Theoretical Method to Predict Internal Force of Crossbeam in Steel–Concrete Composite Twin I-Girder Bridge under Torsional Loading
Abstract
1. Introduction
2. Torsional Effect of Continuous Twin I-Girder Bridge
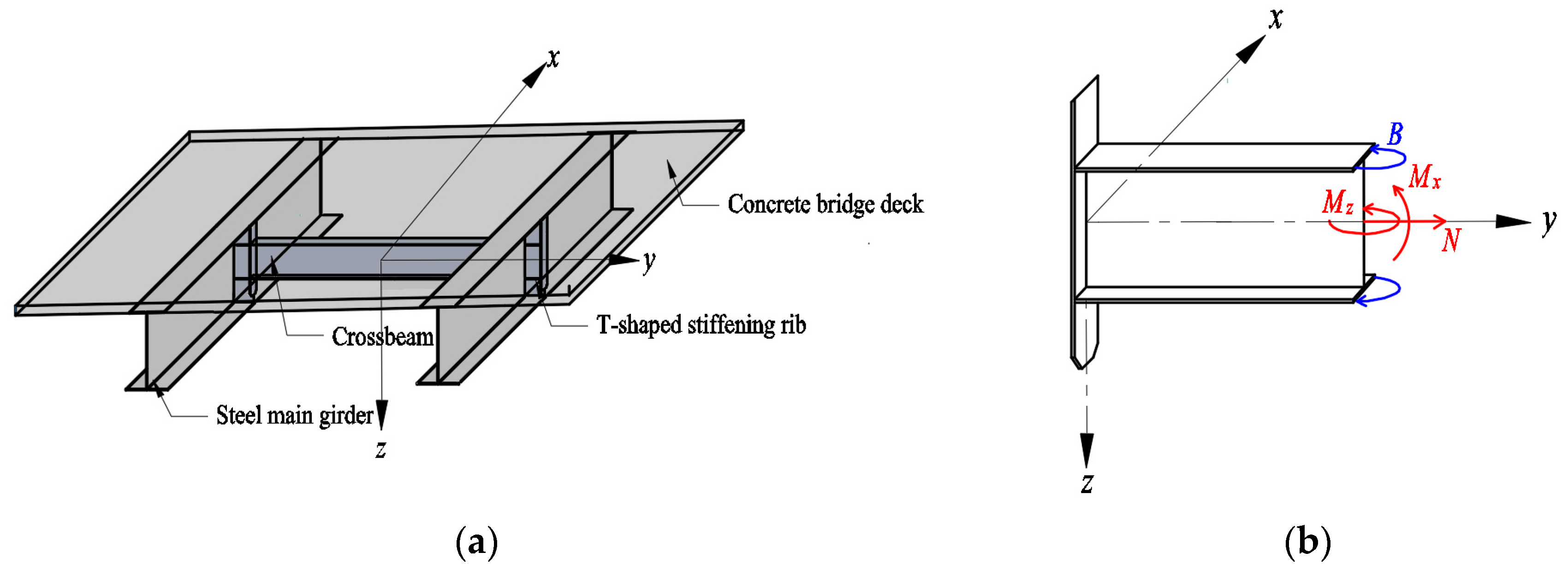
2.1. Section Conversion for Torsion Analysis of Composite Beams
- (1)
- the section profile is not deformed in its plane under small deformations;
- (2)
- the shear strain on the middle face of the bar is zero;
- (3)
- (4)
- both steel and concrete are ideal linear elastic materials.
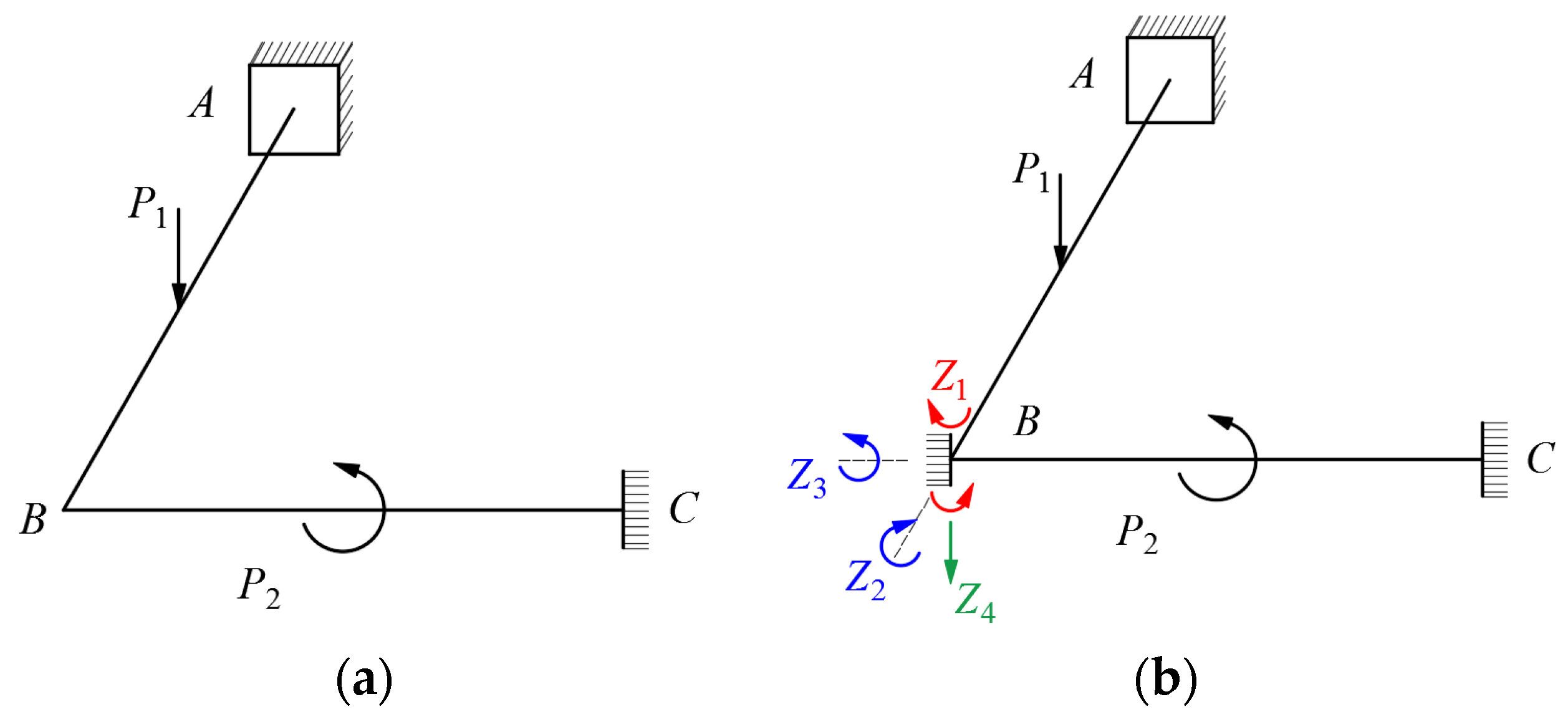
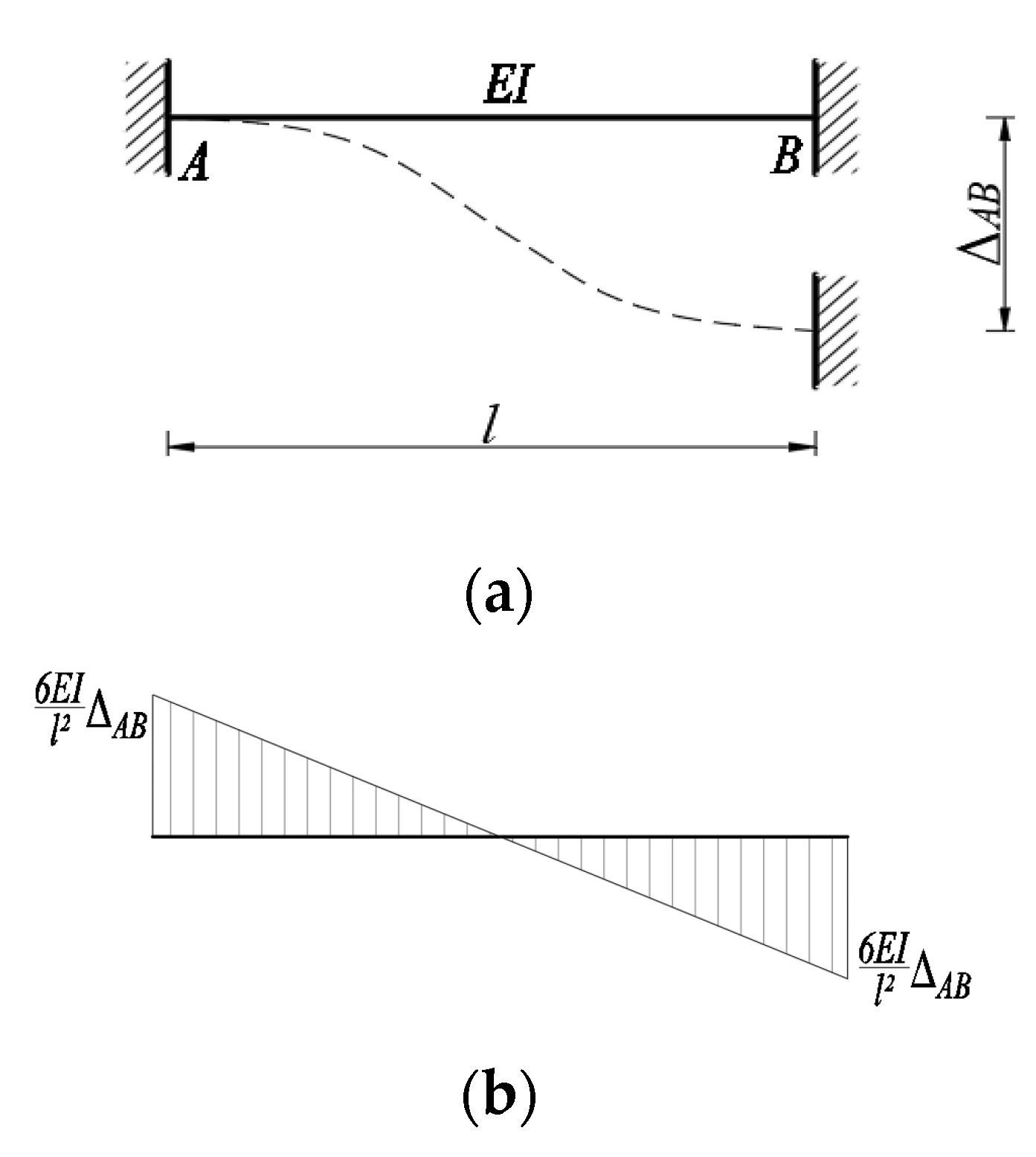
2.2. Application of the Displacement Method to the Analysis of Constrained Torsion in Continuous Beams
- (1)
- Determine which displacements on the structure are to be used as the basic unknown quantities;
- (2)
- Work out the internal forces of a single-span statically indeterminate bar when various displacements and loads occur at the rod ends;
- (3)
- Calculate these displacements.
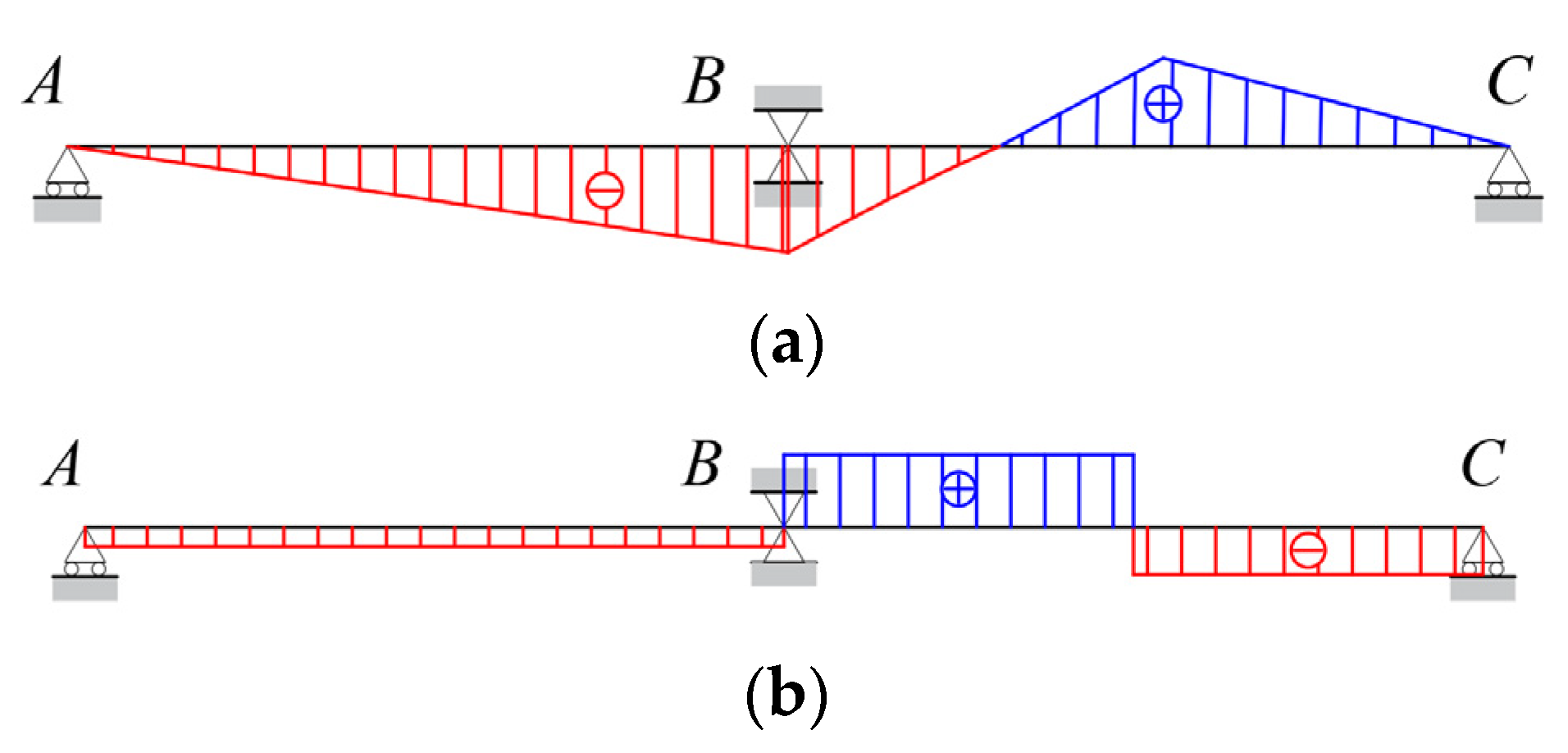
2.3. Effect of Crossbeams on Torsional Effects
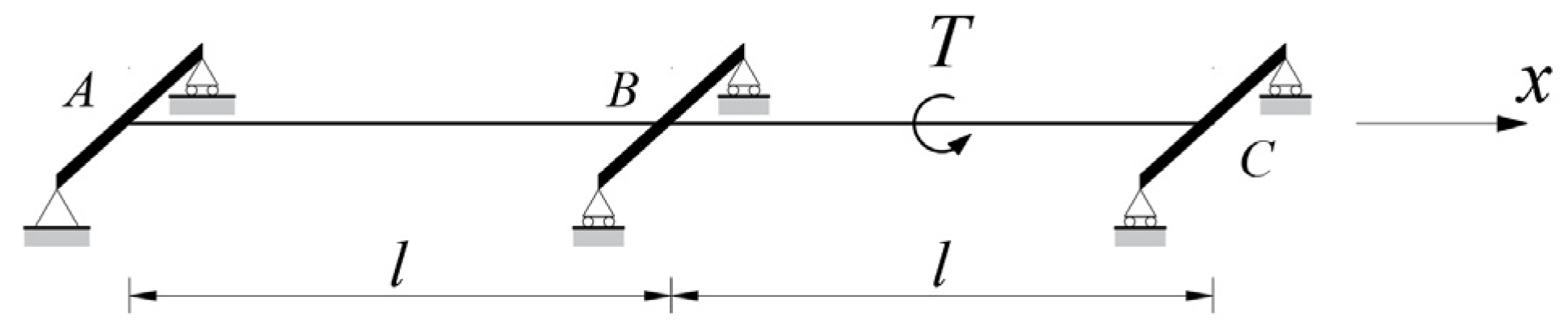
3. Method of Calculating Internal Forces in Crossbeams
3.1. Crossbeam Internal Forces and Deformations
3.2. Calculation of Internal Forces in the Frame Model Considering Warp Deformation of the Main Beam
3.2.1. Internal Forces in the Crossbeam due to Longitudinal Bridge Deformation Lw
3.2.2. Internal Forces in the Crossbeam Due to Torsional Angle βw
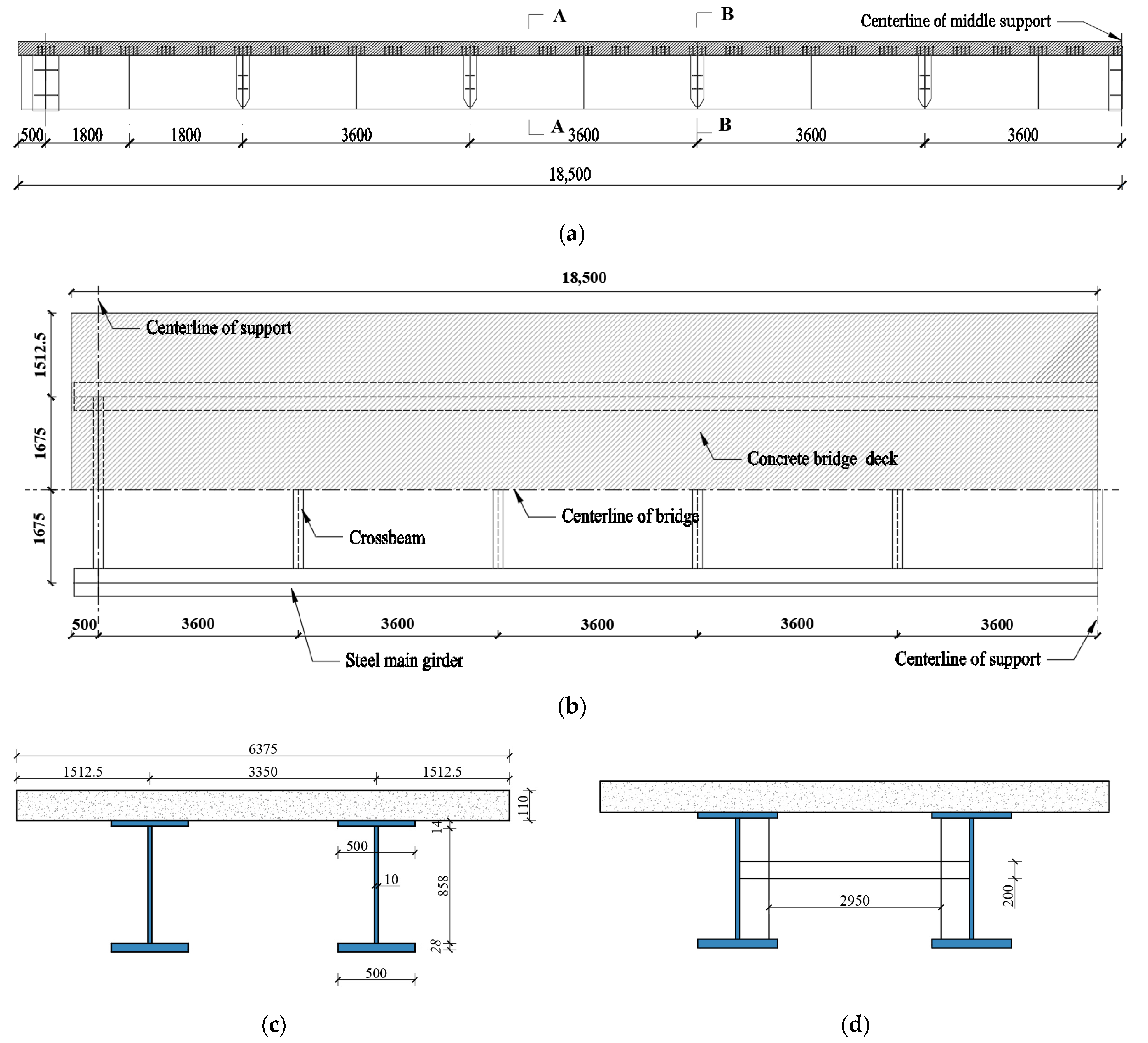
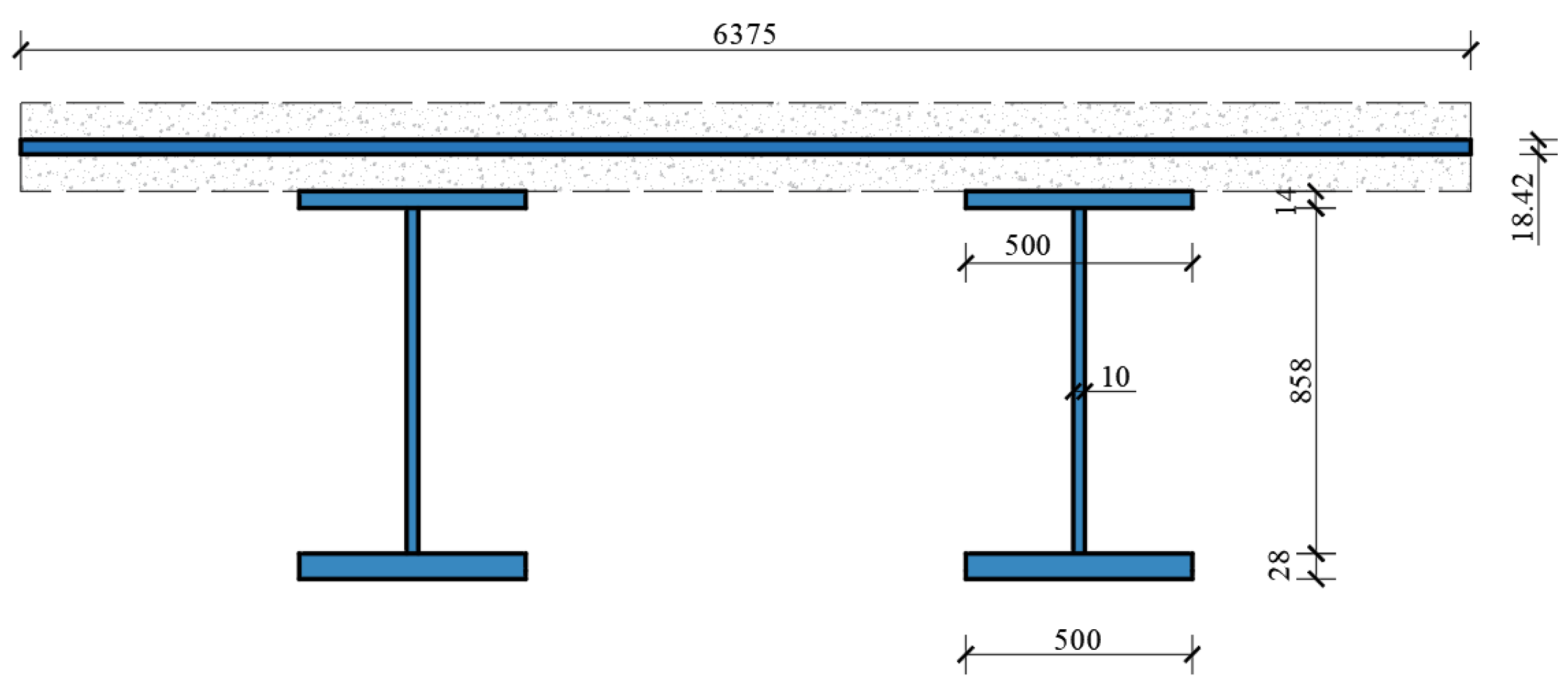
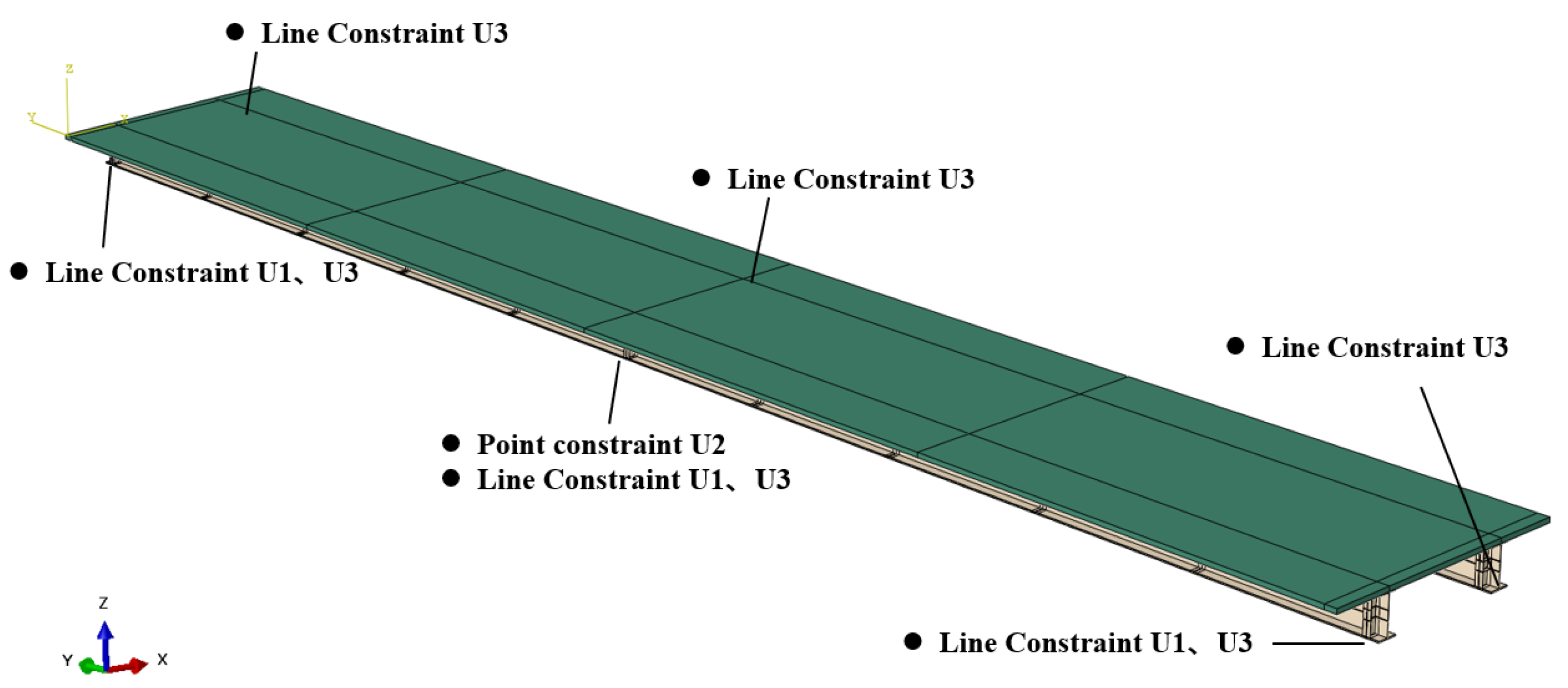
4. Finite Element Verification of Torsional Performance for Continuous Beams
5. Verification of the Crossbeam Internal Force Calculation Formula
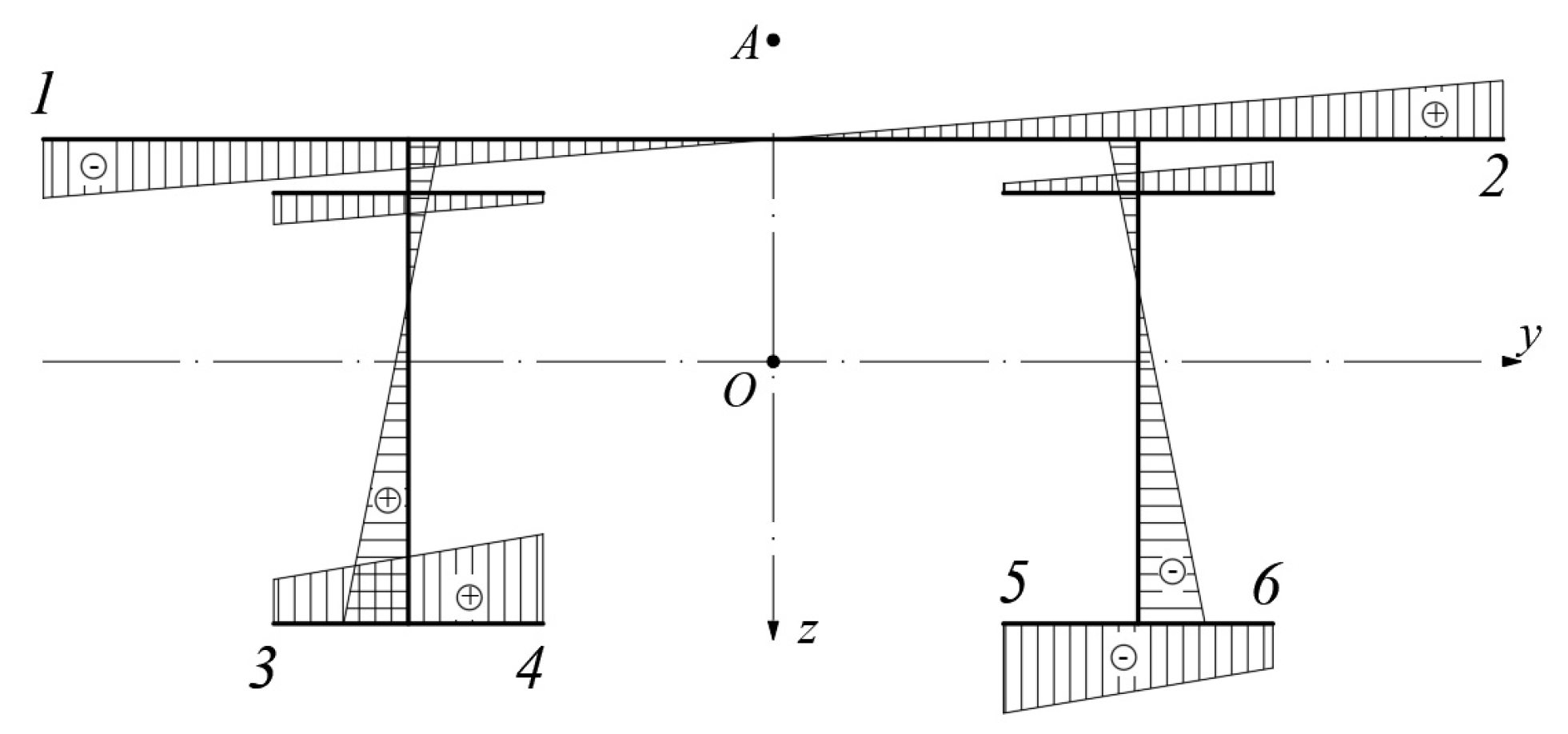
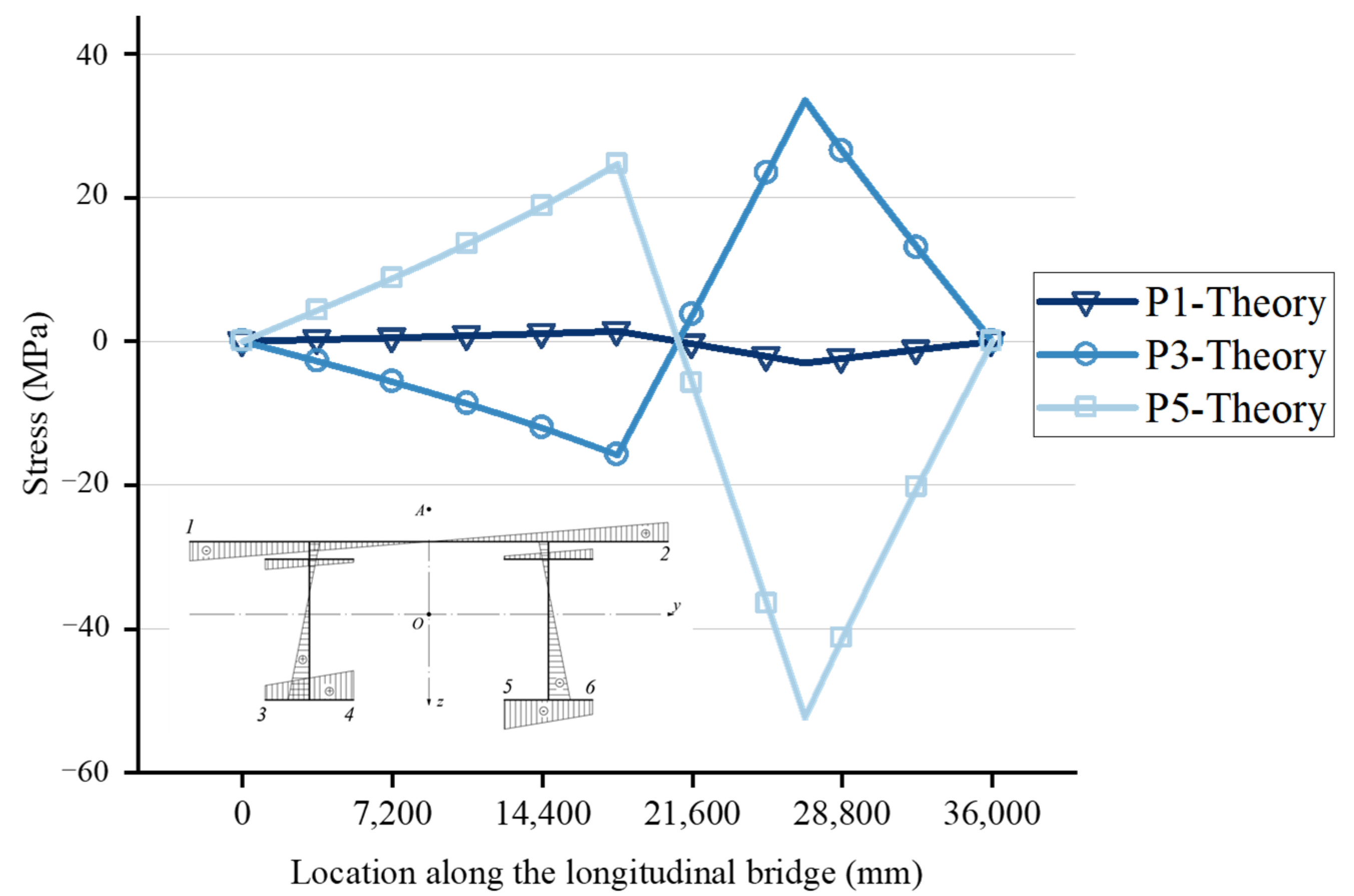
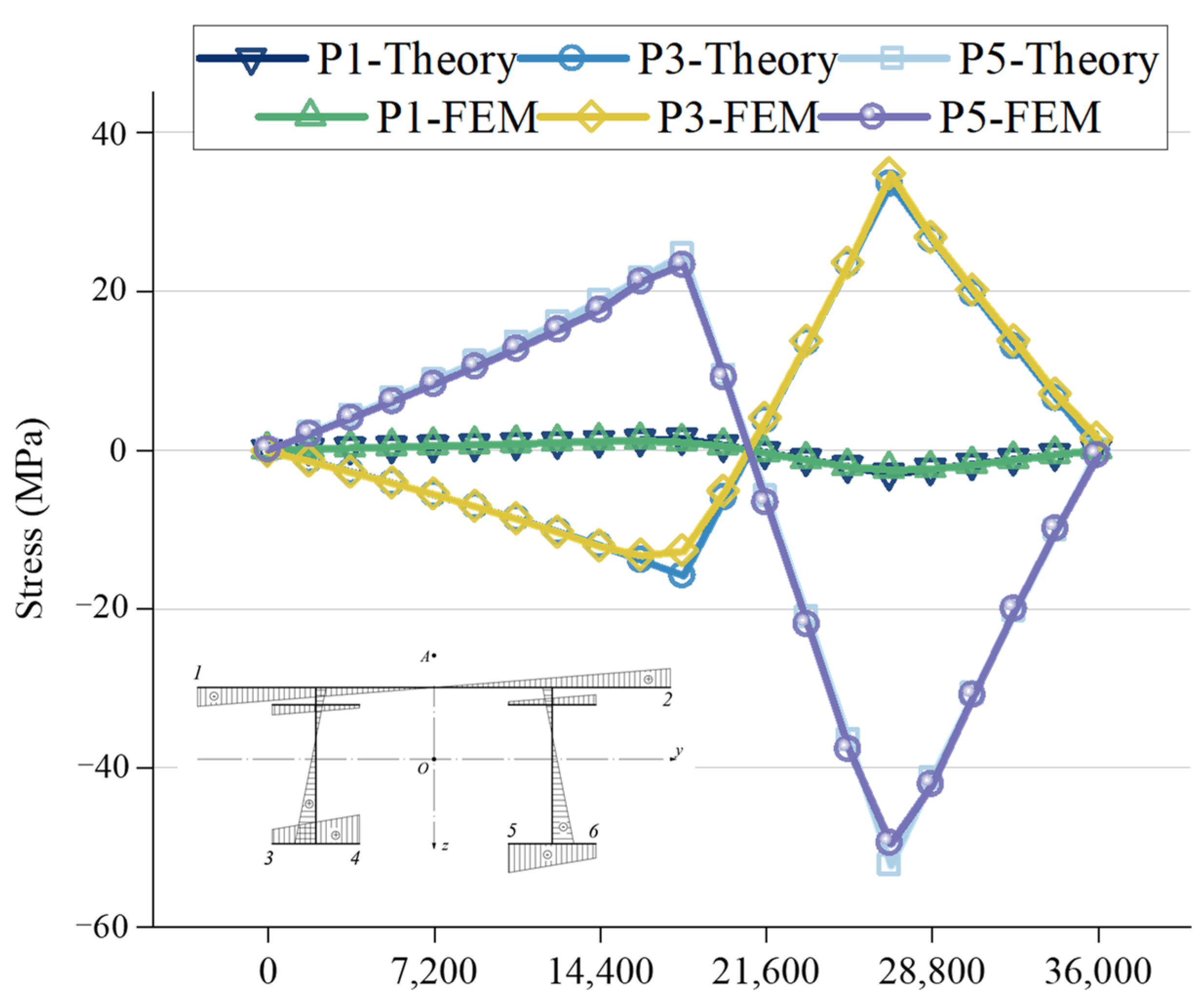
5.1. Extraction of Internal Force Results for Crossbeams
5.2. Verification of Crossbeam Internal Force Results
6. Conclusions
- The torsional performance of the continuous steel–concrete composite twin I-girder bridge can be analysed according to Vlasov’s theory, as verified by the finite element analysis results;
- The bending effects and torsional effects in the longitudinal direction of the crossbeam can be approximately obtained by calculating the warping deformation of the main beam at the same position;
- The internal force calculation formulae in this paper are calculated by simplifying the crossbeam to a bar with two solid ends. For general loading effects (including torsion load and some lateral loads), the internal forces of the crossbeam can be obtained by adding the formulae proposed in this paper to the existing research.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, W.; Jiang, L.; Kang, J.; Bao, M. Distortional buckling analysis of steel-concrete composite girders in gegative moment area. Math. Probl. Eng. 2014, 2014, 635617. [Google Scholar] [CrossRef][Green Version]
- Zhao, R.; Liu, Y.; Jiang, L.; Feng, B.; Fu, Y.; Zhang, C. Experimental study on hot spot stresses of curved composite twin-girder bridges. Materials 2022, 15, 7920. [Google Scholar] [CrossRef] [PubMed]
- Ma, H.; Shi, X.; Zhang, Y. Long-Term behaviour of precast concrete deck using longitudinal prestressed tendons in composite I-girder bridges. Appl. Sci. 2018, 8, 2598. [Google Scholar] [CrossRef]
- Park, S. Cross-Frame Stiffness Modification Factors for Composite Steel I-Girder Bridges; The University of Texas at Austin: Austin, TX, USA, 2021. [Google Scholar]
- Park, Y.; Hwang, S.; Hwang, M.; Choi, B.H. Inelastic buckling of torsionally braced I-girders under uniform bending: I. Numerical parametric studies. J. Constr. Steel Res. 2010, 66, 304–316. [Google Scholar] [CrossRef]
- Nguyen, C.T.; Moon, J.; Le, V.N.; Lee, H. Lateral–torsional buckling of I-girders with discrete torsional bracings. J. Constr. Steel Res. 2010, 66, 170–177. [Google Scholar] [CrossRef]
- Davidson, J.S.; Keller, M.A.; Yoo, C.H. Cross-Frame Spacing and Parametric Effects in Horizontally Curved I-Girder Bridges. J. Struct. Eng. 1996, 122, 1089–1096. [Google Scholar] [CrossRef]
- Sharafbayani, M.; Linzell, D.G. Optimizing horizontally curved, steel bridge, cross-frame arrangements to enhance construction performance. J. Bridge Eng. 2014, 19, 4014021. [Google Scholar] [CrossRef]
- Battistini, A.D.; Donahue, S.; Wang, W.H.; Helwig, T.A.; Engelhardt, M.D.; Frank, K.H. Brace stiffness and forces of X-type, K-type, and Z-type cross frames in steel I-girder bridge systems. In Proceedings of the Structural Stability Research Council/North American Steel Construction Conference, St. Louis, MO, USA, 16 April 2013; p. 2013. [Google Scholar]
- Lebet, J.P.; Hirt, M.A. Conceptual and Structural Design of Steel and Steel-Concrete Composite Bridges; EFPL Press: Lausanne, Switzerland, 2013. [Google Scholar]
- Poellot, W.N. Computer-aided-design of horizontally curved girders by the v-load method engineering journal. Am. Inst. Steel Constr. 1987, 24, 42–50. [Google Scholar]
- Liu, D.; Magliola, R. End forces on crossframes in horizontally curved steel I-girder bridges. Pract. Period. Struct. Des. Constr. 2010, 15, 21–26. [Google Scholar] [CrossRef]
- Gaylord, E.H.; Gaylord, C.N.; Stallmeyer, J.E. Structural Engineering Handbook; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Grubb, M.A. Horizontally curved I-girder bridge analysis: V-load method. Transport. Res. Rec. 1984, 982, 26–36. [Google Scholar]
- Xing, Z. Study on the Stress Mechanism of the Cross Beam of the Curved Twin I-Girder Composite Bridge; Chang’an University: Xi’an, China, 2022. (In Chinese) [Google Scholar]
- Yan, X.; Liu, Y.; Xing, Z.; Feng, B.; Chen, X. Research on internal force of crossbeam in curved steel-concrete composite twin I-girder bridge. J. Archit. Civ. Eng. 2022, 39, 63–73. (In Chinese) [Google Scholar]
- Xiang, D.; Liu, Y.; Yang, F. Numerical and theoretical analysis of slab transverse-moment distributions in twin-girder crossbeam composite bridges. J. Bridge Eng. 2020, 25, 4020004. [Google Scholar] [CrossRef]
- Chen, X.; Zhou, W.; Kong, L. Study on slip effects of simply-supported composite beams. In IOP Conference Series: Earth and Environmental Science; Iop Publishing: Bristol, UK, 2019; p. 32041. [Google Scholar]
- Nie, J.; Cai, C.S. Steel–concrete composite beams considering shear slip effects. J. Struct. Eng. 2003, 129, 495–506. [Google Scholar] [CrossRef][Green Version]
- Nie, J.G.; Cai, C.S.; Zhou, T.R.; Li, Y. Experimental and analytical study of prestressed steel–concrete composite beams considering slip effect. J. Struct. Eng. 2007, 133, 530–540. [Google Scholar] [CrossRef]
- Kollbrunner, C.F.; Basler, K. Torsion in Structures: An Engineering Approach; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Vlasov, V.Z.; Schechtman, Y. Thin-Walled Elastic Beams; Israel Program for Sciemtific Trnsiacionss Ltd.: Jerusalem, Israel, 1987. [Google Scholar]
- Zhang, Y.; Hou, Z.; Li, Y.; Wang, Y. Torsional behaviour of curved composite beams in construction stage and diaphragm effects. J. Constr. Steel Res. 2015, 108, 1–10. [Google Scholar] [CrossRef]








| Load Form | Fixed at One End and Hinged at the Other | Fixed at Both Ends |
|---|---|---|
| Concentrated torque | 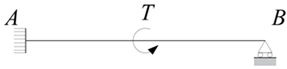 | 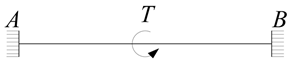 |
| Uniform torque |  |  |
| Unit warping deformation |  |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Liu, Y.; Chai, L.; Xing, Z.; Feng, B.; Jiang, L. Theoretical Method to Predict Internal Force of Crossbeam in Steel–Concrete Composite Twin I-Girder Bridge under Torsional Loading. Appl. Sci. 2023, 13, 6669. https://doi.org/10.3390/app13116669
Li J, Liu Y, Chai L, Xing Z, Feng B, Jiang L. Theoretical Method to Predict Internal Force of Crossbeam in Steel–Concrete Composite Twin I-Girder Bridge under Torsional Loading. Applied Sciences. 2023; 13(11):6669. https://doi.org/10.3390/app13116669
Chicago/Turabian StyleLi, Jiangjiang, Yongjian Liu, Liang Chai, Zihan Xing, Bowen Feng, and Lei Jiang. 2023. "Theoretical Method to Predict Internal Force of Crossbeam in Steel–Concrete Composite Twin I-Girder Bridge under Torsional Loading" Applied Sciences 13, no. 11: 6669. https://doi.org/10.3390/app13116669
APA StyleLi, J., Liu, Y., Chai, L., Xing, Z., Feng, B., & Jiang, L. (2023). Theoretical Method to Predict Internal Force of Crossbeam in Steel–Concrete Composite Twin I-Girder Bridge under Torsional Loading. Applied Sciences, 13(11), 6669. https://doi.org/10.3390/app13116669








