A Novel Classification Method Using the Takagi–Sugeno Model and a Type-2 Fuzzy Rule Induction Approach
Abstract
:1. Introduction
2. Material and Methods
2.1. Materials
2.2. Methods
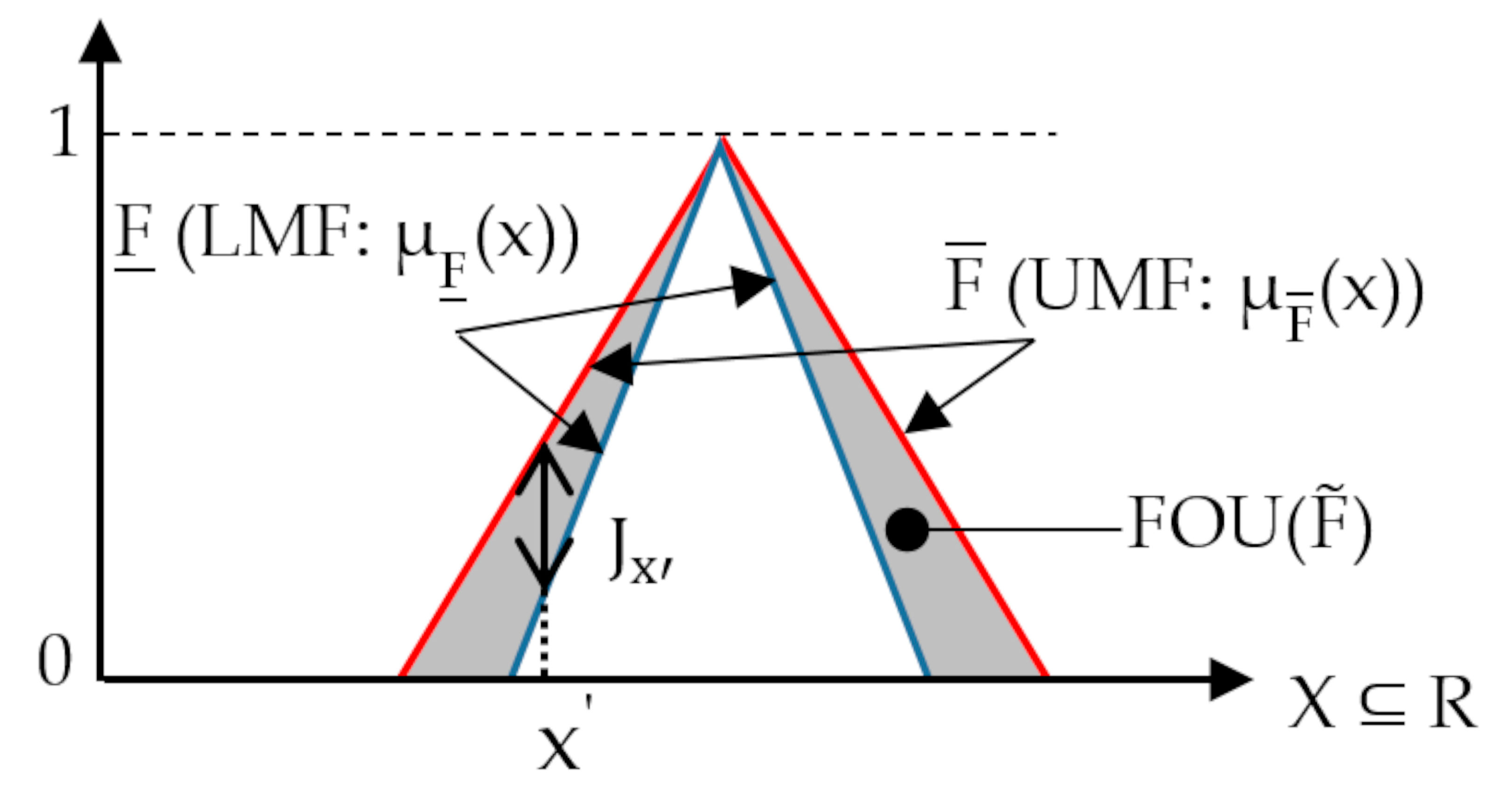
2.2.1. Type-1 and Type-2 Fuzzy Sets
2.2.2. Takagi–Sugeno Type-2 Fuzzy Inference
- (1)
- Compute the membership intervals of for each , , i = 1,…, I; n = 1,…, N (N is the number of rules),
- (2)
- Compute the firing interval of the nth rule:,
- (3)
- Use type reduction to combine with corresponding rule consequents.
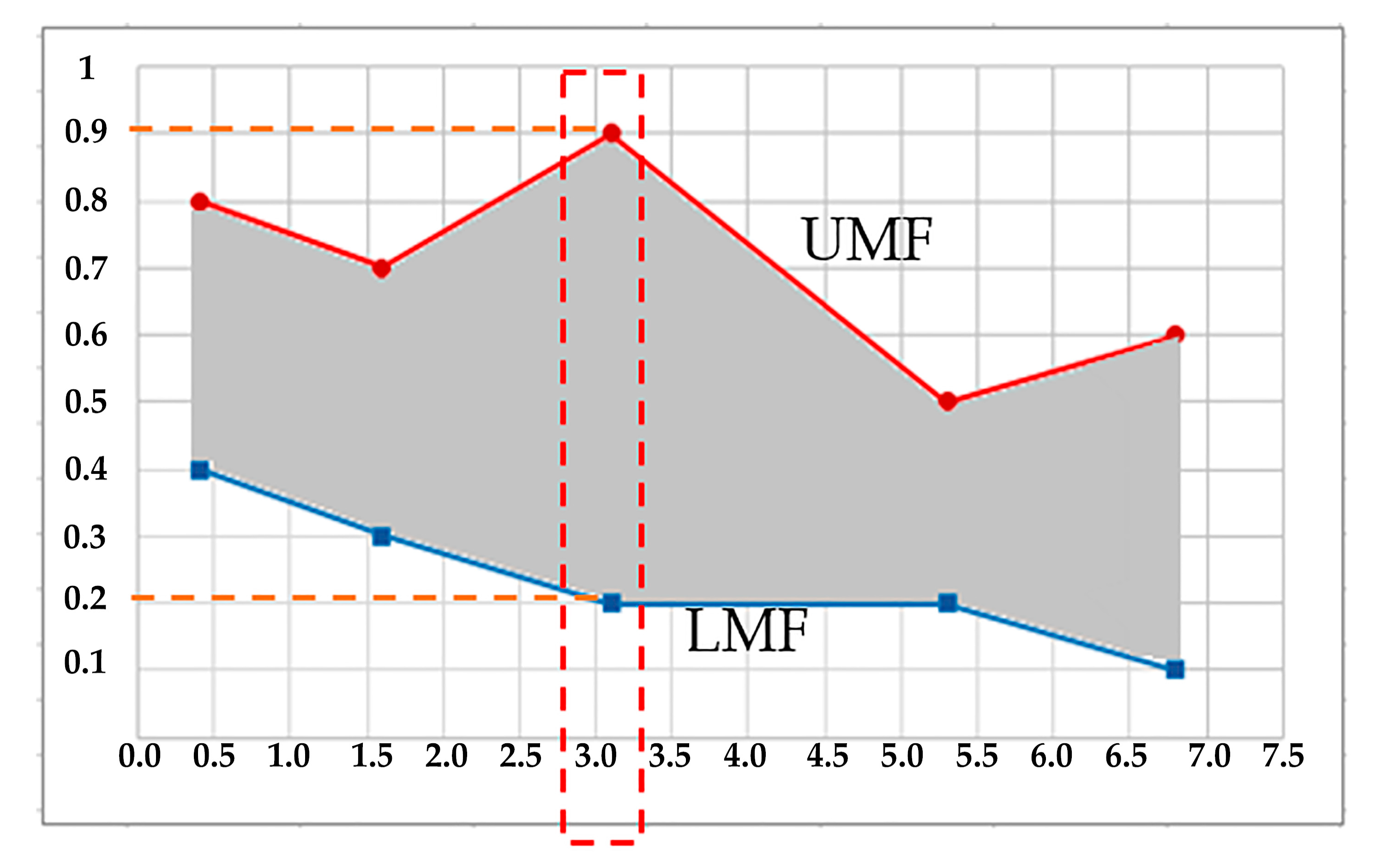
- Sort the rule outputs from all rules into ascending order,
- For each output, define the UMF value using the maximum firing range of the considered rule,
- For each output, define the LMF value using the minimum firing range of the considered rule.
3. Fuzzy Information System with Tagaki-Sugeno Reasoning
3.1. Type-1 Fuzzy Information System and Fuzzy Rule Induction
- decision D: (f(object1, attribute1) ∧ f(object2, attribute2)) ∨ f(object3, attribute1),
- the above rule can be transformed into the following fuzzy rule:
- If ((f(object1, attribute1) is low) ⊗ (f(object2, attribute2) is high)) ⊕ (f(object3,
- attribute1) is medium) Then D.
3.2. Involving Type-2 Fuzzy Sets
3.3. Takagi–Sugeno Reasoning with Optimization
- Split a considered dataset into k-folds.
- For each set of hyperparameters:
- For each cross-validation step:
- Set one fold as held-out for validation, use the rest for training.
- Induce the knowledge base using the training set.
- Infer the crisp value for each sample in the training set with the Takagi–Sugeno model.
- Classify the sample with the threshold function set at 0. Treat the sample as negative if the crisp value is lower than 0.
- Calculate the F1 metric.
- Optimize the parameters of linear functions with CMA-ES, defining the F1 metric as the fitness function.
- Evaluate the model on the validation set when the fitness function is optimized or the maximum number of evaluations passes. Otherwise return to (iii).
- Choose a set of hyperparameters which maximize the mean value of the F1 metric over the validation sets.
- (1)
- Choose the best hyperparameters set for a dataset.
- (2)
- Optimize the fitness function on the training set.
- (3)
- Choose the best parameters of linear functions.
- (4)
- Evaluate the model on a test set.
4. Binary Classification Results
5. Discussion
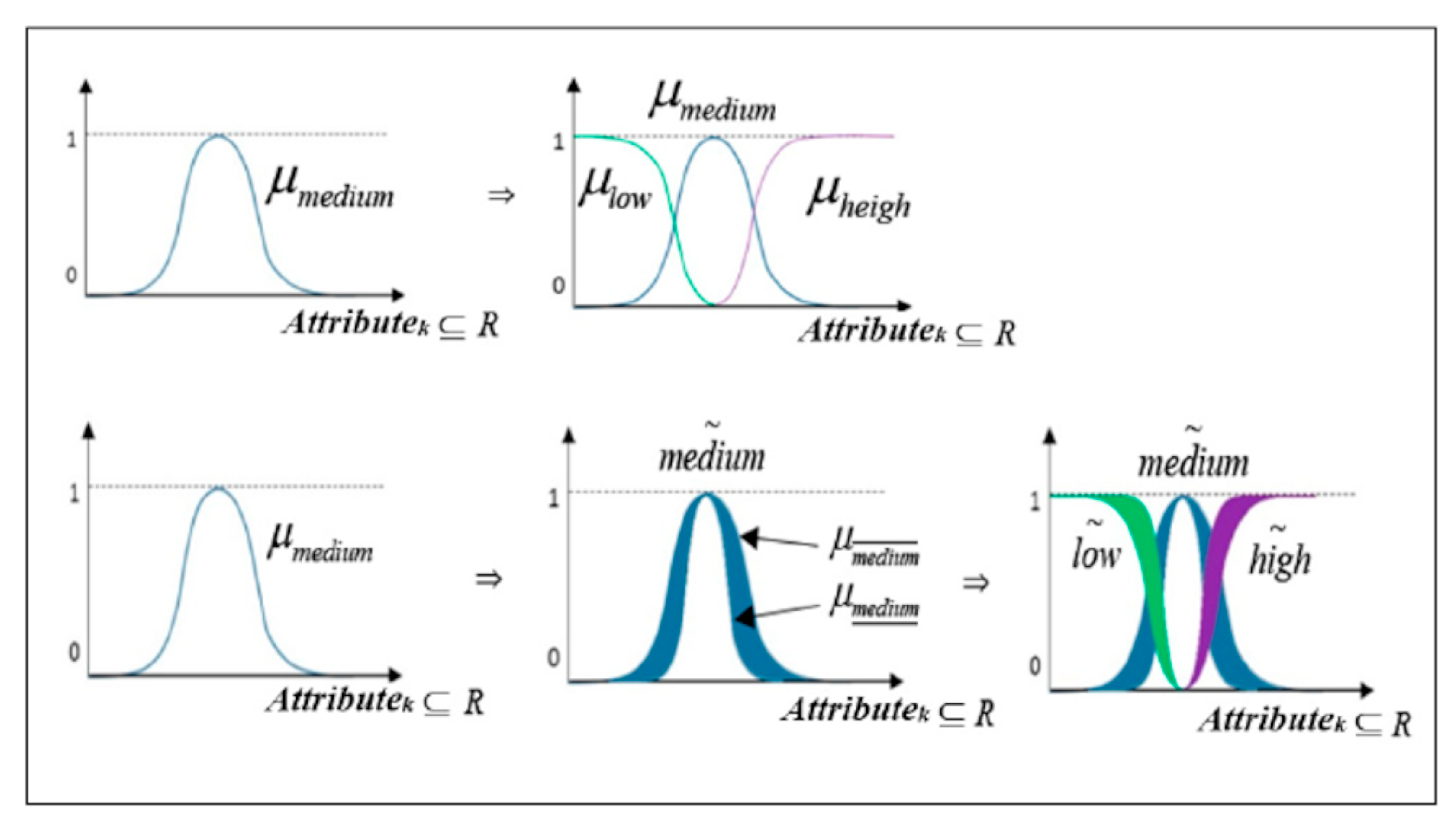
- The information function values are interpreted as fuzzy sets, labeled with corresponding linguistic variables. This gives the possibility to generalize information—we do not consider numerical values for pairs (object, attribute), but general descriptions such as ‘small’, ‘medium’, and ‘high’.
- The decision table used is generated in an automatic manner for a considered data set, as the value ‘medium’ is assumed as the Gaussian distribution of the data for each attribute. Then, the sets ‘low’ and ‘high’ are easy to be defined using the ‘medium’ membership function. Next, a corresponding label (identifying the corresponding fuzzy set) is given for a pair (object, attribute), by using the maximum membership value.
- –
- Defining a decision table with fuzzy values. The fuzzification is provided in an automatic manner directly from a data set.
- –
- Using the rule induction method based on the information system concept, which has a solid mathematical background. Each rule is related to a corresponding class, regarding the classification problem considered.
- –
- Transformation of the induced rules into type-2 fuzzy rules.
- –
- Application of the Takagi–Sugeno model in the classification process. Therefore, there is no need to define the fuzzy rule consequents as fuzzy sets.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rostam Niakan Kalhori, M.; FazelZarandi, M.H. A new interval type-2 fuzzy reasoning method for classification systems based on normal forms of a possibility-based fuzzy measure. Inf. Sci. 2021, 581, 567–586. [Google Scholar] [CrossRef]
- Ghasemi, M.; Kelarestaghi, M.; Eshghi, F.; Sharifi, A. T2-FDL: A robust sparse representation method using adaptive type-2 fuzzy dictionary learning for medical image classification. Expert Syst. Appl. 2020, 158, 113500. [Google Scholar] [CrossRef]
- Xing, H.; He, H.; Hu, D.; Jiang, T.; Yu, X. An interval Type-2 fuzzy sets generation method for remote sensing imagery classification. Comput. Geosci. 2019, 133, 104287. [Google Scholar] [CrossRef]
- Xu, J.; Feng, G.; Zhao, T.; Sun, X.; Zhu, M. Remote sensing image classification based on semi-supervised adaptive interval type-2 fuzzy c-means algorithm. Comput. Geosci. 2019, 131, 132–143. [Google Scholar] [CrossRef]
- Wu, C.; Guo, X. Adaptive enhanced interval type-2 possibilistic fuzzy local information clustering with dual-distance for land cover classification. Eng. Appl. Artif. Intell. 2023, 119, 105806. [Google Scholar] [CrossRef]
- Erozan, İ.; Özel, E.; Erozan, D. A two-stage system proposal based on a type-2 fuzzy logic system for ergonomic control of classrooms and offices. Eng. Appl. Artif. Intell. 2023, 120, 105854. [Google Scholar] [CrossRef]
- Rafiei, H.; Salehi, A.; Baghbani, F.; Parsa, P.; Akbarzadeh-T, M.-R. Interval type-2 Fuzzy control and stochastic modeling of COVID-19 spread based on vaccination and social distancing rates. Comput. Methods Programs Biomed. 2023, 232, 107443. [Google Scholar] [CrossRef]
- Bhandari, G.; Raj, R.; Pathak, P.M.; Yang, J.-M. Robust control of a planar snake robot based on interval type-2 Takagi–Sugeno fuzzy control using genetic algorithm. Eng. Appl. Artif. Intell. 2022, 116, 105437. [Google Scholar] [CrossRef]
- Precup, R.E.; David, R.C.; Roman, R.C.; Szedlak-Stinean, A.I.; Petriu, E.M. Optimal tuning of interval type-2 fuzzy controllers for nonlinear servo systems using Slime Mould Algorithm. Int. J. Syst. Sci. 2021, 1–16. [Google Scholar] [CrossRef]
- Pozna, C.; Precup, R.E.; Horvath, E.; Petriu, E.M. Hybrid Particle filter-particle swarm optimization algorithm and application to fuzzy controlled servo systems. IEEE Trans. Fuzzy Syst. 2022, 30, 4286–4297. [Google Scholar] [CrossRef]
- Cuevas, F.; Castillo, O.; Cortes, P. Optimal Setting of Membership Functions for Interval Type-2 Fuzzy Tracking Controllers Using a Shark Smell Metaheuristic Algorithm. Int. J. Fuzzy Syst. 2022, 24, 799–822. [Google Scholar] [CrossRef]
- Mendel, J.M.; John, R.I. Type-2 fuzzy sets made simple. IEEE Trans. Fuzzy Syst. 2002, 10, 117–127. [Google Scholar] [CrossRef]
- Mendel, J.M. Type-2 Fuzzy Sets and Systems: How to Learn about Them. IEEE Smc Enewsletter 2009, 27, 1–7. [Google Scholar]
- Hagras, H. Type-2 FLCs: A new generation of fuzzy controllers. IEEE Comput. Intell. Mag. 2007, 2, 30–43. [Google Scholar] [CrossRef]
- Castillo, O.; Melin, P. Type-2 Fuzzy Logic Theory and Applications; Springer: Berlin, Germany, 2008. [Google Scholar]
- Pawlak, Z. Information systems—Theoretical foundations. Inf. Syst. 1981, 6, 205–218. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough Sets; Basic notions, Report no 431; Institute of Computer Science, Polish Academy of Sciences: Warsaw, Poland, 1981. [Google Scholar]
- Pawlak, Z. Rough Sets: Theoretical Aspects of Reasoning about Data, System Theory, Knowledge Engineering and Problem Solving; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1991; Volume 9. [Google Scholar]
- Hong, T.-P.; Chen, J.-B. Building a concise decision table for fuzzy rule induction. In Proceedings of the 1998 IEEE International Conference on Fuzzy Systems Proceedings. IEEE World Congress on Computational Intelligence (Cat. No.98CH36228), Anchorage, AK, USA, 4–9 May 1998; Volume 2, pp. 997–1002. [Google Scholar]
- Drwal, G.; Sikora, M. Induction of fuzzy decision rules based upon rough sets theory. In Proceedings of the 2004 IEEE International Conference on Fuzzy Systems (IEEE Cat. No.04CH37542), Budapest, Hungary, 25–29 July 2004; Volume 3, pp. 1391–1395. [Google Scholar]
- Shen, Q.; Chouchoulas, A. Data-driven fuzzy rule induction and its application to systems monitoring. In Proceedings of the FUZZ-IEEE’99. 1999 IEEE International Fuzzy Systems. Conference Proceedings (Cat. No.99CH36315), Seoul, Republic of Korea, 22–25 August 1999; Volume 2, pp. 928–933. [Google Scholar]
- Tabakov, M.; Chlopowiec, A.; Chlopowiec, A.; Dlubak, A. Classification with Fuzzification Optimization Combining Fuzzy Information Systems and Type-2 Fuzzy Inference. Appl. Sci. 2021, 11, 3484. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- Wang, C.; Chen, D.; Hu, Q. Fuzzy information systems and their homomorphisms. Fuzzy Sets Syst. 2014, 249, 128–138. [Google Scholar] [CrossRef]
- Dubois, D. The role of fuzzy sets in decision sciences: Old techniques and new directions. Fuzzy Sets Syst. 2011, 184, 3–28. [Google Scholar] [CrossRef]
- Lee, M.-C.; Chang, T. Rule Extraction Based on Rough Fuzzy Sets in Fuzzy Information Systems. Trans. Comput. Collect. Intell. III 2011, 6560, 115–127. [Google Scholar]
- Cheruku, R.; Edla, D.R.; Kuppili, V.; Dharavath, R. RST-Bat-Miner: A fuzzy rule miner integrating rough set feature selection and bat optimization for detection of diabetes disease. Appl. Soft. Comput. 2018, 67, 764–780. [Google Scholar] [CrossRef]
- Wang, W.; Zhan, J.; Zhang, C.; Herrera-Viedma, E.; Kou, G. A regret-theory-based three-way decision method with a priori probability tolerance dominance relation in fuzzy incomplete information systems. Inf. Fusion 2023, 89, 382–396. [Google Scholar] [CrossRef]
- Kang, Y.; Yu, B.; Cai, M. Multi-attribute predictive analysis based on attribute-oriented fuzzy rough sets in fuzzy information systems. Inf. Sci. 2022, 608, 931–949. [Google Scholar] [CrossRef]
- Mamdani, E.H.; Assilian, S. An Experiment in Linguistic Synthesis with a Fuzzy Logic Controller. Int. J. Man-Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- Dua, D.; Graff, C. UCI Machine Learning Repository; University of California, School of Information and Computer Science: Irvine, CA, USA, 2019; Available online: http://archive.ics.uci.edu/ml (accessed on 31 December 2020).
- Zadeh, L. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Bronstein, I.N.; Semendjajew, K.A.; Musiol, G.; Mühlig, H. Taschenbuch der Mathematik; Verlag Harri Deutsch: Frankfurt, Germany, 2001; p. 1258. [Google Scholar]
- Mendel, J.M. Uncertain Rule-Based Fuzzy Logic Systems: Introduction and New Directions; Prentice-Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Karnik, N.N.; Mendel, J.M.; Liang, Q. Type-2 fuzzy logic systems. IEEE Trans. Fuzzy Syst. 1999, 7, 643–658. [Google Scholar] [CrossRef]
- Wu, D.; Mendel, J.M. Enhanced Karnik–Mendel algorithms. IEEE Trans. Fuzzy Syst. 2009, 17, 923–934. [Google Scholar]
- Wu, D.; Nie, M. Comparison and practical implementation of type reduction algorithms for type-2 fuzzy sets and systems. In Proceedings of the 2011 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE 2011), Taipei, Taiwan, 27–30 June 2011; pp. 2131–2138. [Google Scholar]
- Skowron, A.; Suraj, Z. A Rough Set Approach to Real-Time State Identification for Decision Making; Institute of Computer Science Report 18/93; Warsaw University of Technology: Warsaw, Poland, 1993; p. 27. [Google Scholar]
- Skowron, A.; Suraj, Z. A Rough Set Approach to Real-Time State Identification. Bull. Eur. Assoc. Comput. Sci. 1993, 50, 264. [Google Scholar]
- Hansen, N.; Ostermeier, A. Completely derandomized self-adaptation in evolution strategies. Evol. Comput. 2001, 9, 159–195. [Google Scholar] [CrossRef]
- Hulse, J.V.; Khoshgoftaar, T.; Napolitano, A. Experimental perspectives on learning from imbalanced data. In Proceedings of the Twenty-Fourth International Conference on Machine Learning (ICML 2007), Corvallis, OR, USA, 20–24 June 2007. [Google Scholar]
- Shelke, M.; Deshmukh, D.P.R.; Shandilya, V. A review on imbalanced data handling using undersampling and oversampling technique. Comput. Sci. 2017, 3, 444–449. [Google Scholar]
- Mohammed, R.; Rawashdeh, J.; Abdullah, M. Machine learning with oversampling and undersampling techniques: Overview study and experimental results. In Proceedings of the 2020 11th International Conference on Information and Communication Systems (ICICS), Irbid, Jordan, 7–9 April 2020. [Google Scholar]
- Peng, L.; Chen, W.; Zhou, W.; Li, F.; Yang, J.; Zhang, J. An immune-inspired semi-supervised algorithm for breast cancer diagnosis. Comput. Methods Programs Biomed. 2016, 134, 259–265. [Google Scholar] [CrossRef]
- Utomo, C.P.; Kardiana, A.; Yuliwulandari, R. Breast Cancer Diagnosis using Artificial Neural Networks with Extreme Learning Techniques. Int. J. Adv. Res. Artif. Intell. Ijarai 2014, 3, 10–14. [Google Scholar]
- Akay, A.F. Support vector machines combined with feature selection for breast cancer diagnosis. Expert Syst. Appl. 2009, 36, 3240–3247. [Google Scholar] [CrossRef]
- Kumar, G.R.; Nagamani, K. Banknote authentication system utilizing deep neural network with PCA and LDA machine learning techniques. Int. J. Recent Sci. Res. 2018, 9, 30036–30038. [Google Scholar]
- Kumar, C.; Dudyala, A.K. Bank note authentication using decision tree rules and machine learning techniques. In Proceedings of the 2015 International Conference on Advances in Computer Engineering and Applications, Ghaziabad, India, 19–20 March 2015; pp. 310–314. [Google Scholar]
- Jaiswal, R.; Jaiswal, S. Banknote Authentication using Random Forest Classifier. Int. J. Digit. Appl. Contemp. Res. 2019, 7, 1–4. [Google Scholar]
- Sarma, S.S. Bank Note Authentication: A Genetic Algorithm Supported Neural based Approach. Int. J. Adv. Res. Comput. Sci. 2016, 7, 97–102. [Google Scholar]
- Lyon, R.J.; Stappers, B.W.; Cooper, S.; Brooke, J.M.; Knowles, J.D. Fifty Years of Pulsar Candidate Selection: From simple filters to a new principled real-time classification approach. Mon. Not. R. Astron. Soc. 2016, 459, 1104–1123. [Google Scholar] [CrossRef]
- Wang, Y.; Pan, Z.; Zheng, J.; Qian, L.; Li, M. A hybrid ensemble method for pulsar candidate classification. Astrophys. Space Sci. 2019, 8, 1–13. [Google Scholar] [CrossRef]
- Sağlam, F.; Yıldırım, E.; Cengiz, M.A. Clustered Bayesian classification for within-class separation. Expert Syst. Appl. 2022, 208, 118152. [Google Scholar] [CrossRef]
| Benchmark | Number of Attributes | Number of Samples | Class Proportions |
|---|---|---|---|
| Blood Transfusion | 7 | 748 | 76%/24% |
| Breast Cancer Data | 4 | 569 | 63%/37% |
| Breast Cancer Wisconsin | 9 | 683 | 65%/35% |
| Data Banknote Authentication | 4 | 1372 | 56%/44% |
| Haberman | 3 | 305 | 73%/27% |
| Heart | 13 | 303 | 46%/54% |
| HTRU 2 | 8 | 17,898 | 9%/91% |
| Immunotherapy | 7 | 90 | 79%/21% |
| Indian Liver Patient | 10 | 583 | 71%/29% |
| Ionosphere | 34 | 351 | 64%/36% |
| Parkinson | 22 | 187 | 74%/26% |
| Pima Indians Diabetes | 8 | 768 | 65%/35% |
| Vertebral | 6 | 310 | 68%/32% |
| Rule | Rule Output Value (fk) | Minimum Firing Value | Maximum Firing Value |
|---|---|---|---|
| 1 | 6.8 | 0.1 | 0.6 |
| 2 | 1.6 | 0.3 | 0.7 |
| 3 | 5.3 | 0.2 | 0.5 |
| 4 | 0.4 | 0.4 | 0.8 |
| 5 | 3.1 | 0.2 | 0.9 |
| Sorted in ascending order: | |||
| 4 | 0.4 | 0.4 | 0.8 |
| 2 | 1.6 | 0.3 | 0.7 |
| 5 | 3.1 | 0.2 | 0.9 |
| 3 | 5.3 | 0.2 | 0.5 |
| 1 | 6.8 | 0.1 | 0.6 |
| attribute1 | attribute2 | attribute3 | |
|---|---|---|---|
| object1 | low | medium | low |
| object2 | medium | high | high |
| object3 | medium | high | high |
| object4 | low | medium | low |
 <3 Gausses, Equal, Center> <3 Gausses, Equal, Center> | 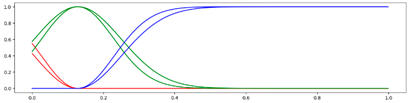 <3 Gausses, Equal, Mean> <3 Gausses, Equal, Mean> |
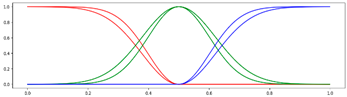 <3 Gausses, Progressive, Center> <3 Gausses, Progressive, Center> | 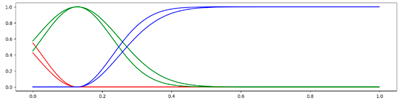 <3 Gausses, Progressive, Mean> <3 Gausses, Progressive, Mean> |
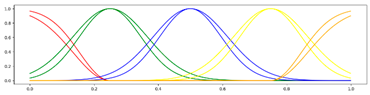 <5 Gausses, Equal, Center> <5 Gausses, Equal, Center> | 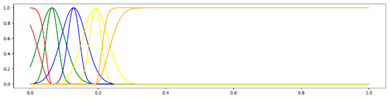 <5 Gausses, Equal, Mean> <5 Gausses, Equal, Mean> |
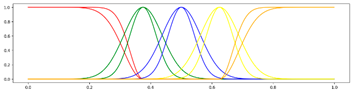 < 5 Gausses, Progressive, Center > < 5 Gausses, Progressive, Center > | 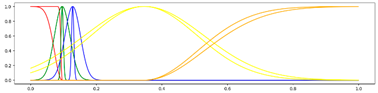 <5 Gausses, Progressive, Mean> <5 Gausses, Progressive, Mean> |
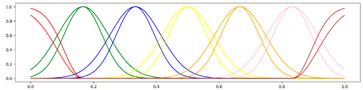 <7 Gausses, Equal, Center> <7 Gausses, Equal, Center> | 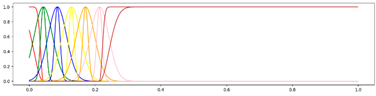 <7 Gausses, Equal, Mean> <7 Gausses, Equal, Mean> |
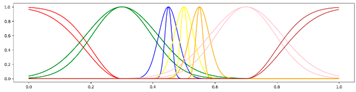 <7 Gausses, Progressive, Center> <7 Gausses, Progressive, Center> | 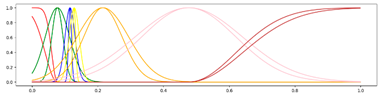 <7 Gausses, Progressive, Mean> <7 Gausses, Progressive, Mean> |
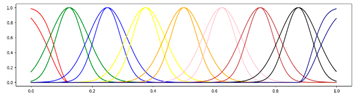 <9 Gausses, Equal, Center> <9 Gausses, Equal, Center> | 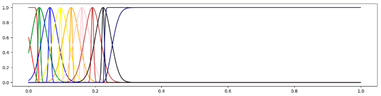 <9 Gausses, Equal, Mean> <9 Gausses, Equal, Mean> |
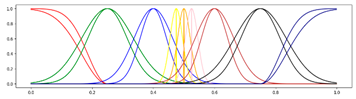 <9 Gausses, Progressive, Center> <9 Gausses, Progressive, Center> | 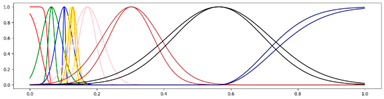 <9 Gausses, Progressive, Mean> <9 Gausses, Progressive, Mean> |
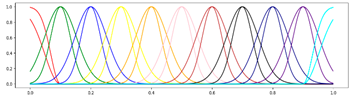 <11 Gausses, Equal, Center> <11 Gausses, Equal, Center> | 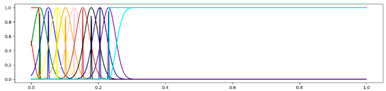 <11 Gausses, Equal, Mean> <11 Gausses, Equal, Mean> |
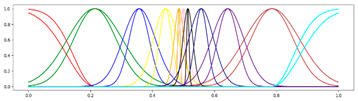 <11 Gausses, Progressive, Center> <11 Gausses, Progressive, Center> | 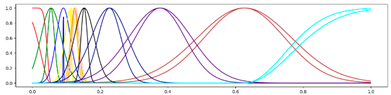 <11 Gausses, Progressive, Mean> <11 Gausses, Progressive, Mean> |
| Hyperparameter | Value |
|---|---|
| Number of Gaussian functions | 3, 5, 7, 9, 11 |
| Whether the std applied to Gaussians are the same | Yes/No |
| If the mean value of the medium membership function is derived directly from mean value of the corresponding feature | Yes/No |
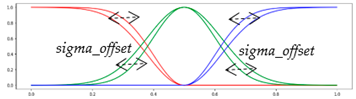
| Sigma_offset | [0.5, 0.9] with step of 0.05 |
| Use PCA | Yes/No |
| Use ROS | Yes/No |
| Hyperparameter | Value |
|---|---|
| Initialization | Random |
| Maximum evaluations of fitness function | 20,000 |
| Number of restarts | 1 |
| Population size increase ratio after restart | 2 |
| Standard deviation in each coordinate | 0.7 |
| Population size | 20 |
| Stagnation tolerance | 100 evaluations |
| Parameters values range | [−400, 400] |
| Benchmark | k-Value |
|---|---|
| Blood Transfusion | 10 |
| Breast Cancer Data | 10 |
| Breast Cancer Wisconsin | 10 |
| Data Banknote Authentication | 10 |
| Haberman | 6 |
| Heart | 5 |
| HTRU | 10 |
| Immunotherapy | 4 |
| Indian Liver Patient | 10 |
| Ionosphere | 6 |
| Parkinson | 4 |
| Pima Indians Diabetes | 10 |
| Vertebral | 5 |
| Dataset | F1 Score (%) | Accuracy (%) | Sensitivity (%) | Hyperparameters | ROS | PCA |
|---|---|---|---|---|---|---|
| Blood Transfusion | 56.6 | 69.3 | 83.3 | <11 Gaussian, equal, mean, 0.75> | Yes | No |
| Breast Cancer Data | 97.6 | 98.2 | 95.2 | <3 Gaussian, equal, center, 0.5> | Yes | Yes |
| Breast Cancer Wisconsin | 96.0 | 97.1 | 100.0 | <3 Gaussian, progressive, mean, 0.85> | Yes | Yes |
| Data Banknote Authentication | 100.0 | 100.0 | 100.0 | <3 Gaussian, equal, mean, 0.65> | Yes | No |
| Haberman | 40.0 | 66.1 | 43.8 | <9 Gaussian, equal, mean, 0.55> | No | No |
| Heart | 85.2 | 85.2 | 92.9 | <3, progressive, mean, 0.6> | Yes | Yes |
| HTRU 2 | 87.8 | 97.8 | 85.4 | <9 Gaussian, equal, center, 0.5> | No | Yes |
| Immunotherapy | 66.7 | 83.3 | 75.0 | <9 Gaussian, equal, mean, 0.75> | Yes | No |
| Indian Liver Patient | 57.4 | 58.1 | 97.1 | <11, Gaussian, equal, center, 0.8> | Yes | Yes |
| Ionosphere | 89.4 | 93.0 | 84.0 | <7 Gaussian, equal, mean, 0.55> | No | Yes |
| Parkinson | 80.0 | 89.7 | 80.0 | <5 Gaussian, progressive, mean, 0.8> | Yes | No |
| Pima Indians Diabetes | 66.2 | 68.8 | 87.0 | <11 Gaussian, equal, center, 0.9> | Yes | Yes |
| Vertebral | 87.1 | 82.3 | 88.1 | <7 Gaussian, progressive, mean, 0.75> | Yes | No |
| Dataset | The Presented Approach (Using the Takagi–Sugeno Model) (%) | Our Previous Approach (Using the Mamdani Model) (%) | Other Classifiers (%) |
|---|---|---|---|
| Breast Cancer Data | 97.6 | 91.2 | Immune-inspired semi-supervised Algorithm, introduced in [44]: 97.3 |
| Breast Cancer Wisconsin | 96.0 | 95.7 | Extreme Learning Machine Neural Networks, introduced in [45]: 97.8 Immune-inspired semi-supervised algorithm, introduced in [44]: 96.5 Support vector machines combined with Feature Selection, introduced in [46]: 99.7 |
| Data Banknote Authentication | 100.0 | 99.3 | Deep Neural Network with PCA and LDA, introduced in [47]: 99 Decision tree approach, introduced in [48]: 99.4 Random Forest approach, introduced in [49]: 94.8 Neural Network-Genetic Algorithm, introduced in [50]: 100 |
| HTRU 2 | 87.8 | 89.0 | Classical classifiers: C4.5: 74; MLP: 75.2; NB: 69.2; SVM: 78.9 GH-VFDT Algorithm, introduced in [51]: 86.2 A hybrid ensemble method, introduced in [52]: 91.8 (with respect to a voting threshold parameter) |
| Ionosphere | 89.4 | 88.8 | Clustered Bayesian classification, 88.5 [53] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tabakov, M.; Chlopowiec, A.B.; Chlopowiec, A.R. A Novel Classification Method Using the Takagi–Sugeno Model and a Type-2 Fuzzy Rule Induction Approach. Appl. Sci. 2023, 13, 5279. https://doi.org/10.3390/app13095279
Tabakov M, Chlopowiec AB, Chlopowiec AR. A Novel Classification Method Using the Takagi–Sugeno Model and a Type-2 Fuzzy Rule Induction Approach. Applied Sciences. 2023; 13(9):5279. https://doi.org/10.3390/app13095279
Chicago/Turabian StyleTabakov, Martin, Adrian B. Chlopowiec, and Adam R. Chlopowiec. 2023. "A Novel Classification Method Using the Takagi–Sugeno Model and a Type-2 Fuzzy Rule Induction Approach" Applied Sciences 13, no. 9: 5279. https://doi.org/10.3390/app13095279
APA StyleTabakov, M., Chlopowiec, A. B., & Chlopowiec, A. R. (2023). A Novel Classification Method Using the Takagi–Sugeno Model and a Type-2 Fuzzy Rule Induction Approach. Applied Sciences, 13(9), 5279. https://doi.org/10.3390/app13095279







