Parasitic Motions of 3-PRS Parallel Mechanisms with Two Different Branch Chain Arrangements
Abstract
:1. Introduction
2. 3-PRS PM I
2.1. 3-PRS PM I Modeling
2.2. Kinematics Analysis
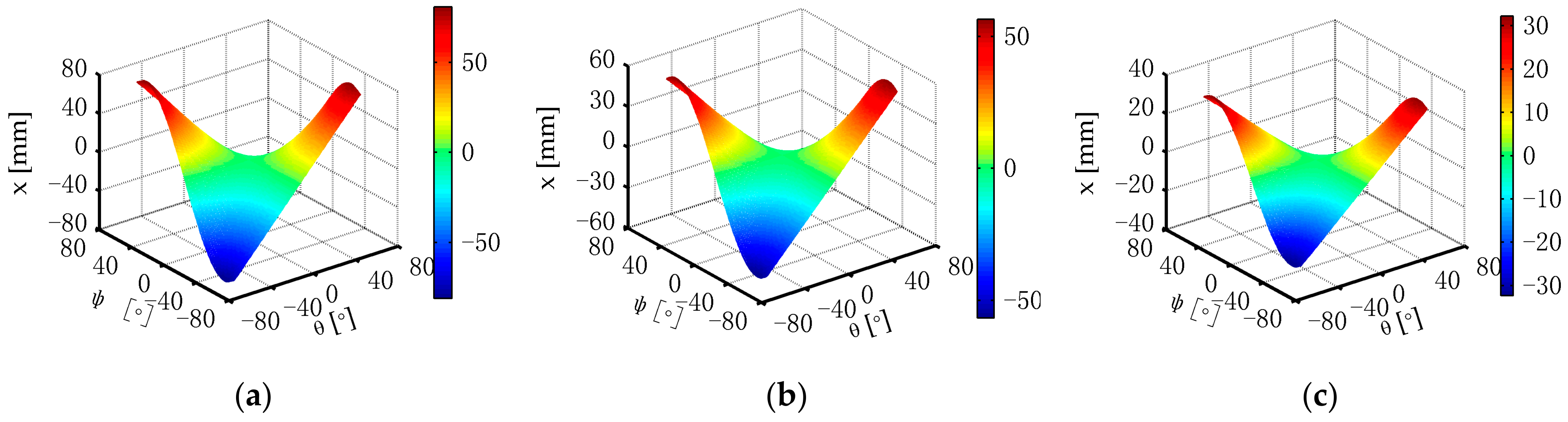
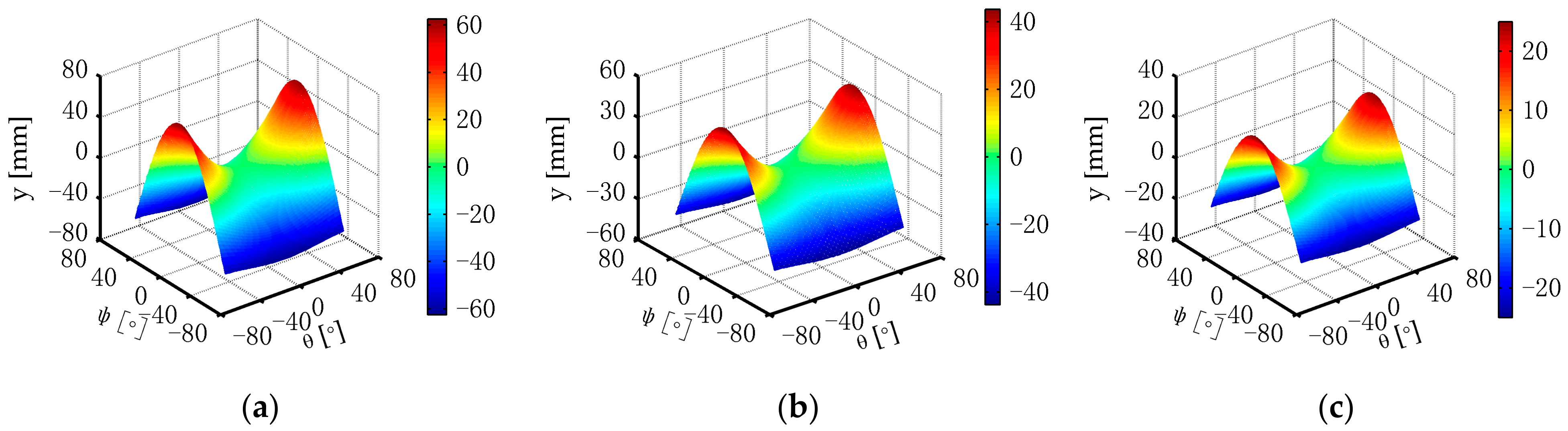
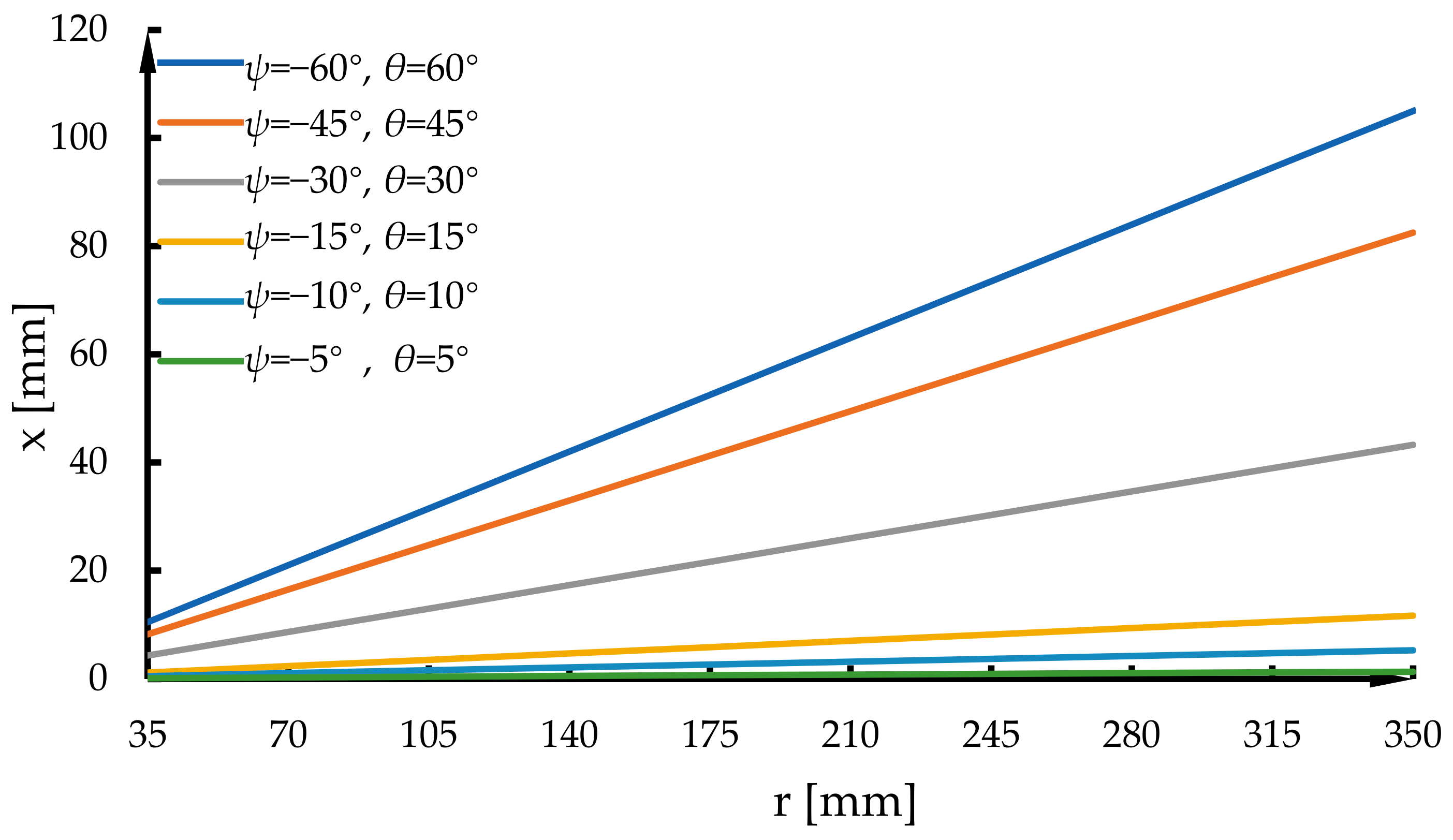
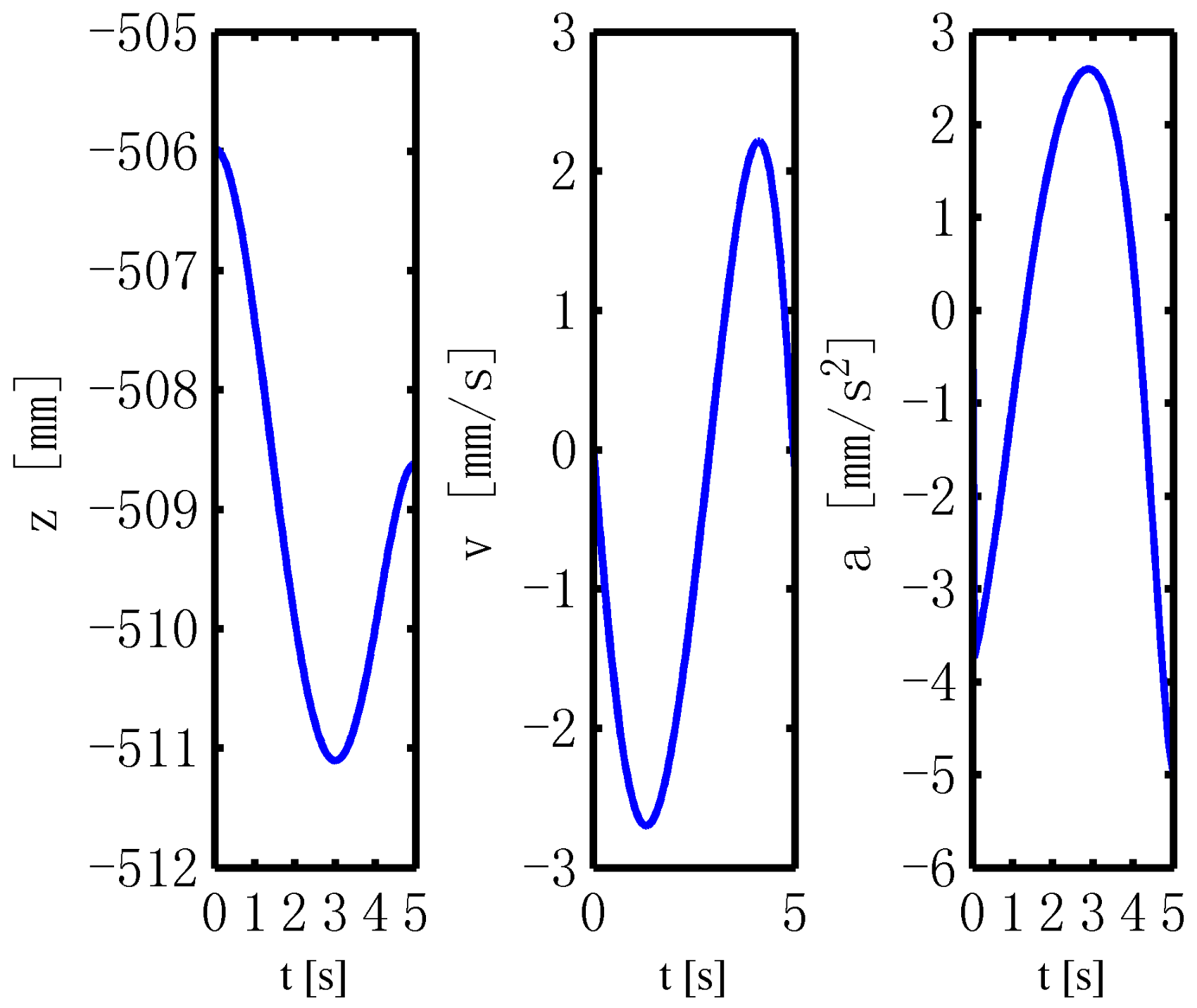
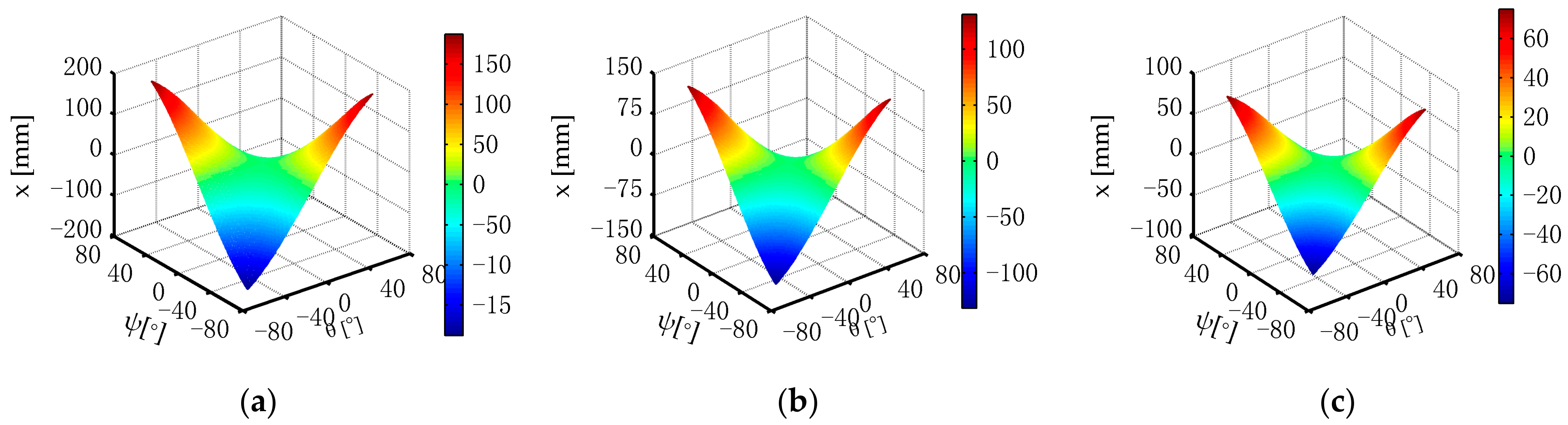
2.3. Parasitic Motion Analysis
2.4. Improved 3-PRS PM I without Parasitic Motion
3. 3-PRS PM II
3.1. 3-PRS PM II Modeling
3.2. Kinematics Analysis
3.3. Parasitic Motion Analysis
3.4. Improved 3-PRS PM II without Parasitic Motion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yao, J.T.; Gu, W.D.; Feng, Z.Q.; Chen, L.P.; Xu, Y.D.; Zhao, Y.S. Dynamic analysis and driving force optimization of a 5-DOF parallel manipulator with redundant actuation. Robot. Comput. Int. Manuf. 2017, 48, 51–58. [Google Scholar] [CrossRef]
- Carabin, G.; Scalera, L.; Wongratanaphisan, T. An energy-efficient approach for 3D printing with a linear Delta robot equipped with optimal springs. Robot. Comput. Int. Manuf. 2021, 67, 102045. [Google Scholar] [CrossRef]
- Rodriguez, E.; Alvares, A.J.; Jaimes, C. Conceptual design and dimensional optimization of the linear delta robot with single legs for additive manufacturing. J. Braz. Soc. Mech. Sci. Eng. 2019, 233, 095965181983691. [Google Scholar] [CrossRef]
- Yang, C.; Ye, W.; Li, Q.C. Review of the performance optimization of parallel manipulators. Mech. Mach. Theory 2022, 170, 104725. [Google Scholar] [CrossRef]
- Li, Y.G.; Liu, H.T.; Zhao, X.M.; Huang, T.; Chetwynd, D.G. Design of a 3-DOF PKM module for large structural component machining. Mech. Mach. Theory 2010, 45, 941–954. [Google Scholar] [CrossRef]
- Xie, F.G.; Mei, B.; Liu, X.J.; Zhang, J.B.; Yue, Y. Novel mode and equipment for machining large complex components. J. Mech. Eng. 2020, 56, 70–78. [Google Scholar] [CrossRef]
- López-Custodio, P.C.; Fu, R.; Dai, J.S.; Jin, Y. Compliance model of Exechon manipulators with an offset wrist. Mech. Mach. Theory 2022, 167, 104558. [Google Scholar] [CrossRef]
- Bi, Z.M.; Jin, Y. Kinematic modeling of Exechon parallel kinematic machine. Robot. Comput. Int. Manuf. 2011, 27, 186–193. [Google Scholar] [CrossRef]
- Liu, X.J.; Xie, F.G.; Wang, J.S. Current opportunities in the field of mechanisms in China. J. Mech. Eng. 2015, 51, 2–12. [Google Scholar] [CrossRef]
- Udomsap, T.; Chinchouryrang, S.; Liampipat, S.; Chanthasopeephan, T. Kinematics of platform stabilization using a 3-PRS parallel manipulator. ROBOMECH J. 2023, 10, 8. [Google Scholar] [CrossRef]
- Gallardo-Alvarado, J.; Orozco, H.; Rico, J.M. Kinematics of 3-RPS parallel manipulators by means of screw theory. Int. J. Adv. Manuf. Technol. 2008, 36, 598–605. [Google Scholar] [CrossRef]
- Tang, T.; Fang, H.; Zhang, J. Hierarchical design, laboratory prototype fabrication and machining tests of a novel 5-axis hybrid serial-parallel kinematic machine tool. Robot. Comput. Int. Manuf. 2020, 64, 101944. [Google Scholar] [CrossRef]
- Liu, M.; Gu, Q.; Yang, B.; Yin, Z.; Liu, S.; Yin, L.; Zheng, W. Kinematics model optimization algorithm for six degrees of freedom parallel platform. Appl. Sci. 2023, 13, 3082. [Google Scholar] [CrossRef]
- Shen, H.P.; Meng, Q.M.; Li, J.; Deng, J.M.; Wu, G.L. Kinematic sensitivity, parameter identification and calibration of a non-fully symmetric parallel Delta robot. Mech. Mach. Theory 2021, 161, 104311. [Google Scholar] [CrossRef]
- Rao, N.M.; Rao, K.M. Dimensional synthesis of a spatial 3-RPS parallel manipulator for a prescribed range of motion of spherical joints. Mech. Mach. Theory 2009, 44, 477–486. [Google Scholar] [CrossRef]
- Malyshev, D.; Rybak, L.; Carbone, G.; Semenenko, T.; Nozdracheva, A. Optimal design of a parallel manipulator for aliquoting of biomaterials considering workspace and singularity zones. Appl. Sci. 2022, 12, 2070. [Google Scholar] [CrossRef]
- Liu, S.Z.; Yu, Y.Q.; Zhu, Z.C.; Su, L.Y.; Liu, Q.B. Dynamic modeling and analysis of 3-RRS parallel manipulator with flexible links. J. Cent. South Univ. Technol. 2010, 17, 323–331. [Google Scholar] [CrossRef]
- Farhat, N.; Mata, V.; Alvaro, P.; Valero, F. Identification of dynamic parameters of a 3-DOF RPS parallel manipulator. Mech. Mach. Theory 2008, 43, 1–17. [Google Scholar] [CrossRef]
- Carretero, J.A.; Podhorodeski, R.P.; Nahon, M.A.; Gosselin, C.M. Kinematic analysis and optimization of a new three degree-of-freedom spatial parallel manipulator. J. Mech. Des. 2000, 122, 17–24. [Google Scholar] [CrossRef]
- Herrero, S.; Pinto, C.; Corral, J.; Altuzarra, O. Actuators orientation influence in the energy consumption of the 3-PRS manipulator. ASME Int. Mech. Eng. Congr. Expo. 2013, 15, 11. [Google Scholar] [CrossRef]
- Alshammari, S.; Al-Sawalha, M.M.; Shah, R. Approximate analytical methods for a fractional-order nonlinear system of Jaulent–Miodek equation with energy-dependent Schrödinger potential. Fractal Fract. 2023, 7, 140. [Google Scholar] [CrossRef]
- Al-Sawalha, M.; Ababneh, O.Y.; Shah, R.; Shah, N.A.; Nonlaopon, K. Combination of Laplace transform and residual power series techniques of special fractional-order non-linear partial differential equations. AIMS Math. 2023, 8, 5266–5280. [Google Scholar] [CrossRef]
- Al-Sawalha, M.M.; Shah, R.; Shah, N.A.; Nonlaopon, K.; Ababneh, O.Y. Numerical investigation of fractional-order wave-like equation. AIMS Math. 2023, 8, 5281–5302. [Google Scholar] [CrossRef]
- Al-Sawalha, M.M.; Shah, R.; Nonlaopon, K.; Khan, I.; Ababneh, O.Y. Fractional evaluation of Kaup–Kupershmidt equation with the exponential-decay kernel. AIMS Math. 2023, 8, 3730–3746. [Google Scholar] [CrossRef]
- Gallardo-Alvarado. An application of the newton-homotopy continuation method for solving the forward kinematic problem of the 3-RRS parallel manipulator. Math. Probl. Eng. 2019, 2019, 3123808. [Google Scholar] [CrossRef]
- Yang, G.; Zhu, R.; Fang, Z.; Chen, C.Y.; Zhang, C. Kinematic design of a 2R1T robotic end-effector with flexure joints. IEEE Access. 2020, 8, 57204–57213. [Google Scholar] [CrossRef]
- Liu, X.J.; Wu, C.; Wang, J.S.; BONEV, I. Attitude description method of [PP]S type parallel robotic mechanisms. Chin. J. Mech. Eng. 2008, 44, 19–23. [Google Scholar] [CrossRef]
- Li, Q.C.; Chen, Z.; Chen, Q.H.; Wu, C.Y.; Hu, X.D. Parasitic motion comparison of 3-PRS parallel mechanism with different limb arrangements. Robot. Comput. Int. Manuf. 2011, 27, 389–396. [Google Scholar] [CrossRef]
- Xu, Y.D.; Zhao, Y.; Yue, Y.; Xi, F.F.; Yao, J.T.; Zhao, Y.S. Type synthesis of overconstrained 2R1T parallel mechanisms with the fewest kinematic joints based on the ultimate constraint wrenches. Mech. Mach. Theory 2020, 147, 103766. [Google Scholar] [CrossRef]
- Hu, B.; Shi, D.S.; Shi, Y.G.; Zhang, D.; Ye, N.J. Kinematically identical manipulators for an asymmetric 3-PRS parallel manipulator and their constraint performance comparison study. J. Mech. Eng. 2020, 56, 31–40. [Google Scholar] [CrossRef]
- Jha, R.; Chablat, D.; Baron, L. Influence of design parameters on the singularities and workspace of a 3-RPS parallel robot. Trans. Can. Soc. Mech. Eng. 2018, 42, 30–37. [Google Scholar] [CrossRef]
- Fang, H.; Xin, B.; Zhang, X. Workspace-constrained optimal design of three-degrees-of-freedom parallel manipulators with minimum parasitic motions by integrating interval analysis, region mapping and differential evolution. Eng. Optimiz. 2015, 47, 407–428. [Google Scholar] [CrossRef]
- Chen, M.; Zhang, Q.; Chen, W.T.; Qin, X.R.; Sun, Y.T. Analysis and type synthesis of parallel mechanisms without parasitic motion based on spatial geometry. J. Mech. Eng. 2021, 57, 77–85. [Google Scholar] [CrossRef]
- Hao, L.L.; Li, H.; Li, R.Q. Workspaces solution of 3-PRS parallel mechanism with simmechanics. Mach. Des. Manuf. 2016, 11, 63–65. (In Chinese) [Google Scholar] [CrossRef]
- Xia, H.; Zhao, Y.H.; Li, R.Q. Concomitant Motion and Positive and Inverse Solutions of UPS+UPR+S Parallel Mechanism. Pack. Eng. 2018, 7, 136–140. (In Chinese) [Google Scholar] [CrossRef]

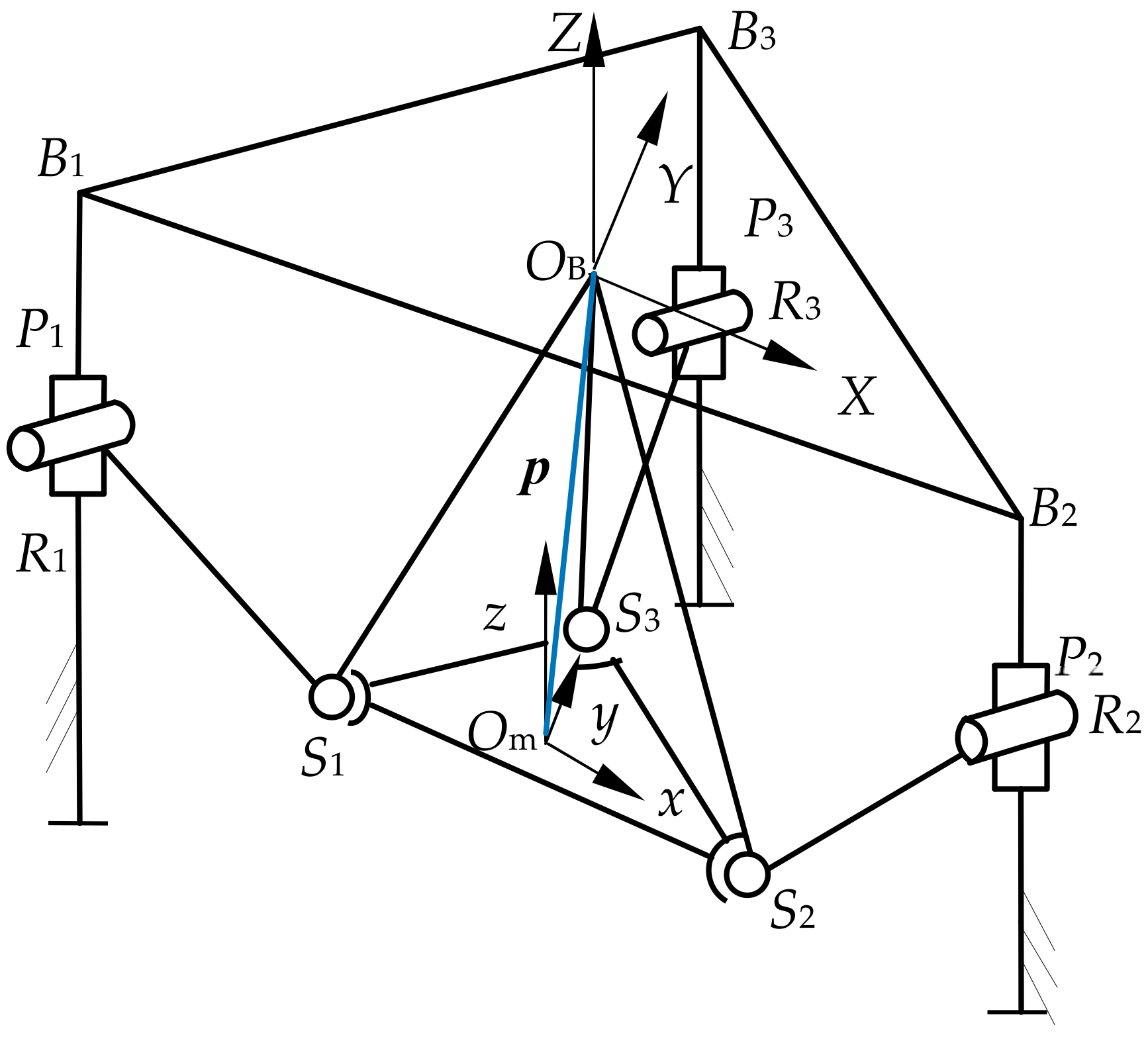
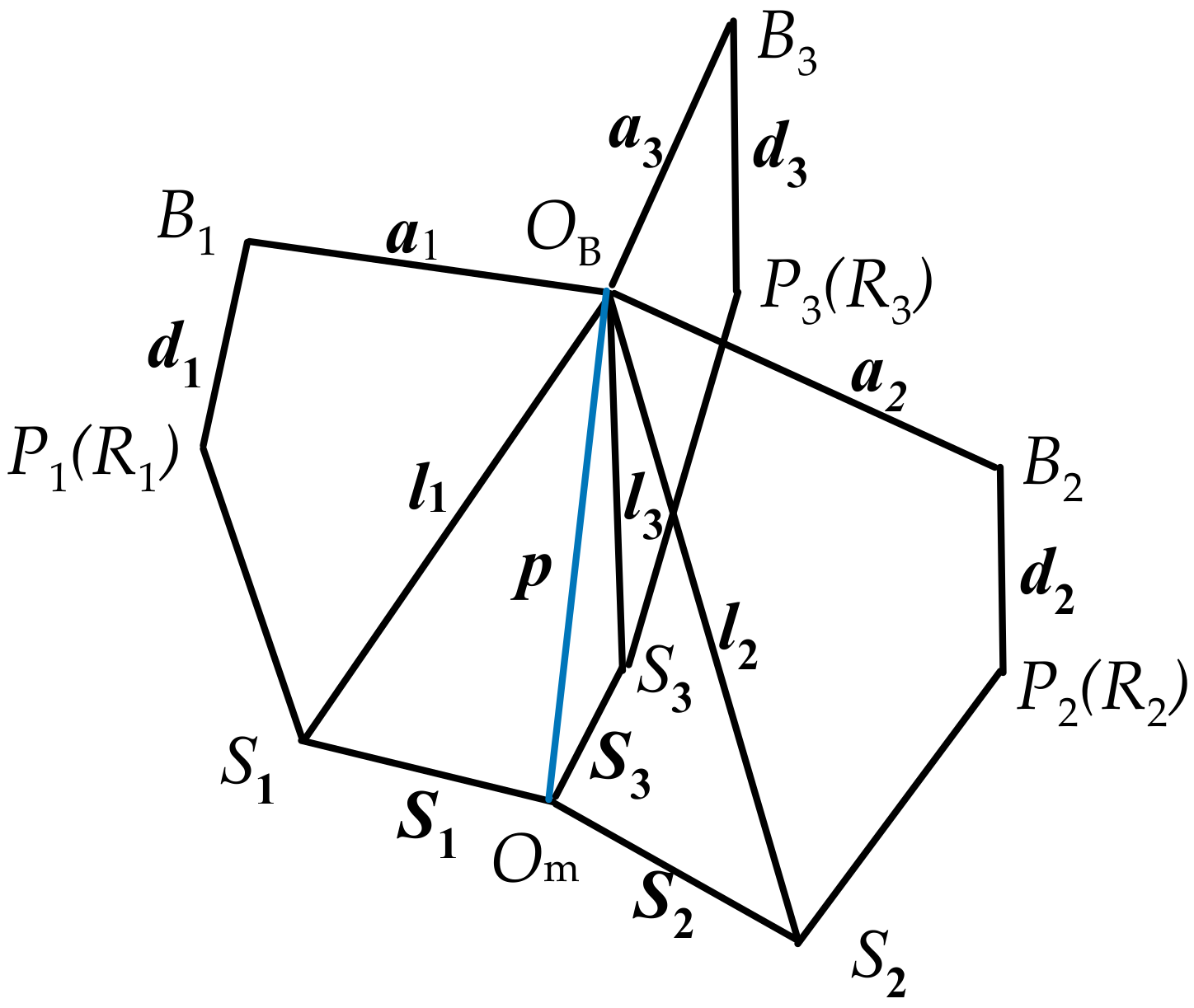
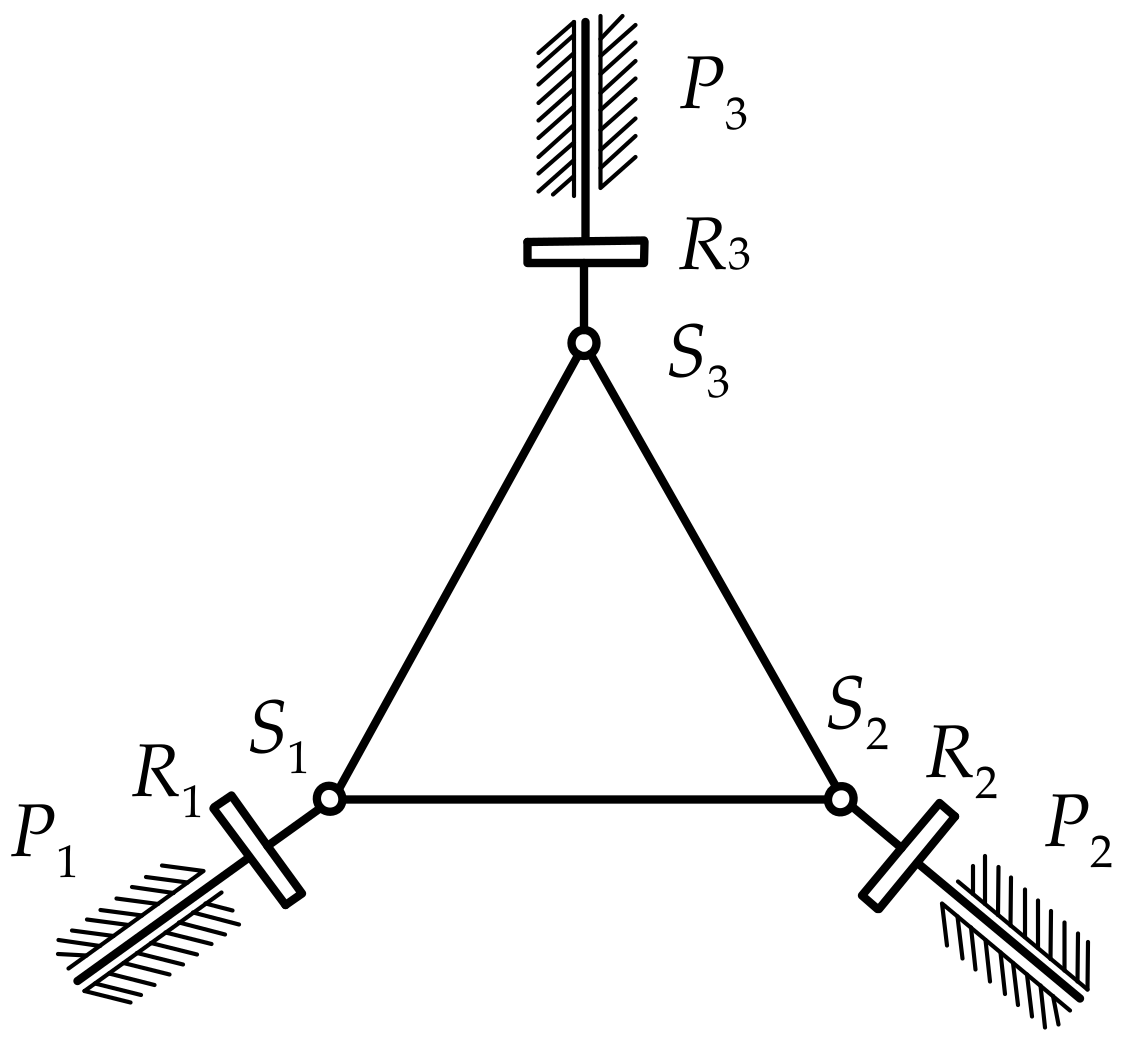




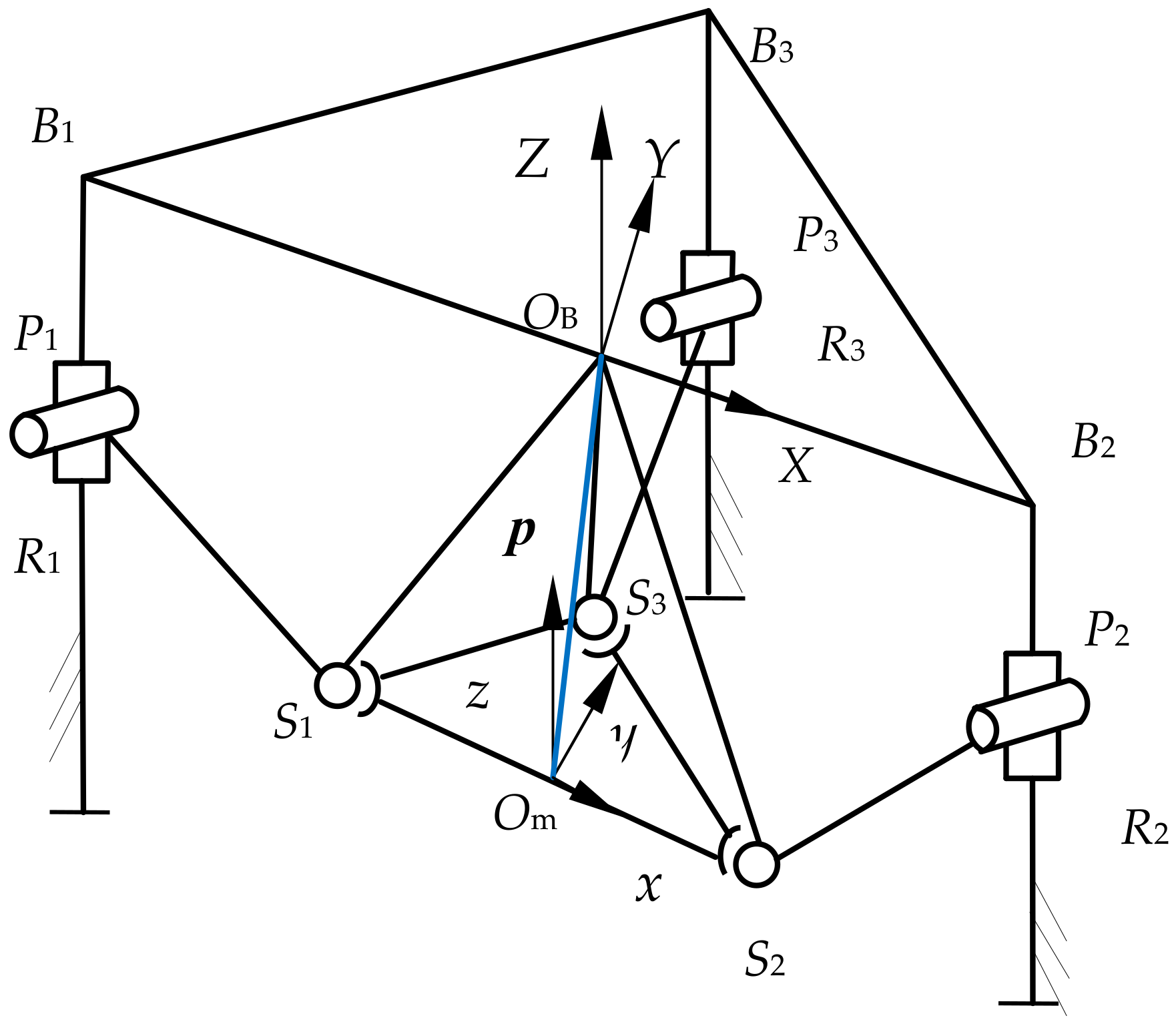
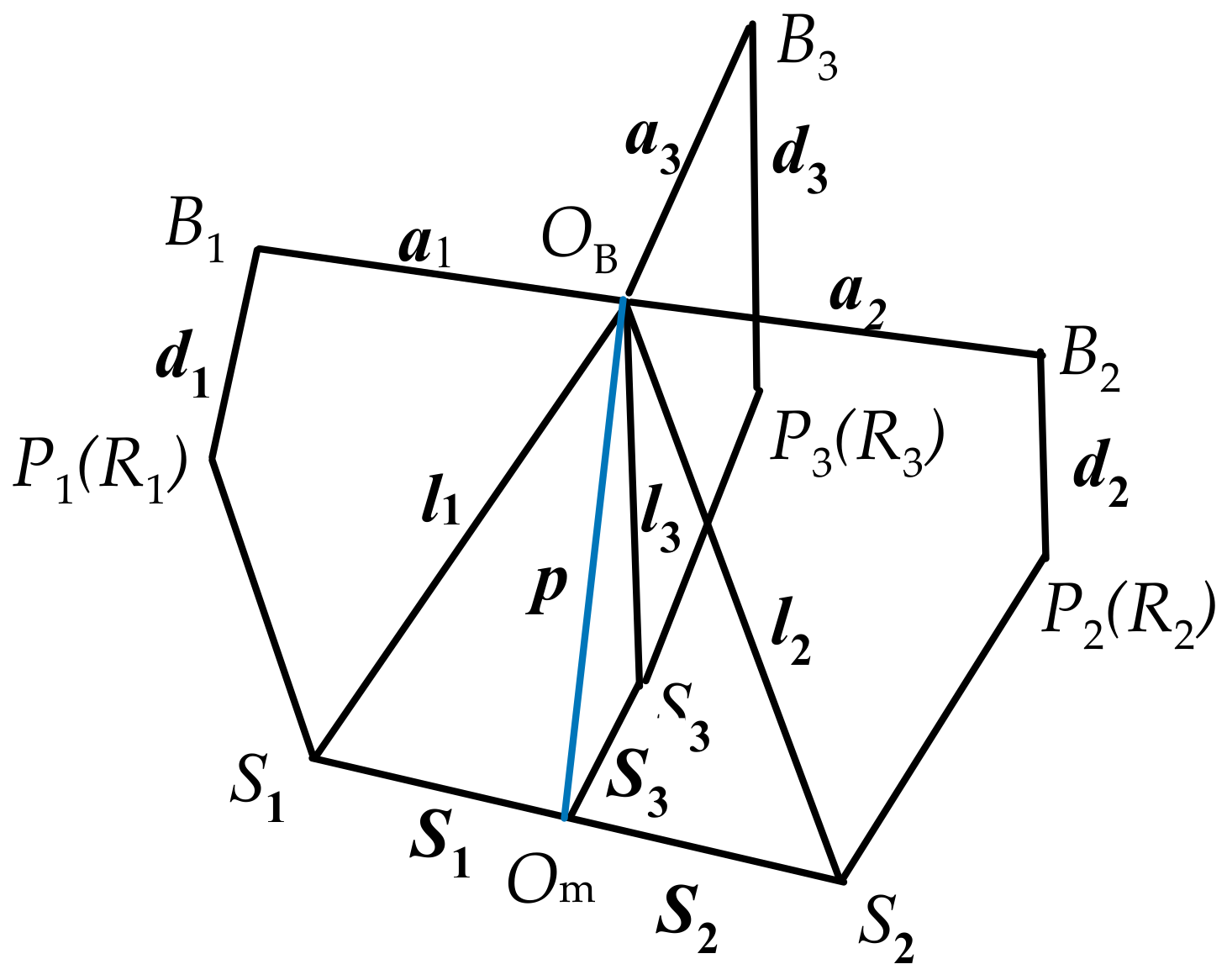




| Expression | Physical Meaning (i = 1, 2, 3) |
|---|---|
| In the {OB} coordinate system, the vector from the origin OB to the origin Om. | |
| In the {OB} coordinate system, the vector from the origin OB to point Bi. | |
| In the {OB} coordinate system, the vector from the origin OB to the spherical joint center Si. | |
| In the {OB} coordinate system, the vector from the origin Om to the spherical joint center Si. | |
| In the {Om} coordinate system, the vector from the origin Om to the spherical joint center Si. | |
| The moving distance of the prismatic pair Pi |
| Parameter | Value |
|---|---|
| Equivalent circumradius of the fixed platform B1B2B3, R [mm] | 125 |
| Equivalent circumradius of the moving platform S1S2S3, r [mm] | 80 |
| Range of the moving distance of the pairs Pi, di [mm] | [105, 195] |
| Ranges of the kinematic parameters ψ and θ | [−60°, 60°] |
| Angles | x-Max [mm] (r = 250) | x-Max [mm] (r = 100) | y-Max [mm] (r = 250) | y-Max [mm] (r = 100) |
|---|---|---|---|---|
| ψ and θ ∈ [−60°, 60°] | 80.6789 | 32.2716 | 62.5000 | 25 |
| ψ and θ ∈ [−45°, 45°] | 58.9256 | 23.5702 | 36.6117 | 14.6447 |
| ψ and θ ∈ [−30°, 30°] | 30.9295 | 12.3718 | 16.7468 | 6.6987 |
| ψ and θ ∈ [−15°, 15°] | 8.3684 | 3.3474 | 4.2593 | 1.7037 |
| ψ and θ ∈ [−10°, 10°] | 3.7688 | 1.5075 | 1.8990 | 0.7596 |
| ψ and θ ∈ [−5°, 5°] | 0.9495 | 0.3798 | 0.4757 | 0.1903 |
| Parameter | Value |
|---|---|
| Length of side OBS2 of the fixed platform B1B2B3, a [mm] | 125 |
| Length of side OBB3 of the fixed platform B1B2B3, b [mm] | 150 |
| Length of side OmS2 of the moving platform S1S2S3, c [mm] | 80 |
| Length of side OmS3 of the moving platform S1S2S3, e [mm] | 60 |
| Range of the equivalent link length of the pairs Pi, di [mm] | [105, 195] |
| Ranges of the kinematic parameters ψ and θ | [−60°, 60°] |
| Angles ψ and θ | x-Max [mm] (e = 250) | x-Max [mm] (e = 100) |
|---|---|---|
| ψ and θ ∈ [−60°, 60°] | 187.5 | 75 |
| ψ and θ ∈ [−45°, 45°] | 125 | 50 |
| ψ and θ ∈ [−30°, 30°] | 62.5 | 25 |
| ψ and θ ∈ [−15°, 15°] | 16.75 | 6.6987 |
| ψ and θ ∈ [−10°, 10°] | 7.5384 | 3.0154 |
| ψ and θ ∈ [−5°, 5°] | 1.8990 | 0.7596 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, Y.; Wu, W.; Li, R.; Zhao, Y. Parasitic Motions of 3-PRS Parallel Mechanisms with Two Different Branch Chain Arrangements. Appl. Sci. 2023, 13, 5425. https://doi.org/10.3390/app13095425
Yao Y, Wu W, Li R, Zhao Y. Parasitic Motions of 3-PRS Parallel Mechanisms with Two Different Branch Chain Arrangements. Applied Sciences. 2023; 13(9):5425. https://doi.org/10.3390/app13095425
Chicago/Turabian StyleYao, Yinyin, Wenge Wu, Ruiqin Li, and Yaohong Zhao. 2023. "Parasitic Motions of 3-PRS Parallel Mechanisms with Two Different Branch Chain Arrangements" Applied Sciences 13, no. 9: 5425. https://doi.org/10.3390/app13095425




