A Comprehensive Review of Soil Remolding Toughness Determination and Its Use in the Classification of Fine-Grained Soils

Abstract

The remolding toughness property of fine-grained soil has not been investigated that much, mainly because it has not lent easily to direct measurement, with soil toughness usually qualitatively described. In practical terms, as the plastic limit w_P is approached, tougher soils require greater rolling effort during the w_P test, such that plasticity and toughness properties can be used to distinguish those plastic soils having greater deformation resistance for various field applications. This state-of-the-art review paper presents a critical appraisal of soil remolding toughness determination and its limited use, to date, in the classification of fine-grained soils. The recent developments reviewed and critically assessed include mechanical thread rolling for nominal toughness measurement during the w_P rolling-out procedure, various extrusion approaches, and proposed correlations between toughness and the plasticity index to liquid limit ratio. From statistical analysis of previously reported toughness–consistency limits data, some new correlations are introduced in the present paper. Soil classification using the traditional Casagrande plasticity chart is not entirely accurate for certain soil types in that one can observe soils that present high toughness (something typical of clay) being incorrectly classified as silt soil. From this perspective, a new toughness chart is introduced to augment (or for use instead of) the Casagrande plasticity chart in obtaining more reliable soil classification. This paper concludes with recommendations on future research efforts for routinely obtaining soil toughness measurements.

1. Introduction

Plasticity can be defined as the material property that enables significant deformation to occur without fracture when sufficiently high stresses are applied (i.e., exceeding the material’s yield stress) and the ability to retain the deformed shape on removal of those stresses. For soils, and specifically fine-grained soils, plasticity is directly related to the platy habit exhibited by most clay mineral particles that favors their sliding with respect to each other when enough moisture is present (i.e., for water content (w) values within the plastic range). The plasticity of these materials is commonly assessed using the manual “rolling of threads” method, with the plastic limit (w_P), originally described by Atterberg [1,2], defined as the water content at which the soil threads just begin to crumble (cracking longitudinally and transversely) during the standardized thread rolling (by hand) test [3,4]. In other words, the w_P defines the ductile–brittle states transition. Attempts to improve on the repeatability and reproducibility of the standard hand rolling w_P test (by minimizing the uncertainties associated with the rolling out (by hand) procedure; i.e., rate of rolling, the hand pressure, and/or the initial and final thread diameter criteria) include the thread rolling device technique proposed by Bobrowski and Griekspoor [5]. Their method, which follows the same basic principles as the standard thread rolling (by hand) test, has been standardized and presented as an alternative method for w_P determination in ASTM D4318 [3] and AASHTO T90 [6]. A comprehensive statistical analysis performed on a database of 60 diverse fine-grained soils demonstrated that these hand and device rolling methods produce essentially similar w_P values for a given fine-grained soil tested [7].

For fine-grained soil (and mainly clays), remolding toughness (T) represents the mechanical resistance offered when its w_P is about to be reached [8] for reducing water content in the plastic range. For instance, as the w_P is approached, tougher soils require noticeably greater rolling effort for reducing the soil thread diameter from a starting 6 mm dia. down to approx. 3 mm dia. at the crumbling condition [3,9]. Together, the plasticity and toughness properties are used to identify soils that provide greater resistance to deformation while retaining plastic behavior for use in various field applications. For instance, soil remolding toughness is important for the choice and performance of field compaction machinery in earthwork construction and it influences the integrity of earthwork components, e.g., the core of earthen dams and clay liners in water-retaining structures and landfills [8].

Greater plasticity and toughness arise from increases in the quantity of expanding lattice-type clay minerals with greater specific surface area (SSA) and cation exchange, and for decreases in the ion concentration of the pore fluid and the valency of exchangeable cations present [10]. Fundamentally, within the plastic range (of water contents), saturated clayey materials develop suction, such that active/high plasticity clays (characterized by the highest air-entry values) have the highest toughness. For instance, at (just above) the w_P, silty, sandy, and peaty soils present slight toughness, whereas low-to-medium plasticity soils (e.g., silty clays) display medium toughness, with active clays exhibiting high toughness [11,12,13]. As stated on page 805 of the paper by Casagrande [14], “the higher the position of a soil above the A-line on the plasticity chart (CL, CH), the stiffer are the soil threads near the plastic limit”. Hence, the concepts of plasticity and toughness could be considered synonymous from a practical standpoint. Note that another term often used to denote toughness is workability [8,9,13], perhaps of more importance for the ceramics and brick-making industries and in an agricultural context [8].

Atterberg [1,2] identified the water content range over which soil behaves in a plastic manner using the plasticity index I_P (= w_L − w_P), where w_L is the liquid limit water content. These index parameters are ubiquitously used for fine-grained soil classification, typically employing the Casagrande plasticity chart that plots I_P against w_L, with the test soil classified as clay or silt material depending on its position relative to the A-line demarcation boundary in the I_P versus w_L plot [14,15,16]. However, the size of the water content range over which the soil behaves plastically (i.e., given by its I_P) or the upper limit of that range (i.e., w_L) are not, by themselves, satisfactory measures of soil toughness. In other words, soil toughness is a more fundamental plasticity property, typically quantified as the amount of work undertaken per unit soil volume necessary to change shape, remold, or, as in the case of the standard w_P test, roll out uniform soil cylinders (threads) applying sufficient finger pressure during the repeated traverses [8,17,18].

The literature presents only a handful of cases employing empirical classifications of soil remolding toughness (these are based on qualitative or subjective assessments/descriptions of the observed soil behavior). A few cases reported in the literature purport to provide semi-quantitative assessments of soil toughness, and apparently, only one reported apparatus and test method [8,17,18] presently exists to provide direct toughness measurements. Neither has the property of soil remolding toughness been used that much in soil classification systems, with all of these points reflected by the sparsity of published work on the subject matter compared to, for instance, the voluminous reported work on the consistency limits (i.e., w_L and w_P) determination. This includes improved knowledge and understanding of the fall cone and Casagrande w_L [19,20,21] and Atterberg w_P [8,17,18,22] state transitions and their experimental determination, methods of relating Casagrande cup and fall cone w_L for a given fine-grained soil investigated [19,23,24], and various alternative proposals for soil plasticity (w_P) determination, mostly based on fall cone approaches. The latter includes using a modified fall cone setup with an enhanced cone mass and incorporating a drop height [25,26] (such that the falling cone hits the surface of the soil test specimen with an impact velocity) for the determination of the “plastic strength limit” PL₁₀₀ parameter [19,22,27,28] and various investigations of the fall cone flow curve for soil plasticity determination [29,30]. Significant recent developments in fine-grained soil classification systems based on plasticity include the proposals of Moreno-Maroto and Alonso-Azcárate [11,31] and Vardanega et al. [32]. Moreno-Maroto and Alonso-Azcárate [11,31] developed their proposal according to objective criteria based on the quantitative measurement of properties, such as soil toughness, the bending capacity of formed soil threads, and the observation of adhesive consistency, whereas the Vardanega et al. [32] system requires only fall cone w_L test results to achieve the classification of fine-grained soils to an acceptable degree of accuracy, i.e., the approach does not require w_P measurement, removing the dependence on the thread rolling w_P test that can have high operator variability [25,33]. There is also greater awareness of the limitations of standard/conventional consistency limits test methods and fine-grained soil classification systems for investigations on unconventional soils, including (fibrous) peats [34] and diatomaceous soil [35]. In other words, the measured consistency limits of these soils do not provide reliable information on the soils’ likely geotechnical properties as they are conventionally expected to do.

On the subject topic of soil toughness, Casagrande [36] introduced an index of toughness at the w_P (denoted herein as I_T(C)), defined as the logarithm of the undrained shear strength (s_u) ratio determined for the w_P-to-w_L water contents. Casagrande [36] also proposed that the value of I_T(C) could be determined as the ratio of I_P to the flow index (I_F), with I_F determined as the gradient of the w versus Log₁₀ N plot obtained from percussion cup test data for w_L determination. However, this approach for I_T(C) determination is not reliable as it assumes a linear Log₁₀ s_u versus w correlation applies over the full plastic range of fine-grained soil, which is generally not the case in practice, instead often exhibiting highly nonlinear behavior [19,37,38,39]. Since the early work of Casagrande [36], the property of soil toughness has not been investigated that much in geotechnical engineering, mostly because it does not lend itself easily to direct measurement. In a follow-up paper, Casagrande [14] gave a qualitative classification of soil toughness considering the “cohesiveness” near the w_P, using the descriptive terms of “very weak”, “weak”, “firm”, “medium tough”, “tough”, and “very tough”. The ASTM visual–tactile field tests [40] include subjective assessments of the finger pressure required in rolling out uniform soil threads and the stiffness of a soil lump formed from amassing those threads, assigning descriptive terms of “non-plastic”, and low, medium, and high toughness accordingly. The US Department of Agriculture Soil Survey Manual [41] considers the relative force required to form 3 mm dia. soil threads at a water content near or at the w_P. In other words, soils are classed as having low, medium, and high toughness for the exertion of <8 N, 8–20 N, or >20 N of force applied by the operator’s finger pressure during the repeated traverses [41] because when testing tougher soils, such as those with a high montmorillonite content, greater force is required to roll out and cause a reduction in diameter of the soil threads prepared at the w_P water content [9,13]. Various attempts have also been presented for soil toughness classification employing the Casagrande plasticity chart, with different zones or classifications of toughness at the w_P identified in the chart. For instance, the Naval Facilities Engineering Command [42] uses the qualitative terms “slight”, “slight to medium”, “medium”, and “high” when identifying toughness zones for soils plotting above and below the A-line boundary marked in the Casagrande plasticity chart.

Some quasi-toughness tests have been developed specifically for the ceramics industry, with various investigations performed to assess soil remolding toughness. These include a novel proposal by Astbury et al. [43], who defined soil toughness considering the amount of energy absorbed by the test specimen during one cycle of a cyclic torsion test and which was quantified as the area within the experimental stress–strain hysteresis loop. The ASTM C181-11 standard [44] presents a test to determine a “workability index” for fireclays and high alumina refractory plastics by measuring the plastic deformation of a molded test specimen when subjected to impact. This approach is comparatively similar in function and outcome to the moisture condition apparatus and test [45] that are used to assess the suitability of mainly cohesive soils for incorporation into earthworks. With tougher soil lumps being more resistant to remolding, thereby requiring more compaction energy and giving higher moisture condition values (MCVs), Barnes [8] suggested that the moisture condition test could potentially be used to assess soil toughness.

Fitzjohn and Worral [46] performed extrusion tests on brick clays, measuring their extrusion rates as a function of the applied extrusion pressure (p_e) for different clay contents. Subsequently, CERAM Research [47,48] developed a ceramic rheology tester, termed the Martin flow instrument (MFI), which is a modified version of the melt flow indexer used for testing the flow properties of plastics and polymers. For the MFI, a standard length of cored soil sample is inserted into a cylindrical barrel that contains a die at the base. A piston placed inside the barrel applies pressure via a deadweight load to cause the extrusion of the soil to occur through the die orifice. The time period required for a known soil volume to flow through the die orifice is measured, with the flow time (extrusion rate) dependent on the soil toughness, with tougher materials taking longer [47]. The soil sample, from soft earthenware clays to some advanced ceramic materials, is tested within a preferred shear rate range (relevant to the subsequent processing of the material) by employing an appropriate deadweight in the range of 2–30 kg applied to the piston [47].

In soil mechanics, the extrusion approach has also been investigated for the testing of fine-grained soils to possibly assess/measure their toughness [12,13], including proposed power-based extrusion approaches for consistency limits determination [13,49]. These aspects will be discussed in detail later in the paper. Closely replicating Atterberg’s hand rolling of threads method, Barnes [8,17,18] developed a mechanical thread rolling apparatus and test that allow nominal applied stress and diametrical strain measurements for a uniform soil cylinder (thread) during the rolling out procedure. The toughness-related soil properties and the value of w_P can be determined from the obtained experimental T–w plots (associated methods are elaborated later in Section 2.1). Based on this research, Barnes [17] proposed a tentative toughness classification based on the remolding toughness mobilized at the w_P water content (i.e., the maximum remolding toughness, T_max). Finally, the work of Moreno-Maroto and Alonso-Azcárate [11] is briefly introduced at this point. They obtained a quantitative relationship between the I_P/w_L ratio and T_max, thereby allowing toughness estimation for fine-grained soil based solely on consistency limits measurements, allowing them to develop a soil plasticity classification system in which the determining factor is toughness.

The aim of the present paper is to present a state-of-the-art review of soil remolding toughness, with emphasis on its experimental determination and the quantification of soil toughness using various related index properties and coefficients. This review focuses particularly on various extrusion proposals [12,13,47,48,49] and Barnes’ mechanical thread rolling apparatus and methodology [8,17,18], which are presently the only means available for obtaining quantitative soil remolding toughness measurements. Challenges arise in the quantification of, and in assigning units of measurement to, the soil remolding toughness. These aspects are discussed in the context of Barnes’ thread rolling approach. Attention then turns to the quantitative assessment of soil toughness via correlations, firstly reporting on the correlation of the T_max to I_P/w_L ratio after Moreno-Maroto and Alonso-Azcárate [11]. Then, employing a large dataset assembly from the available literature, new correlations between T_max and the consistency limits parameters are deduced in the present paper, facilitating the indirect determination of soil remolding toughness from ubiquitously measured Atterberg (consistency) limits parameters. The toughness-based classification of fine-grained soil is discussed, intending to give a more mechanical perspective to fine-grained soil classification. A novel toughness chart is then introduced to augment (or be used instead of) the traditional Casagrande plasticity chart for obtaining more reliable soil classification when investigating some hitherto challenging fine-grained soil types. For instance, based on the toughness criterion, a previous study by the authors has shown that the Casagrande chart tends to classify soils with intermediate characteristics between clays and silts (e.g., silty clays, clayey silts, or clayey sands) as clay if w_L < 50% and as silt if w_L > 50%, while a wide range of clays could be classified as silt for w_L > 65% when using the aforementioned classification [50]. Next, the small number of fundamentally correct approaches for soil remolding toughness determination are compared based on their advantages and disadvantages. This paper concludes with a discussion on recommended future experimental research efforts for soil remolding toughness determination. Note that this review paper concerns itself with the remolding toughness (of ductile soil); for fracture toughness, which applies to brittle soil (i.e., w < w_P), the reader is referred to the papers by Hanson et al. [51] and Wang et al. [52].

2. Soil Remolding Toughness Measurement

2.1. Barnes’ Thread Rolling Apparatus and Method

Barnes [8,17,18] developed an apparatus (see Figure 1) and test method for the rolling of a uniform soil cylinder (thread) between two configured plates. For each traverse, the applied downward force is controlled and recorded, and the actual tread diameter is recorded, such that the graphs of nominal acting stress against the diametrical strain can be computed for a range of investigated water contents (Figure 2a) that reduce in value to the w_P. Based on the areas beneath the produced experimental stress–strain plots, nominal toughness measurements can then be obtained, and are plotted against water content (Figure 2c).

In quantifying remolding toughness, the measurement units of toughness (i.e., work/unit volume) must take into account the number of traverses undergone by the plastic soil thread during the mechanical rolling-out procedure. Barnes [8,17,18] decided that the value of toughness T assigned to the test soil would be based on the cumulative work undertaken per unit soil volume per 100 reversals (i.e., giving units of kJ/m³/100 r) in reducing the soil thread diameter from initially 6 mm down to 4 mm because, over this range of diameters, the soil threads were found to undergo plastic straining in a steady fashion. As described by Barnes [8,17,18], from investigation of the plastic test soil prepared at a range of different water contents, various toughness-related properties can be derived from the obtained experimental T–w plot. For reducing water content, these include the toughness limit w_T (i.e., the water content at zero toughness), the stiffness transition w_S (i.e., the water content below which the remolding toughness increases at a greater rate for many soils), and the maximum remolding toughness T_max, which is mobilized at the w_P and represents the main toughness indicator. Figure 2 shows the experimental sequence carried out by Barnes [8,17,18] in determining the value of T_max (i.e., the value of T corresponding to the measured w_P water content).

Based on the deduced bi-linear T–w relationship (Figure 2c), the plastic range of a given test soil can be subdivided into three distinct regions, namely a workable stiff plastic region for w_P < w < w_S, a workable soft plastic region for w_S < w < w_T, and an adhesive plastic region for w_T < w < w_L [8,18]. In other words, at the w_T, fine-grained soil behavior transforms from workable soft plastic to almost non-workable adhesive plastic. Moreover, for w > w_T, the soil would not only be difficult to form (roll) into a thread to display plasticity, but it would also be very sticky. From the authors’ independent analysis of the experimental data presented for 55 inorganic fine-grained soils reported by Barnes [8], their w_S water contents corresponded to a liquidity index (I_L) of ~0.12 (standard deviation of σ = 0.05), with measurable toughness evident for I_L < 0.43 (σ = 0.14). In other words, w_T could be approximated as follows:

$$w_{\mathrm{T}}=w_{\mathrm{P}}+0.43 I_{\mathrm{P}}$$

(1)

Vinod and Pillai [53] showed that w_T shows a good correlation with the optimum water content for compaction. At all energy levels studied, they found that the maximum dry unit weight displayed a good correlation with the dry unit weight at the w_T water content. Additionally, Shimobe et al. [54] investigated w_T and a soil state index parameter defined as SSI = w_T × e₀, where e₀ is the initial void ratio, as predictors of the compression index (C_c) parameter. The inclusion of e₀ means that the SSI takes into account the effects of several index properties, including the initial density and consistency of soils. They concluded that w_T and, more so, the SSI are reasonable predictors of the C_c parameter.

Furthermore, the toughness coefficients, as given by the gradients of the bi-linear T–w relationship, the workability index I_W (Equation (2)), and the toughness index I_T(B) (= w_T − w_P), can be derived [8,17,18]. Here, the toughness index I_T(B) simply gives the water content range over which the soil would be plastic and workable:

$$I_{\mathrm{W}}=\frac{w-w_{\mathrm{P}}}{w_{\mathrm{T}}-w_{\mathrm{P}}}$$

(2)

where w = soil water content, w_P = plastic limit, and w_T = toughness limit (i.e., water content at zero toughness).

Barnes’ workability index I_W [17] relates the soil’s actual water content to its “workable” range of w_P < w < w_T (i.e., for w = w_T, I_W = 1 ⇒ T = 0 and for w = w_P, I_W = 0 ⇒ T = T_max). In other words, this definition of a workability index does not really relate to the degree of workability (toughness) of the test soil, and, therefore, it does not allow one to discern between silt and clay materials, whose toughness are very different. Note, Barnes’ definition for the toughness index (i.e., I_T(B)) is different from the I_T(C) parameter, after Casagrande [36], previously mentioned in the Introduction. Additionally, as presented in

Table 1. Proposed classification of soil maximum remolding toughness T_max (mobilized at w_P), as determined using Barnes’ thread rolling apparatus [17].

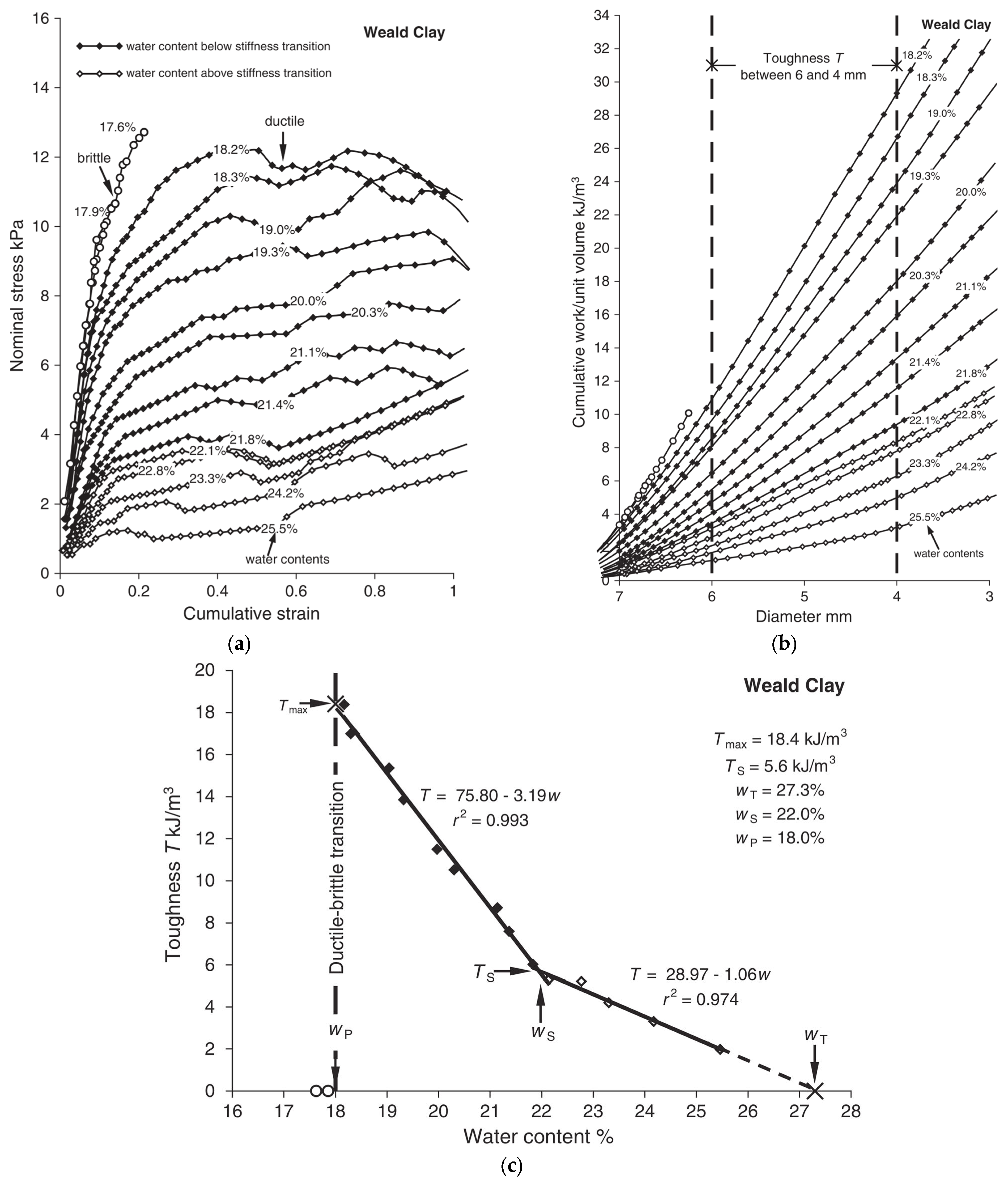
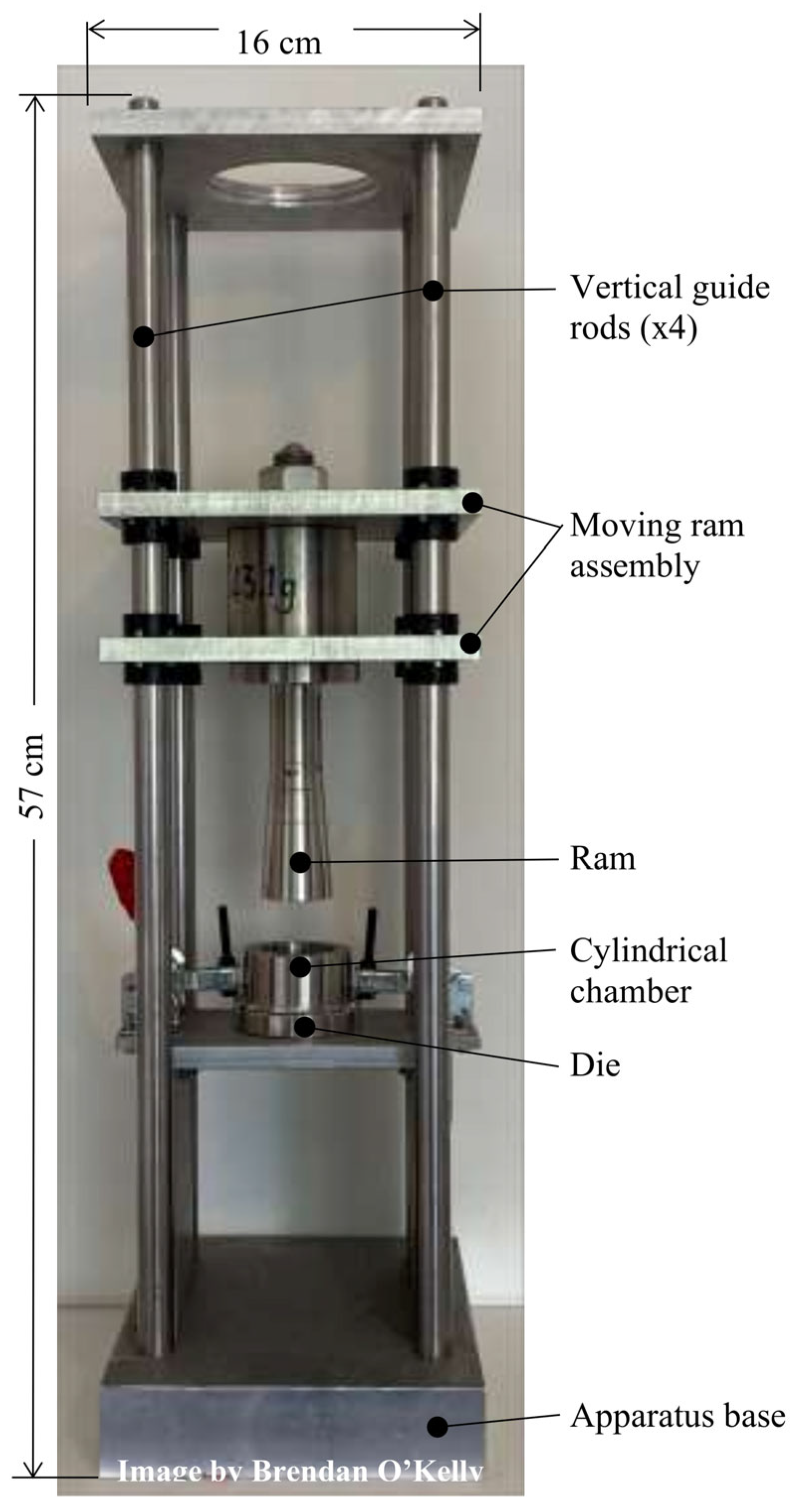
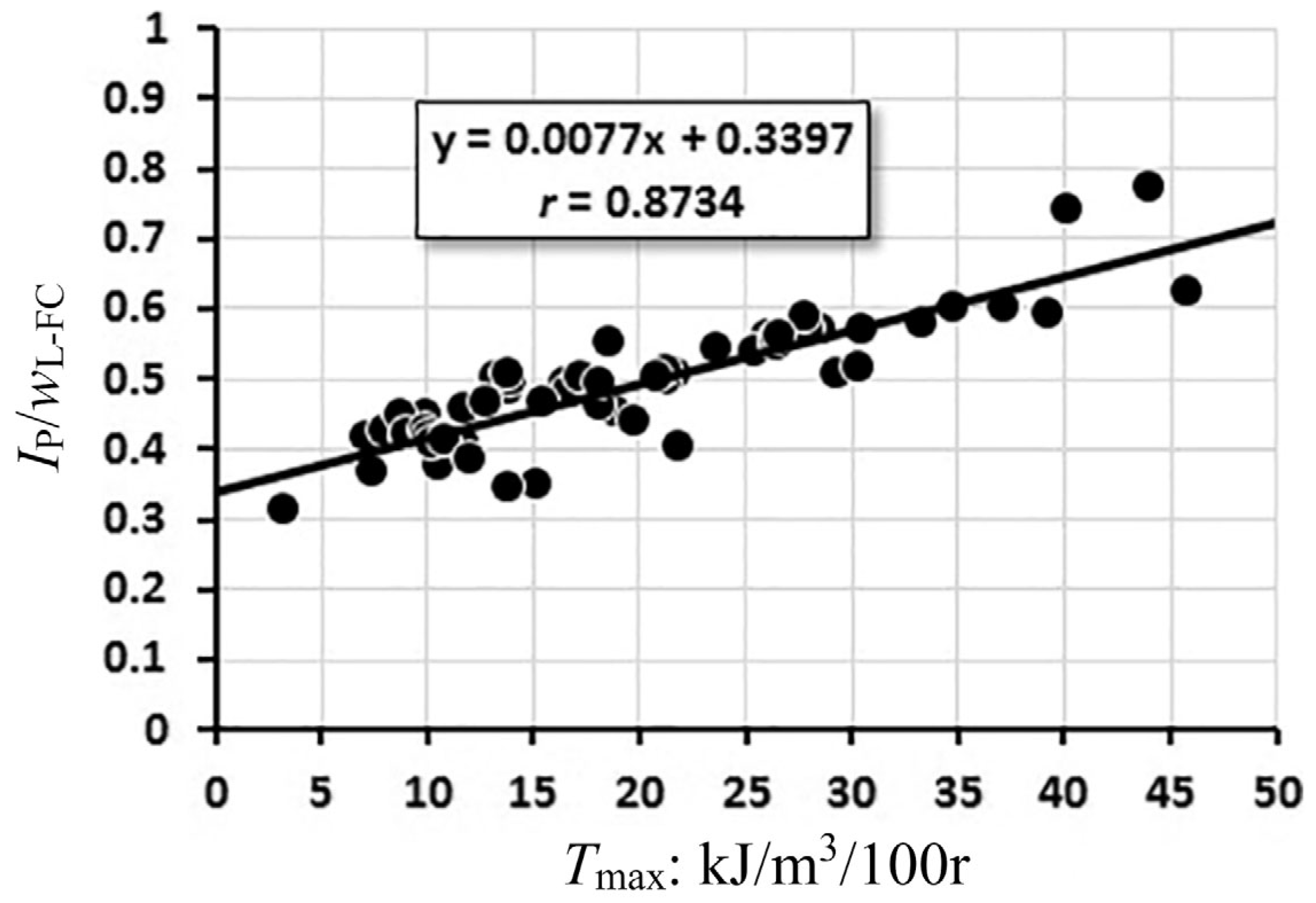
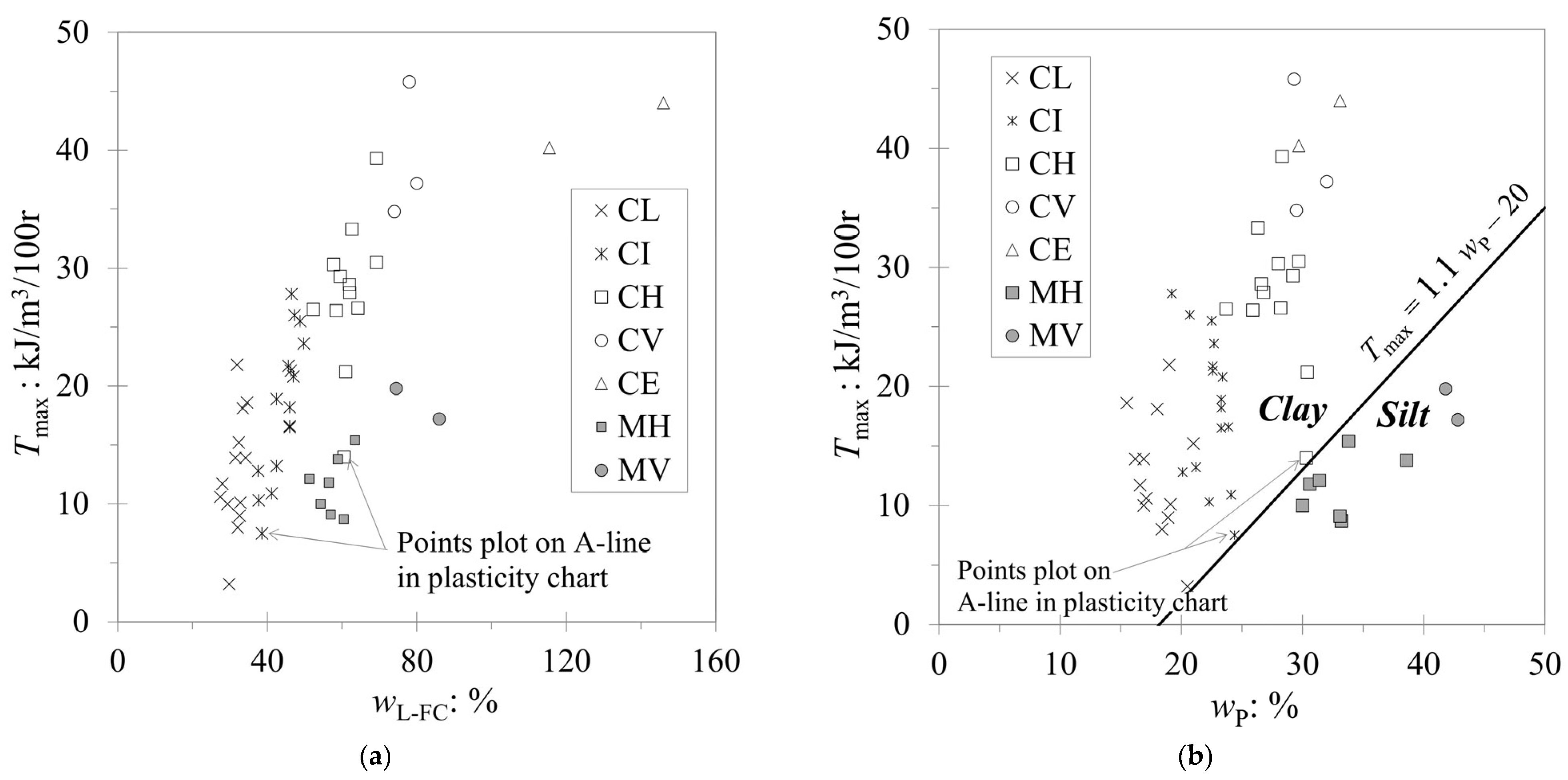
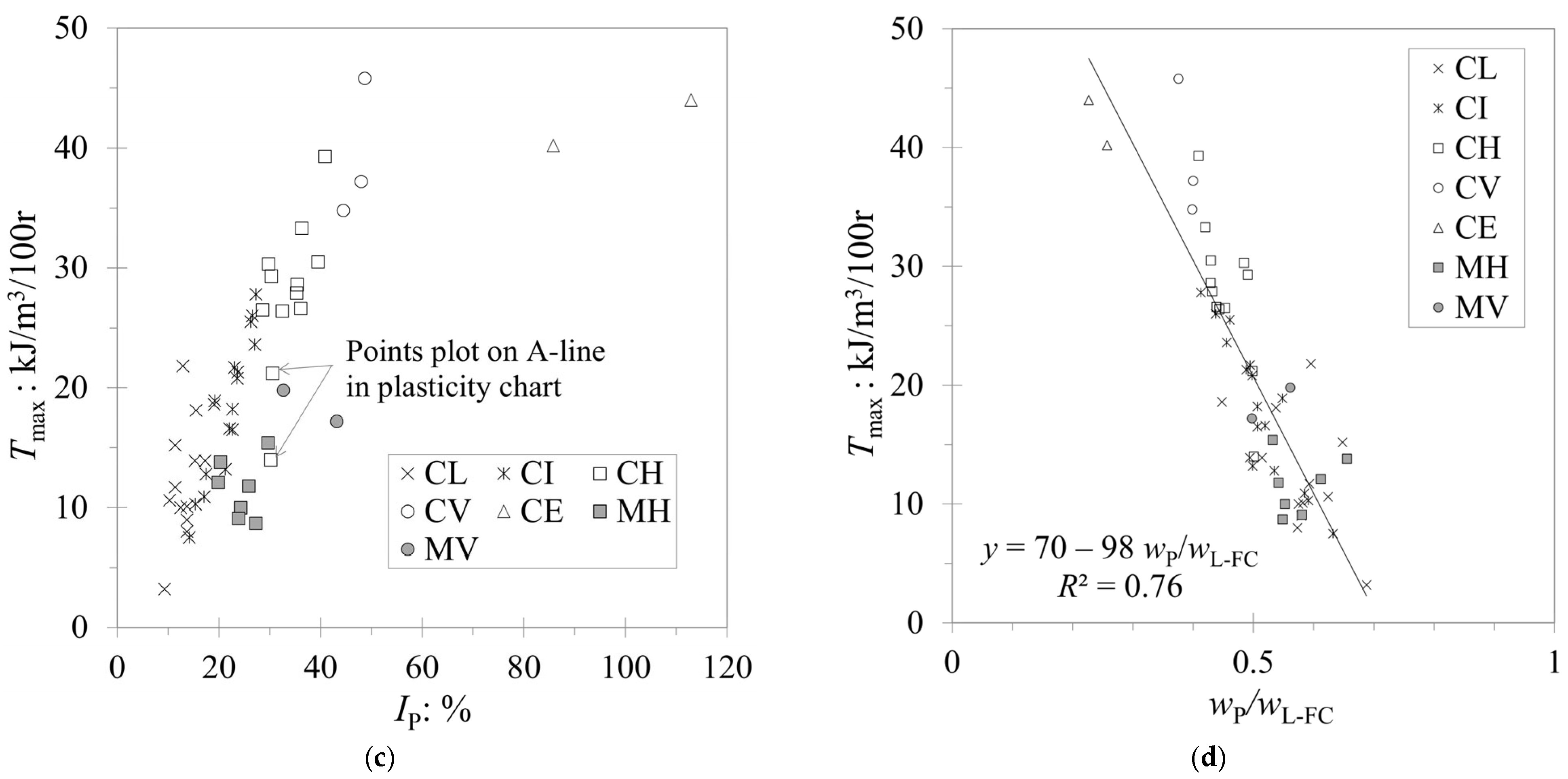
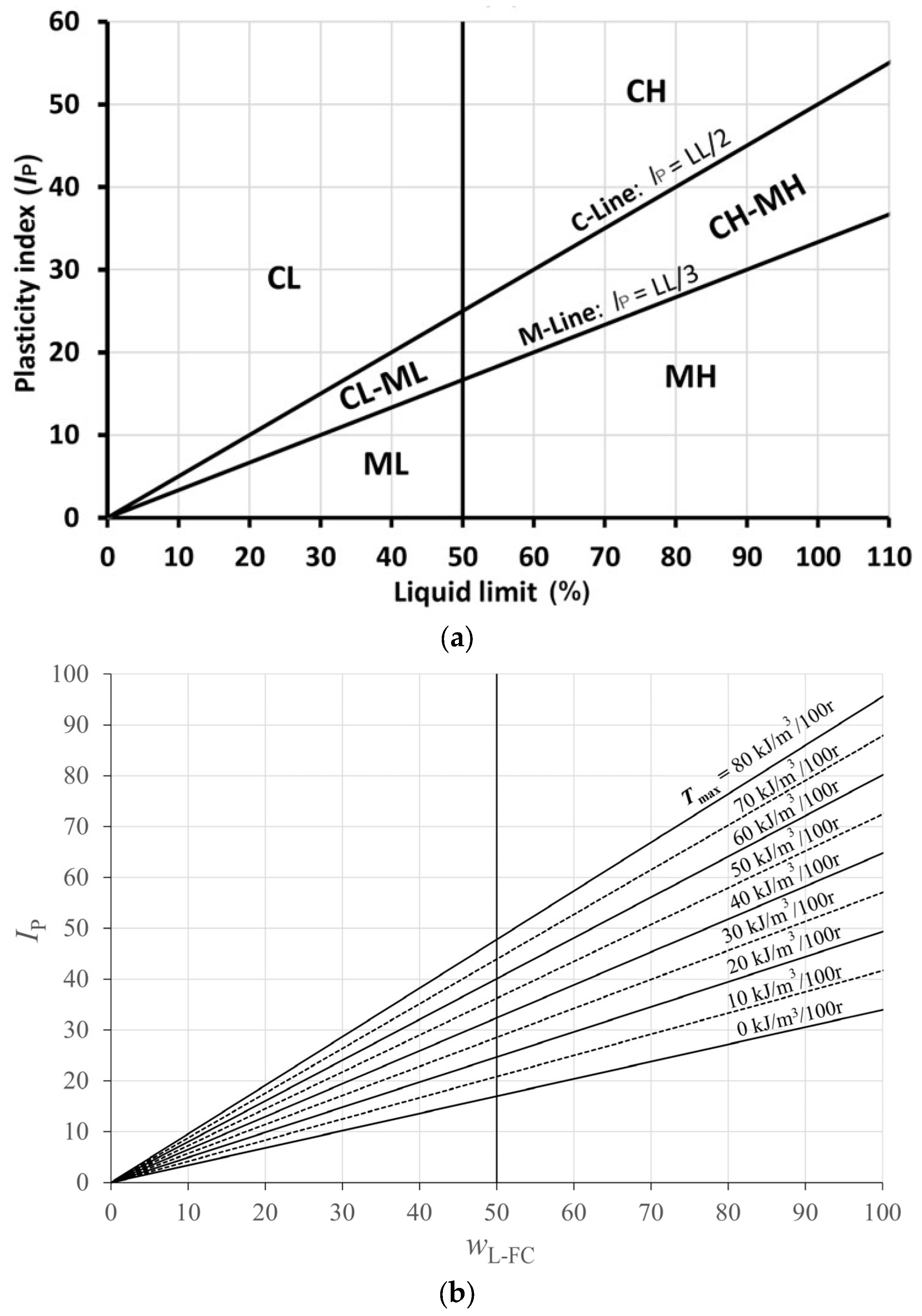
Toughness Classification	Tmax (kJ/m3/100 r)
Very low	<5
Low	5–10
Moderate	10–20
High	20–30
Very high	30–50
Extremely high	>50

, Barnes [17] proposed a tentative classification of soil toughness (from “very low” to “extremely high” toughness) based on assigned ranges of T_max values mobilized at the w_P water content.

Note that Barnes’ definition of and measurement units for soil toughness represent one of many possible ways of quantifying toughness and, therefore, could be viewed as providing relative measures (based on the 100 reversals (i.e., 100 r) definition) of the soil’s toughness properties/characteristics. Barnes could have chosen to base his work calculations on any set number of reversals (e.g., 20 r, 50 r, 120 r, etc.), thereby giving a different definition and hence producing an altered value of T_max for investigating the same fine-grained soil. For instance, compared to the 100 r definition, a greater value of T_max would arise with the toughness calculation defined for a larger number of reversals. From the authors’ viewpoint, if one knows the distance traveled for each reversal during the experimental testing, a possible solution could be to translate those reversals into the distance traveled (in meters), simplifying the measurement units to something like kJ/m⁴, which is the same as kN/m³. Using Barnes’ rolling apparatus, the travel distance in each reversal could be fixed (by the apparatus set-up), or alternatively, it could also be recorded during the testing.

2.2. Proposed Extrusion Approaches

The extrusion method has been recently investigated for the determination of the consistency limits and also possibly of the remolding toughness of fine-grained soils [12,13,28,49,55]. Extrusion involves a reduction in the cross-sectional area of the soil billet (test specimen) by forcing it to flow through a die orifice under the action of a force F_e (extrusion pressure p_e), employing either direct extrusion (DE) or reverse extrusion (RE) approaches [12] (refer to Figure 3). Note, RE is conventionally assumed to require a steady-state p_e (Figure 3d), whereas this is not the case for DE (Figure 3c), which is affected by friction effects at the soil billet–chamber-sidewall interface [12]. Typically, a constant ram/die displacement rate (and hence extrusion velocity of the soil worm) is employed for consistency limits determination and s_u testing. The resulting plot of extrusion force (pressure) against ram/die displacement (Figure 3c,d) can be regarded as the work diagram of extrusion [12].

2.2.1. Extrusion and Remolding Toughness

Based on a reassessment of an extensive RE dataset compiled for many hundreds of different fine-grained soils reported in the existing literature, O’Kelly [12] found that for a given extrusion apparatus with a set die orifice configuration, the p_e value corresponding to the w_P (i.e., p_e(PL)) appeared to show a marginally increasing trend for increasing plasticity (I_P) investigated over a very wide I_P range. Considering that extrusion involves the plastic flow of the test soil, O’Kelly [12] postulated that, whereas s_u is the soil property governing the extrusion resistance capacity for the adhesive plastic region (with zero toughness), when considering the workable soft and stiff plastic regions (i.e., w_P < w < w_T), it is the remolding toughness. Compared with low-plasticity soil, it would follow that for water contents in the workable soft plastic and especially the stiff plastic regions, the superior toughness of fine-grained soils with greater plasticity would require higher ram/die force (i.e., energy) application to produce extrusion. On this basis, the steady-state p_e value mobilized using the RE approach for the workable soft- and stiff-plastic water content ranges would provide a relative measure of the soil toughness (T) [12]. That is, at the same I_L, high values of p_e are needed for tougher soils. Having determined the w_P value for the test soil using the standard thread rolling method [3,4], the associated value of p_e(PL) can then be deduced from the regression analysis of the obtained experimental steady-state p_e—w correlation [12]. To apply this approach for assessing relative values of T_max mobilized between fine-grained soils of different plasticity (toughness) levels, the p_e data employed in the T_max determinations should be for water contents limited to the workable stiff plastic region (w_P < w < w_S), given the characteristic bi-linear nature of the T (p_e)—w relationship [12].

2.2.2. Power-Based Approaches for Consistency Limits Determination

Employing purpose-built DE apparatus, O’Kelly [13] described an investigation of the power concept (i.e., the work undertaken for the extrusion of a known soil volume in a given time period) to potentially determine the consistency limits. Referring to Figure 4, the self-weight of the moving ram assembly applies a constant vertical force (pressure p_e) to the remolded soil sample that initially fills the cylindrical chamber (internally 35 mm dia. × 50 mm deep), causing its downward extrusion to occur via die orifices in the chamber base. This experimental method is analogous to the MFI tester [47,48] approach described in the Introduction, with them both measuring the time period required for the known volume of soil to flow through the die orifice(s) under constant deadweight load action. In other words, for these particular tests, the extrusion process is load/pressure controlled (i.e., not displacement rate controlled). Note that a larger and more complex DE device that essentially follows the same testing methodology as described in [13] is presented by Manafi et al. [49], wherein the power-based extrusion testing approach is termed as a “workability” measurement. O’Kelly [13] hypothesized that the power-based extrusion methodology could potentially serve as an alternative means for the classification of fine-grained soils based on the values of power required to cause extrusion at their w_P water contents.

However, with a given extrusion apparatus and die–orifice combination, the power-based extrusion criterion [13,49] that employs a defined (set) value of power in the determination of the w_P for all inorganic fine-grained soils is fundamentally not correct [9,13,56]. This results from different fine-grained soils invariably having dissimilar values of T_max at their w_p water contents [8,11,12,17,18]. In other words, with the extrusion rate varying according to the soil toughness (e.g., [47]), tougher soils would take longer to flow through the die orifice(s) and, therefore, they would require relatively lower power inputs to cause soil extrusion, and vice versa. The power-based extrusion criterion could be validly applied for the determination of the w_L, as it is defined based on a small (measurable) s_u value (e.g., [19,20,21]), with the experimental p_e for the adhesive plastic region related to the soils’ s_u [12]. However, the w_L can already be reliably determined, e.g., using the simpler fall-cone liquid limit method [4,19,56].

3. Quantitative Assessment of T_max (after Moreno-Maroto and Alonso-Azcárate [11])

As the consistency limits are strongly dependent on the soil mineralogical properties (of the clay fraction) [19], it would be expected for T_max to correlate with the values of w_L, w_P, and hence I_P. Direct experimental measurements of soil remolding toughness were reported by Barnes [8] for 59 inorganic fine-grained soils, including natural clays, brick and ceramic clays, and for different mixtures of clay, silt, and sand materials with pure kaolinite and montmorillonite samples, with these test soils encompassing a very wide range of plasticity/toughness characteristics. Extracting Barnes’ [8] reported data of T_max, the fall cone w_L (i.e., w_L-FC, as obtained using the 80 g/30° fall cone device [4]) and I_P (= w_L-FC − w_P), Moreno-Maroto and Alonso-Azcárate [11] plotted the I_P/w_L-FC ratio against T_max for the 59 investigated soils (Figure 5). In this analysis, they choose the I_P/w_L (I_P/w_L-FC) ratio as it relates to the I_P against w_L plot form of the traditional Casagrande plasticity chart. A good correlation was found between I_P/w_L-FC and T_max (Equation (3) and Figure 5). In particular, based solely on consistency limits measurements, Equation (3) provides a simple means of identifying those fine-grained soils with measurable remolding toughness and then estimating their values of T_max (as defined for Barnes’ thread rolling apparatus in units of kJ/m³/100 r):

$$\frac{I_{\mathrm{P}}}{w_{\mathrm{L}-\mathrm{FC}}}=0.0077 T_{\max }+0.3397 (n=59, R^2=0.76)$$

(3)

4. Correlating T_max with the Consistency Limits

Using tabulated data presented for inorganic fine-grained soils reported on pages 187–191 of Barnes [8], this section investigates new correlations between the consistency limits and T_max (Figure 6). As expected, there are clear trends of T_max increasing overall for increasing w_L-FC, w_P, and I_P (Figure 6a–c), with the clay soils mobilizing significantly greater toughness than the silt soils. Compared to the data plot against I_P (Figure 6c), there appears to be a strong demarcation between clay and silt evident for plotting the data in the T_max versus w_P chart of Figure 6b. The authors have included a tentative demarcation line (i.e., T_max = 1.1 × w_P − 20) in Figure 6b for distinguishing between clay and silt soils, whose original classification, as reported in Barnes [8], was based on the Casagrande plasticity chart. As indicated in Figure 6c, the decision on the positioning of the clay–silt demarcation line in the T_max versus w_P chart was aided by the fact that, when the data were plotted in the Casagrande plasticity chart, three of the investigated soils were plotted on the A-line boundary. Figure 6d presents a plot of T_max against the w_P/w_L-FC ratio, termed the “plasticity ratio” by Shimobe and Spagnoli [57]. They showed that the w_P/w_L ratio inversely correlates with SSA, which is consistent with greater remolding toughness for increasing SSA [10]. From an inspection of Figure 6d, with an increasing plasticity class level from CL to CE, the value of T_max reduces due to the increasing w_P/w_L-FC ratio, according to Equation (4):

T_max = 70 − 98 × w_P/w_L-FC (n = 55, R² = 0.76)

(4)

5. Distinguishing between Clay and Silt Soils Based on the Value of T_max

Based on Equations (3) and (4), there is a real influence of the clay mineral content on soil toughness for w_P/w_L-FC < 0.71 and I_P/w_L-FC > 0.3397 (i.e., ~0.33), with T_max > 0 kJ/m³/100 r mobilized. Conversely, considering that plasticity (toughness) is a property exclusive to clayey materials [14], this means fine-grained soils cannot be considered as clay for w_P/w_L-FC > 0.71 or I_P/w_L-FC ≤ 0.33 (i.e., Equations (3) and (4) give a computed T_max = 0); that is, those inorganic soils would have no workable soft- and stiff-plastic water content ranges. Owing to their lack of toughness, silts and sandy soils produce low plasticity results, only requiring slight finger pressure to be applied during the rolling out of the soil threads for w_P determination, and they also do not present the typical sticky consistency of clays, while non-plastic soils can be considered as materials with an I_P/w_L (I_P/w_L-FC) ratio < 0.1896 (rounded to 0.2) [11]. Relying on Barnes’ toughness classification (see Table 1), “high”, “very high”, and “extremely high” plasticity clay should mobilize a value of T_max ≥ 20 kJ/m³/100 r, which, according to Equation (3), corresponds to I_P/w_L-FC ≥ 0.4937 (i.e., ~0.5). Hence, Moreno-Maroto and Alonso-Azcárate [11] concluded that those fine-grained soils with clay minerals present but which do not exert a significant influence on plasticity would exhibit I_P/w_L-FC ratios of between 0.33 and 0.5.

6. Toughness-Based Classification of Fine-Grained Soils

Soil classification using the Casagrande plasticity chart is not entirely accurate, being inefficient in discerning toughness, e.g., some soils with high toughness (typical of clay) can be incorrectly classified as silt, and vice versa [50]. This observation supports a toughness-based soil classification to augment (or be used instead of) the Casagrande plasticity chart in obtaining more reliable soil classification for some hitherto challenging fine-grained soil types.

Based on fundamental experimental observations described in the previous section and directly connecting plasticity with toughness, Moreno-Maroto and Alonso-Azcárate [11] proposed an updated soil plasticity classification method in which the determining factor is toughness. For measured w_L-FC and I_P, the soil is non-plastic for I_P/w_L-FC < 0.2 and low plastic for 0.2 ≤ I_P/w_L-FC ≤ 0.33 (i.e., silt, organic soil, sandy soil, etc., with computed T_max of ~ 0 kJ/m³/100 r). Soil with a low or moderate influence of clay minerals (i.e., clayey silt, sandy clay, etc., whose T_max < 20 kJ/m³/100 r) has 0.33 < I_P/w_L-FC < 0.5, while clay (i.e., plastic soil with T_max ≥ 20 kJ/m³/100 r) has I_P/w_L-FC ≥ 0.5 [11]. The developed soil classification chart of Moreno-Maroto and Alonso-Azcárate [11] is presented in Figure 7a. Moreno-Maroto et al. [50] investigated the correctness of soil classifications assigned to 31 different inorganic fine-grained soils by applying six of the main plasticity-based soil classification proposals (charts), including the Moreno-Maroto and Alonso-Azcárate [11] and Casagrande plasticity charts, with their research results ranking the Moreno-Maroto and Alonso-Azcárate [11] chart (Figure 7a) as having the strongest predictive capacity among the examined proposals.

An original contribution of the present paper is the chart presented in Figure 7b, which provides a simple and expedient way of estimating the value of T_max from the measured consistency limits values. Taking into account Equation (3), Figure 7b was produced by calculating the T_max isolines (of 0 to 80 kJ/m³/100 r) and then plotted them in the typical plasticity chart (of I_P vs. w_L-FC).

7. Advantages/Limitations of the Existing Methods for Toughness Determination

In the preceding sections, four different approaches were highlighted as the fundamental ones for soil toughness assessment/determination: i.e., manual rolling of soil threads [3,4,40,41], Barnes’ thread rolling apparatus [8,17,18], extrusion approaches [12,13,46,47,48,49], and via various correlations deduced in the present paper and reported in [11] between the consistency limits and values of Barnes’ T_max. Their advantages and disadvantages are summarized in

Table 2. Advantages and weaknesses of the main methods employed for soil toughness determination. Note: w_L, liquid limit; w_P, plastic limit; T_max, maximum remolding toughness (mobilized at w_P).

Method	Type	Advantage	Weakness
Manual thread rolling [3,4,41]	Direct	Meets original definition of toughness.	Qualitative (does not allow obtaining numerical values). Subjectivity; high operator dependence.
Barnes’ thread rolling apparatus [8,17,18]	Direct	Meets original definition of toughness. Objectivity (mechanically determined).	According to [50]: relatively complex measurement approach; slowness (many experimental points required); great skill on operator’s part to reach value of Tmax.
Extrusion [12,13,46,47,48,49]	Indirect	Objectivity (mechanically determined). Good correlation between extrusion resistance and toughness [12,13,46,47].	Non-standardized (features of extruder device and extrusion conditions may give different results). Equipment cost.
Estimation from consistency limits ([11], this paper)	Indirect	wL and wP obtained using standardized and widely known methods. Good correlation with Barnes’ values of Tmax. Speed and low cost.	Of the parameters associated with consistency limits, only the wP test meets toughness definition. Based on estimates according to statistical criteria, outliers may not fit estimated values.

. Manual and mechanical thread rolling are classed as direct methods as they conform to the definition of toughness and the original protocol for its determination.

Considering their various advantages and weaknesses, as listed in Table 2, it is not a simple task to determine which of these four approaches may prove to be the more effective for toughness determination. When the aim is to get accurate results, the use of relatively complex measurement devices, such as Barnes’ thread rolling and various extrusion apparatuses, seems to be a good alternative, particularly the Barnes’ approach, as it is a direct method. However, along with associated equipment costs and complexity, these mechanized methods can present certain operational disadvantages during the testing, as well as a long test duration with associated time/cost implications. On the other hand, manual thread rolling would be the simplest and fastest of all four approaches and the one that most closely approximates the original definition of toughness. However, being qualitative, subjective, and hence highly dependent on the operator’s performance [25,33], the manual thread rolling approach is deemed not suitable when trying to get quantitative and precise results. Therefore, the statistical approximations obtained via consistency limits results (e.g., [11]) do seem to find a balance with what has been said previously, with the obtained toughness predictions conforming satisfactorily to the actual T_max values measured for dozens of different fine-grained soils investigated by Barnes [8,17,18]. Given that the consistency limits are basic index tests performed on fine-grained soils, the use of their parameters for obtaining T_max estimations does not entail any additional testing cost or time (i.e., from the authors’ perspective, the purpose of soil toughness determination is not to replace the ubiquitous consistency limits testing used to obtain w_L and w_P). As it is based on statistical criteria, probably one weakness of this approach is that it could potentially give erroneous T_max predictions for soils with atypical behavior. In this regard, the authors consider that the observations of an experienced operator in judging the relative force and effort required to form and roll out uniform soil cylinders for the thread rolling test method would serve as quality control of the mathematical T_max estimation. Therefore, continued use of standard consistency limits testing along with the estimation of T_max via correlations with I_P/w_L-FC or w_P/w_L-FC (i.e., using Equations (3) and (4)) is judged as the most satisfactory option.

8. Recommendations on Future Research Efforts for Soil Toughness Determination

The authors’ recommendations for future research work on the topic include investigations of soil remolding toughness employing (i) the MFI apparatus and testing approach [47,48] and (ii) the moisture condition test and obtained MCV results [45]. As described earlier in the paper, the MFI tester measures the time period required for a known soil volume to flow through a die orifice under a constant deadweight load action. The mobilized toughness for a particular fine-grained soil (and water content) is related to the flow time (soil extrusion rate), with tougher materials taking longer periods [47]. For the moisture condition test, tougher soils (and for lower water content) give higher MCVs, as more compaction effort is needed to remold the lumps of clay in performing the testing, with Barnes [8] envisaging that the MCV should correlate satisfactorily with the values of toughness. As such, increased research efforts should be directed toward investigating the MFI and/or moisture condition tester for soil toughness determination. Other ways of soil classification, based on remolding toughness parameters or incorporating the concept to complement existing plasticity-based classification systems, also merit investigation for obtaining more reliable soil classification when investigating some hitherto challenging fine-grained soil types.

9. Summary and Conclusions

This review paper covered the basic index (i.e., Atterberg/consistency limits) testing of fine-grained soil, the fundamental understanding of soil plasticity and remolding-toughness properties, and their determination/measurement and use in the classification of fine-grained soils. Plasticity and toughness properties can be used to distinguish plastic soils that provide greater deformation resistance for various field applications. The maximum remolding toughness T_max correlates well to the consistency limits parameters, particularly with the I_P/w_L and w_P/w_L ratios, and the presented Equations (3) and (4) allow indirect T_max estimations via these ratios from consistency limits measurements for fine-grained soils. Being inefficient in discerning toughness, soil classification using the traditional Casagrande plasticity chart system is not entirely accurate (e.g., some soils with high toughness can be incorrectly classified as silt, something typical of clay, and vice versa). As part of the original research work in the present paper, a strong demarcation between clay and silt soils was found in the plot of T_max against w_P for 59 dissimilar fine-grained soils (Figure 6b), giving a more mechanical perspective to soil classification. A new toughness chart, in which the presented T_max isolines were deduced via correlations with the consistency limits parameters (i.e., using Equations (3) and (4)), was introduced as a graphical and simple way to estimate the tenacity of fine-grained soils. This chart, with the inclusion of the demarcation zones of I_P/w_L-FC ≤ 0.33 for silt (ML, MH), I_P/w_L-FC ≥ 0.5 for clay (CL, CH), and 0.33 < I_P/w_L-FC < 0.5 for intermediate soils (0.33 < I_P/w_L-FC < 0.5), augments (or can be used instead of) the Casagrande plasticity chart for obtaining more reliable soil classification. Various useful toughness coefficients and indices can be measured using Barnes’ thread rolling apparatus and method, but this approach is relatively complex and time-consuming. Accordingly, the less complicated and quicker MFI and moisture condition test approaches are recommended for future research investigations in regard to obtaining routine soil toughness measurements.