Wave-Shaped Microstructure Cancer Detection Sensor in Terahertz Band: Design and Analysis
Abstract
:1. Introduction
2. Numerical Analysis
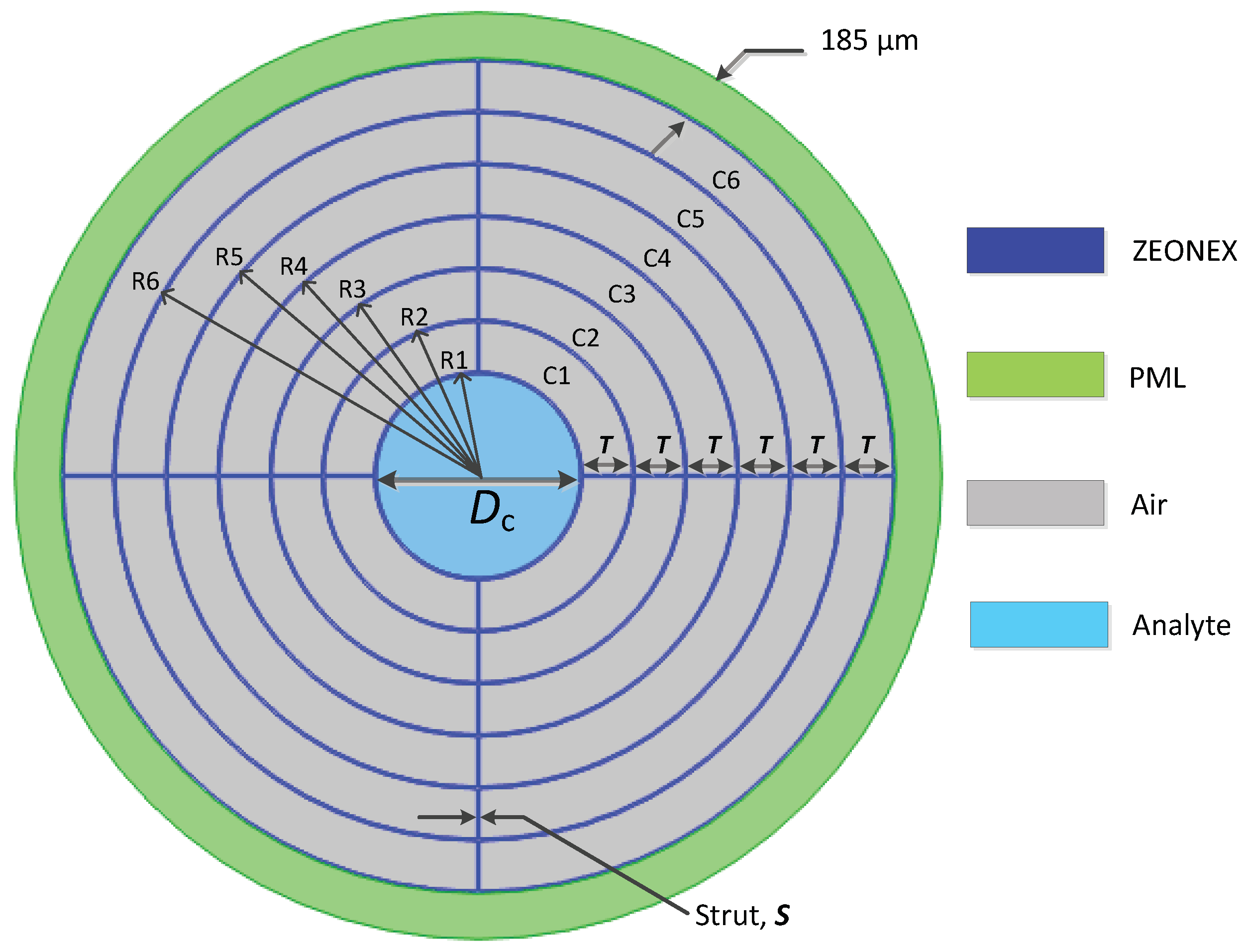
3. Detail Design of the Proposed HC-PCF
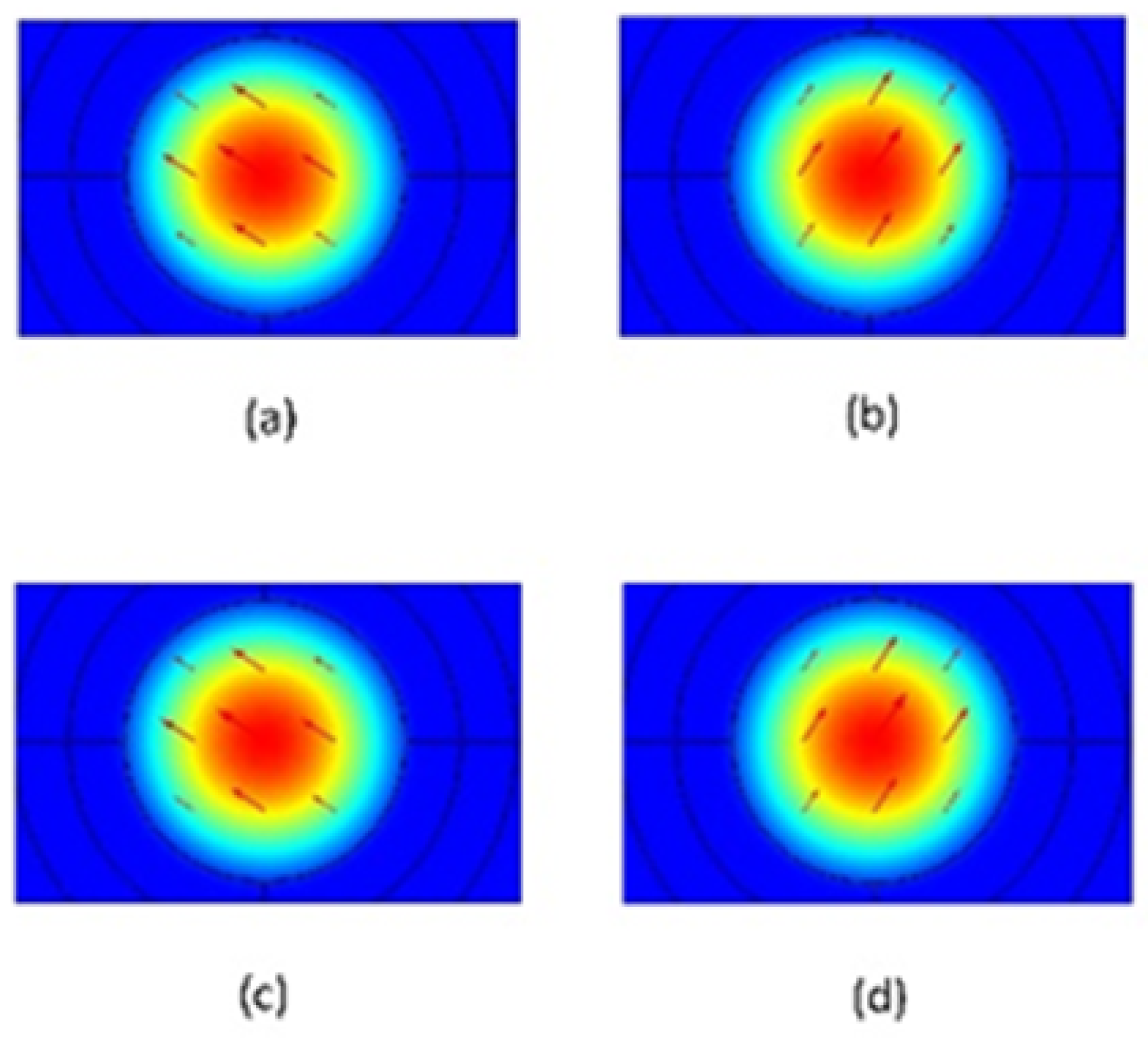
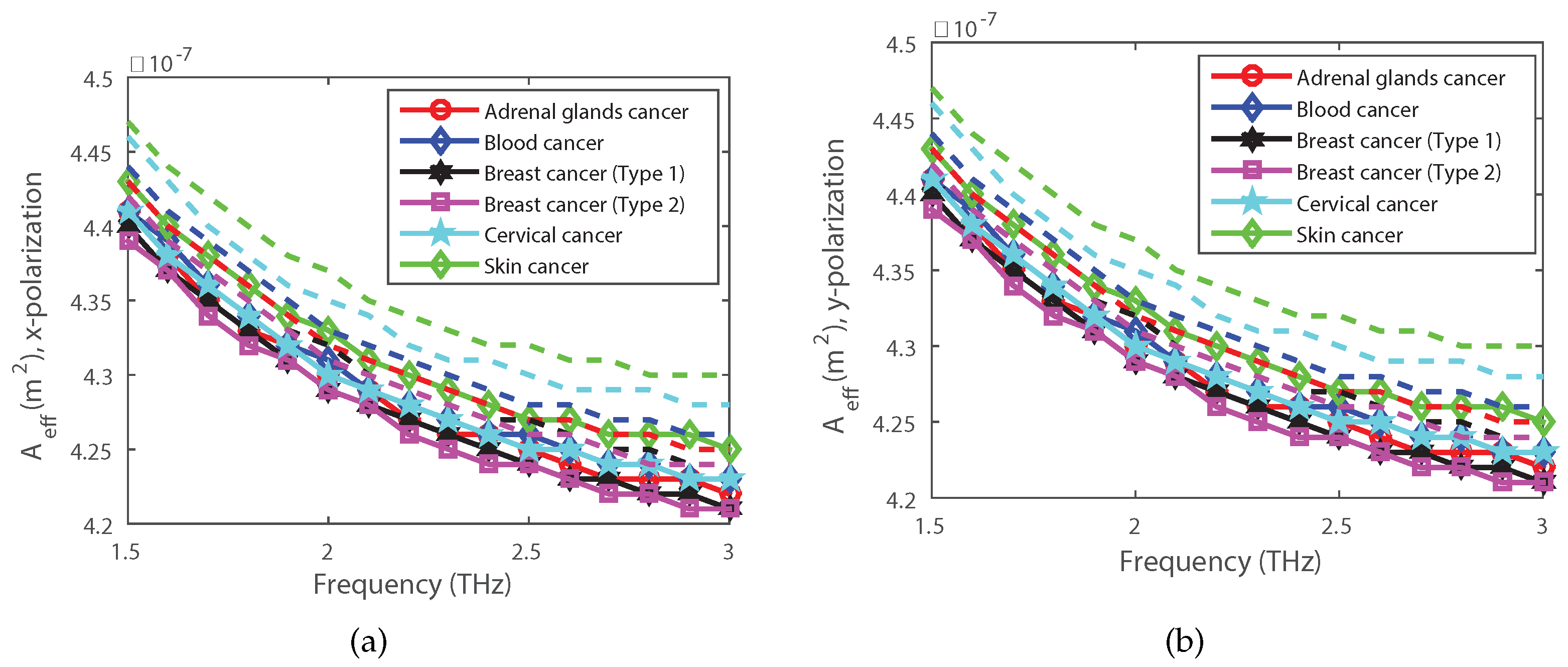
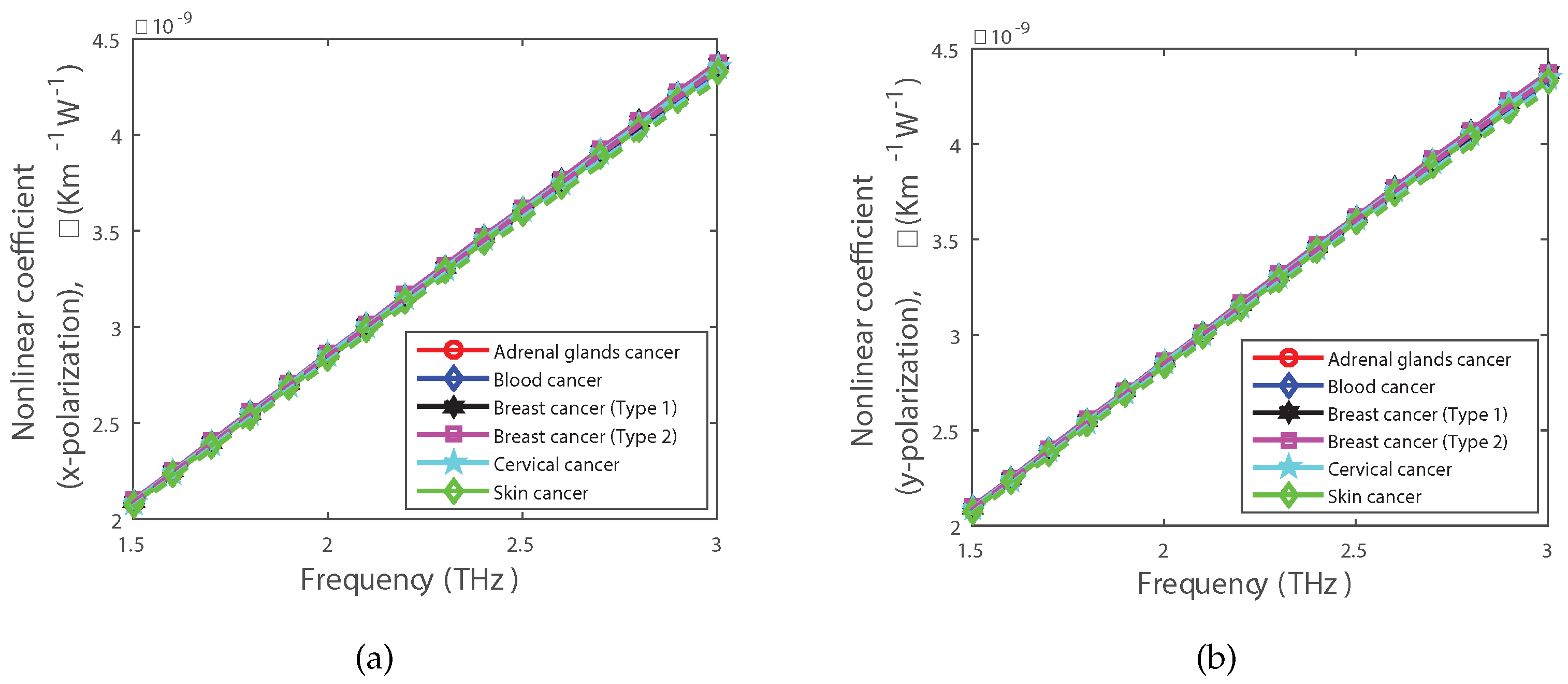
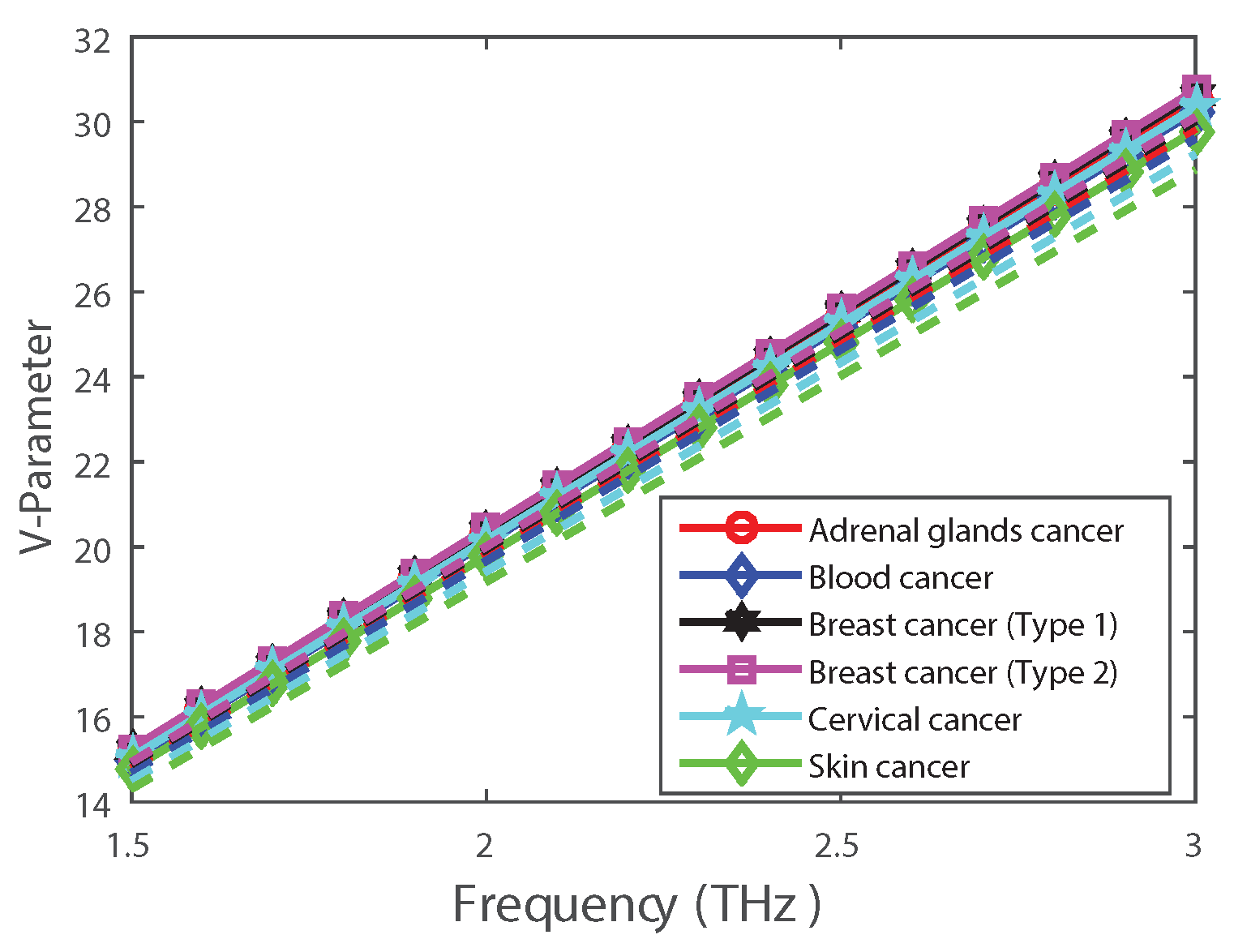
4. Simulation Results and Discussions
5. Fabrication of the Proposed HC-PCF
6. Application Possibilities of the Proposed HC-PCF
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kumar, P.; Kumar, V.; Roy, J.S. Design of quad core photonic crystal fibers with flattened zero dispersion. AEU Int. J. Electron. Commun. 2019, 98, 265–272. [Google Scholar] [CrossRef]
- Kumar, C.S.; Anbazhagan, R. Investigation on chalcogenide and silica based photonic crystal fibers with circular and octagonal core. AEU Int. J. Electron. Commun. 2017, 72, 40–45. [Google Scholar] [CrossRef]
- Saitoh, K.; Koshiba, M. Single-polarization single-mode photonic crystal fibers. IEEE Photonics Technol. Lett. 2003, 15, 1384–1386. [Google Scholar] [CrossRef]
- Buczynski, R. Photonic crystal fibers. Acta Phys. Pol. Ser. A 2004, 106, 141–168. [Google Scholar] [CrossRef]
- Russell, P.S.J. Photonic-crystal fibers. J. Light. Technol. 2006, 24, 4729–4749. [Google Scholar] [CrossRef]
- Folkenberg, J.R.; Nielsen, M.D.; Mortensen, N.; Jakobsen, C.; Simonsen, H.R. Polarization maintaining large mode area photonic crystal fiber. Opt. Express 2004, 12, 956–960. [Google Scholar] [CrossRef]
- Chen, M.Y. Polarization-maintaining large-mode-area photonic crystal fibres with solid microstructured cores. J. Opt. Pure Appl. Opt. 2007, 9, 868. [Google Scholar] [CrossRef]
- Sultana, J.; Islam, M.S.; Faisal, M.; Islam, M.R.; Ng, B.W.H.; Ebendorff-Heidepriem, H.; Abbott, D. Highly birefringent elliptical core photonic crystal fiber for terahertz application. Opt. Commun. 2018, 407, 92–96. [Google Scholar] [CrossRef]
- Sultana, J.; Islam, M.R.; Faisal, M.; Talha, K.M.A.; Islam, M.S. Design and analysis of a Zeonex based diamond-shaped core kagome lattice photonic crystal fiber for T-ray wave transmission. Opt. Fiber Technol. 2019, 47, 55–60. [Google Scholar] [CrossRef]
- Paul, B.K.; Ahmed, K. Highly birefringent TOPAS based single mode photonic crystal fiber with ultra-low material loss for Terahertz applications. Opt. Fiber Technol. 2019, 53, 102031. [Google Scholar] [CrossRef]
- Goto, M.; Quema, A.; Takahashi, H.; Ono, S.; Sarukura, N. Teflon photonic crystal fiber as terahertz waveguide. Jpn. J. Appl. Phys. 2004, 43, L317. [Google Scholar] [CrossRef]
- Hossain, S.; Mollah, A.; Hosain, K.; Ankan, I.M. THz spectroscopic sensing of liquid chemicals using hollow-core anti-resonant fiber. OSA Contin. 2021, 4, 621–632. [Google Scholar] [CrossRef]
- Lanza, R.; Gearhart, J.; Hogan, B.; Melton, D.; Pedersen, R.; Thomas, E.D.; Thomson, J.A. Essentials of Stem Cell Biology; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global cancer statistics 2020: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef]
- Einhorn, L.H. Testicular cancer as a model for a curable neoplasm: The Richard and Hinda Rosenthal Foundation Award Lecture. Cancer Res. 1981, 41, 3275–3280. [Google Scholar] [PubMed]
- Cuzick, J.; Powles, T.; Veronesi, U.; Forbes, J.; Edwards, R.; Ashley, S.; Boyle, P. Overview of the main outcomes in breast-cancer prevention trials. Lancet 2003, 361, 296–300. [Google Scholar] [CrossRef] [PubMed]
- Dressing, G.E.; Thomas, P. Identification of membrane progestin receptors in human breast cancer cell lines and biopsies and their potential involvement in breast cancer. Steroids 2007, 72, 111–116. [Google Scholar] [CrossRef]
- Tajima, K.; Obata, Y.; Tamaki, H.; Yoshida, M.; Chen, Y.T.; Scanlan, M.J.; Old, L.J.; Kuwano, H.; Takahashi, T.; Takahashi, T.; et al. Expression of cancer/testis (CT) antigens in lung cancer. Lung Cancer 2003, 42, 23–33. [Google Scholar] [CrossRef]
- Glunde, K.; Bhujwalla, Z.M. Metabolic tumor imaging using magnetic resonance spectroscopy. Semin. Oncol. 2011, 38, 26–41. [Google Scholar] [CrossRef]
- Furusawa, Y.; Fujiwara, Y.; Campbell, P.; Zhao, Q.L.; Ogawa, R.; Ali Hassan, M.; Tabuchi, Y.; Takasaki, I.; Takahashi, A.; Kondo, T. DNA double-strand breaks induced by cavitational mechanical effects of ultrasound in cancer cell lines. PLoS ONE 2012, 7, e29012. [Google Scholar] [CrossRef]
- Clark, L.C., Jr.; Lyons, C. Electrode systems for continuous monitoring in cardiovascular surgery. Ann. N. Y. Acad. Sci. 1962, 102, 29–45. [Google Scholar] [CrossRef]
- Parvin, T.; Ahmed, K.; Alatwi, A.M.; Rashed, A.N.Z. Differential optical absorption spectroscopy-based refractive index sensor for cancer cell detection. Opt. Rev. 2021, 28, 134–143. [Google Scholar] [CrossRef]
- Habib, A.; Rashed, A.N.Z.; El-Hageen, H.M.; Alatwi, A.M. Extremely Sensitive Photonic Crystal Fiber–Based Cancer Cell Detector in the Terahertz Regime. Plasmonics 2021, 16, 1297–1306. [Google Scholar] [CrossRef]
- Eid, M.; Rashed, A.N.Z.; Bulbul, A.A.M.; Podder, E. Mono-rectangular core photonic crystal fiber (MRC-PCF) for skin and blood cancer detection. Plasmonics 2021, 16, 717–727. [Google Scholar] [CrossRef]
- Bulbul, A.A.M.; Rahaman, H.; Podder, E. Design and quantitative analysis of low loss and extremely sensitive PCF-based biosensor for cancerous cell detection. Opt. Quantum Electron. 2022, 54, 1–16. [Google Scholar] [CrossRef]
- Yadav, S.; Singh, S.; Lohia, D.; Umar, P.; Dwivedi, D.K. Computational Study of a Photonic Crystal Fiber-Based Biosensor for Detection of Breast Cancer Cells in the THz Regime. SSRN Electron. J. 2022, 33, 34. [Google Scholar] [CrossRef]
- Khan, M.R.H.; Ali, F.A.M.; Islam, M.R. THz sensing of CoViD-19 disinfecting products using photonic crystal fiber. Sens. Bio Sens. Res. 2021, 33, 100447. [Google Scholar] [CrossRef]
- Sultana, J.; Islam, M.S.; Ahmed, K.; Dinovitser, A.; Ng, B.W.H.; Abbott, D. Terahertz detection of alcohol using a photonic crystal fiber sensor. Appl. Opt. 2018, 57, 2426–2433. [Google Scholar] [CrossRef]
- Islam, M.S.; Paul, B.K.; Ahmed, K.; Asaduzzaman, S.; Islam, M.I.; Chowdhury, S.; Sen, S.; Bahar, A.N. Liquid-infiltrated photonic crystal fiber for sensing purpose: Design and analysis. Alex. Eng. J. 2018, 57, 1459–1466. [Google Scholar] [CrossRef]
- Arumugam, R.; Babu, P.R.; Senthilnathan, K. Designing a dual steering wheel microstructured blood components sensor in terahertz wave band. Opt. Eng. 2020, 59, 047104. [Google Scholar]
- Fischer, B.; Hoffmann, M.; Helm, H.; Modjesch, G.; Jepsen, P.U. Chemical recognition in terahertz time-domain spectroscopy and imaging. Semicond. Sci. Technol. 2005, 20, S246. [Google Scholar] [CrossRef]
- Islam, M.S.; Sultana, J.; Rifat, A.A.; Dinovitser, A.; Ng, B.W.H.; Abbott, D. Terahertz sensing in a hollow core photonic crystal fiber. IEEE Sens. J. 2018, 18, 4073–4080. [Google Scholar] [CrossRef]
- Sabri, N.; Aljunid, S.; Salim, M.; Ahmad, R.B.; Kamaruddin, R. Toward optical sensors: Review and applications. J. Physics Conf. Ser. 2013, 423, 012064. [Google Scholar] [CrossRef]
- Rahman, M.M.; Mou, F.A.; Bhuiyan, M.I.H.; Mahmud, M.A.A.; Islam, M.R. Design and characterization of a photonic crystal fiber for improved THz wave propagation and analytes sensing. Opt. Quantum Electron. 2022, 54, 669. [Google Scholar] [CrossRef]
- Bise, R.T.; Trevor, D.J. Sol-gel derived microstructured fiber: Fabrication and characterization. In Proceedings of the Optical Fiber Communication Conference, Anaheim, CA, USA, 6–11 March 2005; p. OWL6. [Google Scholar]
- Jabin, M.A.; Ahmed, K.; Rana, M.J.; Paul, B.K.; Islam, M.; Vigneswaran, D.; Uddin, M.S. Surface plasmon resonance based titanium coated biosensor for cancer cell detection. IEEE Photonics J. 2019, 11, 1–10. [Google Scholar] [CrossRef]
- Asaduzzaman, S.; Ahmed, K.; Bhuiyan, T.; Farah, T. Hybrid photonic crystal fiber in chemical sensing. SpringerPlus 2016, 5, 1–11. [Google Scholar] [CrossRef] [PubMed]
- El Hamzaoui, H.; Ouerdane, Y.; Bigot, L.; Bouwmans, G.; Capoen, B.; Boukenter, A.; Girard, S.; Bouazaoui, M. Sol-gel derived ionic copper-doped microstructured optical fiber: A potential selective ultraviolet radiation dosimeter. Opt. Express 2012, 20, 29751–29760. [Google Scholar] [CrossRef]
- Dabas, B.; Sinha, R. Dispersion characteristic of hexagonal and square lattice chalcogenide As2Se3 glass photonic crystal fiber. Opt. Commun. 2010, 283, 1331–1337. [Google Scholar] [CrossRef]
- Kumar, V.R.K.; George, A.; Reeves, W.; Knight, J.; Russell, P.S.J.; Omenetto, F.; Taylor, A. Extruded soft glass photonic crystal fiber for ultrabroad supercontinuum generation. Opt. Express 2002, 10, 1520–1525. [Google Scholar] [CrossRef]
- El-Amraoui, M.; Gadret, G.; Jules, J.; Fatome, J.; Fortier, C.; Désévédavy, F.; Skripatchev, I.; Messaddeq, Y.; Troles, J.; Brilland, L.; et al. Microstructured chalcogenide optical fibers from As 2 S 3 glass: Towards new IR broadband sources. Opt. Express 2010, 18, 26655–26665. [Google Scholar] [CrossRef]
- Talataisong, W.; Ismaeel, R.; Sandoghchi, S.R.; Rutirawut, T.; Topley, G.; Beresna, M.; Brambilla, G. Novel method for manufacturing optical fiber: Extrusion and drawing of microstructured polymer optical fibers from a 3D printer. Opt. Express 2018, 26, 32007–32013. [Google Scholar] [CrossRef]
- Atakaramians, S.; Afshar, S.; Ebendorff-Heidepriem, H.; Nagel, M.; Fischer, B.M.; Abbott, D.; Monro, T.M. THz porous fibers: Design, fabrication and experimental characterization. Opt. Express 2009, 17, 14053–14062. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Tam, H.Y. Fabrication and sensing applications of special microstructured optical fibers. In Selected Topics on Optical Fiber Technologies and Applications; Xu, F., Mou, C., Eds.; Intechopen: London, UK, 2017; pp. 1–20. [Google Scholar]
- Pysz, D.; Kujawa, I.; Stępień, R.; Klimczak, M.; Filipkowski, A.; Franczyk, M.; Kociszewski, L.; Buźniak, J.; Haraśny, K.; Buczyński, R. Stack and draw fabrication of soft glass microstructured fiber optics. Bull. Pol. Acad. Sci. Tech. Sci. 2014, 62, 667–682. [Google Scholar] [CrossRef]
- Cruz, A.L.; Cordeiro, C.; Franco, M.A. 3D printed hollow-core terahertz fibers. Fibers 2018, 6, 43. [Google Scholar] [CrossRef]
- Pysz, D.; Stepien, R.; Kujawa, I.; Kasztelanic, R.; Martynkien, T.; Berghmans, F.; Thienpont, H.; Buczynski, R. Development of silicate hollow core photonic crystal fiber. Photonics Lett. Pol. 2010, 2, 7–9. [Google Scholar]
- Mitrofanov, A.V.; Linik, Y.M.; Buczynski, R.; Pysz, D.; Lorenc, D.; Bugar, I.; Ivanov, A.A.; Alfimov, M.V.; Fedotov, A.B.; Zheltikov, A.M. Highly birefringent silicate glass photonic-crystal fiber with polarization-controlled frequency-shifted output: A promising fiber light source for nonlinear Raman microspectroscopy. Opt. Express 2006, 14, 10645–10651. [Google Scholar] [CrossRef] [PubMed]
- Russell, P. Photonic Crystal Fibers. Science 2003, 299, 358–362. [Google Scholar] [CrossRef]
- Islam, M.R.; Iftekher, A.; Noor, F.; Khan, M.R.H.; Reza, M.; Nishat, M.M. AZO-coated plasmonic PCF nanosensor for blood constituent detection in near-infrared and visible spectrum. Appl. Phys. A 2022, 128, 1–13. [Google Scholar] [CrossRef]
- Hossain, M.B.; Podder, E. Design and investigation of PCF-based blood components sensor in terahertz regime. Appl. Phys. A 2019, 125, 1–8. [Google Scholar] [CrossRef]
- Sokullu, E.; Cücük, Z.L.; Sarabi, M.R.; Birtek, M.T.; Bagheri, H.S.; Tasoglu, S. Microfluidic invasion chemotaxis platform for 3D neurovascular Co-culture. Fluids 2022, 7, 238. [Google Scholar] [CrossRef]
- Rezapour Sarabi, M.; Nakhjavani, S.A.; Tasoglu, S. 3D-Printed microneedles for point-of-care biosensing applications. Micromachines 2022, 13, 1099. [Google Scholar] [CrossRef]









| Cancer Type | Cell Type | RI of Normal Cell (Concentration Range 30–70%) | RI of Cancerous Cell (Concentration Range 80%) |
|---|---|---|---|
| Breast (type 1) | MBA-MD-231 | 1.385 | 1.399 |
| Breast (type 2) | MCF-7 | 1.387 | 1.401 |
| Blood | Jurkat | 1.376 | 1.39 |
| Skin | Basal | 1.36 | 1.38 |
| Cervical | HeLA | 1.368 | 1.392 |
| Adrenal glands | PC-12 | 1.381 | 1.395 |
| Ref. | Cancer Cell | Frequency /Wavelength | RS (%) | CL (dB/cm) | EML (cm) | EA (m) | B |
|---|---|---|---|---|---|---|---|
| [22] | Blood | 2.5 THz | 94.84 | - | - | - | |
| Adrenal Gland | 2.5 THz | 95.15 | - | - | - | ||
| Breast Cancer Type-1 | 2.5 THz | 95.40 | - | - | - | ||
| Breast Cancer Type-2 | 2.5 THz | 95.51 | - | - | - | ||
| Cervical | 2.5 THz | 94.96 | - | - | - | ||
| Skin | 2.5 THz | 94.13 | - | - | - | ||
| [23] | Blood | 2.5 THz | 98.40 | approximately | - | - | |
| Adrenal Gland | 2.5 THz | 98.21 | approximately | - | - | ||
| Breast Cancer Type-1 | 2.5 THz | 98.34 | approximately | - | - | ||
| Breast Cancer Type-2 | 2.5 THz | 98.40 | approximately | - | - | ||
| Cervical | 2.5 THz | 98.12 | approximately | - | - | ||
| Skin | 2.5 THz | 97.95 | approximately | - | - | ||
| [24] | Blood | 2 THz | 96.74 | 0.0006 | |||
| Skin | 2.0 THz | 96.61 | 0.0006 | ||||
| [25] | Blood | 1.3 m | 89.15 | - | |||
| Breast Cancer Type-2 | 1.3 m | 89.53 | - | ||||
| Cervical | 1.3 m | 89.22 | - | ||||
| Skin | 1.3 m | 88.78 | - | ||||
| Proposed HC-PCF | Blood | 3 THz | 99.92 | ||||
| Adrenal Gland | 2.5 THz | 99.92 | |||||
| Breast Cancer Type-1 | 2.5 THz | 99.93 | |||||
| Breast Cancer Type-2 | 2.5 THz | 99.93 | |||||
| Cervical | 2.5 THz | 99.92 | |||||
| Skin | 2.5 THz | 99.91 |
| Analyte | RS (%) | CL (dB/cm) | EML (cm) | EA (m) | B | NA | |
|---|---|---|---|---|---|---|---|
| Adrenal Gland Cancer | 99.9277 | 0.0152 | 0.0865 | ||||
| Blood Cancer | 99.9243 | > | 0.0152 | 0.0864 | |||
| Breast Cancer Type-1 | 99.9302 | > | 0.0152 | 0.0866 | |||
| Breast Cancer Type-2 | 99.9314 | > | 0.0152 | 0.0866 | |||
| Cervical Cancer | 99.9257 | > | 0.0152 | 0.0864 | |||
| Skin Cancer | 99.9169 | > | 0.0153 | 0.0862 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, M.R.H.; Chowdhury, A.A.; Islam, M.R.; Hosen, M.S.; Mim, M.H.; Nishat, M.M. Wave-Shaped Microstructure Cancer Detection Sensor in Terahertz Band: Design and Analysis. Appl. Sci. 2023, 13, 5784. https://doi.org/10.3390/app13095784
Khan MRH, Chowdhury AA, Islam MR, Hosen MS, Mim MH, Nishat MM. Wave-Shaped Microstructure Cancer Detection Sensor in Terahertz Band: Design and Analysis. Applied Sciences. 2023; 13(9):5784. https://doi.org/10.3390/app13095784
Chicago/Turabian StyleKhan, Md Rezaul Hoque, Atiqul Alam Chowdhury, Mohammad Rakibul Islam, Md Sanowar Hosen, Mhamud Hasan Mim, and Mirza Muntasir Nishat. 2023. "Wave-Shaped Microstructure Cancer Detection Sensor in Terahertz Band: Design and Analysis" Applied Sciences 13, no. 9: 5784. https://doi.org/10.3390/app13095784
APA StyleKhan, M. R. H., Chowdhury, A. A., Islam, M. R., Hosen, M. S., Mim, M. H., & Nishat, M. M. (2023). Wave-Shaped Microstructure Cancer Detection Sensor in Terahertz Band: Design and Analysis. Applied Sciences, 13(9), 5784. https://doi.org/10.3390/app13095784











