Computational Accuracy and Efficiency of Room Acoustics Simulation Using a Frequency Domain FEM with Air Absorption: 2D Study
Abstract
:1. Introduction
2. Theory
2.1. Lossy Helmholtz Equation Approach
2.2. Calculation of the Pure-Tone Sound Attenuation Coefficient
2.3. Spatial Discretization with Finite Elements
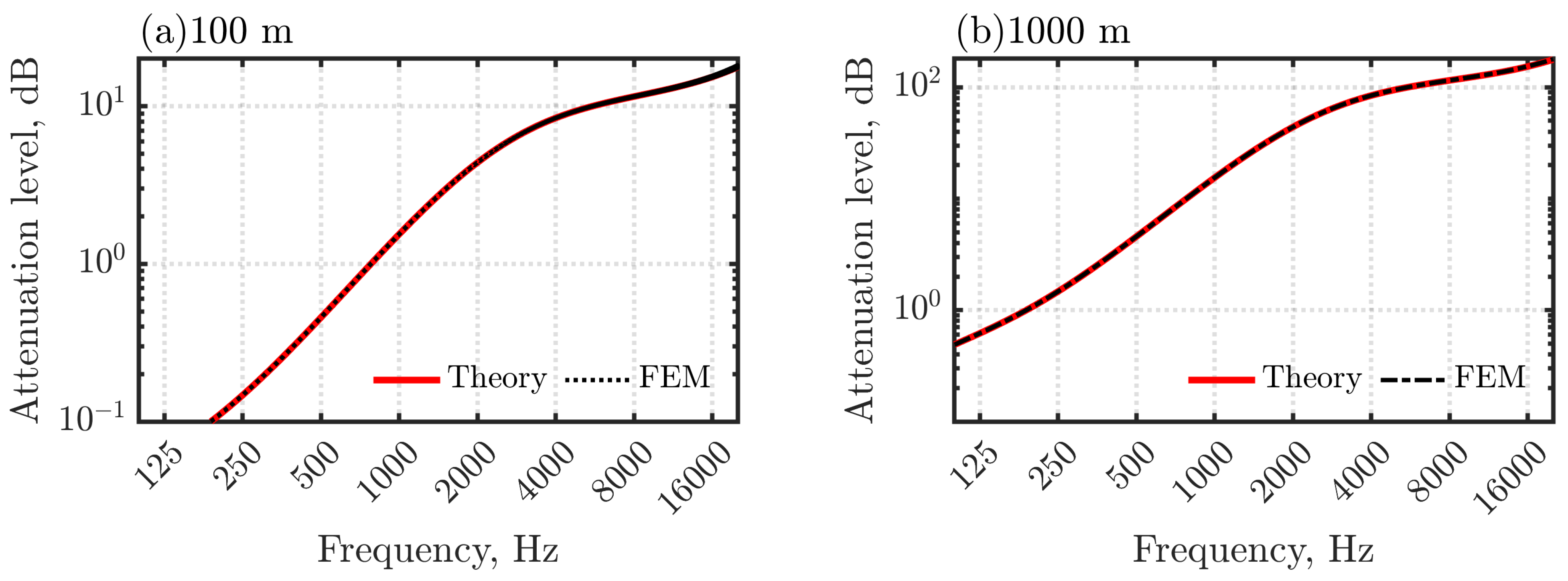
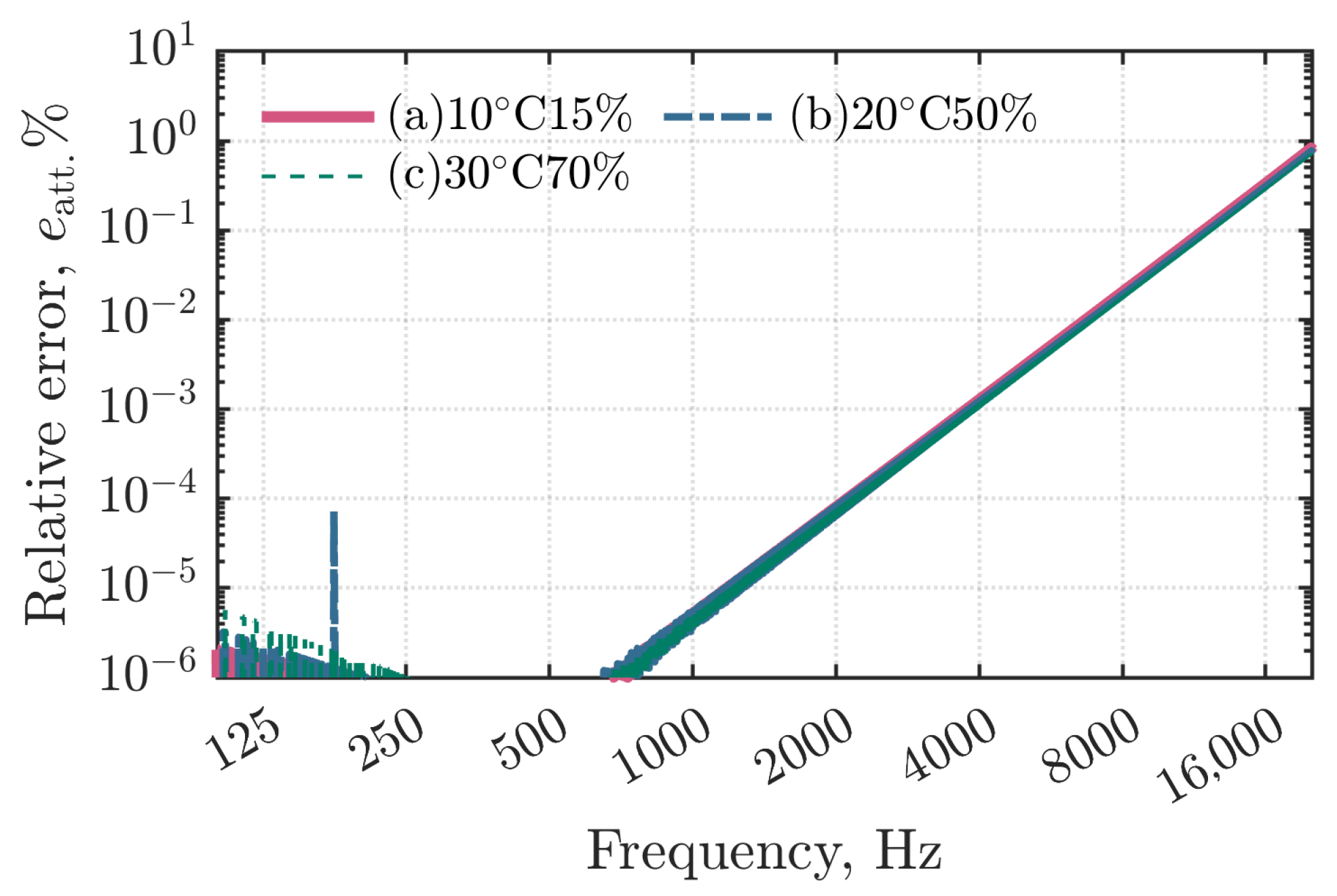
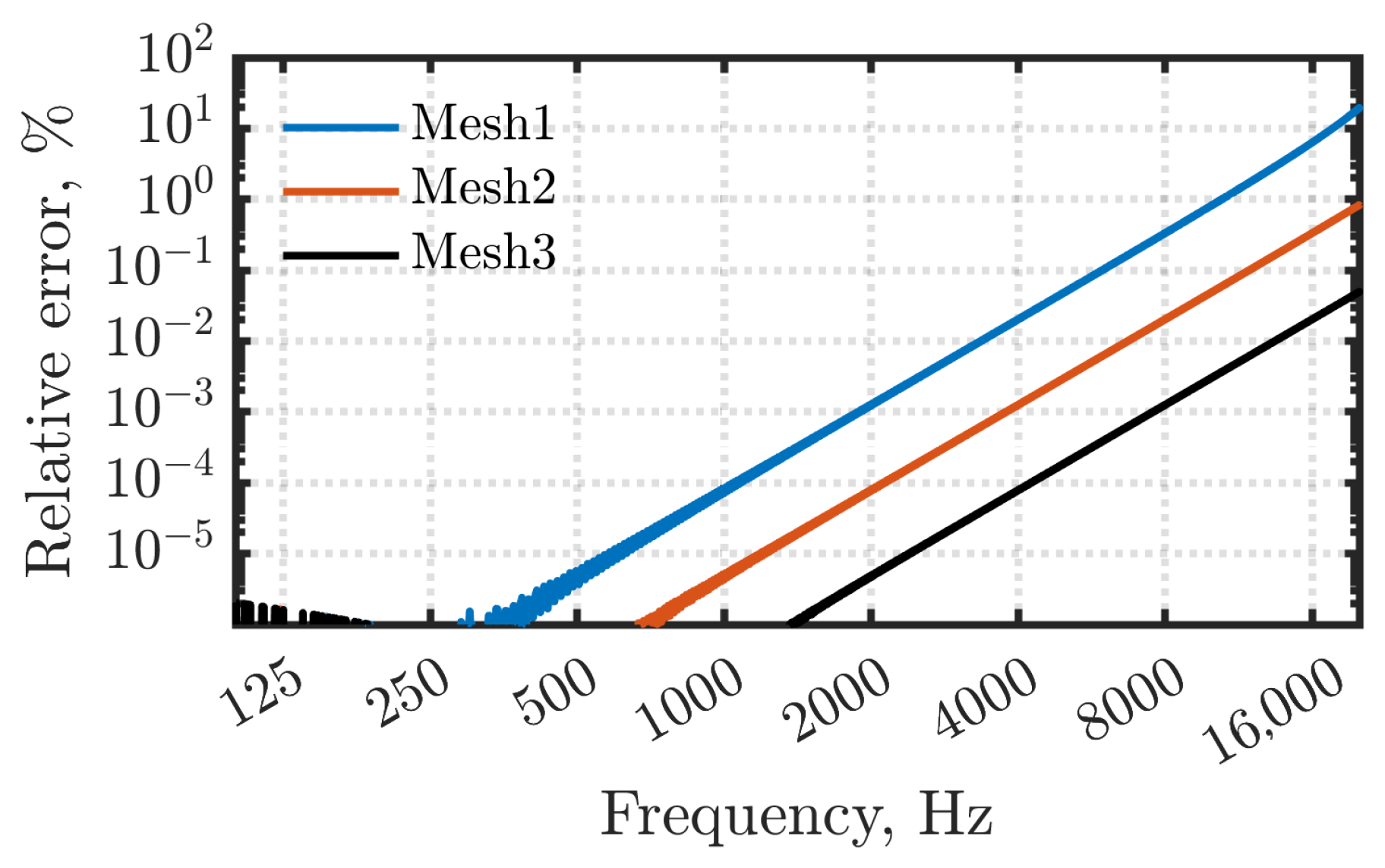
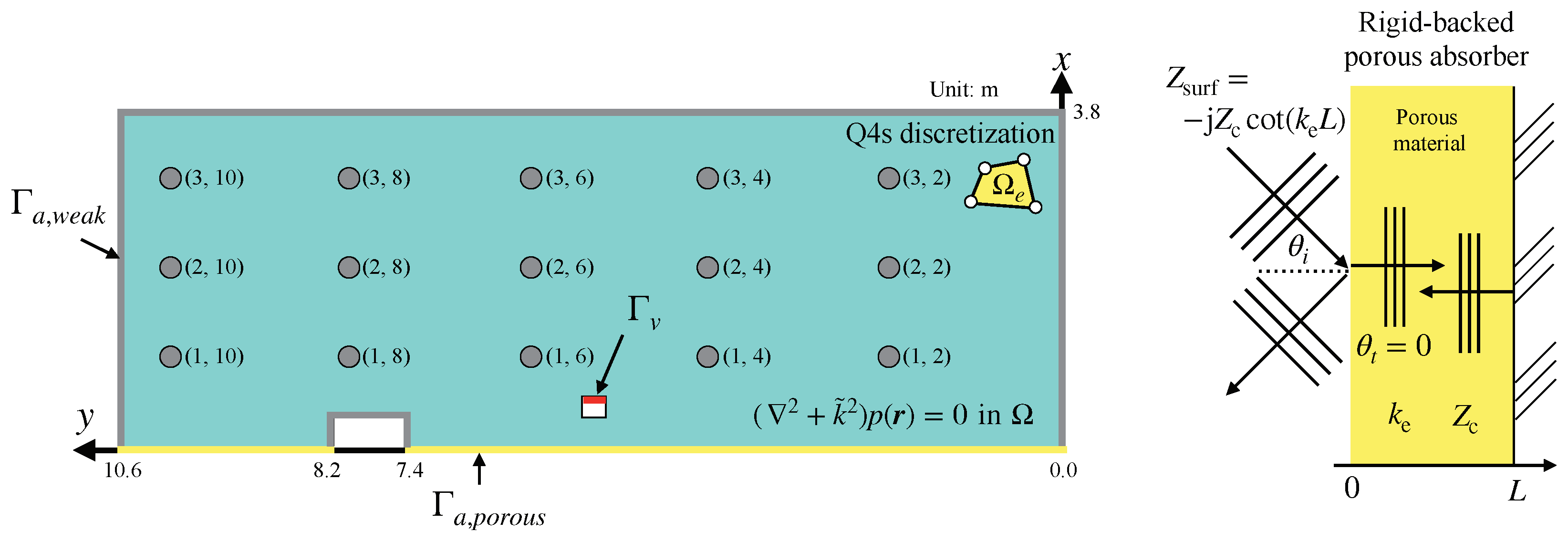
3. Accuracy Assessment with 2D Long Duct Problem
3.1. Outline of the Problem
3.2. Results and Discussion
4. Computational Efficiency Assessment with a 2D Office Problem
4.1. Outline of the Problem
4.2. Results and Discussion
5. Conclusions
- The use of geometrical acoustics simulation methods and presenting methods to improve accuracy, such as phase beam tracing and the novel scattering algorithm [60].
- The use of wave-based acoustics simulation methods and presenting methods to improve their efficiency.
- The use of hybrid techniques that combine geometrical acoustics simulation and wave-based acoustics simulation methods.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FEM | Finite element method |
| FDTD | Finite difference time domain method |
| BEM | Boundary element method |
| IIR | Infinite impulse response |
| FIR | Finite impulse response |
| PARDISO | Parallel direct solver |
| CSQMOR | Complex symmetric quasi-minimal residual method based on coupled two-term |
| biconjugate A-orthonormalization procedure | |
| Q4s | four-node linear quadrilateral elements |
| DOF | Degrees of freedom |
| 2D | Two dimensional |
| GW | Glass wool, 24K, 32K, 96K respectively represent material density in kilograms/m3 |
| SPL | Sound pressure level |
References
- Savioja, L.; Xiang, N. Simulation-based auralization of room acoustics. Acoust. Today 2020, 16, 48–56. [Google Scholar] [CrossRef]
- Vorländer, M. Are virtual sounds real? Acoust. Today 2020, 16, 46–54. [Google Scholar] [CrossRef]
- Savioja, L.; Svensson, U.P. Overview of geometrical room acoustic modeling techniques. J. Acoust. Soc. Am. 2015, 138, 708–730. [Google Scholar] [CrossRef]
- Krokstad, A.; Strøm, S.; Sørsdal, S. Calculating the acoustical room response by the use of a ray tracing technique. J. Sound Vib. 1968, 8, 118–125. [Google Scholar] [CrossRef]
- Allen, J.B.; Berkley, D.A. Image method for efficiently simulating small-room acoustics. J. Acoust. Soc. Am. 1979, 65, 943–950. [Google Scholar] [CrossRef]
- Hodgson, M.; Wareing, A. Comparisons of predicted steady-state levels in rooms with extended- and local-reaction bounding surfaces. J. Sound Vib. 2008, 309, 167–177. [Google Scholar] [CrossRef]
- Hodgson, M.; Behrooz, Y. Energy- and wave-based beam-tracing prediction of room-acoustical parameters using different boundary conditions. J. Acoust. Soc. Am. 2012, 132, 1450–1461. [Google Scholar]
- Jeong, C.H. Absorption and impedance boundary conditions for phased geometrical-acoustics methods. J. Acoust. Soc. Am. 2012, 132, 2347–2358. [Google Scholar] [CrossRef]
- Jeong, C.H.; Ih, J.G.; Rindel, J.H. An approximate treatment of reflection coefficient in the phased beam tracing method for the simulation of enclosed sound fields at medium frequencies. Appl. Acoust. 2008, 69, 601–613. [Google Scholar] [CrossRef]
- Sakamoto, S. Phase-error analysis of high-order finite difference time domain scheme and its influence on calculation results of impulse response in closed sound field. Acoust. Sci. Tech. 2007, 28, 295–309. [Google Scholar] [CrossRef]
- Sakamoto, S.; Nagatomo, H.; Ushiyama, A.; Tachibana, H. Calculation of impulse responses and acoustic parameters in a hall by the finite-difference time-domain method. Acoust. Sci. Tech. 2008, 29, 256–265. [Google Scholar] [CrossRef]
- Kowalczyk, K.; van Walstijn, M. Room acoustics simulation using 3-D compact explicit FDTD schemes. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 34–46. [Google Scholar] [CrossRef]
- Hamilton, B.; Bilbao, S. FDTD methods for 3-D room acoustics simulation with high-order accuracy in space and time. IEEE/ACM Trans. Audio Speech Lang. Process. 2017, 25, 2112–2124. [Google Scholar] [CrossRef]
- Cingolani, M.; Fratoni, G.; Barbaresi, L.; D’Orazio, D.; Hamilton, B.; Garai, M. A trial acoustic improvement in a lecture hall with MPP sound absorbers and FDTD acoustic simulations. Appl. Sci. 2021, 11, 2445. [Google Scholar] [CrossRef]
- Murillo, D.M.; Fazi, F.M.; Astley, J. Room acoustic simulations using the finite element method and diffuse absorption coefficients. Acta Acust. United Acust. 2019, 105, 231–239. [Google Scholar] [CrossRef]
- Pind, F.; Engsig-Karup, A.P.; Jeong, C.-H.; Hesthaven, J.S.; Mejling, M.S.; Strømann-Andersen, J. Time domain room acoustic simulations using the spectral element method. J. Acoust. Soc. Am. 2019, 145, 3299–3310. [Google Scholar] [CrossRef]
- Prinn, A.G. A review of finite element methods for room acoustics. Acoustics 2023, 5, 367–395. [Google Scholar] [CrossRef]
- Yoshida, T.; Okuzono, T.; Sakagami, K. A parallel dissipation-free and dispersion-optimized explicit time-domain FEM for large-scale room acoustics simulation. Buildings 2022, 12, 105. [Google Scholar] [CrossRef]
- Yoshida, T.; Okuzono, T.; Sakagami, K. Binaural auralization of room acoustics with a highly scalable wave-based acoustics simulation. Appl. Sci. 2023, 13, 2832. [Google Scholar] [CrossRef]
- Okuzono, T.; Yoshida, T. High potential of small-room acoustic modeling with 3D time-domain finite element method. Front. Built Environ. 2022, 8, 1006365. [Google Scholar] [CrossRef]
- Hargreaves, J.A.; Cox, T.J. A transient boundary element method model of Schroeder diffuser scattering using well mouth impedance. J. Acoust. Soc. Am. 2008, 124, 2942–2951. [Google Scholar] [CrossRef]
- Yasuda, Y.; Ueno, S.; Kadota, M.; Sekine, H. Applicability of locally reacting boundary conditions to porous material layer backed by rigid wall: Wave-based numerical study in non-diffuse sound field with unevenly distributed sound absorbing surfaces. Appl. Acoust. 2016, 113, 45–57. [Google Scholar] [CrossRef]
- Yasuda, Y.; Saito, K.; Sekine, H. Effects of the convergence tolerance of iterative methods used in the boundary element method on the calculation results of sound fields in rooms. Appl. Acoust. 2020, 157, 106997. [Google Scholar] [CrossRef]
- Gumerov, N.A.; Duraiswami, R. Fast multipole accelerated boundary element methods for room acoustics. J. Acoust. Soc. Am. 2021, 150, 1707–1720. [Google Scholar] [CrossRef]
- Cardoso Soares, M.; Brandão Carneiro, E.; Aizik Tenenbaum, R.; Mareze, P.H. Low-frequency room acoustical simulation of a small room with BEM and complex-valued surface impedances. Appl. Acoust. 2022, 188, 108570. [Google Scholar] [CrossRef]
- Aretz, M.; Vorländer, M. Combined wave and ray based room acoustic simulations of audio systems in car passenger compartments, Part I: Boundary and source data. Appl. Acoust. 2014, 76, 82–99. [Google Scholar] [CrossRef]
- Aretz, M.; Vorländer, M. Combined wave and ray based room acoustic simulations of audio systems in car passenger compartments, Part II: Comparison of simulations and measurements. Appl. Acoust. 2014, 76, 52–65. [Google Scholar] [CrossRef]
- Cox, T.J.; Peter, D. Porous sound absorption. In Acoustic Absorbers and Diffusers: Theory, Design and Application; Taylor & Francis: London, UK, 2017; pp. 175–224. [Google Scholar]
- Cox, T.J.; Peter, D. Resonant absorbers. In Acoustic Absorbers and Diffusers: Theory, Design and Application; Taylor & Francis: London, UK, 2017; pp. 225–264. [Google Scholar]
- ISO 10534-2:1998; Acoustics—Determination of Sound absorption Coefficient and Impedance in Impedance Tubes—Part 2: Transfer-Function Method. International Organization for Standardization: Geneva, Switzerland, 1998.
- Brandão, E.; Lenzi, A.; Paul, S. A review of the In Situ impedance and sound absorption measurement techniques. Acta Acust. United Acust. 2015, 101, 443–463. [Google Scholar] [CrossRef]
- Allard, J.; Atalla, N. Modeling multilayered systems with porous materials using the transfer matrix method. In Propagation of Sound in Porous Media: Modeling Sound Absorbing Materials; John Wiley & Sons: Chichester, UK, 2009; pp. 243–281. [Google Scholar]
- Craggs, A. A finite element model for rigid porous absorbing materials. J. Sound Vib. 1978, 61, 101–111. [Google Scholar] [CrossRef]
- Craggs, A. Coupling of finite element acoustic absorption models. J. Sound Vib. 1979, 66, 605–613. [Google Scholar] [CrossRef]
- Allard, J.; Atalla, N. Finite element modelling of poroelastic materials. In Propagation of Sound in Porous Media: Modeling Sound Absorbing Materials; John Wiley & Sons: Chichester, UK, 2009; pp. 309–349. [Google Scholar]
- Kates, J.M.; Brandewie, E.J. Adding air absorption to simulated room acoustic models. J. Acoust. Soc. Am. 2020, 148, EL408–EL413. [Google Scholar] [CrossRef]
- ISO 9613-1:1993; Acoustics—Attenuation of Sound during Propagation Outdoors. Part 1: Calculation of the Absorption of Sound by the Atmosphere. International Organization for Standardization: Geneva, Switzerland, 1993.
- Saarelma, J.; Savioja, L. Audibility of dispersion error in room acoustic finite-difference time-domain simulation in the presence of absorption of air. J. Acoust. Soc. Am. 2016, 140, EL545–EL550. [Google Scholar] [CrossRef]
- Hamilton, B. Air absorption filtering method based on approximate green function for Stokes equation. In Proceedings of the 24th International Conference on Digital Audio Effects, Vienna, Austria, 8–10 September 2021; pp. 160–167. [Google Scholar]
- Hamilton, B.; Bilbao, S. Time-domain modeling of wave-based room acoustics including viscothermal and relaxation effects in air. JASA Express Lett. 2021, 1, 092401-1–092401-8. [Google Scholar] [CrossRef]
- Ihlenburg, F. Sound in vibrating cabins: Physical effects, mathematical formulation, computational simulation with FEM. In Computational Aspects of Structural Acoustics and Vibration; Sandberg, G., Ohayon, R., Eds.; Springer: Wien, Austria, 2008; pp. 103–170. [Google Scholar]
- Sakuma, T.; Iwase, T.; Yasuoka, M. Prediction of sound fields in rooms with membrane materials: Development of a limp membrane element in acoustical FEM analysis and its application. J. Archit. Plann. Environ. Eng. 1998, 505, 1–8. [Google Scholar]
- Chen, W.H.; Lee, F.C.; Chiang, D.M. On the acoustic absorption of porous materials with different surface shapes and perforated plates. J. Sound Vib. 2000, 237, 337–355. [Google Scholar] [CrossRef]
- Tomiku, R.; Otsuru, T. Sound fields analysis in an irregular-shaped reverberation room by finite element method. J. Archit. Plann. Environ. Eng. 2002, 551, 9–15. [Google Scholar] [CrossRef]
- Aretz, M.; Vorländer, M. Efficient modeling of absorbing boundaries in room acoustic FE simulations. Acta Acust. United Acust. 2010, 96, 1042–1050. [Google Scholar] [CrossRef]
- Kim, K.H.; Yoon, G.H. Absorption performance optimization of perforated plate using multiple-sized holes and a porous separating partition. Appl. Acoust. 2017, 120, 21–37. [Google Scholar] [CrossRef]
- Okuzono, T.; Sakagami, K. Dispersion error reduction of absorption finite elements based on equivalent fluid model. Acoust. Sci. Tech. 2018, 39, 362–365. [Google Scholar] [CrossRef]
- Carbajo, J.; Ramis, J.; Godinho, L.; Mendes, P.A. Assessment of methods to study the acoustic properties of heterogeneous perforated panel absorbers. Appl. Acoust. 2018, 133, 1–7. [Google Scholar] [CrossRef]
- Okuzono, T.; Nitta, T.; Sakagami, K. Note on microperforated panel model using equivalent-fluid-based absorption elements. Acoust. Sci. Tech. 2019, 40, 221–224. [Google Scholar] [CrossRef]
- Davis, T.A. Direct Methods for Sparse Linear Systems; SIAM: Philadelphia, PA, USA, 2006. [Google Scholar]
- Barrett, R.; Berry, M.; Chan, T.; Demmel, J.; Donato, J.; Dongarra, J.; Eijkhout, V.; Pozp, R.; Romine, C.; van der Vorst, H. Nonstationary iterative methods. In Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods; SIAM: Philadelphia, PA, USA, 1994; pp. 14–20. [Google Scholar]
- Zhang, J.; Dai, H. A new quasi-minimal residual method based on a biconjugate A-orthonormalization procedure and coupled two-term recurrences. Numer. Algorithms 2015, 70, 875–896. [Google Scholar] [CrossRef]
- Guddati, M.N.; Yue, B. A Modified integration rules for reducing dispersion error in finite element methods. Comput. Methods Appl. Mech. Engrg. 2004, 193, 275–287. [Google Scholar] [CrossRef]
- Okamoto, N.; Tomiku, R.; Otsuru, T.; Yasuda, Y. Numerical analysis of large-scale sound fields using iterative methods part II: Application of Krylov subspace methods to finite element analysis. J. Comput. Acoust. 2007, 15, 473–493. [Google Scholar] [CrossRef]
- Okuzono, T.; Sakagami, K. A frequency domain finite element solver for acoustic simulations of 3D rooms with microperforated panel absorbers. Appl. Acoust. 2018, 129, 1–12. [Google Scholar] [CrossRef]
- Okuzono, T.; Mohamed, M.S.; Sakagami, K. Potential of room acoustic solver with plane-wave enriched finite element method. Appl. Sci. 2020, 10, 1969. [Google Scholar] [CrossRef]
- Okuzono, T.; Yoshida, T.; Sakagami, K. Efficiency of room acoustic simulations with time-domain FEM including frequency-dependent absorbing boundary conditions: Comparison with frequency-domain FEM. Appl. Acoust. 2021, 182, 108212. [Google Scholar] [CrossRef]
- Miki, Y. Acoustical properties of porous materials – Modifications of Delany–Bazley models. J. Acoust. Soc. Jpn. 1990, 11, 19–24. [Google Scholar] [CrossRef]
- Diwan, G.C.; Mohamed, M.S. Pollution studies for high order isogeometric analysis and finite element for acoustic problems. Comput. Methods Appl. Mech. Eng. 2019, 350, 701–718. [Google Scholar] [CrossRef]
- Autio, H.; Nilsson, E. A novel algorithm for directional scattering in acoustic ray tracers. Acoustics 2023, 5, 928–947. [Google Scholar] [CrossRef]


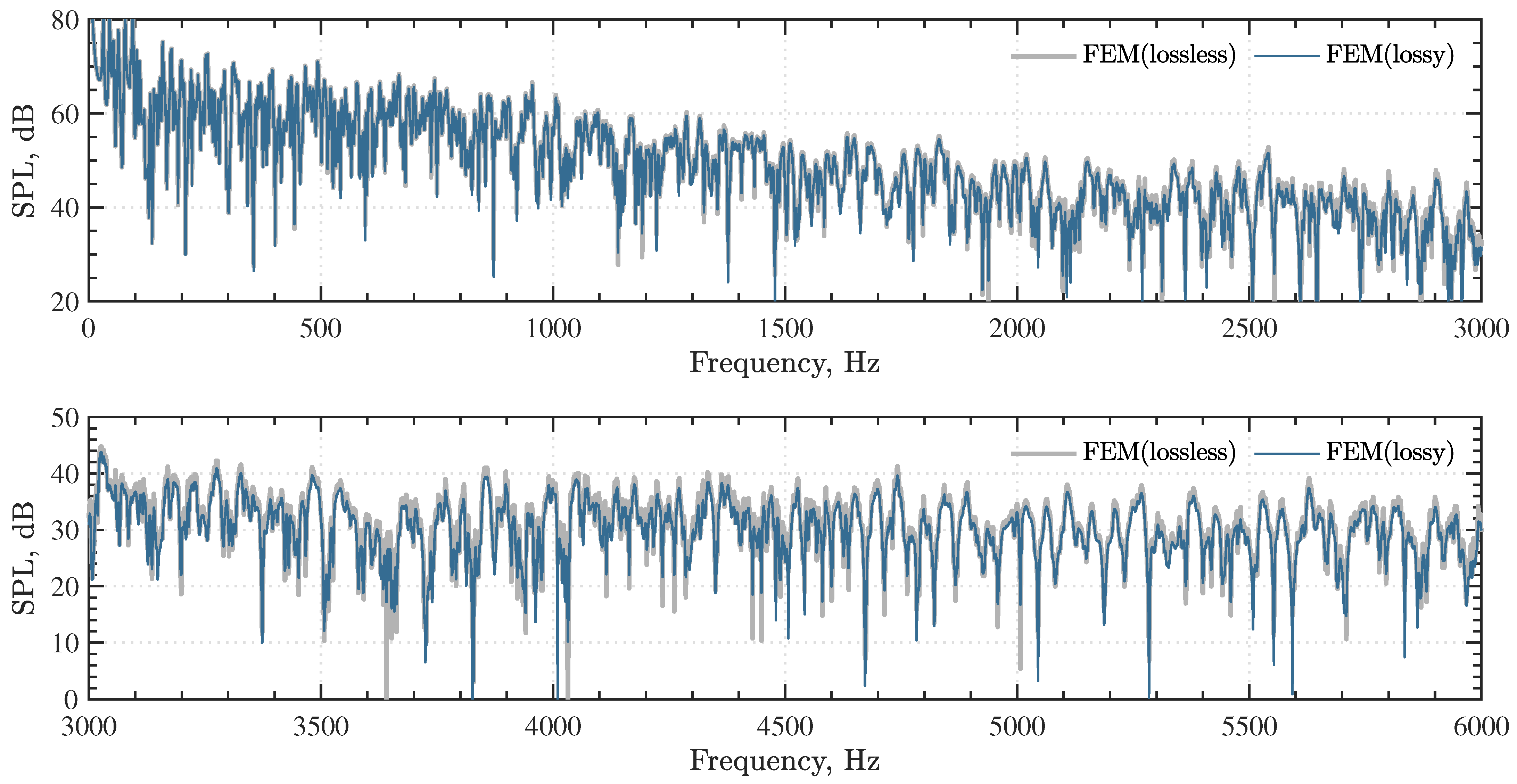

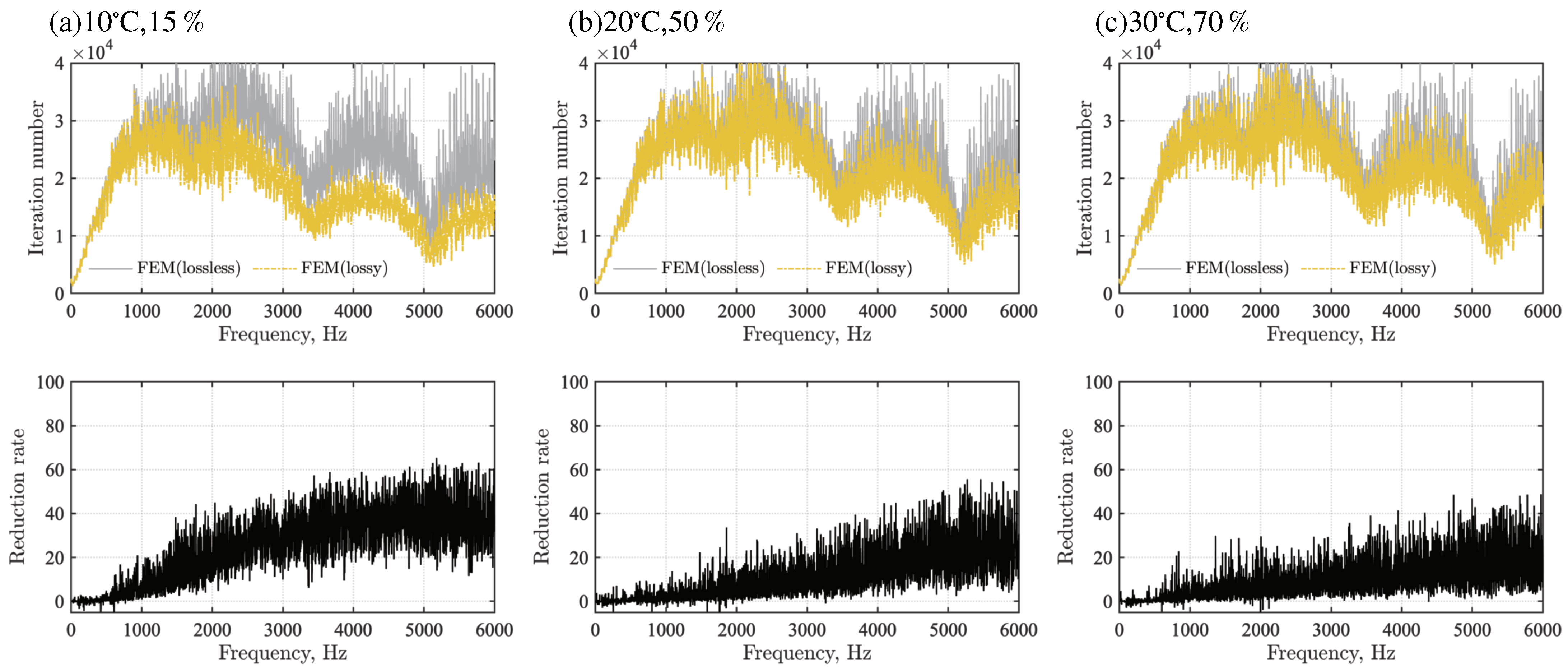
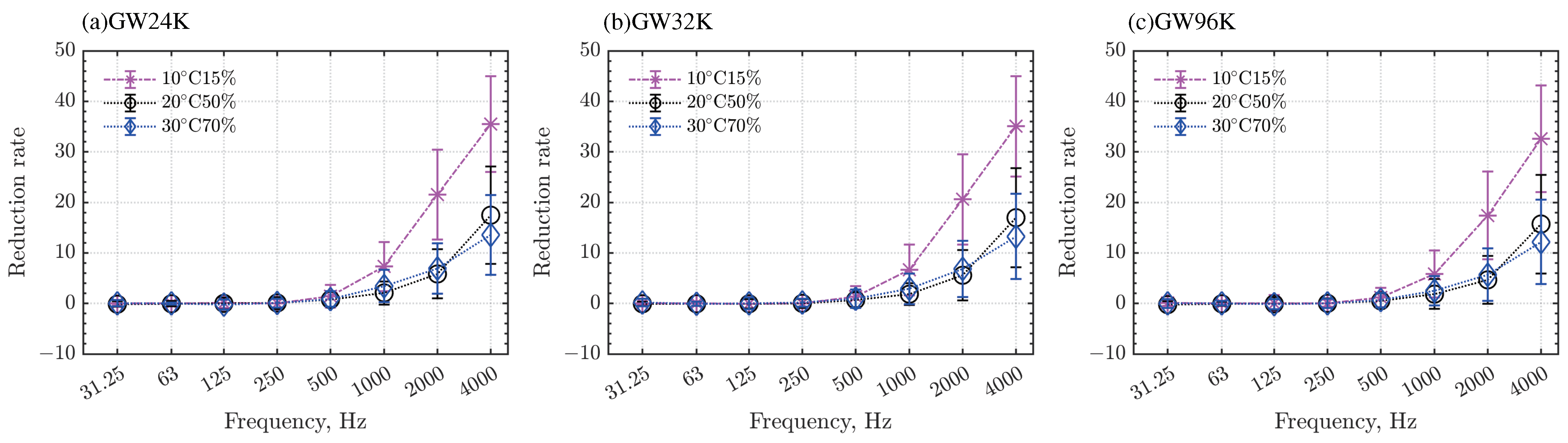

| FEM (Lossless) | FEM (Lossy) | |||
|---|---|---|---|---|
| Frequency, Hz | , s | (, %) | , s (, %) | |
| 3000 | 40,561 | 200 | 29,334 (27.7) | 145 (27.5) |
| 4000 | 36,883 | 183 | 24,615 (33.3) | 123 (32.7) |
| 5000 | 24,477 | 121 | 16,567 (32.3) | 83 (31.1) |
| 6000 | 37,811 | 187 | 23,132 (38.8) | 114 (39.2) |
| Frequency, Hz | Mesh1 | Mesh2 | |
|---|---|---|---|
| 3000 | 19.1 | 1.8 | 1.5 |
| 4000 | 15.2 | 1.5 | 1.6 |
| 5000 | 9.3 | 1.0 | 1.8 |
| 6000 | 14.4 | 1.4 | 1.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Okuzono, T. Computational Accuracy and Efficiency of Room Acoustics Simulation Using a Frequency Domain FEM with Air Absorption: 2D Study. Appl. Sci. 2024, 14, 194. https://doi.org/10.3390/app14010194
Okuzono T. Computational Accuracy and Efficiency of Room Acoustics Simulation Using a Frequency Domain FEM with Air Absorption: 2D Study. Applied Sciences. 2024; 14(1):194. https://doi.org/10.3390/app14010194
Chicago/Turabian StyleOkuzono, Takeshi. 2024. "Computational Accuracy and Efficiency of Room Acoustics Simulation Using a Frequency Domain FEM with Air Absorption: 2D Study" Applied Sciences 14, no. 1: 194. https://doi.org/10.3390/app14010194
APA StyleOkuzono, T. (2024). Computational Accuracy and Efficiency of Room Acoustics Simulation Using a Frequency Domain FEM with Air Absorption: 2D Study. Applied Sciences, 14(1), 194. https://doi.org/10.3390/app14010194






