Fault Feature Extraction of Parallel-Axis Gearbox Based on IDBO-VMD and t-SNE
Abstract
:1. Introduction
2. Algorithm Principle
2.1. Variational Mode Decomposition (VMD)
2.2. Dung Beetle Optimizer (DBO)
2.2.1. Dung Beetle Ball Rolling
2.2.2. Foraging
2.2.3. Breed
2.2.4. Thief
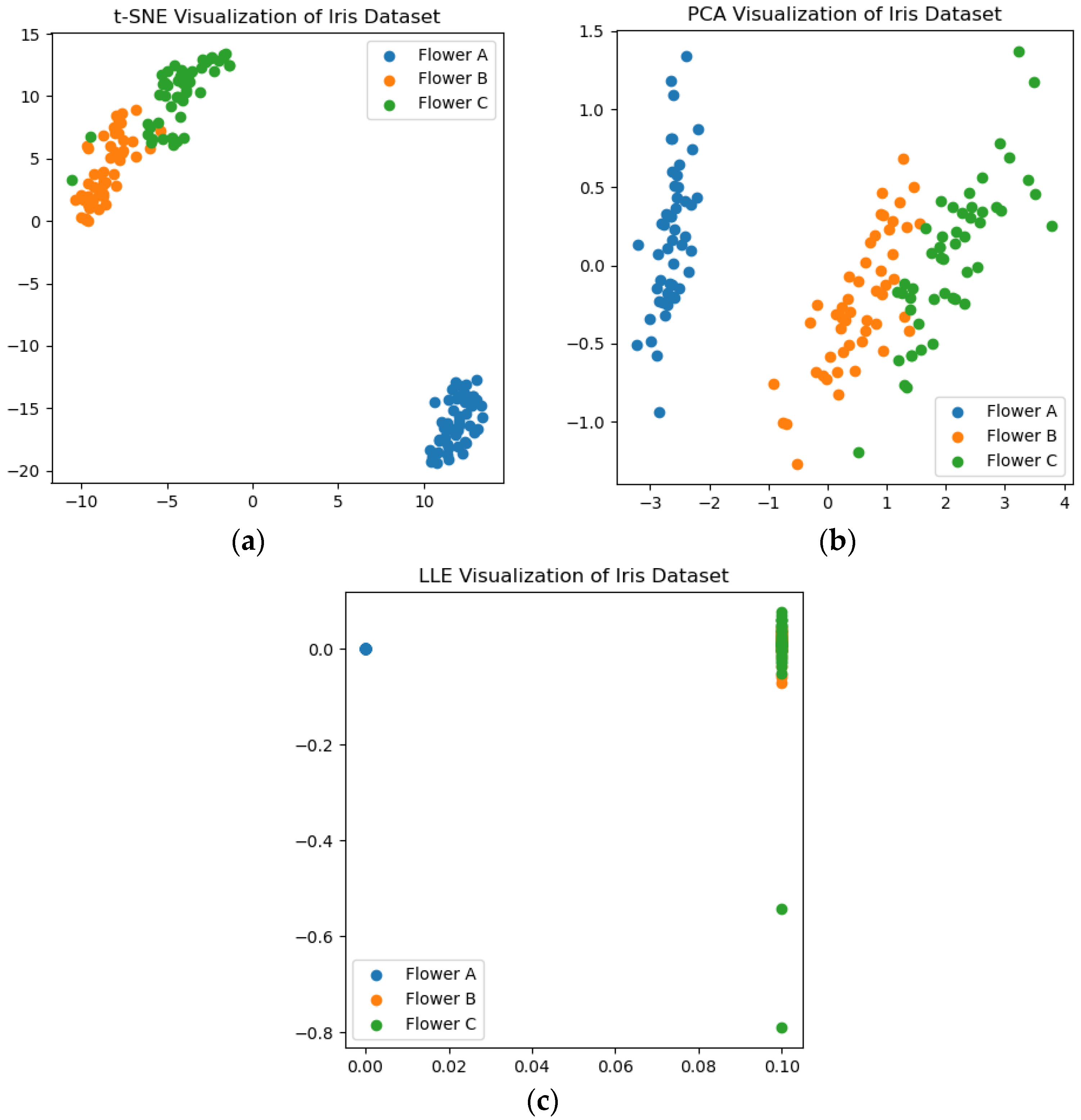
2.3. t-Distributed Stochastic Neighbor Embedding (t-SNE)
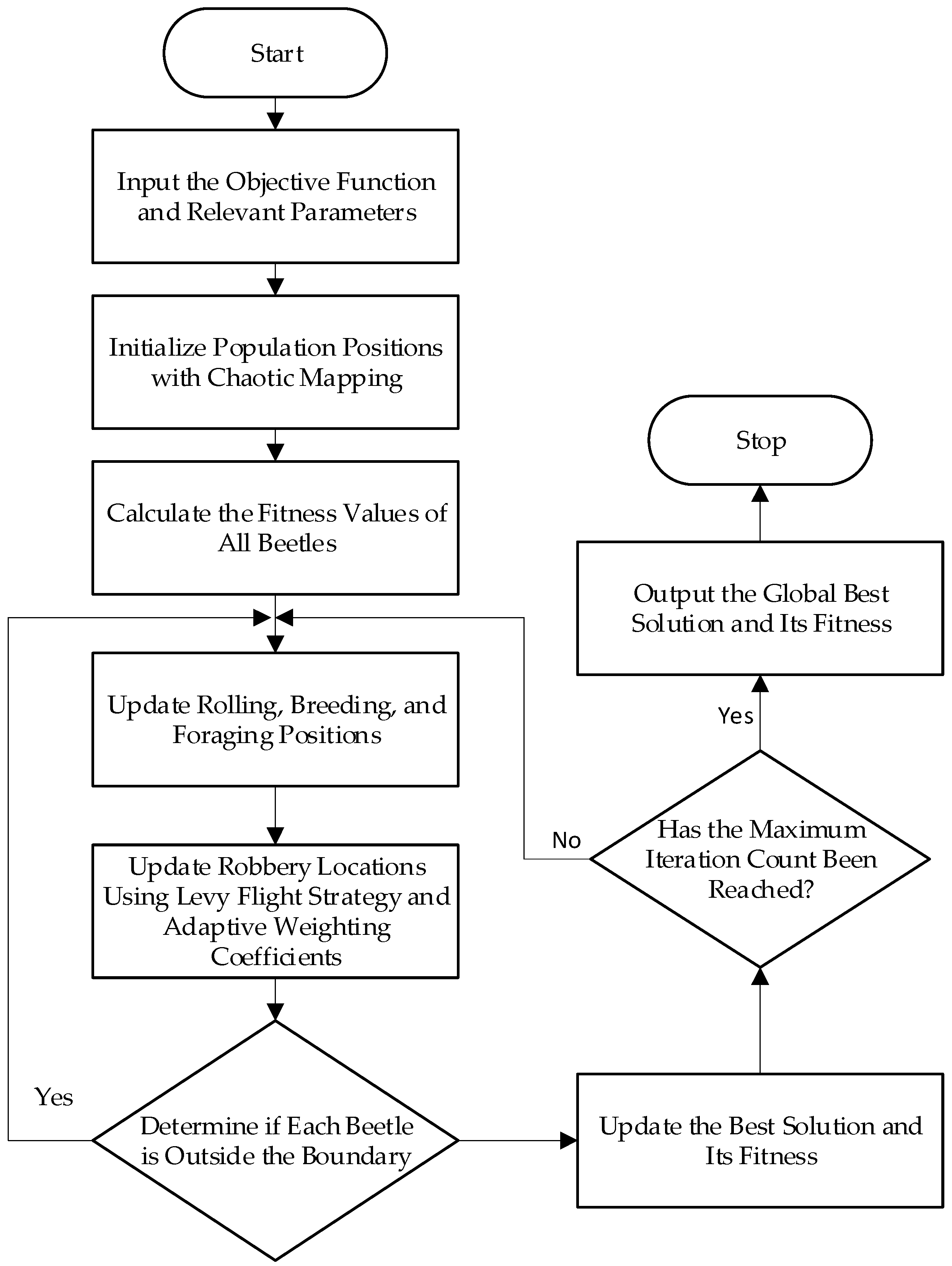
3. Improved Dung Beetle Optimization Algorithm (IDBO)
3.1. Cubic Mapping
3.2. Levy Flight Strategy
3.3. Dynamic Adaptive Weight
4. Fault Diagnosis Process for Parallel-Axis Gearboxes Based on WOA-VMD and t-SNE
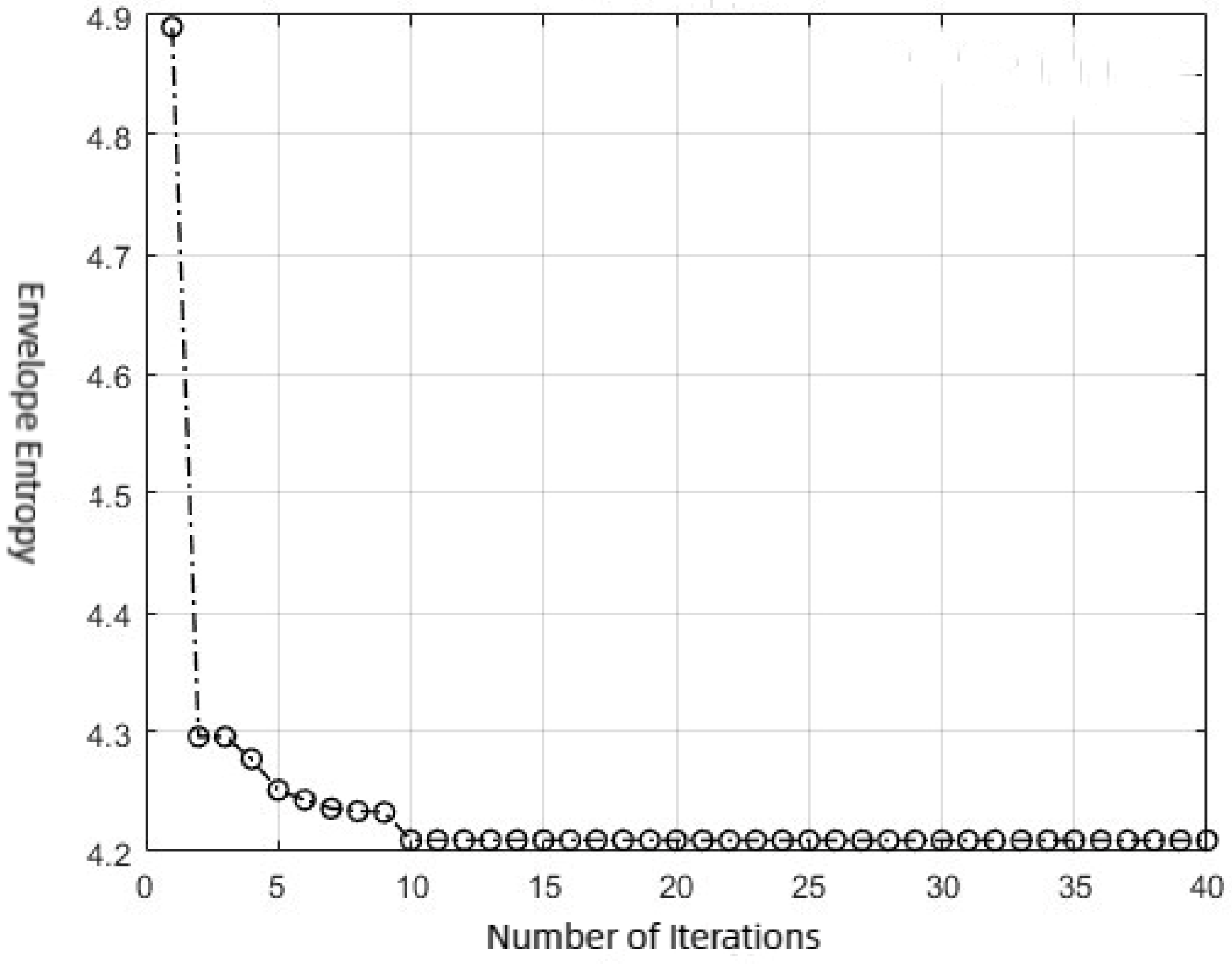
4.1. Optimizing VMD with IDBO
- Set the IDBO population size and the number of iterations, and define a suitable range for [K, α] values for VMD decomposition. Ensure that the range is not too narrow to avoid losing essential feature information in the modal components.
- Use VMD to decompose the vibration signal from the gearbox, resulting in several intrinsic mode functions (IMFs).
- Calculate the fitness function value for each set of [K, α] values and continually update the iterations to find the best fitness function value.
- Determine if the iteration is completed, i.e., whether the maximum number of iterations has been reached. When the maximum number of iterations is reached, terminate the iteration and save the optimal parameters [K, α].
4.2. Kurtosis-Based Signal Reconstruction
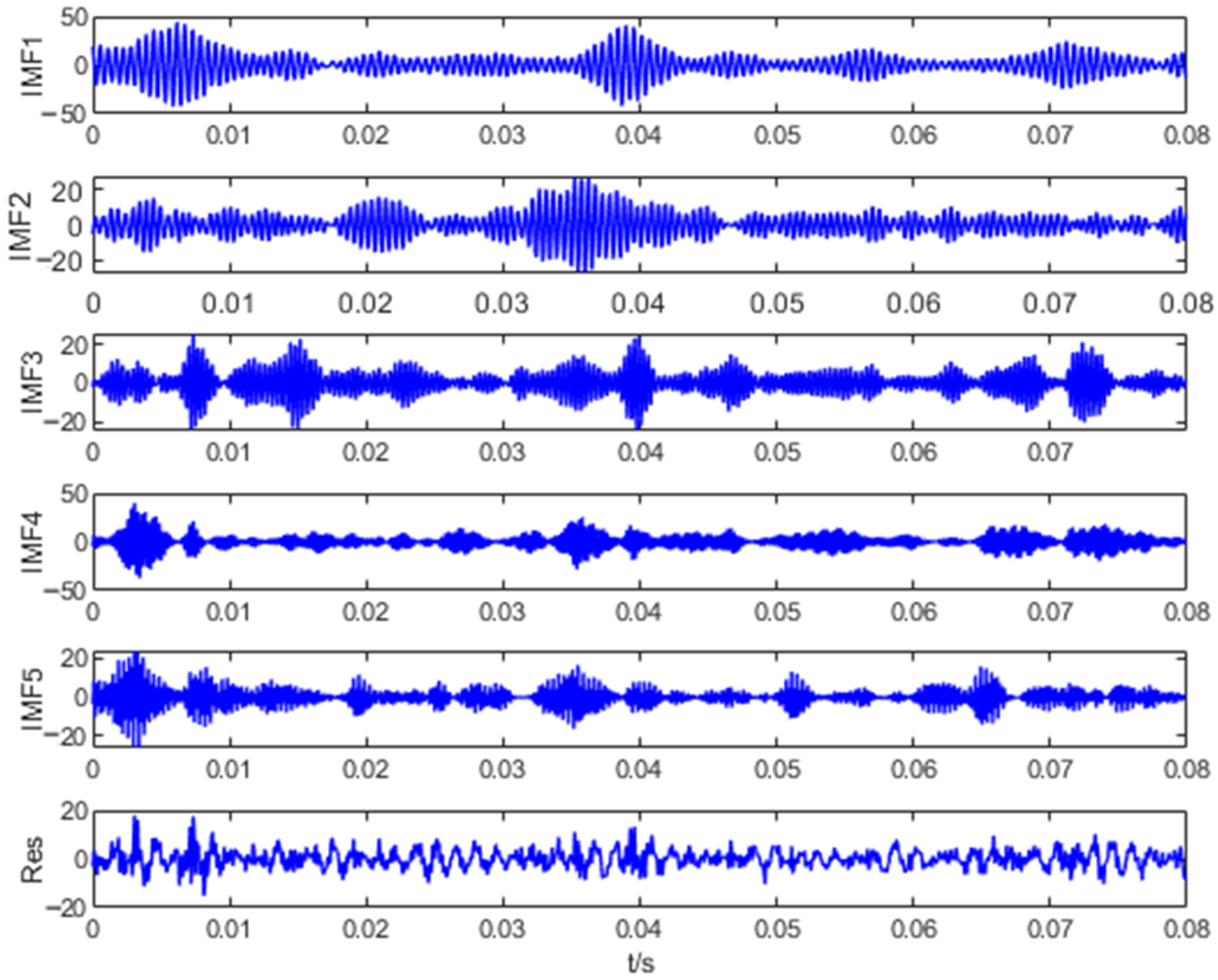
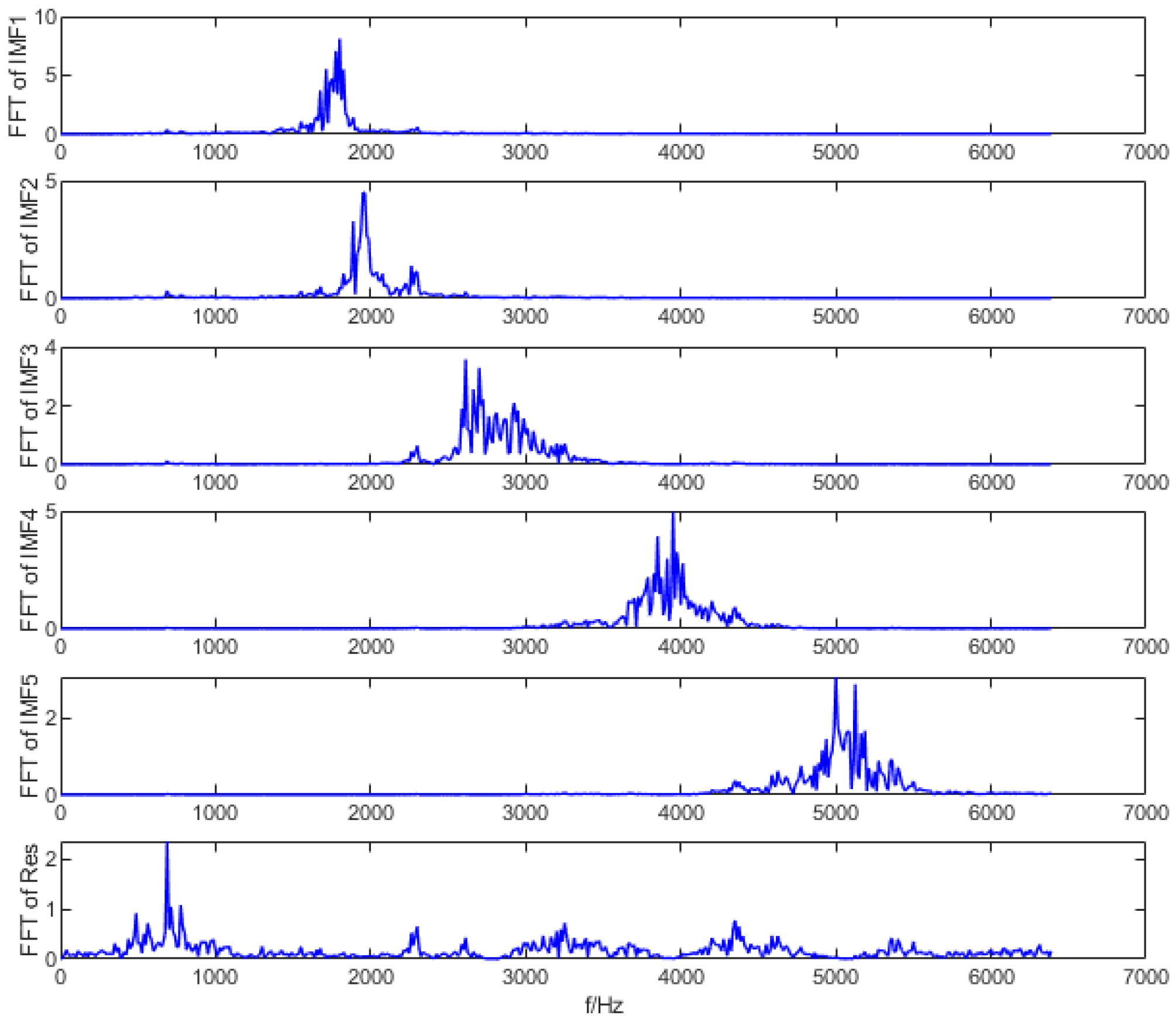
4.3. Feature Extraction
- Obtain vibration signals for various states using an accelerometer sensor.
- Use the IDBO algorithm to search the optimal parameters of VMD for each state. After parameter optimization, apply VMD to decompose the signals from various states, resulting in K IMF components.
- Apply the kurtosis criterion to filter the obtained IMF components, selecting the best IMF.
- Perform feature extraction on the chosen IMF, recombine the extracted 20 feature values to create a new feature vector.
- Utilize the t-SNE method for dimensionality reduction, obtaining a two-dimensional feature vector.
- Input the feature vectors of the training dataset into an SVM for training, creating an SVM classification model.
- Input the feature vectors of the testing dataset into the trained SVM model to perform fault diagnosis.
5. Simulation Testing
6. Experimental Verification
6.1. Description of Experimental Data
6.2. The Extraction of Fault Signal Features
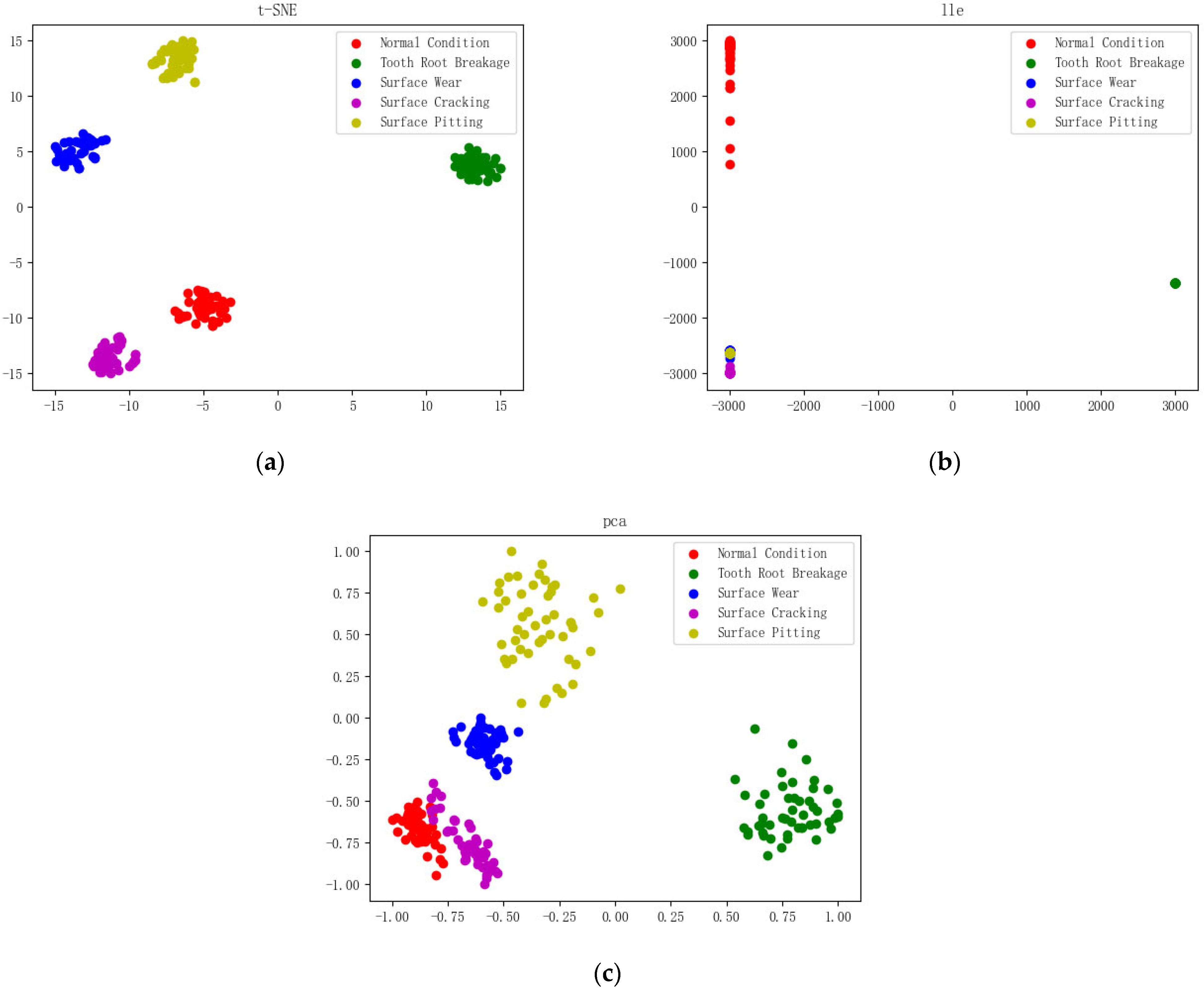
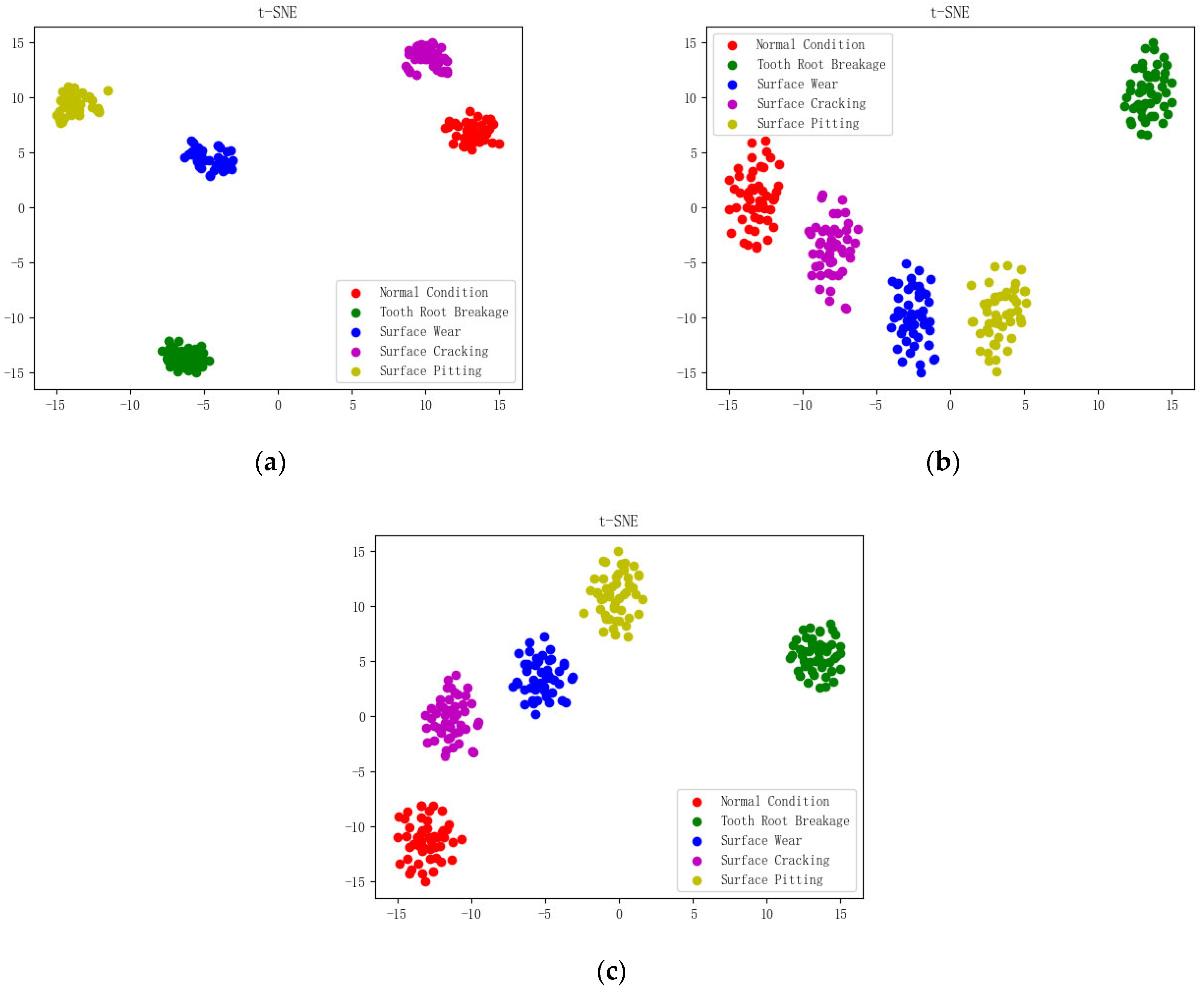
6.3. t-SNE Dimensionality Reduction Effect
6.4. Fault Feature Dimensionality Reduction
6.5. Fault Classification
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| DBO | dung beetle optimization |
| EMD | empirical mode decomposition |
| GWO | grey wolf optimization |
| IDBO | improved dung beetle optimization |
| IMFs | intrinsic mode functions |
| K | decomposition quantity |
| LLE | locally linear embedding |
| PCA | principal component analysis |
| PSO | particle swarm optimization |
| SSA | sparrow search algorithm |
| SVM | support vector machine |
| t-SNE | t-distributed stochastic neighbor embedding |
| VMD | variational modal decomposition |
| α | penalty factor |
References
- Vachtsevanos, G.J.; Lewis, F.; Roemer, M.; Hess, A.; Wu, B. Intelligent Fault Diagnosis and Prognosis for Engineering Systems; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Hirani, H.; Athre, K.; Biswas, S. Comprehensive Design Methodology for an Engine Journal Bearing. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2000, 214, 401–412. [Google Scholar] [CrossRef]
- Hotait, M.A.; Kahraman, A. Experiments on the Relationship between the Dynamic Transmission Error and the Dynamic Stress Factor of Spur Gear Pairs. Mech. Mach. Theory 2013, 70, 116–128. [Google Scholar] [CrossRef]
- Kahraman, A. Effect of axial vibrations on the dynamics of a helical gear pair. J. Vib. Acoust. 1993, 115, 33–39. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, T.; Chen, Y.; Song, L. The Effect of Parallel-Axis Helix Gear Pair on Wind Turbine Gearbox Vibration Control. Shock. Vib. 2020, 2020, 8893890. [Google Scholar] [CrossRef]
- Huang, E.N.; Shen, Z.; Long, R.S.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Zhang, Y.T.; Li, C.L.; Jiang, Y.Q.; Sun, L.; Zhao, R.B.; Yan, K.F.; Wang, W.H. Accurate prediction of water quality in urban drainage network with integrated EMD-LSTM model. J. Clean. Prod. 2022, 354, 131724. [Google Scholar] [CrossRef]
- Deng, Y.; Zhu, K.H.; Zhao, G.J.; Zhu, J.Y. Efficient partial discharge signal denoising method via adaptive variational modal decomposition for infrared detectors. Infrared Phys. Technol. 2022, 125, 104230. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Zhan, J.; Cheng, L.; Peng, Z. Based on VMD and Improved Multi-Classification Matian Series Integrated Intelligent Diagnosis of Rolling Bearing Faults. Vib. Shock 2020, 39, 32–39. [Google Scholar]
- Tang, G.; Wang, X. Parameter Optimized Variational Mode Decomposition Method with Application to Incipient Fault Diagnosis of Rolling Bearing. J. Xi’an Jiaotong Univ. 2015, 49, 73–81. [Google Scholar]
- Ding, J.; Wang, Z.; Yao, L.; Cai, Y. Rolling Bearing Fault Diagnosis Based on GCMWPE and Parameter Optimization SVM. China Mech. Eng. 2021, 32, 147–155. [Google Scholar] [CrossRef]
- Shen, T.; Huang, S.; Han, S. Extracting Information Entropy Features for Rotating Machinery Vibration Signals. Chin. J. Mech. Eng. 2001, 37, 94–98. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Chen, X.; Wei, J. Feature Extraction and Classification of Ship Radiated Noise Based on VMD and SVM. J. Natl. Univ. Def. Technol. 2019, 41, 89–94. [Google Scholar]
- Li, Z.; Jiang, Y.; Guo, Q.; Hu, C.; Peng, Z. Multi-dimensional Variational Mode Decomposition for Bearing-Crack Detection in Wind Turbines with Large Driving-Speed Variations. Renew. Energy 2018, 116, 55–73. [Google Scholar] [CrossRef]
- Wang, C.; Li, H.; Huang, G.; Ou, J. Early Fault Diagnosis for Planetary Gearbox Based on Adaptive Parameter Optimized VMD and Singular Kurtosis Difference Spectrum. IEEE Access 2019, 7, 31501–31516. [Google Scholar] [CrossRef]
- Zhang, M.; Jiang, Z.; Feng, K. Research on Variational Mode Decomposition in Rolling Bearings Fault Diagnosis of the Multistage Centrifugal Pump. Mech. Syst. Signal Process. 2017, 93, 460–493. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung Beetle Optimizer: A New Meta-Heuristic Algorithm for Global Optimization. J. Supercomput. 2022, 79, 7305–7336. [Google Scholar] [CrossRef]
- Ge, Y.; Guo, L.Z.; Niu, S.G.; Dou, Y. Prediction of Remaining Useful Life Based on t-SNE and LSTM for Rotating Machinery. J. Vib. Shock 2020, 39, 223–231. [Google Scholar]
- Zhang, J.; Zheng, J.; Xie, X.; Lin, Z.; Li, H. Mayfly Sparrow Search Hybrid Algorithm for RFID Network Planning. IEEE Sens. J. 2022, 22, 16673–16686. [Google Scholar] [CrossRef]
- Feng, J.; Zhang, J.; Zhu, X.; Lian, W. A Novel Chaos Optimization Algorithm. Multimed. Tools Appl. 2017, 76, 17405–17436. [Google Scholar] [CrossRef]
- Reynolds, A. Cooperative Random Levy Flight Searches and the Flight Patterns of Honeybees. Phys. Lett. A 2006, 354, 384–388. [Google Scholar] [CrossRef]
- Yang, C.-Y.; Ma, Y.-W.; Chen, J.-L.; Lin, C.-J.; Lee, W.-L. Novel Dynamic KNN with Adaptive Weighting Mechanism for Beacon-Based Indoor Positioning System. J. Internet Technol. 2019, 20, 1601–1610. [Google Scholar]
- Hu, A.J.; Ma, W.L. Rolling Bearing Fault Feature Extraction Method Based on Ensemble Empirical Mode Decomposition and Kurtosis Criterion. Proc. CSEE 2012, 32, 106–111+153. [Google Scholar]
- Liu, C.L.; Wu, Y.J.; Zhen, C.G. Rolling Bearing Fault Diagnosis Based on Variational Mode Decomposition and Fuzzy C-Means Clustering. Proc. CSEE 2015, 35, 3358–3365. [Google Scholar]
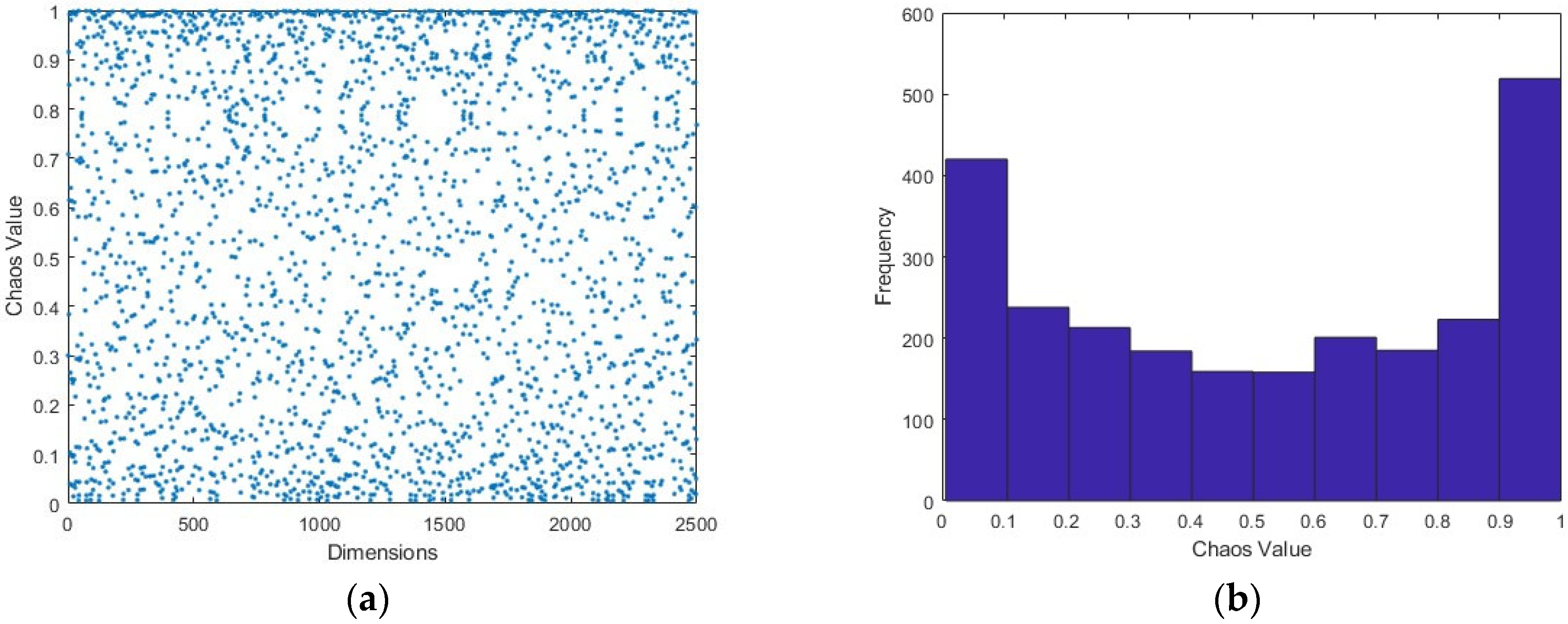


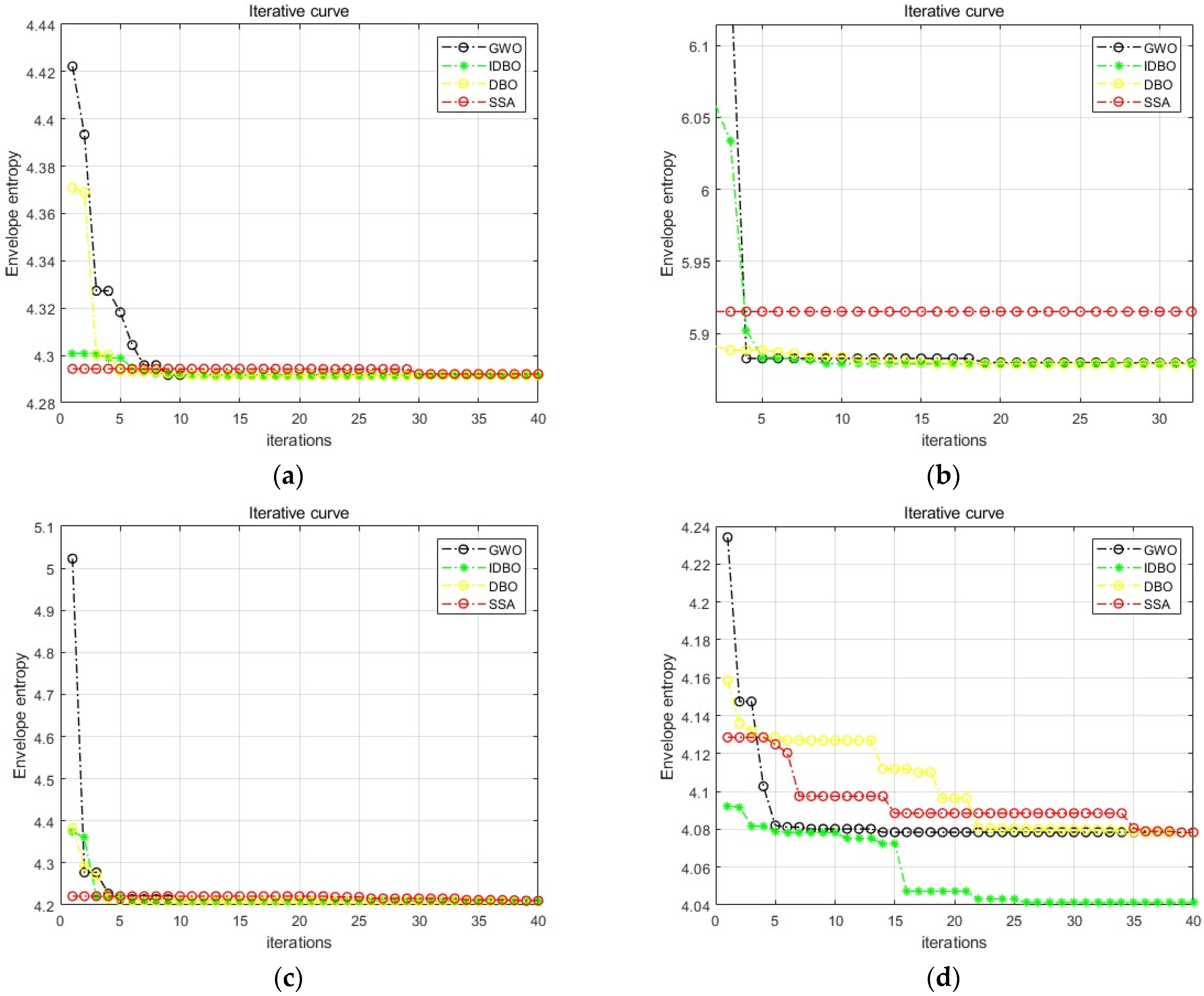

| Test Functions | Dimension | Range | Optimal Value |
|---|---|---|---|
| 30 | [−100, 100] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−30, 30] | 0 | |
| 30 | [−500, 500] | 0 | |
| 30 | [−32, 32] | 0 | |
| 30 | [−50, 50] | 0 |
| IDBO | DBO | GWO | SSA | |
|---|---|---|---|---|
| F1 | ||||
| Optimal value | 0 | 2.4081 × 10−176 | 5.5438 × 10−29 | 7.1886 × 10−100 |
| Mean value | 0 | 6.0809 × 10−107 | 6.7022 × 10−28 | 3.7487 × 10−60 |
| Standard deviation | 0 | 1.9229 × 10−106 | 1.3445 × 10−27 | 1.1854 × 10−59 |
| F2 | ||||
| Optimal value | 0 | 1.4802 × 10−76 | 4.9103 × 10−17 | 5.0108 × 10−81 |
| Mean value | 0 | 1.0308 × 10−58 | 8.2908 × 10−17 | 5.4129 × 10−32 |
| Standard deviation | 0 | 3.2597 × 10−58 | 2.9568 × 10−17 | 1.6937 × 10−31 |
| F3 | ||||
| Optimal value | 0 | 3.2393 × 10−76 | 2.2534 × 10−7 | 2.8709 × 10−93 |
| Mean value | 3.6372 × 10−90 | 1.8364 × 10−54 | 7.4764 × 10−7 | 7.0487 × 10−31 |
| Standard deviation | 1.1299 × 10−89 | 5.8014 × 10−54 | 5.1431 × 10−7 | 2.2202 × 10−30 |
| F4 | ||||
| Optimal Value | 0 | 4.3236 × 10−304 | 3.0912 × 10−53 | 5.4264 × 10−243 |
| Mean Value | 0 | 4.1335 × 10−210 | 1.7039 × 10−50 | 3.8374 × 10−124 |
| Standard Deviation | 0 | 0 | 3.7227 × 10−50 | 1.2135 × 10−123 |
| F5 | ||||
| Optimal value | 0 | 1.2767 × 10−162 | 7.9735 × 10−105 | 6.3863 × 10−119 |
| Mean value | 0 | 6.2664 × 10−114 | 3.5699 × 10−100 | 4.1615 × 10−44 |
| Standard deviation | 0 | 1.9816 × 10−113 | 9.4946 × 10−100 | 1.316 × 10−43 |
| F6 | ||||
| Optimal value | 4.4409 × 10−16 | 4.4409 × 10−16 | 7.5051 × 10−14 | 4.4409 × 10−16 |
| Mean value | 4.4409 × 10−16 | 4.4409 × 10−16 | 1.0134 × 10−13 | 4.4409 × 10−16 |
| Standard deviation | 0 | 0 | 3.8454 × 10−14 | 0 |
| Gear Condition | [K, α] |
|---|---|
| Normal condition | [6, 2232] |
| Tooth root breakage | [5, 648] |
| Surface pitting | [4, 476] |
| Surface cracking | [5, 741] |
| Surface wear | [4, 2678] |
| State | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 |
|---|---|---|---|---|---|---|
| Normal | 3.25 | 4.29 | 3.82 | 4.20 | 3.49 | 3.89 |
| Breakage | 2.44 | 2.95 | 3.20 | 2.89 | 4.26 | |
| Pitting | 3.15 | 3.44 | 3.58 | 4.41 | ||
| Cracking | 2.66 | 4.13 | 3.25 | 4.84 | 5.22 | |
| Wear | 2.89 | 13.95 | 15.22 | 8.79 |
| Method | Classification Accuracy/% |
|---|---|
| EMD + t-SNE | 95 |
| VMD + t-SNE | 98 |
| IDBO-VMD + t-SNE | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Wang, S.; Cheng, Y. Fault Feature Extraction of Parallel-Axis Gearbox Based on IDBO-VMD and t-SNE. Appl. Sci. 2024, 14, 289. https://doi.org/10.3390/app14010289
Wang Z, Wang S, Cheng Y. Fault Feature Extraction of Parallel-Axis Gearbox Based on IDBO-VMD and t-SNE. Applied Sciences. 2024; 14(1):289. https://doi.org/10.3390/app14010289
Chicago/Turabian StyleWang, Zhen, Shuaiyu Wang, and Yiyang Cheng. 2024. "Fault Feature Extraction of Parallel-Axis Gearbox Based on IDBO-VMD and t-SNE" Applied Sciences 14, no. 1: 289. https://doi.org/10.3390/app14010289
APA StyleWang, Z., Wang, S., & Cheng, Y. (2024). Fault Feature Extraction of Parallel-Axis Gearbox Based on IDBO-VMD and t-SNE. Applied Sciences, 14(1), 289. https://doi.org/10.3390/app14010289






