An Improved Contact Force Model of Polyhedral Elements for the Discrete Element Method
Abstract
:1. Introduction
2. Experimental Method
2.1. Design and Properties of Specimens
2.2. Experimental Equipment
2.3. Experimental Procedure
- (1)
- The upper specimen was struck by controlling the angle of the impact force hammer, and the force was transmitted to the contact surface between the specimens through the compression caused by the impact.
- (2)
- When impacted, the pressure sensor on the impact force hammer generated a charge signal, which was converted into a voltage signal by the signal converter. The thin-film pressure sensor generated a corresponding current signal when sensing pressure, which was converted into a voltage signal by a linear voltage conversion module. The strain gauge changed its resistance due to deformation, and the signal amplifier converted it into a voltage signal. These three sets of signals were transmitted to the dynamic signal acquisition instrument.
- (3)
- The dynamic signal acquisition instrument transmitted the data to the dynamic signal testing and analysis software on the PC through a network cable, and generated data waveforms collected by the force hammer pressure sensor, thin-film pressure sensor, and strain gauge, thereby obtaining the time–domain curve of the impact force of the force hammer, the contact force between the blocks, and the strain curve.
2.4. Magnitude of Impact Force
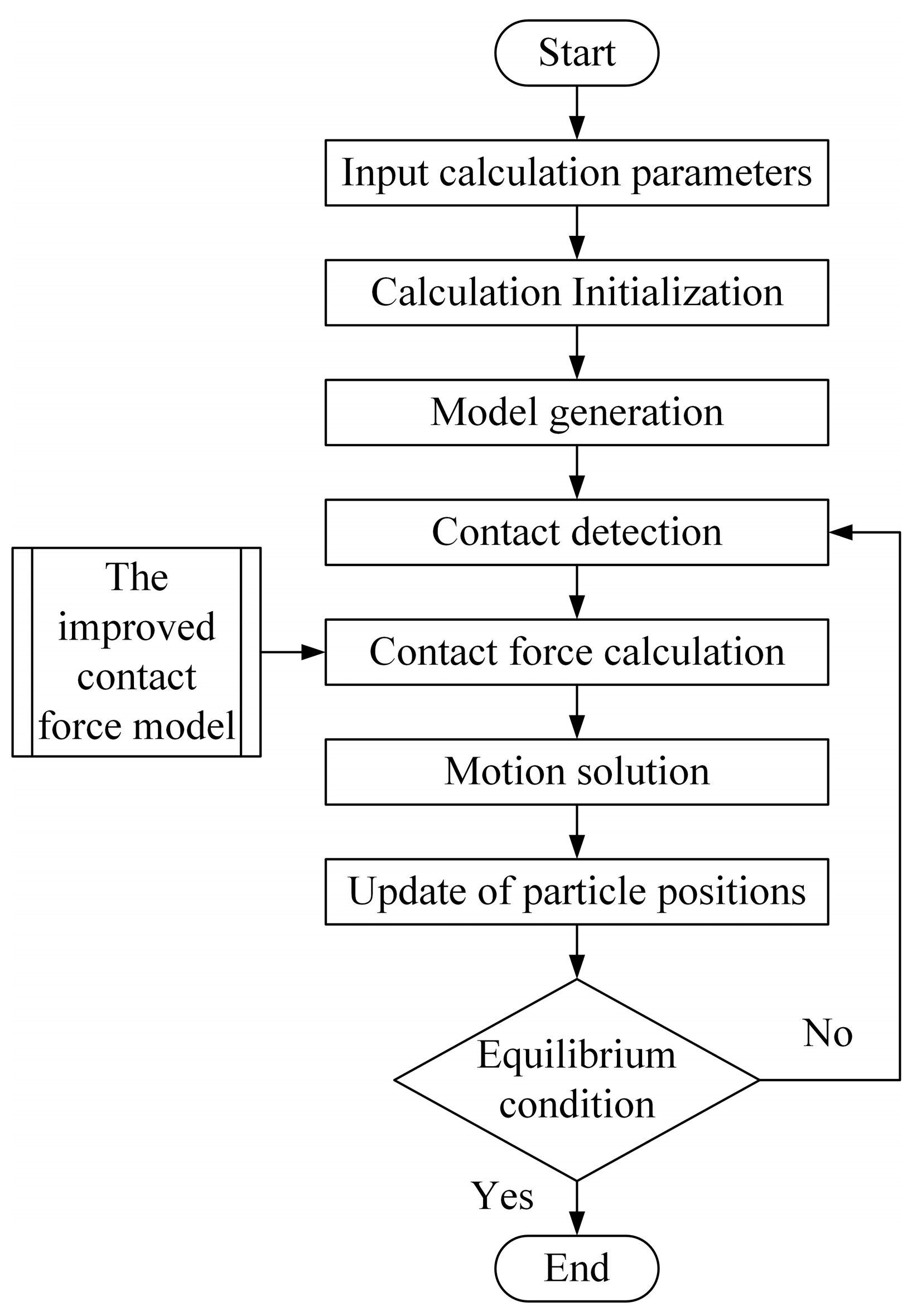
3. Calculation of Contact Force
3.1. Contact Depth
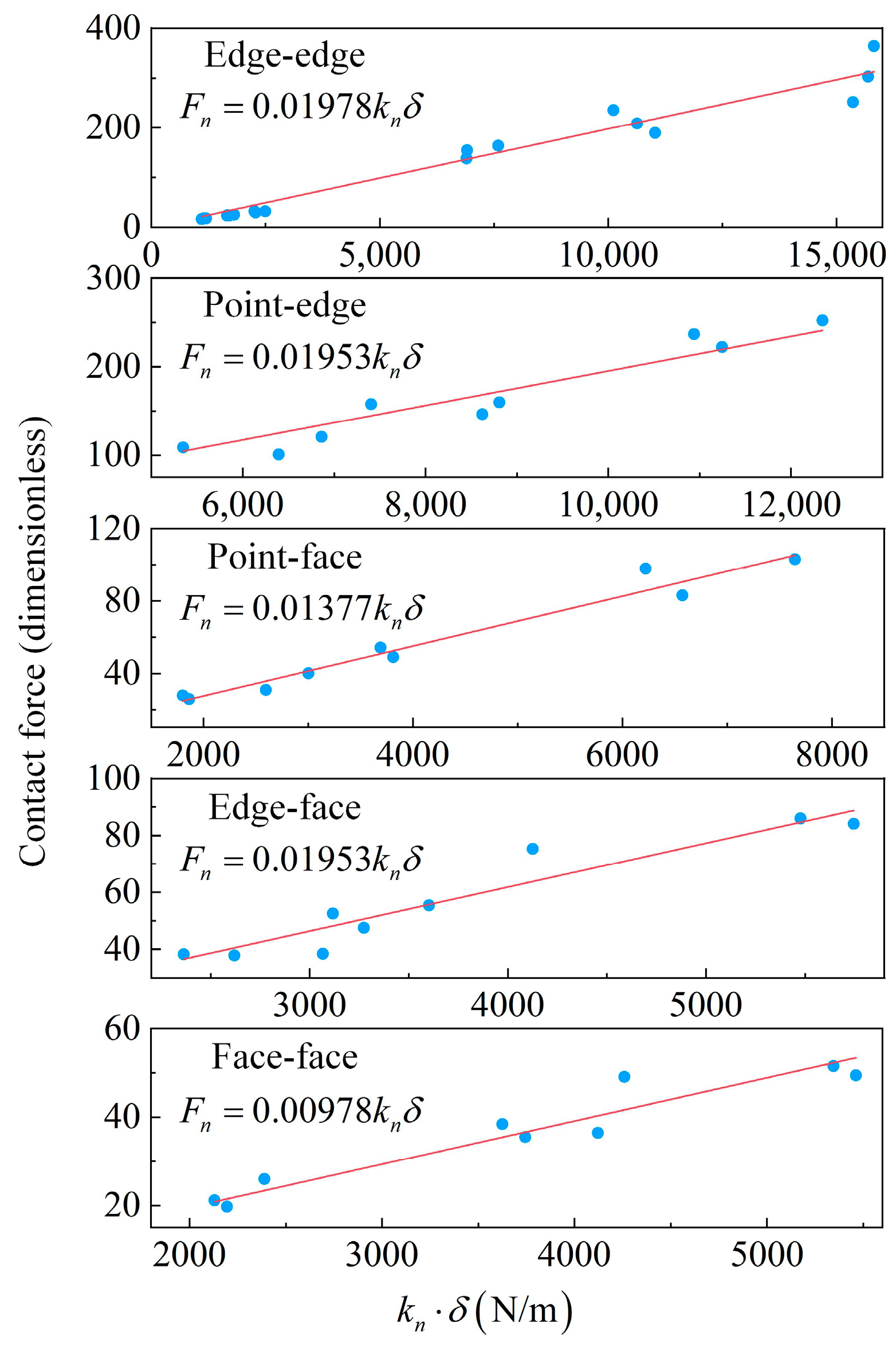
3.2. Normal Stiffness
3.3. Stiffness Correction Factor
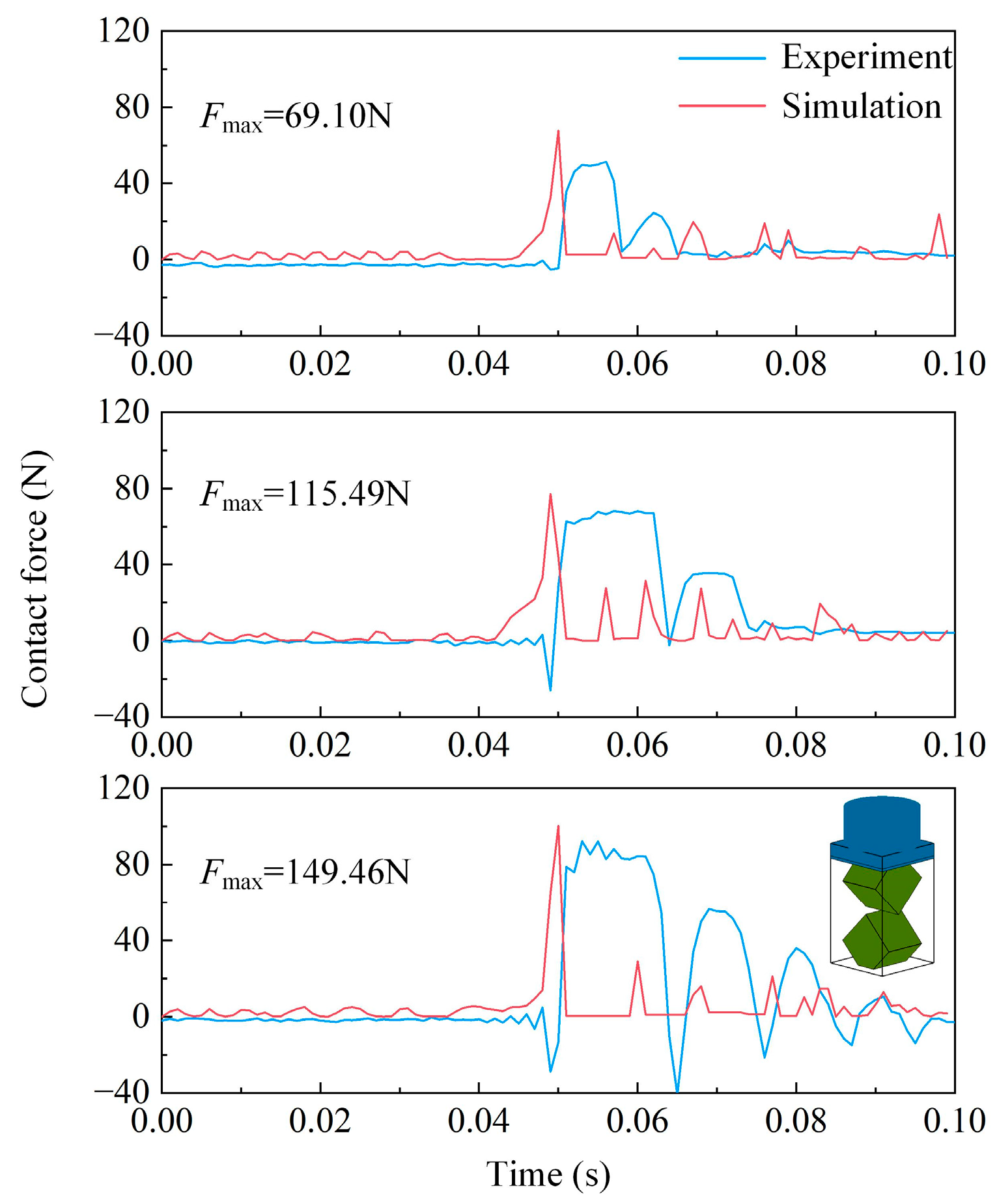
4. Comparison between DEM and Experimental Results
4.1. Two Elements under Edge–Edge Contact Mode
4.1.1. Collinear
4.1.2. Non-Collinear
4.2. Two Elements under Point–Edge Contact Mode
4.3. Two Elements under Point–Face Contact Mode
4.4. Two Elements under Edge–Face Contact Mode
4.5. Two Elements under Face–Face Contact Mode
5. Verification of Simulation
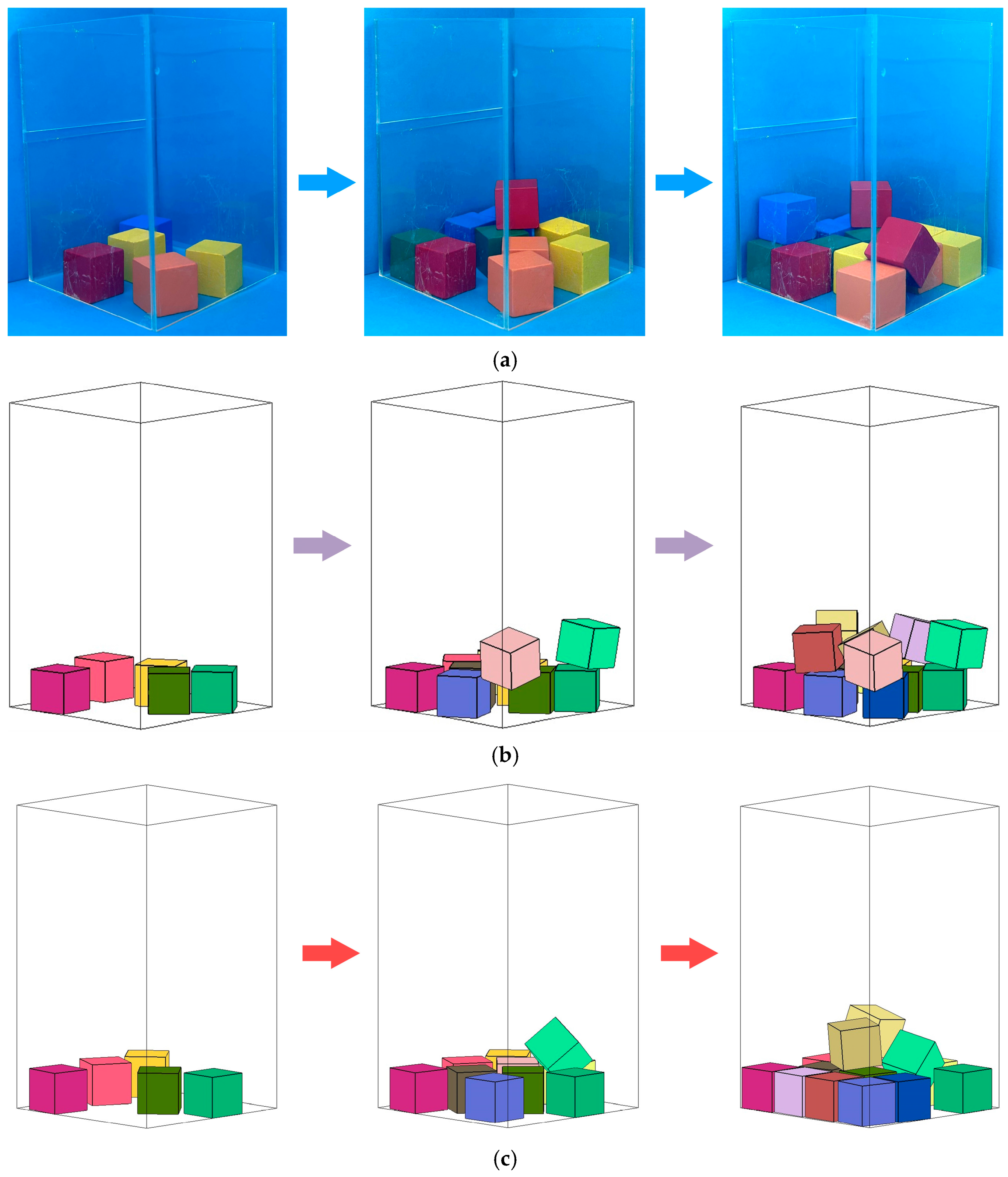
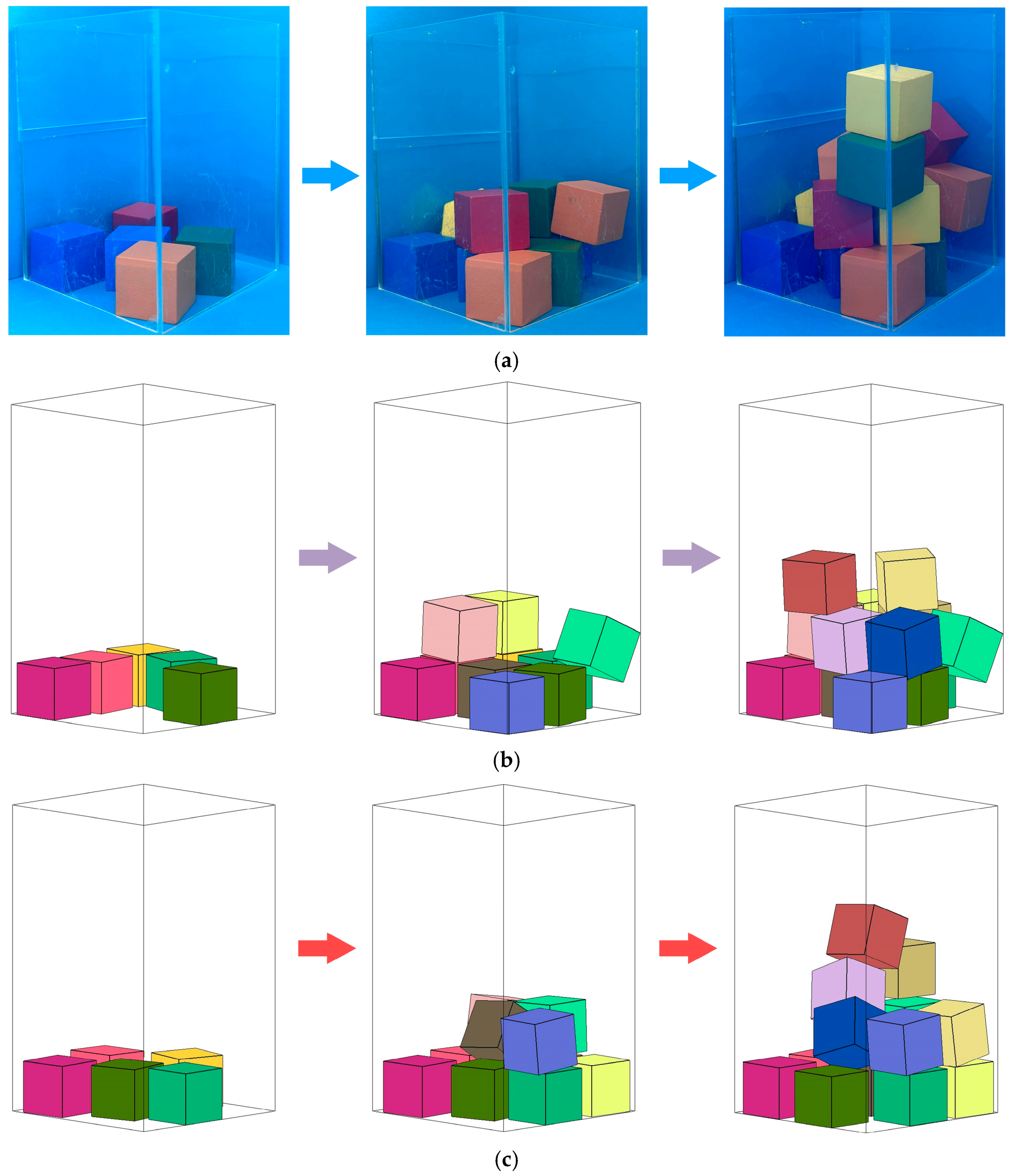
5.1. Packing Experiment of Multiple Cubes
5.2. Comparison between Packing Experiment and Simulation
5.2.1. Cubes with an Edge Length of 20 mm
5.2.2. Cubes with an Edge Length of 25 mm
5.2.3. Cubes with an Edge Length of 30 mm
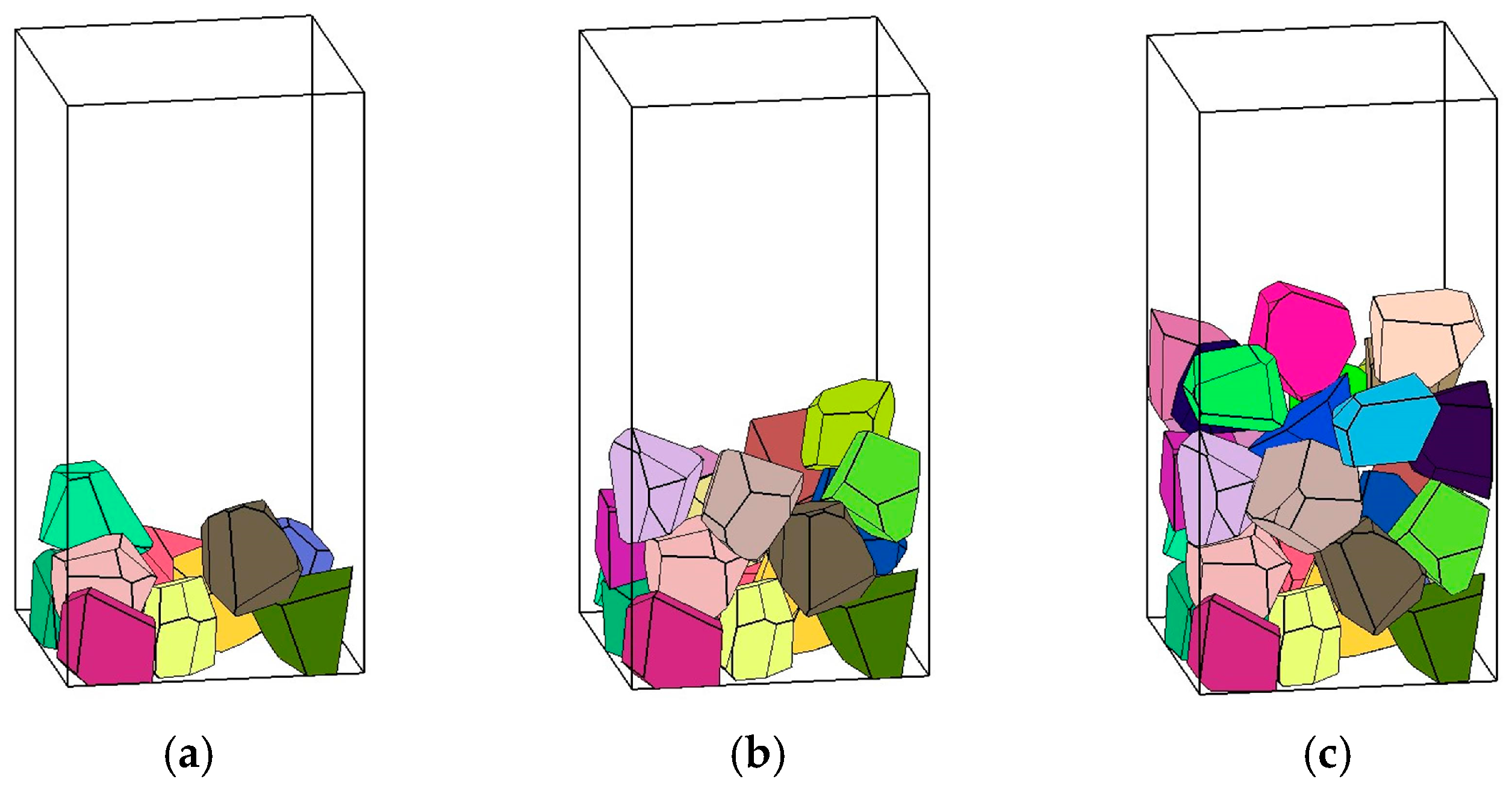
5.3. Packing Simulation of Randomly Shaped Polyhedral Elements
6. Conclusions
- The experimental method designed in this study can be employed to test the contact forces between polyhedral blocks under different modes. A contact stiffness correction coefficient was introduced into the Cundall model, leading to the construction of an improved contact force model suitable for polyhedral elements.
- The improved contact force model was incorporated into the DEM. An analysis of simulated contact force peaks and force patterns revealed an improved accuracy of the model, and this would affect the motion behavior of polyhedral elements.
- The DEM simulation methods, both before and after the improvement, were applied to packing experiments with cubic specimens. A comparative analysis of the results confirmed the improved accuracy and reliability of the improved contact force model in simulating the contact of polyhedral elements.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Horabik, J.; Molenda, M. Parameters and contact models for DEM simulations of agricultural granular materials: A review. Biosyst. Eng. 2016, 147, 206–225. [Google Scholar] [CrossRef]
- Petalas, A.L.; Dafalias, Y.F.; Papadimitriou, A.G. SANISAND-F: Sand constitutive model with evolving fabric anisotropy. Int. J. Solids Struct. 2020, 188, 12–31. [Google Scholar] [CrossRef]
- Das, S.K.; Das, A. Influence of quasi-static loading rates on crushable granular materials: A DEM analysis. Powder Technol. 2019, 344, 393–403. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.T.; Li, X.Z. Analysis of particle crushing in rolling compaction for rockfill dam using DEM. Appl. Mech. Mater. 2013, 353, 702–705. [Google Scholar] [CrossRef]
- Toe, D.; Bourrier, F.; Dorren, L.; Berger, F. A novel DEM approach to simulate block propagation on forested slopes. Rock Mech. Rock Eng. 2018, 51, 811–825. [Google Scholar] [CrossRef]
- Gong, H.; Song, W.; Huang, B.; Shu, X.; Han, B.; Wu, H.; Zou, J. Direct shear properties of railway ballast mixed with tire derived aggregates: Experimental and numerical investigations. Constr. Build. Mater. 2019, 200, 465–473. [Google Scholar] [CrossRef]
- Cil, M.B.; Alshibli, K.A. 3D analysis of kinematic behavior of granular materials in triaxial testing using DEM with flexible membrane boundary. Acta Geotech. 2014, 9, 287–298. [Google Scholar] [CrossRef]
- Liu, G.; Li, J. A three-dimensional discontinuous deformation analysis method for investigating the effect of slope geometrical characteristics on rockfall behaviors. Int. J. Comp. Meth. 2019, 16, 455–471. [Google Scholar] [CrossRef]
- Chen, G.; Zheng, L.; Zhang, Y.; Wu, J. Numerical simulation in rockfall analysis: A close comparison of 2-D and 3-D DDA. Rock Mech. Rock Eng. 2013, 46, 527–541. [Google Scholar] [CrossRef]
- Munjiza, A.A. The Combined Finite-Discrete Element Method; John Wiley Sons: London, UK, 2004. [Google Scholar]
- Mahabadi, O.K.; Randall, N.X.; Zong, Z.; Grasselli, G. A novel approach for micro-scale characterization and modeling of geomaterials incorporating actual material heterogeneity. Geophys. Res. Lett. 2012, 39, 1303. [Google Scholar] [CrossRef]
- Kang, G.; Ning, Y.; Liu, R. Simulation of force chains and particle breakage of granular material by numerical manifold method. Powder Technol. 2021, 390, 464–472. [Google Scholar] [CrossRef]
- Seyedan, S.; Sołowski, W.T. From solid to disconnected state and back: Continuum modelling of granular flows using material point method. Comput. Struct. 2021, 251, 106545. [Google Scholar] [CrossRef]
- Liu, C.; Sun, Q.; Zhou, G.G.D. Coupling of material point method and discrete element method for granular flows impacting simulations. Int. J. Numer. Meth. Eng. 2018, 115, 172–188. [Google Scholar] [CrossRef]
- Cundall, P.A. A computer model for simulating progressive, large-scale movement in blocky rock system. In Proceedings of the International Symposium on Rock Mechanics, Nancy, France, 4–6 October 1971; pp. 129–136. [Google Scholar]
- Huang, Y.; Sun, W.; Xie, Q.; You, H.; Wu, K. Discrete Element Simulation of the Shear Behavior of Binary Mixtures Composed of Spherical and Cubic Particles. Appl. Sci. 2023, 13, 9163. [Google Scholar] [CrossRef]
- Nassauer, B.; Kuna, M. Contact forces of polyhedral particles in discrete element method. Granul. Matter. 2013, 15, 349–355. [Google Scholar] [CrossRef]
- Orozco, L.F.; Delenne, J.Y.; Sornay, P.; Radjai, F. Discrete-element model for dynamic fracture of a single particle. Int. J. Solids Struct. 2019, 166, 47–56. [Google Scholar] [CrossRef]
- Kildashti, K.; Dong, K.; Yu, A. Contact force models for non-spherical particles with different surface properties: A review. Powder Technol. 2023, 418, 118323. [Google Scholar] [CrossRef]
- Cundall, P.A. Formulation of a three-dimensional distinct element model—Part I. A scheme to detect and represent contacts in a system composed of many polyhedral blocks. A scheme to detect and represent contacts in a system composed of many polyhedral blocks. Int. J. Rock Mech. Min. 1988, 25, 107–116. [Google Scholar] [CrossRef]
- Liu, G.; Xu, W.; Zhou, Q. DEM contact model for spherical and polyhedral particles based on energy conservation. Comput. Geotech. 2023, 153, 105072. [Google Scholar] [CrossRef]
- Feng, Y.T.; Owen, D.R.J. A 2D polygon/polygon contact model: Algorithmic aspects. Eng. Comput. 2004, 21, 265–277. [Google Scholar] [CrossRef]
- Feng, Y.T.; Han, K.; Owen, D.R.J. Energy-conserving contact interaction models for arbitrarily shaped discrete elements. Comput. Method. Appl. Mech. 2012, 205, 169–177. [Google Scholar] [CrossRef]
- Rojek, J.; Karlis, G.F.; Malinowski, L.J.; Beer, J. Setting up virgin stress conditions in discrete element models. Comput. Geotech. 2013, 48, 228–248. [Google Scholar] [CrossRef] [PubMed]
- Minamoto, H.; Kawamura, S. Effects of material strain rate sensitivity in low speed impact between two identical spheres. Int. J. Impact Eng. 2009, 36, 680–686. [Google Scholar] [CrossRef]
- Cole, D.M.; Mathisen, L.U.; Hopkins, M.A.; Knapp, B.R. Normal and sliding contact experiments on gneiss. Granul. Matter 2010, 12, 69–86. [Google Scholar] [CrossRef]
- Ouyang, Y.; Yang, Q.; Chen, X. Bonded-particle model with nonlinear elastic tensile stiffness for rock-like materials. Appl. Sci. 2017, 7, 686. [Google Scholar] [CrossRef]
- Liu, P.; Liu, J.; Gao, S.; Wang, Y.; Zheng, H.; Zhen, M.; Zhao, F.; Liu, Z.; Ou, C.; Zhuang, R. Calibration of Sliding Friction Coefficient in DEM between Different Particles by Experiment. Appl. Sci. 2023, 13, 11883. [Google Scholar] [CrossRef]
- Nadler, B.; Guillard, F.; Einav, I. Kinematic model of transient shape-induced anisotropy in dense granular flow. Phys. Rev. Lett. 2018, 120, 198003. [Google Scholar] [CrossRef]
- Malone, K.F.; Xu, B.H. Determination of contact parameters for discrete element method simulations of granular systems. Particuology 2008, 6, 521–528. [Google Scholar] [CrossRef]
- Mack, S.; Langston, P.; Webb, C.; York, T. Experimental validation of polyhedral discrete element model. Powder Technol. 2011, 214, 431–442. [Google Scholar] [CrossRef]








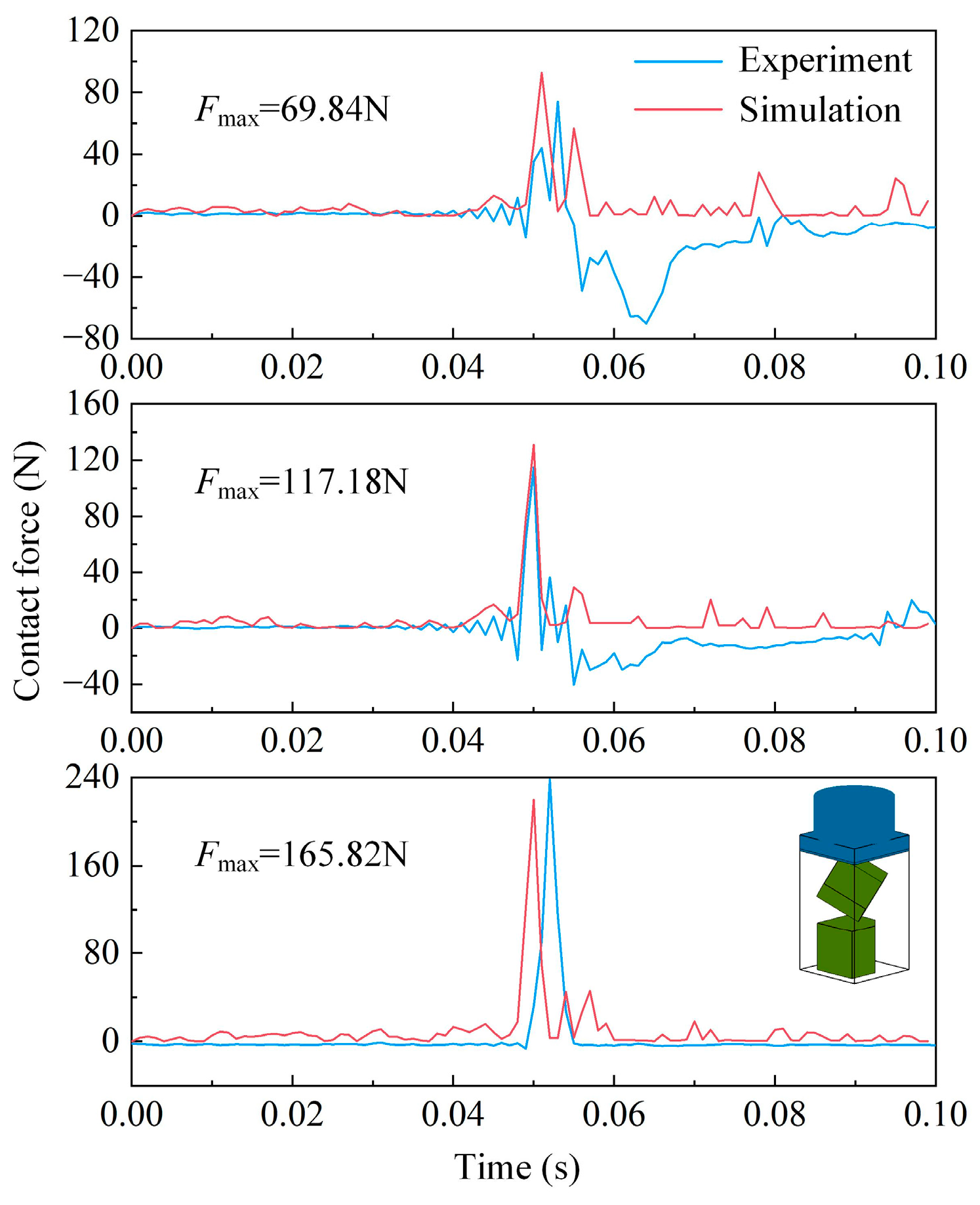
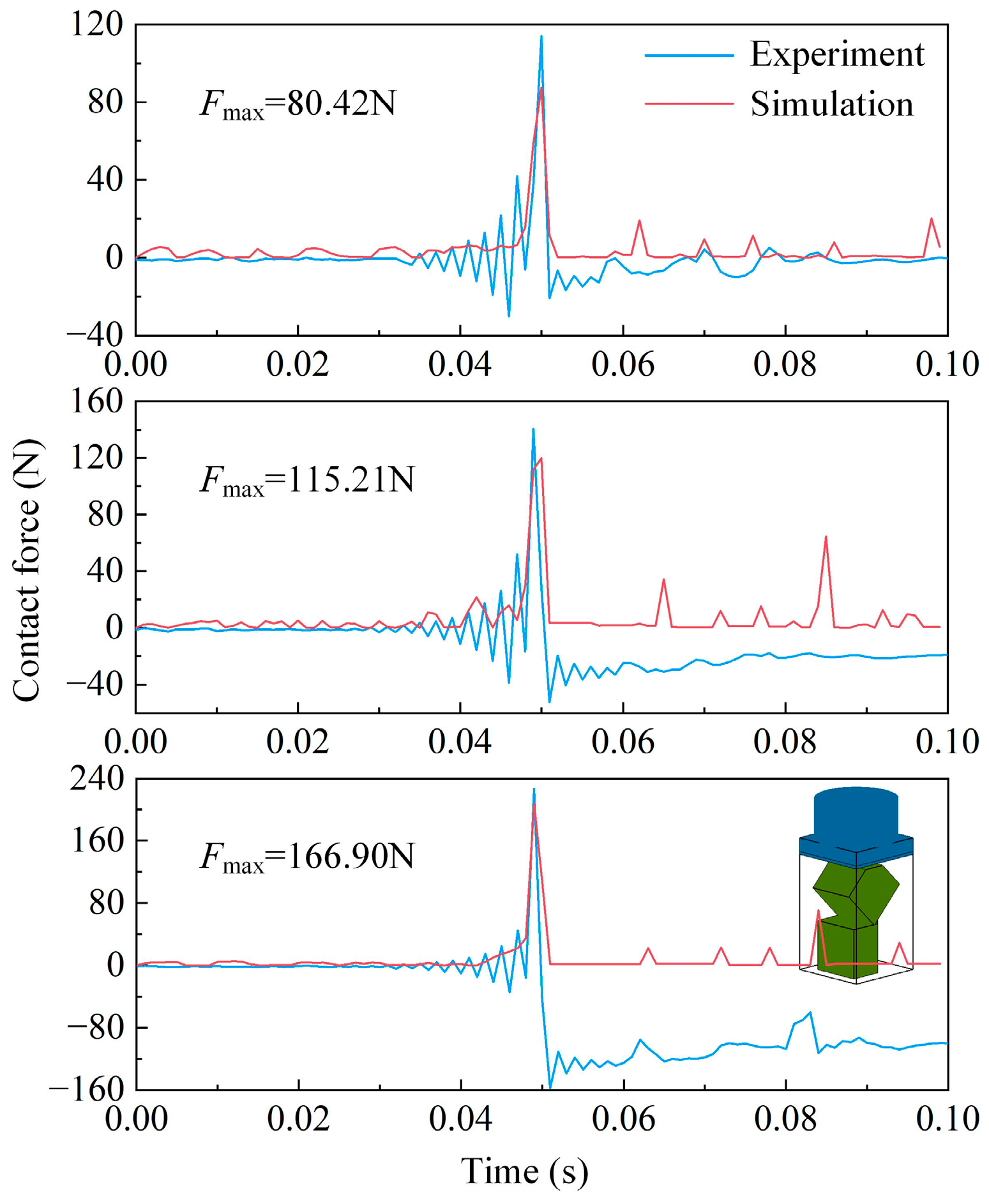
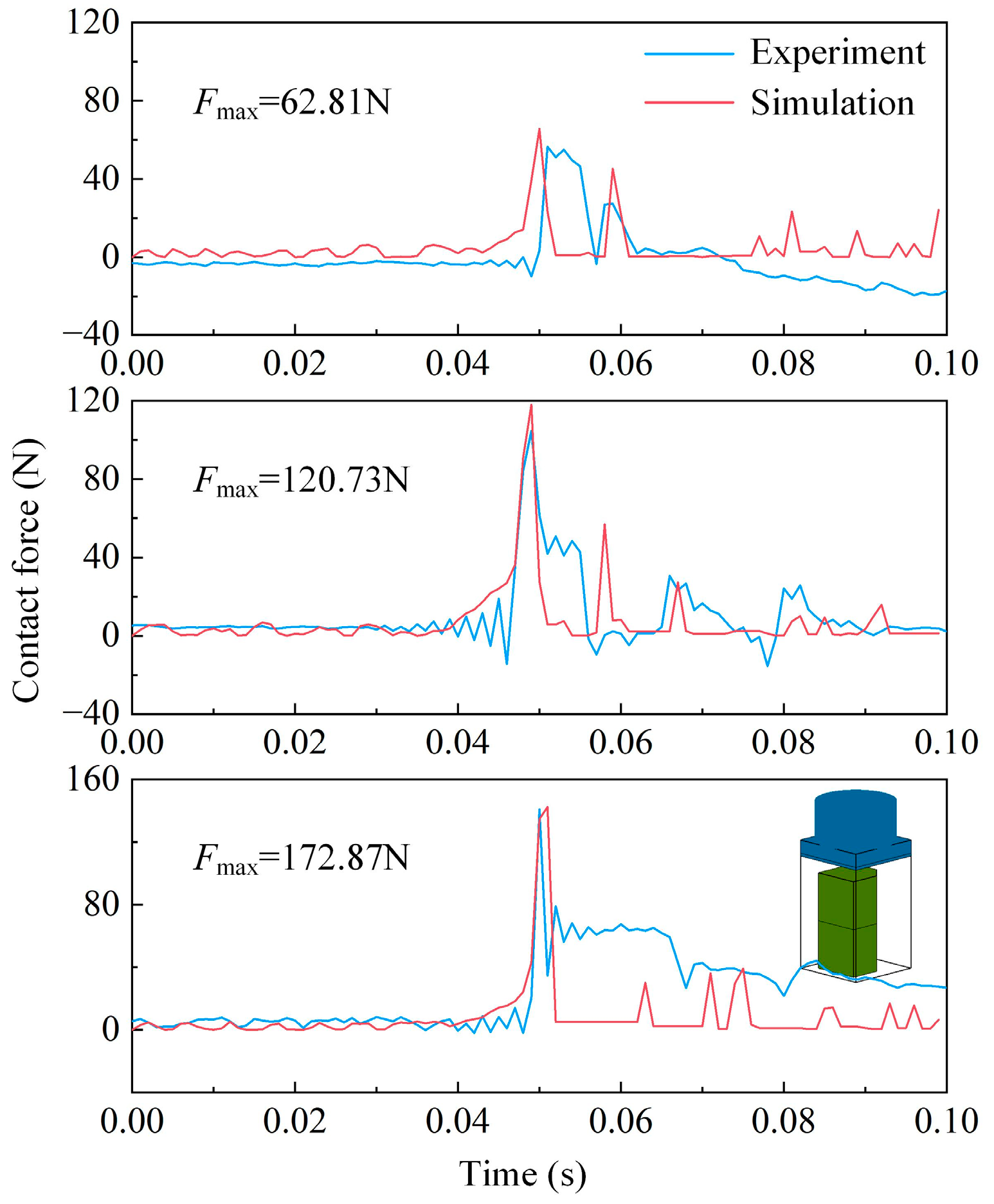


| Group | Edge–Edge (Collinear) | Point–Edge | Point–Face | Edge–Edge (Non-Collinear) | Edge–Face | Face–Face |
|---|---|---|---|---|---|---|
| 1 | 65.31 | 68.60 | 69.84 | 69.10 | 80.42 | 62.81 |
| 2 | 72.28 | 70.14 | 71.26 | 70.35 | 83.64 | 68.11 |
| 3 | 78.18 | 73.53 | 74.20 | 72.49 | 87.37 | 73.58 |
| 4 | 111.14 | 114.52 | 117.18 | 115.49 | 115.21 | 120.73 |
| 5 | 115.79 | 118.85 | 121.55 | 118.68 | 118.96 | 124.65 |
| 6 | 121.82 | 125.21 | 122.59 | 123.01 | 123.51 | 127.09 |
| 7 | 176.68 | 165.72 | 165.82 | 149.46 | 166.90 | 172.87 |
| 8 | 177.35 | 169.34 | 168.69 | 155.23 | 170.21 | 173.62 |
| 9 | 179.68 | 175.09 | 173.92 | 160.57 | 174.86 | 176.82 |
| Group | Edge–Edge (Collinear) | Point–Edge | Point–Face | Edge–Edge (Non-Collinear) | Edge–Face | Face–Face |
|---|---|---|---|---|---|---|
| 1 | −9.1 × 10−8 | −8.4 × 10−8 | −6.1 × 10−8 | −6.9 × 10−8 | −8.6 × 10−8 | −7.2 × 10−8 |
| 2 | −9.1 × 10−8 | −7 × 10−8 | −5.9 × 10−8 | −7.3 × 10−8 | −1 × 10−7 | −7 × 10−8 |
| 3 | −1 × 10−7 | −9 × 10−8 | −8.5 × 10−8 | −6.7 × 10−8 | −7.8 × 10−8 | −7.8 × 10−8 |
| 4 | −1.4 × 10−7 | −9.7 × 10−8 | −9.8 × 10−8 | −9.6 × 10−8 | −1.1 × 10−7 | −1.4 × 10−7 |
| 5 | −1.4 × 10−7 | −1.1 × 10−7 | −1.2 × 10−7 | −8.2 × 10−8 | −1 × 10−7 | −1.2 × 10−7 |
| 6 | −1.3 × 10−7 | −1.2 × 10−7 | −1.2 × 10−7 | −1.1 × 10−7 | −1.2 × 10−7 | −1.2 × 10−7 |
| 7 | −2 × 10−7 | −1.5 × 10−7 | −2.2 × 10−7 | −1.4 × 10−7 | −1.4 × 10−7 | −1.4 × 10−7 |
| 8 | −2.1 × 10−7 | −1.4 × 10−7 | −2 × 10−7 | −1.2 × 10−7 | −1.9 × 10−7 | −1.8 × 10−7 |
| 9 | −2.1 × 10−7 | −1.6 × 10−7 | −2.5 × 10−7 | −1.5 × 10−7 | −1.8 × 10−7 | −1.8 × 10−7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Liu, J.; Zhen, M.; Liu, Z.; Zheng, H.; Zhao, F.; Ou, C.; Liu, P. An Improved Contact Force Model of Polyhedral Elements for the Discrete Element Method. Appl. Sci. 2024, 14, 311. https://doi.org/10.3390/app14010311
Wang Y, Liu J, Zhen M, Liu Z, Zheng H, Zhao F, Ou C, Liu P. An Improved Contact Force Model of Polyhedral Elements for the Discrete Element Method. Applied Sciences. 2024; 14(1):311. https://doi.org/10.3390/app14010311
Chicago/Turabian StyleWang, Yue, Jun Liu, Mengyang Zhen, Zheng Liu, Haowen Zheng, Futian Zhao, Chen Ou, and Pengcheng Liu. 2024. "An Improved Contact Force Model of Polyhedral Elements for the Discrete Element Method" Applied Sciences 14, no. 1: 311. https://doi.org/10.3390/app14010311






