Simulation of Spinal Cord Reflexes
Abstract
:1. Introduction
1.1. The Myotatic (Stretch) Reflex and the Reciprocal Inhibition in the Stretch Reflex
1.2. The Autogenic Inhibition Reflex and the Reciprocal Excitation in the Autogenic Inhibition Reflex
1.3. The Flexion Reflex and the Reciprocal Inhibition for the Flexion Reflex and Crossed Extension Reflex
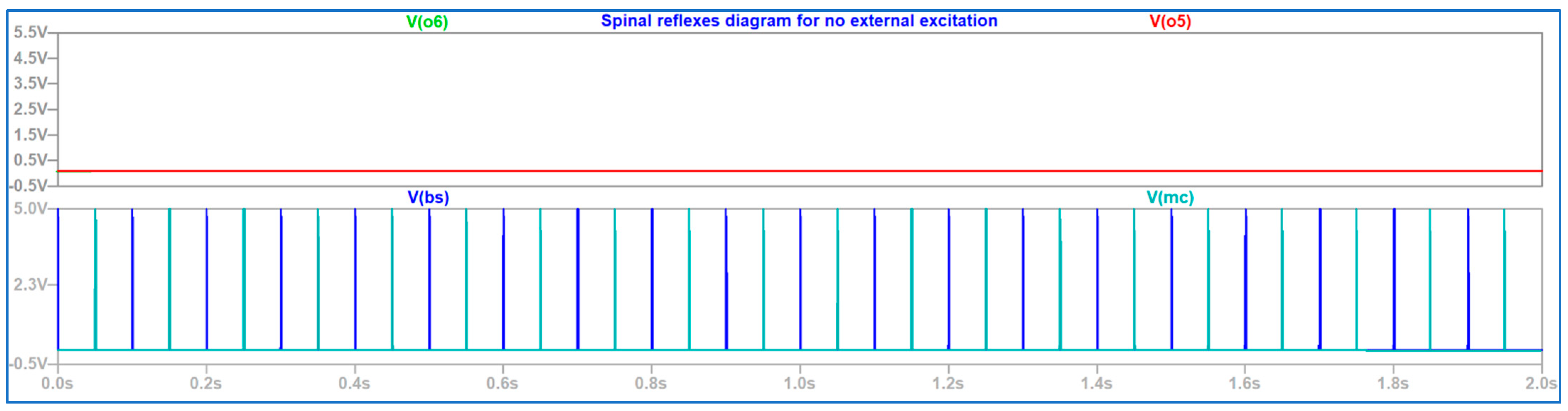
1.4. The Recurrent Inhibition of Motor Neurons
2. Theoretical Considerations
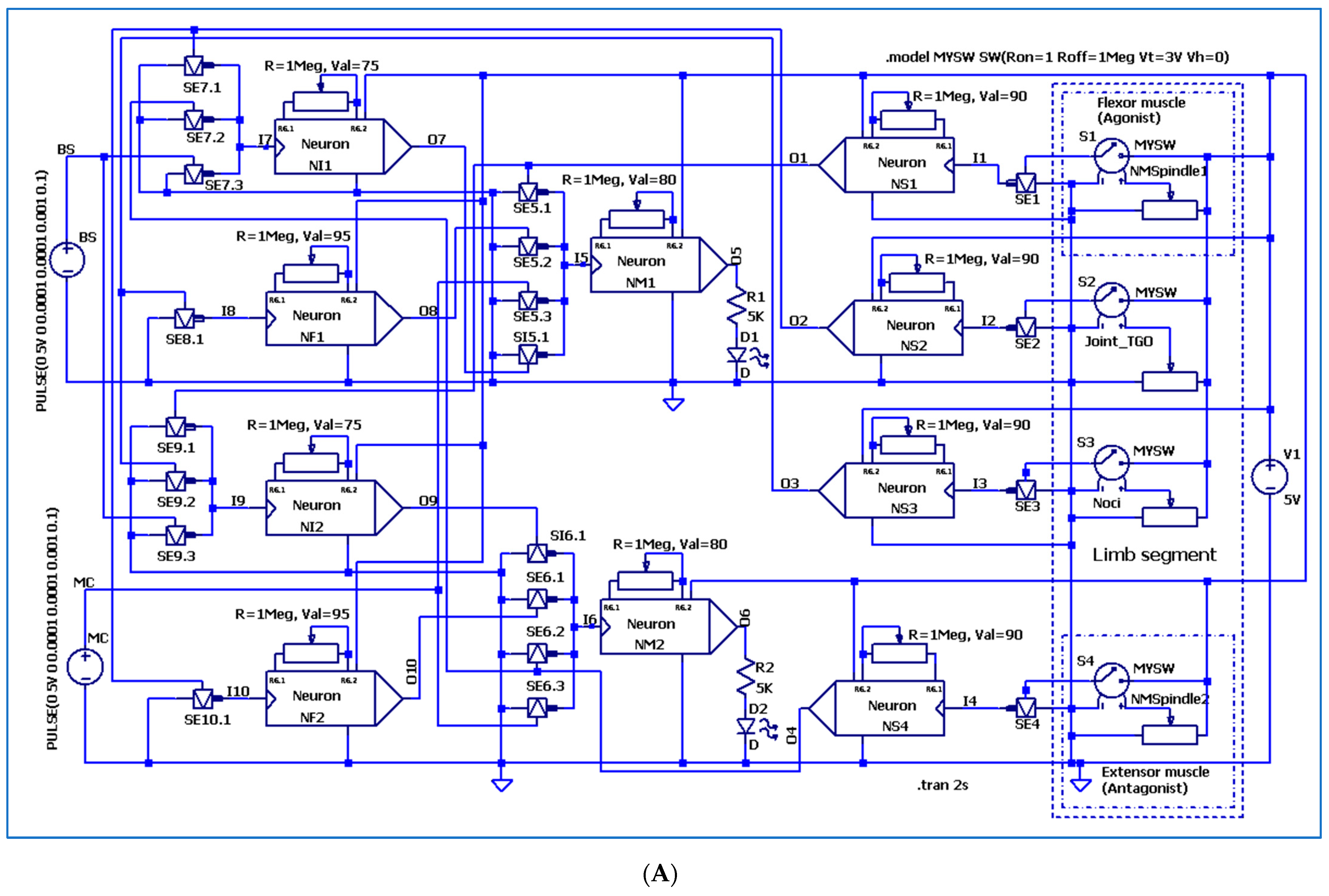
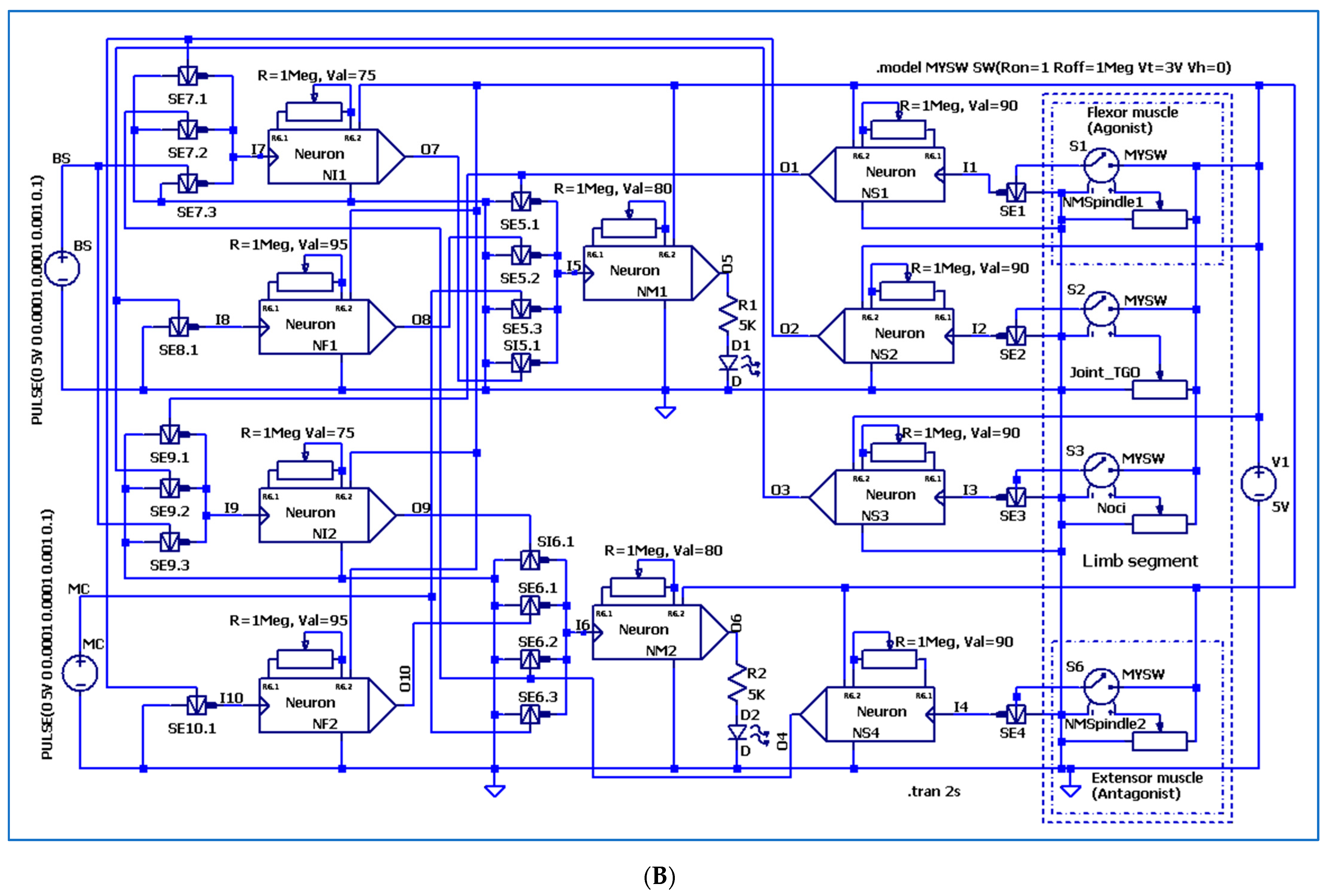
3. The Electronic Circuitry for the Models of Different Neuron Types
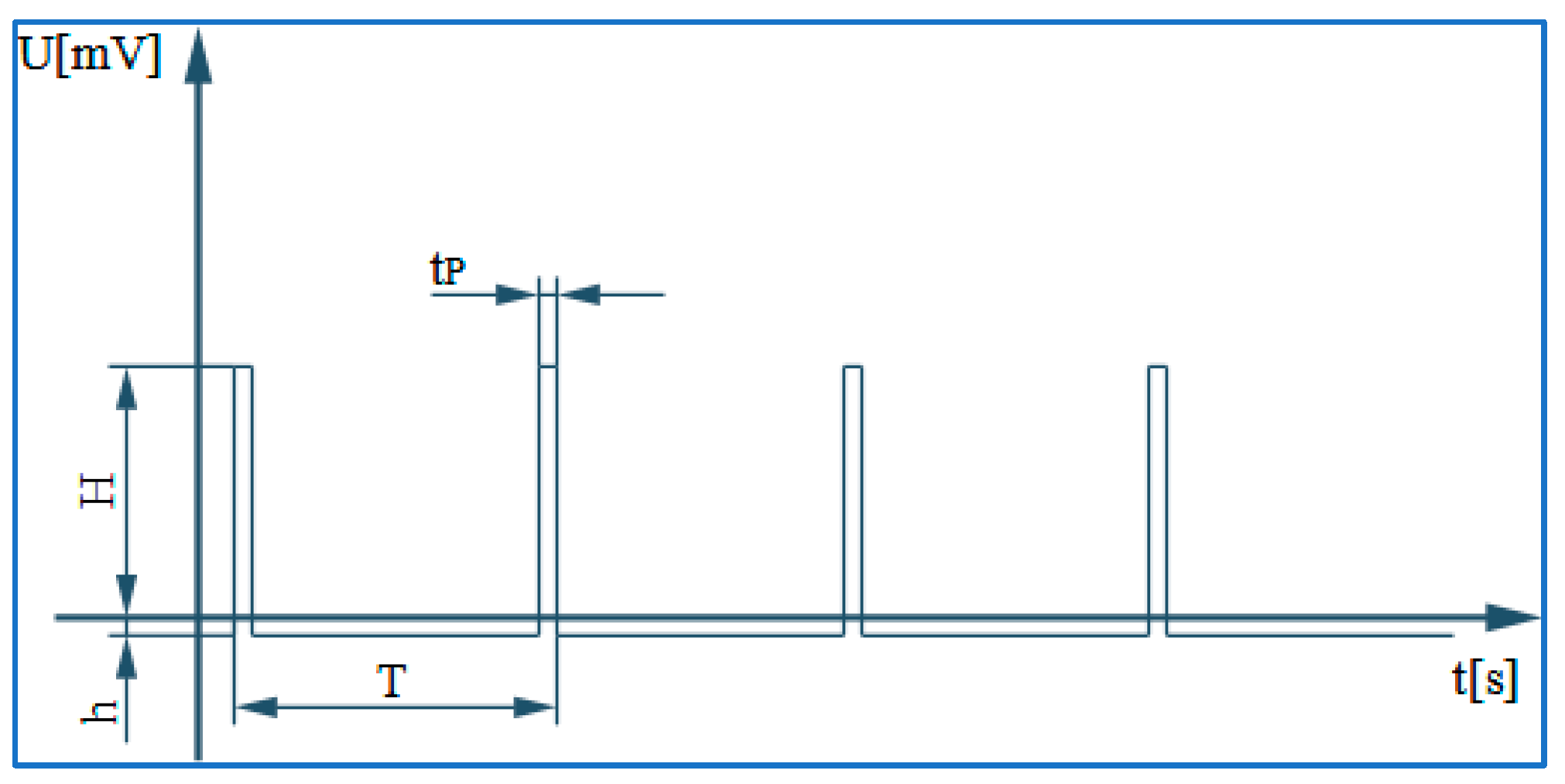
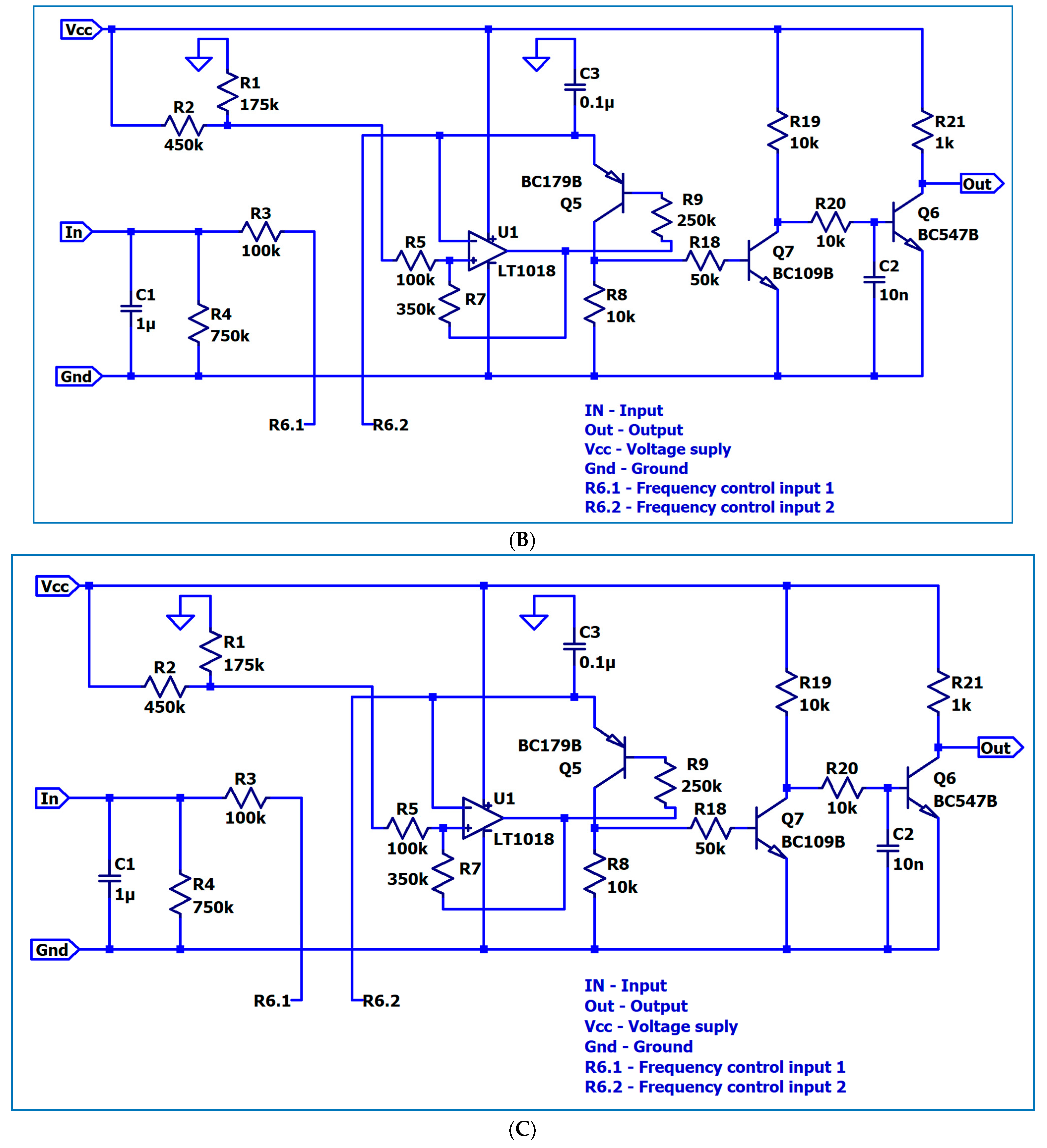
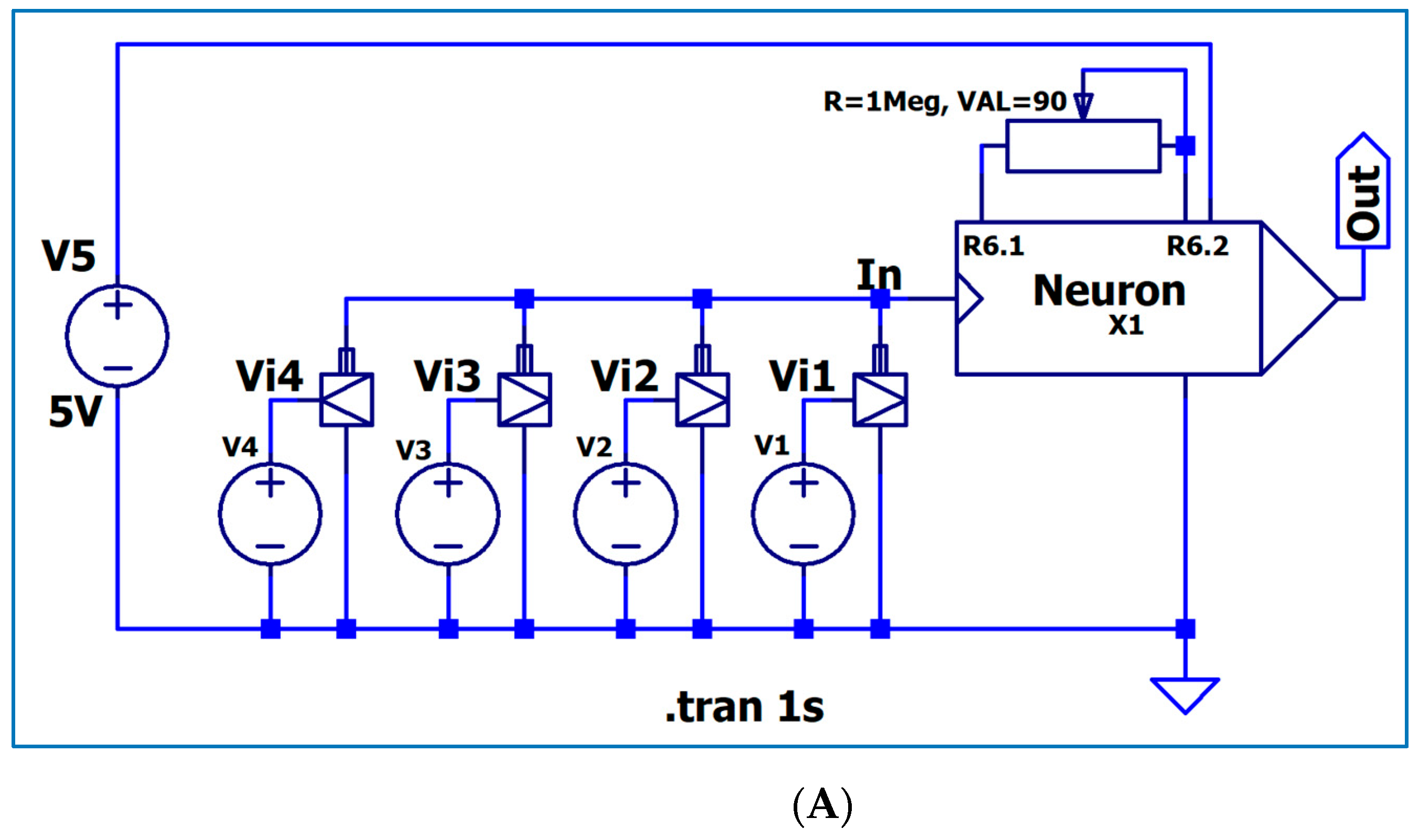
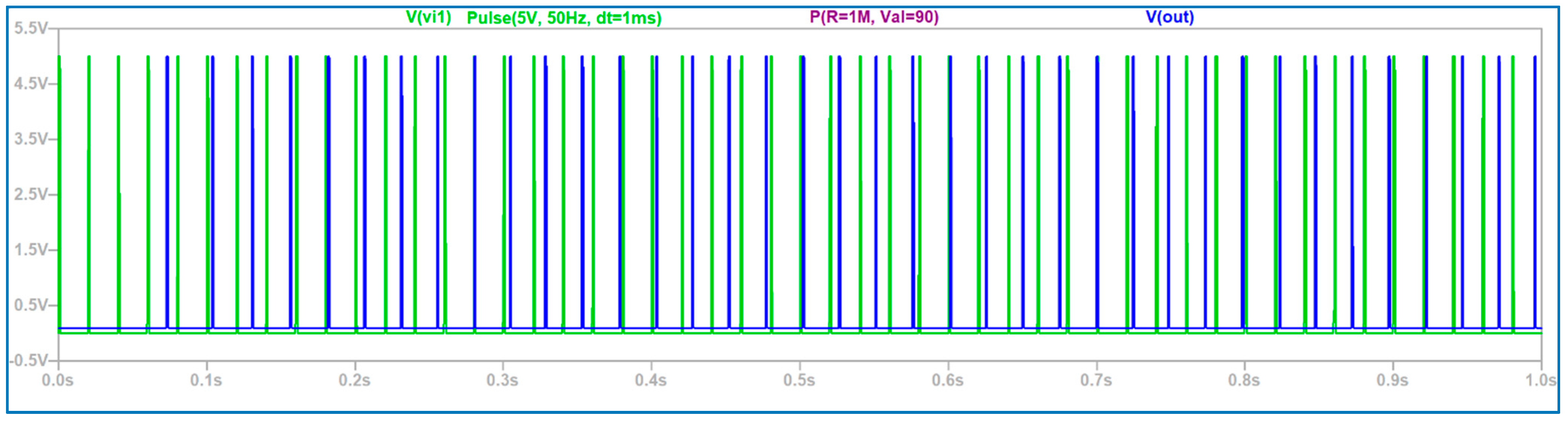
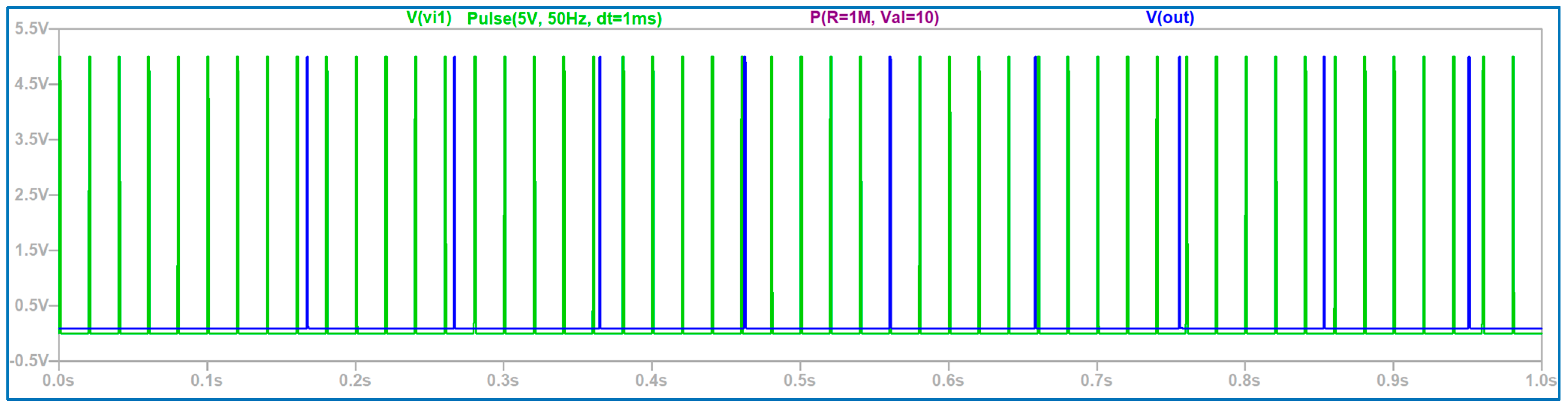
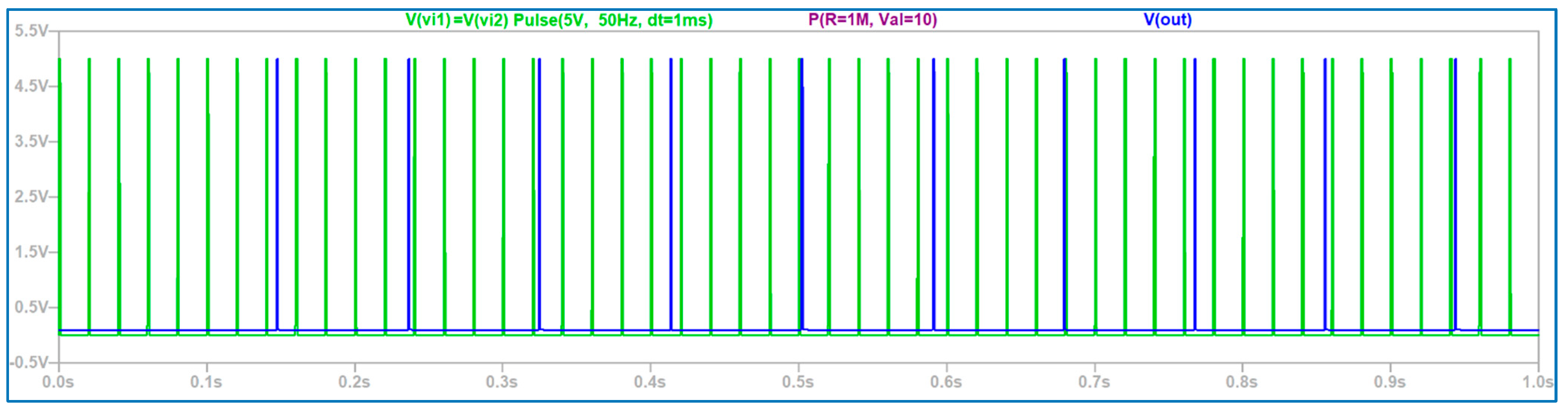
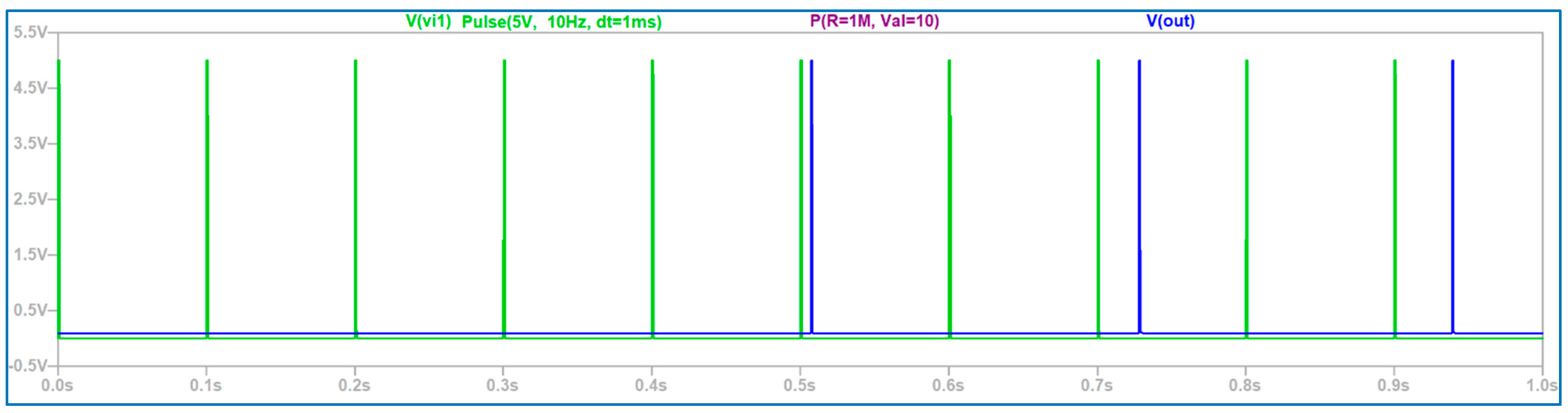
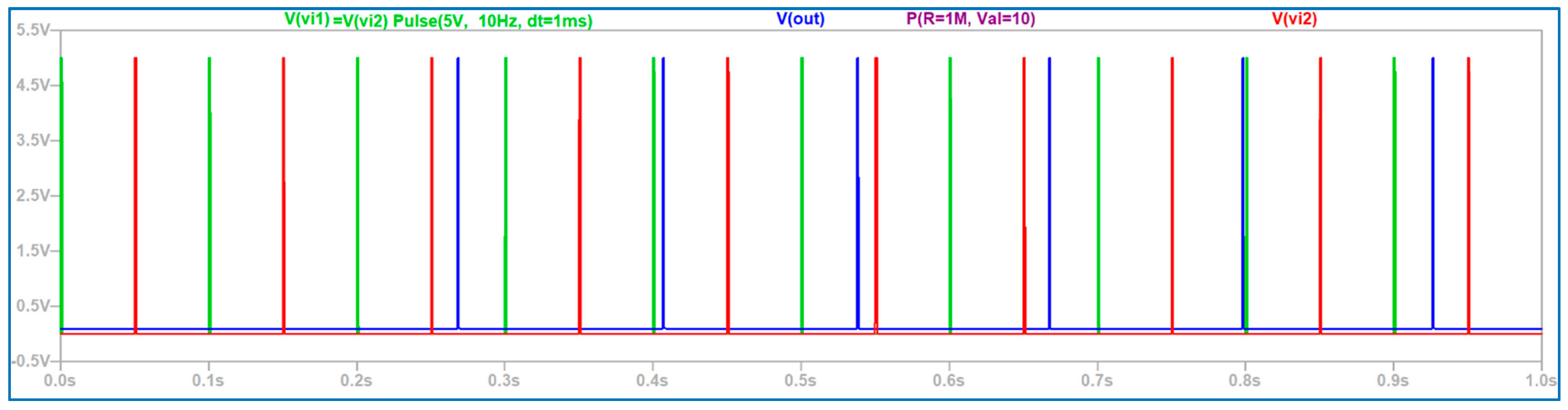
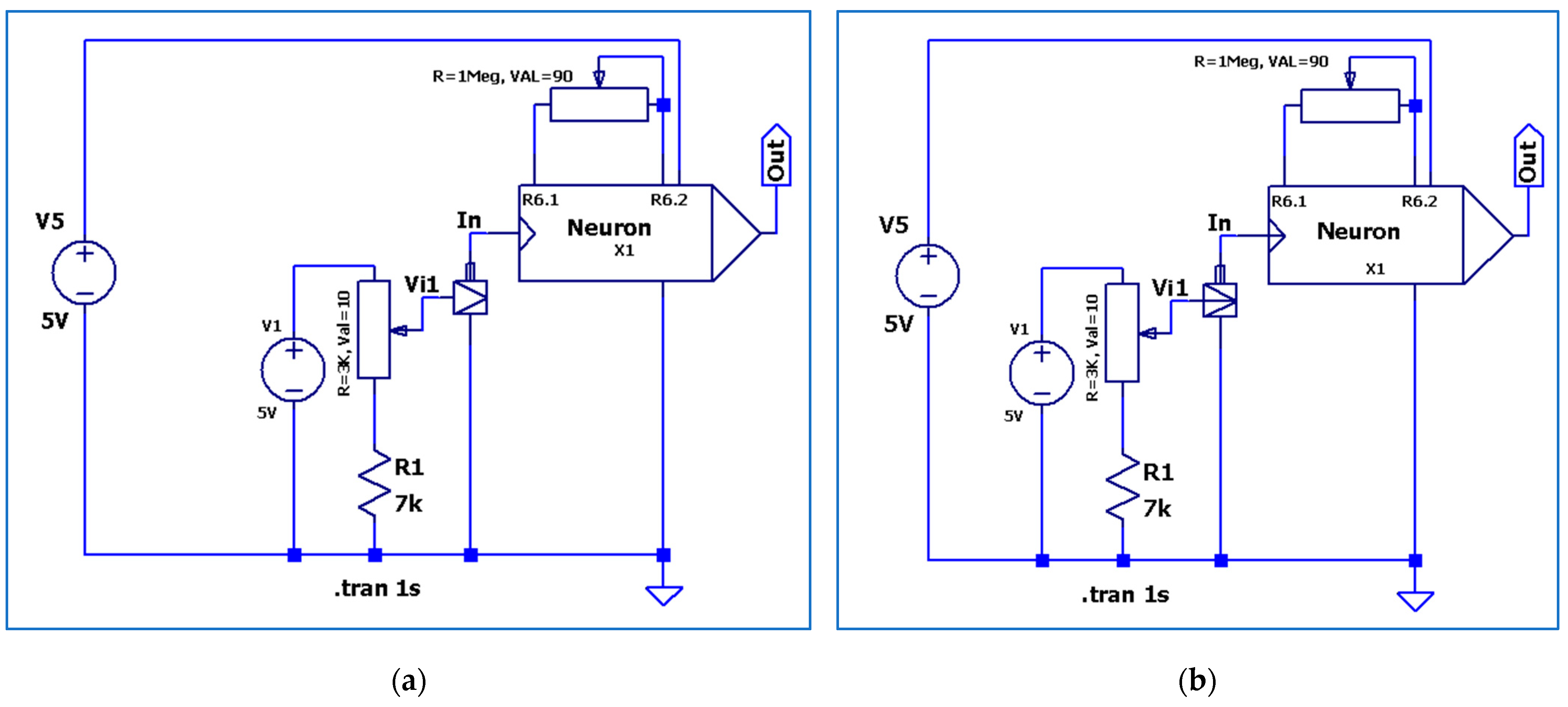
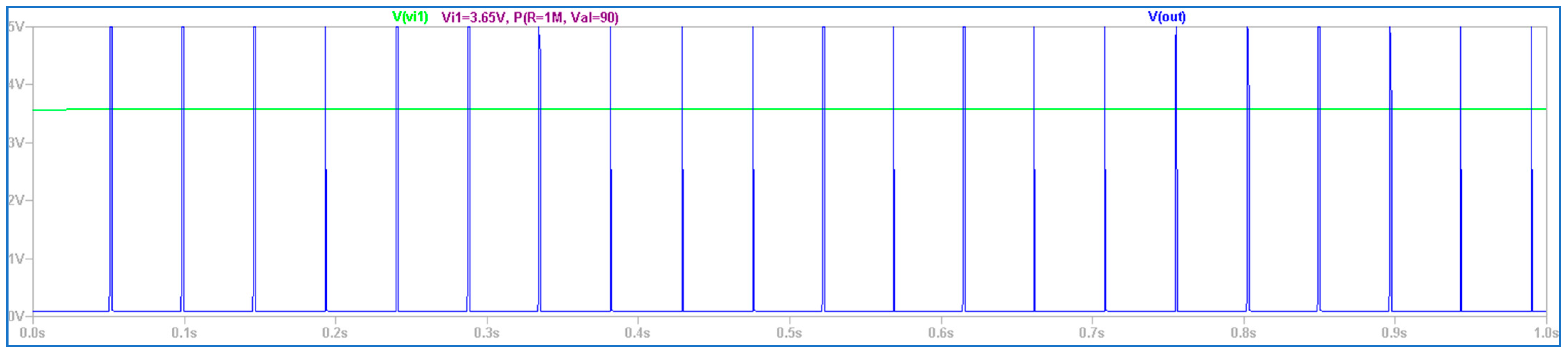
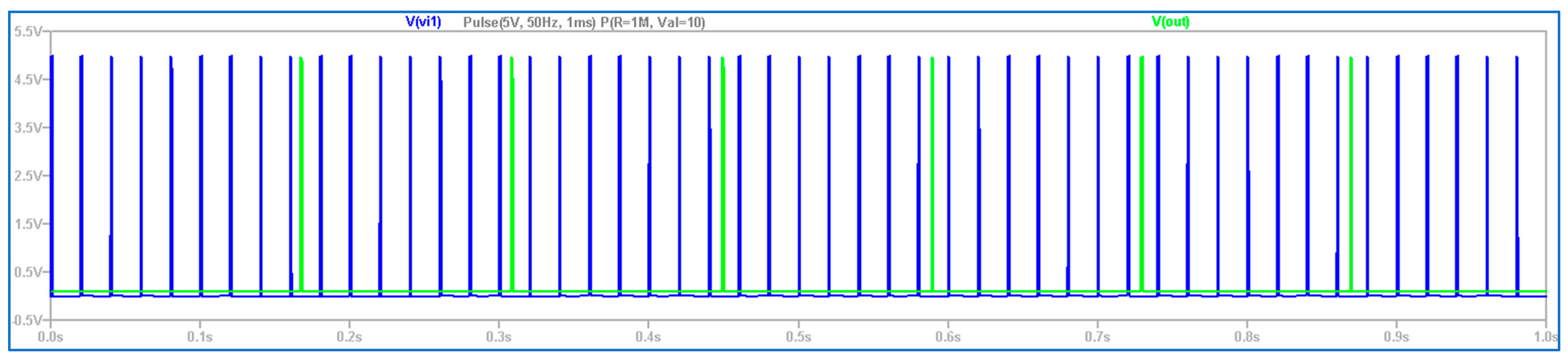
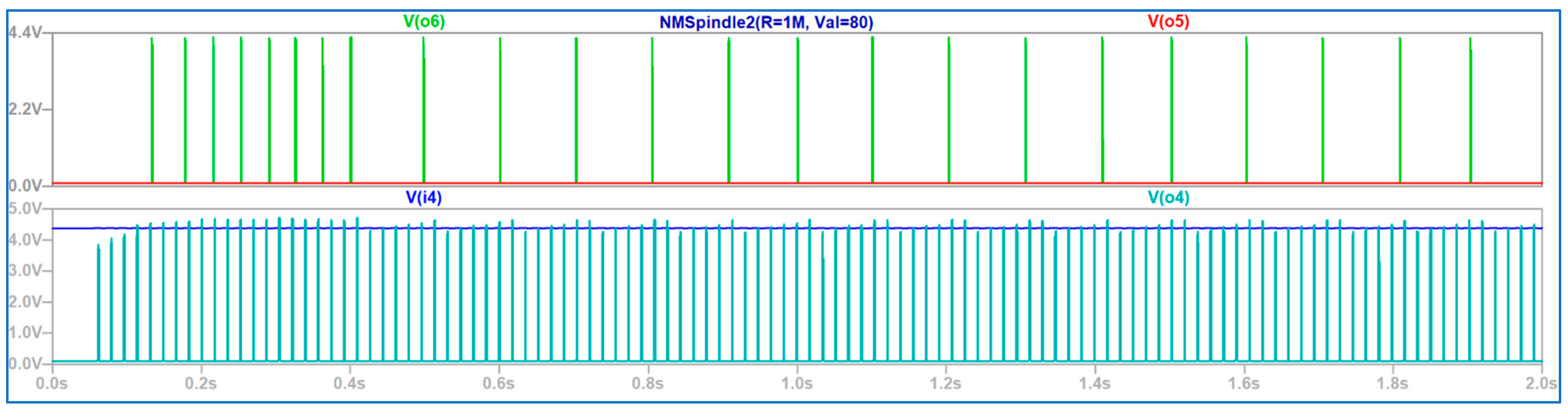
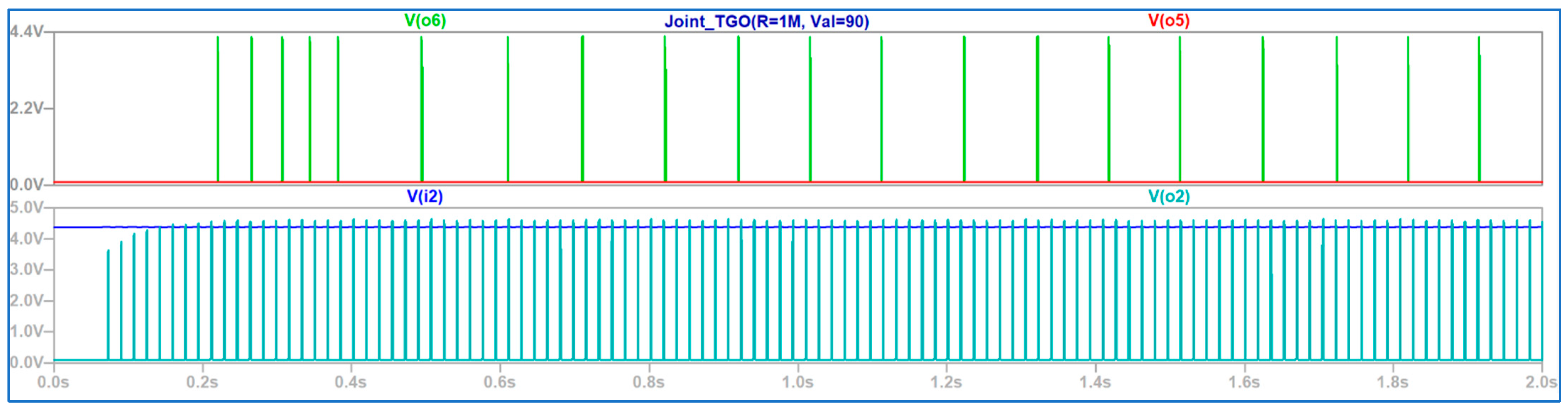
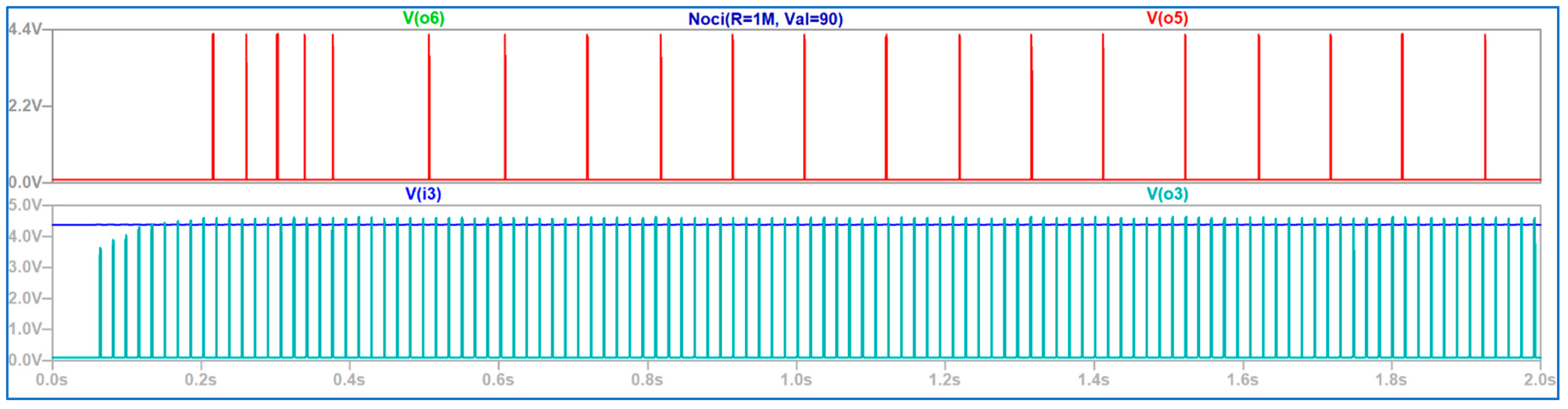
3.1. The Electronic Scheme Model and Signal Diagram for the Common Neuron Type
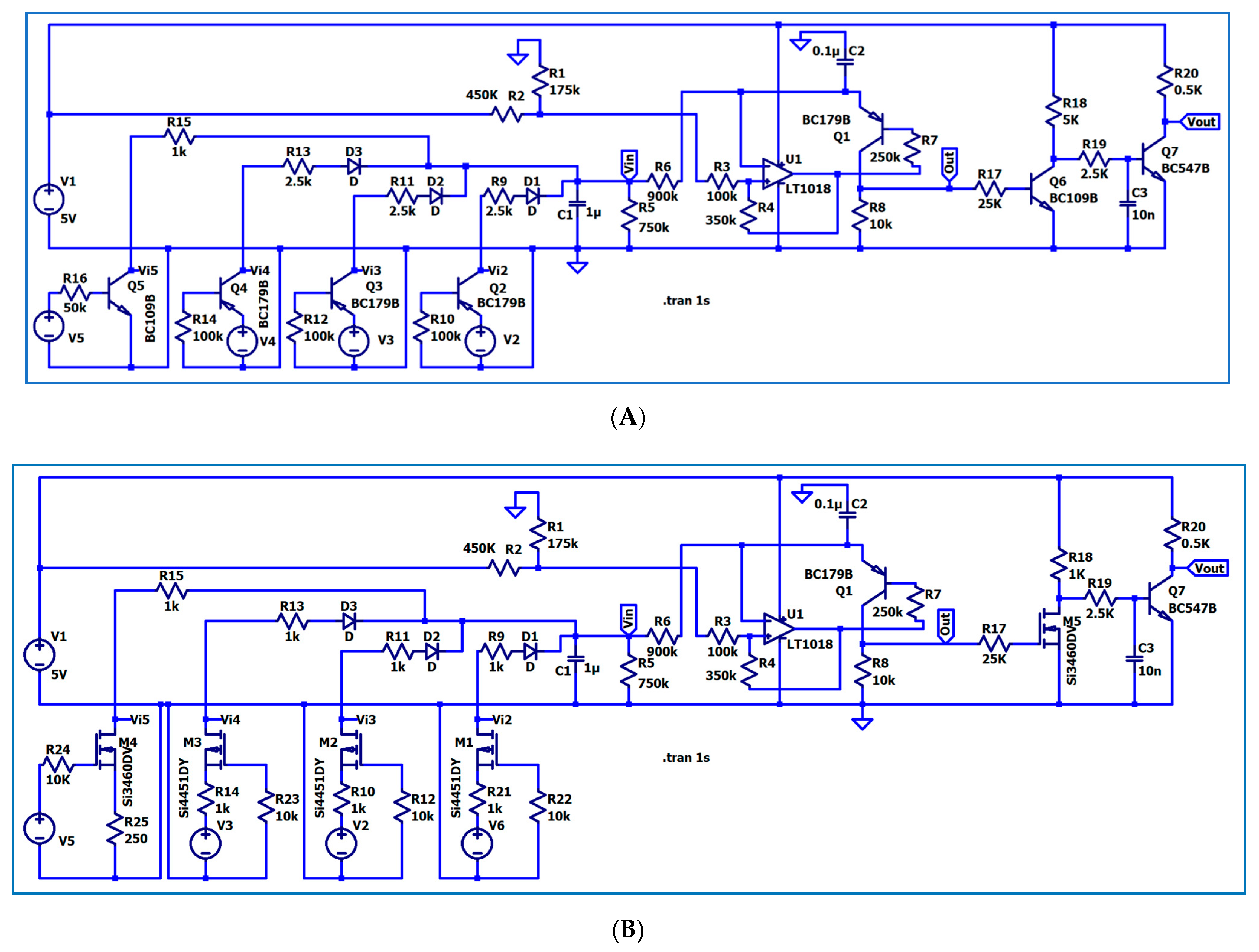
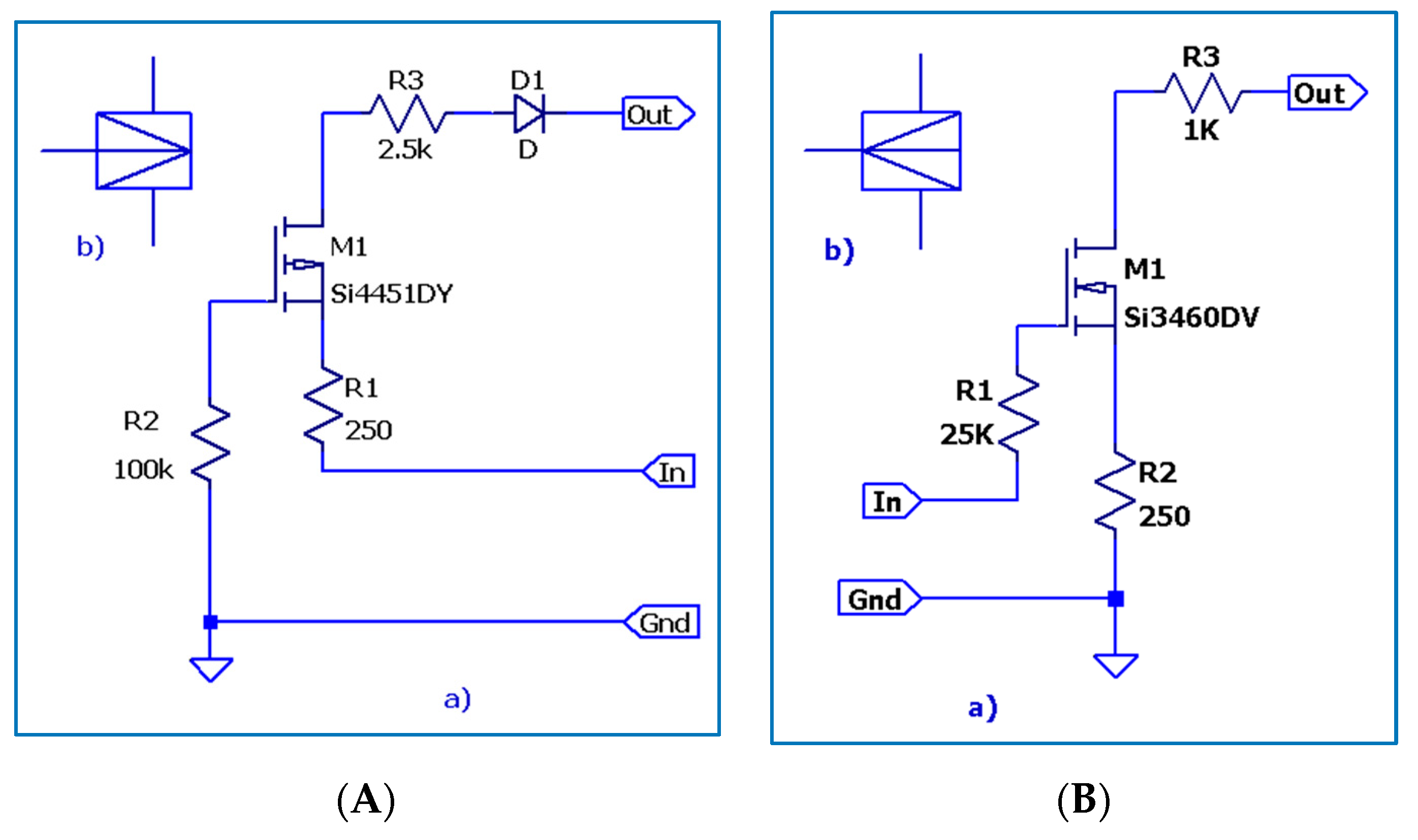
3.2. The Electronic Scheme Model and Signal Diagram for the Sensitive Neuron
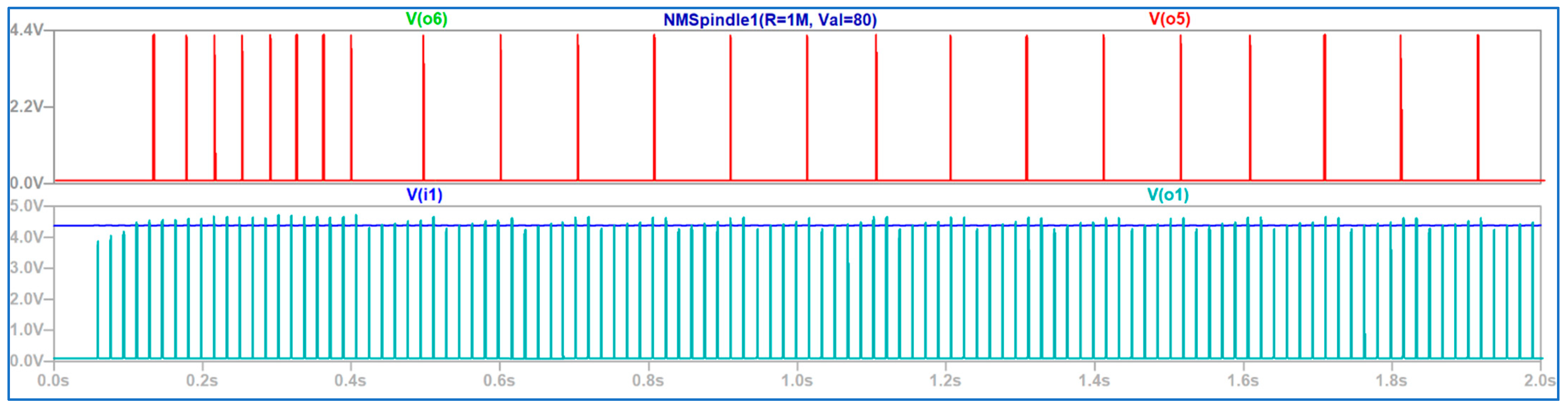
3.3. The Electronic Scheme Model and Signal Diagram for the Recurrent Inhibition Reflex
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Byrne, G.H.; Dafny, N. Neuroscience Online: An Electronic Textbook for the Neurosciences; Department of Neurobiology and Anatomy, University of Texas Medical School at Houston: Houston, TX, USA, 1997; Available online: https://nba.uth.tmc.edu/neuroscience/m/ (accessed on 1 December 2023).
- Guertin, P.A. Central pattern generator for locomotion: Anatomical, physiological, and pathophysiological considerations. Front. Neurol. 2013, 3, 183. [Google Scholar] [CrossRef] [PubMed]
- Mescher, A.L. Junqueira’s Basic Histology: Text and Atlas; McGraw Hill: New York, NY, USA, 2018. [Google Scholar]
- Morega, M. Bioelectromagnetism, 1st ed.; Matrix Rom: Bucharest, Romania, 1999; pp. 57–128. [Google Scholar]
- Cruz, P.M.R.; Cossins, J.; Beeson, D.; Vincent, A. The Neuromuscular Junction in Health and Disease: Molecular Mechanisms Governing Synaptic Formation and Homeostasis. Front. Mol. Neurosci. 2020, 13, 610964. [Google Scholar] [CrossRef] [PubMed]
- Balal, A.; Rukh, S.; Balali, S. Designing a Dual Active Transformer DC-DC Forward Converter for DC Micro-Grid Applications Using LTSPICE. Int. J. Appl. Eng. Res. 2021, 16, 327–331. [Google Scholar]
- Engelhardt, M. Using Transformers in LTspice/SwitcherCAD III. Linear Technol. Mag. 2006, 23–24. [Google Scholar]
- Ahmed, M.R.; Todd, R.; Forsyth, A.J. Predicting SiC MOSFET behavior under hard-switching, soft-switching, and false turn-on conditions. IEEE Trans. Ind. Electron. 2017, 64, 9001–9011. [Google Scholar] [CrossRef]
- Babacan, Y. An operational transconductance amplifier-based memcapacitor and meminductor. Electrica 2018, 18, 36–38. [Google Scholar] [CrossRef]
- Wang, X.; Jin, C.; Eshraghian, J.K.; Iu HH, C.; Ha, C. A behavioral spice model of a binarized memristor for digital logic implementation. Circuits Syst. Signal Process. 2021, 40, 2682–2693. [Google Scholar] [CrossRef]
- Alonso, G. Get Up and Running with LTspice. 41 Underst. Fundam. Earthq. Signal Sens. Netw. 2019, 53, 60. [Google Scholar]
- Akram, S.; Bertilsson, K.; Siden, J. LTspice electro-thermal model of joule heating in high density polyethylene optical fiber microducts. Electronics 2019, 8, 1453. [Google Scholar] [CrossRef]
- Viswanathan, S.M. Design and Analysis of Operational Transconductance Amplifier (OTA) Under 180 nm Technology Using LTspice. JASC 2020, 1076–5131, 107–115. [Google Scholar]
- Liu, G.; Shen, S.; Jin, P.; Wang, G.; Liang, Y. Design of memristor-based combinational logic circuits. Circuits Syst. Signal Process. 2021, 40, 5825–5846. [Google Scholar] [CrossRef]
- Menzio, L.U.C.A.; Arcidiacono, R.; Borghi, G.; Boscardin, M.; Cartiglia, N.; Vignali, M.C.; Costa, M.; Dalla Betta, G.F.; Ferrero, M.; Ficorella, F.; et al. DC-coupled resistive silicon detectors for 4D tracking. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2022, 1041, 167374. [Google Scholar] [CrossRef]
- Khawaldeh, H.A.; Al-Soeidat, M.; Lu DD, C.; Li, L. Simple and Fast Dynamic Photovoltaic Emulator based on a Physical Equivalent PV-cell Model. J. Eng. 2021, 2021, 276–285. [Google Scholar] [CrossRef]
- Özer, E.; Başak, M.E.; Kaçar, F. Realizations of lossy and lossless capacitance multiplier using CFOAs. AEU-Int. J. Electron. Commun. 2020, 127, 153444. [Google Scholar] [CrossRef]
- Başak, M.E.; Kaçar, F. Lossy/lossless grounded inductance simulators using current feedback operational amplifier (CFOA). Electrica 2018, 18, 95–99. [Google Scholar]
- Grasso, F.; Manetti, S.; Piccirilli, M.C.; Reatti, A. A Laplace transform approach to the simulation of DC-DC converters. Int. J. Numer. Model. Electron. Netw. Devices Fields 2019, 32, e2618. [Google Scholar] [CrossRef]
- Maranhão, G.; Guimarães, J.G. Low-power hybrid memristor-CMOS spiking neuromorphic STDP learning system. IET Circuits Devices Syst. 2021, 15, 237–250. [Google Scholar] [CrossRef]
- Choi, M.; Jang, M.; Yoo, S.S.; Noh, G.; Yoon, K. Deep Neural Network for Navigation of a Single-Element Transducer During Transcranial Focused Ultrasound Therapy: Proof of Concept. IEEE J. Biomed. Health Inform. 2022, 26, 5653–5664. [Google Scholar] [CrossRef]
- Mikkelsen, J.H. Ltspice—An Introduction; Technical Report; Institute of Electronic Systems, Aalborg University: Aalborg, Denmark, 2005. [Google Scholar]
- Chung, E.J.; Yang, B.E.; Park, I.Y.; Yi, S.; On, S.W.; Kim, Y.H. Effectiveness of cone-beam computed tomography-generated cephalograms using artificial intelligence cephalometric analysis. Sci. Rep. 2022, 12, 20585. [Google Scholar] [CrossRef]
- Moon, H.C.; Park, S.J.; Kim, Y.D.; Kim, K.M.; Kang, H.; Lee, E.J.; Kim, M.S.; Kim, J.W.; Kim, Y.H.; Park, C.K.; et al. Navigation of Frameless Fixation for Gama Knife Radiosurgery Using Fixed Augumented Reality. Sci. Rep. 2022, 12, 4486. [Google Scholar] [CrossRef]
- Marican, N.D.; Halim, M.H.A.; Nor, M.A.M.; Nasir, M.F.M. Reflexology, A Modality in Manipulative and Body Based Method. Indian J. Public Health Res. 2019, 10, 515–519. [Google Scholar] [CrossRef]
- Kaur, N.; Bhanot, K.; Ferreira, G. Lower Extremity and Trunk Electromyographic Muscle Activity During Performance of the Y-Balance Test on Stable and Unstable Surfaces. Int. J. Sports Phys. Ther. 2022, 17, 483–486. [Google Scholar] [CrossRef] [PubMed]
- Voicu, M. Systems Theory; Romanian Academy: Bucharest, Romania, 2008; pp. 29–89. [Google Scholar]
- Eigenschink, M.; Dearing, L.; Dablander, T.E.; Maier, J.; Sitte, H.H. A critical examination of the main premises of Traditional Chinese Medicine. Wien. Clin. Wkly. J. 2020, 132, 260–273. [Google Scholar] [CrossRef] [PubMed]
- Procacini, C.; Pucino, V.; De Rosa, V.D.; Marone, G.; Matarese, G. Neuro-Endocrine Networks Controlling Immune System in Health and Disease. Front. Immunol. 2014, 5, 143. [Google Scholar]
- Mueler, B.; Figueroa, A.; Papp, J.R. Structural and Functional Connection Between the Autonomic Nervous System, Hypothalamic-Pituitary-Adrenal Axis, and the Immune System: A Contex and Time Dependant Stress Response Network. Neurol. Sci. 2022, 43, 951–960. [Google Scholar] [CrossRef]
- Dantzer, R. Neuroimune Interactions: From the Brain to the Immune System and Vice Versa. Physiol. Rev. 2018, 98, 477–504. [Google Scholar] [CrossRef]
- Fang, X.; Collins, S.; Nanivadekar, A.C.; Jantz, M.; Gaunt, R.A.; Capogrosso, M. An Open-source Computational Model of Neurostimulation of the Spinal Pudendo-Vesical Reflex for the Recovery of Bladder Control After Spinal Cord Injury. In Proceedings of the 2022 44th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Glasgow, Scotland, UK, 11–15 July 2022; pp. 1607–1610. [Google Scholar] [CrossRef]
- Perreault, E.J.; Crago, P.E.; Kirsch, R.F. Estimation of intrinsic and reflex contributions to muscle dynamics: A modeling study. IEEE Trans. Biomed. Eng. 2000, 47, 1413–1421. [Google Scholar] [CrossRef]
- Zheng, Z.; Mo, F.; Liu, T.; Li, X. A Novel Neuromuscular Head-Neck Model and Its Application on Impact Analysis. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 1394–1402. [Google Scholar] [CrossRef]
- Fortuna, L.; Buscarino, A. Spiking neuron mathematical models: A compact overview. Bioengineering 2023, 10, 174. [Google Scholar] [CrossRef]
- Jolivet, R.; Kobayashi, R.; Rauch, A.; Naud, R.; Shinomoto, S.; Gerstner, W. A benchmark test for a quantitative assessment of simple neuron models. J. Neurosci. Methods 2008, 169, 417–424. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popescu, M.; Ravariu, C. Simulation of Spinal Cord Reflexes. Appl. Sci. 2024, 14, 310. https://doi.org/10.3390/app14010310
Popescu M, Ravariu C. Simulation of Spinal Cord Reflexes. Applied Sciences. 2024; 14(1):310. https://doi.org/10.3390/app14010310
Chicago/Turabian StylePopescu, Mihai, and Cristian Ravariu. 2024. "Simulation of Spinal Cord Reflexes" Applied Sciences 14, no. 1: 310. https://doi.org/10.3390/app14010310
APA StylePopescu, M., & Ravariu, C. (2024). Simulation of Spinal Cord Reflexes. Applied Sciences, 14(1), 310. https://doi.org/10.3390/app14010310







