Climate Change Impact on Corrosion of Reinforced Concrete Bridges and Their Seismic Performance
Abstract
:1. Introduction
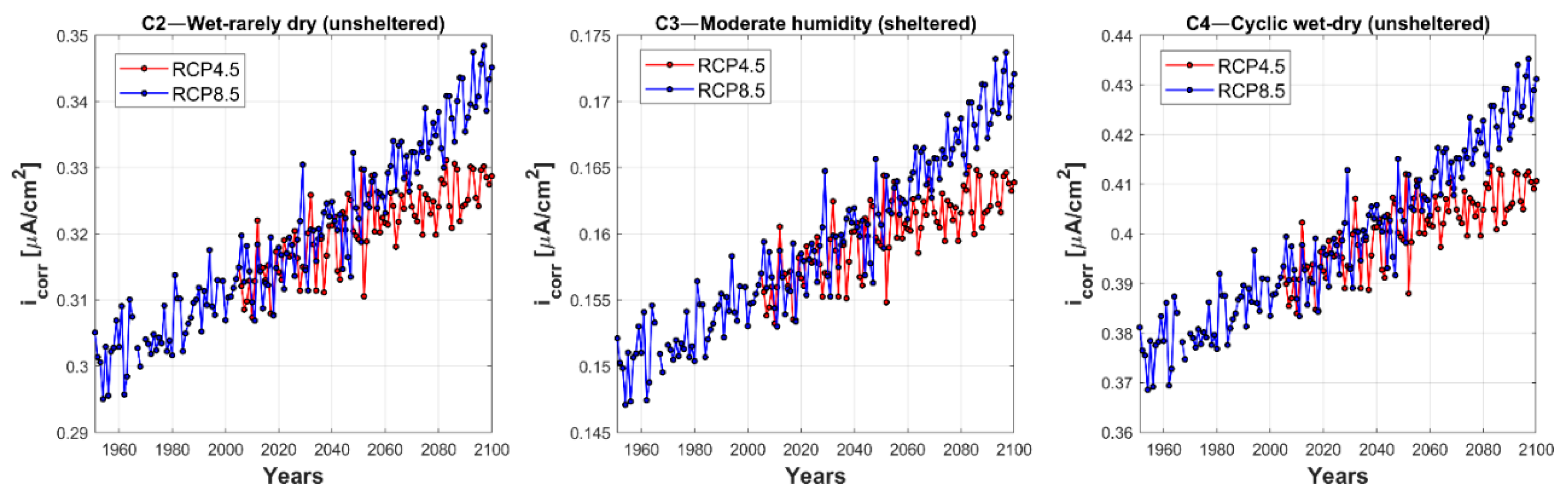
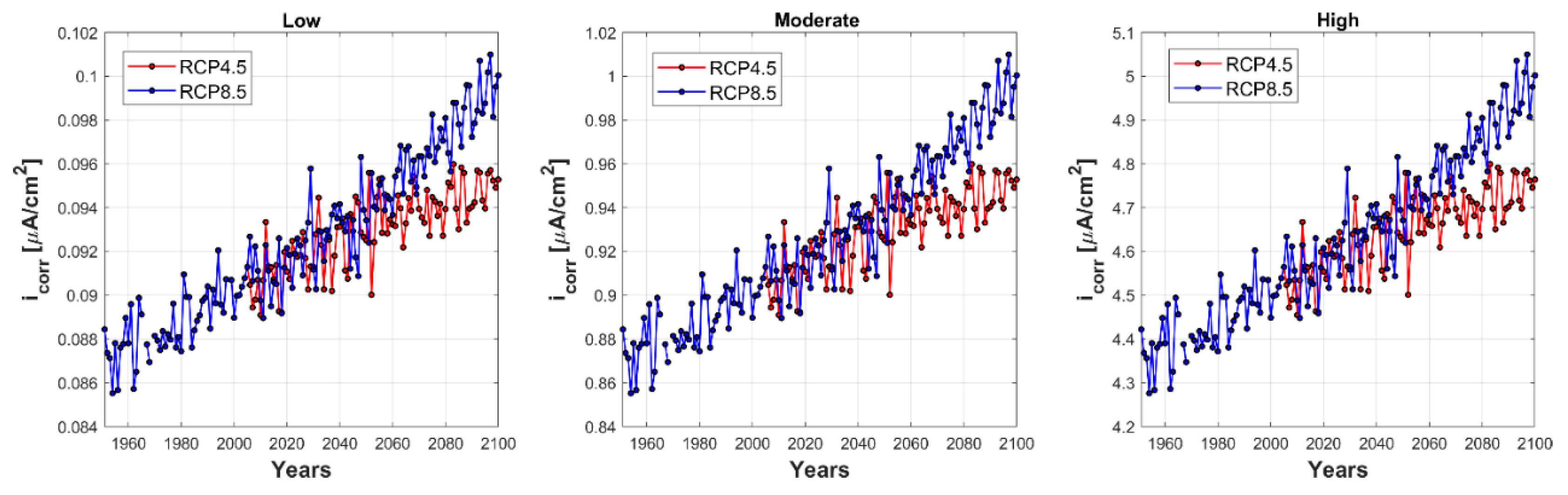
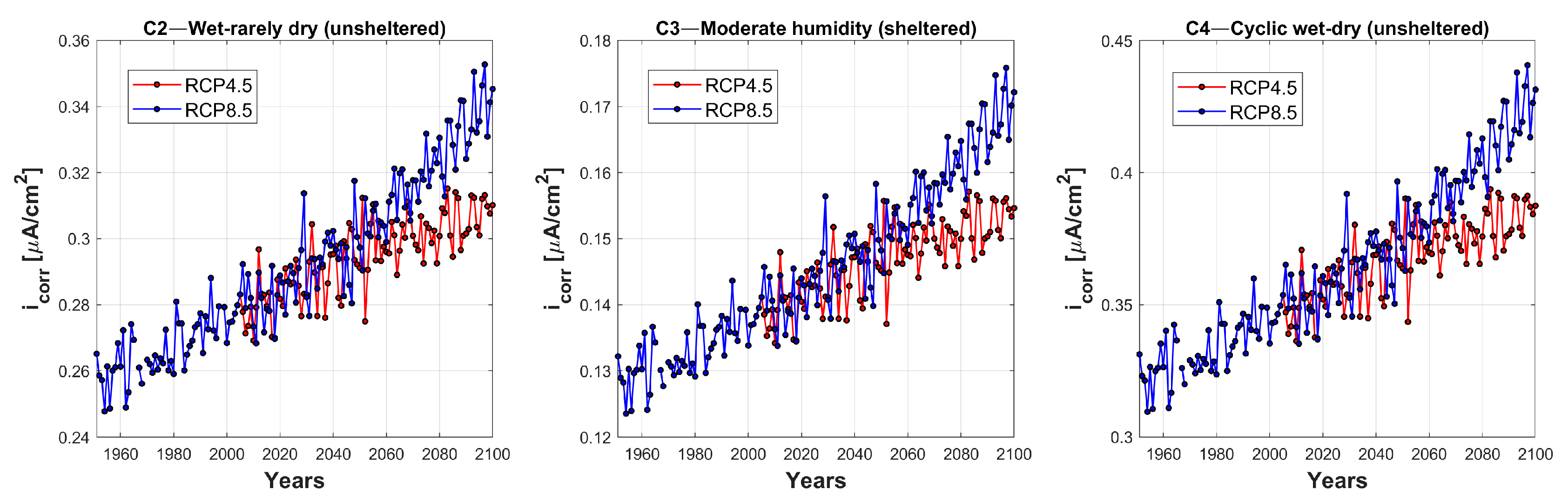
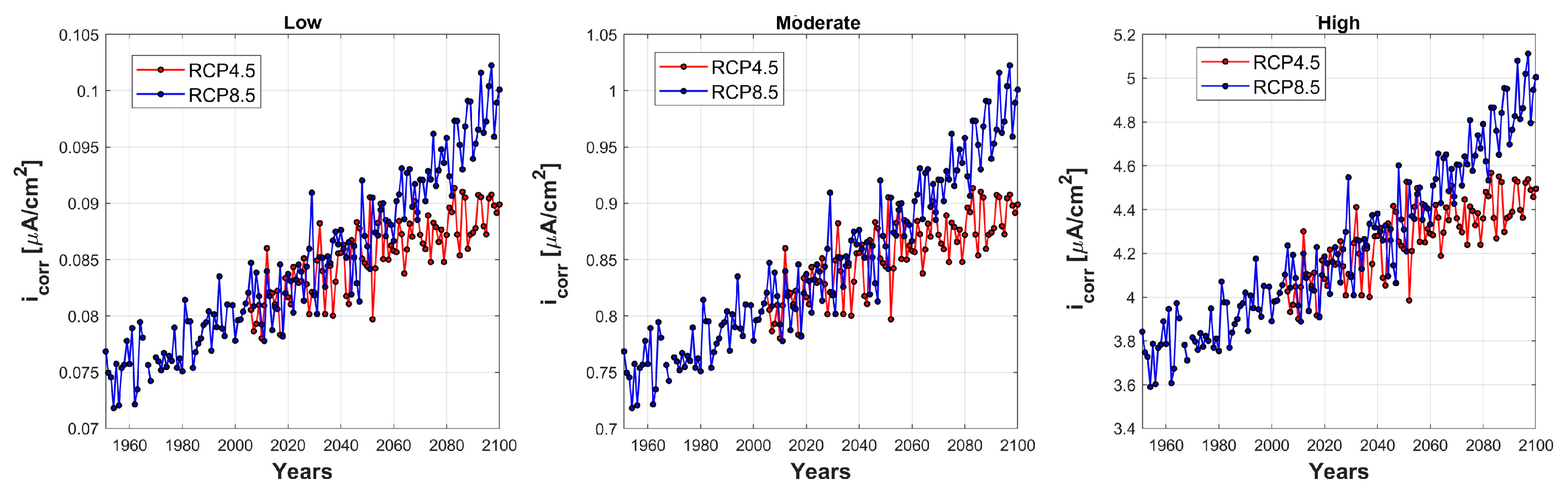
2. Climate Change’s Impact on the Corrosion Rate
3. Structural Modelling and Analysis Method
4. Case Study
5. Conclusions
- The values of icorr calculated considering the climate change impact through the indications suggested by Stewart et al. are lower than those obtained considering the results reported in DuraCrete, except for the slight corrosion scenario, which does not significantly influence the seismic performance of the viaduct;
- The corrosion effects, expressed in terms of the reduction in steel reinforcement, influence the brittle failure mechanism more significantly than the ductile one;
- Considering the corrosion scenarios obtained from the above-mentioned climate change impact prediction model, a significant reduction in the risk indices, which characterize the seismic vulnerability of the viaduct, are observed only for the high corrosion level (icorr = 0.431 μA/cm2) with the brittle collapse mechanism;
- Different conclusions can be observed when considering the icorr values proposed by DuraCrete, where an important decrease in risk index values is obtained for the moderate and high corrosion scenarios. Focusing on the high corrosion level, the reduction in the risk index values exceeds 90% for the brittle collapse mechanism and 80% for the ductile collapse mechanism;
- The corrosion levels obtained from DuraCrete lead to more critical scenarios compared to those obtained from climate change projections for the area where the analyzed viaduct was built, when the corrosion rates proposed by Stewart et al. are considered.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| icorr | Mean corrosion current density |
| icorr,20 | Mean corrosion current density at 20 °C |
| K | Environmental exposure factor |
| E | Activation energy of the diffusion process (40 kJ/mol) |
| R | Gas constant (8.314 × 10−3 kJ/mol K) |
| s | Carbonated layer thickness |
| k | Penetration rate coefficient |
| n | Parameters related to the concrete characteristics |
| d0 | Initial diameter of the steel reinforcement |
| P(t) | Corroded thickness |
| ti | Initiation time of the corrosion process |
| fck | Concrete compressive strength |
| εu,0 | Steel ultimate deformation |
| c | Concrete cover thickness |
| w/c | Water/cement ratio |
References
- Xiong, W.; Cai, C.S.; Zhang, R.; Shi, H.; Xu, C. Review of Hydraulic Bridge Failures: Historical Statistic Analysis, Failure Modes, and Prediction Methods. J. Bridge Eng. 2023, 28, 4. [Google Scholar] [CrossRef]
- Menga, A.; Kenstad, K.; Cantero, D.; Bathen, L.; Hornbostel, K.; Klausen, A. Corrosion-induced damages and failures of posttensioned bridges: A literature review. Struct. Concr. 2023, 24, 84–99. [Google Scholar] [CrossRef]
- Zucca, M.; Crespi, P.; Stochino, F.; Puppio, M.L.; Coni, M. Maintenance interventions period of existing RC motorway viaducts located in moderate/high seismicity zones. Structures 2023, 47, 976–990. [Google Scholar] [CrossRef]
- Santarsiero, G.; Picciano, V.; Masi, A. Structural rehabilitation of half-joints in RC bridges: A state-of-the-art review. Struct. Infrastruct. Eng. 2023. [Google Scholar] [CrossRef]
- Fan, Y.; Zhu, J.; Pei, J.; Li, Z.; Wu, Y. Analysis for Yangmingtan bridge collapse. Eng. Fail. Anal. 2015, 56, 20–27. [Google Scholar] [CrossRef]
- Biondini, F.; Camnasio, E.; Palermo, A. Lifetime seismic performance of concrete bridges exposed to corrosion. Struct. Infrastruct. Eng. 2014, 10, 880–900. [Google Scholar] [CrossRef]
- Berto, L.; Saetta, A.V.; Simioni, P. Structural risk assessment of corroding RC structures under seismic excitation. Constr. Build. Mater. 2012, 30, 803–813. [Google Scholar] [CrossRef]
- Kassir, M.K.; Ghosn, M. Chloride-induced corrosion of reinforced concrete bridge decks. Cem. Concr. Res. 2002, 32, 139–143. [Google Scholar] [CrossRef]
- Pour-Ghaz, M.; Burkan Isgor, O.; Ghods, P. The effect of temperature on the corrosion of steel in concrete. Part 1: Simulated polarization resistance tests and model development. Corros. Sci. 2009, 51, 415–425. [Google Scholar] [CrossRef]
- Bastidas-Arteaga, E.; Schoefs, F.; Stewart, M.G.; Wang, X. Influence of global warming on durability of corroding RC structures: A probabilistic approach. Eng. Struct. 2013, 51, 259–266. [Google Scholar] [CrossRef]
- Sousa, M.L.; Dimova, A.; Athanasopoulou, A.; Rianna, G.; Mercogliano, P.; Villani, V.; Nogal, M.; Gervasio, H.; Neves, L.; Bastidas-Arteaga, E.; et al. Expected Implications of Climate Change on the Corrosion of Structures; EUR 30303 EN; Publications Office of the European Union: Luxembourg, 2020; ISBN 978-92-76-20782-5. [Google Scholar]
- Nasr, A.; Honfi, D.; Larsson Ivanov, O. Probabilistic analysis of climate change impact on chloride-induced deterioration of reinforced concrete considering Nordic climate. J. Infrastruct. Preserv. Resil. 2022, 3, 8. [Google Scholar] [CrossRef]
- Landi, F.; Croce, P.; Marsili, F.; Kessler, S. Prediction of RC bridge deterioration under changing environmental conditions. In Life-Cycle of Structures and Infrastructure Systems; Biondini, F., Frangopol, D.M., Eds.; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar] [CrossRef]
- Sassu, M.; Giresini, L.; Puppio, M.L. Failure scenarios of small bridges in case of extreme rainstorms. Sustain. Resilient Infrastruct. 2017, 2, 108–116. [Google Scholar] [CrossRef]
- Pucci, A.; Hélder, S.; Giresini, L.; Matos, J.C.; Castelli, F. Fragility of bridge decks exposed to hydraulic and driftwood actions. Struct. Infrastruct. Eng. 2023. [Google Scholar] [CrossRef]
- Decreto Ministeriale 17/01/2018, Ministero delle Infrastrutture e dei Trasporti, G.U. Serie Generale n.42 del 20/02/2018—S.O.8.
- Estes, A.C.; Frangopol, D.M. Updating Bridge Reliability Based on Bridge Management Systems Visual Inspection Results. J. Bridge Eng. 2003, 8, 6. [Google Scholar] [CrossRef]
- Quirk, L.; Matos, J.; Murphy, J.; Pakrashi, K. Visual inspection and bridge management. Struct. Infrastruct. Eng. 2018, 14, 320–332. [Google Scholar] [CrossRef]
- Bertola, N.J.; Brühwiler, E. Risk-based methodology to assess bridge condition based on visual inspection. Struct. Infrastruct. Eng. 2023, 19, 575–588. [Google Scholar] [CrossRef]
- Deng, Z.; Huang, M.; Wan, N.; Zhang, J. The Current Development of Structural Health Monitoring for Bridges: A Review. Buildings 2023, 13, 1360. [Google Scholar] [CrossRef]
- Luo, J.; Huang, M.; Lei, Y. Temperature Effect on Vibration Properties and Vibration-Based Damage Identification of Bridge Structures: A Literature Review. Buildings 2022, 12, 1209. [Google Scholar] [CrossRef]
- Gul, M.; Necati Catbas, F. Statistical pattern recognition for Structural Health Monitoring using time series modelling: Theory and experimental verifications. Mech. Syst. Signal Process. 2009, 23, 2194–2204. [Google Scholar] [CrossRef]
- Valente, M.; Milani, G. Alternative retrofitting strategies to prevent the failure of an under-designed RC frame. Eng. Fail. Anal. 2018, 89, 271–285. [Google Scholar] [CrossRef]
- Adhikari, G.; Pinho, R. Development and Application of Nonlinear Static Procedures for Plan-Asymmetric Buildings; Research Report No. ROSE-2010/01; ROSE School, IUSS Pavia: Pavia, Italy, 2010. [Google Scholar]
- Stefanidou, S.; Kappos, A. Methodology for the development of bridge-specific fragility curves. Earthq. Eng. Struct. Dyn. 2017, 46, 73–93. [Google Scholar] [CrossRef]
- Contiguglia, C.P.; Pelle, A.; Briseghella, B.; Nuti, C. IMPA versus Cloud Analysis and IDA: Different Methods to Evaluate Structural Seismic Fragility. Appl. Sci. 2022, 12, 3687. [Google Scholar] [CrossRef]
- Karimi-Moridani, K.; Zarfam, P.; Ghafory-Ashtiany, M. A Novel and Efficient Hybrid Method to Develop the Fragility Curves of Horizontally Curved Bridges. KSCE J. Civ. Eng. 2020, 24, 508–524. [Google Scholar] [CrossRef]
- Bernuzzi, C.; Rodigari, D.; Simoncelli, M. Incremental dynamic analysis for assessing the seismic performance of moment resisting steel frames. Ing. Sismica 2020, 4, 23–44. [Google Scholar]
- Concu, G.; Deligia, M.; Sassu, M. Seismic Analysis of Historical Urban Walls: Application to the Volterra Case Study. Infrastructures 2023, 8, 18. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Cornell, C.A. Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- Paraskeva, T.S.; Kappos, A.J.; Sextos, A.G. Extension of modal pushover analysis to seismic assessment of bridges. Earthq. Eng. Struct. Dyn. 2006, 35, 1269–1293. [Google Scholar] [CrossRef]
- Paraskeva, T.S.; Kappos, A.J. Further development of a multimodal pushover procedure for seismic assessment of bridges. Earthq. Eng. Struct. Dyn. 2010, 39, 211–222. [Google Scholar] [CrossRef]
- Chopra, A.K.; Goel, R.K. A modal pushover analysis procedure for estimating seismic demands for buildings. Earthq. Eng. Struct. Dyn. 2002, 31, 561–582. [Google Scholar] [CrossRef]
- Chopra, A.K.; Goel, R.K. A modal pushover analysis procedure to estimate seismic demands for unsymmetric-plan buildings. Earthq. Eng. Struct. Dyn. 2004, 33, 903–927. [Google Scholar] [CrossRef]
- De Domenico, D.; Messina, D.; Recupero, A. Seismic vulnerability assessment of reinforced concrete bridge piers with corroded bars. Struct. Concr. 2023, 24, 56–83. [Google Scholar] [CrossRef]
- Dizaj, E.A.; Salami, M.R.; Kashani, M.M. Seismic vulnerability analysis of irregular multi-span concrete bridges with different corrosion damage scenarios. Soil Dyn. Earthq. Eng. 2023, 165, 107678. [Google Scholar] [CrossRef]
- Ge, B.; Yang, Y.; Kim, S. Time-dependent multi-hazard seismic vulnerability and risk assessment of deteriorating reinforced concrete bridges considering climate change. Structures 2023, 55, 995–1010. [Google Scholar] [CrossRef]
- Zhong, J.; Mao, Y.; Yuan, X. Lifetime seismic risk assessment of bridges with construction and aging considerations. Structures 2023, 47, 2259–2272. [Google Scholar] [CrossRef]
- Nasr, A.; Björnsson, I.; Honfi, D.; Larsson Ivanov, O.; Johansson, J.; Kjellström, E. A review of the potential impacts of climate change on the safety and performance of bridges. Sustain. Resilient Infrastruct. 2021, 6, 1–21. [Google Scholar] [CrossRef]
- Mondoro, A.; Frangopol, D.M.; Liu, L. Multi-criteria robust optimization framework for bridge adaptation under climate change. Struct. Saf. 2018, 74, 14–23. [Google Scholar] [CrossRef]
- Kaewunruen, S.; AbdelHadi, M.; Kongpuang, M.; Pansuk, W.; Remennikov, A.M. Digital Twins for Managing Railway Bridge Maintenance, Resilience, and Climate Change Adaptation. Sensors 2023, 23, 252. [Google Scholar] [CrossRef]
- Moro, F.; Kessler, S.; Landi, F. Prediction of corrosion rates in view of climate change with rising temperatures. Ce/Pap. 2023, 6, 1044–1047. [Google Scholar] [CrossRef]
- van Vuuren, D.P.; Edmonds, J.; Kainuma, M.; Riahi, K.; Thomson, A.; Hibbard, K.; Hurtt, G.C.; Kram, T.; Krey, V.; Lamarque, G.F.; et al. The representative concentration pathways: An overview. Clim. Chang. 2011, 109, 5–31. [Google Scholar] [CrossRef]
- O’Neill, B.C.; Carter, T.R.; Ebi, K.; Harrison, P.A.; Kemp-Benedict, E.; Kok, K.; Kriegler, E.; Preston, B.L.; Riahi, K.; Sillmann, J.; et al. Achievements and needs for the climate change scenario framework. Nat. Clim. Chang. 2020, 10, 1074–1084. [Google Scholar] [CrossRef]
- Schwalm, C.R.; Glendon, S.; Duffy, P.B. RCP8.5 tracks cumulative CO2 emissions. Proc. Natl. Acad. Sci. USA 2020, 117, 19656–19657. [Google Scholar] [CrossRef]
- Li, S.H. Effect of nonstationary extreme wind speeds and ground snow loads on the structural reliability in a future Canadian changing climate. Struct. Saf. 2023, 101, 102296. [Google Scholar] [CrossRef]
- Jacob, D.; Petersen, J.; Eggert, B.; Alias, A.; Christensen, O.B.; Bouwer, L.M.; Braun, A.; Colette, A.; Déqué, M.; Georgievski, G.; et al. EURO-CORDEX: New high-resolution climate change projections for European impact research. Reg. Environ. Chang. 2014, 14, 563–578. [Google Scholar] [CrossRef]
- Masson-Delmotte, V.; Zhai, P.; Pirani, A.; Connors, S.L.; Péan, C.; Berger, S.; Caud, N.; Chen, Y.; Goldfarb, L.; Gomis, M.I.; et al. IPCC, 2021: Summary for Policymakers. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; pp. 3–32. [Google Scholar]
- Croce, P.; Formichi, P.; Landi, F. Enhancing the Output of Climate Models: A Weather Generator for Climate Change Impact Studies. Atmosphere 2021, 12, 1074. [Google Scholar] [CrossRef]
- Maraun, D.; Wetterhall, F.; Ireson, A.M.; Chandler, R.E.; Kendon, E.J.; Widmann, M.; Brienen, S.; Rust, H.W.; Sauter, T.; Themeßl, M.; et al. Precipitation downscaling under climate change: Recent developments to bridge the gap between dynamical models and the end user. Rev. Geophys. 2010, 48, RG3003. [Google Scholar] [CrossRef]
- Ho, C.K.; Stephenson, D.B.; Collins, M.; Ferro, C.A.T.; Brown, S.J. Calibration Strategies: A Source of Additional Uncertainty in Climate Change Projections. Bull. Am. Meteorol. Soc. 2012, 93, 21–26. [Google Scholar] [CrossRef]
- Maraun, D. Bias Correcting Climate Change Simulations—A Critical Review. Curr. Clim. Chang. Rep. 2016, 2, 211–220. [Google Scholar] [CrossRef]
- Stewart, G.M.; Wang, X.; Nguyen, M.N. Climate change impact and risks of concrete infrastructure deterioration. Eng. Struct. 2011, 33, 1326–1337. [Google Scholar] [CrossRef]
- DuraCrete. Statistical quantification of the variables in the limit state functions. Dura-Crete-Probabilistic performance-based durability design of concrete structures. EU-brite EuRam III. Contract BRPR-CT95-0132. Project BE95-1347/R9. January 2000.
- fib Bullettin 34. Model Code for Service Life Design; FIB: Lausanne, Switzerland, 2006. [Google Scholar]
- Crespi, P.; Zucca, M.; Valente, M.; Longarini, N. Influence of corrosion effects on the seismic capacity of existing RC bridges. Eng. Fail. Anal. 2022, 140, 106546. [Google Scholar] [CrossRef]
- MIDAS Civil. Analysis Reference. 2023. Available online: https://www.midasoft.com/bridge-library/civil/products/midascivil (accessed on 5 October 2023).
- EN 1337-3:2005; Structural Bearings—Part 3: Elastomeric Bearings. British Standards: London, UK, 2005.
- EN 1998-3:2005; Eurocode 8: Design of Structures for Earthquake Resistance—Part 3: Assessment and Retrofitting Buildings. CEN (European Committee for Standardization), Management Centre: Brussels, Belgium, 2005.
- Chen, W.F.; Duan, L. Bridge Engineering—Seismic Design, 1st ed.; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Miluccio, G.; Losanno, D.; Parisi, F.; Cosenza, E. Traffic-load fragility models for prestressed concrete girder decks of existing Italian highway bridges. Eng. Struct. 2021, 249, 113367. [Google Scholar] [CrossRef]
- Kent, D.C.; Park, R. Flexural members with confined concrete. ASCE-J. Struct. Div. 1971, 97, 1969–1990. [Google Scholar] [CrossRef]
- Park, R.; Paulay, T. Reinforced Concrete Structures, 1st ed.; John Wiley and Sons: New York, NY, USA, 1975. [Google Scholar]
- EN 1998-2:2005; Eurocode 8: Design of Structures for Earthquake Resistance—Part 2: Bridges. CEN (European Committee for Standardization), Management Centre: Brussels, Belgium, 2005.
- Saetta, A.V.; Vitaliani, R. Experimental investigation and numerical modeling of carbonation process in reinforced concrete structures: Part I: Theoretical formulation. Cem. Concr. Res. 2004, 34, 571–579. [Google Scholar] [CrossRef]
- ATC-40:1996; Seismic Evaluation and Retrofitting of Concrete Buildings. Applied Technology Council, 8.1–8.66: Redwood City, CA, USA, 1996.
- Causevic, M.; Mitrovic, S. Comparison between non-linear dynamic and static seismic analysis of structures according to European and US provisions. Bull. Earthq. Eng. 2011, 9, 467–489. [Google Scholar] [CrossRef]
- Lee, H.S.; Cho, Y.S. Evaluation of the mechanical properties of steel reinforcement embedded in concrete specimen as a function of the degree of reinforcement corrosion. Int. J. Fract. 2009, 157, 81–88. [Google Scholar] [CrossRef]


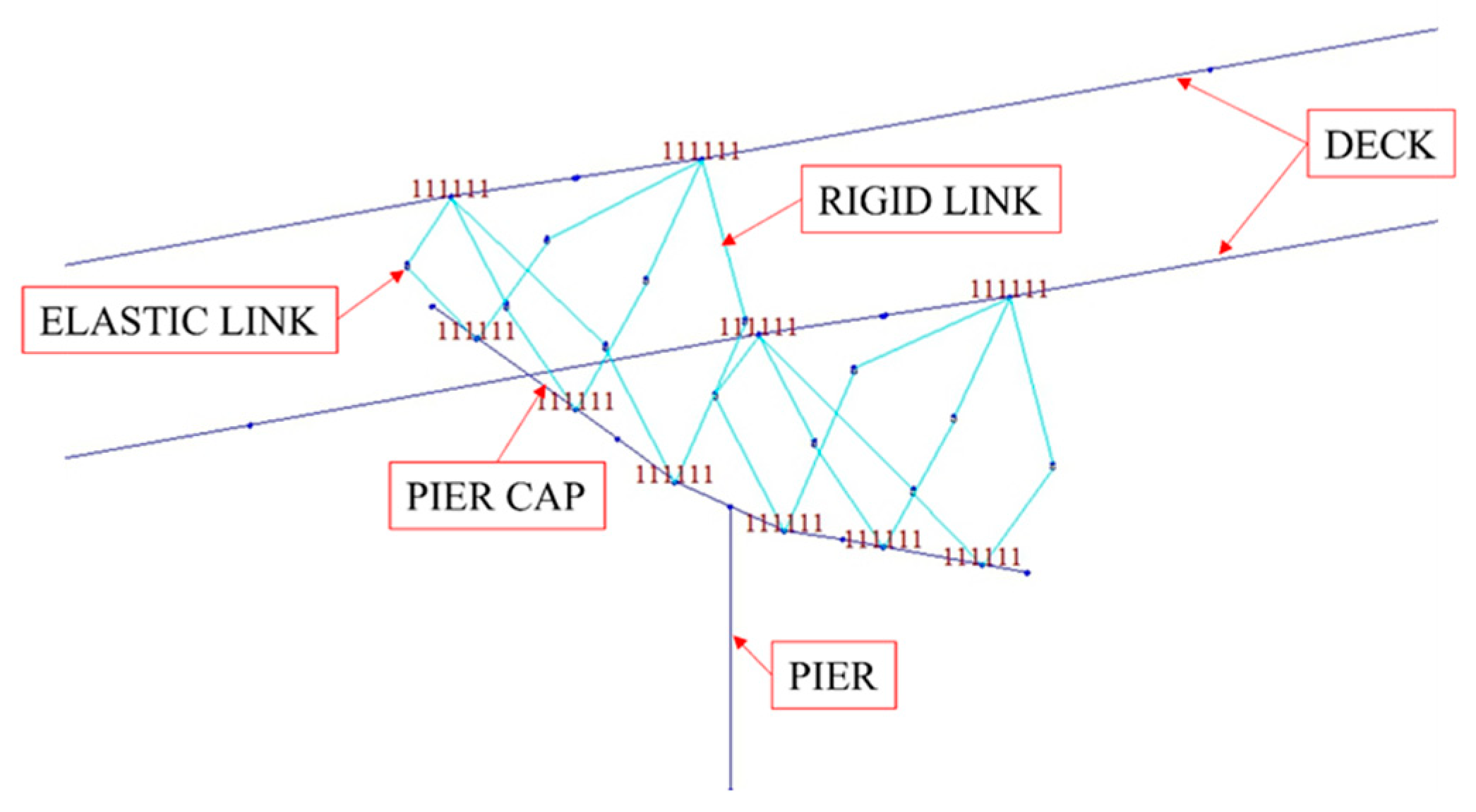
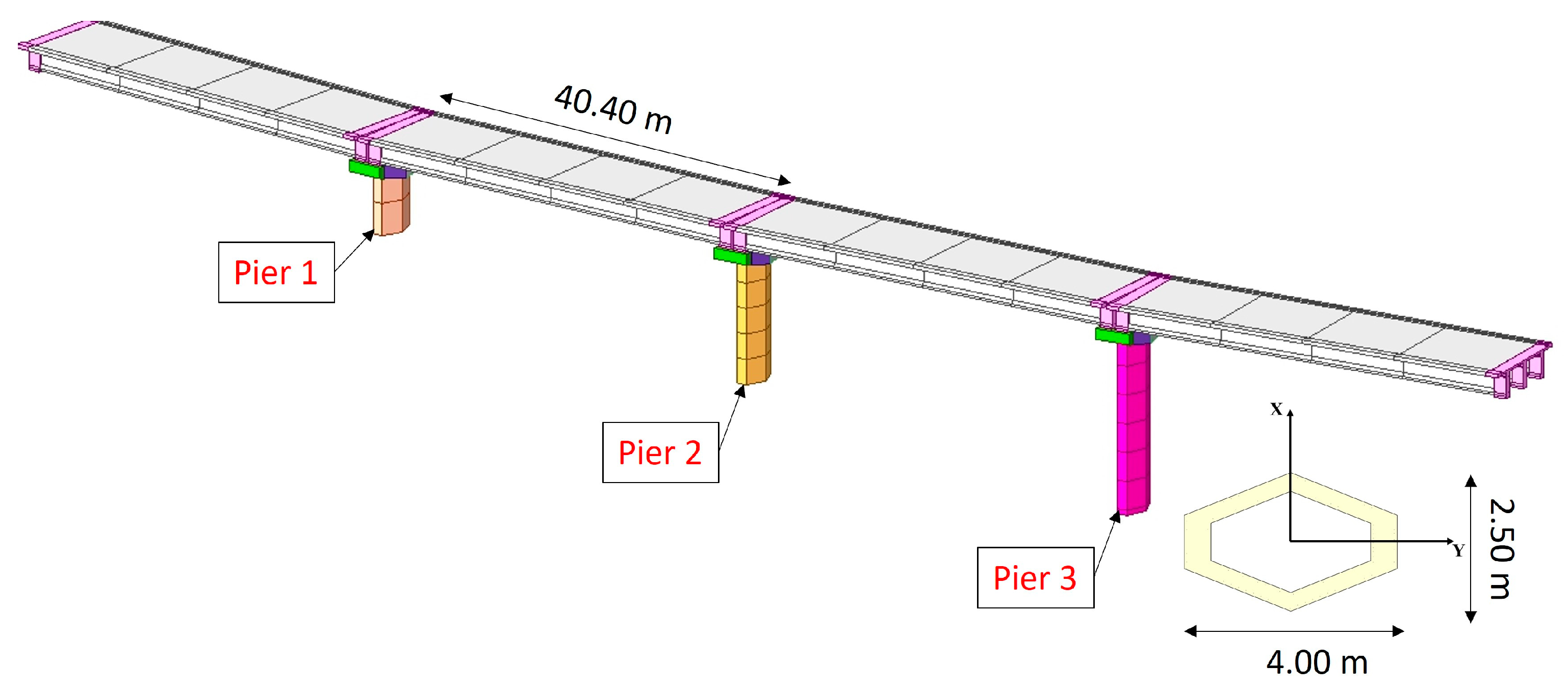


| fck | k | εu,0 | w/c | ti |
|---|---|---|---|---|
| [MPa] | [-] | [%] | [-] | [year] |
| 28 | 0.0116 | 9 | 0.6 | 13.5 |
| Piers | Cross-Section | Height | Longitudinal Steel Rebar | Stirrups |
|---|---|---|---|---|
| [n°] | [m] | [m] | [-] | [-] |
| 1 | 4.0 × 2.5 | 5.06 | 148Φ14 | Φ10/20 |
| 2 | 4.0 × 2.5 | 10.84 | 148Φ14 | Φ10/20 |
| 3 | 4.0 × 2.5 | 15.51 | 148Φ14 | Φ10/20 |
| Span | Length | Bearings | Pier | Pier Shape | Pier Thickness |
|---|---|---|---|---|---|
| [n°] | [m] | [-] | [n°] | [-] | [m] |
| 4 | 200 | 2 × 3 | 3 | Hexagonal hollow | 0.35 |
| t | Corrosion Scenario | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Slight | Moderate | High | ||||||||||
| icorr = 0.172 [μA/cm2] | icorr = 0.345 [μA/cm2] | icorr = 0.431 [μA/cm2] | ||||||||||
| d0 | d | ΔAs | εu | d0 | d | ΔAs | εu | d0 | d | ΔAs | εu | |
| [Years] | [mm] | [mm] | [%] | [%] | [mm] | [mm] | [%] | [%] | [mm] | [mm] | [%] | [%] |
| 0–13.5 | 10.00 | 10.00 | 0.00 | 9.00 | 10.00 | 10.00 | 0.00 | 9.00 | 10.00 | 10.00 | 0.00 | 9.00 |
| 14.00 | 14.00 | 0.00 | 9.00 | 14.00 | 14.00 | 0.00 | 9.00 | 14.00 | 14.00 | 0.00 | 9.00 | |
| 50 | 10.00 | 9.85 | 1.46 | 8.79 | 10.00 | 9.71 | 2.92 | 8.59 | 10.00 | 9.64 | 3.65 | 8.36 |
| 14.00 | 13.85 | 1.04 | 8.85 | 14.00 | 13.71 | 2.09 | 8.70 | 14.00 | 13.64 | 2.61 | 8.54 | |
| 75 | 10.00 | 9.75 | 2.45 | 8.57 | 10.00 | 9.51 | 4.92 | 8.14 | 10.00 | 9.39 | 6.15 | 7.92 |
| 14.00 | 13.75 | 1.75 | 8.69 | 14.00 | 13.51 | 3.52 | 8.38 | 14.00 | 13.39 | 4.39 | 8.23 | |
| 100 | 10.00 | 9.65 | 3.45 | 8.39 | 10.00 | 9.31 | 6.92 | 7.78 | 10.00 | 9.14 | 8.65 | 7.48 |
| 14.00 | 13.65 | 2.47 | 8.57 | 14.00 | 13.31 | 4.95 | 8.13 | 14.00 | 13.14 | 6.18 | 7.92 | |
| t | Corrosion Scenario | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Slight | Moderate | High | ||||||||||
| icorr = 0.1 [μA/cm2] | icorr = 1 [μA/cm2] | icorr = 5 [μA/cm2] | ||||||||||
| d0 | d | ΔAs | εu | d0 | d | ΔAs | εu | d0 | d | ΔAs | εu | |
| [Years] | [mm] | [mm] | [%] | [%] | [mm] | [mm] | [%] | [%] | [mm] | [mm] | [%] | [%] |
| 0–13.5 | 10.00 | 10.00 | 0.00 | 9.00 | 10.00 | 10.00 | 0.00 | 9.00 | 10.00 | 10.00 | 0.00 | 9.00 |
| 14.00 | 14.00 | 0.00 | 9.00 | 14.00 | 14.00 | 0.00 | 9.00 | 14.00 | 14.00 | 0.00 | 9.00 | |
| 50 | 10.00 | 9.92 | 0.85 | 8.88 | 10.00 | 9.15 | 8.47 | 7.80 | 10.00 | 5.77 | 42.34 | 1.57 |
| 14.00 | 13.92 | 0.60 | 8.91 | 14.00 | 13.15 | 6.05 | 8.15 | 14.00 | 9.77 | 30.24 | 3.69 | |
| 75 | 10.00 | 9.86 | 1.43 | 8.75 | 10.00 | 8.57 | 14.27 | 6.50 | 10.00 | 2.87 | 71.34 | 1.17 |
| 14.00 | 13.86 | 1.02 | 8.82 | 14.00 | 12.57 | 10.19 | 7.21 | 14.00 | 6.87 | 50.96 | 2.33 | |
| 100 | 10.00 | 9.80 | 2.01 | 8.65 | 10.00 | 7.99 | 20.07 | 5.48 | 10.00 | 0.00 | 100.00 | 0.00 |
| 14.00 | 13.80 | 1.43 | 8.75 | 14.00 | 11.99 | 14.33 | 6.48 | 14.00 | 3.97 | 71.67 | 1.01 | |
| Corrosion Level | Ductile Failure Mechanism | ||||||
|---|---|---|---|---|---|---|---|
| 50 Years | 75 Years | 100 Years | |||||
| X | Y | X | Y | X | Y | ||
| RIPGA | Slight | 5.342 (0.00%) | 3.936 (0.00%) | 5.342 (0.00%) | 3.936 (0.00%) | 5.231 (−2.08%) | 3.851 (−2.16%) |
| Moderate | 5.262 (−1.50%) | 3.888 (−1.22%) | 5.201 (−2.64%) | 3.866 (−1.79%) | 5.171 (−3.20%) | 3.815 (−3.07%) | |
| High | 5.231 (−2.08%) | 3.851 (−2.16%) | 5.171 (−3.20%) | 3.815 (−3.07%) | 5.100 (−4.20%) | 3.799 (−4.14%) | |
| RIRP | Slight | 9.804 (0.00%) | 6.464 (0.00%) | 9.804 (0.00%) | 6.464 (0.00%) | 9.597 (−2.11%) | 6.303 (−2.49%) |
| Moderate | 9.686 (−1.20%) | 6.387 (−1.19%) | 9.583 (−2.25%) | 6.356 (−1.67%) | 9.502 (−3.08%) | 6.288 (−2.72%) | |
| High | 9.597 (−2.11%) | 6.303 (−2.49%) | 9.502 (−3.08%) | 6.288 (−2.72%) | 9.480 (−3.30%) | 6.200 (−4.08%) | |
| Brittle failure mechanism | |||||||
| RIPGA | Slight | 1.379 (0.00%) | 0.959 (0.00%) | 1.379 (0.00%) | 0.959 (0.00%) | 1.257 (−8.46%) | 0.889 (−7.30%) |
| Moderate | 1.313 (−4.79%) | 0.913 (−4.80%) | 1.297 (−5.94%) | 0.901 (−6.04%) | 1.221 (−11.45%) | 0.836 (−12.82%) | |
| High | 1.257 (−8.46%) | 0.889 (−7.30%) | 1.221 (−11.45%) | 0.836 (−12.82%) | 1.144 (−17.04%) | 0.632 (−34.09%) | |
| RIRP | Slight | 1.547 (0.00%) | 0.949 (0.00%) | 1.547 (0.00%) | 0.949 (0.00%) | 1.421 (−8.15%) | 0.882 (−7.06%) |
| Moderate | 1.478 (−4.46%) | 0.906 (−4.53%) | 1.459 (−5.68%) | 0.893 (−5.90) | 1.398 (−9.63%) | 0.855 (−9.90%) | |
| High | 1.421 (−8.15%) | 0.882 (−7.06%) | 1.398 (−9.63%) | 0.855 (−9.90%) | 1.200 (−22.43%) | 0.627 (−33.93%) | |
| Corrosion Level | Ductile Failure Mechanism | ||||||
|---|---|---|---|---|---|---|---|
| 50 Years | 75 Years | 100 Years | |||||
| X | Y | X | Y | X | Y | ||
| RIPGA | Slight | 5.342 (0.00%) | 3.936 (0.00%) | 5.342 (0.00%) | 3.936 (0.00%) | 5.342 (0.00%) | 3.936 (0.00%) |
| Moderate | 5.100 (−4.20%) | 3.799 (−4.14%) | 5.083 (−4.84%) | 3.801 (−3.43%) | 4.537 (−15.01%) | 3.004 (−23.68%) | |
| High | 4.968 (−7.00%) | 3.782 (−4.56%) | 3.194 (−40.21%) | 2.348 (−40.35%) | 1.114 (−79.15%) | 0.876 (−77.74%) | |
| RIRP | Slight | 9.804 (0.00%) | 6.464 (0.00%) | 9.804 (0.00%) | 6.464 (0.00%) | 9.804 (0.00%) | 6.464 (0.00%) |
| Moderate | 9.480 (−3.30%) | 6.200 (−4.08%) | 9.322 (−4.92%) | 6.208 (−3.96%) | 8.374 (−14.58%) | 5.233 (−19.04%) | |
| High | 8.879 (−9.34%) | 6.122 (−5.29%) | 4.862 (−50.41%) | 3.198 (−50.53%) | 2.256 (−76.99%) | 1.635 (−74.70) | |
| Brittle failure mechanism | |||||||
| RIPGA | Slight | 1.379 (0.00%) | 0.959 (0.00%) | 1.379 (0.00%) | 0.959 (0.00%) | 1.379 (0.00%) | 0.959 (0.00%) |
| Moderate | 1.144 (−17.04%) | 0.632 (−34.09%) | 1.003 (−27.26%) | 0.413 (−56.93%) | 0.829 (−39.88%) | 0.222 (−76.85%) | |
| High | 0.937 (−32.05%) | 0.299 (−68.82%) | 0.442 (−67.95%) | 0.241 (−74.87%) | 0.123 (−91.08%) | 0.054 (−94.37%) | |
| RIRP | Slight | 1.547 (0.00%) | 0.949 (0.00%) | 1.547 (0.00%) | 0.949 (0.00%) | 1.547 (0.00%) | 0.949 (0.00%) |
| Moderate | 1.200 (−22.43%) | 0.627 (−33.93%) | 1.102 (−28.76%) | 0.389 (−59.01) | 0.966 (−37.56) | 0.237 (−75.03%) | |
| High | 0.984 (−36.39%) | 0.267 (−71.87%) | 0.503 (−67.49%) | 0.230 (−75.76%) | 0.159 (−89.72%) | 0.062 (−93.46%) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zucca, M.; Landi, F.; Puppio, M.L.; Mistretta, F.; Formichi, P.; Croce, P. Climate Change Impact on Corrosion of Reinforced Concrete Bridges and Their Seismic Performance. Appl. Sci. 2024, 14, 60. https://doi.org/10.3390/app14010060
Zucca M, Landi F, Puppio ML, Mistretta F, Formichi P, Croce P. Climate Change Impact on Corrosion of Reinforced Concrete Bridges and Their Seismic Performance. Applied Sciences. 2024; 14(1):60. https://doi.org/10.3390/app14010060
Chicago/Turabian StyleZucca, Marco, Filippo Landi, Mario Lucio Puppio, Fausto Mistretta, Paolo Formichi, and Pietro Croce. 2024. "Climate Change Impact on Corrosion of Reinforced Concrete Bridges and Their Seismic Performance" Applied Sciences 14, no. 1: 60. https://doi.org/10.3390/app14010060
APA StyleZucca, M., Landi, F., Puppio, M. L., Mistretta, F., Formichi, P., & Croce, P. (2024). Climate Change Impact on Corrosion of Reinforced Concrete Bridges and Their Seismic Performance. Applied Sciences, 14(1), 60. https://doi.org/10.3390/app14010060











