Fatigue Damage of Rubber Concrete Backfill at Arch Springing Influence on Surrounding Rock Deformation in Tunnel Engineering
Abstract
:1. Introduction
2. Test Materials and Methods
2.1. Raw Materials
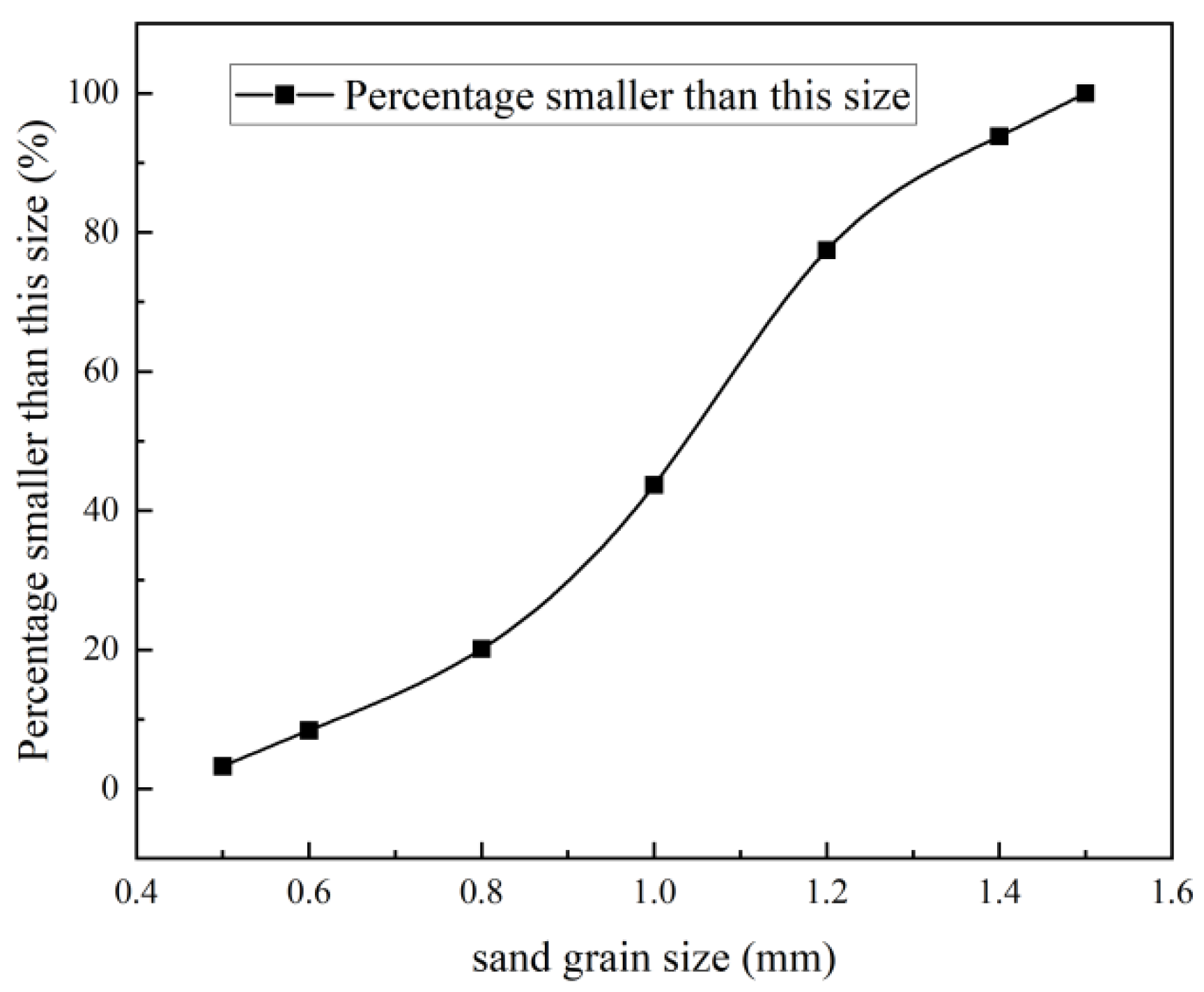
2.2. Preparation of Specimens
2.3. Test Setup and Method
3. Test Results and Discussion
3.1. Crack Morphology and Deformation Characteristics
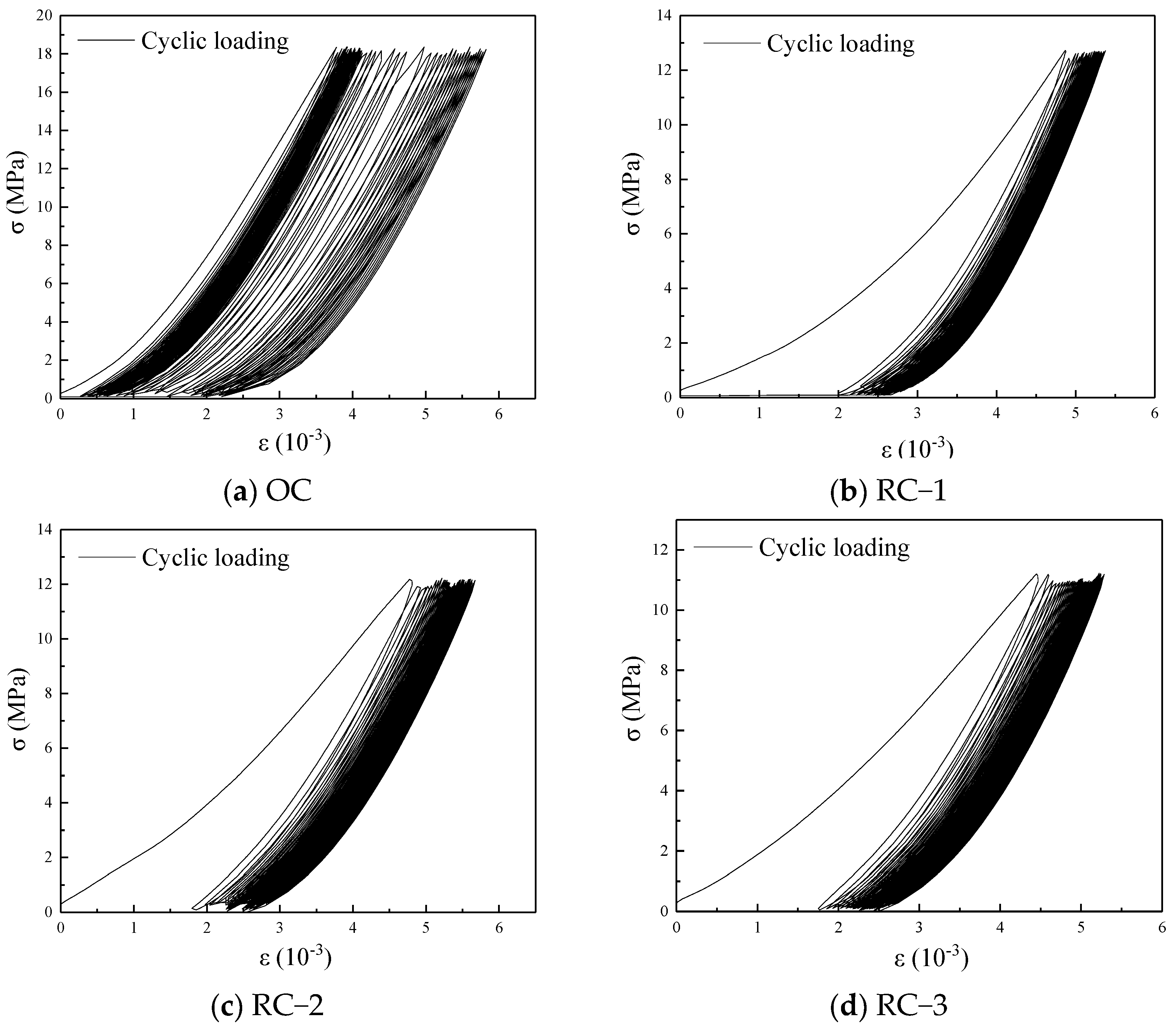
3.2. Stress–Strain Curves
4. Degradation Analysis
4.1. Compressive Characteristics
- (1)
- Elastic modulus
- (2)
- Toughness index
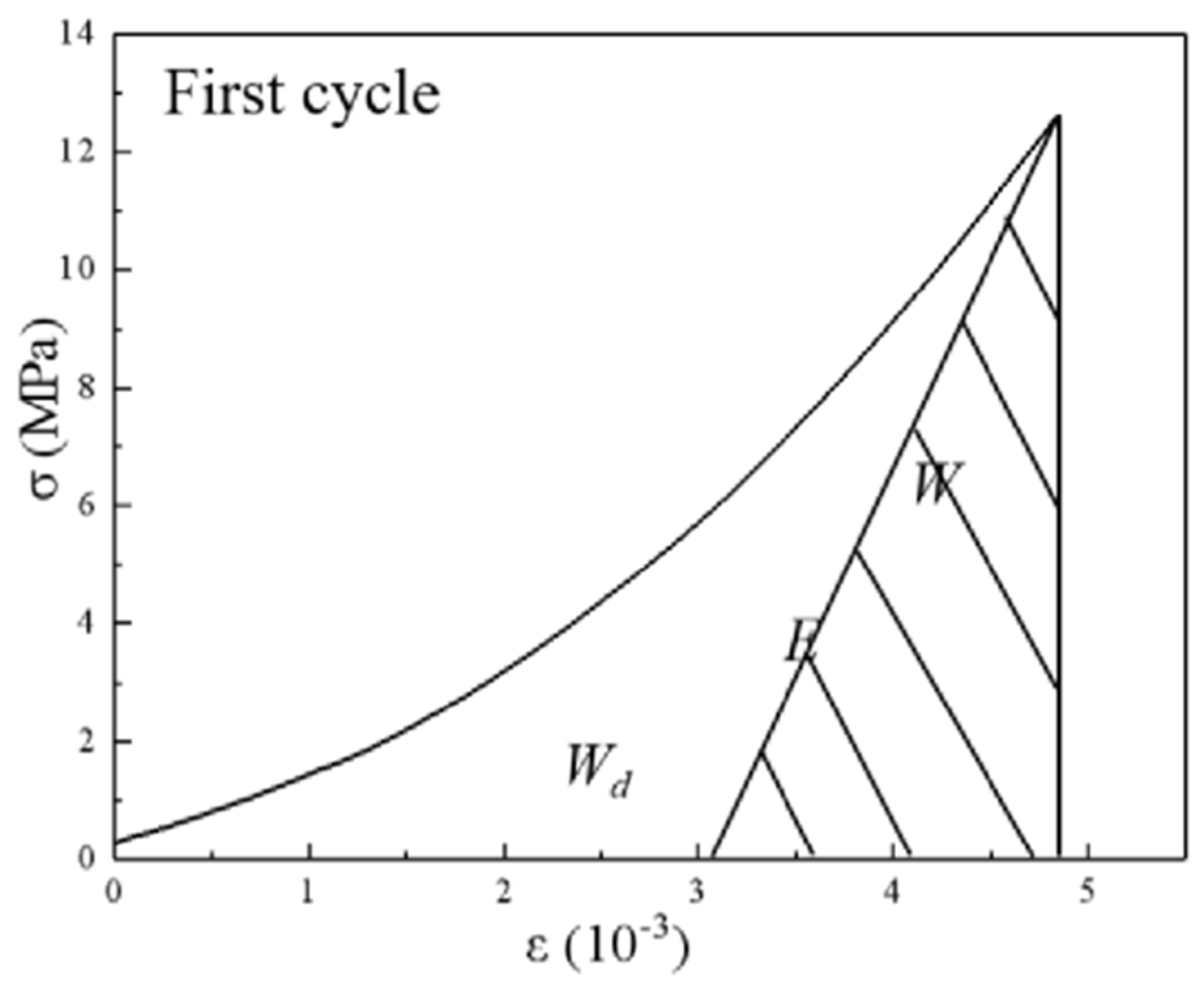
4.2. Energy Dissipation Feature
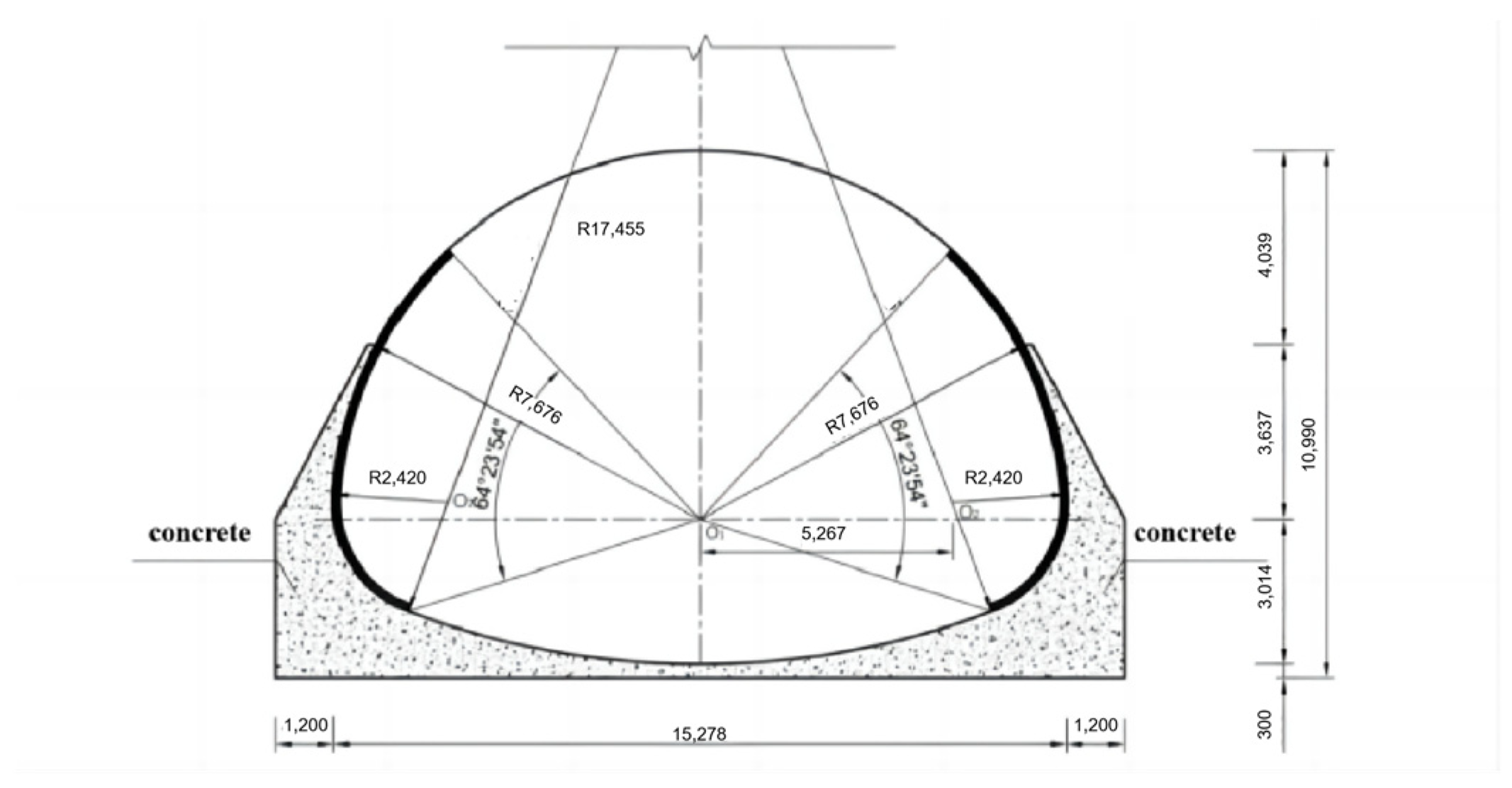
5. Engineering Application
Determination of Material Parameters
6. Conclusions
- (1)
- The purpose of the test was to analyze the effect of adding different-sized rubber particles on concrete material via the stress–strain curve of materials under cyclic loading and observe microcracks on the concrete specimens before and after fatigue loading. The outcome demonstrated that the compressive strength of concrete material decreased with the addition of rubber particles, but the surface crack propagation was inhibited and the deformation resistance was improved. With the increase in rubber particle size, the crack resistance and deformation resistance of rubber concrete decreased. Therefore, 0.85 mm rubber particles resulted in better stability.
- (2)
- The elastic modulus and toughness indices of concrete materials with different mixing quantities of rubber particles before and after fatigue load were measured and calculated, and the energy dissipation of the specimens was analyzed. The result revealed that, after fatigue loading, the incorporation of rubber particles significantly alleviated the decrease in elastic modulus and toughness index of concrete materials, and RC-1 showed better resistance to elastic deformation, toughness, and ductility. At the same time, the energy dissipation method acquired the loss variables of each cycle accurately. The constant amplitude cyclic loading made the loss accumulate slowly, but it could be found that the damage variable of RC was in a narrow range and resulted in remarkable crack resistance and fatigue resistance.
- (3)
- Tunnel-surrounding rock deformation and the stress of lining structure using two kinds of backfill concrete were calculated by the finite element method, and the safety and stability of the tunnel structure are contrasted and analyzed. The outcome shows that the deformation and stress of the surrounding rock are lower than those of plain concrete when rubber concrete is used as backfill material. The vault settlement and arch bottom settlement are reduced by 0.4 mm and 0.6 mm, respectively, and the maximum principal stress is increased by 11.5%. Therefore, the stability of the tunnel structure is enhanced by employing rubber concrete backfill.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| OC | Ordinary concrete |
| RC | Rubber concrete |
| RC-1 | Rubber concrete with a grain size of 0.85 mm |
| RC-2 | Rubber concrete with a grain size of 1–3 mm |
| RC-3 | Rubber concrete with a grain size of 3–6 mm |
| σ | Test compressive strength |
| σr | Standard compressive strength |
| E | Elastic modulus |
| D | Damage variables |
| K | Elastic resistance coefficient |
References
- Meng, J. Research on structural force characteristics and scheme optimization of backfilling construction of open-cut tunnel group, Southwest. Jiaotong Univ. 2021. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, R.; Goh, A. Multivariate Adaptive Regression Splines Approach to Estimate Lateral Wall Deflection Profiles Caused by Braced Excavations in Clays. Geotech. Geol. Eng. 2018, 36, 1349–1363. [Google Scholar] [CrossRef]
- Zhang, R.; He, C.G.; Fei, W.; Li, J. Experimental study on dynamic pore water pressure of saturated cohesive soil and gravel. Rock Mech. 2006, 10, 1805–1810. [Google Scholar] [CrossRef]
- Chen, Y.; Ma, Y.F.; Tang, Q.S.; Zhou, Y. Influence of elastic modulus of back-fill concrete above mid-wall on stability of multi-arch tunnel. J. Central South Univ. Sci. Technol. 2012, 43, 1138–1143. [Google Scholar]
- Xu, H.F.; Zeng, C.C. Optimization Design and Construction of Backfilling Materials for the Arch Foot of Long Distance Open Excavation Section of Submarine Tunnel. Portal. Highw. 2021, 66, 376–379. [Google Scholar]
- Yao, Z.M.; Zhang, M.H.; Chen, J.H. Cyclic Accumulative Pore Pressure Explicit Model of Saturated Soft Clay and Long-term Settlement Calculation of Subway Tunnel Roadbed. J. China Railw. Soc. 2012, 34, 87–92. [Google Scholar] [CrossRef]
- Wang, J.; Li, X.; Guo, B.; Ding, G.; Liu, T.; Sun, Y.; Yu, M. Test Study on Settlement Model of Ultra-Thick Backfill in High-Speed Railway Tunnel through Giant Karst Cave. China Railw. Sci. 2022, 43, 84–95. [Google Scholar] [CrossRef]
- Zhao, Y.; Shang, Y.H. Study on Dynamic Characteristics and Cumulative Deformation Law of Subgrade under Dynamic Load of High-speed Train. Railw. Stand. Des. 2017, 61, 56–61. [Google Scholar] [CrossRef]
- Ishikawa, T.; Sekine, E.; Miura, S. Cyclic Deformation of Granular Material Subjected to MovingWheel Loads. Can. Geotech. J. 2011, 48, 691–703. [Google Scholar] [CrossRef]
- Yang, B.M.; Liu, B.G. Analysis of Long-Term Settlement of Shield Tunnel in Soft Soil Areatunder Cyclic Loading of Subway Train. China Railw. Sci. 2016, 37, 61–67. [Google Scholar]
- Jiang, Z.; Gao, G.Y.; Zhao, H.; Chen, G.Q. Long-term settlement of tunnels induced by subway moving load in soft soil districts. Chin. J. Geotech. Eng. 2013, 35, 301–307. [Google Scholar]
- Pang, D.P.; Liu, F.; Li, L.J. Survey of application and research of rubber concrete. China Rubber Ind. 2007, 54, 182–185. [Google Scholar]
- Sgobba, S.; Borsa, M.; Molfetta, M.; Marano, G.C. Mechanical performance and medium-term degradation of rubberised concrete. Constr. Build. Mater. 2015, 98, 820–831. [Google Scholar] [CrossRef]
- Elchalakani, M. High strength rubberized concrete containing silica fume for the construction of sustainable road side barriers. Structures 2015, 1, 20–38. [Google Scholar] [CrossRef]
- Yang, R.; Wang, Z. Application Research of Rolled Rubber Concrete in Engineering. Concrete 2011, 12, 139–141. [Google Scholar]
- Sofi, A. Effect of waste tyre rubber on mechanical and durability properties of concrete–A review. Ain Shams Eng. J. 2018, 9, 2691–2700. [Google Scholar] [CrossRef]
- Hu, P.; Zhu, H. Experimental study on permeability of crumb rubber concrete. J. Tianjin Univ. Technol. 2006, 22, 8–12. [Google Scholar] [CrossRef]
- Jie, X.U.; Yao, Z.Y.; Yang, G.; Han, Q.H. Research on crumb rubber concrete: From a multi-scale review. Constr. Build. Mater. 2020, 232, 117282. [Google Scholar] [CrossRef]
- Jing, X.U.; Hong, J.X.; Wan, Y.; Liu, J.P. In fluence of rubber powder on shrinkage cracking of concrete. Concrete 2009, 10, 96–98. [Google Scholar]
- Suad, A.B. Investigation of corrosion damage in a reinforced concrete structure in Kuwait. ACI Mater. J. 1998, 3, 226–231. [Google Scholar] [CrossRef]
- Nehdi, M.; Khan, A. Cementitious composites containing recycled tire rubber: An overview of engineering properties and potential applica-tions. Cem. Concr. Aggreg. 2001, 23, 3–10. [Google Scholar] [CrossRef]
- Toutanji, H.A. The use of rubber tire particles in concrete to replace mineral aggregate. Cem. Concr. Compos. 1996, 18, 135–139. [Google Scholar] [CrossRef]
- Wang, B.M.; Guo, Z.Q.; Han, Y. The research progress of rubberied concrete on the shrinkage and cracking property. Low Temp. Arch. Technol. 2012, 34, 4–6. [Google Scholar] [CrossRef]
- Chen, W.W. Research on Toughness of Crumb Rubber Concrete. Tianjin Univ. 2014. [Google Scholar]
- Son, K.S.; Iman, H.; Kypros, P.K. Strength and deformability of waste tyre rubber-filled reinforced concrete columns. Constr. Build. Mater. 2011, 25, 218–226. [Google Scholar] [CrossRef]
- Han, J.H.; Yuan, Q.; Feng, L.Y.; Wang, W.W.; Zhao, F. Research on Shock Resistance of Rubber Concrete. Yellow River 2018, 40, 107–114. [Google Scholar]
- Khaloo, A.R.; Dehestani, M.; Rahmatabadi, P. Mechanical properties of concrete containing a high volume of tire–rubber particles. Waste Manag. 2008, 28, 2472–2482. [Google Scholar] [CrossRef] [PubMed]
- Pang, J.Y.; Chen, Y.; Huang, X.; Liu, G.C.; Huang, J. Impact of Equal-amplitude Cyclic High Stress Loading on Mechanical and Deformation Properties of Rubber Concrete. J. Changjiang River Sci. Res. Inst. 2020, 37, 142–148. [Google Scholar]
- Huang, X.; Pang, J.; Liu, G.; Chen, Y. The influence of equal amplitude high stress repeated loading on the mechanical and deformation characteristics of rubber concrete—ScienceDirect. Constr. Build. Mater. 2020, 266, 121–135. [Google Scholar] [CrossRef]
- Gholampour, A.; Fallah Pour, A.; Hassanli, R.; Ozbakkaloglu, T. Behavior of actively confined rubberized concrete under cyclic axial compression. J. Struct. Eng. 2019, 145, 04019131. [Google Scholar] [CrossRef]
- Li, P.D.; Wu, Y.F. Stress-strain behavior of actively and passively confined concrete under cyclic axial load. Compos. Struct. 2016, 149, 369–384. [Google Scholar] [CrossRef]
- Song, Z.T.; Thomas, F.H.; Heinz, K. Inhomogeneous mechanical behaviour of concrete subjected to monotonic and cyclic loading. Int. J. Fatigue 2020, 132, 105383. [Google Scholar] [CrossRef]
- Song, Z.; Konietzky, H.; Frühwirt, T. Hysteresis energy-based failure indicators for concrete and brittle rocks under the condition of fatigue loading. Int. J. Fatigue 2018, 114, 298–310. [Google Scholar] [CrossRef]
- Jiang, D.Y.; Liu, Y.H.; Chen, J. Fatigue performance of ordinary concrete subjected to stepwise discontinuous cyclic loading. J. Southeast Univ. 2019, 49, 631–637. [Google Scholar]
- Abusharar, S.W. Effect of Particle Sizes on Mechanical Properties of Concrete Containing Crumb Rubber. Innov. Syst. Des. Eng. 2015, 6, 114–125. [Google Scholar]
- JGJ55-2011; Specification for Mix Proportion Design of Ordinary Concrete. China Architecture & Building Press: Beijing, China, 2011.
- GB/T 50081-2002; Standard for Test Method of Mechanical Properties on Ordinary Concrete. China Architecture & Building Press: Beijing, China, 2003.
- Liu, H.R.; Xia, L.L.; Dai, Y.; Zhao, M.; Zhou, Z.; Liu, H.B. Fabrication and characterization of novel hydroxyapatite/porous carbon composite scaffolds. Mater. Lett. 2012, 66, 36–38. [Google Scholar] [CrossRef]
- JGJ/T70-2009; Standard for Test Method of Basic Properties of Construction Mortar. China Architecture & Building Press: Beijing, China, 2009.
- Hany, N.F.; Hantoche, E.G.; Harajli, M.H. Axial stress-strain model of CFRP-confined concrete under monotonic and cyclic loading. J. Com. Constr. 2015, 19, 1–16. [Google Scholar] [CrossRef]
- Wang, C.L.; Xu, B.G.; Li, S.L.; Tang, H.Y. Study on a constitutive model of damage of SFRC under uniaxial compression. Rock Soil Mech. 2006, 27, 151–154. [Google Scholar] [CrossRef]
- Hu, S.C. Study on mechanical properties and energy response characteristics of high-porosity concrete under cyclic loading and unloading. China Univ. Min Technol. 2018. [Google Scholar]
- Yue, X.G. Numerical simulation analysis on the influence of blasting construction of small clear distance tunnel. Railw. Constr. Technol. 2018, 4, 9–12. [Google Scholar]
- Chen, W.Z.; Tian, H.M.; Yang, F.D.; Geng, Y.M. Study of effects of foam concrete preset deformation layer on long-term stability of deep soft rock tunnel. Rock Soil Mech. 2011, 32, 2577–2583. [Google Scholar] [CrossRef]








| Composition | CaO | SiO2 | Al2O3 | MgO | Fe2O3 | Na2O | SO3 | Ignition Loss | |
|---|---|---|---|---|---|---|---|---|---|
| Content | Cement | 63.11 | 22.60 | 5.03 | 1.46 | 4.38 | - | 2.24 | 1.18 |
| Fly ash | 2.47 | 53.26 | 34.72 | 0.39 | 4.07 | 1.90 | - | 4.07 | |
| Sample | fp/MPa | ff/MPa | E1/GPa | E2/GPa | T1 | T2 |
|---|---|---|---|---|---|---|
| OC | 20.3 | 18.3 | 2.46 | 1.47 | 2.87 | 2.51 |
| RC-1 | 14.1 | 12.7 | 1.68 | 1.54 | 3.91 | 3.52 |
| RC-2 | 13.6 | 12.3 | 1.55 | 1.46 | 3.66 | 3.33 |
| RC-3 | 12.4 | 11.2 | 1.82 | 1.29 | 3.12 | 2.76 |
| Test Piece Number | 1/n | 2/n | 10/n | 20/n | 30/n | 40/n | 50/n | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Wd | W | Wd | W | Wd | W | Wd | W | Wd | W | Wd | W | Wd | W | |
| OC | 2.4 | 28.9 | 1.1 | 26.2 | 1.9 | 26.0 | 2.6 | 25.9 | 2.3 | 27.2 | 2.4 | 25.8 | 2.6 | 25.7 |
| RC-1 | 12.3 | 24.1 | 1.3 | 14.7 | 1.2 | 14.1 | 1.2 | 13.7 | 1.2 | 13.6 | 1.4 | 13.6 | 1.4 | 13.9 |
| RC-2 | 13.6 | 25.8 | 1.6 | 16.1 | 1.9 | 15.9 | 1.8 | 15.4 | 1.3 | 15.5 | 1.6 | 15.5 | 1.7 | 15.4 |
| RC-3 | 12.3 | 22.3 | 1.5 | 13.9 | 1.4 | 12.7 | 1.3 | 12.5 | 1.3 | 12.5 | 1.3 | 12.7 | 1.4 | 12.4 |
| Test Piece Number | Weigh γ (kN/m3) | E (MPa) | K (MPa/m) | ν | Hydraulic Conductivity (m/s) |
|---|---|---|---|---|---|
| OC | 24 | 1470 | 231.1 | 0.2 | 2.3 × 10−6 |
| RC-1 | 21 | 1540 | 242.1 | 0.2 | 2.1 × 10−6 |
| Evaluating Indicator | OC | RC-1 |
|---|---|---|
| Crown settlement (mm) | 29.1 | 28.7 |
| Bottom settlement (mm) | −26.4 | −27.0 |
| Horizontal displacement of left arch waist (mm) | 8.58 | 7.61 |
| Horizontal displacement of right arch waist (mm) | −8.39 | −7.40 |
| Maximum principal stress (MPa) | 0.96 | 1.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, B.; Zhu, R.; Liu, Z.; Zeng, J.; Liu, C. Fatigue Damage of Rubber Concrete Backfill at Arch Springing Influence on Surrounding Rock Deformation in Tunnel Engineering. Appl. Sci. 2024, 14, 4129. https://doi.org/10.3390/app14104129
Wu B, Zhu R, Liu Z, Zeng J, Liu C. Fatigue Damage of Rubber Concrete Backfill at Arch Springing Influence on Surrounding Rock Deformation in Tunnel Engineering. Applied Sciences. 2024; 14(10):4129. https://doi.org/10.3390/app14104129
Chicago/Turabian StyleWu, Bo, Ruonan Zhu, Zhaochun Liu, Jiajia Zeng, and Cong Liu. 2024. "Fatigue Damage of Rubber Concrete Backfill at Arch Springing Influence on Surrounding Rock Deformation in Tunnel Engineering" Applied Sciences 14, no. 10: 4129. https://doi.org/10.3390/app14104129
APA StyleWu, B., Zhu, R., Liu, Z., Zeng, J., & Liu, C. (2024). Fatigue Damage of Rubber Concrete Backfill at Arch Springing Influence on Surrounding Rock Deformation in Tunnel Engineering. Applied Sciences, 14(10), 4129. https://doi.org/10.3390/app14104129





