Research on the Capillary Filling Behavior of Liquid Solder Al-12Si under the Action of Electromagnetic Ultrasonic Wave

Abstract

To address the issues of high cost, low welding efficiency, and complex processes in vacuum brazing, we proposed a method of electromagnetic ultrasonic (EU)-assisted brazing with Al-12Si solder to join SiC ceramic and TC4 alloy. The results showed that the maximum magnetic induction strength (MIS) on the surface of the liquid solder was 0.629 T when subjected to a static and alternating magnetic field (MF). Additionally, the combined action of MF and eddy current generated a downward Lorentz force (LF) in the liquid solder, with the maximum LF in the horizontal and vertical directions being 48.91 kN m⁻³ and 60.93 kN m⁻³, respectively. Under the influence of an EU wave, the liquid solder exhibited capillary filling (CF) behavior. At 26 ms, the maximum length of CF was 12.21 mm.

1. Introduction

SiC ceramics are widely used in armor materials of protective equipment such as tanks and armored vehicles because of their high temperature resistance, high hardness, high compressive strength, and strong oxidation resistance [1,2]. However, SiC ceramics have low ductility and poor toughness, and are easily broken when impacted. Therefore, they cannot be used alone, but need to be welded with metal materials to form composite armor to improve impact toughness and strength [3,4]. Titanium alloy has the characteristics of high strength, excellent toughness and tensile properties, and good corrosion resistance [5,6,7]. Therefore, the composite structure plate composed of the two can avoid the brittleness of SiC ceramics and give full play to the armor protection characteristics of SiC ceramics [8]. At present, vacuum brazing technology is one of the most potential technologies for welding SiC ceramics and metal materials.

Vacuum brazing is a welding method in which the brazing filler metal is melted by heating in a vacuum or inert gas environment, so that it penetrates into the surface of the base metal and solidifies, and finally forms a solid connection. Due to the advantages of high quality and strong corrosion resistance, the welded joints prepared by this method have received extensive attention in recent years [9,10]. Ma et al. [11] inserted a 3D-SiO₂ fiber interlayer between SiC and TC4 alloy (with a nominal composition of Ti-6Al-4V), and then performed vacuum brazing. The results showed that the welded joints contained abundant and dispersed TiSi₂, TiCu₂, TiSi, and α-Ti particles, which effectively reduced residual stresses. The shear strength of the welded joints reached 40 MPa. Wang et al. [12] used Cu foam as a liquid solder to join ZrB₂-SiC ceramics and TC4 alloy by vacuum brazing. They found that the shear strength of the welded joints reached 435 MPa when the holding time was 20 min. However, with an increase in holding time, the content of Ti₂Cu compounds increased, which was detrimental to the mechanical properties of the welded joints. Gao et al. [13] also used liquid solder AgCuTi-Al to braze C_f/SiC composites and TC4 titanium alloy in vacuum brazing. The welded joint contained the intermetallic compound Ti₃Al, which effectively reduced the residual thermal stress and resulted in a maximum shear strength of 149 MPa.

However, vacuum brazing has several disadvantages, including high welding equipment costs, a complex process, and low welding efficiency [14,15,16]. In addition, the application of an EU wave in liquid metal can also refine the grains and improve the mechanical properties of the metal, and can effectively solve these problems [17,18]. At present, the application of electromagnetic field in the field of welding is mainly combined with other welding processes as an auxiliary means. Farhang et al. [19] used electromagnetic field-assisted laser welding technology to connect NiTi/316L stainless steel joints. The results showed that compared with the traditional laser welding, the Ti-Fe-based intermetallic compounds in the welding area were suppressed, and the strength and toughness of the welded joints were increased by 28% and 137%, respectively. Bachmann et al. [20] analyzed the influence of an external transverse electromagnetic field on the flow phenomenon of molten pool by establishing a three-dimensional steady-state laminar numerical model. The results showed that the application of a transverse electromagnetic field during laser welding of aluminum alloy could significantly inhibit the metal flow in the molten pool. In summary, the current application of electromagnetic field in the field of welding was mainly to prepare better welded joints by affecting the arc or molten pool generated by other welding processes in the working process. However, there were few studies on the LF generated by electromagnetic field as the main welding method. Therefore, a new welding method of EU-assisted brazing was proposed. The method generated an LF with a vibration frequency of 20 kHz inside the liquid solder by means of an electromagnetic field, which controlled the CF behavior of the liquid solder within the gap of the substrate. This method did not require contact with materials, and has the advantages of low cost, simple process control, and low pollution. As a continuation and expansion of research by Ref. [21], the CF behavior of liquid solder Al-12Si on the surface of SiC ceramic and TC4 alloy under the action of an EU wave is studied in this paper. Firstly, this article establishes the CF model of liquid solder under the influence of an EU wave by COMSOL Multiphysics software. Then, it analyzes the generation of the MF and its mechanism of action on the liquid solder, thereby improving the relevant theoretical system of EU-assisted brazing.

2. Physical Model

2.1. Governing Equation

Under the action of the EU wave, the essence of the CF behavior of the liquid solder is the forced movement of the fluid, that is, the flow of the liquid solder is fundamentally caused by the pressure change. Because the pressure measurement inside the liquid solder is extremely difficult to obtain, it is necessary to use the computational fluid dynamics method for calculation and analysis. Computational fluid dynamics is based on the basic theory of fluid mechanics. According to Newton’s fluid mechanics theory, the flow of any particle or system follows the law of conservation of mass, energy, and momentum. The basic equations describing the fluid are the continuity equation, momentum equation, and energy equation [22].

According to the theory of fluid mechanics, the basic governing equations describing the flow field can be expressed as follows [23,24]:

(1) Continuity equation:

$$\frac{\partial \rho }{\partial t}+\nabla •\left(\rho v\right)=0$$

(1)

(2) Momentum equation:

$$\frac{\partial \rho v}{\partial t}+\nabla •\left(\rho vv\right)=\rho F+\nabla •p$$

(2)

(3) Energy equation:

$$\frac{\partial E}{\partial t}+\nabla •\left[\left(E+p\right)v\right]=\rho F•v+\nabla •\left(\tau •v\right)+\nabla •\left(k•T\right)$$

(3)

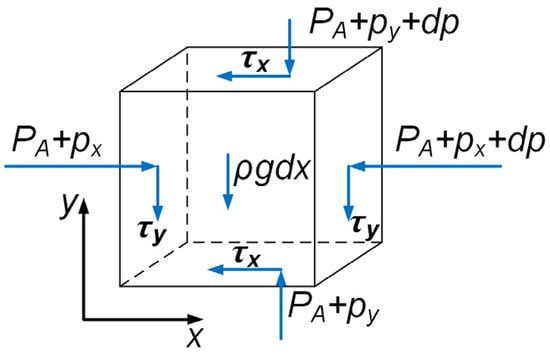
where ρ is the density of liquid solder, v is the velocity vector, ∇ is the Hamiltonian operator, F is the source term, p is the pressure, E is the internal energy, τ is the stress tensor, T is the temperature, k is the thermal coefficient.

2.2. Establishment of the Model

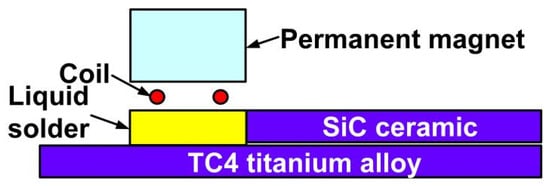
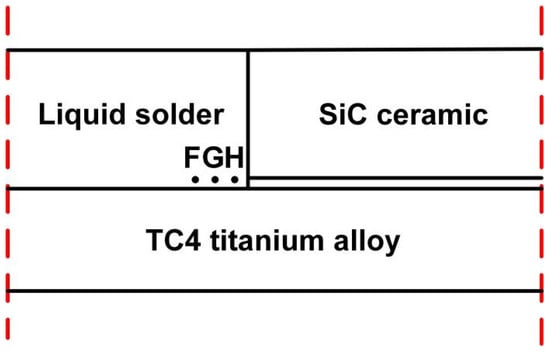
In order to analyze whether composite components could be formed from SiC ceramic and metal material under the influence of the EU wave, the SiC ceramic and TC4 alloy were chosen as the substrates. The size of TC4 alloy was 60 × 3 mm, and the size of SiC ceramic was 30 × 3 mm. The surface roughness of both was 10 μm. Because Al could form effective metallurgical bonding with SiC and TC4 alloys, and the presence of Si could inhibit the formation of Al₄C₃ metal compounds at the Al/SiC interface and the chemical reaction between Ti/Al, therefore, Al-12Si was selected as the liquid solder. The physical properties of the substrate and the liquid solder are shown in

Table 1. Physical parameters of substrates [25,26,27].

Substrate	Elastic Modulus (GPa)	Poisson Ratio	Density (g/cm3)
SiC	450	0.142	3.1
TC4	110	0.31	4.44

and

Table 2. Physical parameters of Al-12Si [28,29,30].

Solder	Melting (°C)	Viscosity (mPa·s)	Density (g/cm3)
Al-12Si	577	0.88 (700 °C)	2.654

, respectively. In this paper, a two-dimensional plane model of CF behavior was established using COMSOL Multiphysics software, as depicted in Figure 1.

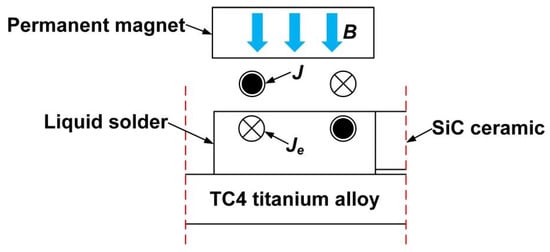
At the beginning, the SiC ceramic was placed on the top of the TC4 alloy with a gap of 0.2 mm, and the liquid solder Al-12Si was placed at the edge of the substrate gap. Subsequently, the coil and the permanent magnet were placed on the top of the liquid solder. The alternating current flowing into the coil can be given by the following:

$$I=A\times \sin \left(2\pi ft\right)$$

(4)

where A is the peak current, f is the current frequency. The model’s initial parameters are as shown in

Table 3. Model’s initial parameters.

Parameter Name	Value
Peak current	50 A
Current frequency	20 kHz
Number of coils	30
Static MF	1 T

. According to previous studies, the peak current and the static MF strength had a great influence on the LF generated in the liquid solder; therefore, they play a key role in the flow behavior of the liquid solder. To achieve the coupling of the magnetic and flow fields, the analysis modules “MF”, “MF, no current”, and “two-phase flow, level set” were used. Finally, the model was divided into 138,862 free triangular meshes, and the transient solver was used to solve the flow process of the liquid solder.

3. Results

3.1. MIS and Distribution

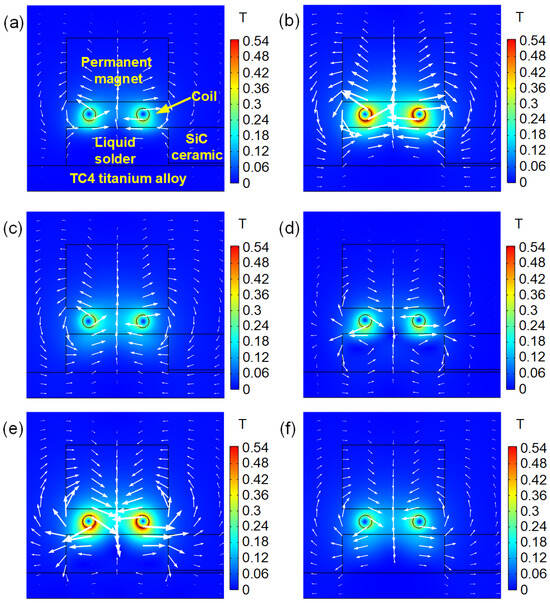
Figure 2 shows the distribution of the alternating MF near the liquid solder. When the strength of the field was between 1/6 period and 3/6 period, the field induced clockwise and counterclockwise rotation around the left and right sides of the coil, respectively. The MIS first increased and then decreased, with the maximum value of 0.529 T near the coil. Between 4/6 period and 6/6 period, the MF directions were reversed, and the MIS again increased and then decreased, with a maximum value of 0.526 T.

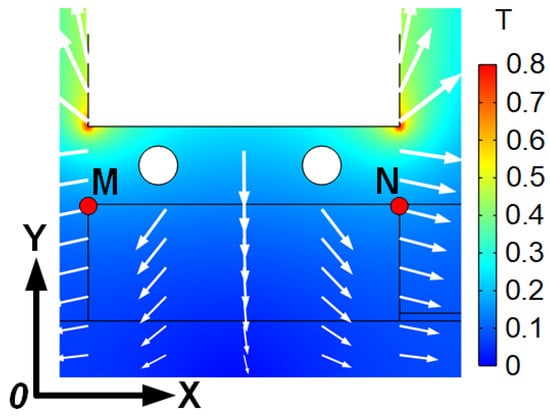
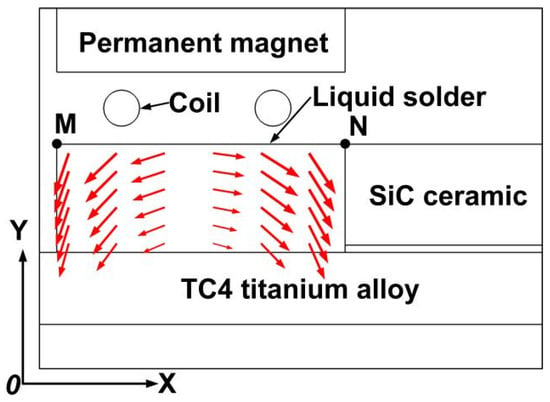
Figure 3 indicates the magnetic induction distribution near the liquid solder at a static MF strength of 1 T. The static MF direction received by the liquid solder under the permanent magnet was mainly vertical, while the edge part of the solder received a static MF direction that tended to deflect outwards.

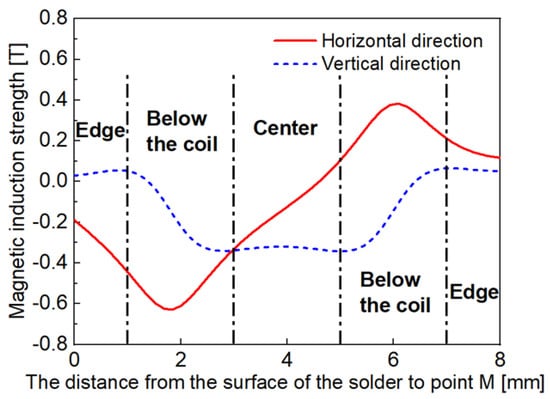
The M point and N point at the top of the liquid solder were extracted from Figure 3, and the MIS on the surface of the liquid solder was analyzed, as shown in Figure 4. It could be seen that the MIS of the liquid solder below the coil was larger, and the maximum MIS in the horizontal and vertical directions was 0.629 T and 0.342 T, respectively. The liquid solder at the edge was less affected by the alternating magnetic field due to the distance from the coil. This indicates that the liquid solder located below the coil would produce a large LF.

3.2. CF Process of Liquid Solder

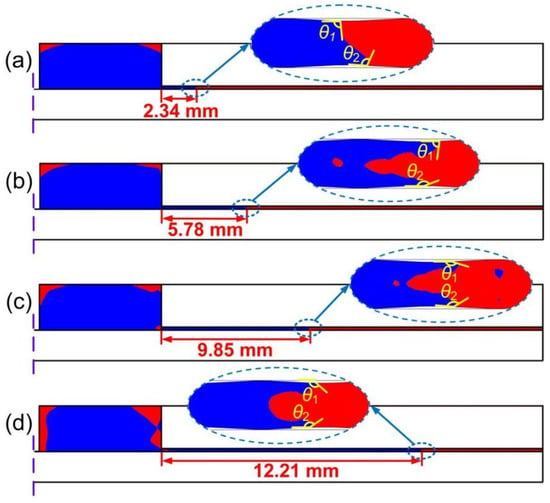
Figure 5 shows the CF process of liquid solder under the action of the EU wave. The contact angles between the liquid solder and the upper and lower substrate surfaces were denoted as θ₁ and θ₂, respectively. At 5 ms, the liquid solder in contact with the substrate surface first began to move and the top began to collapse. Then, the liquid solder continued to fill the gap, and the gap was filled to 9.85 mm at 17 ms. At this time, a small amount of splash occurred. At 26 ms, the CF length of liquid solder reached the maximum value of 12.21 mm.

4. Discussion

4.1. Driving Force Analysis of Liquid Solder CF Process

For the analysis of the LF production mechanism in liquid solder, a 2D theoretical model of the EU wave production was constructed, as shown in Figure 6. The AC flowing J into the coil can be given by the following:

$$J=\sqrt{2}{J}_A\cos \left(\omega t\right)$$

(5)

where J_A is the effective current density. At present, an alternating MF B_e was induced in the surrounding air, which in turn induced an eddy current J_e of the same magnitude and frequency as the AC but in the opposite direction in the liquid solder. Due to the J_e and the static MF B, the LF F₁ was generated inside the liquid solder, which can be expressed by the following formula [31]:

$$F_1=J_e•B=\sqrt{2}{J}_e•B\exp \left(-\frac{x}{\delta }\right)\cos \left(-\frac{x}{\delta }+\omega t\right)$$

(6)

F₂ was produced by a combination of the J_e and B_e in the air as given by the following:

$$F_2=J_e•B_e=\sqrt{2}{J}_e•B_e\exp \left(-\frac{x}{\delta }\right)\cos \left(-\frac{x}{\delta }+\omega t\right)$$

(7)

The distribution of the LF in the liquid solder is shown in Figure 7. The LF as a whole was outwardly directed, with a right to left direction on the left coil and an opposite direction on the right. The presence of an alternating MF resulted in a macroscopic vertical downward repulsion, which was attributed to the vertical component of the LF.

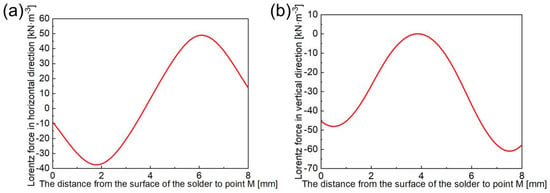
The LF on the surface of the liquid solder in all directions is shown in Figure 8, since the LF in Figure 7 had horizontal and vertical components. The liquid solder under the coil was subjected to a high LF, and the maximum horizontal and vertical values were 48.91 kN·m⁻³ and 60.93 kN·m⁻³, respectively. This indicates that the liquid solder under the coil plays a major role in the CF process of the liquid solder.

Under the influence of LF F₁ and F₂, the liquid solder occurred periodic vibration, extrusion, and stretching when the AC frequency was 20 kHz. This resulted in a change in the density state in the liquid solder, ultimately forming the EU wave. According to Refs. [32,33], ultrasonic vibration could produce pressure in the liquid, that is, sound pressure. In addition, according to Newton’s second law, when the liquid only receives the action of sine or cosine pressure, it will perform a reciprocating motion with the initial position as the center. Therefore, in order to analyze the mechanism of an EU wave on liquid solder, it is necessary to analyze the variation law of sound pressure in the liquid solder.

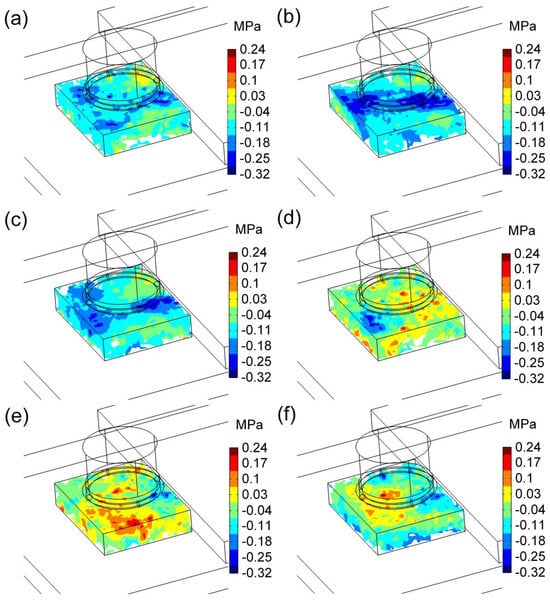
Figure 9 shows the sound pressure distribution in the liquid solder under the influence of the EU wave. In the first half of the cycle, the top and bottom were dominated by negative pressure and positive pressure, respectively. When the time was 60 μs, the maximum sound pressure value in the liquid solder was 0.309 MPa. Subsequently, the direction of the alternating current changed, and the positive and negative pressures in the liquid solder were converted to each other. The maximum sound pressure value in the second half of the cycle was 0.227 MPa.

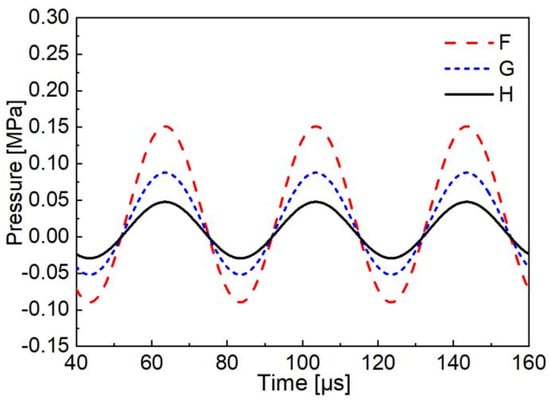
To analyze the sound pressure change of the liquid solder entering the substrate gap, micro-points F, G, and H were taken at the bottom of the liquid solder. Figure 10 shows the sound pressure change analysis of three micro-points.

The sound pressure variation curve for each micro-point is shown in Figure 11. The curve for each micro-point exhibited a sinusoidal periodic change. The sound pressure value was highest at point F, followed by point G, and lowest at point H, which was far from the coil.

The sound pressure change curve in Figure 11 was fitted, and the corresponding expression of the data can be given by the following:

$$P=P_0\times \sin \left[2\pi f\left(t-t_0\right)\right]+P_s$$

(8)

where P is the pressure on the micro-point, P₀ is the sound pressure amplitude, f is the sound pressure frequency, t is the action time of the EU wave; t₀ is the initial phase, P_s is the half-wave offset. According to Refs. [34,35], the half-wave offset is the offset resulting from the fact that when the acoustic energy density is high, the sound pressure within the liquid solder no longer varies ideally linearly.

Table 4. The sound pressure expression parameters of each micro-point.

Micro-Point	Sound Pressure Amplitude (MPa)	Sound Pressure Frequency (kHz)	Initial Phase (μs)	Half-Wave Offset (MPa)
F	0.121	20	13.501	0.092
G	0.07	20	13.025	0.031
H	0.039	20	13.115	0.018

shows the sorted parameter values of the sound pressure function expression for each micro-point. The absolute value of the sound pressure difference between the micro-points was |P_F − P_G| = 0.051 MPa and |P_G − P_H| = 0.031 MPa, respectively. Since the half-wave offset of each micro-point was positive, and the sound pressure difference was |P_F − P_G| > |P_G − P_H|, it follows that the repulsion between the FG points was greater than that between the GH points, indicating that the liquid solder near the coil pushed the right part to fill the gap.

4.2. Interface Mechanical Analysis of Liquid Solder CF Process

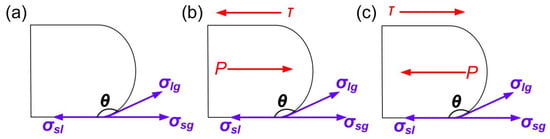
Figure 12 displays the physical model of the liquid solder’s front-end during the CF process. This model included surface tension values at the interfaces between liquid and solid, gas and solid, and gas and liquid, which were represented by symbols σ_sl, σ_sg, and σ_lg, respectively. The surface tension caused the three-phase interface to balance at the front-end of the liquid solder before the EU wave was applied. When the EU wave was applied, the sound pressure difference was generated inside the liquid solder. When the sound pressure difference was greater than 0 and greater than the surface tension σ and friction τ, the liquid solder had a tendency to move forward. When the acoustic pressure difference was less than 0 and greater than the surface tension σ and friction τ, the liquid solder was hindered from moving forward. Due to the friction force and half-wave offset, the liquid solder could not be retracted to its original position. Over time, the liquid solder was able to fill the gap.

To analyze the driving force of the liquid solder from the microscopic point of view, it is necessary to extract a micro-element in the liquid solder and establish a mathematical model, as shown in Figure 13. Before the EU wave was applied, the micro-element was subjected to gravity and the static pressure P_A with equal direction. After the EU wave was applied, it was subjected to the sound pressure p and the viscous resistance τ when the micro-element moves.

During the CF process of liquid solder, the micro-element motion in the gap of the substrate still satisfies Newton’s law. The two-dimensional Newton’s motion equation can be expressed as follows [36,37]:

$$\rho \frac{du}{dt}=-\Delta P_{ux}-\eta \frac{du}{dy}-\left({\sigma }_{\lg }\cos \theta -{\sigma }_{sl}+{\sigma }_{sg}\right)/S$$

(9)

where P_ux is the sound pressure difference in the X direction, η is the viscosity of the liquid solder, and S is a cross-sectional area of the micro-element. Extending the analysis to a liquid layer consisting of continuous microelements with all cross-sectional areas S, the overall equation of motion can be given by the following:

$$-\rho \frac{du}{dt}=\Delta P_{ul}-P_{\sigma }-{\displaystyle \underset{0}{\overset{d}{\int }}\eta \frac{\partial u}{\partial y}dx}$$

(10)

where P_ul is the sound pressure difference in the X direction of the liquid layer with a length of l and a thickness of d. P_σ is the surface additional pressure formed by the surface tension pointing to the inside of the liquid solder, which can be expressed as follows:

$$P_{\sigma }=\frac{{\sigma }_{\lg }}{l}=\frac{2{\sigma }_{\lg }\cos \theta }{d}$$

(11)

According to Equation (8), the general expression of the sound pressure gradient on the liquid layer during the CF process of the liquid solder can also be expressed as follows:

$$\Delta P_u=P_0\times \sin \left[2\pi f\left(t-t_0\right)\right]+P_s$$

(12)

According to Equation (12), it could be concluded that the sound pressure gradient changed with time, so it could explain why the liquid solder had an instantaneous process of repeated forward and contraction motion during the CF process. According to Equation (10), it could be concluded that if the liquid layer moved in the X direction, the sound pressure gradient satisfied the following equation:

$$-\Delta P_u>P_{\sigma }+{\displaystyle \underset{0}{\overset{d}{\int }}\eta \frac{\partial u}{\partial y}dx}$$

(13)

Equation (13) indicated that the positive sound pressure gradient was greater than the surface tension additional pressure and friction resistance. In summary, the continuous forward and contraction movement finally realized the CF process of the liquid solder because of the asymmetry of the positive and negative half waves, and there was an offset Ps, so that the forward degree of the liquid solder in a cycle was greater than the degree of contraction.

4.3. Interface Mechanical Analysis of Liquid Solder CF Process

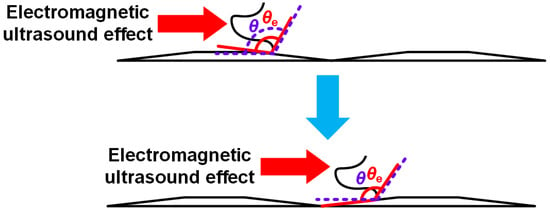
During the movement of the liquid solder, the change of the front contact angle also played a role in promoting and hindering. Assuming that the surface of the substrate was smooth and uniform, the contact angle θ can be expressed by Young’s equation [38,39,40]:

$$\cos \theta =\frac{{\sigma }_{sg}-{\sigma }_{sl}}{{\sigma }_{\lg }}$$

(14)

When the contact angle was less than 90°, the liquid solder could easily wet the substrate surface. Conversely, the liquid solder was difficult to wet the substrate surface when the contact angle was greater than 90°.

Since the actual substrate surface was not smooth, it was more in line with the corrected wetting equation proposed by Wenzel. The expression can be expressed as follows [41,42,43]:

$$r=\frac{\cos {\theta }_e}{\cos \theta }$$

(15)

where θ_e is the contact angle between the actual contact surface and the liquid solder, r is the roughness factor, which represents the ratio of the actual flux contact surface to the ideal contact surface, where r must be greater than or equal to 1.

When θ_e < θ < 90°, the liquid solder could also wet the rough substrate surface. However, in the actual CF process, the contact angle was still greater than 90° for most of the time, which hindered the forward movement of the liquid solder, as shown in Figure 5. When the liquid solder passed through the surface of the substrate in the concave part, it underwent a small amount of CF behavior due to the force of gravity, in addition to the driving force of the EU wave. In Figure 14, it can be observed that as the liquid solder flowed to the convex part of the substrate, θ and θ_e increased, resulting in an increased resistance to move forward. However, the EU wave facilitated the movement of the liquid solder to the next concave part surface.

In future research, the effect of EU-assisted brazing on liquid solder can be improved by changing the shape of the coil and the size of the permanent magnet. Furthermore, the flow state of the liquid solder can be regulated by adjusting the number of turns of the coil and the spacing between the permanent magnet, the coil, and the liquid solder.

5. Conclusions

In order to solve the problems of high cost, low welding efficiency, and complex process in vacuum brazing, the welding method of EU-assisted brazing was proposed, and the CF behavior of liquid solder Al-12Si in the gap between SiC ceramic and TC4 alloy under the action of an EU wave was analyzed. The following findings were revealed:

(1) After the alternating current was introduced, a periodically rotating alternating magnetic field was induced in the air near the coil. The static MF generated by the permanent magnet was directed vertically downwards. Under the combined action of the two MFs, the maximum MIS of the liquid solder in the horizontal and vertical directions was 0.629 T and 0.342 T, respectively.

(2) The eddy current generated in the liquid solder interacts with both the alternating and static MFs, resulting in a downward deflection trend of the LF inside the liquid solder. The maximum LF in the horizontal and vertical directions was 48.91 kN m⁻³ and 60.93 kN m⁻³, respectively.

(3) Under the influence of the LF with a frequency of 20 kHz, an EU wave was generated in the liquid solder, resulting in sinusoidal sound pressure at multiple positions within the liquid solder. The liquid solder moved due to the combined effect of the acoustic pressure difference and positive half-wave offset between different positions. At 26 ms, the maximum CF length of the liquid solder was 12.21 mm. These results indicate that applying a high-frequency MF to the liquid solder could make the liquid solder undergo macroscopic fluid movement, and then complete the connection between dissimilar materials.