Magnetic Negative Stiffness Devices for Vibration Isolation Systems: A State-of-the-Art Review from Theoretical Models to Engineering Applications
Abstract
1. Introduction
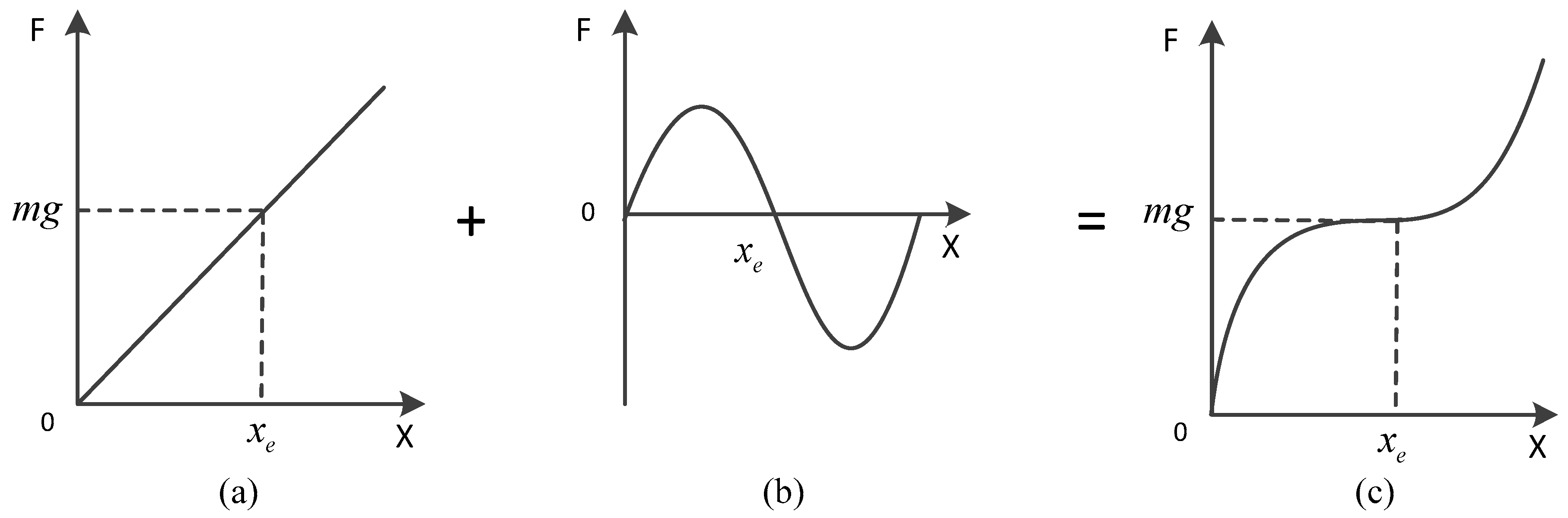
2. Fundamental Principles of Quasi-Zero Stiffness
2.1. Basic Principles of QZS
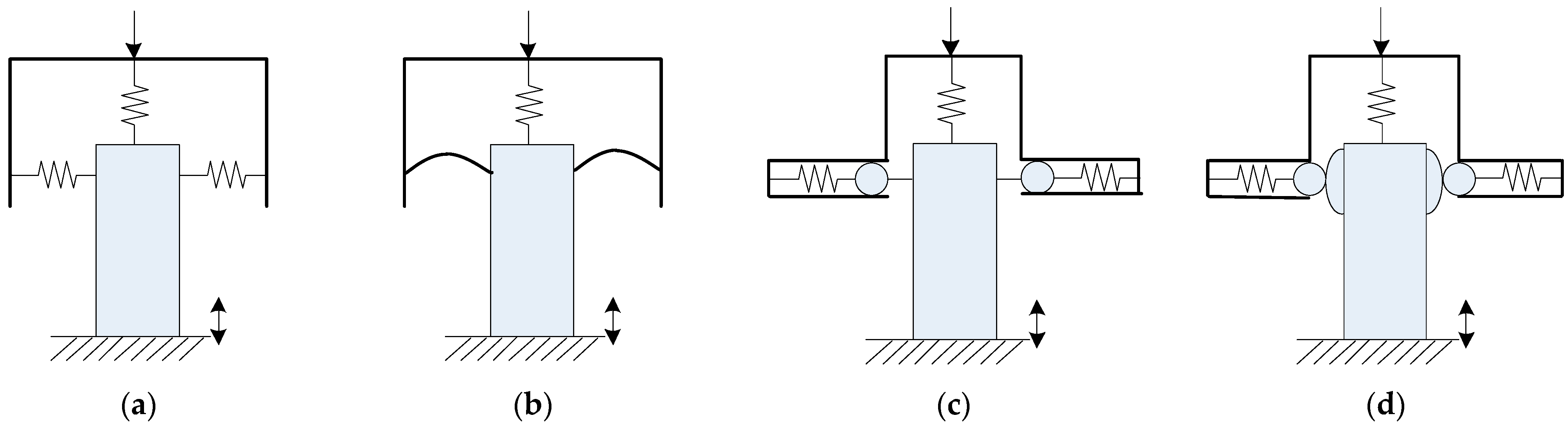
2.2. Basic Types of QZS Vibration Isolators
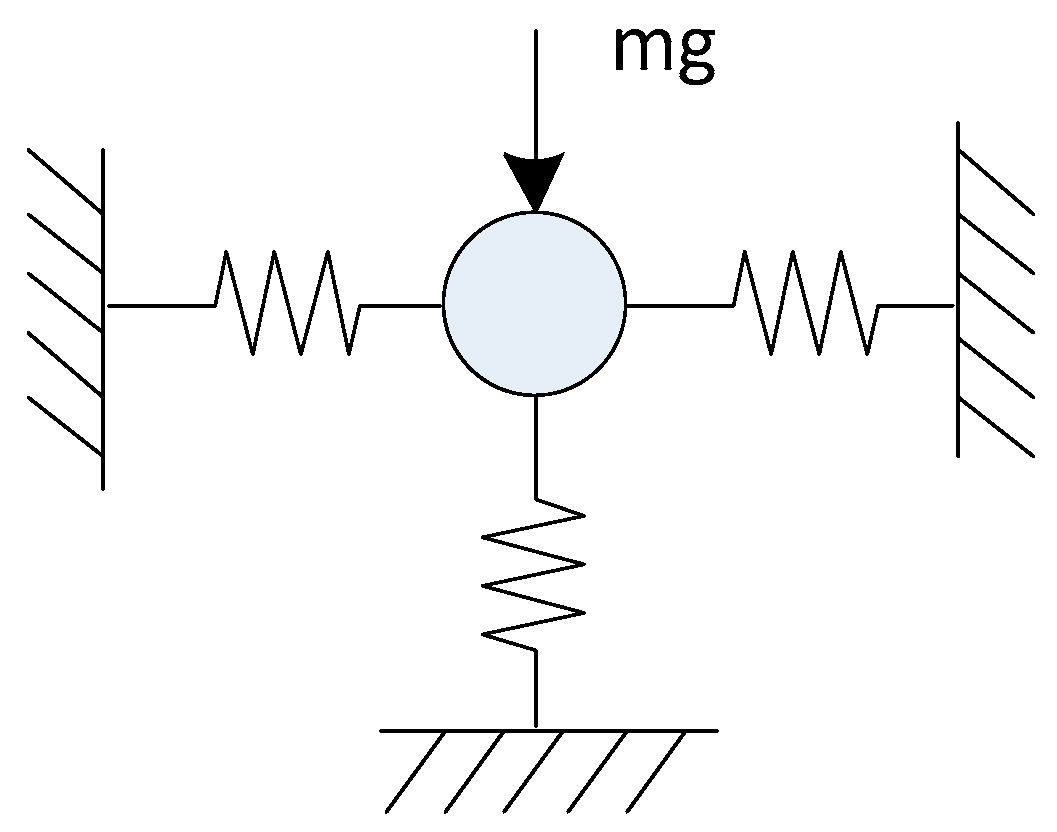
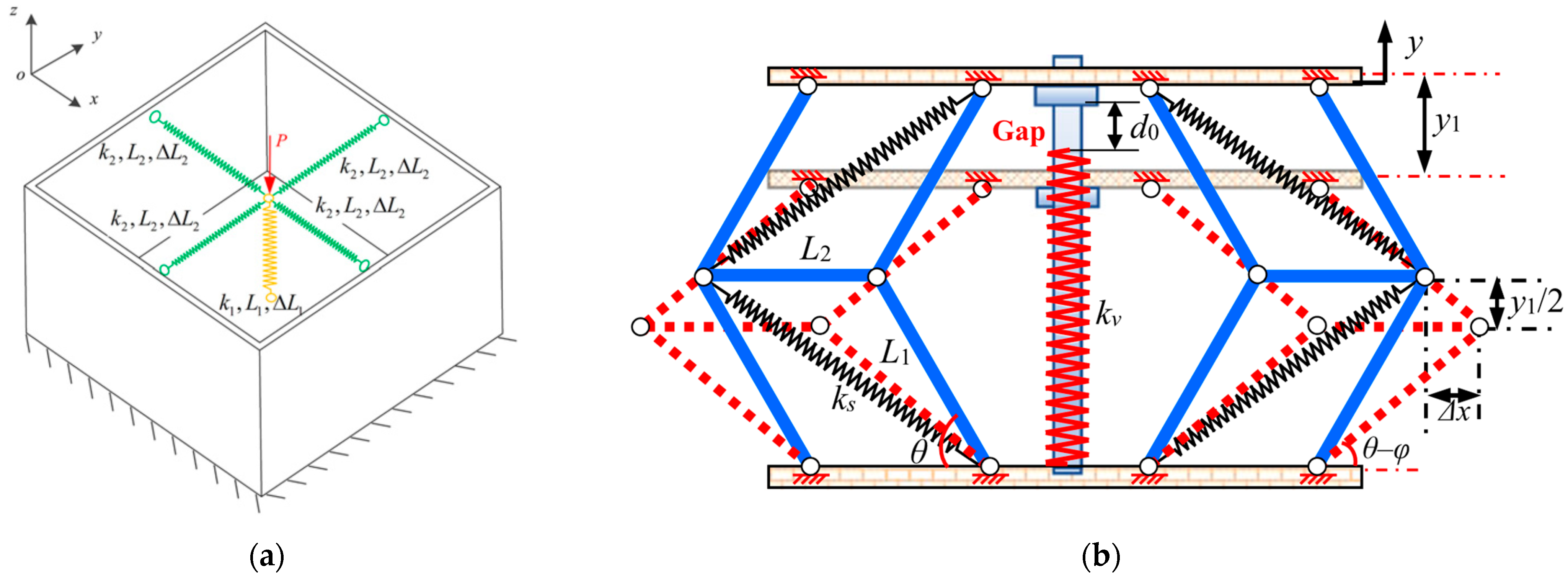
2.2.1. Linear Spring as Negative Stiffness Mechanism
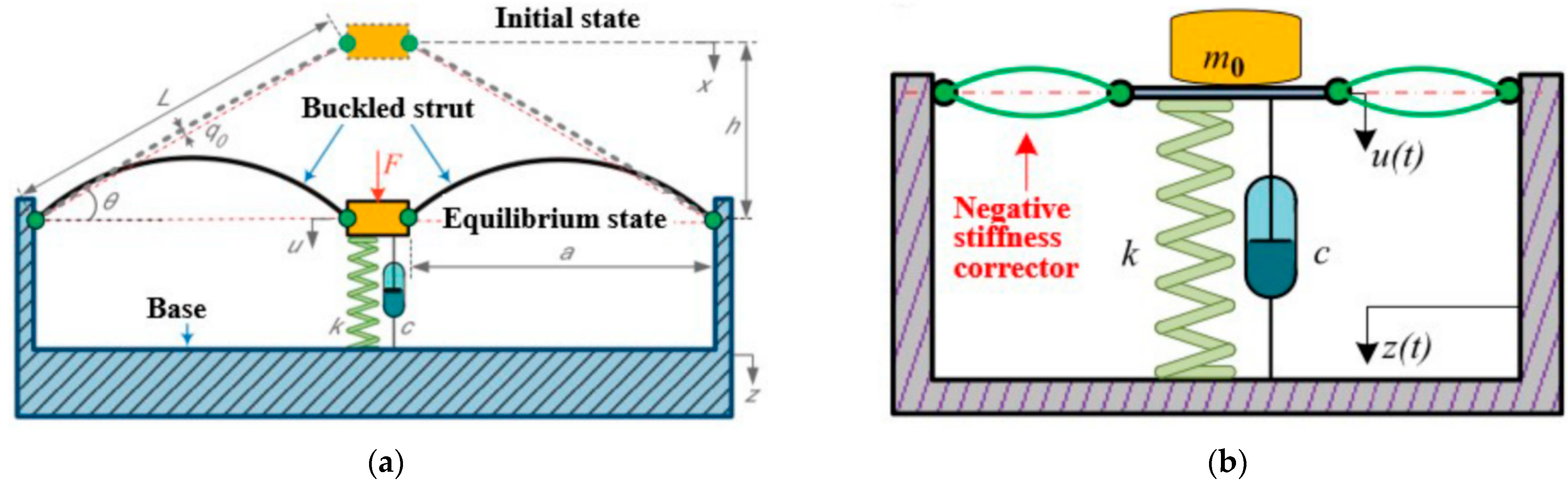
2.2.2. Buckled Beam as Negative Stiffness Mechanism
2.2.3. Level Spring-Link as Negative Stiffness Mechanism
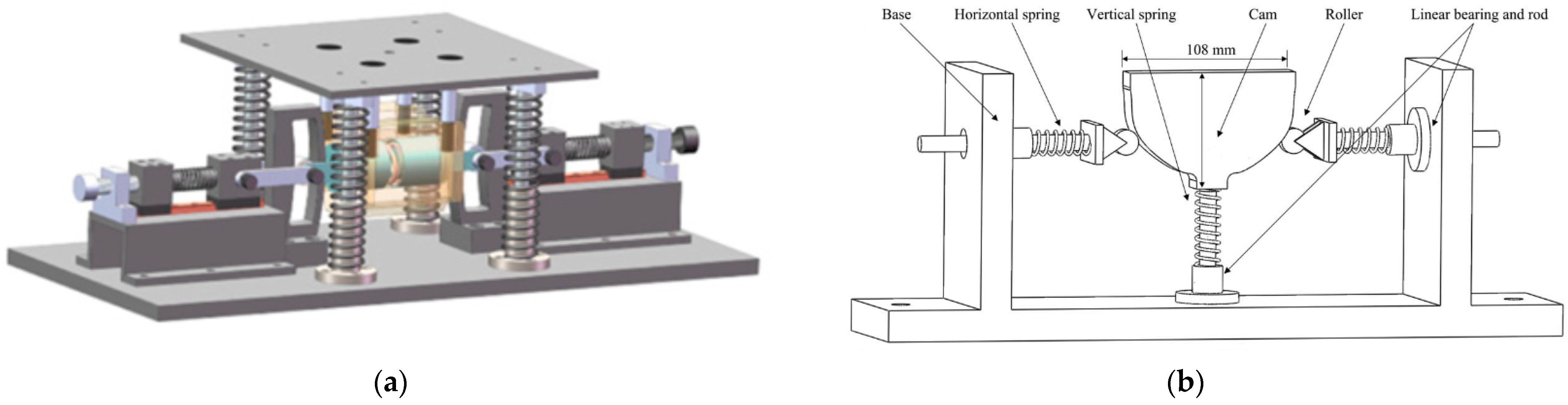
2.2.4. Cam-Roller as Negative Stiffness Mechanism
2.3. Several Types of Negative Stiffness Actuator
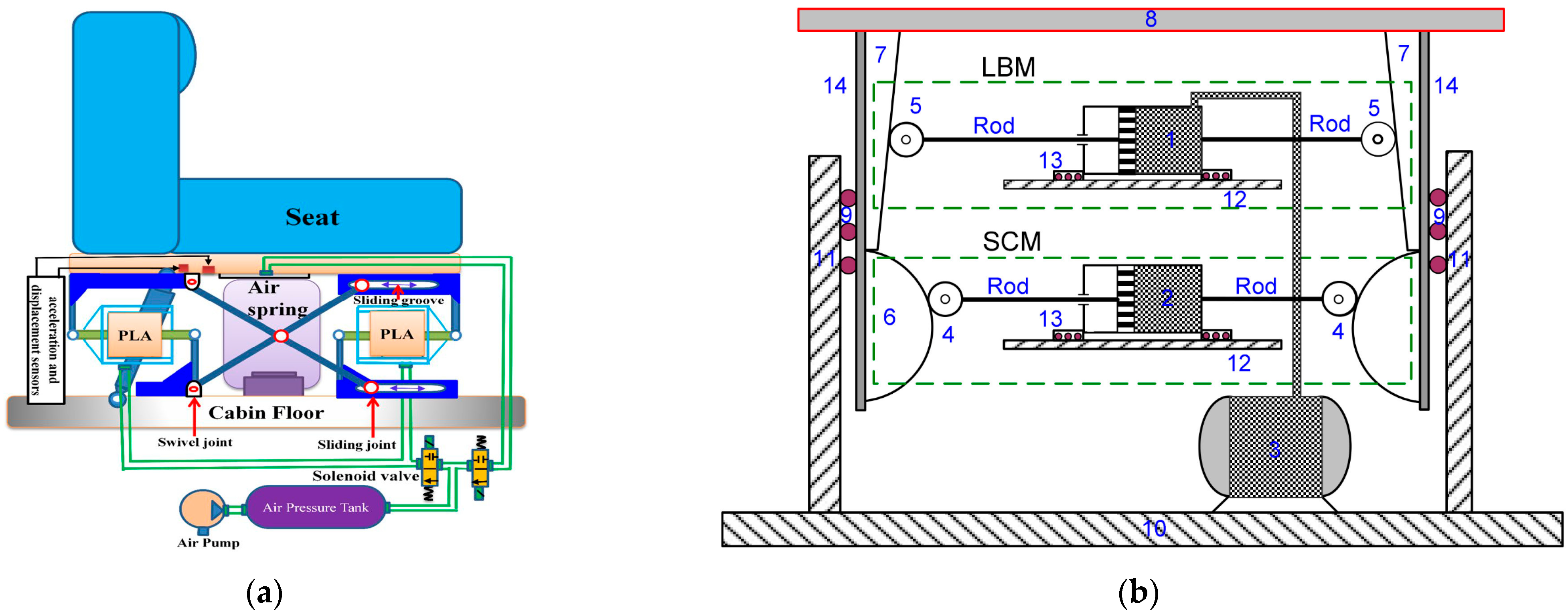
2.3.1. Air Spring as Negative Stiffness Actuator
2.3.2. Disc Spring as Negative Stiffness Actuator
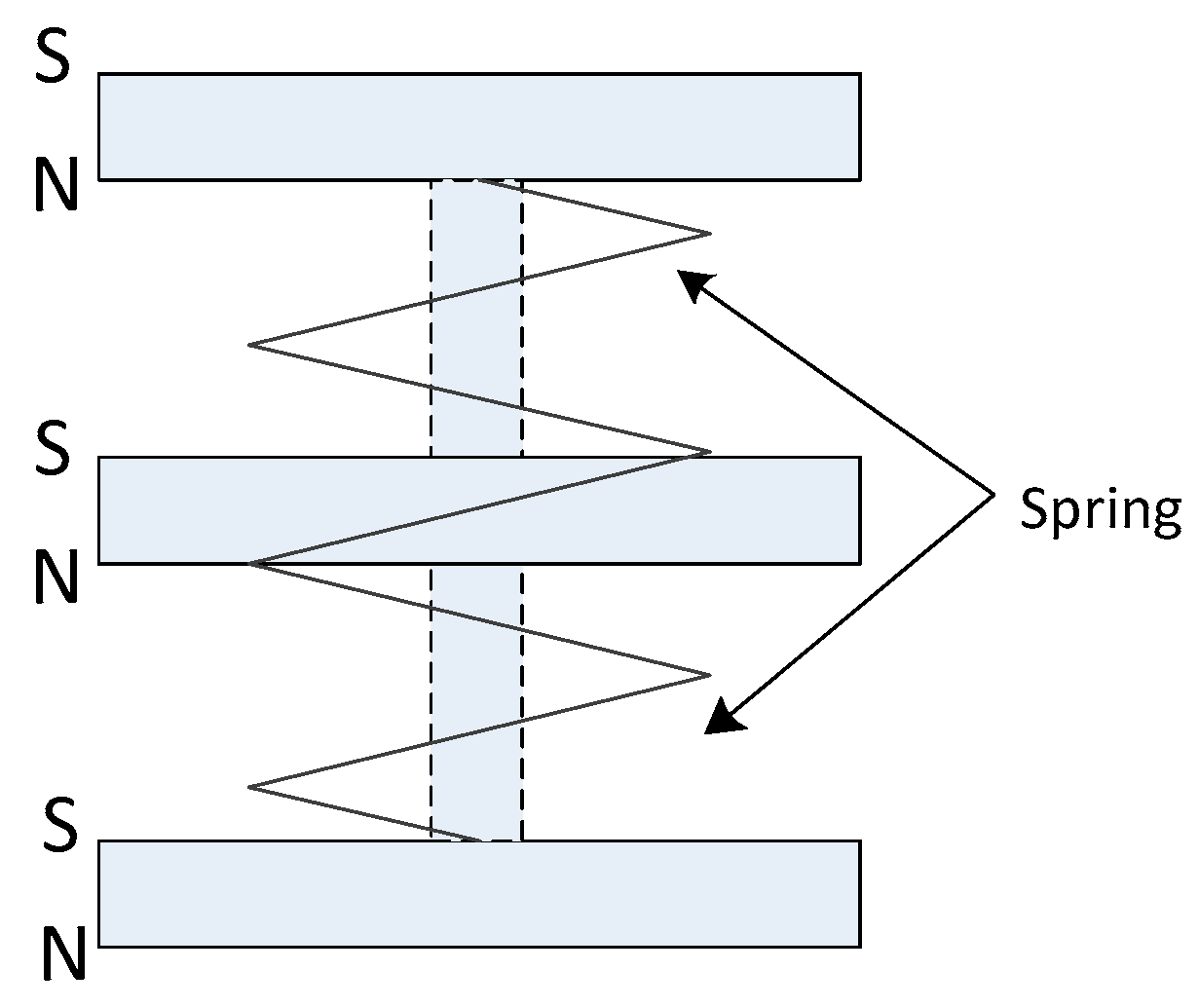
2.3.3. Magnetic Spring as Negative Stiffness Actuator
3. Magnetic Negative Stiffness in QZS Isolators
3.1. Introduction to Magnetic Negative Stiffness
3.2. Mathematical Modeling of Permanent Magnet Negative Stiffness Elements
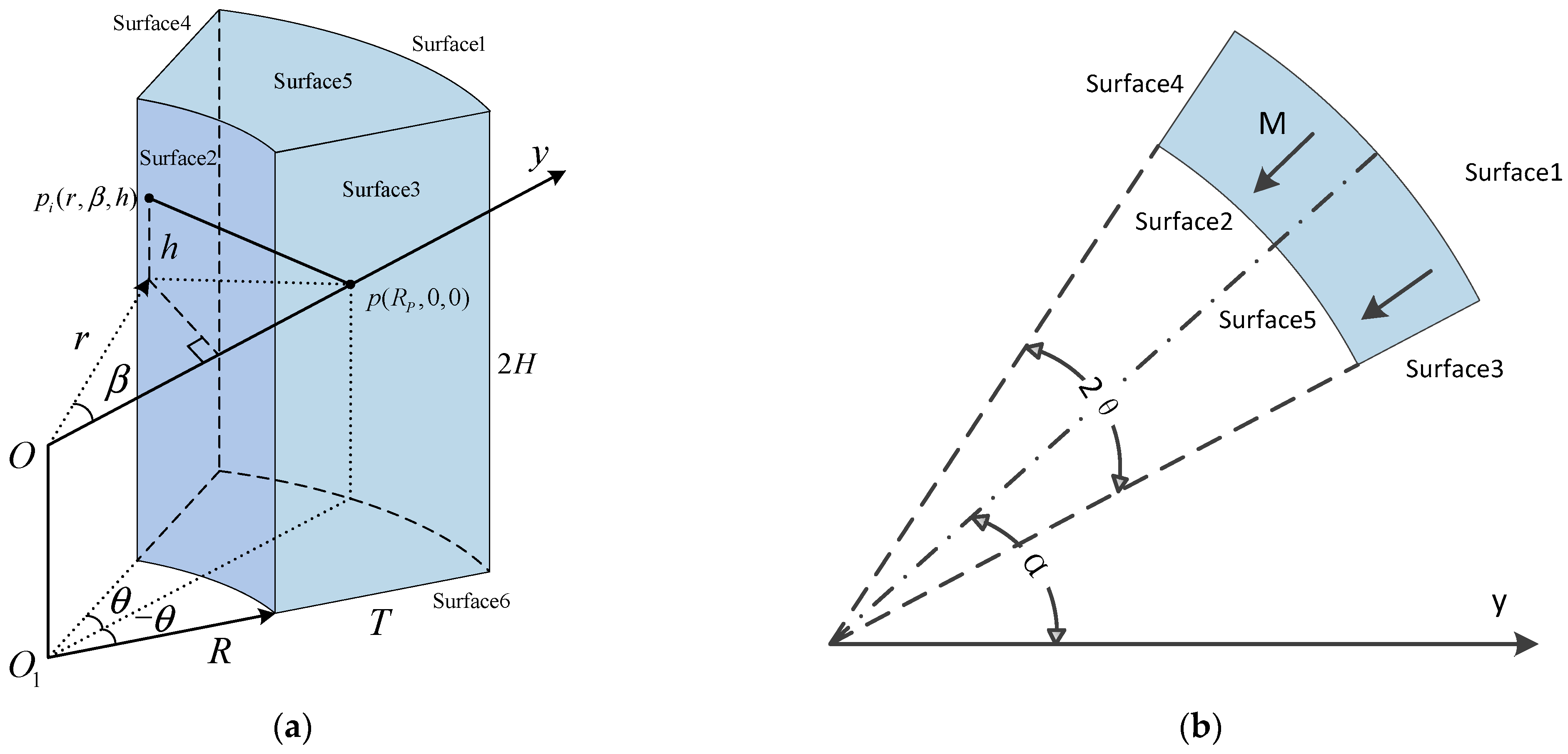
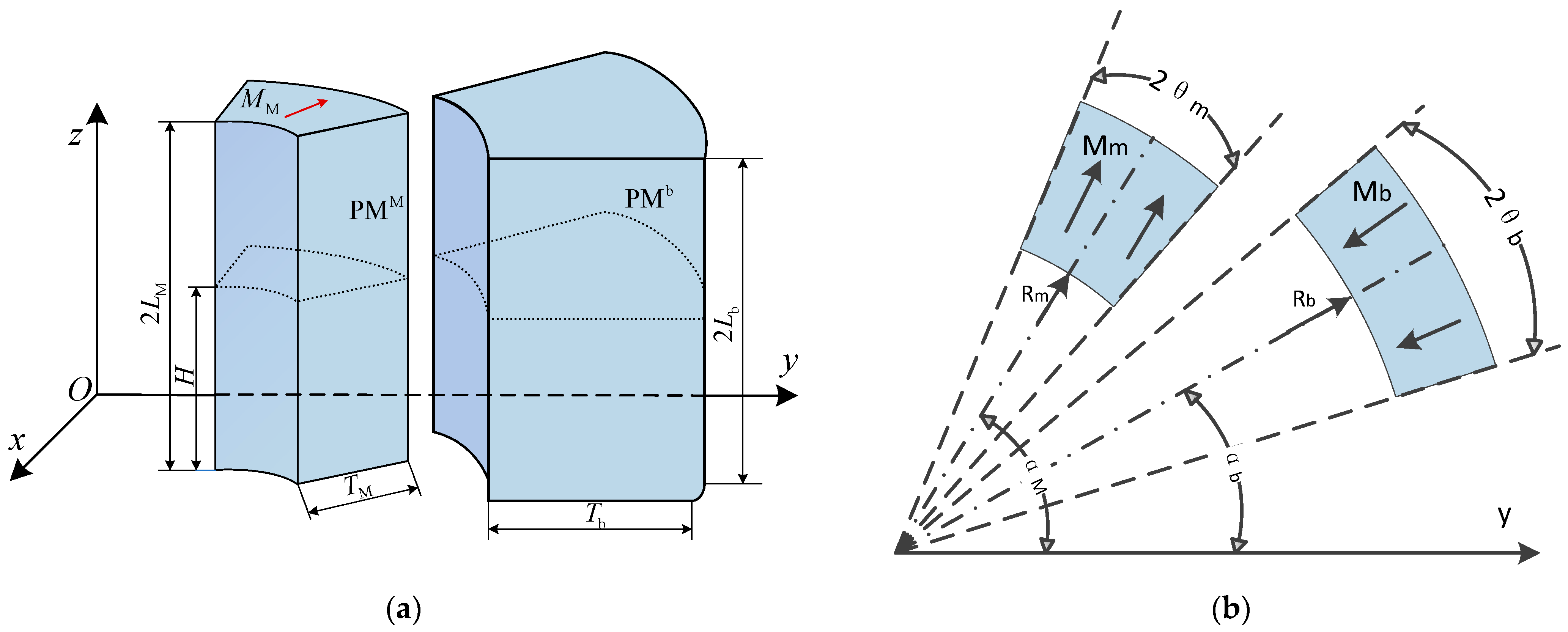
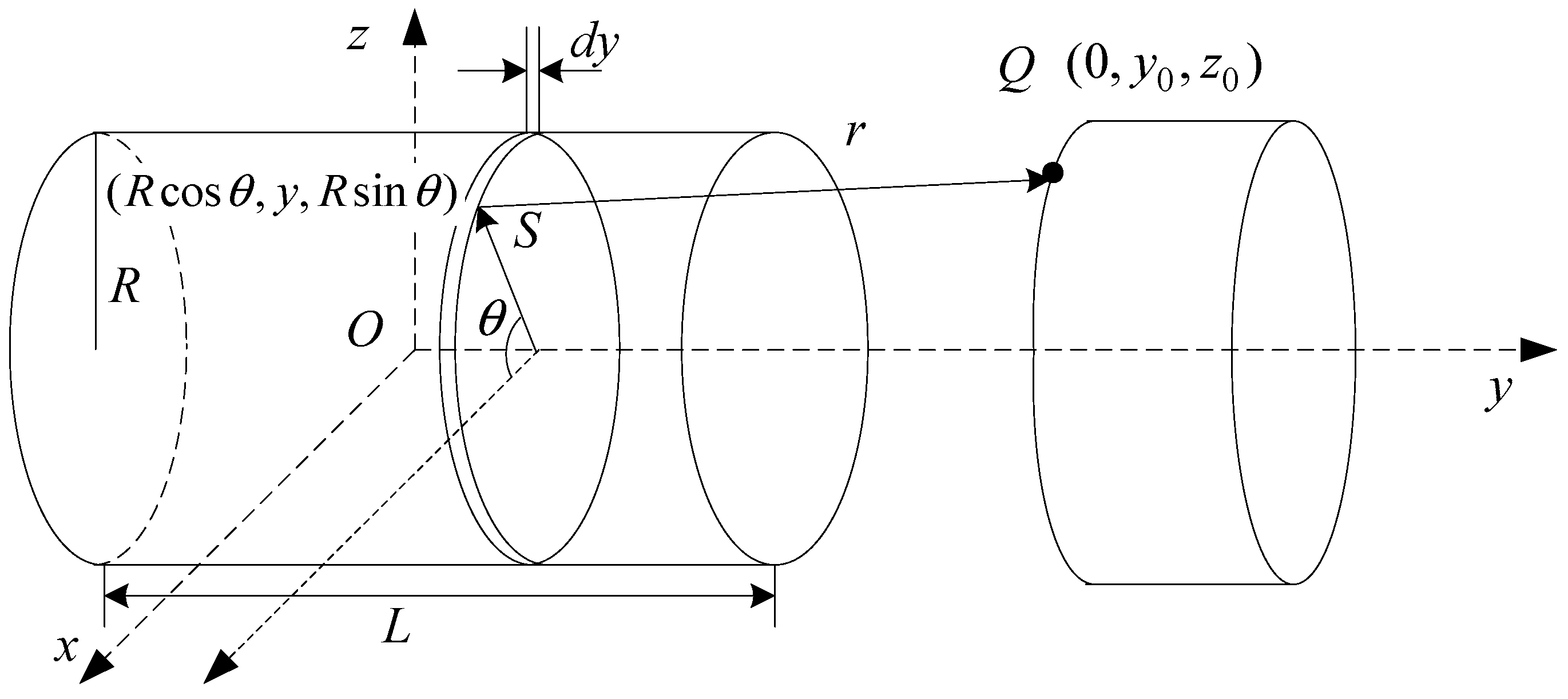
3.2.1. Mechanical Modeling of Magnetic Springs with Negative Stiffness of Magnetic Rings
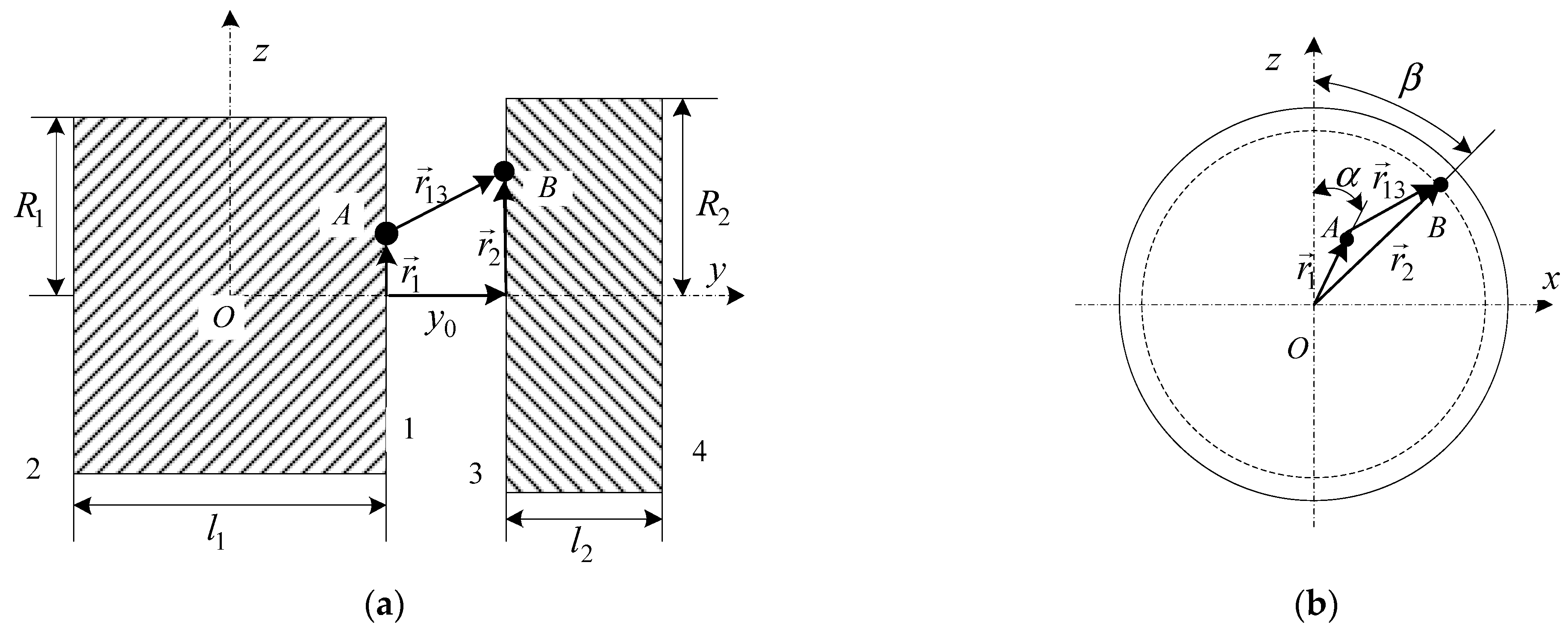
3.2.2. Mechanical Modeling of Rectangular Magnet Negative Stiffness Springs
3.2.3. Mechanical Modeling of Wedge-Shape Magnet Negative Stiffness Springs
3.3. Mathematical Modeling of Electromagnetic Negative Stiffness Elements
4. Current Progress of Magnetic Negative Stiffness in QZS Isolators
4.1. QZS-Based Permanent Magnet Negative Stiffness Elements
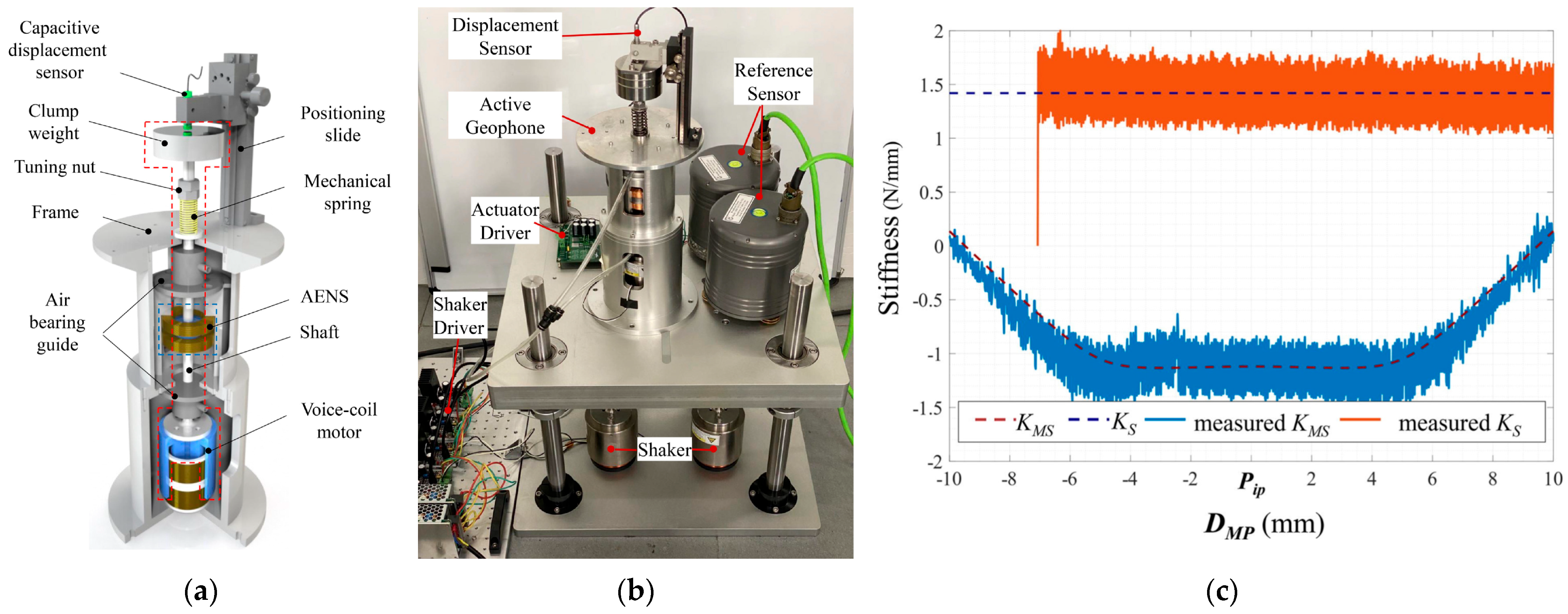
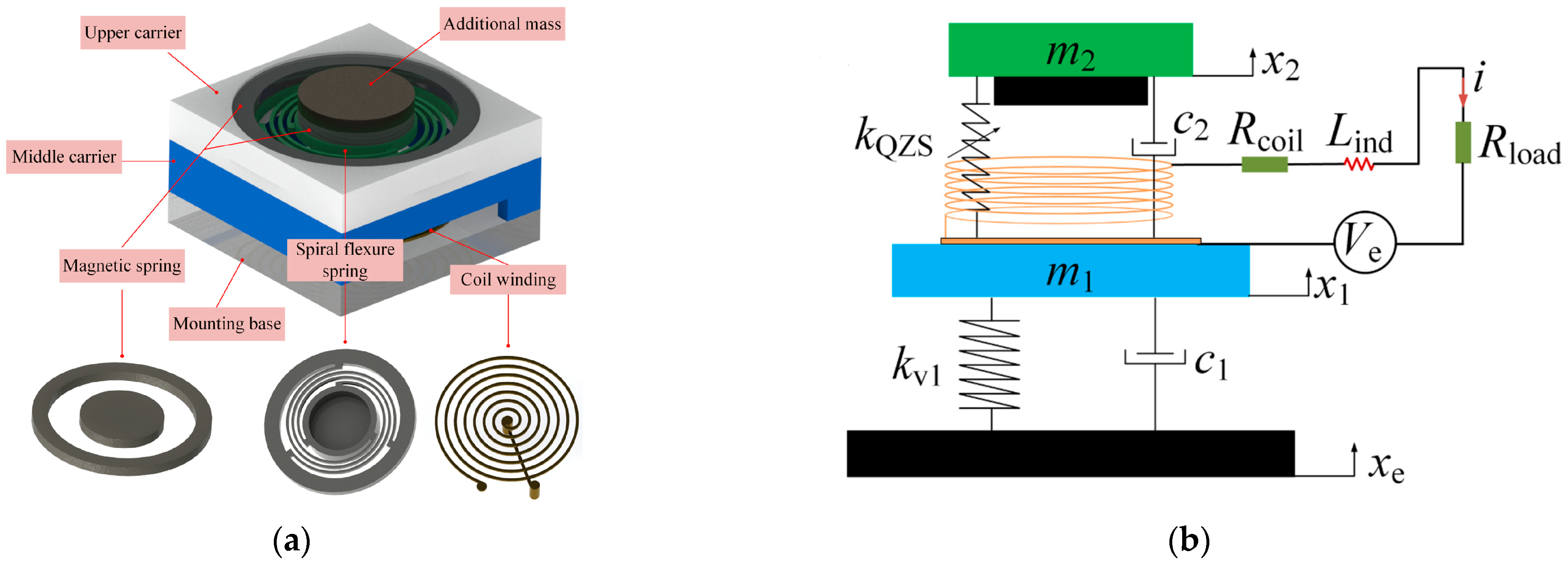
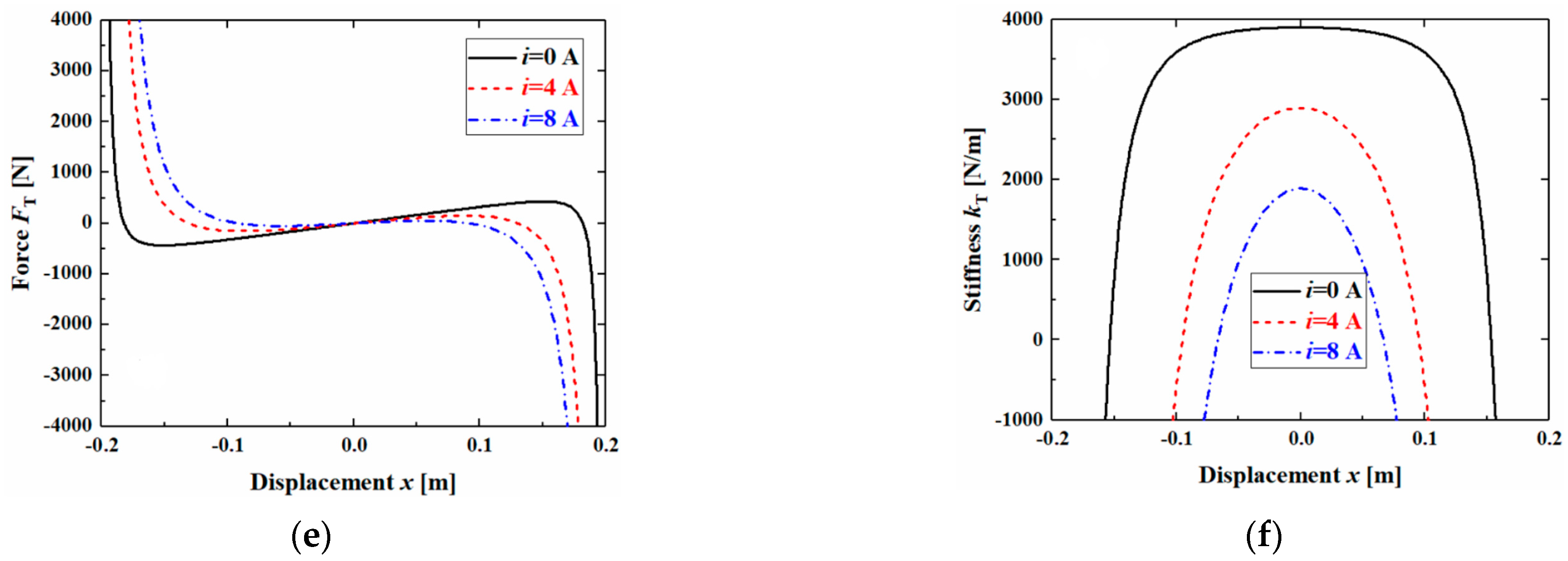
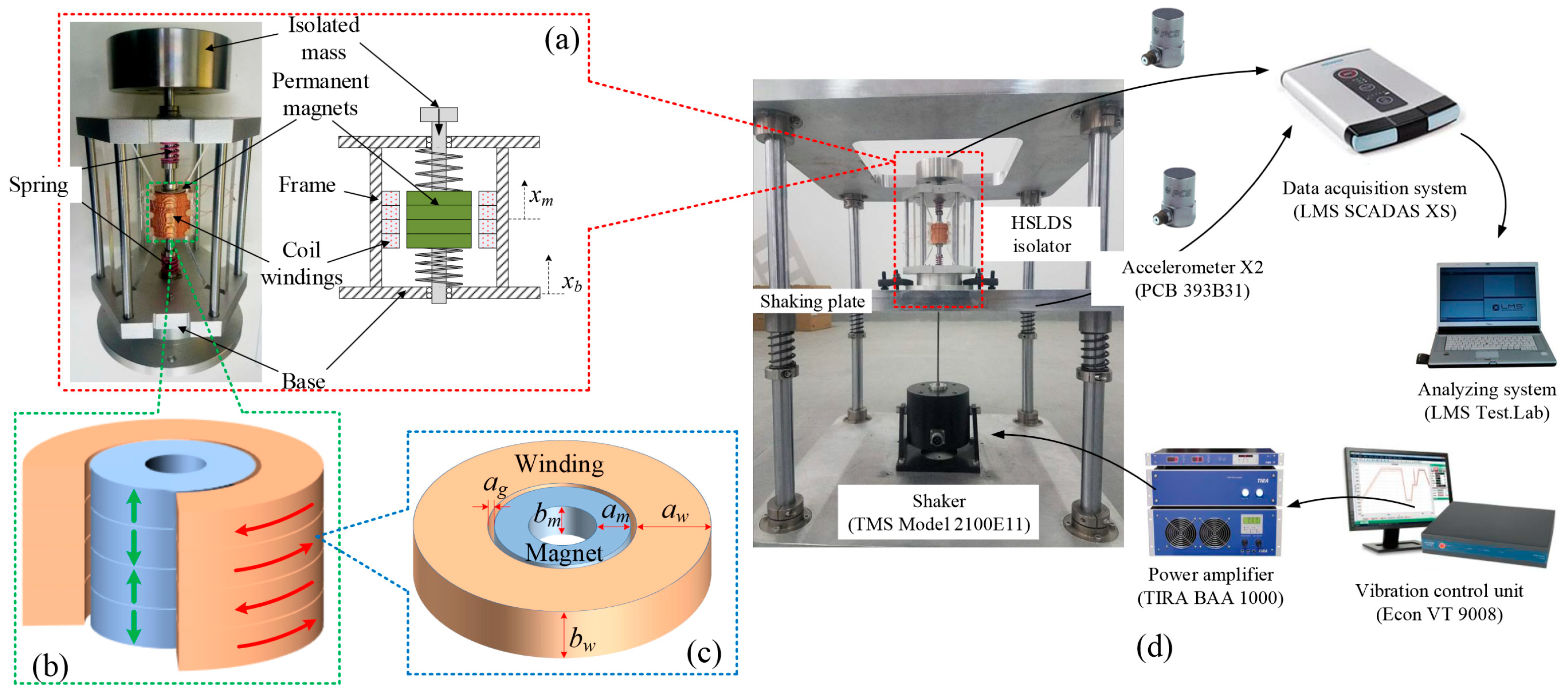
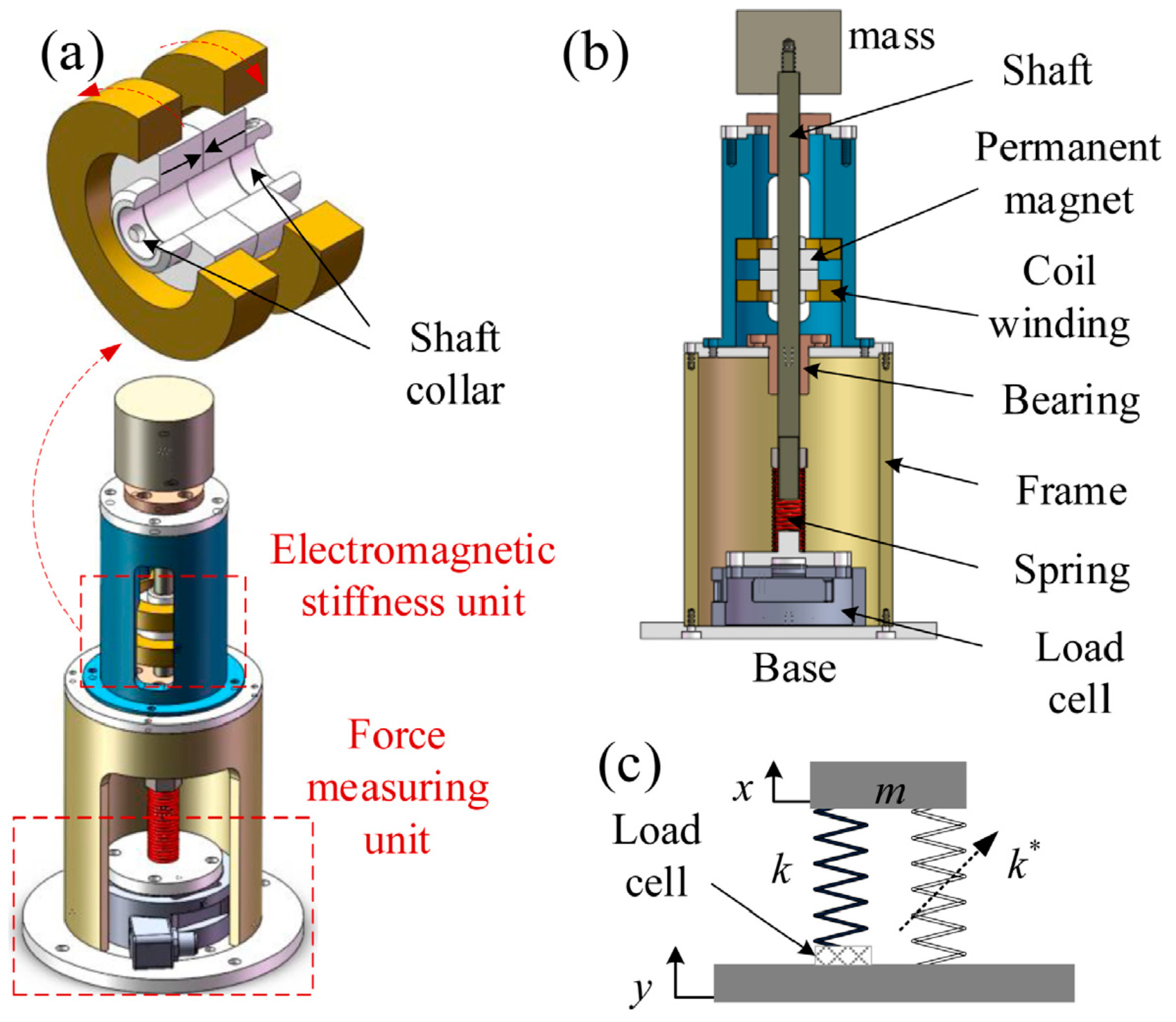
4.2. QZS-Based Electromagnetic Negative Stiffness Elements
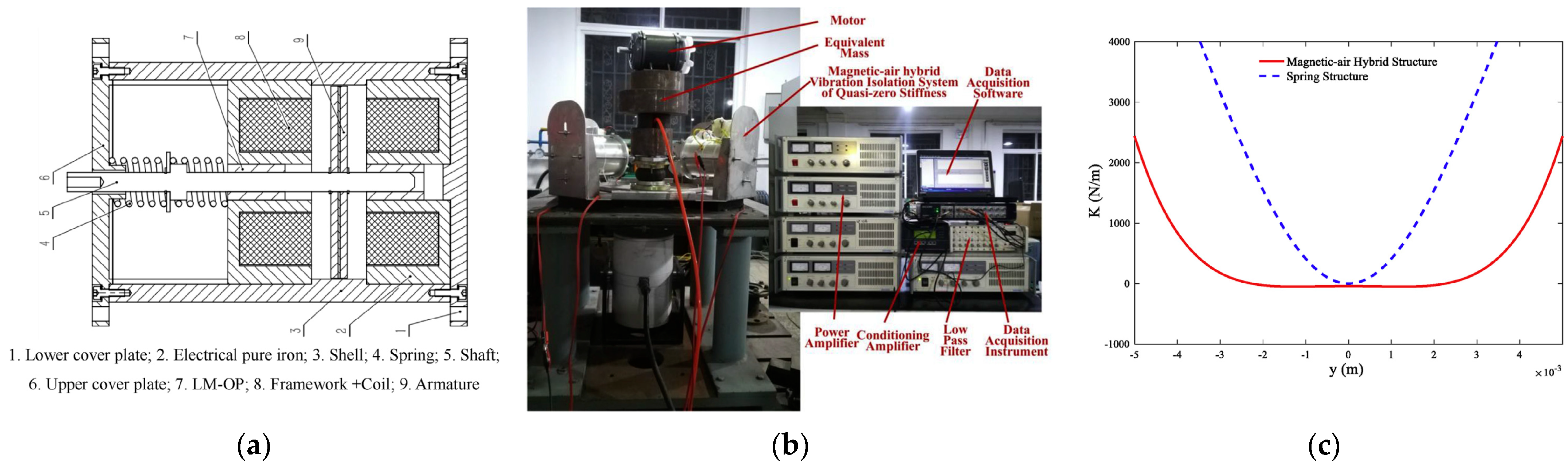
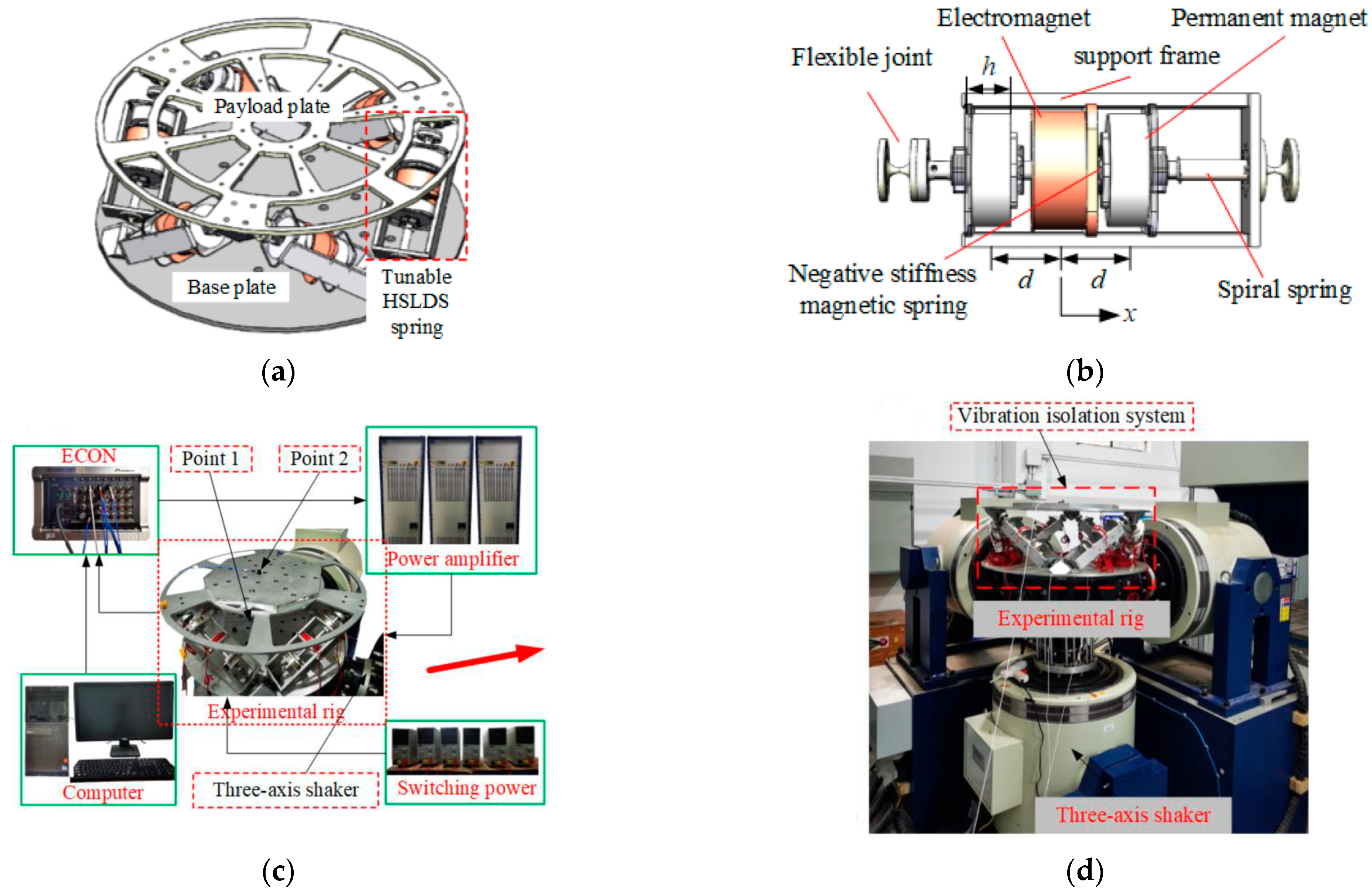
4.3. QZS-Based Hybrid Magnetic Negative Stiffness Elements
5. Summary and Outlook
5.1. Concluding Discussion
5.2. Future Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, B.; Shuai, C.; Ma, J. Shock Performance Analysis of High-Static-Low-Dynamic Stiffness Floating Raft Vibration Isolation System. ACTA Mech. 2024, 235, 1623–1635. [Google Scholar] [CrossRef]
- Li, Y.; Xu, D. Chaotification of Quasi-Zero-Stiffness System with Time Delay Control. Nonlinear Dyn. 2016, 86, 353–368. [Google Scholar] [CrossRef]
- Li, Y.; Xu, D. Spectrum Reconstruction of Quasi-Zero Stiffness Floating Raft Systems. Chaos Solitons Fractals 2016, 93, 123–129. [Google Scholar] [CrossRef]
- Li, S.; Feng, G.; Zhao, Q. Design and Research of Semiactive Quasi-Zero Stiffness Vibration Isolation System for Vehicles. Shock. Vib. 2021, 2021, 5529509. [Google Scholar] [CrossRef]
- Han, H.; Sorokin, V.; Tang, L.; Cao, D. Lightweight Origami Isolators with Deployable Mechanism and Quasi-Zero-Stiffness Property. Aerosp. Sci. Technol. 2022, 121, 107319. [Google Scholar] [CrossRef]
- Moghadam, S.R.; Konstantinidis, D. Experimental and Analytical Studies on the Horizontal Behavior of Elastomeric Bearings under Support Rotation. J. Struct. Eng. 2021, 147, 04021024. [Google Scholar] [CrossRef]
- Abolfathi, A. Can a Nonlinear Quasi-Zero-Stiffness Spring Improve the Ride Quality of a Vehicle? Veh. Syst. Dyn. 2024, 62, 330–346. [Google Scholar] [CrossRef]
- Abuabiah, M.; Dabbas, Y.; Herzallah, L.; Alsurakji, I.H.; Assad, M.; Plapper, P. Analytical Study on the Low-Frequency Vibrations Isolation System for Vehicle’s Seats Using Quasi-Zero-Stiffness Isolator. Appl. Sci. 2022, 12, 2418. [Google Scholar] [CrossRef]
- Chen, L.; Xu, X.; Liang, C.; Jiang, X.; Wang, F. Semi-Active Control of a New Quasi-Zero Stiffness Air Suspension for Commercial Vehicles Based on H2H∞ State Feedback. J. Vib. Control. 2023, 29, 1910–1926. [Google Scholar] [CrossRef]
- Cao, L.; Xiao, B.; Golestani, M. Robust Fixed-Time Attitude Stabilization Control of Flexible Spacecraft with Actuator Uncertainty. Nonlinear Dyn. 2020, 100, 2505–2519. [Google Scholar] [CrossRef]
- Dai, H.; Jing, X.; Wang, Y.; Yue, X.; Yuan, J. Post-Capture Vibration Suppression of Spacecraft via a Bio-Inspired Isolation System. Mech. Syst. Signal Process. 2018, 105, 214–240. [Google Scholar] [CrossRef]
- Liu, F.; Yu, D.; Wang, C.; Wang, G. Advances in Variable Stiffness Vibration Isolator and Its Application in Spacecraft. Int. J. Struct. Stab. Dyn. 2022, 22, 2230004. [Google Scholar] [CrossRef]
- Ahn, H.-J.; Lim, S.-H.; Park, C. An Integrated Design of Quasi-Zero Stiffness Mechanism. J. Mech. Sci. Technol. 2016, 30, 1071–1075. [Google Scholar] [CrossRef]
- Li, J.; Cao, S.; Zheng, J. On the Characteristic of a Small-Scale Isolation Mechanism With Three-Dimensional Quasi-Zero Stiffness. J. Mech. Des. 2020, 142, 095001. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Waters, T.P.; Lopes, V., Jr. Force and Displacement Transmissibility of a Nonlinear Isolator with High-Static-Low-Dynamic-Stiffness. Int. J. Mech. Sci. 2012, 55, 22–29. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhang, Z.; Zeng, L.; Li, X. Microvibration Isolation in Sensitive Payloads: Methodology and Design. Nonlinear Dyn. 2023, 111, 19563–19611. [Google Scholar] [CrossRef]
- Li, S.; Nguyen, V.; Jiao, R.; Ni, D.; Zhou, H. Isolation Efficiency of Vehicle Seat Suspension with Three Quasi-Zero Stiffness Models. Int. J. Acoust. Vib. 2022, 27, 210–220. [Google Scholar] [CrossRef]
- Eskandary-Malayery, F.; Ilanko, S.; Mace, B.; Mochida, Y.; Pellicano, F. Experimental and Numerical Investigation of a Vertical Vibration Isolator for Seismic Applications. Nonlinear Dyn. 2022, 109, 303–322. [Google Scholar] [CrossRef]
- Wu, Z.; Jing, X.; Sun, B.; Li, F. A 6DOF Passive Vibration Isolator Using X-Shape Supporting Structures. J. Sound Vib. 2016, 380, 90–111. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, L.; Shi, W. Seismic Control of Adaptive Variable Stiffness Intelligent Structures Using Fuzzy Control Strategy Combined with LSTM. J. Build. Eng. 2023, 78, 107549. [Google Scholar] [CrossRef]
- Farshidianfar, A.; Saghafi, A.; Kalami, S.M.; Saghafi, I. Active Vibration Isolation of Machinery and Sensitive Equipment Using H a Control Criterion and Particle Swarm Optimization Method. Meccanica 2012, 47, 437–453. [Google Scholar] [CrossRef]
- Li, Z.; Peng, X.; Hu, G.; Zhang, D.; Xu, Z.; Peng, Y.; Xie, S. Towards Real-Time Self-Powered Sensing with Ample Redundant Charges by a Piezostack-Based Frequency-Converted Generator from Human Motions. Energy Convers. Manag. 2022, 258, 115466. [Google Scholar] [CrossRef]
- Chai, Y.; Jing, X.; Chao, X. X-Shaped Mechanism Based Enhanced Tunable QZS Property for Passive Vibration Isolation. Int. J. Mech. Sci. 2022, 218, 107077. [Google Scholar] [CrossRef]
- Wang, L.; Nagarajaiah, S.; Zhou, Y.; Shi, W. Experimental Study on Adaptive-Passive Tuned Mass Damper with Variable Stiffness for Vertical Human-Induced Vibration Control. Eng. Struct. 2023, 280, 115714. [Google Scholar] [CrossRef]
- Wang, L.; Nagarajaiah, S.; Shi, W.; Zhou, Y. Seismic Performance Improvement of Base-Isolated Structures Using a Semi-Active Tuned Mass Damper. Eng. Struct. 2022, 271, 114963. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, Y.; Shi, W. Seismic Response Control of a Nonlinear Tall Building Under Mainshock-Aftershock Sequences Using Semi-Active Tuned Mass Damper. Int. J. Struct. Stab. Dyn. 2023, 23, 2340027. [Google Scholar] [CrossRef]
- Zhu, Z.; Tang, H.; Huang, Y.; Lin, Z.; Tian, Y.; Yu, P.; Su, C. A Compliant Self-Stabilization Nanopositioning Device With Modified Active-Passive Hybrid Vibration Isolation Strategy. IEEE-ASME Trans. Mechatron. 2023, 28, 3305–3316. [Google Scholar] [CrossRef]
- Ren, M.; He, P.; Xie, X.; Zhang, Z. Active/Passive Vibration Isolation with Multi-Axis Transmission Control: Analysis and Experiment. J. Vib. Control. 2023, 29, 5090–5106. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhu, L.; Dong, Q.; Sui, J.; Sun, M.; Wang, J.; Yu, X. Experimental Study on the Active Control and Dynamic Characteristics of Electromagnetic Active-Passive Hybrid Vibration Isolation System. Appl. Sci. 2023, 13, 10565. [Google Scholar] [CrossRef]
- Xie, X.; Diao, J.; Xu, Y.; Zhang, Z. Performance of a Low-Frequency Hybrid Vibration Isolation Platform for Vibration-Sensitive Devices. J. Low Freq. Noise Vib. Act. Control. 2018, 37, 1164–1175. [Google Scholar] [CrossRef]
- Jin, S.; Sun, S.; Yang, J.; Deng, L.; Du, H.; Li, W. A Hybrid MRE Isolation System Integrated with Ball-Screw Inerter for Vibration Control. Smart Mater. Struct. 2022, 31, 025009. [Google Scholar] [CrossRef]
- Alabuzhev, P. Vibration Protection and Measuring Systems With Quasi-Zero Stiffness; CRC Press: Boca Raton, FL, USA, 1989. [Google Scholar]
- Carrella, A.; Brennan, M.J.; Waters, T.P. Optimisation of a Quasi-Zero-Stiffness Isolator. J. Mech. Sci. Technol. 2007, 21, 946–949. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Waters, T.P. Static Analysis of a Passive Vibration Isolator with Quasi-Zero-Stiffness Characteristic. J. Sound Vib. 2007, 301, 678–689. [Google Scholar] [CrossRef]
- Wu, T.-H.; Lan, C.-C. A Wide-Range Variable Stiffness Mechanism for Semi-Active Vibration Systems. J. Sound Vib. 2016, 363, 18–32. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, X.; Luo, Y.; Xie, S.; Zhang, Y. Harnessing the Compressed-Spring Mechanism for a Six-Degrees-of-Freedom Quasi-Zero-Stiffness Vibration Isolation Platform. J. Vib. Control 2021, 27, 1793–1805. [Google Scholar] [CrossRef]
- Chai, Y.; Bian, J.; Li, M. A Novel Quasi-Zero-Stiffness Isolation Platform via Tunable Positive and Negative Stiffness Compensation Mechanism. Nonlinear Dyn. 2024, 112, 101–123. [Google Scholar] [CrossRef]
- Liu, T.; Bi, S.; Yao, Y.; Dong, Z.; Yang, Q.; Liu, L. Research on Zero-Stiffness Flexure Hinge (ZSFH) Based on Spring Four-Bar Linkage(4BSL). Mech. Mach. Theory 2020, 143, 103633. [Google Scholar] [CrossRef]
- Kovacic, I.; Teofanov, L.; Kanovic, Z.; Zhao, J.; Zhu, R.; Rajs, V. On the Influence of Internal Oscillators on the Performance of Metastructures: Modelling and Tuning Conditions. Mech. Syst. Signal Process. 2023, 205, 110861. [Google Scholar] [CrossRef]
- Zuo, S.; Wang, D.; Zhang, Y.; Luo, Q. Design and Testing of a Parabolic Cam-Roller Quasi-Zero-Stiffness Vibration Isolator. Int. J. Mech. Sci. 2022, 220, 107146. [Google Scholar] [CrossRef]
- Huang, X.; Liu, X.; Sun, J.; Zhang, Z.; Hua, H. Vibration Isolation Characteristics of a Nonlinear Isolator Using Euler Buckled Beam as Negative Stiffness Corrector: A Theoretical and Experimental Study. J. Sound Vib. 2014, 333, 1132–1148. [Google Scholar] [CrossRef]
- Kang, B.; Li, H.; Zhang, Z.; Zhou, H. A Study of a Ruzicka Vibration Isolator Model with High-Static-Low-Dynamic Characteristic. Mechanika 2018, 24, 422–431. [Google Scholar]
- Niu, F.; Meng, L.; Wu, W.; Sun, J.; Zhang, W.; Meng, G.; Rao, Z. Design and Analysis of a Quasi-Zero Stiffness Isolator Using a Slotted Conical Disk Spring as Negative Stiffness Structure. J. Vibroengineering 2014, 16, 1769–1785. [Google Scholar]
- Cai, C.; Zhou, J.; Wu, L.; Wang, K.; Xu, D.; Ouyang, H. Design and Numerical Validation of Quasi-Zero-Stiffness Metamaterials for Very Low-Frequency Band Gaps. Compos. Struct. 2020, 236, 111862. [Google Scholar] [CrossRef]
- Lan, C.-C.; Yang, S.-A.; Wu, Y.-S. Design and Experiment of a Compact Quasi-Zero-Stiffness Isolator Capable of a Wide Range of Loads. J. Sound Vib. 2014, 333, 4843–4858. [Google Scholar] [CrossRef]
- Zhang, Y.; Wei, G.; Wen, H.; Jin, D.; Hu, H. Design and Analysis of a Vibration Isolation System with Cam-Roller-Spring-Rod Mechanism. J. Vib. Control. 2022, 28, 1781–1791. [Google Scholar] [CrossRef]
- Li, M.; Cheng, W.; Xie, R. Design and Experiments of a Quasi-Zero-Stiffness Isolator with a Noncircular Cam-Based Negative-Stiffness Mechanism. J. Vib. Control 2020, 26, 1935–1947. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, X.; Li, H. Design and Analysis of a High-Static-Low-Dynamic Stiffness Isolator Using the Cam-Roller-Spring Mechanism. J. Vib. Acoust. 2020, 142, 021009. [Google Scholar] [CrossRef]
- Le Thanh, D.; Ahn, K.K. Active Pneumatic Vibration Isolation System Using Negative Stiffness Structures for a Vehicle Seat. J. Sound Vib. 2014, 333, 1245–1268. [Google Scholar] [CrossRef]
- Atindana, V.A.; Xu, X.; Huan, L.; Nirere, A.; Nyedeb, A.N.; Quaisie, J.K.; Kwaku, N.J.; Assam, S.P. Experimental Design and Optimization of Pneumatic Low-Frequency Driver Seat for off-Road Vehicles: Quasi-Zero Negative Stiffness and Gray Wolf Optimization Algorithm. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 502. [Google Scholar] [CrossRef]
- Vo, N.Y.P.; Le, T.D. Dynamic Analysis of Quasi-Zero Stiffness Pneumatic Vibration Isolator. Appl. Sci. 2022, 12, 2378. [Google Scholar] [CrossRef]
- An, J.; Chen, G.; Deng, X.; Xi, C.; Wang, T.; He, H. Analytical Study of a Pneumatic Quasi-Zero-Stiffness Isolator with Mistuned Mass. Nonlinear Dyn. 2022, 108, 3297–3312. [Google Scholar] [CrossRef]
- Liu, Y.; Ji, W.; Gu, H.; Deng, E.; Wang, X.; Song, C. Force Transmissibility of a 6-DOF Passive Quasi-Zero Stiffness Vibration Isolation Platform. J. Mech. Sci. Technol. 2021, 35, 2313–2324. [Google Scholar] [CrossRef]
- Meng, L.; Sun, J.; Wu, W. Theoretical Design and Characteristics Analysis of a Quasi-Zero Stiffness Isolator Using a Disk Spring as Negative Stiffness Element. Shock. Vib. 2015, 2015, 813763. [Google Scholar] [CrossRef]
- Yu, K.; Chen, Y.; Yu, C.; Zhang, J.; Lu, X. A Compact Nonlinear Stiffness-Modulated Structure for Low-Frequency Vibration Isolation under Heavy Loads. Nonlinear Dyn. 2024, 112, 5863–5893. [Google Scholar] [CrossRef]
- Ma, Z.; Zhou, R.; Yang, Q.; Lee, H.P.; Chai, K. A Semi-Active Electromagnetic Quasi-Zero-Stiffness Vibration Isolator. Int. J. Mech. Sci. 2023, 252, 108357. [Google Scholar] [CrossRef]
- Yuan, S.; Sun, Y.; Wang, M.; Ding, J.; Zhao, J.; Huang, Y.; Peng, Y.; Xie, S.; Luo, J.; Pu, H.; et al. Tunable Negative Stiffness Spring Using Maxwell Normal Stress. Int. J. Mech. Sci. 2021, 193, 106127. [Google Scholar] [CrossRef]
- Jiang, Y.; Song, C.; Ding, C.; Xu, B. Design of Magnetic-Air Hybrid Quasi-Zero Stiffness Vibration Isolation System. J. SOUND Vib. 2020, 477, 106127. [Google Scholar] [CrossRef]
- Zhou, Z.; Dai, Z.; Liu, Z.; Liu, X.; Chen, S.; Li, Z.; Zhou, M. An Adjustable Low Frequency Vibration Isolation with High-Static-Stiffness Low-Dynamic-Stiffness Property Using a Novel Negative Stiffness Element. Appl. Acoust. 2022, 188, 108571. [Google Scholar] [CrossRef]
- Yan, B.; Ma, H.; Jian, B.; Wang, K.; Wu, C. Nonlinear Dynamics Analysis of a Bi-State Nonlinear Vibration Isolator with Symmetric Permanent Magnets. Nonlinear Dyn. 2019, 97, 2499–2519. [Google Scholar] [CrossRef]
- Yan, B.; Yu, N.; Wang, Z.; Wu, C.; Wang, S. Wenming Lever-Type Quasi-Zero Stiffness Vibration Isolator with Magnetic Spring. J. Sound Vib. 2022, 527, 116865. [Google Scholar] [CrossRef]
- Zhao, J.; Sun, Y.; Li, J.; Yuan, S.; Wang, M.; Ding, J.; Pu, H.; Luo, J.; Peng, Y.; Xie, S. A Novel Electromagnet-Based Absolute Displacement Sensor with Approximately Linear Quasi-Zero-Stiffness. Int. J. Mech. Sci. 2020, 181, 105695. [Google Scholar] [CrossRef]
- Kozakiewicz, B.; Winiarski, T. Spring based on Flat Permanent Magnets: Design, Analysis and Use in Variable Stiffness Actuator. Facta Univ.-Ser. Mech. Eng. 2023, 21, 101–120. [Google Scholar] [CrossRef]
- Li, R.; Qin, W.; Li, G.; Shou, M.; Wang, X.; Huang, X.; Gong, X.; Lee, C.-H.; Chen, Y. Design and Optimization of the Magnetic Field-Driven Spherical Gripper with Adjustable Stiffness. Mater. Des. 2023, 235, 112391. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, W.; Liu, W.; Li, Z.; Lv, S.; Sang, X.; Yang, Y. Verification of the Microgravity Active Vibration Isolation System Based on Parabolic Flight. Microgravity Sci. Technol. 2017, 29, 415–426. [Google Scholar] [CrossRef]
- Ni, D.; Jiao, R.; Nguyen, V.; Zhang, J. Enhancing the Ride Comfort of Off-Road Vibratory Rollers with Seat Suspension Using Optimal Quasi-Zero Stiffness. Proc. Inst. Mech. Eng. PART C-J. Mech. Eng. Sci. 2023, 237, 482–496. [Google Scholar] [CrossRef]
- Akoun, G.; Yonnet, J.-P. 3D Analytical Calculation of the Forces Exerted between Two Cuboidal Magnets. IEEE Trans. Magn. 1984, 20, 1962–1964. [Google Scholar] [CrossRef]
- Bancel, F. Magnetic Nodes. J. Phys. Appl. Phys. 1999, 32, 2155. [Google Scholar] [CrossRef]
- Dong, G.; Ma, C.; Zhang, F.; Luo, Y.; Bi, C. Non-Resonant Response of the Novel Airborne Photoelectric Quasi-Zero Stiffness Platform with Friction Damping. Int. J. Appl. Electromagn. Mech. 2020, 64, 315–324. [Google Scholar] [CrossRef]
- Zhao, Y.; Cui, J.; Zou, L. Magnetic Ring Array with High-Amplitude Negative Stiffness for High Performance Micro-Vibration Isolation. J. Vib. Control 2023, 29, 2609–2622. [Google Scholar] [CrossRef]
- Oyelade, A.O. Experiment Study on Nonlinear Oscillator Containing Magnetic Spring with Negative Stiffness. Int. J. Non-Linear Mech. 2020, 120, 103396. [Google Scholar] [CrossRef]
- Zhang, F.; Shao, S.; Tian, Z.; Xu, M.; Xie, S. Active-Passive Hybrid Vibration Isolation with Magnetic Negative Stiffness Isolator Based on Maxwell Normal Stress. Mech. Syst. Signal Process. 2019, 123, 244–263. [Google Scholar] [CrossRef]
- Ding, J.; Wang, Y.; Wang, M.; Sun, Y.; Peng, Y.; Luo, J.; Pu, H. An Active Geophone with an Adjustable Electromagnetic Negative Stiffness for Low-Frequency Vibration Measurement. Mech. Syst. Signal Process. 2022, 178, 109207. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, J.; Wang, K.; Lin, Q.; Xu, D.; Wen, G. A Compact Quasi-Zero-Stiffness Device for Vibration Suppression and Energy Harvesting. Int. J. Mech. Sci. 2023, 250, 108284. [Google Scholar] [CrossRef]
- Hao, R.-B.; Lu, Z.-Q.; Ding, H.; Chen, L.-Q. Orthogonal Six-DOFs Vibration Isolation with Tunable High-Static-Low-Dynamic Stiffness: Experiment and Analysis. Int. J. Mech. Sci. 2022, 222, 107237. [Google Scholar] [CrossRef]
- Sun, Y.; Zhao, J.; Wang, M.; Sun, Y.; Pu, H.; Luo, J.; Peng, Y.; Xie, S.; Yang, Y. High-Static-Low-Dynamic Stiffness Isolator With Tunable Electromagnetic Mechanism. IEEE-ASME Trans. Mechatron. 2020, 25, 316–326. [Google Scholar] [CrossRef]



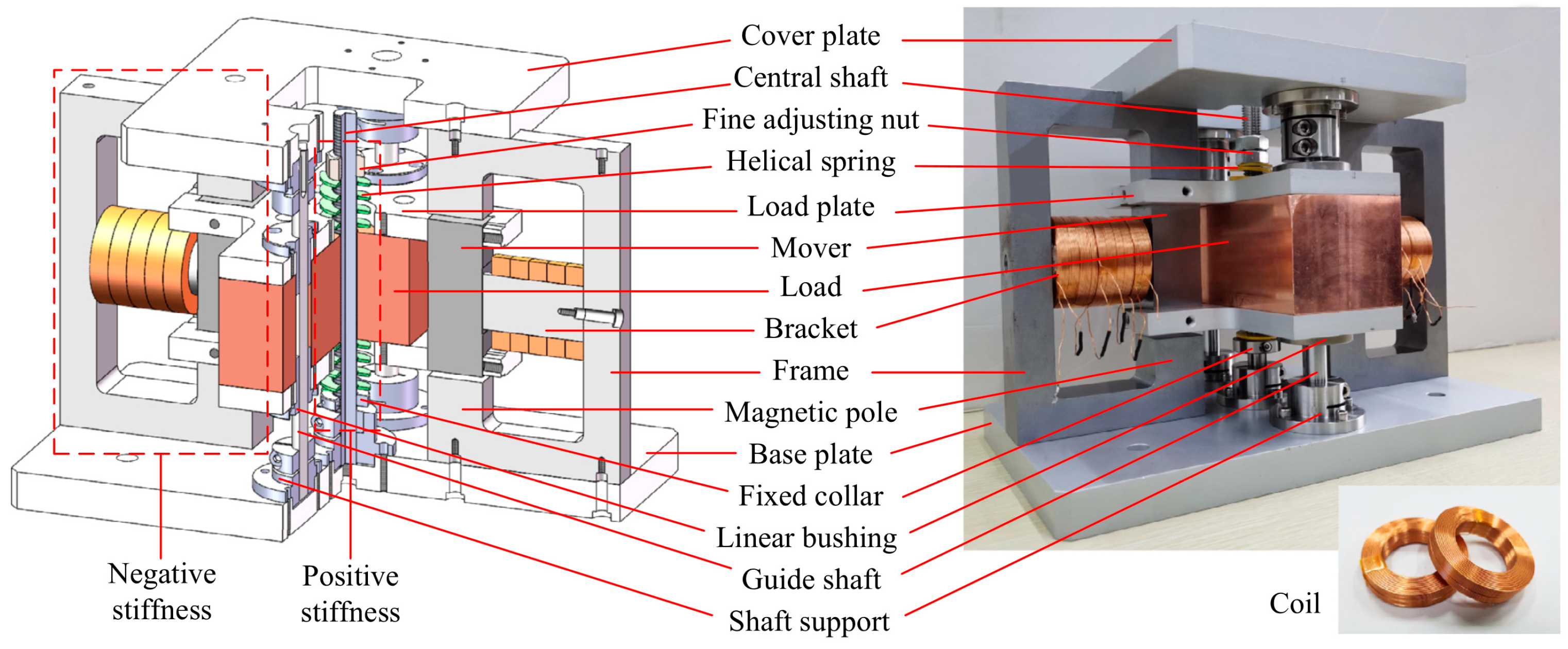
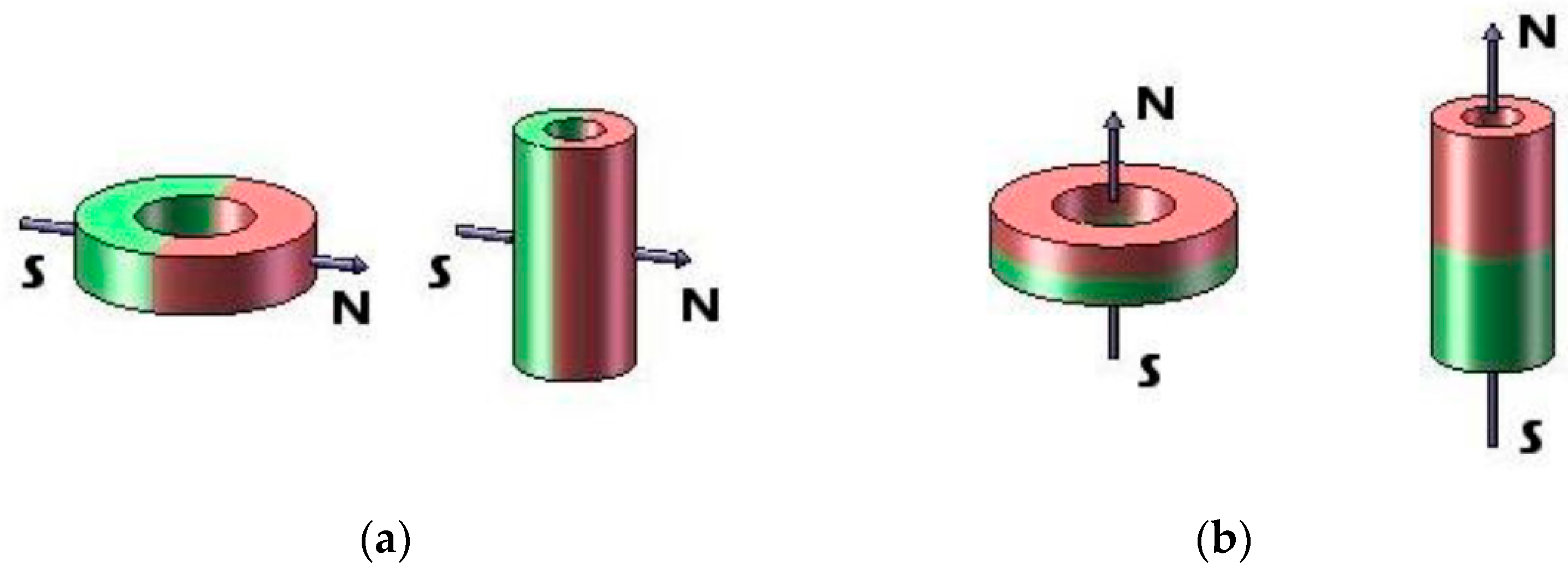


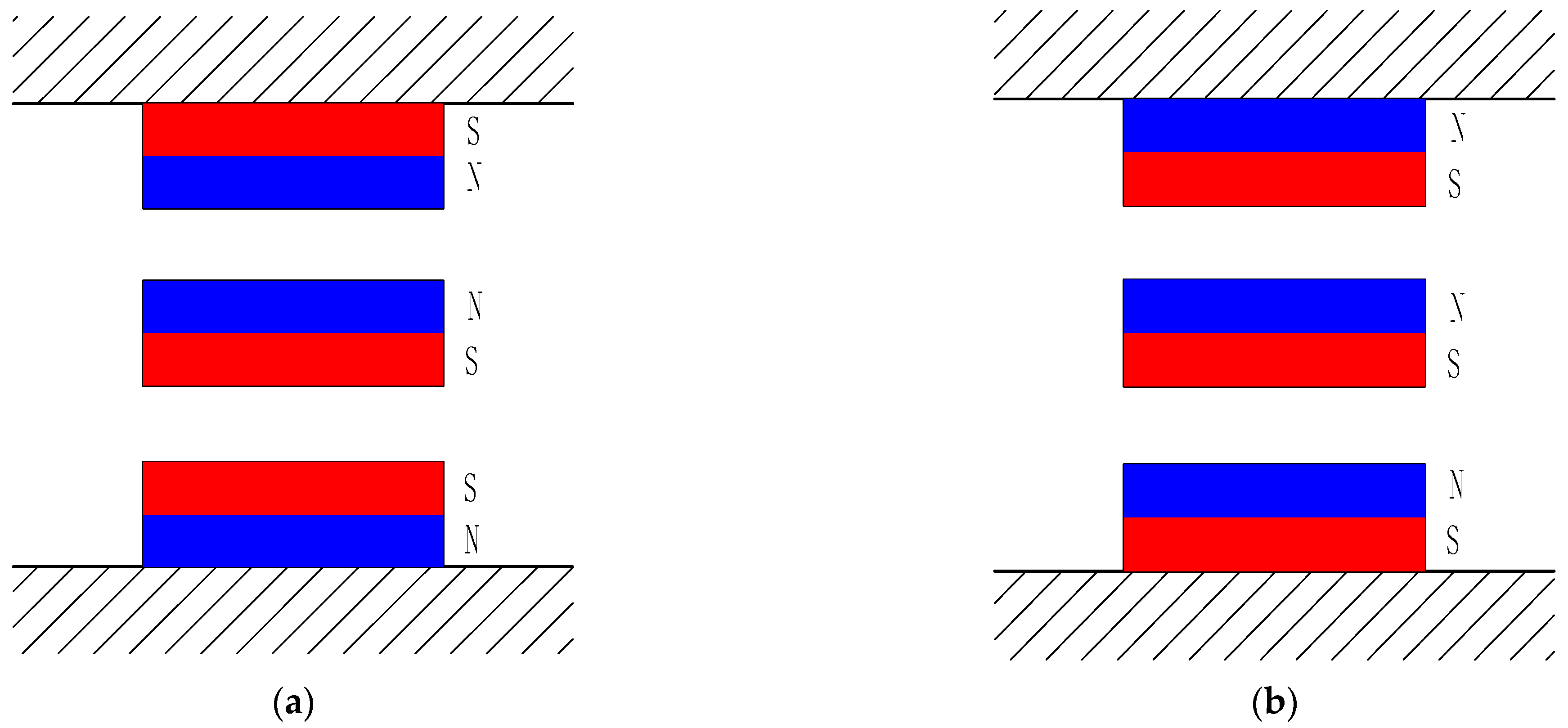
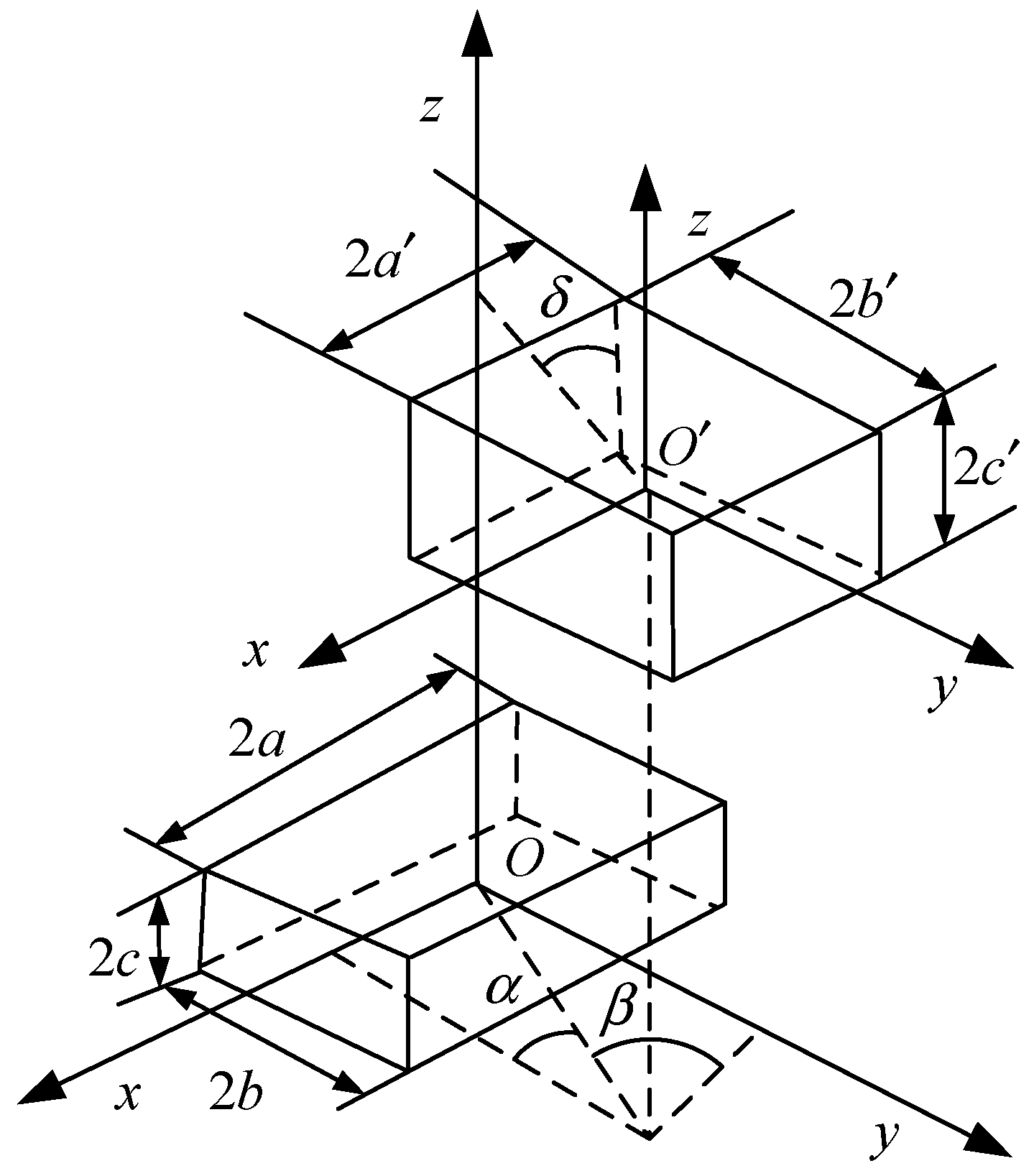

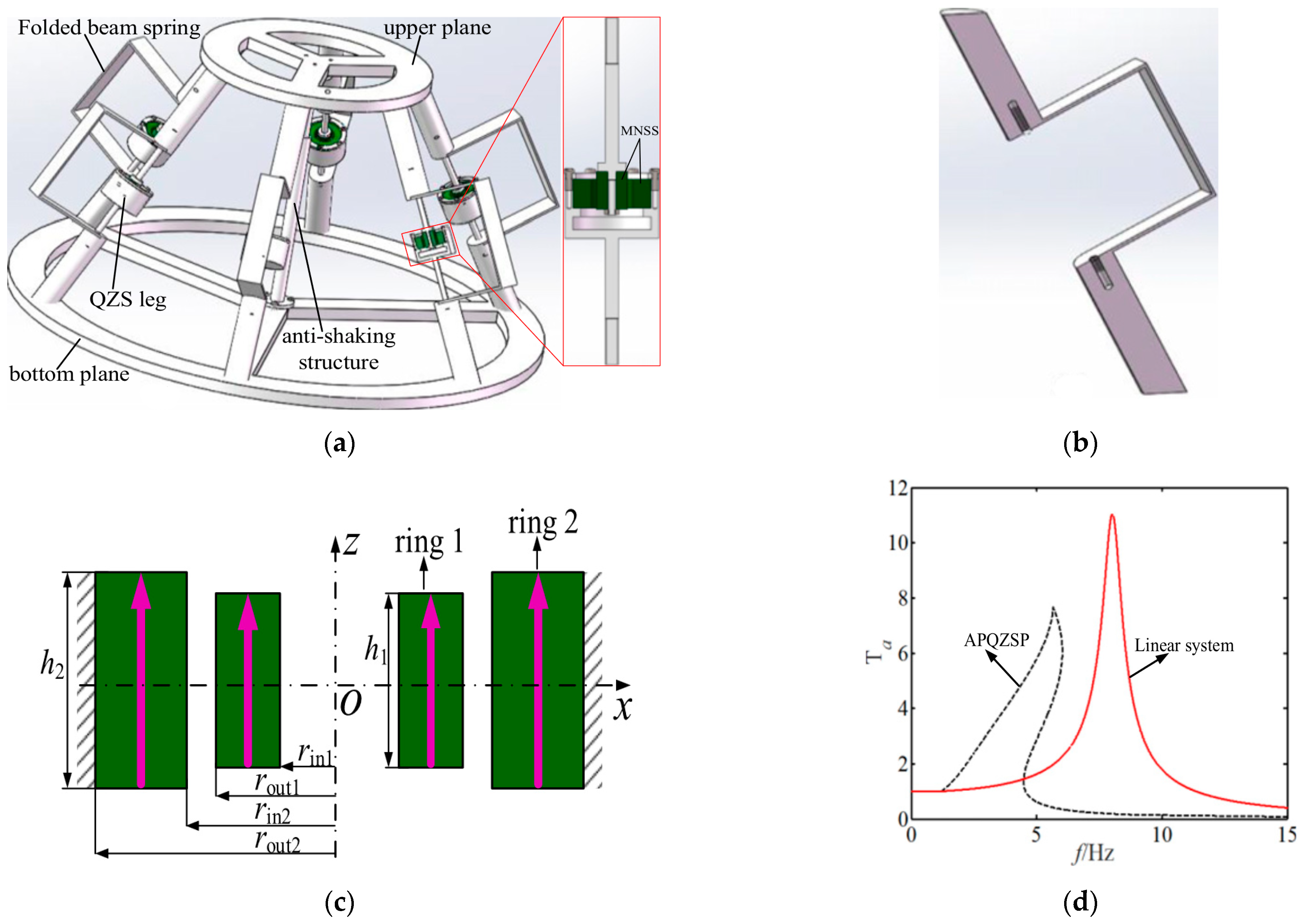
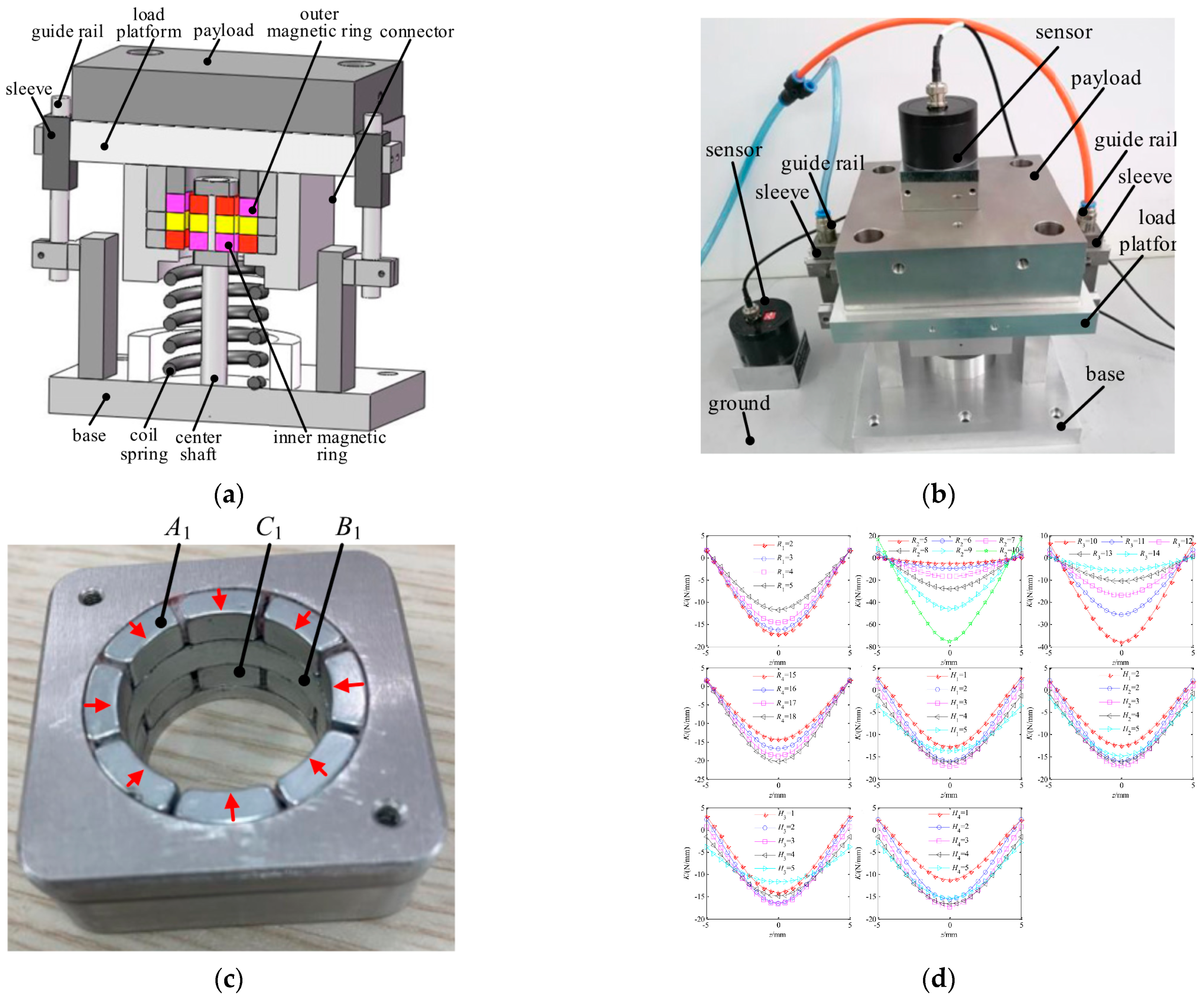
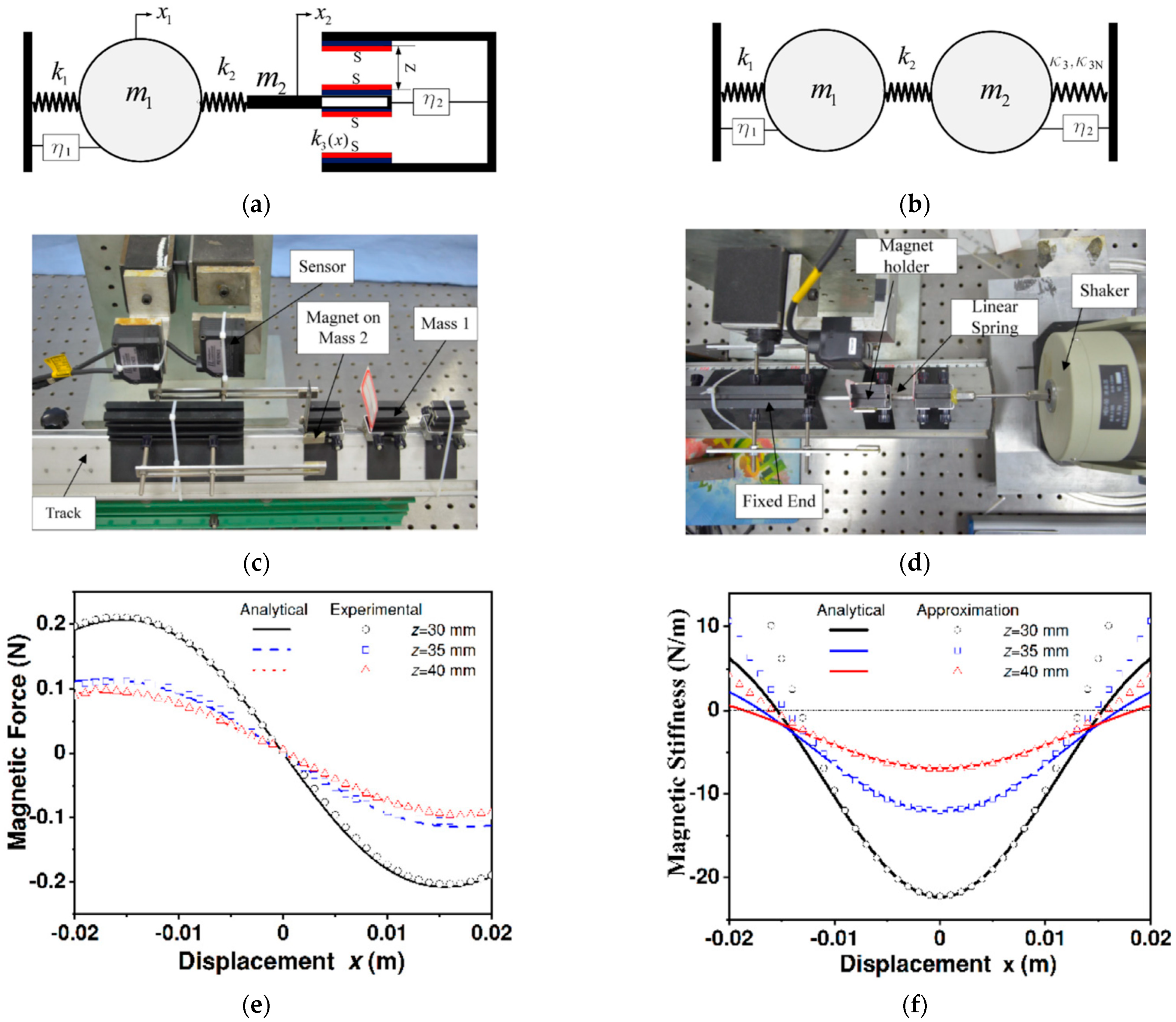
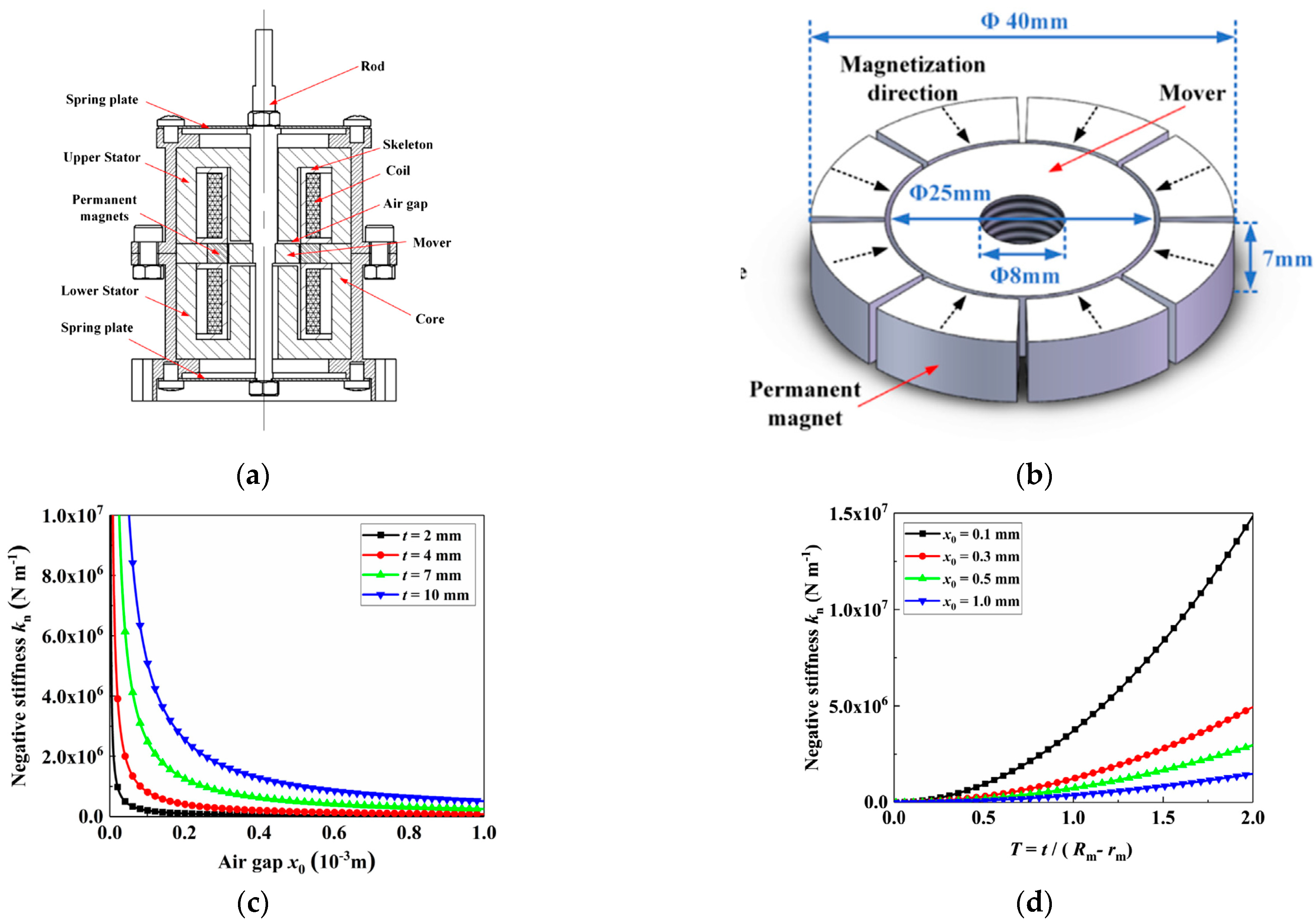

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Q.; Chai, K. Magnetic Negative Stiffness Devices for Vibration Isolation Systems: A State-of-the-Art Review from Theoretical Models to Engineering Applications. Appl. Sci. 2024, 14, 4698. https://doi.org/10.3390/app14114698
Zhu Q, Chai K. Magnetic Negative Stiffness Devices for Vibration Isolation Systems: A State-of-the-Art Review from Theoretical Models to Engineering Applications. Applied Sciences. 2024; 14(11):4698. https://doi.org/10.3390/app14114698
Chicago/Turabian StyleZhu, Qingbo, and Kai Chai. 2024. "Magnetic Negative Stiffness Devices for Vibration Isolation Systems: A State-of-the-Art Review from Theoretical Models to Engineering Applications" Applied Sciences 14, no. 11: 4698. https://doi.org/10.3390/app14114698
APA StyleZhu, Q., & Chai, K. (2024). Magnetic Negative Stiffness Devices for Vibration Isolation Systems: A State-of-the-Art Review from Theoretical Models to Engineering Applications. Applied Sciences, 14(11), 4698. https://doi.org/10.3390/app14114698





