Design and Control of a Shape Memory Alloy-Based Idle Air Control Actuator for a Mid-Size Passenger Vehicle Application
Abstract
1. Introduction
2. Materials and Methods
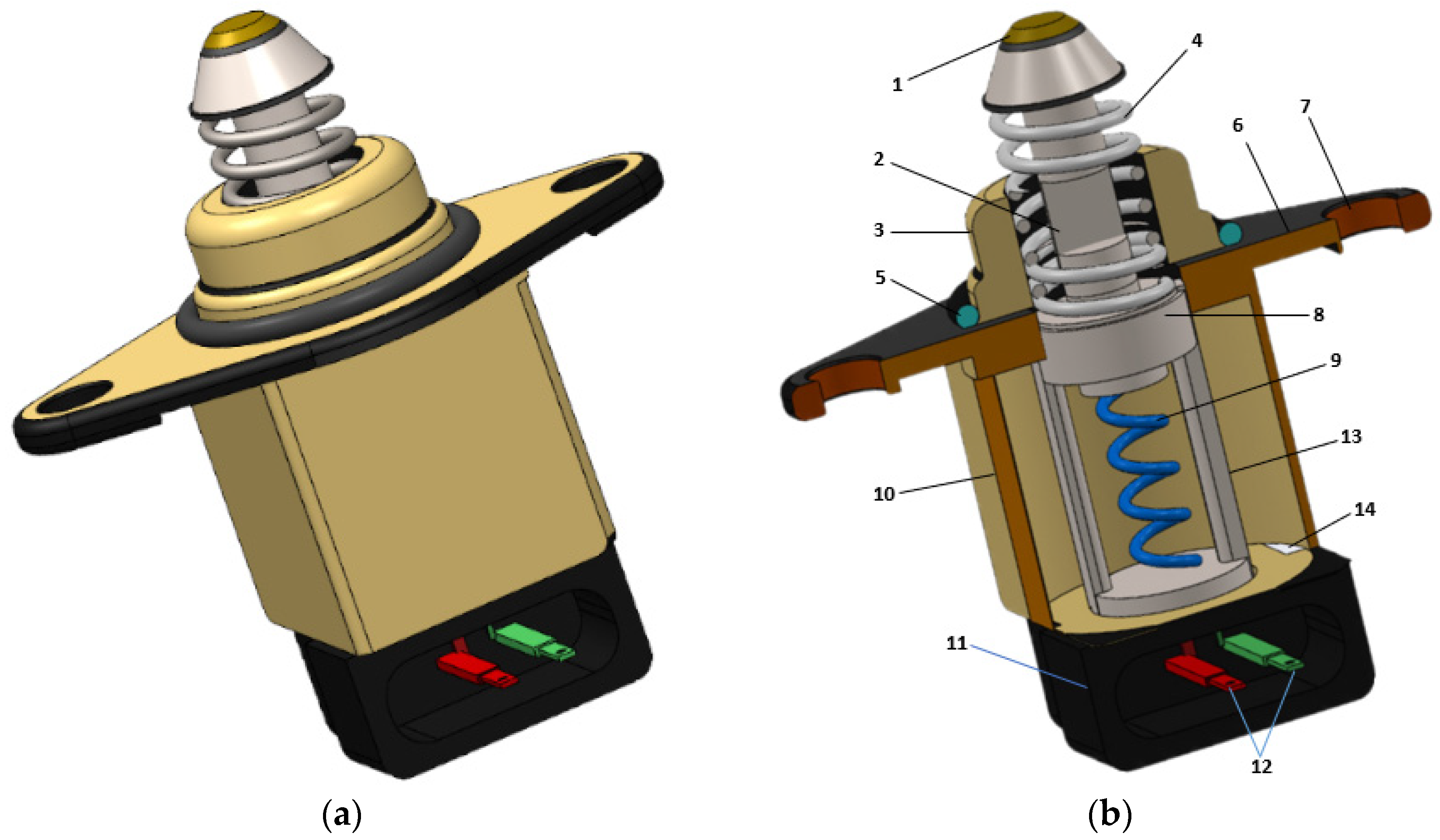
2.1. Structural Configuration of Proposed IAC Actuator
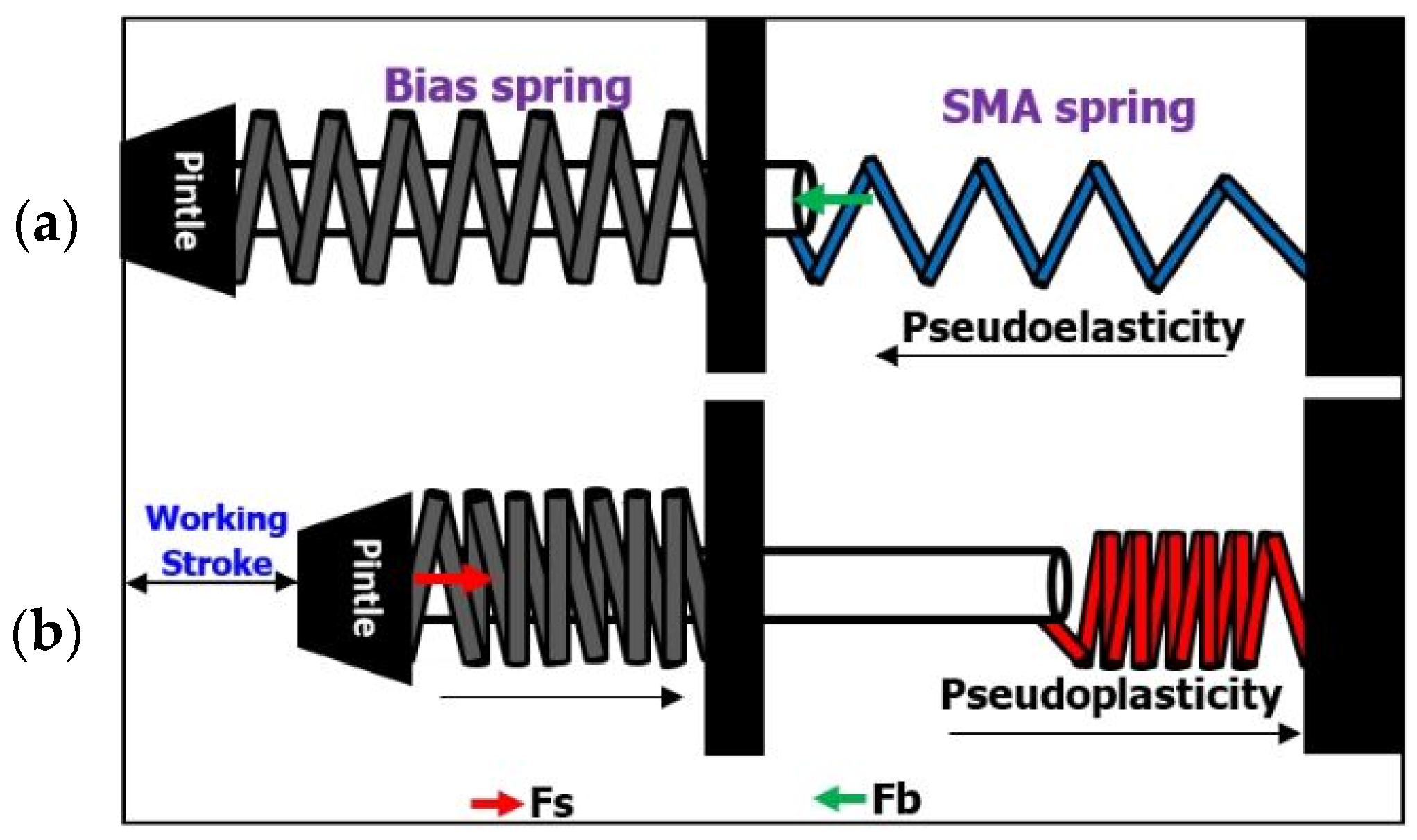
2.2. Actuation Mechanism of SMA-Based IAC Actuator
2.2.1. Actuation Requirements of Proposed Actuator
2.2.2. Working Principle of SMA-Based Actuator
2.3. Analytical Modelling of the Proposed IAC Actuator
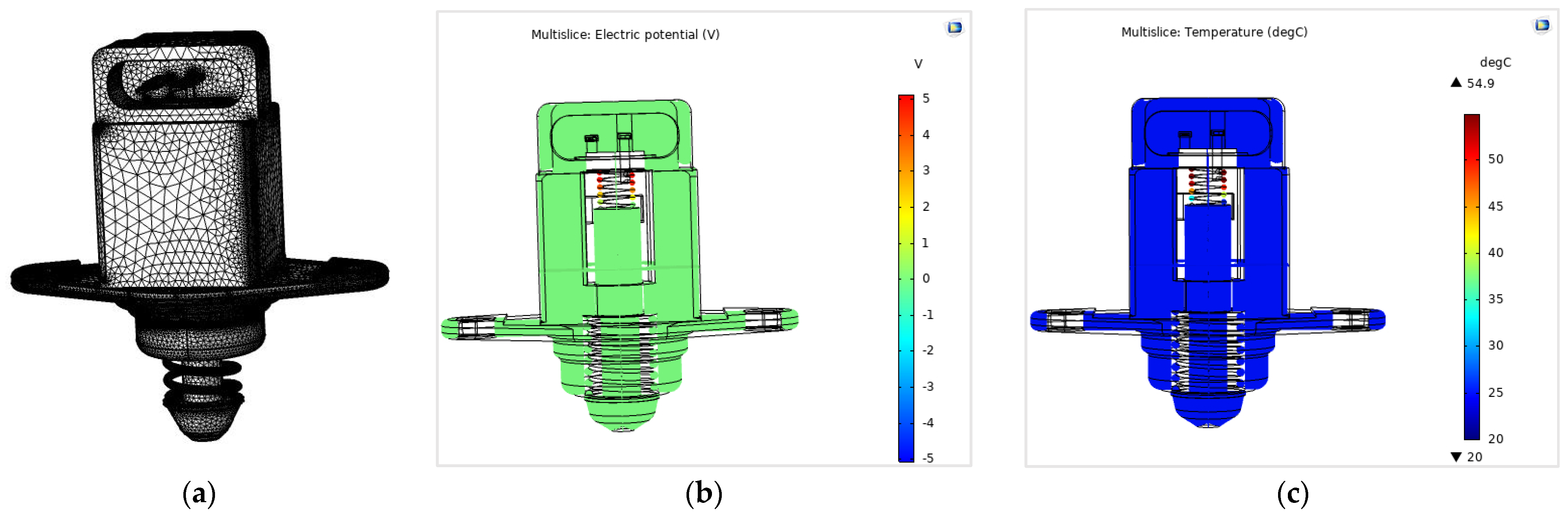
2.4. Numerical Analysis of SMA-Based IAC Actuator
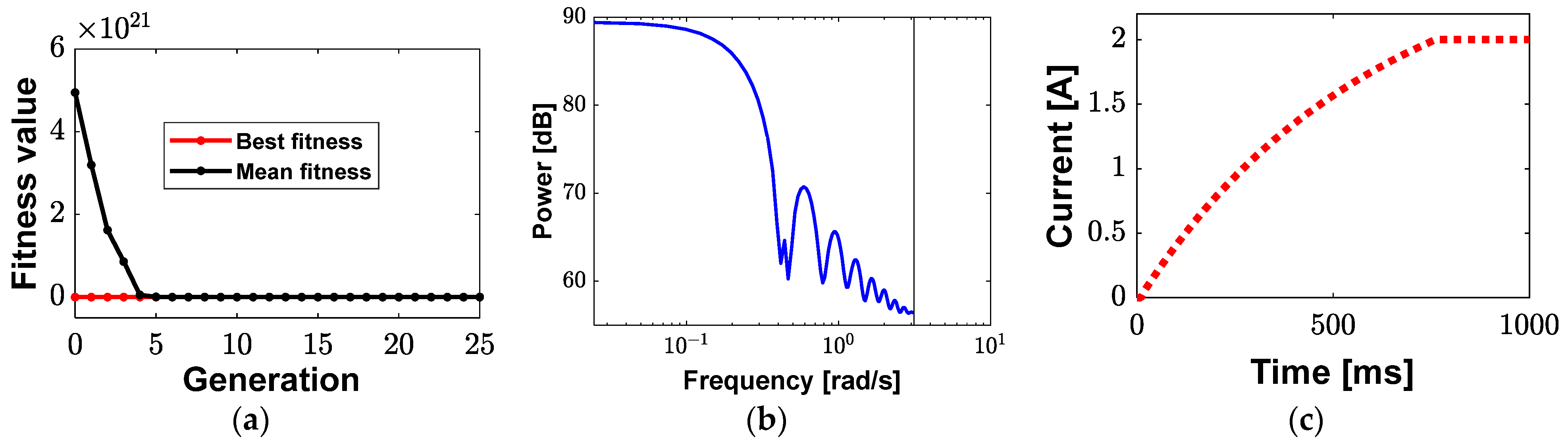
2.5. Performance Evaluation of the Proposed IAC Actuator
3. Results and Discussion
3.1. Analytical Results
3.2. Numerical Simulations
3.3. Performance Evaluation Outputs
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Mathematical Variables and Their Descriptions
| Variable | Description | Variable | Description |
| Indication of Bias spring | SMA spring’s area | ||
| Indication of SMA spring | Density of SMA spring | ||
| Shear stress correction factor | The total volume of SMA spring | ||
| The outer coil diameter of the bias spring | Specific heat | ||
| Cooling cycle | The electric resistance of the SMA spring | ||
| The wire diameter of the bias spring | Convective coefficient | ||
| Spring index | Operational time | ||
| Spring’s maximum shear stress | Ambient temperature | ||
| Force from the pressure difference between the inlet and outlet of the bypass | A mechanical driving force to extend the SMA spring | ||
| Spring constant of SMA spring | Heating cycle | ||
| Spring constant of bias spring | Austenite final temperature | ||
| Generated force by SMA spring to compress the bias spring | Austenite starting temperature | ||
| SMA spring’s wire diameter | Martensite final temperature | ||
| SMA spring’s coil mean diameter | Martensite stating temperature | ||
| SMA spring’s number of active coils | Austenite fraction volume | ||
| Transient flow force | Martensite fraction volume | ||
| Spring displacement | Detwinned martensite fraction volume | ||
| Parameters associated with the stress–strain curve | Temperature coefficient from material’s resistance | ||
| SMA spring working strain | SMA spring’s shear modulus | ||
| Tensile detwinned martensite | Change in vertical pitch for spring | ||
| Compressive detwinned martensite | Cristal variable speed coefficients of Nitinol | ||
| Transformation strain | Density of air to flow in the intake manifold | ||
| Air pressure difference | Slope of Austenite limit curve | ||
| Air Flowing length | Slope of martensite limit curve | ||
| Air flow coefficient | Initial martensite fraction volume | ||
| Pintle diameter | Initial austenite fraction volume | ||
| Pintle’s conic angle | Initial detwinned fraction volume | ||
| Transformation modulus | Minimum allowable stress | ||
| Electric current | Maximum allowable stress | ||
| Temperature in the SMA spring | Minimum strain | ||
| Actuator’s defined stroke | Initial vertical pitch of the coil spring | ||
| Air mass flow through pintle of SMA-based IAC actuator | Air mass flow rate passes through the IAC actuator and induced by the engine | ||
| Ambient temperature | Volume of the intake manifold | ||
| Atmospheric pressure | Temperature in the intake manifold | ||
| Air pressure in the intake manifold | Air fuel ratio | ||
| Air constant | Stochiometric air-fuel ratio | ||
| Engine torque | Volumetric efficiency | ||
| Ignition parameter | Piston displacement volume | ||
| Piston’s friction coefficient | Engine speed | ||
| Heating due to ignition | Austenite young’s modulus | ||
| Twinned young’s modulus | Detwinned young’s modulus |
References
- Chakirov, R.; Vagapov, Y. Rapid Control Prototyping Platform for the Design of Control Systems for Automotive Electromechanical Actuators [Internet]. IFAC Proc. Vol. 2010, 43, 646–651. [Google Scholar] [CrossRef]
- Battaglia, A.R.M.; Sellitto, A.; Giamundo, A.; Visone, M. Shape Memory Alloys Applied to Automotive Adaptive Aerodynamics. Materials 2023, 16, 4832. [Google Scholar] [CrossRef] [PubMed]
- Dezaki, M.L.; Bodaghi, M.; Serjouei, A.; Afazov, S.; Zolfagharian, A. Adaptive reversible composite-based shape memory alloy soft actuators. Sens. Actuators A Phys. 2022, 345, 113779. [Google Scholar] [CrossRef]
- Purohit, R.; Patel, K.K.; Gupta, G.K.; Rana, R.S. Development of Ni-Ti Shape Memory Alloys through Novel Powder Metallurgy Route and Effect of Rolling on their properties. Mater. Today Proc. 2017, 4, 5330–5335. [Google Scholar] [CrossRef]
- Kanada, T.; Enokizono, M. A slant type shape memory alloy. J. Magn. Magn. Mater. 2000, 215–216, 573–575. [Google Scholar] [CrossRef]
- Benafan, O.; Gaydosh, D.J. Scale-up of NiTiHf shape memory alloy tubes with high torque capability. Smart Mater. Struct. 2019, 28, 085035. [Google Scholar] [CrossRef]
- Copaci, D.; Blanco, D.; Moreno, L.E. Flexible shape-memory alloy-based actuator: Mechanical design optimization according to application. Actuators 2019, 8, 63. [Google Scholar] [CrossRef]
- Song, G.; Kelly, B.; Agrawal, B.N. Active position control of a shape memory alloy wire actuated composite beam. Smart Mater. Struct. 2000, 9, 711–716. [Google Scholar] [CrossRef]
- Fann, K.J.; Su, J.Y. Cold Forming of Ni-Ti Shape Memory Alloy Sheet. IOP Conf. Ser. Mater. Sci. Eng. 2018, 317, 012079. [Google Scholar] [CrossRef]
- Costanza, G.; Tata, M.E. Shape Memory Alloys for Aerospace, Recent Developments, and New Applications: A Short Review. Materials 2020, 13, 1856. [Google Scholar] [CrossRef]
- Prendota, W.; Goc, K.; Strączek, T.; Yamada, E.; Takasaki, A.; Przewoźnik, J.; Radziszewska, A.; Uematsu, S.; Kapusta, C. Properties of NiTi shape memory alloy micro-foils obtained by pulsed-current sintering of Ni/Ti foils. Metals 2019, 9, 323. [Google Scholar] [CrossRef]
- Tomus, D.; Tsuchiya, K.; Inuzuka, M.; Sasaki, M.; Imai, D.; Ohmori, T.; Umemoto, M. Fabrication of shape memory TiNi foils via Ti/Ni ultrafine laminates. Scr. Mater. 2003, 48, 489–494. [Google Scholar] [CrossRef]
- Turabimana, P.; Sohn, J.W.; Choi, S.B. A Novel Active Cooling System for Internal Combustion Engine Using Shape Memory Alloy Based Thermostat. Sensors 2023, 23, 3972. [Google Scholar] [CrossRef]
- Spaggiari, A.; Spinella, I.; Dragoni, E. Design equations for binary shape memory actuators under arbitrary external forces. J. Intell. Mater. Syst. Struct. 2013, 24, 682–694. [Google Scholar] [CrossRef]
- Bhaskar, J.; Sharma, A.K.; Bhattacharya, B.; Adhikari, S. A review on shape memory alloy reinforced polymer composite materials and structures. Smart Mater. Struct. 2020, 29, 073001. [Google Scholar] [CrossRef]
- Mizzi, L.; Hoseini, S.F.; Formighieri, M.; Spaggiari, A. Development and prototyping of SMA-metamaterial biaxial composite actuators. Smart Mater. Struct. 2023, 32, 035027. [Google Scholar] [CrossRef]
- Serrano, D.; Copaci, D.S.; Moreno, L.; Blanco, D. SMA based wrist exoskeleton for rehabilitation therapy. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 2318–2323. [Google Scholar] [CrossRef]
- Hamid, Q.Y.; Hasan, W.Z.W.; Hanim, M.A.A.; Nuraini, A.A.; Hamidon, M.N.; Ramli, H.R. Shape memory alloys actuated upper limb devices: A review. Sens. Actuators Rep. 2023, 5, 100160. [Google Scholar] [CrossRef]
- Liu, Q.; Ghodrat, S.; Jansen, K.M.B. Modelling and mechanical design of a flexible tube-guided SMA actuator. Mater. Des. 2022, 216, 110571. [Google Scholar] [CrossRef]
- Jiang, S.; Zhang, Y.; Zheng, Y.; Li, C. Deformation mechanism of hot spinning of NiTi shape memory alloy tube based on FEM. J. Wuhan Univ. Technol. Mater. Sci. Ed. 2012, 27, 811–814. [Google Scholar] [CrossRef]
- Sohn, J.W.; Ruth, J.S.; Yuk, D.G.; Choi, S.B. Application of Shape Memory Alloy Actuators to Vibration and Motion Control of Structural Systems: A Review. Appl. Sci. 2023, 13, 995. [Google Scholar] [CrossRef]
- Liu, R.; Zhang, C.; Ji, H.; Zhang, C.; Qiu, J. Training, Control and Application of SMA-Based Actuators with Two-Way Shape Memory Effect. Actuators 2023, 12, 25. [Google Scholar] [CrossRef]
- Hao, L.; Qiu, J.; Ji, H.; Nie, R. Numerical analysis on shape memory alloy–based adaptive shock control bump. J. Intell. Mater. Syst. Struct. 2018, 29, 3055–3066. [Google Scholar] [CrossRef]
- John, S.; Hariri, M. Effect of shape memory alloy actuation on the dynamic response of polymeric composite plates. Compos. Part A Appl. Sci. Manuf. 2008, 39, 769–776. [Google Scholar] [CrossRef]
- Koh, J.S. Design of shape memory alloy coil spring actuator for improving performance in cyclic actuation. Materials 2018, 11, 2324. [Google Scholar] [CrossRef] [PubMed]
- Soother, D.K.; Daudpoto, J.; Chowdhry, B.S. Challenges for practical applications of shape memory alloy actuators. Mater. Res. Express 2020, 7, 073001. [Google Scholar] [CrossRef]
- Bhatt, N.; Gurung, H.; Soni, S.; Singla, A. Effect of biasing conditions on the performance of a SMA spring actuator under thermo-mechanical loading. Mech. Adv. Mater. Struct. 2022, 29, 4599–4613. [Google Scholar] [CrossRef]
- Song, G.; Ma, N.; Lee, H.J.; Arnold, S. Design and control of a proof-of-concept variable area exhaust nozzle using shape-memory alloy actuators. Smart Mater. Struct. 2007, 16, 1342–1347. [Google Scholar] [CrossRef]
- Fawcett, J.N.; Burdess, J.S. Application of a shape memory alloy in a smart thermal clutch or brake. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 1999, 213, 21–26. [Google Scholar] [CrossRef]
- Palaniappan, S.K.; Rathanasamy, R.; Chellamuthu, S.; Pal, S.K. Development of Shape Memory Alloy Based Quarter Car Suspension System. J. Mech. Eng. Res. 2020, 3, 21–24. [Google Scholar] [CrossRef]
- Hübler, M.; Nissle, S.; Gurka, M.; Breuer, U. Active aerodynamic components for automotive applications—FRP spoiler with integrated SMA actuation. ICCM Int. Conf. Compos. Mater. 2015, 2015, 1–6. [Google Scholar] [CrossRef]
- Leal, P.B.C.; Savi, M.A. Shape memory alloy-based mechanism for aeronautical application: Theory, optimization and experiment. Aerosp. Sci. Technol. 2018, 76, 155–163. [Google Scholar] [CrossRef]
- Chillara, V.S.C.; Headings, L.M.; Tsuruta, R.; Itakura, E.; Gandhi, U.; Dapino, M.J. Shape memory alloy–actuated prestressed composites with application to morphing automotive fender skirts. J. Intell. Mater. Syst. Struct. 2019, 30, 479–494. [Google Scholar] [CrossRef]
- Sazonov, E.; Daoud, W.A. Grand Challenges in Wearable Electronics. Front. Electron. 2021, 2, 668619. [Google Scholar] [CrossRef]
- Shimoga, G.; Kim, T.H.; Kim, S.Y. An intermetallic niti-based shape memory coil spring for actuator technologies. Metals 2021, 11, 1212. [Google Scholar] [CrossRef]
- Ishii, T. Design of shape memory alloy (SMA) coil springs for actuator applications [Internet]. In Shape Memory and Superelastic Alloys; Woodhead Publishing Limited: Cambridge, UK, 2011; pp. 63–76. [Google Scholar] [CrossRef]
- An, L.; Huang, W.M.; Fu, Y.Q.; Guo, N.Q. A note on size effect in actuating NiTi shape memory alloys by electrical current. Mater. Des. 2008, 29, 1432–1437. [Google Scholar] [CrossRef]
- Mozhi, G.T.; Dhanalakshmi, K.; Choi, S.B. Design and Control of Monolithic Compliant Gripper Using Shape Memory Alloy Wires. Sensors 2023, 23, 2052. [Google Scholar] [CrossRef] [PubMed]
- Grigorie, T.L.; Botez, R.M. A Self–Tuning Intelligent Controller for a Smart Actuation Mechanism of a Morphing Wing Based on Shape Memory Alloys. Actuators 2023, 12, 350. [Google Scholar] [CrossRef]
- Pillai, R.R.; Murali, G.; Gopal, M. Modeling and Simulation of a Shape Memory Alloy Spring Actuated Flexible Parallel Manipulator. Procedia Comput. Sci. 2018, 133, 895–904. [Google Scholar] [CrossRef]
- Qian, H.; Li, H.; Song, G.; Guo, W. A constitutive model for superelastic shape memory alloys considering the influence of strain rate. Math. Probl. Eng. 2013, 2013, 248671. [Google Scholar] [CrossRef]
- Kittinanthapanya, R.; Sugahara, Y.; Matsuura, D.; Takeda, Y. Development of a novel SMA-driven compliant rotary actuator based on a double helical structure. Robotics 2019, 8, 12. [Google Scholar] [CrossRef]
- Turabimana, P. Design of Automobile Concrete Pump. IOSR J. Mech. Civ. Eng. 2019, 15, 1–5. [Google Scholar] [CrossRef]
- Meng, L.; Luo, J.; Yang, X.; Zeng, C. Intake air mass observer design based on extended Kalman filter for air-fuel ratio control on SI engine. Energies 2019, 12, 3444. [Google Scholar] [CrossRef]
- Amaral, A.A.D.C.; Saidatin, N.; Mahmud, R.; Maulana, H.S. Experimental Study of Spark Ignition Engine Performance under Different Electronic Control Units, Hole Injectors and Spark Plugs. J. Mech. Eng. Sci. Innov. 2023, 3, 22–29. [Google Scholar] [CrossRef]
- Wong, P.K.; Tam, L.M.; Li, K.; Vong, C.M. Engine idle-speed system modelling and control optimization using artificial intelligence. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2010, 224, 55–72. [Google Scholar] [CrossRef]
- Gharib, A.R.; Gharib, M.R.; Mousavi, S.A.S.; Gorkani, M.R. Control of Throttle Valve in idle speed condition. In Proceedings of the 2010 International Conference on Modelling, Identification and Control, ICMIC, Okayama, Japan, 17–19 July 2010; pp. 394–399. [Google Scholar]
- Shamekhi, A.M.; Taghavipour, A.; Shamekhi, A.H. Engine idle speed control using nonlinear multiparametric model predictive control. Optim. Control Appl. Methods 2020, 41, 960–979. [Google Scholar] [CrossRef]
- Nikzadfar, K.; Noorpoor, A.; Shamekhi, A.H. Design of an optimal idle speed controller for a turbocharged diesel engine using fuzzy logic method. J. Mech. Sci. Technol. 2012, 26, 2325–2336. [Google Scholar] [CrossRef]
- Hashemi, Y.M.; Kadkhodaei, M.; Mohammadzadeh, M.R. Fatigue analysis of shape memory alloy helical springs. Int. J. Mech. Sci. 2019, 161–162, 105059. [Google Scholar] [CrossRef]
- Di Cairano, S.; Yanakiev, D.; Bemporad, A.; Kolmanovsky, I.V.; Hrovat, D. Model predictive idle speed control: Design, analysis, and experimental evaluation. IEEE Trans. Control Syst. Technol. 2012, 20, 84–97. [Google Scholar] [CrossRef]
- Yin, F.; Sun, J.; Wang, W. Engine Idle Speed Control Research Status and Development Trend; no. Icmmcce; Atlantis Press: Berlin/Heidelberg, Germany, 2015; pp. 1884–1888. [Google Scholar] [CrossRef]
- Shulga, E.; Lanusse, P.; Airimitoaie, T.B.; Maurel, S.; Trutet, A. Model Predictive Control of engine intake manifold pressure with an uncertain model. IFAC-PapersOnLine 2021, 54, 335–340. [Google Scholar] [CrossRef]
- Wei, H.; Chen, Y.L.; Yu, W.; Su, L.; Wang, X.; Tang, D. Study on corrosion resistance of high-strength medium-carbon spring steel and its hydrogen-induced delayed fracture. Constr. Build. Mater. 2020, 239, 117815. [Google Scholar] [CrossRef]
- Nov, Z.; Salvetr, P.; Kotous, J.; Moty, P.; Gokhman, A. Enhanced Spring Steel’s Strength Using Strain Assisted Tempering. Materials 2022, 15, 7354. [Google Scholar] [CrossRef] [PubMed]
- Mirzaeifar, R.; Desroches, R.; Yavari, A. A combined analytical, numerical, and experimental study of shape-memory-alloy helical springs. Int. J. Solids Struct. 2011, 48, 611–624. [Google Scholar] [CrossRef]
- Zhang, B.; Zeng, S.; Tang, F.; Hu, S.; Zhou, Q.; Jia, Y. Experimental and numerical analysis of the mechanical properties of a pretreated shape memory alloy wire in a self-centering steel brace. Processes 2021, 9, 80. [Google Scholar] [CrossRef]
- Yildiz, Y.; Annaswamy, A.M.; Yanakiev, D.; Kolmanovsky, I. Spark-ignition-engine idle speed control: An adaptive control approach. IEEE Trans. Control Syst. Technol. 2011, 19, 990–1002. [Google Scholar] [CrossRef]




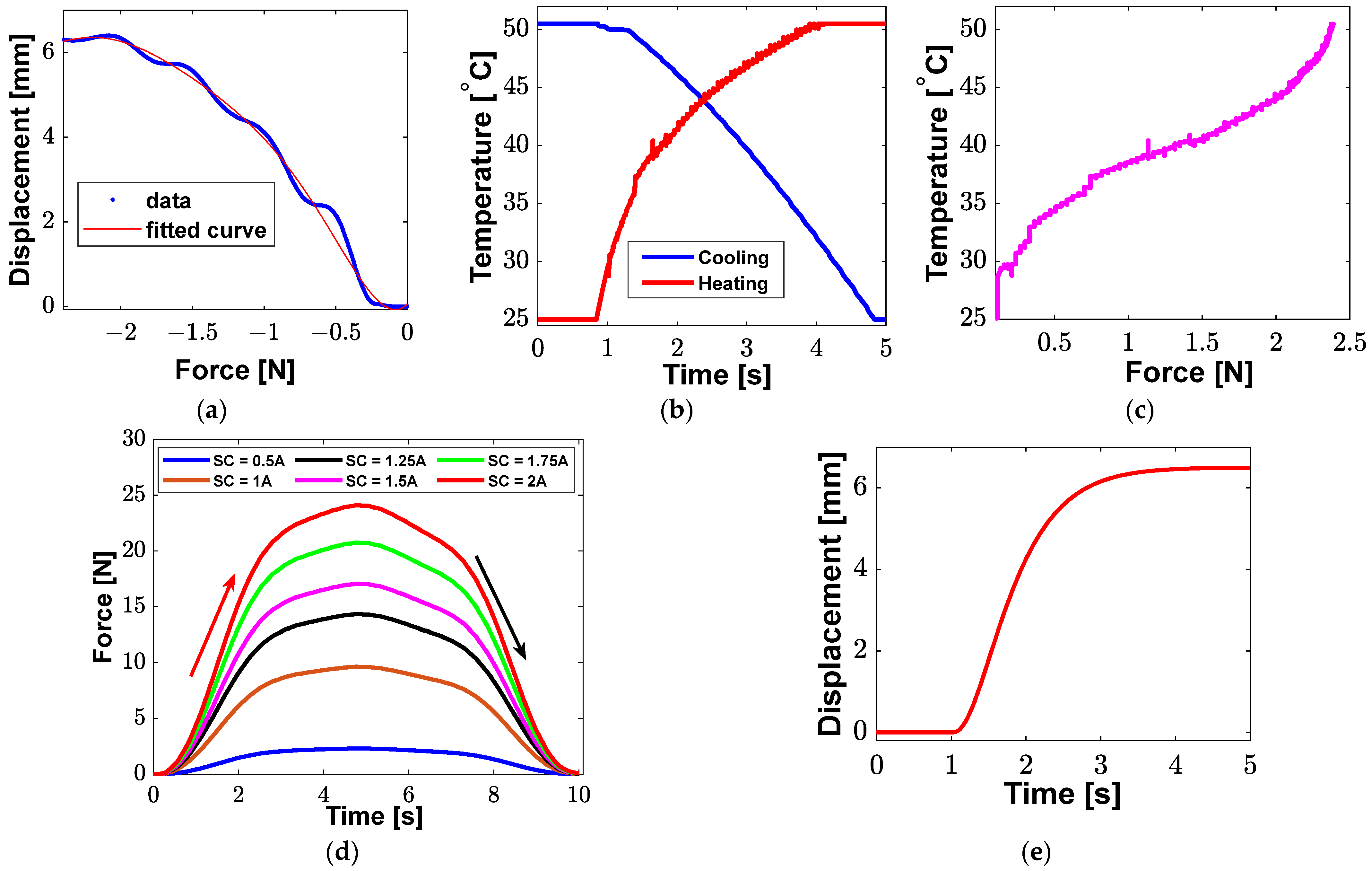

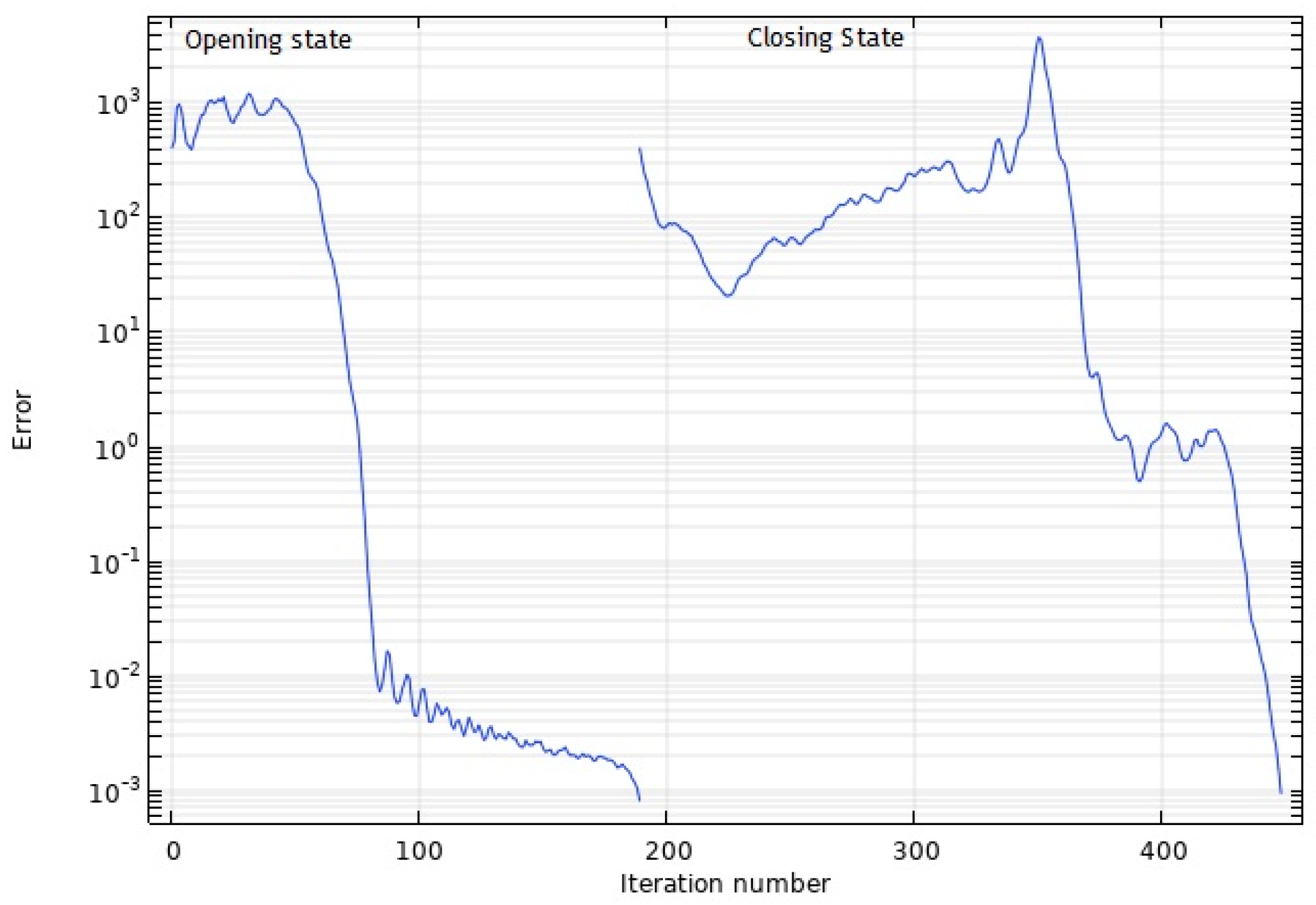


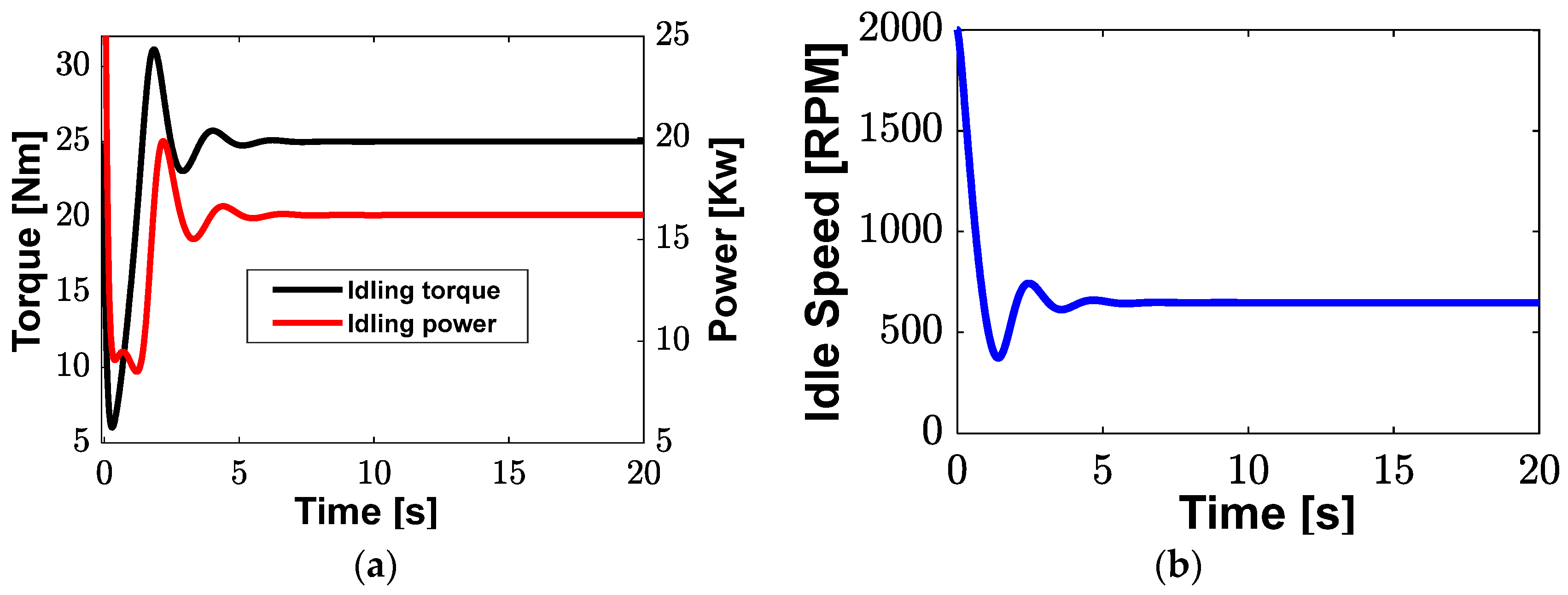
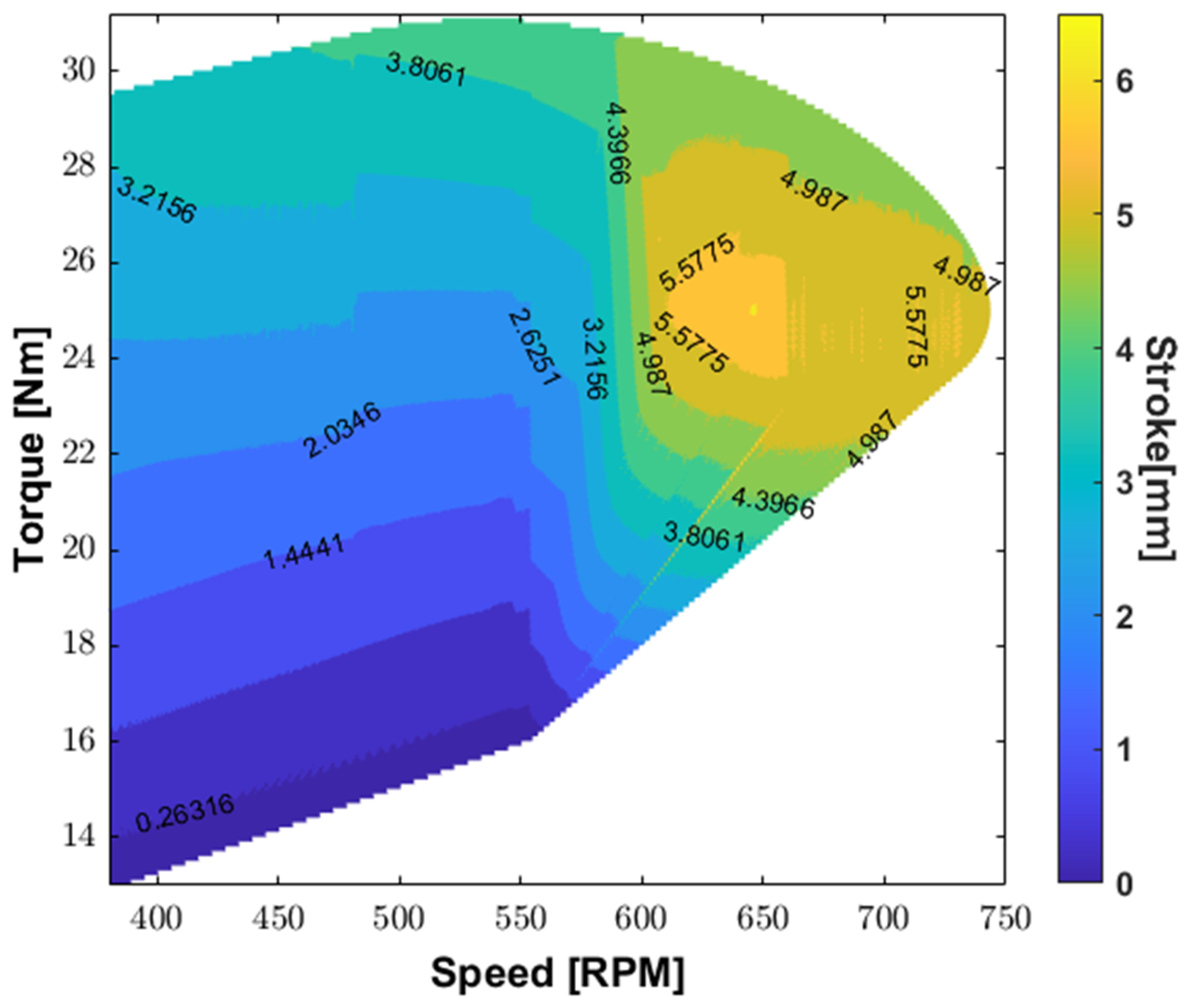
| Parameter | Value | |
|---|---|---|
| Bias Spring () | SMA Spring () | |
| Wire diameter () | 2 mm | 1.7 mm |
| Free length of coil () | 23 mm | 15.5 mm |
| Coil diameter () | 16 mm | 10.2 mm |
| Spring index () | 8 | 6 |
| Generated force () | 2.25 N | 2.416 N |
| Number of active coils () | 7 | 5 |
| Property | Value |
|---|---|
| Maximum allowable stress () | |
| Minimum allowable stress () | |
| Operating number of cycles () | |
| Operating temperature | 0–60 |
| Ambient temperature () | |
| Density () | |
| Poison’s ratio () | 0.33 |
| Electric resistivity_Martensite () | |
| Electric resistivity_Austenite () | |
| Specific heat () | |
| Martensite young’s modulus () | 33,500 |
| Austenite young’s modulus () | 62,500 |
| Coefficient of thermal expansion () | |
| Maximum pulling force ( |
| Parameter | Value | Reference |
|---|---|---|
| Martensite starting temperature () | [40] | |
| Martensite final temperature () | ||
| Austenite starting temperature () | ||
| Austenite final temperature () | ||
| Slope of Austenite limit curve () | ||
| Slope of martensite limit curve () | ||
| Maximum transformation strain ( | [41] |
| Model Builder and Setting | IAC Actuator’s Operating Mode | |
|---|---|---|
| Closing State | Opening State | |
| Physics interface | Structure Mechanics/Multibody dynamics | Structure Mechanics/Joule Heating and Thermal Expansion |
| Study | Stationary | Stationary |
| Physics constraints | Rigid fixed domain (supports), Prescribed displacement, (Assigned on the Pintle as the desired displacement), and Boundary load ( used as pressure and assigned on the bias spring) | Fixed constraint (supports), Temperature (), Ground (negative connector), Electric terminal (positive connector linked with the SMA spring). |
| Meshing | Free tetrahedral extra fine | Free tetrahedral extra fine |
| Solver configurations | Stationary nonlinear solver with segregated steps | Stationary nonlinear solver with segregated steps |
| Property | Material | ||||
|---|---|---|---|---|---|
| Stainless Steel 405 (Bias Spring, Rod Holder, and Rod) | Low Carbon Steel 1008 (Fixture Plate and Vertical Support) | Grey Cast Iron (Housings) | Ductile Cast iron (Connection Box) | Nitrile Rubber (O Ring) | |
| Young’s modulus | |||||
| Poison’s ratio | |||||
| Density | |||||
| Thermal conductivity | |||||
| Specific heat capacity | |||||
| Coefficient of thermal expansion | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turabimana, P.; Sohn, J.W.; Choi, S.-B. Design and Control of a Shape Memory Alloy-Based Idle Air Control Actuator for a Mid-Size Passenger Vehicle Application. Appl. Sci. 2024, 14, 4784. https://doi.org/10.3390/app14114784
Turabimana P, Sohn JW, Choi S-B. Design and Control of a Shape Memory Alloy-Based Idle Air Control Actuator for a Mid-Size Passenger Vehicle Application. Applied Sciences. 2024; 14(11):4784. https://doi.org/10.3390/app14114784
Chicago/Turabian StyleTurabimana, Pacifique, Jung Woo Sohn, and Seung-Bok Choi. 2024. "Design and Control of a Shape Memory Alloy-Based Idle Air Control Actuator for a Mid-Size Passenger Vehicle Application" Applied Sciences 14, no. 11: 4784. https://doi.org/10.3390/app14114784
APA StyleTurabimana, P., Sohn, J. W., & Choi, S.-B. (2024). Design and Control of a Shape Memory Alloy-Based Idle Air Control Actuator for a Mid-Size Passenger Vehicle Application. Applied Sciences, 14(11), 4784. https://doi.org/10.3390/app14114784









