A Study of Cavitation Erosion in Artificial Submerged Water Jets
Abstract
:1. Introduction
2. Numerical Simulation
2.1. Turbulence Model
2.2. Cavitation Model
2.3. Mesh Configuration and Boundary Conditions in Flow Domain
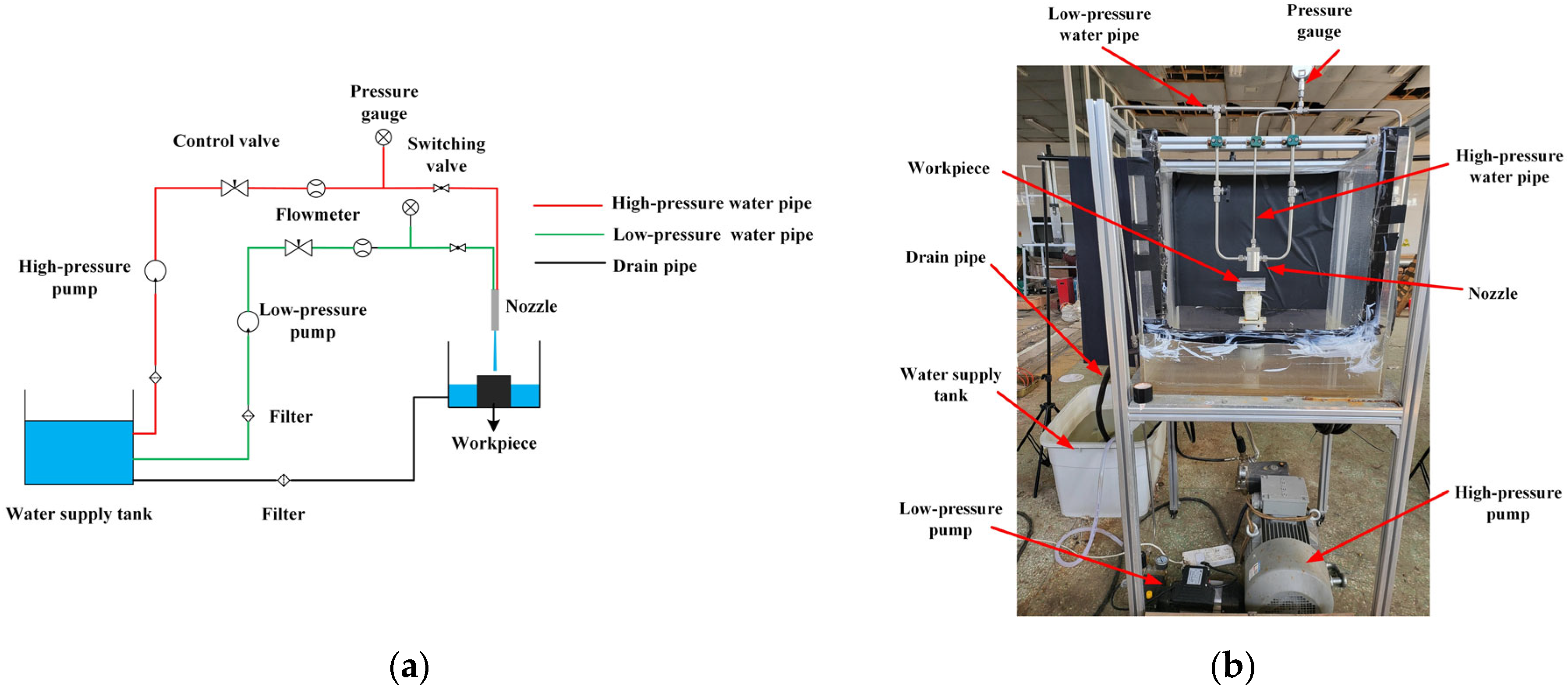
2.4. Experimental Procedure
3. Results and Discussion
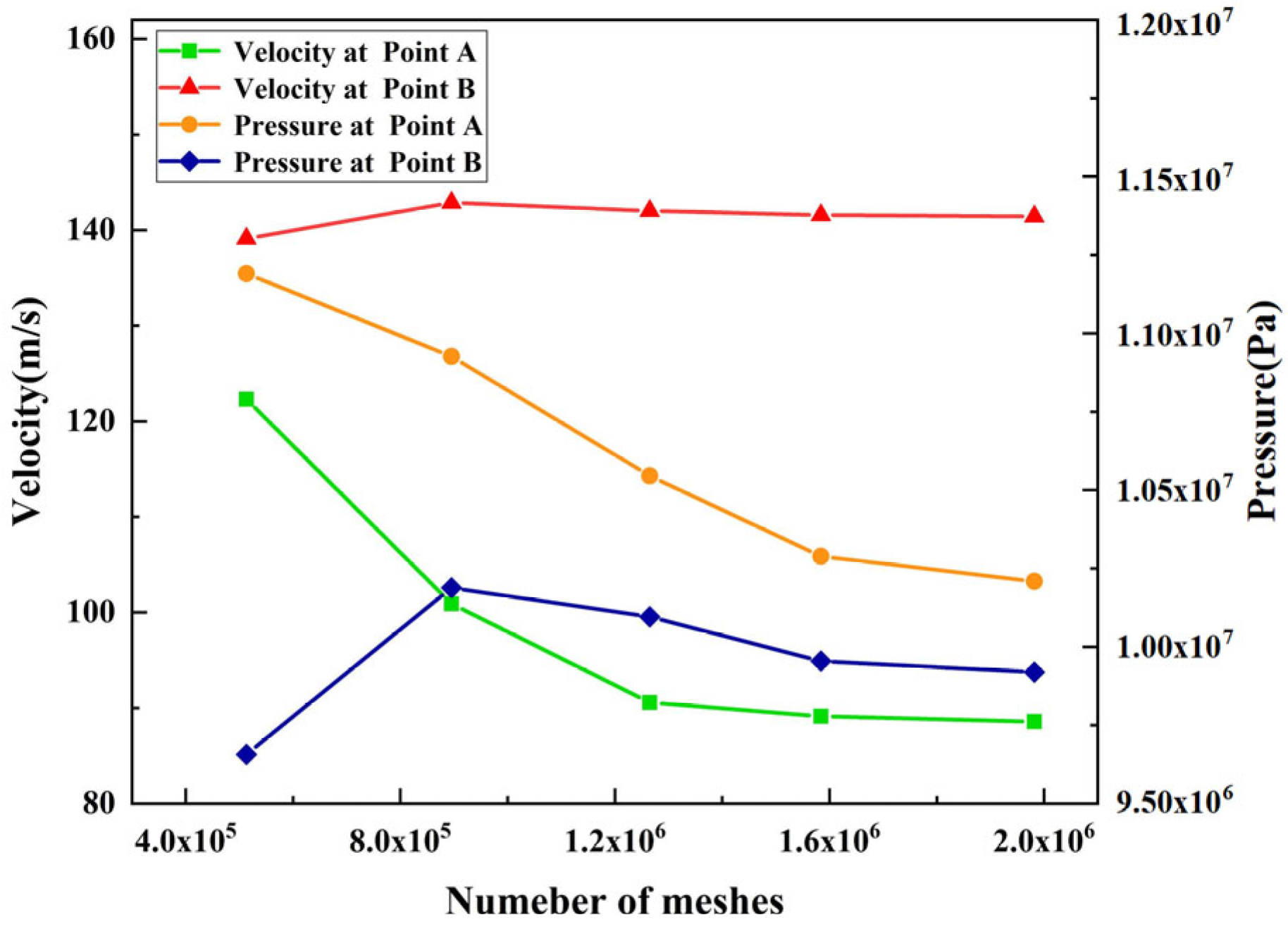
3.1. Mesh Independence Analysis
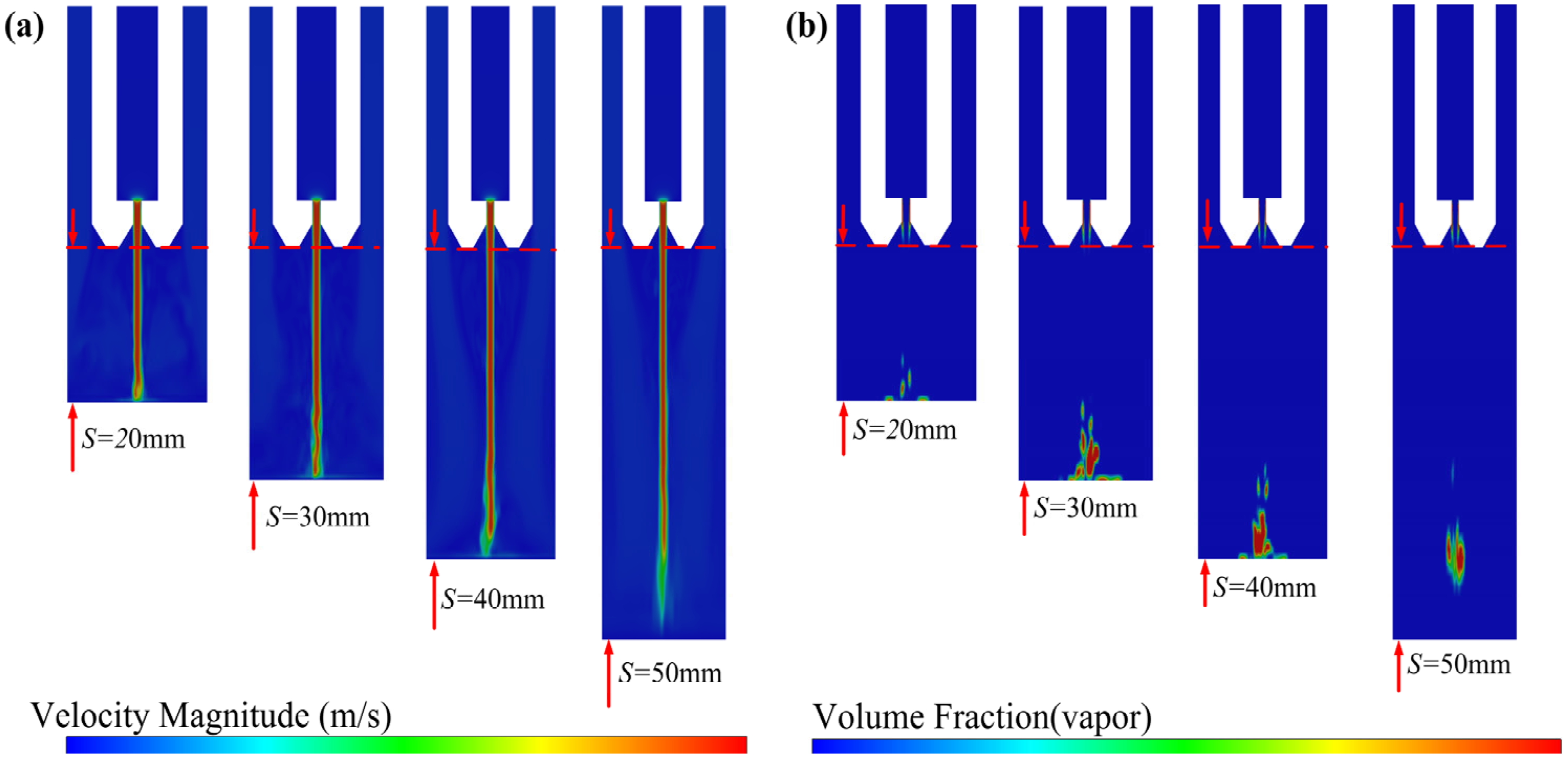
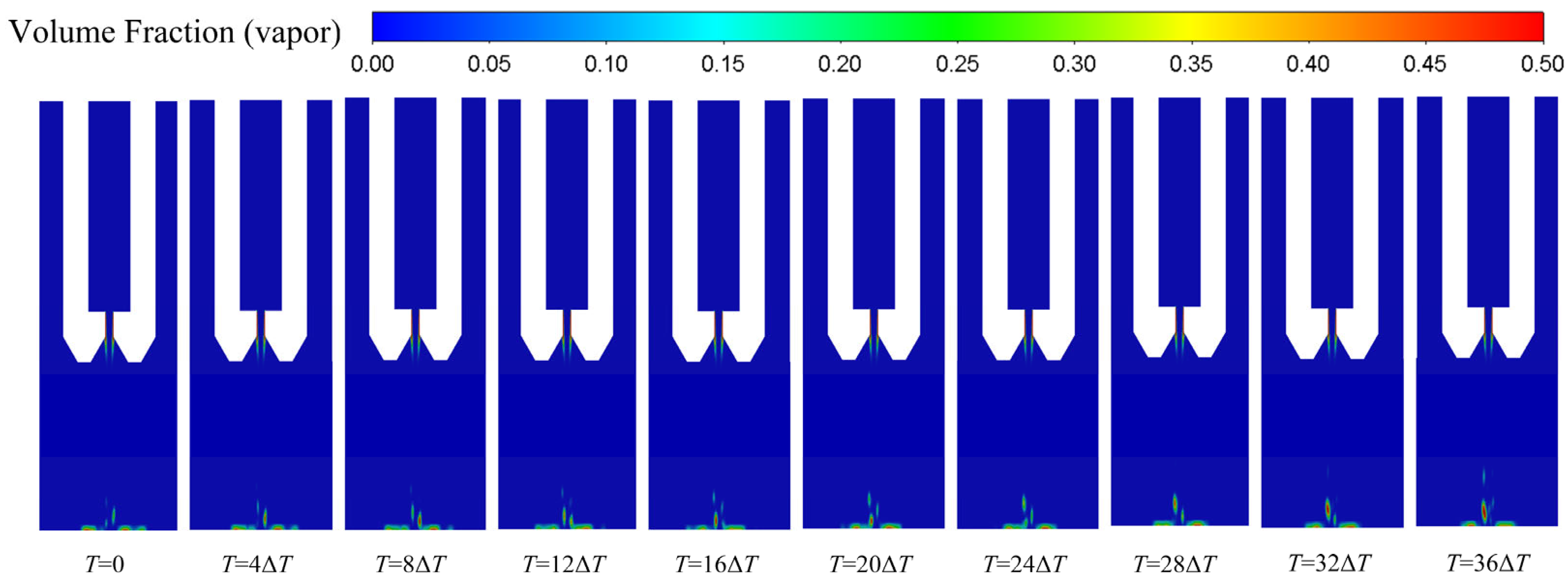
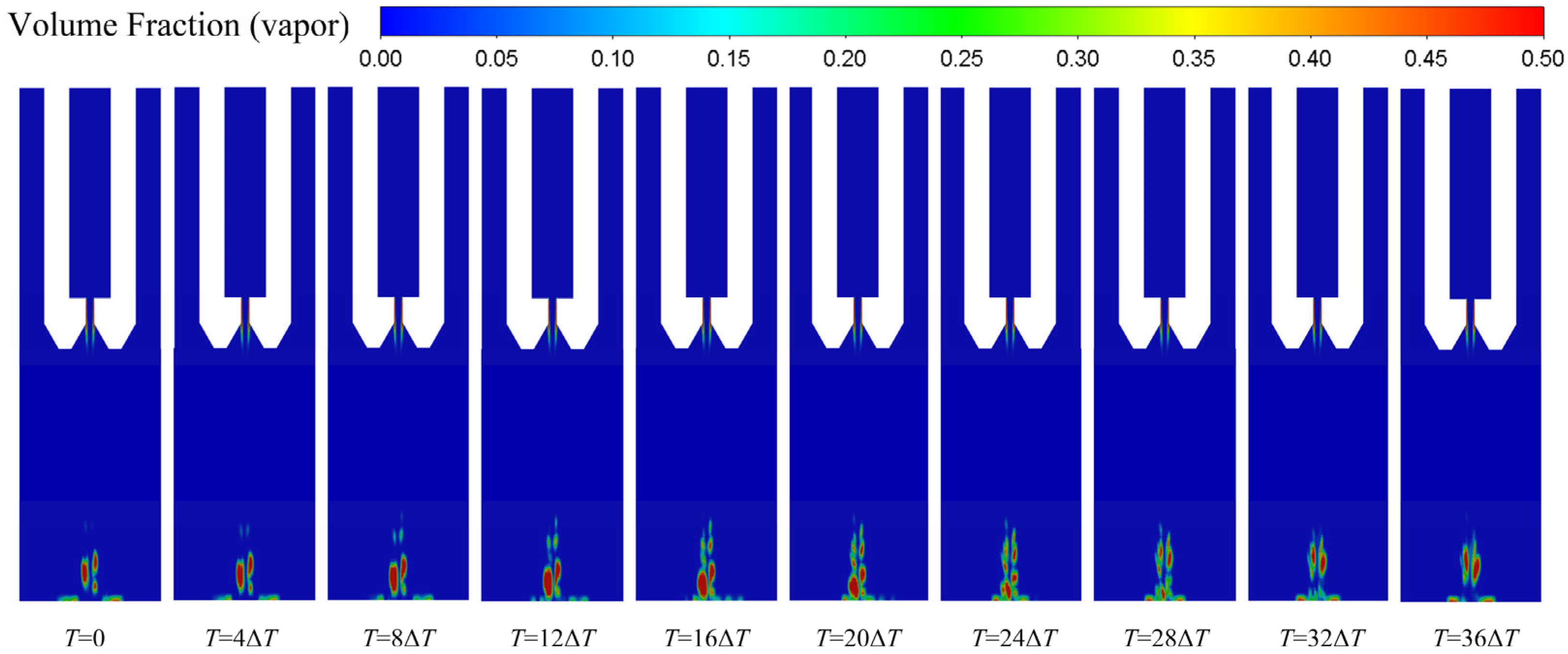
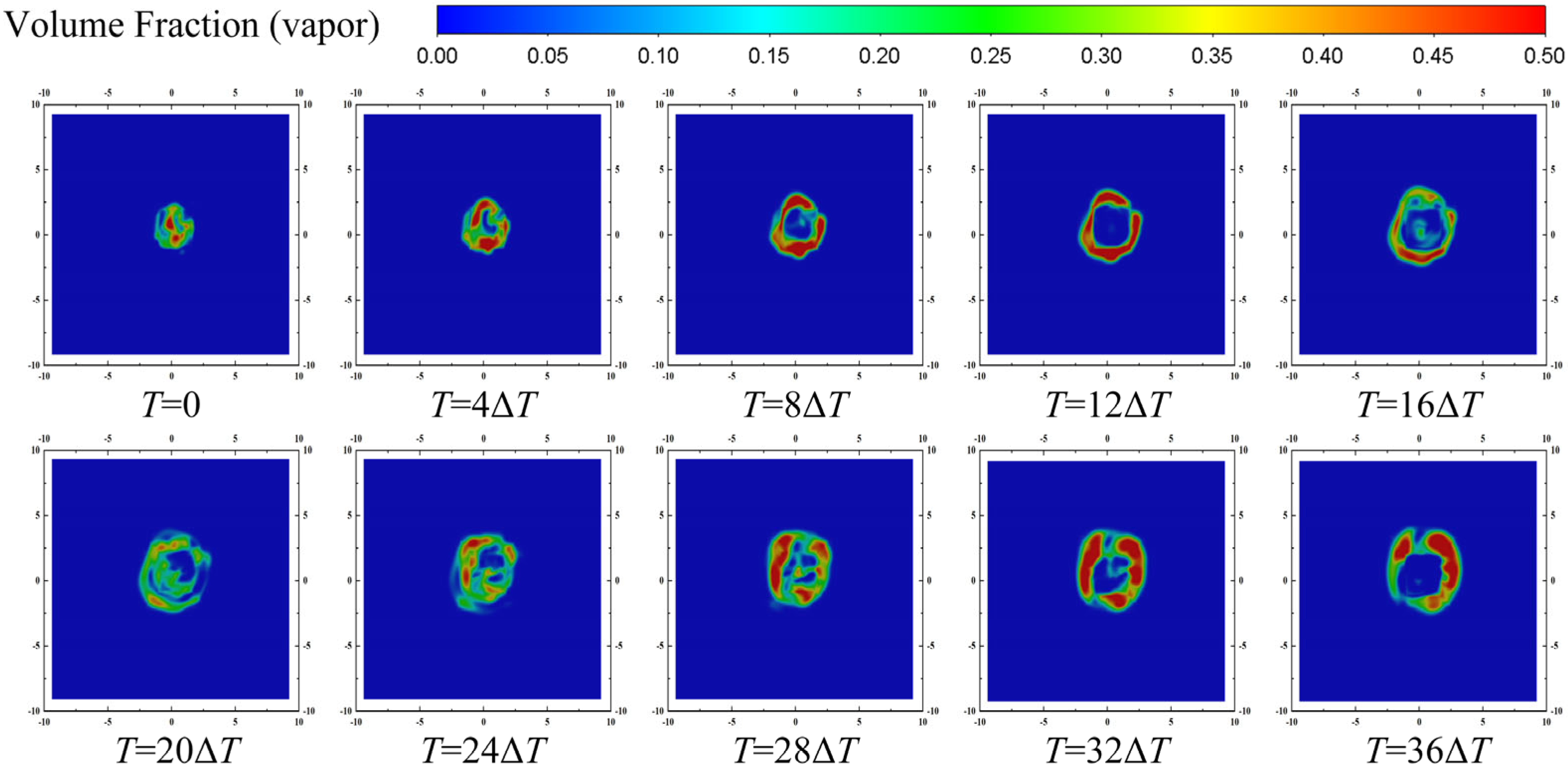
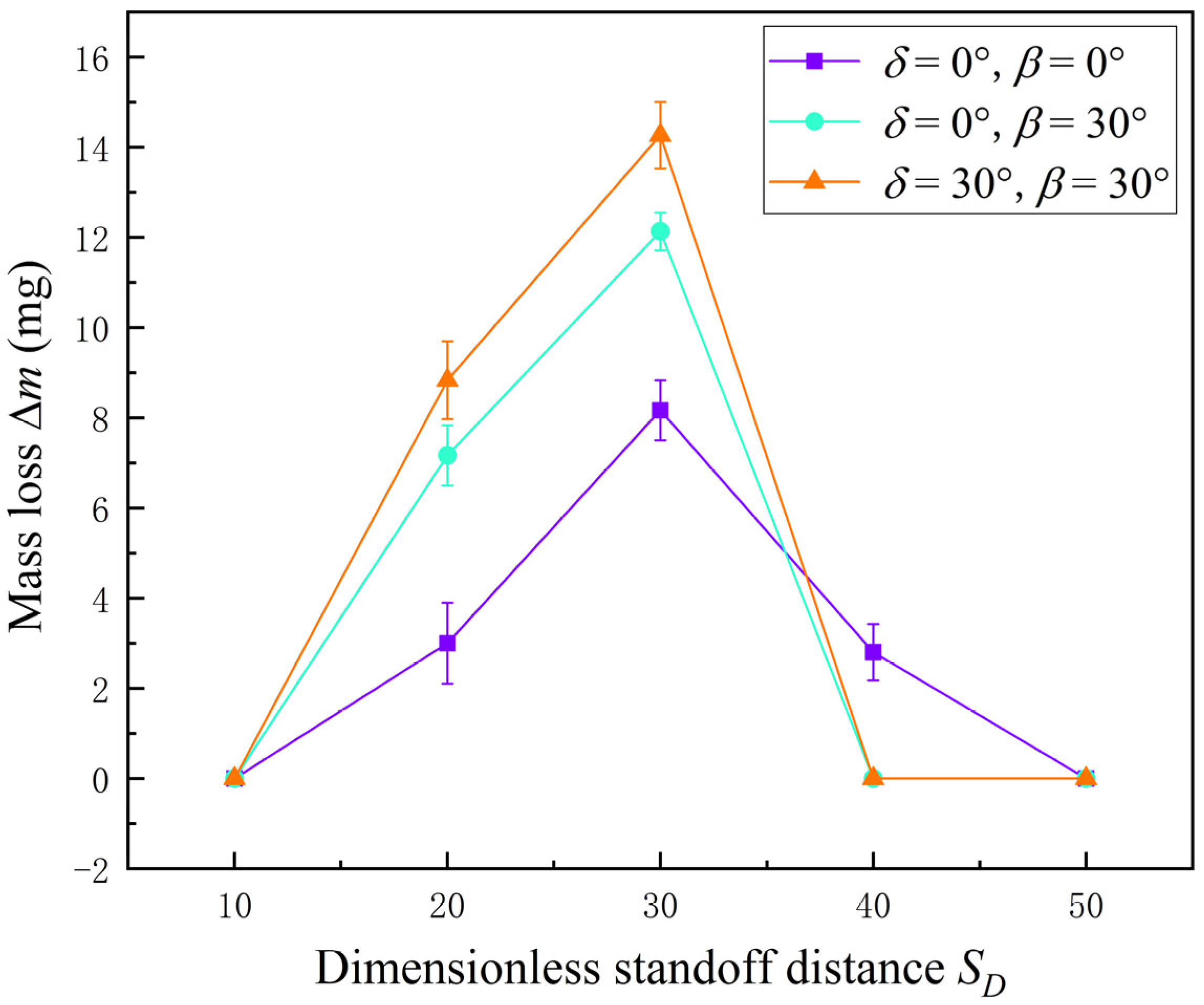
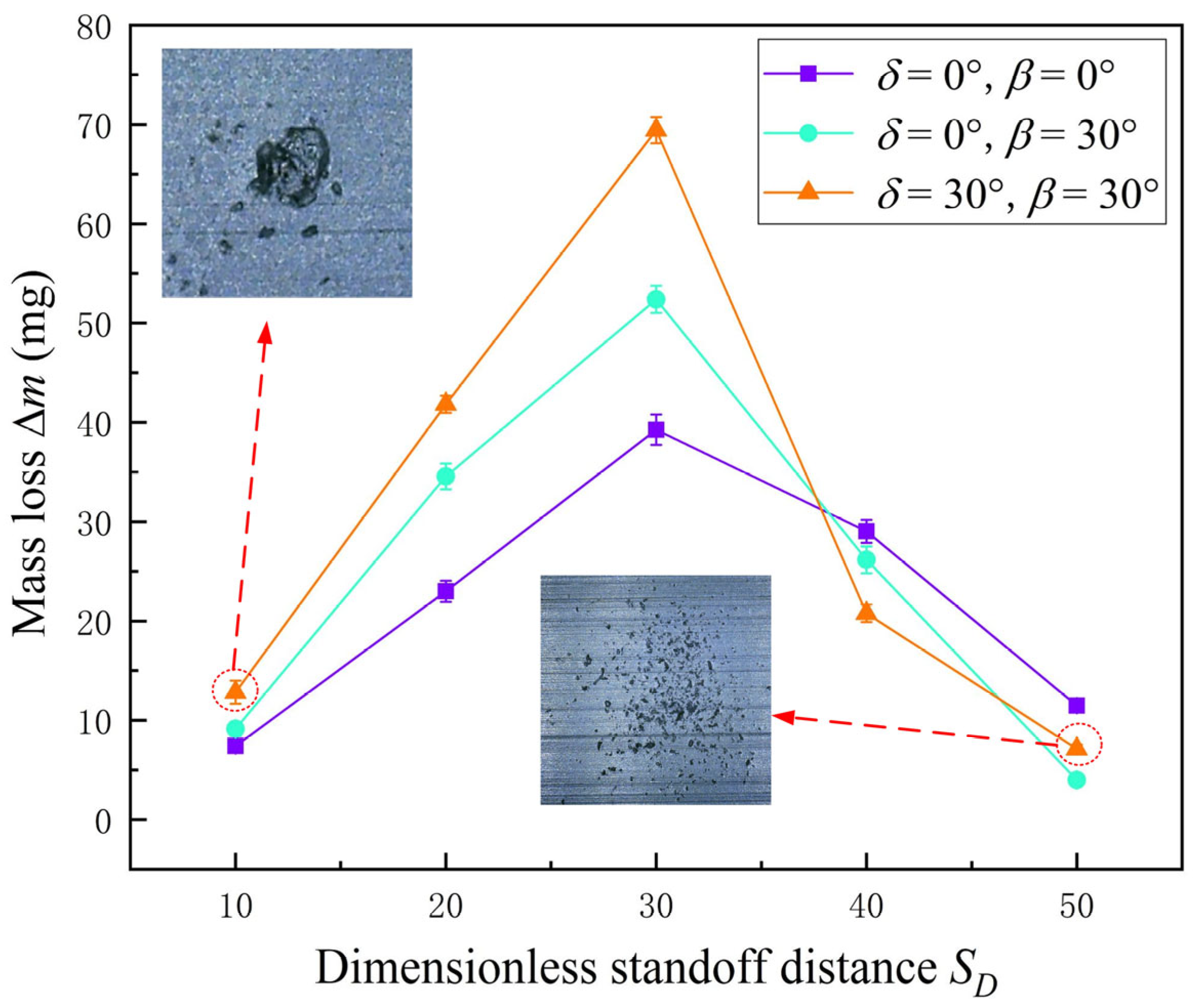
3.2. Effects of Dimensionless Standoff Distance between Nozzle and Workpiece
3.3. Effects of Nozzle Structure and High-Pressure Inlet Condition at Different Dimensionless Standoff Distance between the Nozzle and Workpiece
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Young, F.R. Cavitation; World Scientific: Singapore, 1999. [Google Scholar]
- Soyama, H. Cavitation peening: A review. Metals 2020, 10, 270. [Google Scholar] [CrossRef]
- Soyama, H. High-speed observation of a cavitating jet in air. J. Fluids Eng. 2005, 127, 1095–1101. [Google Scholar] [CrossRef]
- Rayleigh, L. VIII. On the pressure developed in a liquid during the collapse of a spherical cavity. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1917, 34, 94–98. [Google Scholar] [CrossRef]
- Noltingk, B.E.; Neppiras, E.A. Cavitation produced by ultrasonics. Proc. Phys. Society. Sect. B 1950, 63, 674. [Google Scholar] [CrossRef]
- Ivany, R.D.; Hammitt, F.G. Cavitation bubble collapse in viscous, compressible liquids—Numerical analysis. J. Basic Eng. 1965, 87, 977–985. [Google Scholar] [CrossRef]
- Ye, L.; Zhu, X.; Liu, Y. Numerical study on dual-frequency ultrasonic enhancing cavitation effect based on bubble dynamic evolution. Ultrason. Sonochem. 2019, 59, 104744. [Google Scholar] [CrossRef] [PubMed]
- Laguna-Camacho, J.; Lewis, R.; Vite-Torres, M.; Mendez-Mendez, J.V. A study of cavitation erosion on engineering materials. Wear 2013, 301, 467–476. [Google Scholar] [CrossRef]
- Soyama, H. Effect of nozzle geometry on a standard cavitation erosion test using a cavitating jet. Wear 2013, 297, 895–902. [Google Scholar] [CrossRef]
- Hattori, S.; Hirose, T.; Sugiyama, K. Prediction method for cavitation erosion based on measurement of bubble collapse impact loads. Wear 2010, 269, 507–514. [Google Scholar] [CrossRef]
- Ashrafizadeh, S.M.; Ghassemi, H. Experimental and numerical investigation on the performance of small-sized cavitating venturis. Flow Meas. Instrum. 2015, 42, 6–15. [Google Scholar] [CrossRef]
- Coutier-Delgosha, O.; Stutz, B.; Vabre, A.; Legoupil, S. Analysis of cavitating flow structure by experimental and numerical investigations. J. Fluid Mech. 2007, 578, 171–222. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, B.; Zhang, M.; Wang, G. Experimental and numerical investigation of ventilated cavitating flow structures with special emphasis on vortex shedding dynamics. Int. J. Multiph. Flow 2018, 98, 79–95. [Google Scholar] [CrossRef]
- Chen, Y.; Hu, Y.; Zhang, S. Structure optimization of submerged water jet cavitating nozzle with a hybrid algorithm. Eng. Appl. Comput. Fluid Mech. 2019, 13, 591–608. [Google Scholar] [CrossRef]
- Qiu, T.; Wang, K.; Lei, Y.; Wu, C.; Liu, Y.; Chen, X.; Guo, P. Investigation on effects of back pressure on submerged jet flow from short cylindrical orifice filled with diesel fuel. Energy 2018, 162, 964–976. [Google Scholar] [CrossRef]
- Wu, X.-Y.; Zhang, Y.-Q.; Tan, Y.-W.; Li, G.-S.; Peng, K.-W.; Zhang, B. Flow-visualization and numerical investigation on the optimum design of cavitating jet nozzle. Pet. Sci. 2022, 19, 2284–2296. [Google Scholar] [CrossRef]
- Dular, M.; Coutier-Delgosha, O. Numerical modelling of cavitation erosion. Int. J. Numer. Methods Fluids 2009, 61, 1388–1410. [Google Scholar] [CrossRef]
- Luo, X.; Qian, Z.; Wang, X.; Yu, A. Mode vortex and turbulence in ventilated cavitation over hydrofoils. Int. J. Multiph. Flow 2022, 157, 104252. [Google Scholar] [CrossRef]
- Li, X.-s.; Wu, Q.-t.; Miao, L.-y.; Yak, Y.-y.; Liu, C.-b. Scale-resolving simulations and investigations of the flow in a hydraulic retarder considering cavitation. J. Zhejiang Univ.-Sci. A 2020, 21, 817–833. [Google Scholar] [CrossRef]
- Liu, C.; Yan, Q.; Wood, H.G. Numerical investigation of passive cavitation control using a slot on a three-dimensional hydrofoil. Int. J. Numer. Methods Heat Fluid Flow 2020, 30, 3585–3605. [Google Scholar] [CrossRef]
- Marcon, A.; Melkote, S.N.; Yoda, M. Effect of nozzle size scaling in co-flow water cavitation jet peening. J. Manuf. Process. 2018, 31, 372–381. [Google Scholar] [CrossRef]
- Straka, W.A.; Meyer, R.S.; Fontaine, A.A.; Welz, J.P. Cavitation inception in quiescent and co-flow nozzle jets. J. Hydrodyn. Ser. B 2010, 22, 813–819. [Google Scholar] [CrossRef]
- Vickers, G.; Harrison, P.; Houlson, R. Extending the range of cavitation cleaning jets. In Proceedings of the Fifth International Symposium on Jet Cutting Technology, Hannover, Germany, 2–4 June 1980; pp. 403–412. [Google Scholar]
- Vijay, M.; Zou, C.; Hu, S.; Remisz, J.; Tavoularis, S. A study of the practicality of cavitating water jets. Jet Cut. Technol. 1992, 13, 75–99. [Google Scholar]
- Vijey, M.; Brierley, W. Cutting rocks and other materials by cavitating and non-cavitating jets. In Proceedings of the 4th International Symposium on Jet Cutting Technology, Canterbury, UK, 12–14 April 1978; pp. 51–66. [Google Scholar]
- Guo, Q.; Huang, X.; Qiu, B. Numerical investigation of the blade tip leakage vortex cavitation in a waterjet pump. Ocean Eng. 2019, 187, 106170. [Google Scholar] [CrossRef]
- Peng, K.; Tian, S.; Li, G.; Huang, Z.; Zhang, Z. Cavitation in water jet under high ambient pressure conditions. Exp. Therm. Fluid Sci. 2017, 89, 9–18. [Google Scholar] [CrossRef]
- Zhu, R.; Zhu, H.; Zhang, X. Numerical investigation about the unsteady behavior of a free submerged cavitation jet using the SBES approach. Ocean Eng. 2023, 281, 115010. [Google Scholar] [CrossRef]
- Yang, Y.; Shi, W.; Tan, L.; Li, W.; Chen, S.; Pan, B. Numerical research of the submerged high-pressure cavitation water jet based on the RANS-LES hybrid model. Shock Vib. 2021, 2021, 6616718. [Google Scholar] [CrossRef]
- Kawamura, T.; Sakoda, M. Comparison of bubble and sheet cavitation models for simulation of cavitating flow over a hydrofoil. In Proceedings of the Fifth International Symposium on Cavitation (Cav2003), Osaka, Japan, 1–4 November 2003. [Google Scholar]
- Kozubková, M.; Rautová, J.; Bojko, M. Mathematical model of cavitation and modelling of fluid flow in cone. Procedia Eng. 2012, 39, 9–18. [Google Scholar] [CrossRef]
- Som, S.; Aggarwal, S.K.; El-Hannouny, E.; Longman, D. Investigation of nozzle flow and cavitation characteristics in a diesel injector. J. Eng. Gas Turbines Power 2010, 132, 042802. [Google Scholar] [CrossRef]
- Yang, Y.; Li, W.; Shi, W.; Zhang, W.; A. El-Emam, M. Numerical investigation of a high-pressure submerged jet using a cavitation model considering effects of shear stress. Processes 2019, 7, 541. [Google Scholar] [CrossRef]
- Mednikov, A.; Zilova, O.; Tkhabisimov, A.; Dasaev, M.; Grigoriev, S. Parametric Studies of Effect of Cavitation Jet Modes on Wear Rate of Surface of Structural Materials. Metals 2022, 13, 48. [Google Scholar] [CrossRef]
- Lin, Y.; Guo, J.; Li, H.; Wang, Z.; Chen, Y.; Huang, H. Improvement of hydrodynamic performance of the disk-shaped autonomous underwater helicopter by local shape modification. Ocean Eng. 2022, 260, 112056. [Google Scholar] [CrossRef]
- Dong, J.; Li, S.; Meng, R.; Zhong, X.; Pan, X. Research on Cavitation Characteristics of Two-Throat Nozzle Submerged Jet. Appl. Sci. 2022, 12, 536. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| d | 1 mm |
| L1 | 3 mm |
| L2 | 3 mm |
| δ | 0, 30° |
| β | 0, 30° |
| D | 3 mm |
| S | 20, 30, 40, 50 mm |
| ɸw | 80 mm |
| SD | 20, 30, 40, 50 |
| Al | Si | Cu | Mg | Zn | Mn | Ti | Fe |
|---|---|---|---|---|---|---|---|
| 99.6 | ≤0.25 | ≤0.05 | ≤0.03 | ≤0.05 | ≤0.03 | ≤0.03 | ≤0.35 |
| Density/kg∙m−3 | Elasticity Modulus/GPa | Tensile Strength/MPa | Offset Yield Strength/MPa | Surface Roughness/μm | Vickers Hardness HV0.2 |
|---|---|---|---|---|---|
| 2710 | 71 | 80 | 35 | 1.5 | 31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Chen, J.; Guo, J.; Zhu, H.; Lin, Y.; Ge, H. A Study of Cavitation Erosion in Artificial Submerged Water Jets. Appl. Sci. 2024, 14, 4804. https://doi.org/10.3390/app14114804
Li H, Chen J, Guo J, Zhu H, Lin Y, Ge H. A Study of Cavitation Erosion in Artificial Submerged Water Jets. Applied Sciences. 2024; 14(11):4804. https://doi.org/10.3390/app14114804
Chicago/Turabian StyleLi, Haonan, Jiawang Chen, Jin Guo, Hai Zhu, Yuan Lin, and Han Ge. 2024. "A Study of Cavitation Erosion in Artificial Submerged Water Jets" Applied Sciences 14, no. 11: 4804. https://doi.org/10.3390/app14114804
APA StyleLi, H., Chen, J., Guo, J., Zhu, H., Lin, Y., & Ge, H. (2024). A Study of Cavitation Erosion in Artificial Submerged Water Jets. Applied Sciences, 14(11), 4804. https://doi.org/10.3390/app14114804







