Decoupled MPC Power Balancing Strategy for Coupled Inductor Flying Capacitor DC–DC Converter
Abstract
1. Introduction
2. Basic Principle Analysis of Coupled Inductor FCDC
3. Decoupled MPC Power Balancing Strategy for Coupled Inductor FCDC
3.1. Decoupled Mathematical Model of Coupled Inductor FCDC
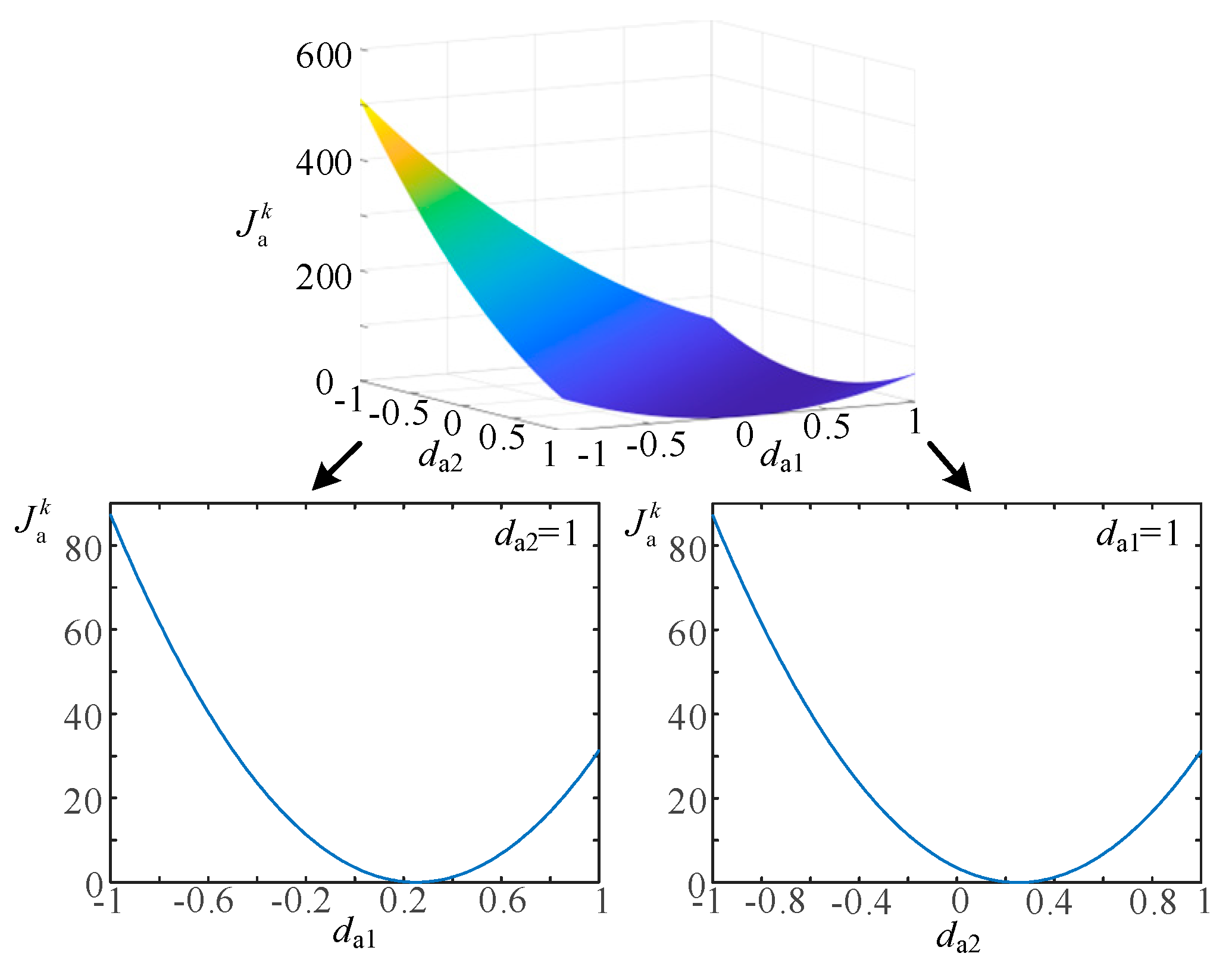
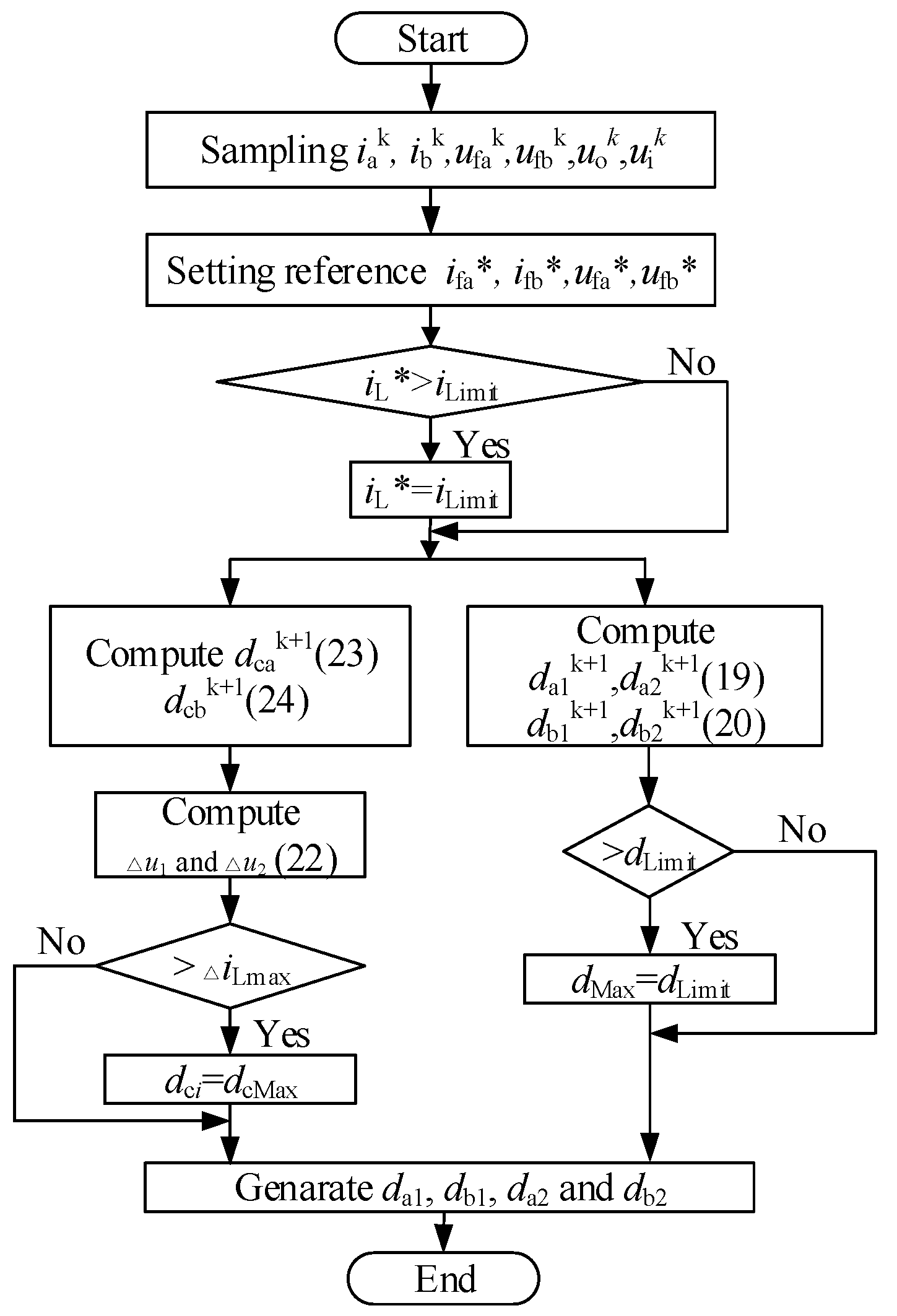
3.2. Multi-Objective MPC Strategy Design
- (1)
- Taking phase a as an example, when the converter operates under steady-state iak ≈ ia*, ufak ≈ uik/2 and uok ≈ uo*, we can have da1k ≈ da2k. Under this situation, da1k and da2k are derived by optimizing control ia, and ufa cannot be controlled by (19). The operation principle of phase b is the same as that of phase a.
- (2)
- With the aid of (19) and (20), the optimal duty ratio to track the current reference can be obtained through a single calculation, greatly reducing the computational burden.
3.3. Stability Analysis
4. Experimental Verification
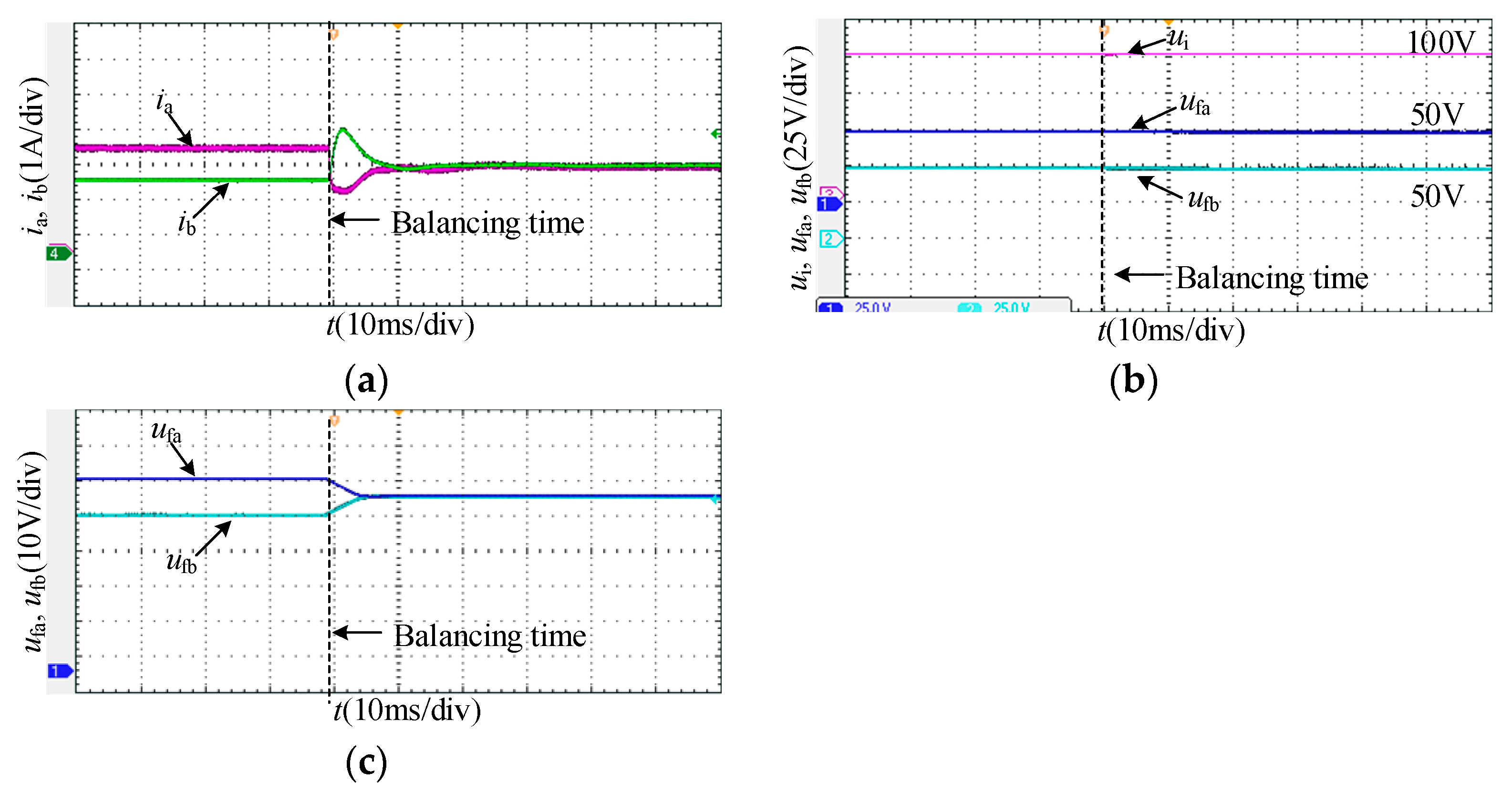
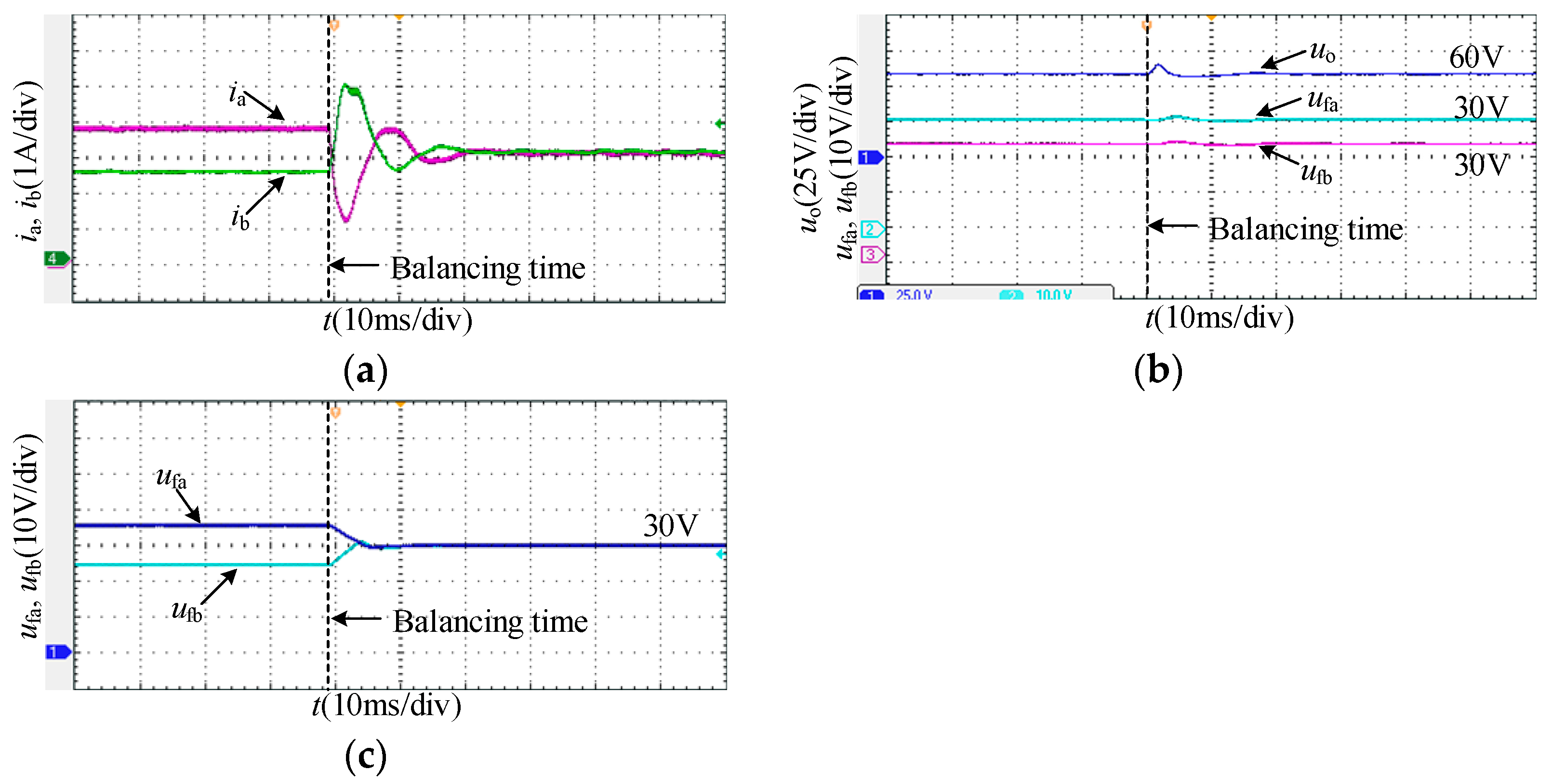
4.1. Experimental Results
4.2. Performance Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Yang, Z.; Zhan, M.; Liu, D.; Ye, C.; Cao, K.; Cheng, S. Small-Signal Synchronous Stability of a New-generation Power System with 100% Renewable Energy. IEEE Trans. Power Syst. 2022, 38, 4269–4280. [Google Scholar] [CrossRef]
- Holttinen, H.; Kiviluoma, J.; Flynn, D.; Smith, J.C.; Orths, A.; Eriksen, P.B.; Cutululis, N.; Soder, L.; Korpas, M.; Estanqueiro, A.; et al. System Impact Studies for Near 100% Renewable Energy Systems Dominated by Inverter Based Variable Generation. IEEE Trans. Power Syst. 2020, 37, 3249–3258. [Google Scholar] [CrossRef]
- Xiong, L.; Liu, X.; Liu, Y.; Zhuo, F. Modeling and Stability Issues of Voltage-source Converter-dominated Power Systems: A Review. CSEE J. Power Energy Syst. 2022, 8, 1530–1549. [Google Scholar]
- Fan, H.; Zhou, S.; Wei, Q.; Hu, X. Honeycomb-like carbon for electrochemical energy storage and conversion. Renew. Sustain. Energy Rev. 2022, 165, 112585. [Google Scholar] [CrossRef]
- Argyrou, M.C.; Christodoulides, P.; Kalogirou, S.A. Energy storage for electricity generation and related processes: Technologies appraisal and grid scale applications. Renew. Sustain. Energy Rev. 2018, 94, 804–821. [Google Scholar] [CrossRef]
- Rocabert, J.; Capo-Misut, R.; Munoz-Aguilar, R.S.; Candela, J.I.; Rodriguez, P. Control of Energy Storage System Integrating Electrochemical Batteries and Supercapacitors for Grid-Connected Applications. IEEE Trans. Ind. Appl. 2018, 55, 1853–1862. [Google Scholar] [CrossRef]
- Chen, H.; Wang, D.; Tang, S.; Yin, X.; Wang, J.; Shen, Z.J. Continuous Control Set Model Predictive Control for Three-Level Flying Capacitor Boost Converter with Constant Switching Frequency. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 5996–6007. [Google Scholar] [CrossRef]
- Ye, Z.; Lei, Y.; Liao, Z.; Pilawa-Podgurski, R.C.N. Investigation of Capacitor Voltage Balancing in Practical Implementations of Flying Capacitor Multilevel Converters. IEEE Trans. Power Electron. 2022, 37, 2921–2935. [Google Scholar] [CrossRef]
- Zhang, J.; He, Y.; Hang, L. A Novel Interleaved Parallel Cascaded Three-Level PFC with Low Inductance Volt-Second and Low Common-Mode Noise. IEEE Trans. Power Electron. 2023, 38, 17–21. [Google Scholar] [CrossRef]
- Jovanovic, D.P.; Broadmeadow, M.A.H.; Taylor, R.R.; Walker, G.R.; Ledwich, G.F. Decoupling of Current Balancing and Reference Tracking Control in Parallel Interleaved Converters. IEEE Trans. Power Electron. 2020, 35, 4286–4295. [Google Scholar] [CrossRef]
- Lu, S.; Mu, M.; Jiao, Y.; Lee, F.C.; Zhao, Z. Coupled Inductors in Interleaved Multiphase Three-Level DC–DC Converter for High-Power Applications. IEEE Trans. Power Electron. 2016, 31, 120–134. [Google Scholar] [CrossRef]
- Moradisizkoohi, H.; Elsayad, N.; Mohammed, O.A. An Integrated Interleaved Ultrahigh Step-Up DC–DC Converter Using Dual Cross-Coupled Inductors with Built-In Input Current Balancing for Electric Vehicles. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 644–657. [Google Scholar] [CrossRef]
- Mayer, R.; El Kattel, M.B.; Oliveira, S.V.G. Multiphase Interleaved Bi-directional DC/DC Converter with Coupled Inductor for Electrified-Vehicle Applications. IEEE Trans. Power Electron. 2021, 36, 2533–2547. [Google Scholar] [CrossRef]
- Naseem, N.; Cha, H. Quad-Active-Bridge Converter with Current Balancing Coupled Inductor for SST Application. IEEE Trans. Power Electron. 2021, 36, 12528–12539. [Google Scholar] [CrossRef]
- Dou, Y.; Ouyang, Z.; Anderson, M.A.E. Integrated Coupled Inductors with Functionality of Current Balancing Transformer for Two-Phase Synchronous DC–DC Converters. IEEE Trans. Power Electron. 2020, 35, 4472–4476. [Google Scholar] [CrossRef]
- Pan, T.; Wang, Y.; Qu, Z.; Tao, W. Topology optimisation and current sharing strategy of interleaved bidirectional dc/dc converter with coupling technique. IET Power Electron. 2018, 11, 2470–2480. [Google Scholar] [CrossRef]
- Capella, G.J.; Pou, J.; Ceballos, S.; Zaragoza, J.; Agelidis, V.G. Current-Balancing Technique for Interleaved Voltage Source Inverters with Magnetically Coupled Legs Connected in Parallel. IEEE Trans. Ind. Electron. 2015, 62, 1335–1344. [Google Scholar] [CrossRef]
- McGrath, B.P.; Holmes, D.G. Analytical modeling of voltage balance dynamics for a flying capacitor multilevel converter. IEEE Trans. Power Electron. 2008, 23, 543–550. [Google Scholar] [CrossRef]
- Stala, R. The switch-mode flying-capacitor dc-dc converters with improved natural balancing. IEEE Trans. Ind. Electron. 2010, 57, 1369–1382. [Google Scholar] [CrossRef]
- Chen, H.-C.; Lu, C.-Y.; Lien, W.-H. Active Capacitor Voltage Balancing Control for Three-Level Flying Capacitor Boost Converter Based on Average-Behavior Circuit Model. IEEE Trans. Ind. Appl. 2019, 55, 1628–1638. [Google Scholar] [CrossRef]
- Lu, C.-Y.; Lin, D.-H.; Chen, H.-C. Decoupled Design of Voltage Regulating and Balancing Controls for Four-Level Flying Capacitor Converter. IEEE Trans. Ind. Electron. 2021, 68, 12152–12161. [Google Scholar] [CrossRef]
- Jayan, V.; Ghias, A.; Merabet, A. Modeling and control of three level bi-directional flying capacitor DC–DC converter in DC microgrid. In Proceedings of the 45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 4113–4118. [Google Scholar]
- Thielemans, S.; Vyncke, T.J.; Melkebeek, J.A.A. Weight factor selection for model-based predictive control of a four-level flying capacitorinverter. IET Power Electron. 2012, 5, 323–333. [Google Scholar] [CrossRef]
- Davari, S.A.; Khaburi, D.A.; Kennel, R. An improved FCS-MPC algorithm for an induction motor with an imposed optimized weighting factor. IEEE Trans. Power Electron. 2012, 27, 1540–1551. [Google Scholar] [CrossRef]
- Dragi, T.; Novak, M. Weighting factor design in model predictive control of power electronic converters: An artificial neural network approach. IEEE Trans. Ind. Electron. 2019, 66, 8870–8880. [Google Scholar]
- Bi, K.; Lv, H.; Chen, L.; Li, J.; Zhu, Y.; Huang, W.; Fan, Q. A Model Predictive Controlled Bidirectional Four Quadrant Flying Capacitor DC/DC Converter Applied in Energy Storage System. IEEE Trans. Power Electron. 2022, 37, 7705–7717. [Google Scholar] [CrossRef]
- Ruan, X.; Li, B.; Chen, Q.; Tan, S.C.; Tse, C.K. Fundamental considerations of three-level DC–DC converters: Topologies analyses and control. IEEE Trans. Circuits Syst. I Regul. Pap. 2008, 55, 3733–3743. [Google Scholar] [CrossRef]
- Meynard, T.A.; Foch, H.; Thomas, P.; Courault, J.; Jakob, R.; Nahrstaedt, M. Multicell converters: Basic concepts and industry applications. IEEE Trans. Ind. Electron. 2002, 49, 955–964. [Google Scholar] [CrossRef]

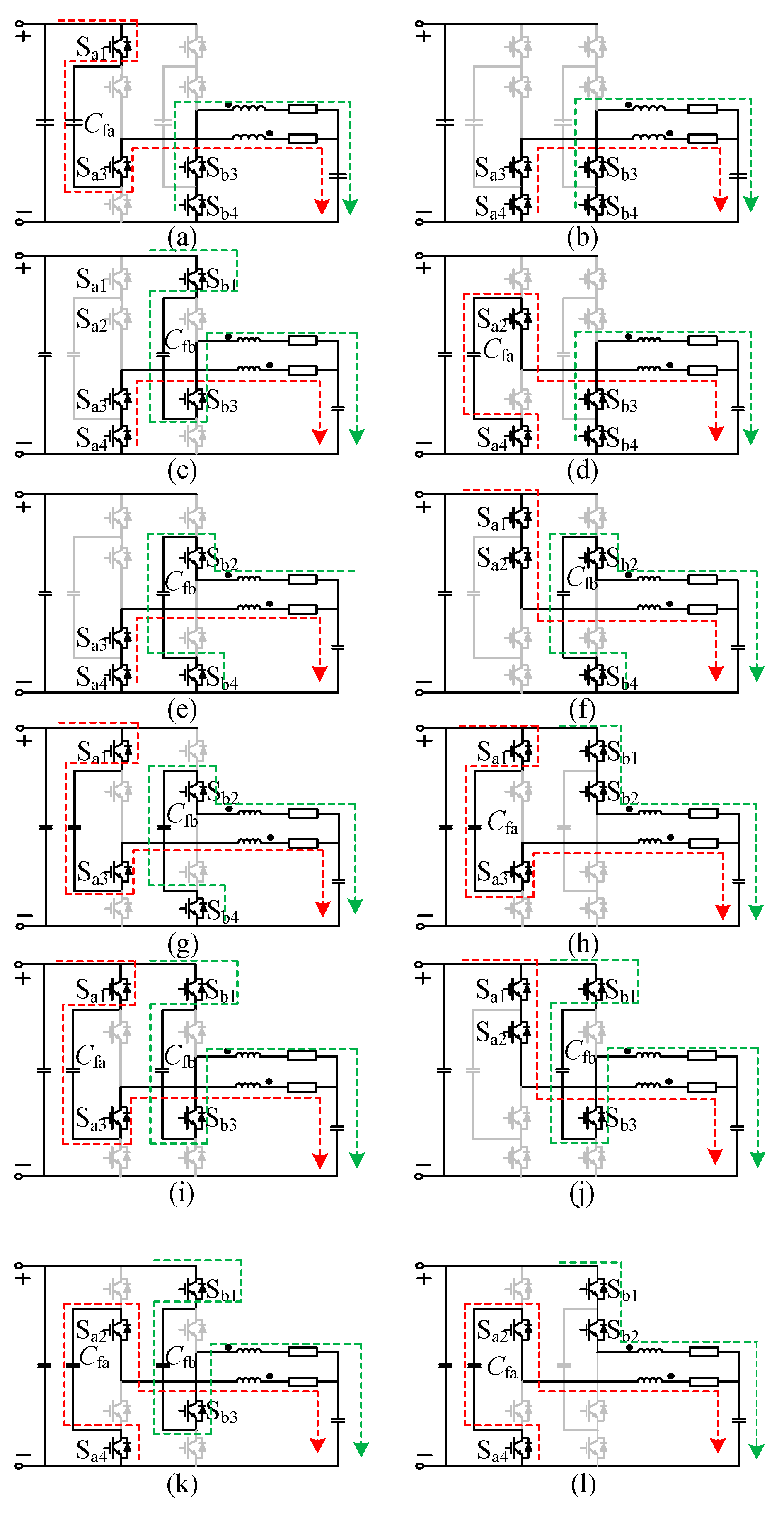





| Duty Ratio Range | Operating State |
|---|---|
| −1 < D < −0.5 | a, b, c, d, e |
| D = −0.5 | a, c, d, e |
| −0.5 < D < 0 | a, c, d, e, g, i, k, m |
| D = 0 | g, i, k, m |
| 0 < D < 0.5 | f, g, h, i, j, k, l, m |
| D = 0.5 | f, h, j, l |
| 0.5 < D < 1 | f, h, j, l, n |
| Item | Value | Unit |
|---|---|---|
| Maximum input voltage | 100 | V |
| Maximum operating power | 300 | W |
| Switching frequency | 10 | kHz |
| Self-inductance of phase a and b | 1 | mH |
| Mutual inductance | −0.33 | mH |
| Flying capacitor | 220 | μF |
| Output voltage under Buck mode | 50 | V |
| Load | 12 | Ω |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, X.; Bi, K.; Lan, G.; Li, W.; Cui, J. Decoupled MPC Power Balancing Strategy for Coupled Inductor Flying Capacitor DC–DC Converter. Appl. Sci. 2024, 14, 4813. https://doi.org/10.3390/app14114813
Wei X, Bi K, Lan G, Li W, Cui J. Decoupled MPC Power Balancing Strategy for Coupled Inductor Flying Capacitor DC–DC Converter. Applied Sciences. 2024; 14(11):4813. https://doi.org/10.3390/app14114813
Chicago/Turabian StyleWei, Xin, Kaitao Bi, Genlong Lan, Wei Li, and Jin Cui. 2024. "Decoupled MPC Power Balancing Strategy for Coupled Inductor Flying Capacitor DC–DC Converter" Applied Sciences 14, no. 11: 4813. https://doi.org/10.3390/app14114813
APA StyleWei, X., Bi, K., Lan, G., Li, W., & Cui, J. (2024). Decoupled MPC Power Balancing Strategy for Coupled Inductor Flying Capacitor DC–DC Converter. Applied Sciences, 14(11), 4813. https://doi.org/10.3390/app14114813






