Behavior of Circular Hollow Steel-Reinforced Concrete Columns under Axial Compression
Abstract
:1. Introduction
2. Experimental Procedures and Results
2.1. Experimental Design
2.2. Material Properties
2.3. Specimen Preparation
2.4. Test Setup and Measurements
2.5. Failure Modes
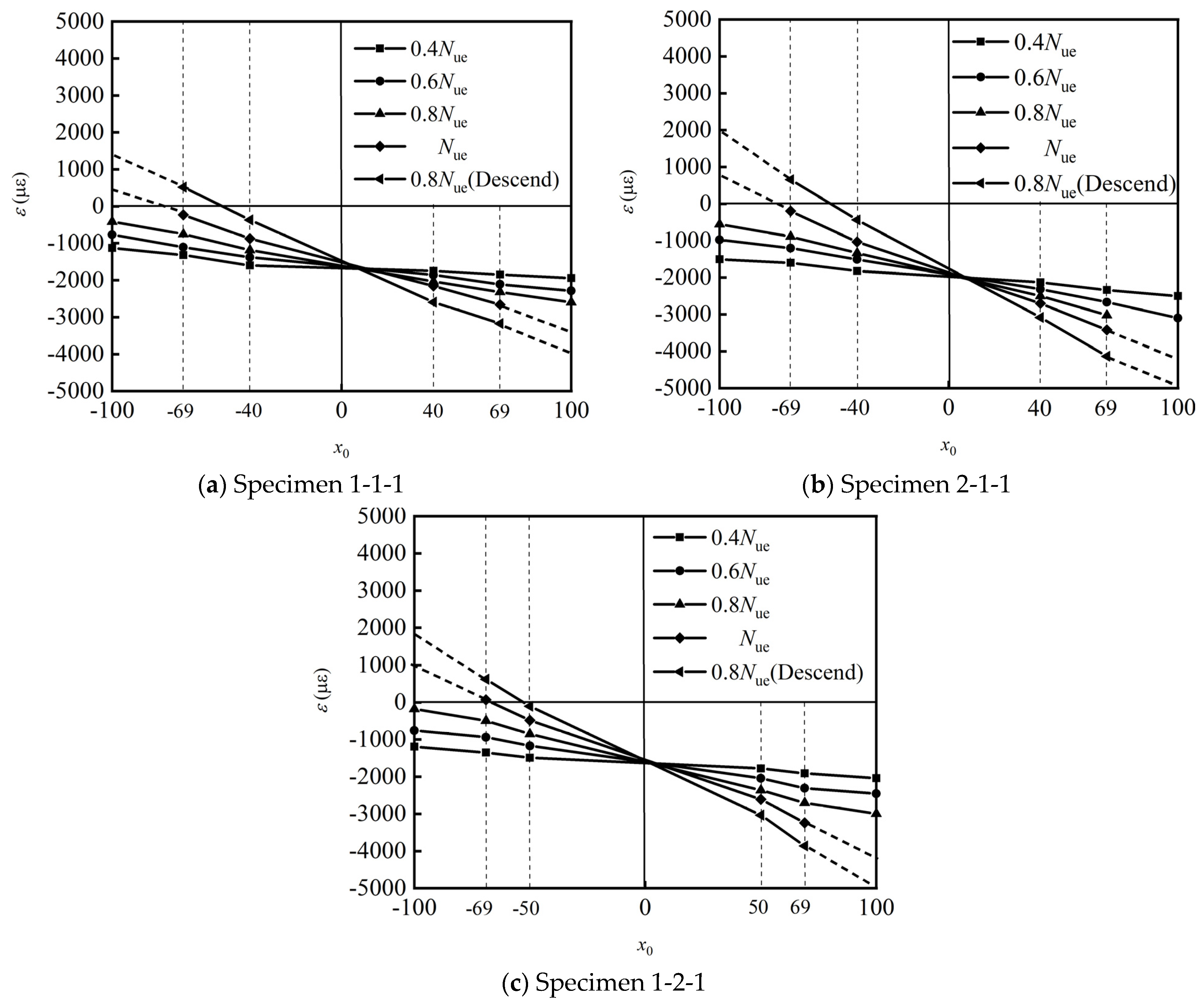
2.6. Strain Analysis
2.7. Ultimate Compressive Strength
2.8. Ductility Index
3. Finite Element Modeling
3.1. Material Models
3.1.1. Steel
3.1.2. Concrete
3.2. Element Type, Meshing, and Boundary Conditions
3.3. Verification of Finite Element Model
4. Analytical Behavior
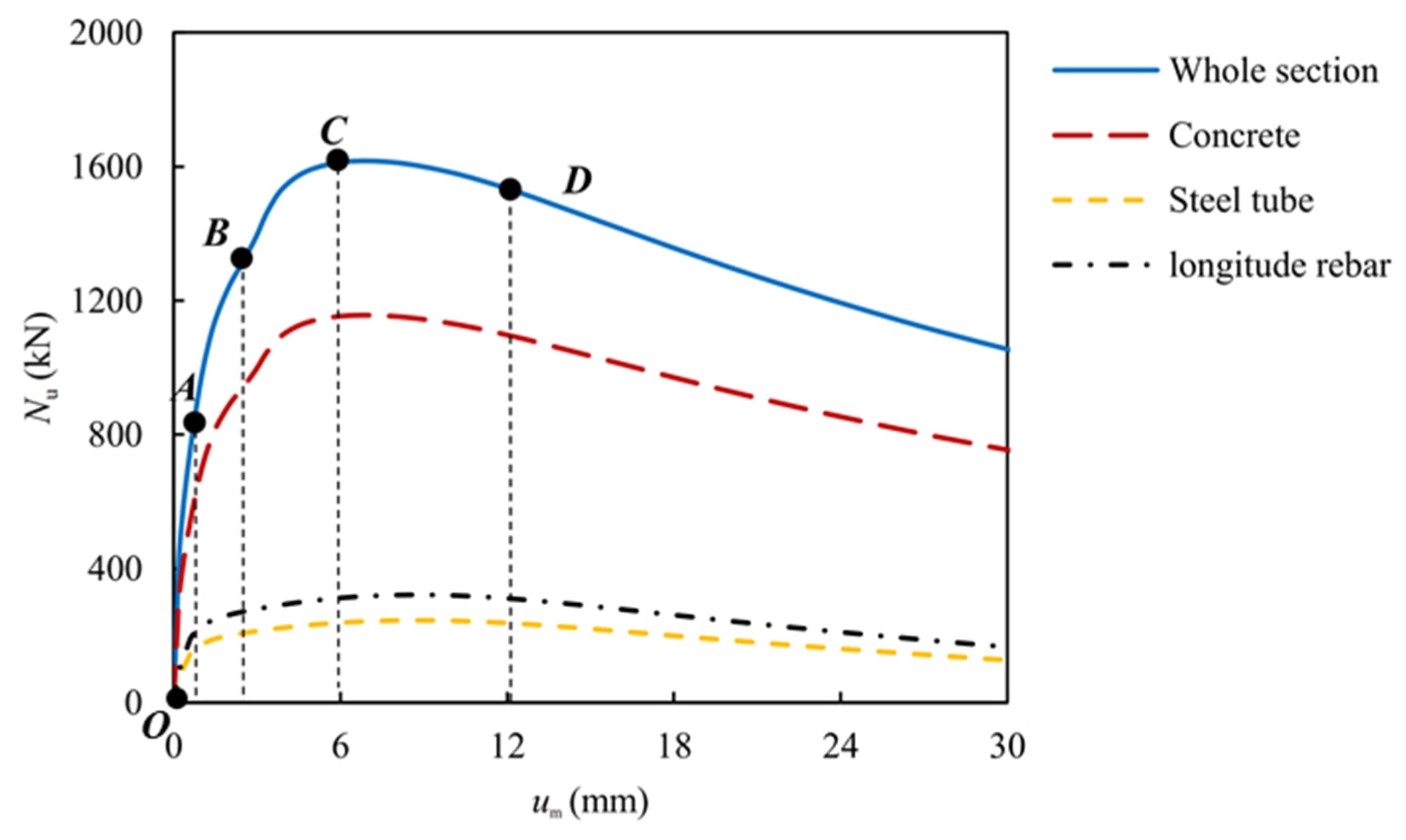
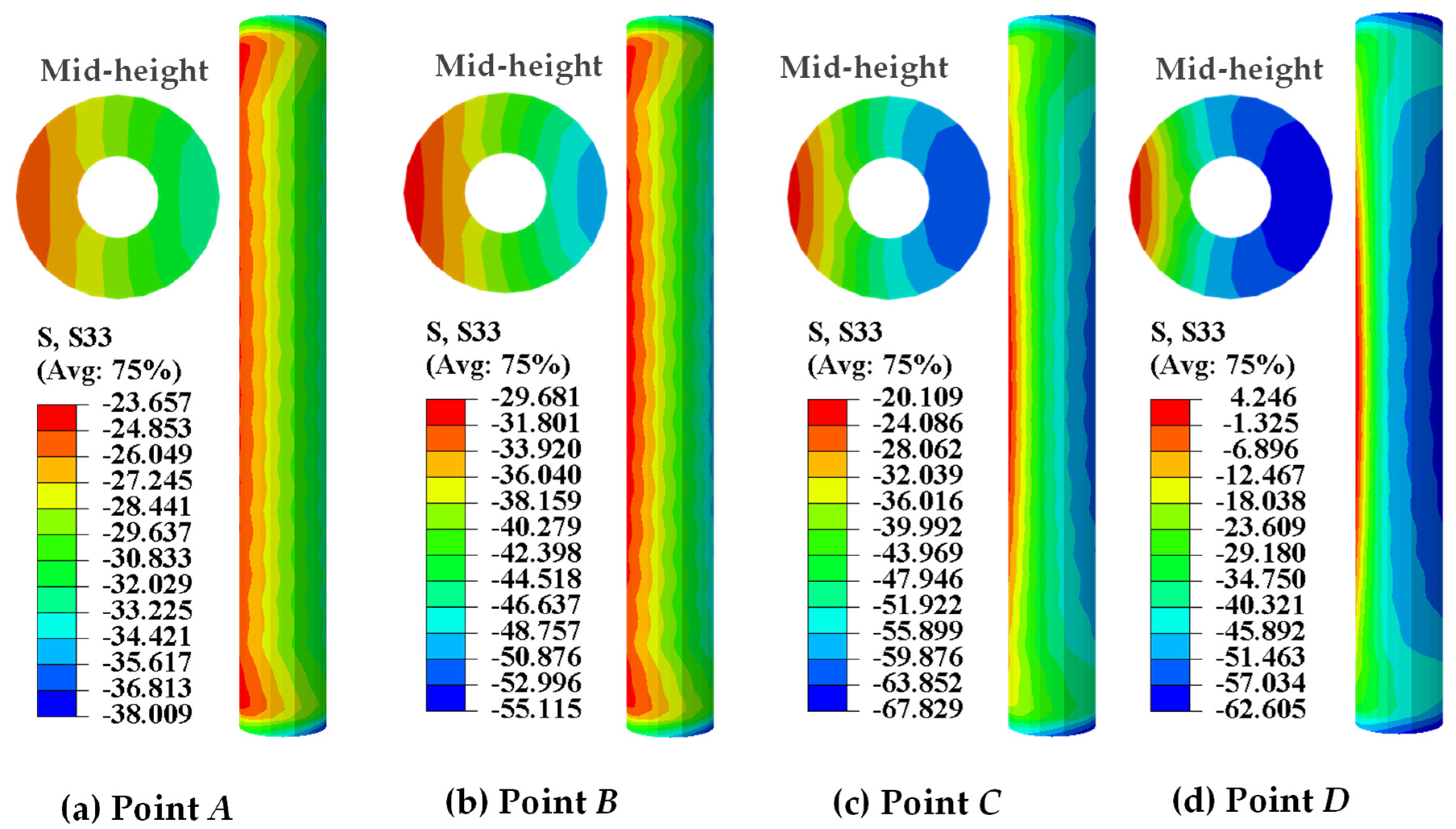
4.1. Complete Mechanism of Circular HSRC Columns
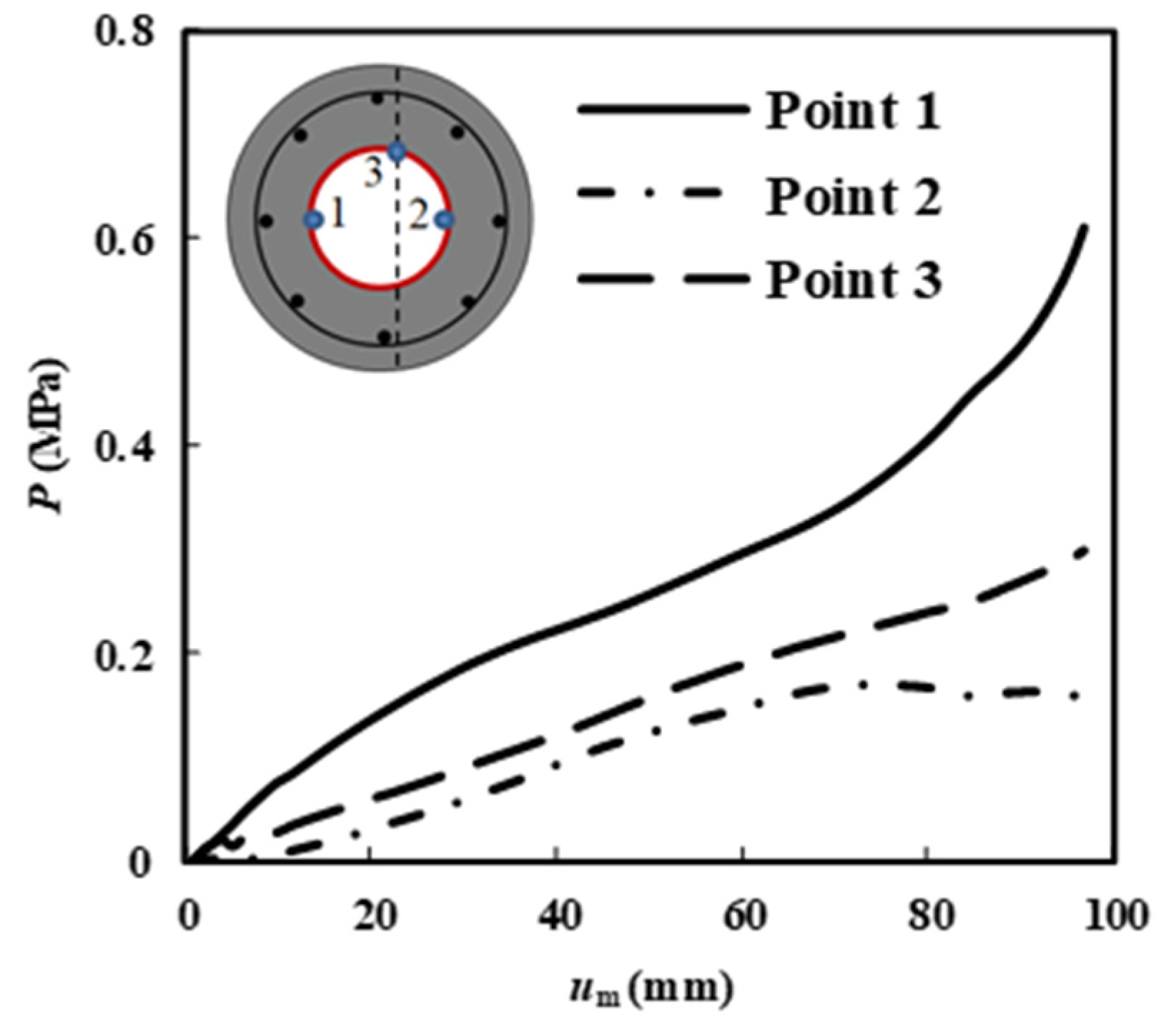
4.2. Interactions between Steel and Concrete
5. Parametric Analysis
5.1. Diameter of Steel Tube
5.2. Thickness of the Steel Tube
5.3. Slenderness Ratio
5.4. Strength of Concrete
5.5. Strength of Steel Tube
5.6. Strength of Longitudinal Rebar
5.7. Strength of Stirrup
5.8. Spacing of Stirrup
6. Calculations of Ultimate Strength
6.1. Proposed Design Procedures
6.2. Evaluation of Proposed Design Procedures
7. Conclusions
- Cracks appeared on the left side of the concrete surface when the load decreased to approximately 0.9Nue. At a load of 0.5Nue to 0.7Nue, the outer surface of the concrete on the right side was crushed, causing the inner steel tube to buckle inward. The strain on the components exceeded their yield strain. Based on the values of SI and DI, the circular HSRC columns exhibited good ductility and stiffness, with a bearing capacity higher than the sum of the compressive strengths of the components.
- A finite element model considering material nonlinearity and the interaction between the concrete and the steel tube was established for the circular HSRC column under axial compression. The model-calculated results showed excellent agreement with the measured data. The parameters that significantly influenced the column’s bearing capacity under axial compression were the concrete strength, slenderness ratio, steel tube diameter, yield strength of the longitudinal rebar, and yield strength of the steel tube. The parameters that had a significant impact on the column’s stiffness were the slenderness ratio and concrete strength.
- Three superimposition models were evaluated for calculating the ultimate strength of circular HSRC columns under axial compression. The evaluated methods were based on codes T/CECS663–2020, GB50010-2019, AIJ, Eurocode 4.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Method 1
| L (mm) | 3200 | 1800 | 1600 | 1500 | 1200 |
|---|---|---|---|---|---|
| φ | 0.875 | 0.973 | 0.987 | 0.993 | 1.000 |
Appendix A.2. Method 2
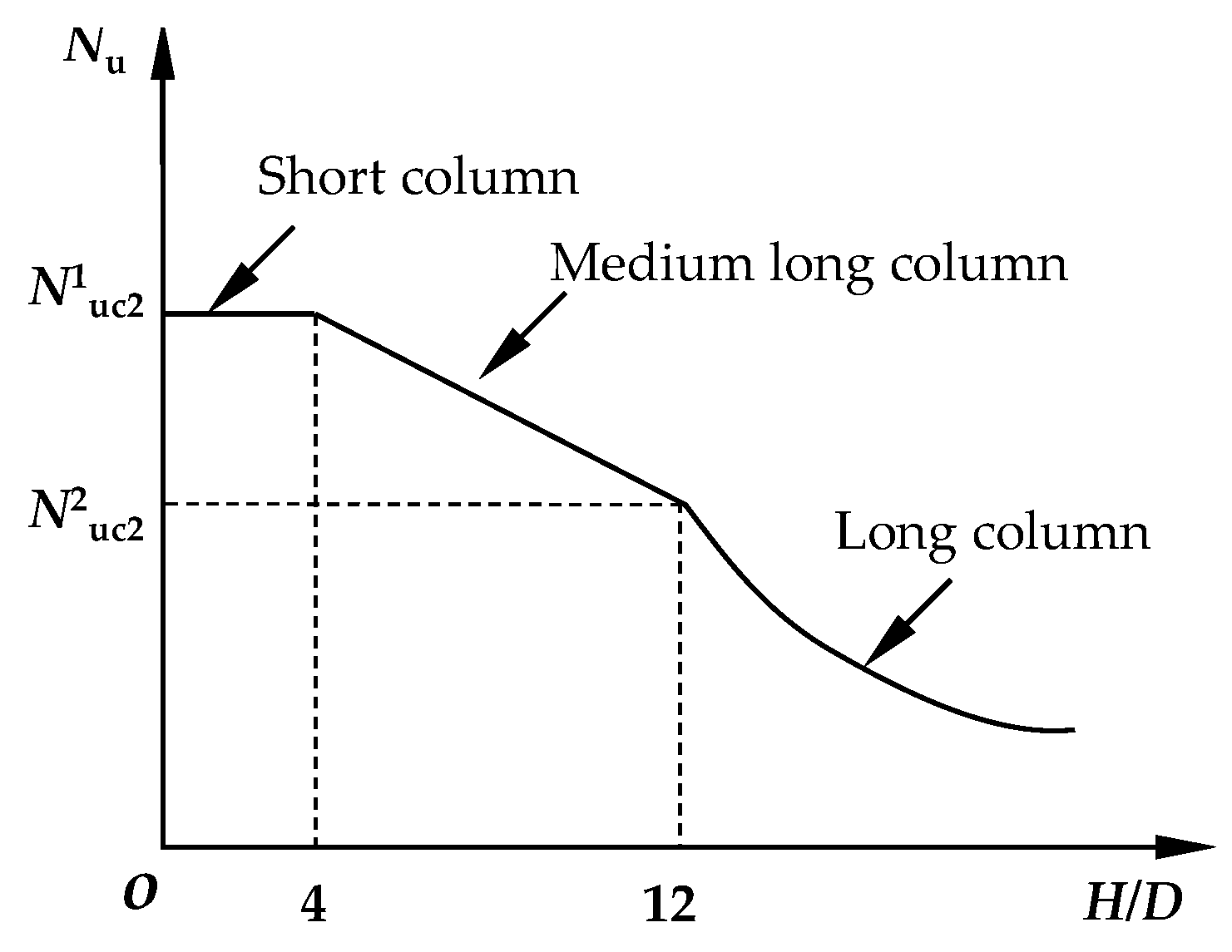
Appendix A.2.1. Short Columns (H/D ≤ 4)
Appendix A.2.2. Medium–Long Columns (4 < H/D ≤ 12)
Appendix A.2.3. Long Columns (H/D > 12)
Appendix A.3. Method 3
Appendix B
Appendix B.1. Mechanical Parameters Adopted for the Damage Plasticity Model for Concrete
| Dilation Angle (°) | Eccentricity | fb0/fc0 | k | Viscosity Parameter |
|---|---|---|---|---|
| 30° | 0.1 | 1.16 | 0.667 | 0.015 |
| Yield Stress (N/(mm2)) | Inelastic Strain |
|---|---|
| 13.57795546 | 0 |
| 13.924074 | 0.00013829 |
| 17.402848 | 0.000220006 |
| 20.31775 | 0.000319012 |
| 22.679232 | 0.000434996 |
| 24.497746 | 0.000567646 |
| 25.783744 | 0.000716649 |
| 26.547678 | 0.000881693 |
| 26.8 | 0.001062463 |
| 26.51798268 | 0.00125967 |
| 25.79416175 | 0.00147047 |
| 24.79210696 | 0.001689825 |
| 23.63948447 | 0.001913801 |
| 22.42726595 | 0.002139594 |
| Yield Stress (N/(mm2)) | Fracture Energy (N/(mm0.5)) |
|---|---|
| 3.0141926622 | 1 |
| Maximum Number of Increments | 10,000 | ||
|---|---|---|---|
| Increment size | Initial | Minimum | Maximum |
| 0.001 | 1 × 10−6 | 0.01 | |
References
- Wang, R.; Han, L.H.; Lam, D.; Sheehan, T. Behavior of octagonal steel-reinforced concrete box columns under compressive load. Mag. Concr. Res. 2018, 70, 38–855. [Google Scholar] [CrossRef]
- An, Y.F.; Han, L.H.; Zhao, X.L. Experimental behavior of box concrete-encased CFST eccentrically loaded column. Mag. Concr. Res. 2013, 65, 1219–1235. [Google Scholar] [CrossRef]
- Won, D.H.; Han, T.H.; Kim, S.; Jang, I.S.; Kang, Y.J. Optimum confining effect in steel composite hollow RC column with inner tube under compressive load. Mag. Concr. Res. 2014, 66, 433–446. [Google Scholar] [CrossRef]
- Han, T.H.; Stallings, J.M.; Cho, S.K.; Kang, Y.J. Behavior of a hollow RC column with an internal tube. Mag. Concr. Res. 2010, 62, 25–38. [Google Scholar] [CrossRef]
- Han, T.H.; Yoon, K.Y.; Kang, Y.J. Compressive strength of circular hollow reinforced concrete confined by an internal steel tube. Constr. Build. Mater. 2010, 24, 1690–1699. [Google Scholar] [CrossRef]
- Alajarmeh, O.; Manalo, A.; Benmokrane, B.; Ferdous, W.; Mohammed, A.; Abousnina, R.; Elchalakani, M.; Edoo, A. Behavior of circular concrete columns reinforced with hollow composite sections and GFRP bars. Mar. Struct. 2020, 72, 102785. [Google Scholar] [CrossRef]
- Ren, Q.X.; Ding, J.N.; Wang, Q.H.; Lou, H.Q. Behavior of slender square hollow steel-reinforced concrete columns under eccentric compression. J. Build. Eng. 2021, 43, 103133. [Google Scholar] [CrossRef]
- AS 5100.6-2004: 2004; Bridge Design, Part 6: Steel and Composite Construction. The Council of Standards: Sydney, NSW, Australia, 2004.
- ANSI/AISC 360-05: 2005; Specification for Structural Steel Buildings. The AISC Committee on Specifications: Chicago, IL, USA, 2005.
- DBJ/T 13-51-2010: 2010; Technical Specification for Concrete-Filled Steel Tubular Structures. Provincial Department of Housing and Urban Rural Development: Fuzhou, China, 2010. (In Chinese)
- Mat, S.C.; Mitani, I.; Kawano, A. AIJ Design method for concrete filled steel tubular structures. In Proceedings of the International Conference on Composite Construction Conventional and Innovative, Innsbruck, Austria, 14–18 July 1997. [Google Scholar]
- EN1994-1-1: 2004; Design of Composite Steel and Concrete Structures—Part 1–1: General Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004.
- Hadi, M.; Goaiz, H.A.; Yu, T. Experimental investigation of CFRP confined hollow core Reactive Powder Concrete columns. Constr. Build. Mater. 2018, 74, 343–355. [Google Scholar] [CrossRef]
- Bai, Y.; Nie, J.G.; Cai, C.S. New connection system for confined concrete columns and beams. I I: Theoretical Modeling. J. Struct. Eng. ASCE 2008, 134, 1800–1809. [Google Scholar] [CrossRef]
- Li, Y.J.; Han, L.H.; Xu, W.; Tao, Z. Circle concrete-encased concrete-filled steel tube (CFST) stub columns subjected to axial compression. Mag. Concr. Res. 2016, 68, 995–1010. [Google Scholar] [CrossRef]
- Hibbitt, K.; Sorenson, I. ABAQUS, Version 6.14: Theory Manual, Users’ Manual, Verification Manual and Example Problems Manual; Dassault Systèmes: Providence, RI, USA, 2014.
- Han, L.H. Concrete Filled Steel Tubular Structures—Theory and Practice, 3rd ed.; Science Press: Beijing, China, 2016. [Google Scholar]
- Guo, Z.H.; Shi, X.D. Principle and Analysis of Reinforced Concrete, 3rd ed.; Tsinghua University Press: Beijing, China, 2013. [Google Scholar]
- ACI318-11: 2011; Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute: Detroit, MI, USA, 2011.
- Hillerborg, A.; Modéer, M.; Petersson, P.E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–782. [Google Scholar] [CrossRef]
- Xiao, L.; Sritharan, S. Effects of confinement in square hollow concrete column sections. Eng. Struct. 2019, 19, 526–535. [Google Scholar] [CrossRef]
- T/CECS 188-2019: 2020; Technical Specification for Steel Tube-Reinforced Concrete Column Structures. Tsinghua University and China Association for Standardization of Engineering Construction: Beijing, China, 2020. (In Chinese)
- GB50010-2010: 2015; Code for Design of Concrete Structures. Ministry of Housing and Urban-Rural Development of the PRC and General Adminstration of Quality Supervision Inspection and Quarantine: Beijing, China, 2015. (In Chinese)
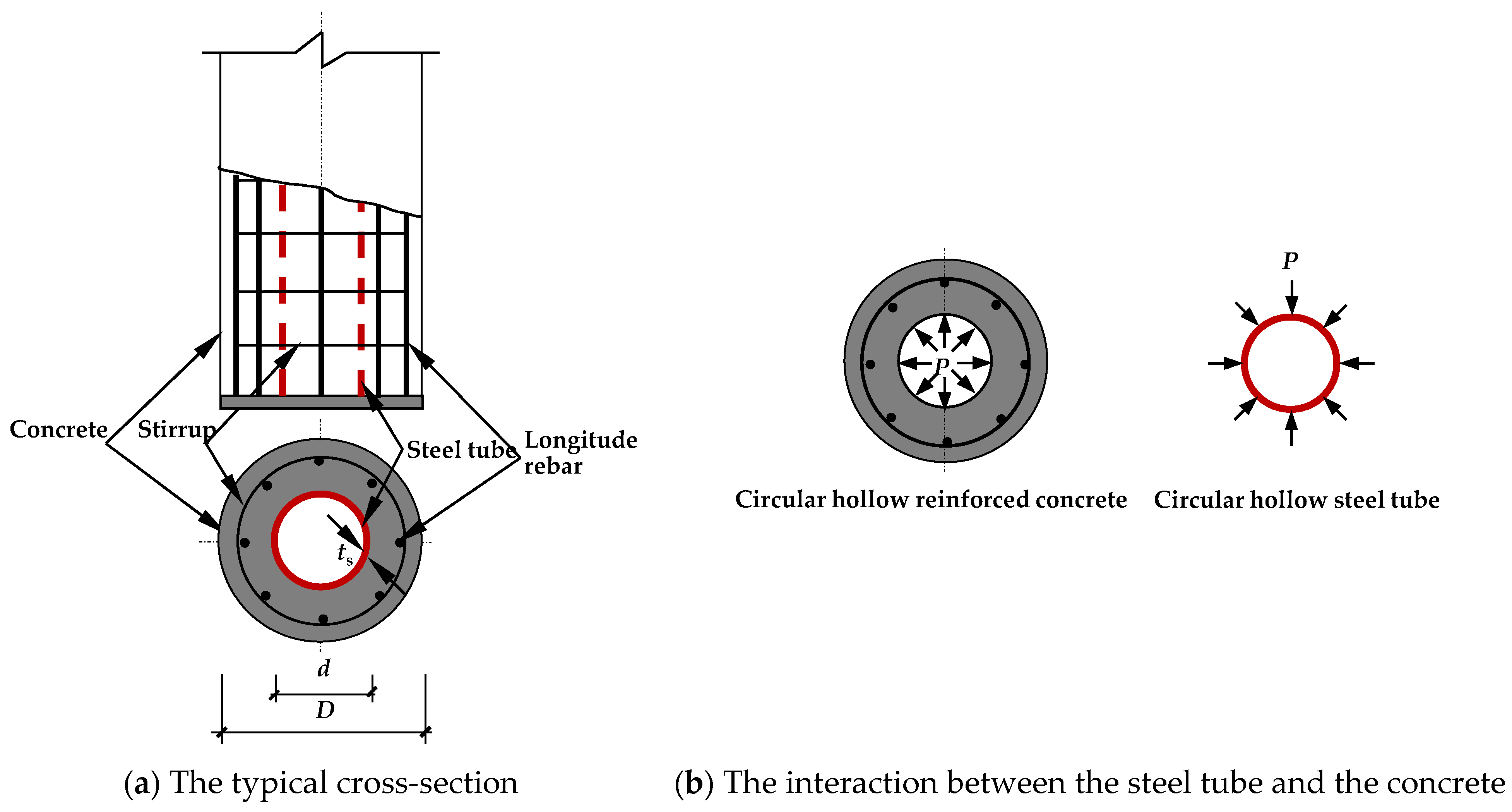
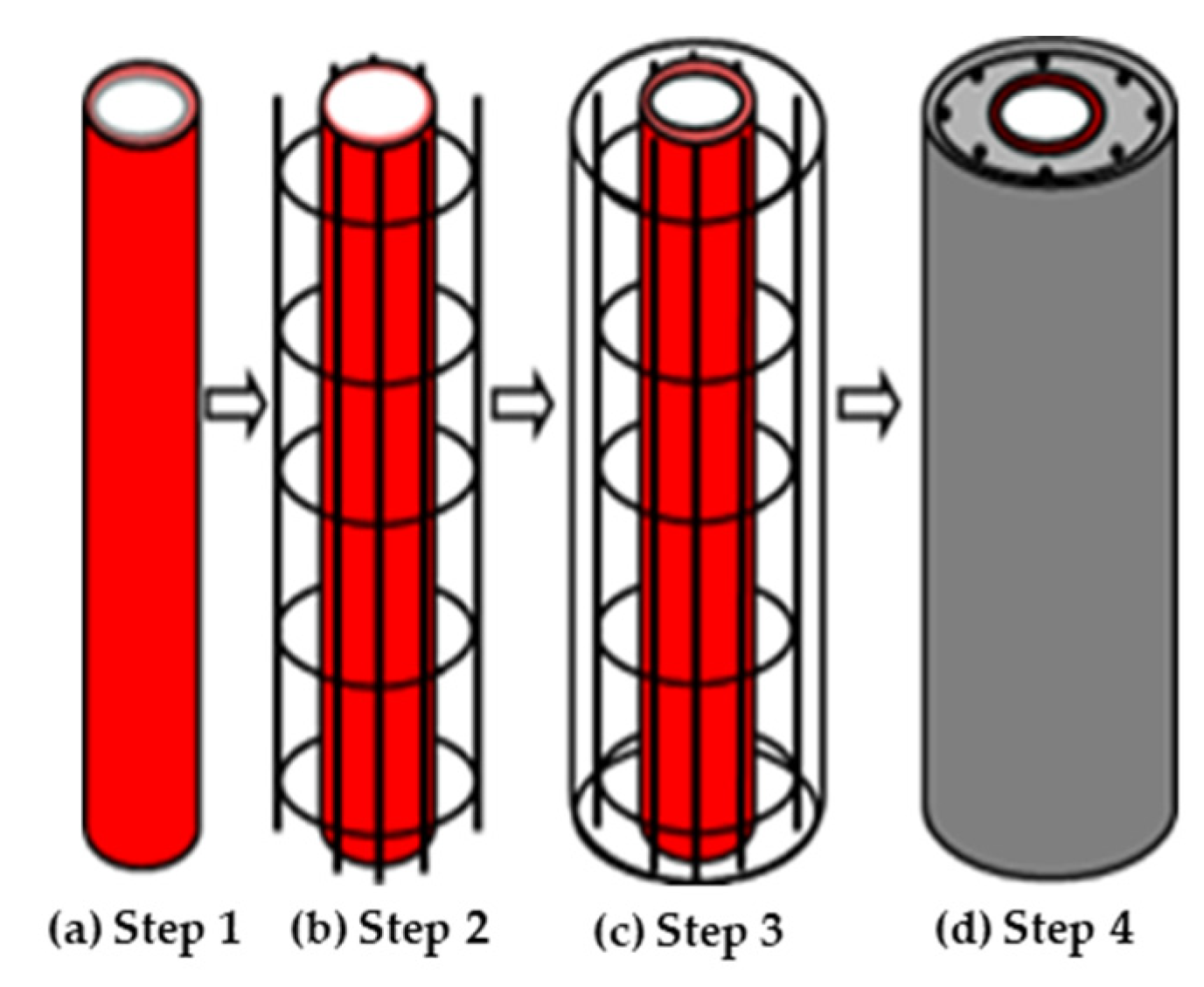
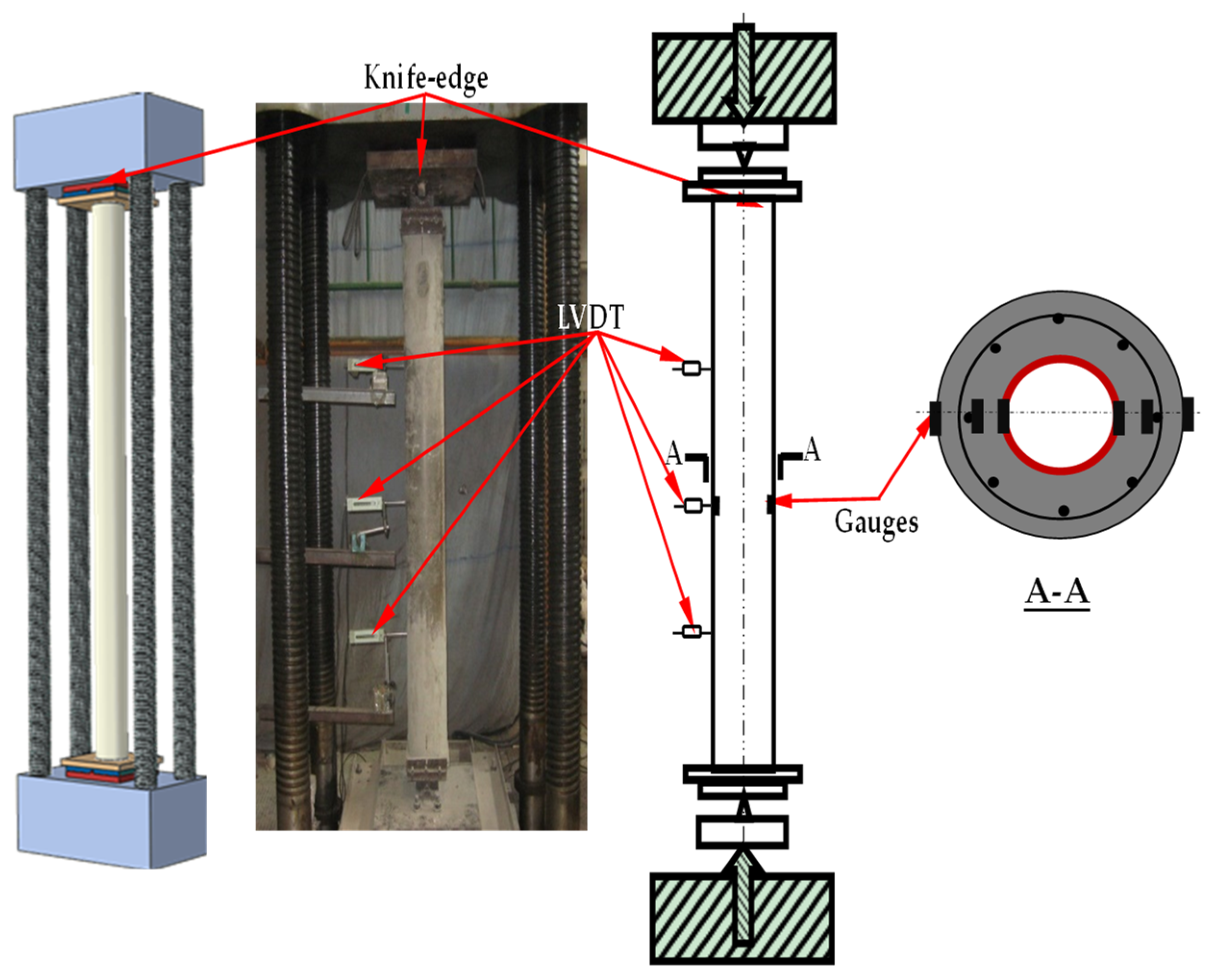
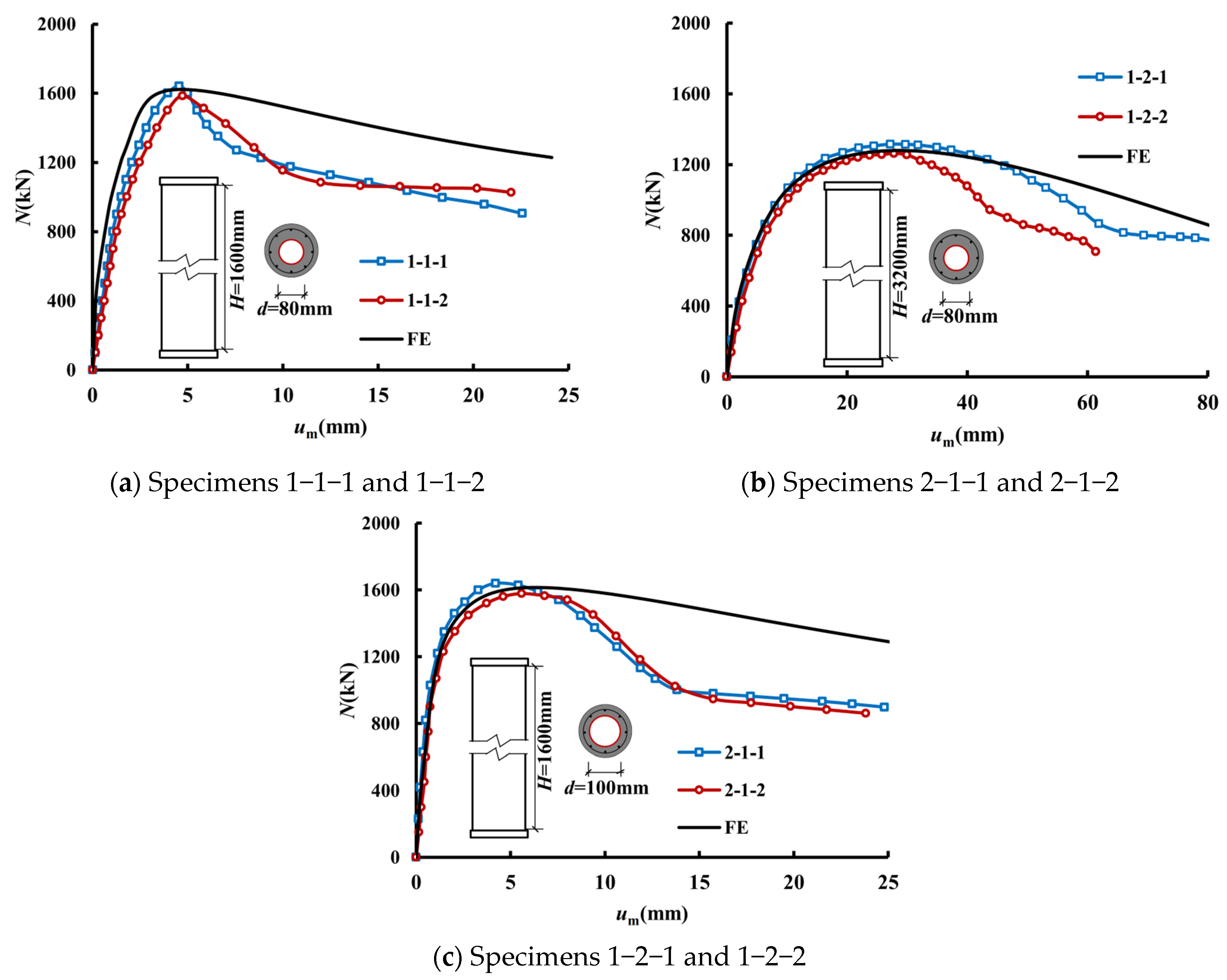
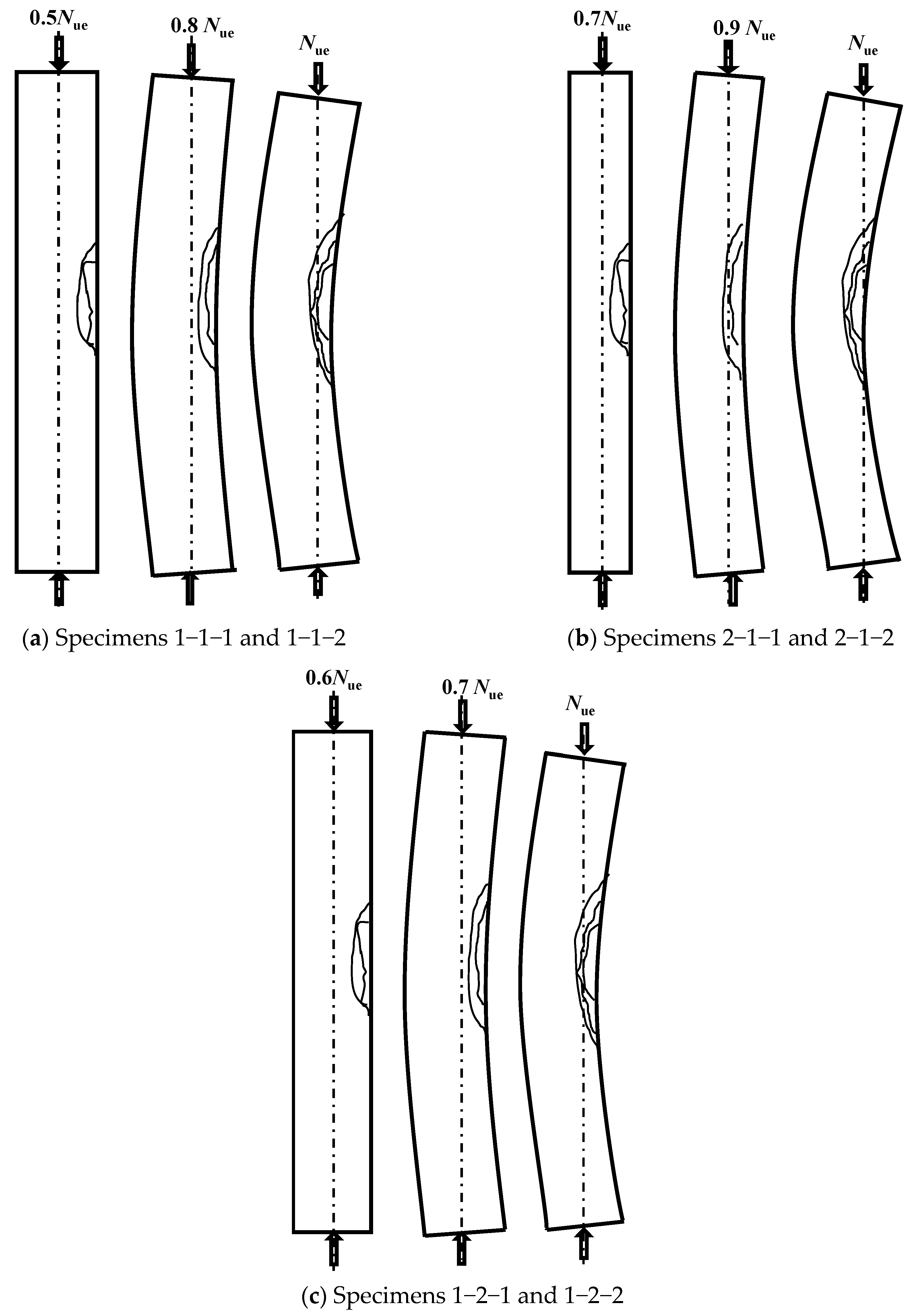

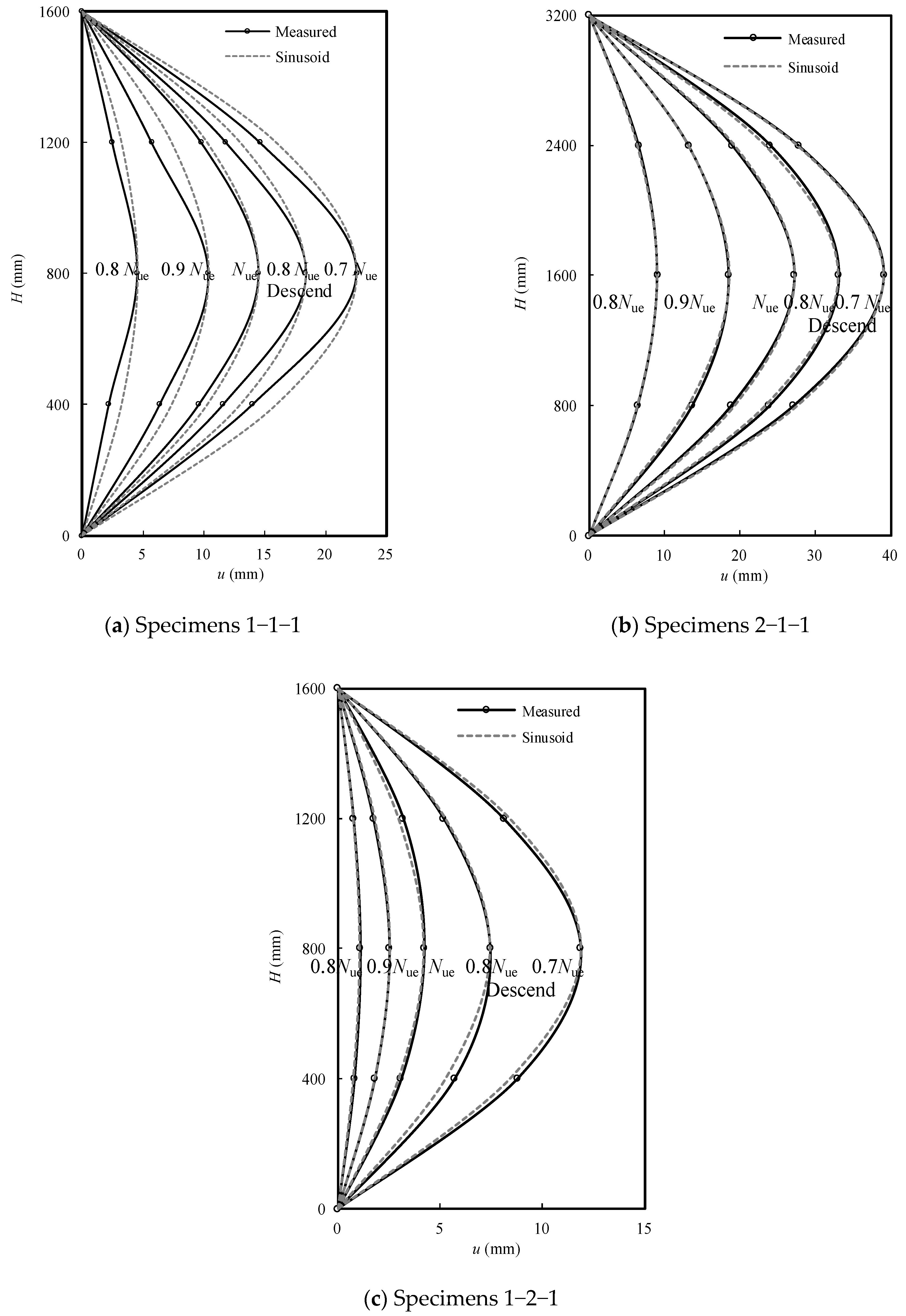
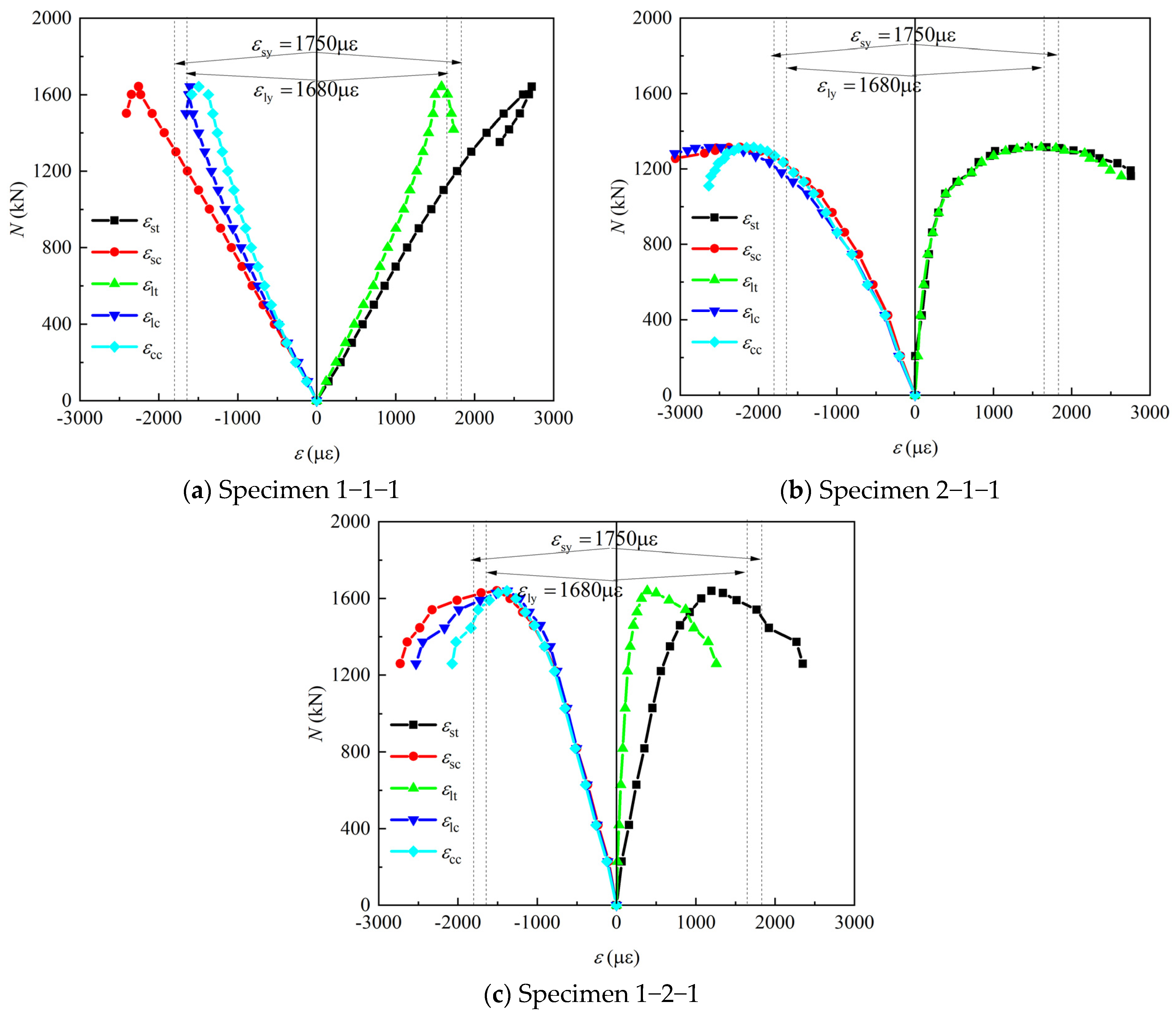



| Label | Section D × L (mm) | Steel Tube d × t (mm) | SI | DI | Nue(kN) |
|---|---|---|---|---|---|
| 1−1−1 | 200 × 1600 | 80 × 2.78 | 1.234 | 1.656 | 1642 |
| 1−1−2 | 200 × 1600 | 80 × 2.78 | 1.278 | 1.363 | 1585 |
| 2−1−1 | 200 × 3200 | 80 × 2.78 | 1.155 | 1.852 | 1315 |
| 2−1−2 | 200 × 3200 | 80 × 2.78 | 1.109 | 1.619 | 1263 |
| 1−2−1 | 200 × 1600 | 100 × 2.78 | 1.290 | 2.198 | 1639 |
| 1−2−2 | 200 × 1600 | 100 × 2.78 | 1.258 | 1.835 | 1578 |
| Steel Type | d | ts | fy | fu | E | νs |
|---|---|---|---|---|---|---|
| Steel tube | 80.0 | 2.78 | 378 | 519 | 206 | 0.296 |
| Longitudinal bar | 12.0 | - | 384 | 503 | 204 | 0.289 |
| Stirrup | 6.40 | - | 326 | 452 | 196 | 0.293 |
| Cement | Water | Fly Ash | Sand | Coarse Aggregate | Water Reducer | fcu,test | Ec | νc |
|---|---|---|---|---|---|---|---|---|
| 300 | 156 | 100 | 730 | 1130 | 4.5 | 45.2 | 32.0 | 0.201 |
| Label. | Nue (kN) | Nuc (kN) | Nuc/Nue | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| NuFEM | Nuc1 | Nuc2 | Nuc3 | A | B | C | D | |||
| 1−1−1 | 1642 | 1622 | 1549 | 1644 | 1697 | 1.023 | 0.977 | 1.037 | 1.071 | |
| 1−1−2 | 1585 | 0.988 | 0.944 | 1.001 | 1.034 | |||||
| 2−1−1 | 1315 | 1280 | 1356 | 1278 | 1301 | 0.973 | 1.031 | 0.982 | 0.989 | |
| 2−1−2 | 1263 | 1.013 | 1.073 | 1.022 | 1.030 | |||||
| 1−2−1 | 1639 | 1614 | 1494 | 1579 | 1684 | 0.985 | 0.911 | 0.963 | 1.027 | |
| 1−2−2 | 1578 | 1.023 | 0.947 | 1.000 | 1.067 | |||||
| Mean | 1.001 | 0.981 | 0.997 | 1.036 | ||||||
| Standard deviation | 0.022 | 0.061 | 0.026 | 0.029 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Q.; Ren, Q.; Wang, Q.; Zhang, Y. Behavior of Circular Hollow Steel-Reinforced Concrete Columns under Axial Compression. Appl. Sci. 2024, 14, 4833. https://doi.org/10.3390/app14114833
Wei Q, Ren Q, Wang Q, Zhang Y. Behavior of Circular Hollow Steel-Reinforced Concrete Columns under Axial Compression. Applied Sciences. 2024; 14(11):4833. https://doi.org/10.3390/app14114833
Chicago/Turabian StyleWei, Qiuyu, Qingxin Ren, Qinghe Wang, and Yannian Zhang. 2024. "Behavior of Circular Hollow Steel-Reinforced Concrete Columns under Axial Compression" Applied Sciences 14, no. 11: 4833. https://doi.org/10.3390/app14114833
APA StyleWei, Q., Ren, Q., Wang, Q., & Zhang, Y. (2024). Behavior of Circular Hollow Steel-Reinforced Concrete Columns under Axial Compression. Applied Sciences, 14(11), 4833. https://doi.org/10.3390/app14114833







