Design of a New Supersonic Shock Wave Generator and Application in Power Generation

Featured Application

The shock wave generator developed in this article is easy to operate and reusable. It can generate high-pressure and high-speed shock waves. Therefore, it can be widely used in the design and development of various devices, such as shock-driven power generation devices, pipeline obstruction removal devices, geothermal well productivity enhancement devices, lightweight rock fracture devices for disaster relief, shock wave soil loosening and hole fertilization devices that can reduce soil carbon emissions, etc.

Abstract

Wind energy is a kind of renewable energy with great potential for development. This study mainly investigated the application of shock waves generated by high-pressure gases (wind energy) for generating energy. In this study, we designed a new supersonic shock wave generator that can be reused without disassembling and assembling bolts and developed a shock wave monitoring system. It could measure the velocity of the generated shock waves at about Mach 3–5, and the output pressure exceeded 900 kg/cm² (more than 100 times the input pressure). Then, we developed a power generation system driven by supersonic shock waves based on the characteristics of the new shock wave generator, which could generate high-pressure and high-speed blast waves and could be reused. The shock wave generator can repeatedly generate high-pressure waves to drive the Tesla turbine and then rotate the magnetic energy generator for power generation. This paper used tank pressure, output pressure, gas flow, rotation speed, voltage, and current detected by the system to conduct power generation performance analysis. When the minimum rotation speed was set to 1500 rpm and three bulbs were turned on as loads, the system could generate an average voltage of 36.64 V and an average current of 211.01 mA as output (power about 7731.41 mW).

1. Introduction

The current approach to utilizing wind energy drives power generators by rotating wind turbines. The entire mechanical–electrical facilities used to match the generated electricity to the power grid or meet the power supply specifications of existing tools are very complicated [1,2]. As for the existing wind generation facilities, giant windmills capture wind energy directly but represent only a tiny proportion of the total cost. The wind is free, but wind power generation is more expensive than thermal power generation. This is why countries tend to build larger and larger wind turbines [3,4,5]. Large wind turbines can reduce the unit cost of mechanical and electrical facilities but cause many other problems. For example, the wind energy conversion efficiency of large wind turbines is low because the difference between wind farms caused by large blade spans makes it challenging to optimize blade design; in addition, it is difficult to popularize wind energy because of the stringent conditions to locate large wind turbines.

Wind turbine blades are critical components in wind power generation; long blades lead to great twisting forces and high-power generation; thus, it is essential to develop large wind turbines with high power and long blades [5,6]. On the other hand, the longer the blades of a wind generator are, the higher it will be and the more space it will take up. According to the American Wind Energy Association, from 2000 to 2018, the average height of grid wind generators in the United States significantly increased from 58 m to 88 m, and the average blade diameter increased from 48 m to 116 m [6,7].

From the perspective of fluid energy, with current technologies, it is much easier to store high-pressure gases than high-temperature heat because its energy increases very quickly, unlike batteries that take a long time to recharge. Moreover, high-pressure gases are easy to store and not easy to escape, so it is a good option for short-term (compared with chemical energy) energy storage. It is also challenging to convert compressed high-pressure gases into mechanical energy, even with compressed high-pressure gases. For example, high-pressure molecules in internal combustion engines move in all directions but not just toward pistons, losing a lot of energy as heat energy. However, if low-pressure zones are deliberately created in front of high-pressure gases to guide all the molecules in that direction, it is called a shock wave [8,9]. Shock waves propagating in steady flows are usually generated at gas interfaces with differential pressure, such as shock tubes and explosion shock waves [10,11]. Studies on detonation waves generated by explosions have been conducted for more than half a century, including shock wave reflection, diffraction, the interaction between shock waves, and the interaction between shock waves and vortices [12,13,14]; these are essential bases for safety assessment and disaster prediction techniques in the military and industry [15,16,17,18]. A study proposed using dynamic vortex generators to control SWBLI in supersonic inlets, significantly improving aerodynamic performance by reducing separation bubble lengths and increasing total pressure recovery [19]. Recent investigations have focused on the complex interactions between shock waves and boundary layers, including the effects of duct geometry and flow conditions on shock wave behavior [20]. Discussing these interactions can help explain the operational dynamics of a shock wave generator and its performance under various conditions.

The shock wave is a supersonic shock wave when its speed exceeds Mach 1 (the speed of sound, about 340.3 m/s). Supersonic fluids have been applied in missiles, supersonic vehicles, space rockets, and the operations or experimental research of high-speed vacuum flow. Various research institutions and industries are currently experimenting with supersonic fluid by using the shock waves generated by the intense compression of fluid between high-pressure and low-pressure zones. As for the design of existing devices used to generate supersonic shock waves, firing pins are mainly used to impact the metal partition (a thin aluminum sheet) between high-pressure and low-pressure zones to rupture them and create gaps, or the difference between high and low pressures is used to rupture a metal partition and create gaps so that a large amount of high-pressure gases can rush out of the gap to generate shock waves [21]. Figure 1 shows the structure of a shock wave generator that uses a striker to break a metal partition. Figure 2a shows a metal partition with a score in the middle. Figure 2b shows a metal partition broken by impact.

However, such shock wave generation devices have the following shortcomings: (1) it is necessary to disassemble screw locks and a large number of joint bolts each time when devices are used, which is labor consuming and time costing; (2) thin aluminum sheets need to be notched, with too shallow notches affecting the impact, and too deep notches cause devices to be easily torn and unavailable; (3) fragments of broken thin aluminum sheets are often directed downward by airflow, affecting the shock wave generation efficiency and becoming dangerous factors for operators; and (4) the devices cannot be reused directly, since operators must replace the thin aluminum sheet after each use. The above problems not only seriously reduce the operating efficiency of such shock wave-generating devices but also greatly limit the scope of their applications.

This study first designed a new shock wave generator structure to address the problems existing in current shock wave generation devices. Then, we conducted CFD numerical simulations of shock wave generation and monitoring and developed a shock wave monitoring system. This system can monitor the velocity and pressure of the generated shock waves and verify the efficiency of repeated operations. Furthermore, to improve the problem that wind power generation often relies on giant blades to provide enough torque to drive high-power generators, this study further developed an experimental system for shock wave-driven power generation based on this new generator. This system can automatically control the power generation process and measure parameters such as storage tank pressure, output pressure, gas flow, rotation speed, voltage, current, and power for the performance analysis of shock wave-driven power generation experiments. Through these analysis results, we can verify the feasibility of using supersonic shock waves as the source of aerodynamic force to drive power generation.

Therefore, this study’s main innovation is proposing a control mechanism for a new supersonic shock wave generator that can generate high-pressure shock waves and be reusable. We verified the results and efficiency of generating supersonic shock waves through CFD numerical simulation and monitoring experiments. Furthermore, this study also shows the importance of new shock wave generators in designing and developing aerodynamic power generation systems and their potential for broader applications.

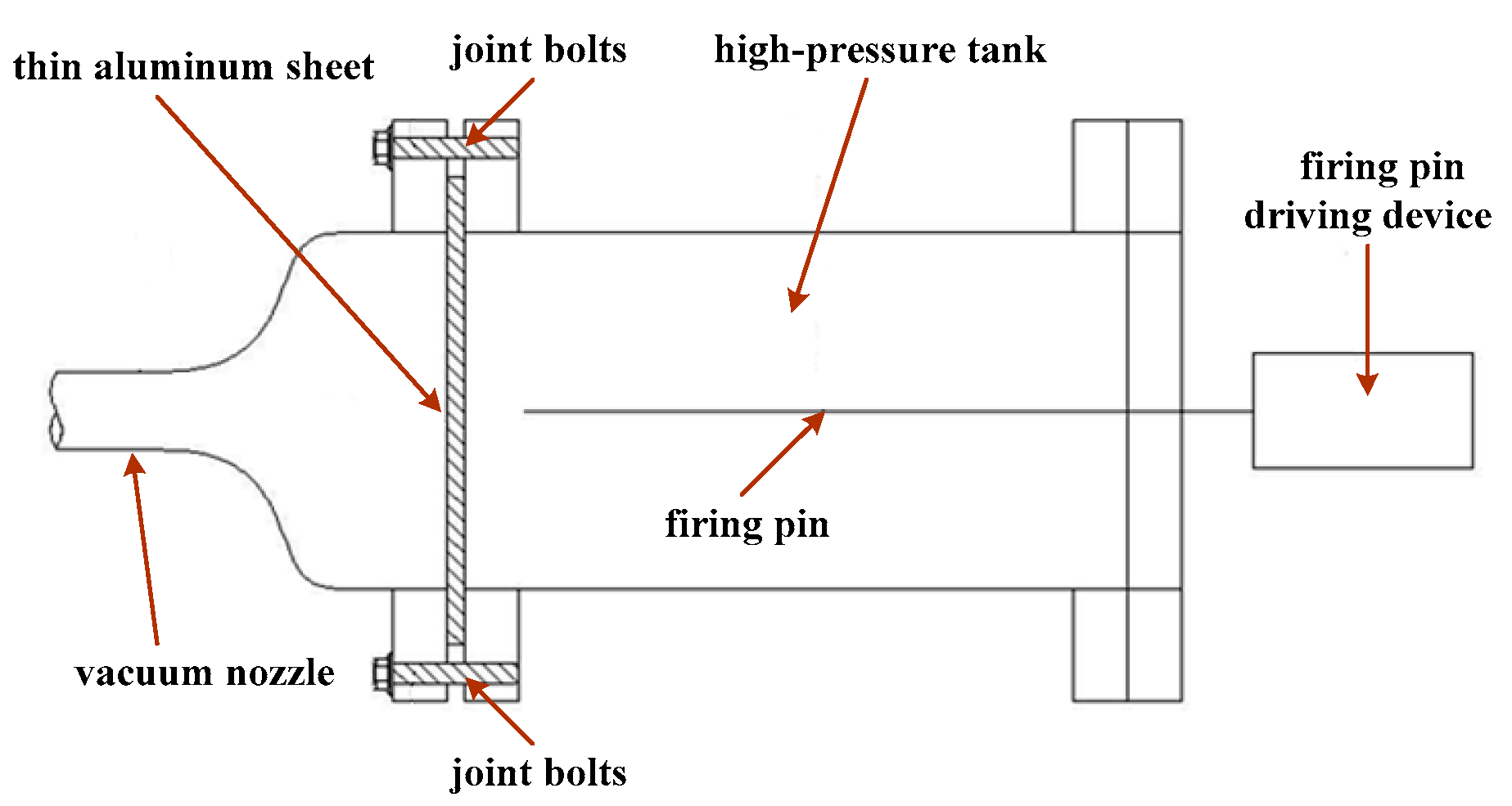
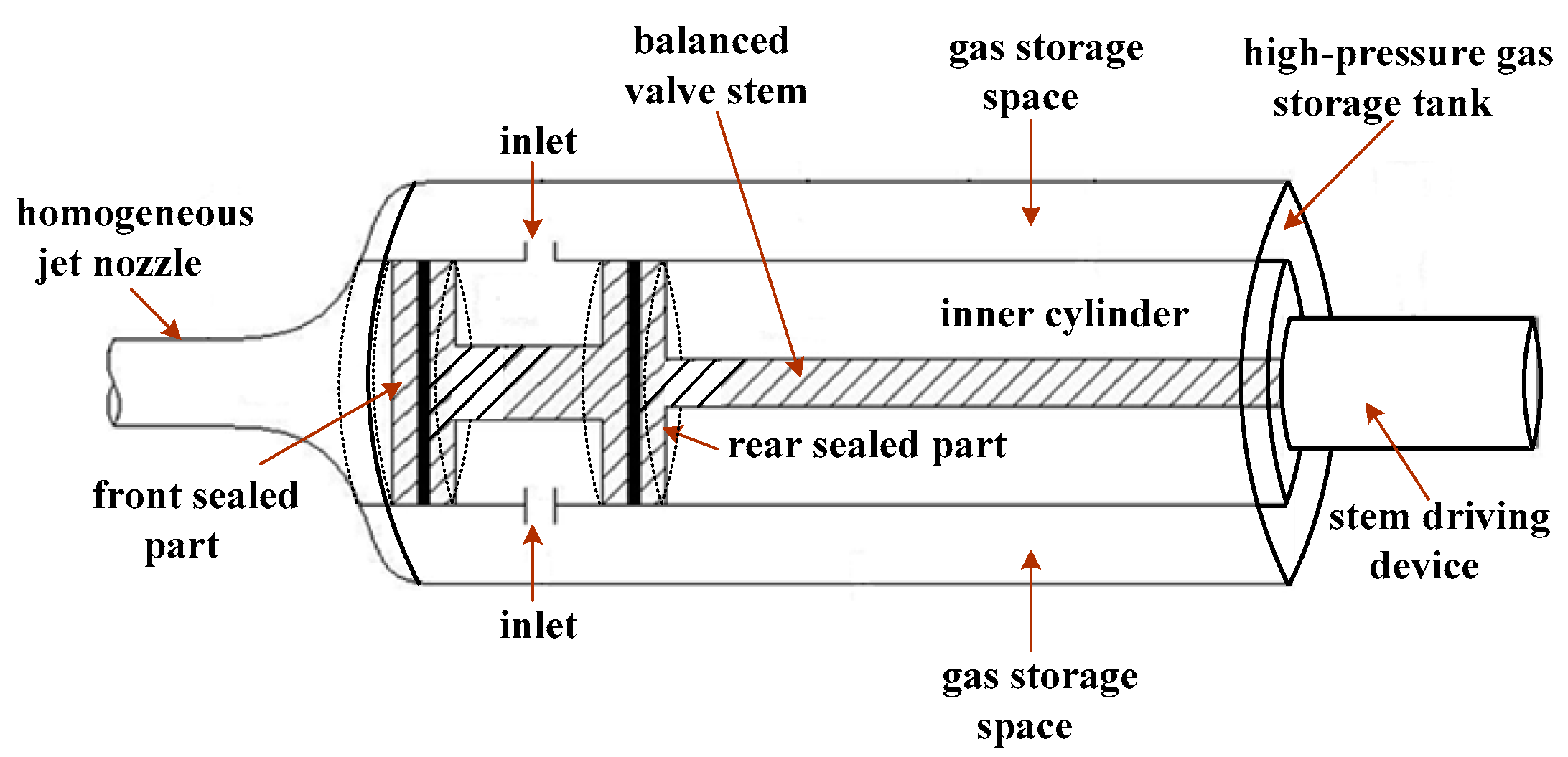
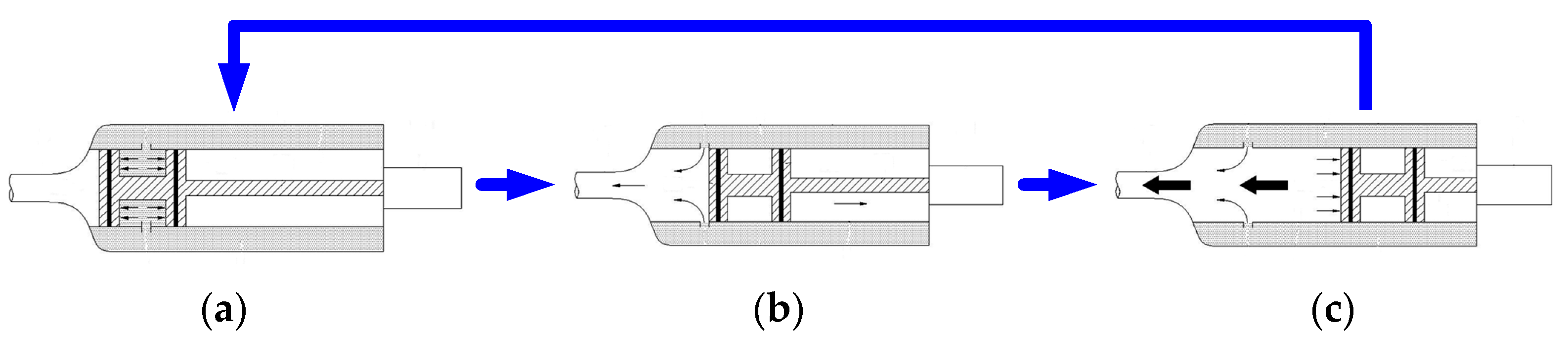
2. Design of a New Shock Wave Generator

This study proposes a new shock wave generator [22], comprising a high-pressure storage tank and a balanced valve stem (as shown in Figure 3). The gas storage space is arranged on the outer ring inside the high-pressure storage tank and is joined to a high-pressure gas inlet unit by a pin. An inner cylinder is set in the center of the gas storage tank to connect it to the outside world, and there is an inlet in front of the inner cylinder to connect it to the gas storage space. A homogeneous jet nozzle is arranged at the front end of the high-pressure storage tank, and the front end of the nozzle is joined to a shock tube by a pin. The balanced valve stem is in the inner cylinder of the high-pressure storage tank, with a front and rear sealed part. The rear end is jointed with a stem driving device by a pin, which can drive the valve stem forward and backward in the inner cylinder by gas pressure.

This supersonic shock wave generator works as follows: (1) when the high-pressure gases enter the front and rear sealed parts, due to their equal stressed area and acting force, the balanced valve stem creates static balance, which can effectively prevent the high-pressure gas from flowing into the homogeneous jet nozzle and shock tube (Figure 4a); (2) the balanced valve stem is driven to move backward, and the high-pressure gas in the gas storage space is rushed into the homogeneous jet nozzle and shock tube to cause shock waves (Figure 4b,c); and (3) when it works again, the balanced valve stem is driven to move forward so that the inlet of the high-pressure storage tank is precisely between the front and rear sealed parts of the balanced valve stem, then high-pressure gases can be input again to prepare to generate shock waves (as shown in Figure 4a).

Compared with current generators, the new shock wave generator has the following advantages: (1) low labor cost: there is no need to notch the metal partition and to disassemble screw locks and a large number of joint bolts, which is easy and can reduce the labor cost; (2) high operating efficiency: the shock wave generation process needs no manual intervention, which can reduce the experimental failure rate and improve the shock wave generation efficiency; (3) high safety: no foreign matter and debris are rushed into the shock tube with airflow, which can improve the safety of the operator and reduce the need for equipment maintenance; and (4) repeatability: after shock waves are generated, as long as the high-pressure storage tank is filled again, the generator can generate shock waves again. Hence, this generator enables supersonic shock wave generation experiments to be repeated dozens to hundreds of times each day and helps to design the automatic control architecture of the continuous shock wave generator, for example, the application in the power generation systems driven by supersonic shock waves.

3. Supersonic Shock Wave Monitoring

3.1. Monitoring System Architecture

To verify the function and efficiency of the new shock wave generator, a supersonic shock wave monitoring system was developed in this study to monitor the speed and pressure of the generated shock waves. Figure 5 shows the shock wave monitoring system architecture. The black line represents the gas, the red dotted line represents the signal, and the blue line represents the fluid. The functions of all components in the system architecture are described as follows:

(1)

Shock wave generator: this is a device used to generate supersonic shock waves.

(2)

Activation control valve: this is controlled by the monitoring host and is used to activate the shock wave generator to generate supersonic shock waves.

(3)

Shock tube: this is a cylindrical steel tube, with water as the carrier, and the shock waves generated enter the steel tube to be moved and reflected quickly.

(4)

High-pressure gas supply unit: this is used to generate high-pressure gases and provide gases to the shock wave generator to generate shock waves. It can be an air compressor or a high-pressure gas cylinder.

(5)

Inlet valve: this is used to control high-pressure gases entering the gas storage tank of the shock wave generator.

(6)

Input pressure gauge: this is used to monitor the pressure of the gases entering the gas storage tank of the shock wave generator.

(7)

Output pressure gauge: this is a mechanical pressure gauge with residual pressure used to monitor and display the maximum pressure in the shock tube.

(8)

Front-end pressure sensor: this is a high-pressure and high-speed pressure sensor installed at the front end of the shock tube.

(9)

Rear-end pressure sensor: this is also a high-pressure and high-speed pressure sensor installed at the rear end of the shock tube.

(10)

Water inlet valve: this is used to assess and control whether to input water into the shock tube and is installed below the shock tube.

(11)

Water source: this provides water for the shock tube and is used as a water bucket or tap.

(12)

Exhaust drainage valve: this is a control valve installed at the top of the shock tube for exhaust or drainage, so the shock tube is filled with water when water flows out of the valve.

(13)

Drainage tank: this is used to receive water or gases from the exhaust drainage valve.

(14)

Drainage valve: this is a control valve for removing residual water from the shock tube.

(15)

Signal transformation unit: This is a data acquisition and control card for acquiring pressure signals measured by the front-end and rear-end pressure sensors and then transmitting them to the monitoring host for processing. It also transmits the command of the monitoring host to the activation control valve to activate the shock wave generator to generate supersonic shock waves.

(16)

Monitoring host: This is a personal computer that executes monitoring software developed with LabVIEW 2014 SPI. Through the signal transformation unit, the monitoring host commands the activation control valve to activate the shock wave generator to generate supersonic shock waves. Additionally, it synchronously acquires the pressure signals measured by the front-end and rear-end pressure sensors. It then calculates and analyzes supersonic shock waves’ movement speed and output pressure in the shock tube.

Figure 5. The architecture of the shock wave monitoring system.

Figure 5. The architecture of the shock wave monitoring system.

3.2. Numerical Simulation of the Shock Wave Monitoring

3.2.1. Governing Equations and Preconditioning System

For the numerical simulation of supersonic, high-temperature, and high-pressure flow fields in a long cylindrical shock tube [23], this study uses a multi-block grid approach, using a CFD (computational fluid dynamics) code based on the control volume method and the preconditioning method for solving Navier–Stokes equations to model compressible and incompressible coupling problems. We define the inviscid flux vector $\overrightarrow{F}$ in the standard conservation form as follows:

$$\overrightarrow{F}=\left[\begin{array}{c}\rho \overrightarrow{V}\\ \begin{array}{c}\rho \overrightarrow{V}{v}_x+p\overrightarrow{i}\\ \rho \overrightarrow{V}{v}_y+p\overrightarrow{j}\\ \rho \overrightarrow{V}{v}_z+p\overrightarrow{k}\end{array}\\ \rho \overrightarrow{V}E+p\overrightarrow{V}\end{array}\right]$$

(1)

where ρ is the density, $\overrightarrow{V}$ is the velocity vector, v_x, v_y, and v_z are the velocity components in the x, y, and z directions, respectively, p is the pressure, E is the total energy per unit mass, and the relationship between E and the total enthalpy H is H = E − p/ρ, where H = C_pT + V²/2 (C_p is the constant pressure specific heat and T is the temperature). This system is closed by the equation of state, which usually has the form ρ = ρ(p, T). The low diffusion flux splitting method of AUSM+ is used here [24], then the inviscid interface flux F_i+1/2 in the x direction can be decomposed into the sum of the convection contribution $F_{1/2}^c$ and the pressure contribution $F_{1/2}^p$, where the subscript 1/2 represents the center of the grid, and the convection term $F_{1/2}^c$ and the pressure term $F_{1/2}^p$ can be defined as follows:

$$F_{1/2}^c={\left(\rho v_x\right)}_{1/2}{\left[\begin{array}{c}1\\ \begin{array}{c}{v}_x\\ v_y\\ v_z\end{array}\\ H\end{array}\right]}_{i/i+1}, F_{1/2}^p={\left(\rho v_x\right)}_{1/2}\left[\begin{array}{c}0\\ \begin{array}{c}{p}_{1/2}\\ 0\\ 0\end{array}\\ 0\end{array}\right]$$

(2)

In the convection term $F_{1/2}^c$, if interface mass flux (ρv_x)_1/2 is non-negative, then state i is selected for column vector (1, v_x, v_y, v_z, H)^T; if (ρv_x)_1/2 is negative, then state i + 1 is selected. The interface quantities (ρv_x)_1/2 and p_1/2 are defined as follows:

$${\left(\rho v_x\right)}_{1/2}=a_{1/2}\left({\rho }_i{m}_{1/2}^{+}+{\rho }_{i+1}{m}_{1/2}^{-}\right)$$

(3)

$$p_{1/2}=P_{\left(5\right)}^{+}\left(M_i\right)p_i+P_{\left(5\right)}^{-}\left(M_{i+1}\right)p_{i+1}$$

(4)

Among them, a_1/2 is the interface sound speed, M_i is the MACH number, M_i = v_xi/a_1/2, and $m_{1/2}^{+}$ and $m_{1/2}^{-}$ are defined as follows:

$$m_{1/2}^{+}=M_{\left(4\right)}^{+}\left(M_i\right)+M_{\left(4\right)}^{-}\left(M_{i+1}\right)$$

(5)

$$m_{1/2}^{-}=\frac{1}{2}\left(M_{1/2}+\left|M_{1/2}\right|\right)$$

(6)

$P_{\left(5\right)}^{+}$ and $P_{\left(5\right)}^{-}$ in Equation (4) are both fifth-degree polynomials of M, and their definitions are as follows:

$$P_{\left(5\right)}^{\pm }\left\{\begin{array}{c}\frac{1}{4}{\left(M\pm 1\right)}^2\left(2\mp M\right)\pm \frac{3}{16}M{\left(M^2-1\right)}^2, \left|M\right|<1\\ \frac{1}{2M}\left(M+\left|M\right|\right), otherwise\end{array}\right.$$

(7)

$M_{\left(4\right)}^{+}$ and $M_{\left(4\right)}^{-}$ in Equation (5) are both fourth-degree polynomials of M, and their definitions are as follows:

$$M_{\left(4\right)}^{\pm }\left\{\begin{array}{c}\pm \frac{1}{4}{\left(M\pm 1\right)}^2, \left|M\right|<1\\ \frac{1}{2}\left(M\pm \left|M\right|\right), otherwise\end{array}\right.$$

(8)

Next, we use the following Navier–Stokes equations as governing equations:

$$\frac{\partial }{\partial t}\iiint Wd\Omega +\iint \left[\overrightarrow{F}-\overrightarrow{G}\right]·d\overrightarrow{A}=0$$

(9)

where Ω is an arbitrary control volume, $\overrightarrow{A}$ is the surface area, W is the dependent vector of conservative variables, and $\overrightarrow{G}$ is the viscous flux vector in the standard conservation form. W and $\overrightarrow{G}$ are defined as follows:

$$W=\left[\begin{array}{c}\rho \\ \begin{array}{c}\rho v_x\\ \rho v_y\\ \rho v_z\end{array}\\ \rho E\end{array}\right], \overrightarrow{G}=\left[\begin{array}{c}0\\ \begin{array}{c}{\tau }_{xi}\\ {\tau }_{yi}\\ {\tau }_{zi}\end{array}\\ {\tau }_{ij}{v}_j+q\end{array}\right]$$

(10)

In the preconditioning method, we convert the governing equations defined by the conservative variable W into the form defined by the primitive variable Q = (p, v_x, v_y, v_z, T)^T as follows:

$$\mathrm{\Gamma }\frac{\partial }{\partial t}\iiint QdV+\iint \left[\overrightarrow{F}-\overrightarrow{G}\right]·d\overrightarrow{A}=0$$

(11)

where Γ is the preconditioning matrix, which is based on the matrix proposed by Choi and Merkle [25] and further expanded by Weiss and Smith [26]. Γ is defined as follows:

$$\mathrm{\Gamma }=\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{ccc}\Theta +\frac{1}{RT}& \begin{array}{ccc}0& 0& 0\end{array}& -\frac{\rho }{T}\end{array}\\ \begin{array}{ccc}\begin{array}{cc}{v}_x\left(\Theta +\frac{1}{RT}\right) & \rho \end{array} & 0 & \begin{array}{cc}0& -\frac{\rho v_x}{T}\end{array}\end{array}\end{array}\\ \begin{array}{ccc}{v}_y\left(\Theta +\frac{1}{RT}\right) & 0& \begin{array}{cc}\rho & \begin{array}{cc}0& -\frac{\rho v_y}{T}\end{array}\end{array}\end{array}\end{array}\\ \begin{array}{ccc}{v}_z\left(\Theta +\frac{1}{RT}\right) & 0 & \begin{array}{cc}0& \begin{array}{cc}\rho & -\frac{\rho v_z}{T}\end{array}\end{array}\end{array}\end{array}\\ \begin{array}{ccc}H\left(\Theta +\frac{1}{RT}\right)-1 & \rho v_x & \begin{array}{cc}\rho v_y & \begin{array}{cc}\rho v_z& \rho \left[C_p-\left(\frac{H}{T}\right)\right]\end{array}\end{array}\end{array}\end{array}\right]$$

(12)

where R is the gas constant, and Θ and H are defined as follows:

$$\Theta =\frac{1}{U_{ref}^2}-\frac{1}{a^2}$$

(13)

$$U_{ref}^2=min\left\{a^2, max\left({\left|V\right|}^2,K{\left|V_{\infty }\right|}^2\right)\right\}$$

(14)

$$H=C_{p}T+\frac{1}{2}({v_x}^2+{v_y}^2+{v_z}^2)$$

(15)

where |V| is the local velocity, |V_∞| is the fixed reference velocity, a is the speed of sound, and K is the constant. The Weiss–Smith preconditioner is formed by adding the vector [1, v_x, v_y, v_z, T]^T to the Jacobian matrix ∂W/∂Q, where W is a vector of conservative variables. In this study, K is fixed at 0.25, and the eigenvalues of Γ⁻¹A (A = ∂F/∂W) are v_x, v_x’ ± a’, where v_x is the velocity component in the x direction, and

$${v_x}^{\prime }\pm a^{\prime }=\frac{1}{2}\left|(1+M_{ref}^2)v_x\pm a\sqrt{{\left(1-M_{ref}^2\right)}^2{M}^2+4M_{ref}^2}\right|$$

(16)

$$M_{ref}^2=\frac{U_{ref}^2}{a^2}$$

(17)

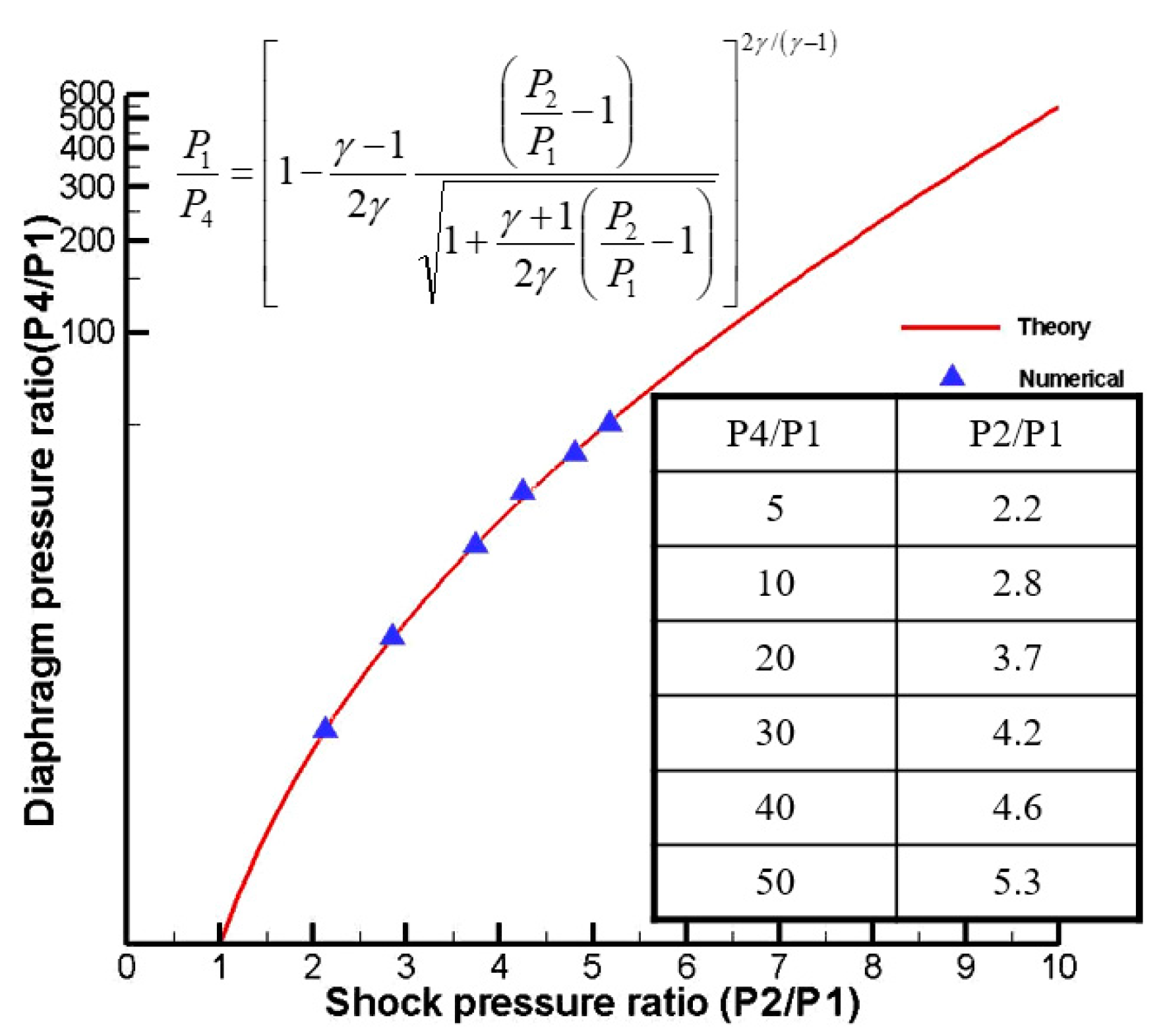
3.2.2. Scheme Validation

The basic assumptions of the numerical simulation method in this study are as follows:

• The fluid is compressible flow.
• The viscous effect (inviscid) is not considered.
• The fluid is a perfect ideal gas.
• We do not consider chemical reactions.

This study selected six sets of theoretical high and low pressure values as the initial settings for numerical simulation. By recording the pressure changes in shock waves at various positions within the tube during their propagation, the pressure values on both sides of the contact surface formed during shock wave transmission were extracted. This allowed for the calculation of the pressure ratios P₂/P₁ and P₄/P₃.

A comparison of the numerical simulation and theoretical calculation pressure values is shown in Figure 6. The results indicate that the numerical simulation results align with the trend of the theoretical calculation pressure values, thereby demonstrating the credibility of the numerical program and boundary settings used in this study for obtaining shock wave phenomena.

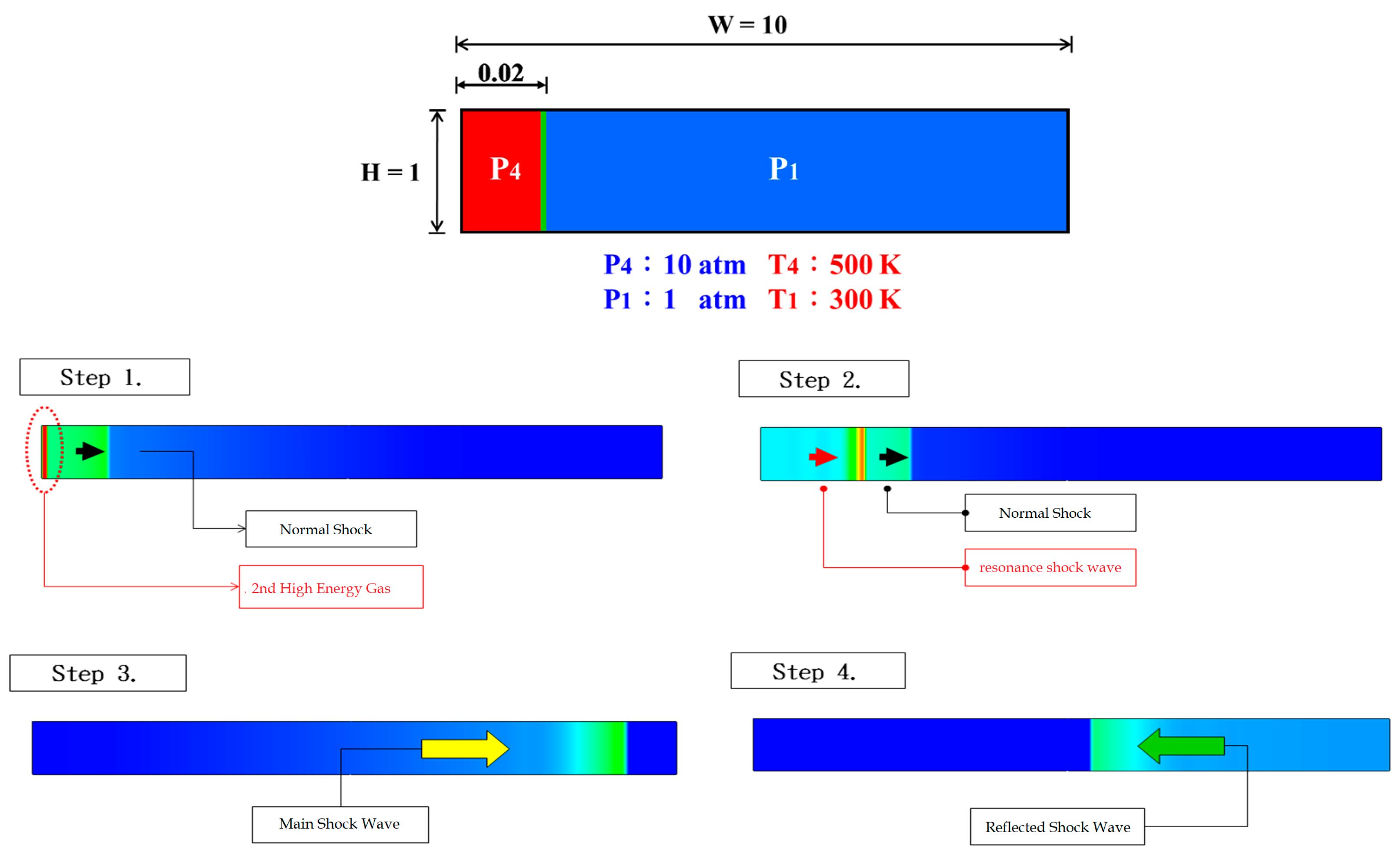
3.2.3. Resonance Shock Wave Monitoring

Based on the components established in Figure 3, a numerical model was created to simulate the shock wave resonance flow field phenomenon (as shown in Figure 7). Using the aforementioned numerical simulation method, starting from the formation of the initial forward shock wave, six instances of high-pressure gas were applied to enable continuous shock wave resonance. Pressure data were recorded at a detection point set on the bottom wall of the tube, as shown in Figure 8.

From the pressure curve graph, it is observed that the initial forward shock wave impact on the wall yielded a pressure value of approximately 0.4. As high-pressure gas was successively introduced at optimal timings, providing energy for the continuous operation of the shock wave in the tube, the pressure values recorded at the detection point gradually increased. Examining the highest pressure values from the six shock wave resonance impacts on the wall, it is noted that after the fourth shock wave impact, the pressure increase slowed down. The fifth and sixth measured pressure values were approximately 0.8.

Therefore, it can be concluded that the pressure values in this shock wave resonance case reached a saturation state, where the resonance effect increased the overpressure value in the tube by about two times.

3.3. Development of the Shock Wave Monitoring System

Figure 9 shows the entity of a supersonic shock wave monitoring system prepared according to the system architecture in Figure 5. In the entity monitoring system, the gas storage tank volume of the shock wave generator is 2 L, and the length of the shock wave tube is 1 M. We use an air compressor as the high-pressure gas supply unit and set the gas pressure at 5 kg. Moreover, Model 113B23 pressure sensors that can measure gas with high pressure and high speed are adopted as the front-end and rear-end pressure sensors [27], with a resonant frequency ≥500 kHz. The pressure sensing (P_min~P_max) ranges from 0 psi to 15,000 psi (equivalent to 0 kg/cm² to 1054 kg/cm²), the output voltage (V_min~V_max) of the two pressure sensors ranges from 0 V to 7.5 V, and the distance (Δd) between the two pressure sensors is 35 cm. The signal transformation unit uses NI USB-6341 X Series data acquisition and control card [28], with a sampling rate of 500 KS/s and input–output channels (pins) including 16 AIs, 24 DIOs, and two AOs. In this monitoring system, two analog input channels (AI0 and AI1) are used to acquire the pressure signals measured by the front-end and rear-end pressure sensors, respectively. A digital output channel (PA00) transmits DO commands to the activation control valve.

3.4. Experimental Analysis of Supersonic Shock Wave Monitoring

In this study, we used the LabVIEW graphical language [29,30,31] to develop the monitoring software for the shock wave monitoring system. Figure 10 shows the screen of the shock wave monitoring results, the upper left corner shows that the sample number n_s of this monitoring system is 100,000 points (Pt), and the sampling rate r_s is 100,000 Pt/s; namely, the sampling time t_s of each Pt is 1/100,000 s. Buffered sampling [28] was adopted in this study. At a sampling rate of 100,000 points per sec, the pressure values of 100,000 points measured at each end were collected (lasting for 1 s) to draw the pressure curve in the middle of the screen. A monitoring result display zone is located on the right side of the screen to display the monitored data and the calculated result of shock wave speed and shock wave pressure.

The pressure curve chart shows two curves in blue and red. The blue curve represents the front-end pressure curve, while the red curve represents the rear-end pressure curve. The system automatically displays the pressure pulses with the maximum peak (namely, the first measured shock wave) in the center of the chart. In this chart, a blue (front-end) pressure pulse appears first, followed by a red (rear-end) pressure pulse (we can ignore noises with slight pressure), indicating that the shock wave first passes through the front-end pressure sensor and then the rear-end pressure sensor. After that, a red-pressure pulse follows another red-pressure pulse, giving rise to another blue-pressure pulse. This phenomenon indicates that after passing through the rear-end pressure sensor for the first time, the shock wave reaches the bottom of the shock tube and is reflected; the reflected shock wave first passes through the rear-end pressure sensor and then the front-end pressure sensor.

The measurements and calculated parameters in the monitoring result display zone on the right side of Figure 10 are analyzed from top to bottom as follows:

(1)

Maximum voltage measured: The maximum peak voltage of the pressure pulse measured appears at the peak, where “Ch1 Max” represents the maximum voltage (v_fmax) of the front-end pressure curve (channel 1), and “Ch2 Max” represents the maximum voltage (v_rmax) of the rear-end pressure curve (channel 2). At this point, v_fmax = 6.756 V and v_rmax = 6.728 V.

(2)

Location with the maximum pressure: “Ch1 Max Pos” represents the location (l_fmax) with the maximum value of the front-end pressure curve, and “Ch2 Max Pos” represents the location (l_rmax) with the maximum value of the rear-end pressure curve. At this point, l_fmax = 8959 Pt and l_rmax = 8983 Pt.

(3)

Distance and time differences between both ends: The distance Δd between the front-end pressure sensor and the rear-end pressure sensor was 0.35 m, and the system calculates the time difference Δt of two pressure pulses based on the difference between the rear end and the front end in positions of the maximum pressure, namely,

Δt = (l_rmax − l_fmax) × t_s

(18)

Therefore, Δt = (8983 − 8959) × 0.00001 = 24 × 0.00001 = 0.00024 s, where t_s is the time of each sampling (0.00001 s).

(4)

Shock wave velocity and Mach: The shock wave velocity in the x direction can be calculated by dividing the distance between the front end and rear end by the time difference between the shock wave passing through the front-end and rear-end sensors. Namely, shock wave velocity v_x (m/s) was calculated as follows:

v_x = Δd/Δt

(19)

Therefore, v_x = 0.35 m/0.00024 s = 1458.33 m/s. In addition, because Mach 1 (Ma) was about 340.3 m/s, the shock wave velocity M_x in Mach was calculated as follows:

M_x = v_x/340.3 = 1458.33/340.3 = 4.29 (Mach)

(20)

(5)

Input pressure and output pressure: We fixed the input pressure p_in at 5 kg/cm² in the shock wave monitoring. However, the maximum peak voltage of the pressure pulse measured appeared at the peak. Therefore, the output pressure p_out of the shock wave was calculated from the maximum peak voltage (V_fpeak) of the front-end pressure pulse or the maximum peak voltage (V_rpeak) of the rear-end pressure pulse. The equation is as follows:

V_peak = max(V_fpeak, V_rpeak)

(21)

$$p_{out}=p_{in}+\frac{V_{peak}-V_{min}}{V_{max}-V_{min}}\left(P_{max}-P_{min}\right)$$

(22)

Since V_fpeak = 6.756 V and V_rpeak = 6.728 V, V_peak = 6.756 V. And, V_min = 0 V, V_max = 7.5 V, P_min = 0 kg/cm², and P_max = 1054 kg/cm²; therefore, the calculated output pressure is p_out = (6.756 V/7.5 V) × 1054 kg/cm² = 945.51 kg/cm². We can compare the output pressure of the shock wave measured by this monitoring system with the value measured by the magnetic output pressure gauge on the shock tube for verification. The data measured by the output pressure gauge on the shock tube were all about 945 kg/cm², verifying the pressure measured by this monitoring system.

(6)

Magnification ratio: The pressure magnification ratio r_p is the ratio of the output pressure p_out to the input pressure p_in, namely

r_p = p_out/p_in

(23)

Therefore, the pressure magnification ratio r_p = 945.51/5 = 188.3 (times).

In this study, 20 shock wave monitoring experiments were conducted. We fixed the input pressure at 5 kg, and the system calculated the time difference (Δt) between the front and rear ends, velocity (v_x), Mach (M_x), output pressure (p_out), and magnification ratio (r_p) in each experiment. A list of the 20 experiment results is shown in

Table 1. List of 20 shock wave monitoring experiment results.

No.	Δt (s)	vx (m/s)	Mx (Mach)	pout (kg/cm2)	rp
1	0.00025	1400	4.12	935.7	187.14
2	0.00024	1458.33	4.29	942.85	188.57
3	0.00024	1458.33	4.29	943.27	188.65
4	0.00027	1296.3	3.81	906.01	181.2
5	0.00027	1296.3	3.81	908.49	181.7
6	0.00021	1666.67	4.9	964.94	192.99
7	0.00022	1590.91	4.68	956.19	191.24
8	0.00022	1590.91	4.68	956.57	191.31
9	0.00022	1590.91	4.68	956.01	191.2
10	0.00023	1521.74	4.48	951.92	190.38
11	0.00026	1346.15	3.96	931.17	186.23
12	0.00025	1400	4.12	938.37	187.67
13	0.00026	1346.15	3.96	926.23	185.25
14	0.00026	1346.15	3.96	928.19	185.64
15	0.00021	1666.67	4.9	965.08	193.02
16	0.00022	1590.91	4.68	957.25	191.45
17	0.00022	1590.91	4.68	958.81	191.76
18	0.00022	1590.91	4.68	958.75	191.75
19	0.00023	1521.74	4.48	950.7	190.14
20	0.00025	1400	4.12	939.33	187.87
Avg	0.00024	1480.33	4.36	943.31	188.7

. According to Table 1, for the 20 shock wave monitoring experiments, the average speed was 1480.33 m/s and equivalent to Mach 4.36, the average pressure was 943.31 kg/cm², and the average magnification ratio was 188.7 times. On the other hand, the table also shows that the shock wave speed was proportional to the pressure generated; the higher the speed, the higher the pressure.

4. Design of a Power Generation System Driven by Supersonic Shock Waves

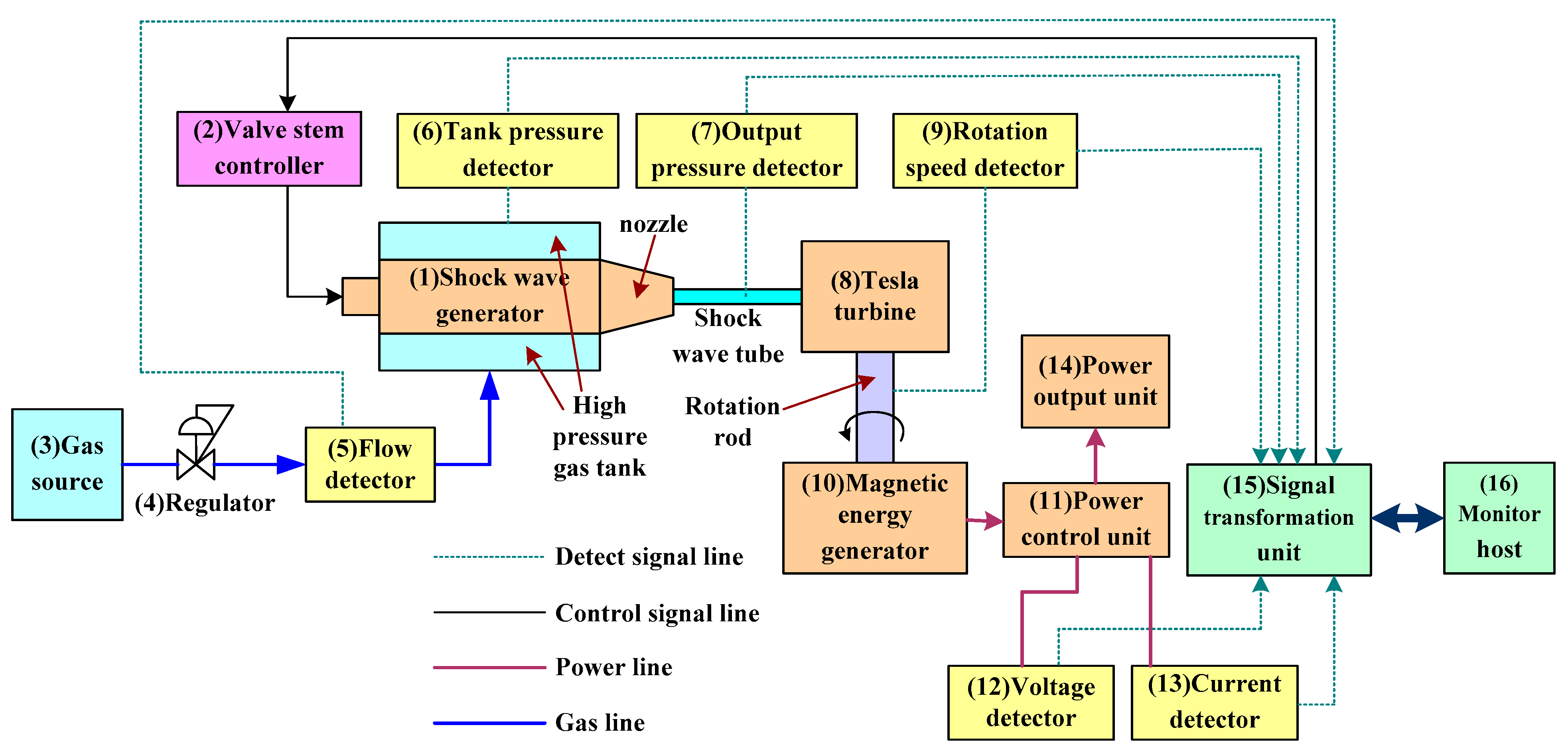
4.1. System Design

We designed and developed a power generation system based on the new shock wave generator [32]. Figure 11 shows the architecture of the power generation system driven by supersonic shock waves.

The functions of the components in the system architecture in Figure 11 are described as below:

(1)

Shock wave generator: This comprises a high-pressure storage tank and a balanced valve stem. When the balanced valve stem moves backward and the gases in the high-pressure storage tank reach the set pressure, the generator can generate shock waves that rush out of the homogeneous jet nozzle.

(2)

Valve stem controller: This can drive the balanced valve stem of the shock wave generator forward and backward. When the balanced valve stem moves backward (ON), the generator generates a shock wave, and high-pressure gas rushes out to drive the Tesla turbine to rotate. When the balanced valve stem moves forward (OFF), the output of high-pressure gases stops.

(3)

Gas source: this is a high-pressure gas cylinder or an air compressor that provides high-pressure gases for the high-pressure storage tank of the shock wave generator.

(4)

Regulator: this can adjust the gas pressure output from the gas source.

(5)

Flow detector: this detects the gas flow f_g delivered from the gas source to the high-pressure gas storage tank. The flow signals detected can be transmitted to the monitoring host through the signal transformation unit.

(6)

Tank pressure detector: This can detect the gas pressure p_t in the high-pressure storage tank of the shock wave generator. The pressure signals detected can be transmitted to the monitoring host through the signal transformation unit.

(7)

Output pressure detector: This can detect the gas pressure p_o output from the shock wave generator. The pressure signals detected are transmitted to the monitoring host through the signal transformation unit.

(8)

Tesla turbine: The turbine can rotate through the impact of shock waves and high-pressure gas and can continue to rotate after the high-pressure gas stops through its energy storage inertia. The rotated turbine can rotate the rotating rod and then drive the magnetic energy generator to work.

(9)

Rotation speed detector: This can detect the rotation speed s_r of the rotation rod. The speed signals detected are transmitted to the monitoring host through the signal transformation unit.

(10)

Magnetic energy generator: This comprises a rotating permanent magnet and a stationary coil. The rotating rod rotates to rotate the magnet to cut magnetic lines and generate power. According to the principle that magnet motors can rotate sustainably due to magnetic action, it can supplement the heat consumed by friction, increase the continuous high-speed magnet rotation time, and improve the power generation efficiency.

(11)

Power control unit: this can convert the alternating current generated by the magnetic energy generator into direct current and provide it to the power output unit.

(12)

Voltage detector: This can detect the voltage V_p of power generated by the magnetic energy generator. The voltage signals detected are transmitted to the monitoring host through the signal transformation unit.

(13)

Current detector: This can detect the current I_p of power generated by the magnetic energy generator. The current signals detected are transmitted to the monitoring host through the signal transformation unit.

(14)

Power output unit: This contains an energy storage battery and a load unit. The load unit is a light bulb box containing three parallel light bulbs. Users can turn each light bulb on or off. The power provided by the power control unit can charge the energy storage battery or directly supply the power required by the load unit.

(15)

Signal transformation unit: This is an Advantech USB-4711A multi-functional high-speed signal acquisition and control card [33]. It can transmit signals measured by the tank pressure detector, output pressure detector, rotation detector, and power control unit to the monitoring host for processing. It further transmits driving commands from the monitoring host to drive the valve stem controller.

(16)

Monitoring host: This is a personal computer that executes LabVIEW monitoring software. It receives the signals of tank pressure, output pressure, gas flow, rotation speed, voltage and current. Then, it sends the control signals to drive the valve stem controller to carry out the control process of power generation driven by shock waves.

The developed power generation system entity, according to the system architecture in Figure 11, is shown in Figure 12.

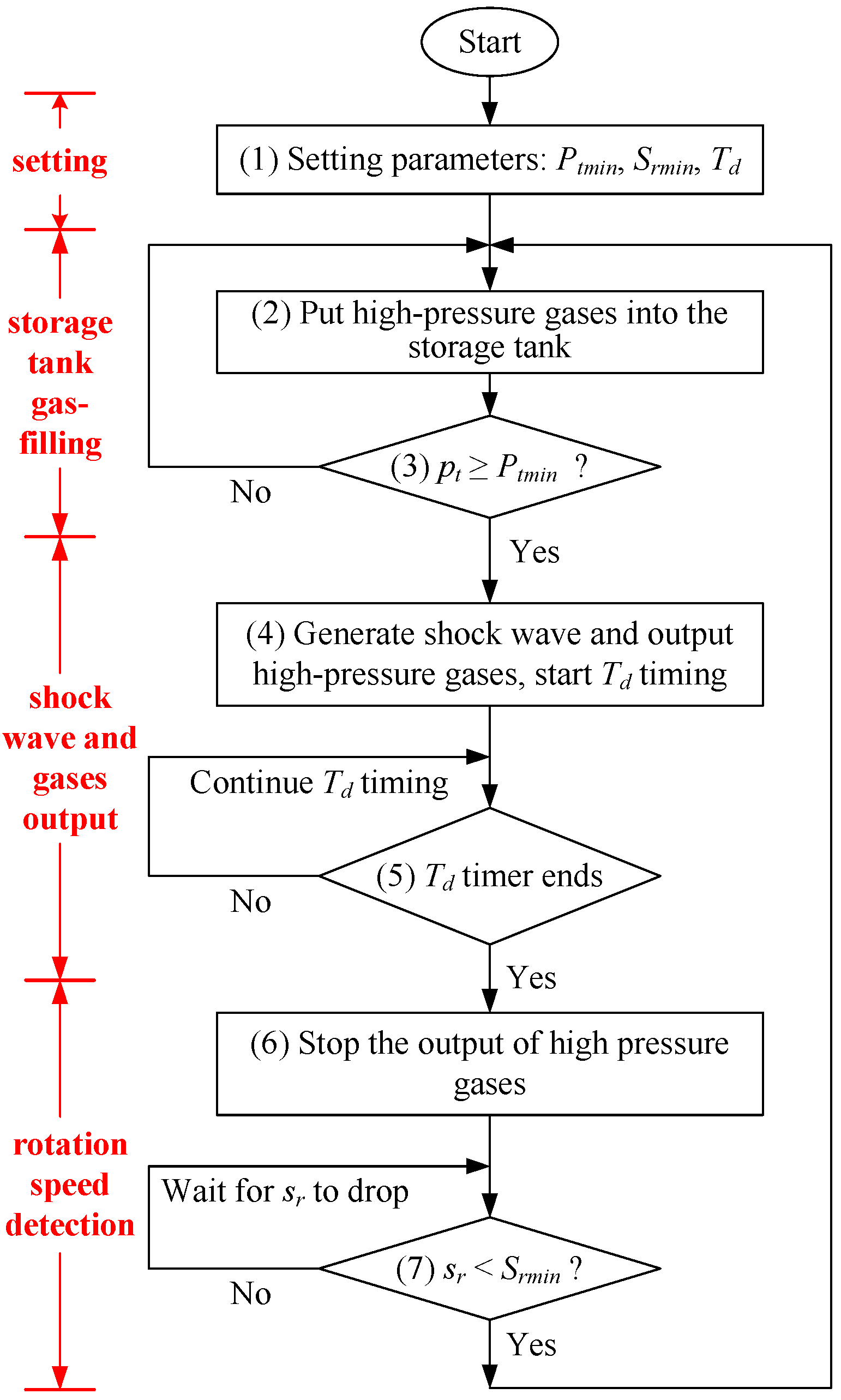
4.2. Shock Wave-Driven Control Process

In this study, we developed an automatic monitoring software in the LabVIEW graphical language [29,30,31] for power generation systems driven by supersonic shock waves. Figure 13 shows the control process of this software. The symbols used in this control process have the following meanings: (a) P_tmin: the lower threshold of pressure in a high-pressure storage tank; (b) S_rmin: the lower threshold of rotation speed; and (c) T_d: the delay time for high-pressure gas output. The control process consists of four stages: setting, storage tank gas filling, shock wave and gas output, and rotation speed detection, which includes seven steps. Step (1) is in the setting stage, steps (2) and (3) are in the storage tank gas filling stage, steps (4) and (5) are in the shock wave and gases output stage, and steps (6) and (7) are in the rotation speed detecting stage. This control process automatically monitors the shock wave-driven power generation experiments [34,35].

4.3. Power Generation Experiments and Analysis

Figure 14 shows the execution screen of the power generation monitoring software. This monitoring software can execute the automatic control program shown in Figure 13. The control parameters set by the user are displayed in the upper left corner of the execution screen in Figure 14, such as the minimum tank pressure (P_tmin), minimum rotation speed (S_rmin), and delay time (T_d), where P_tmin = 3.5 kg/cm², S_rmin = 1200 rpm, and T_d = 2 s. The square light “Low pressure” on the left side of the screen indicates whether the tank pressure is too low (p_t < P_tmin), the red light means too low, and the green light means sufficient. The square light “Low rotation” indicates whether the rotational speed is insufficient (s_r < S_rmin). The circular light “Activation” represents the activation of shock wave output. The sampling rate, elapsed time, and number of data records are displayed at the bottom of the screen.

During the monitoring process of the shock-driven power generation, the system will automatically capture six measurement data, including storage tank pressure p_t, output pressure p_o, rotation speed s_r, gas flow rate f_g, voltage V_p, and current I_p, at a sampling rate of once every 0.2 s. The curves of these measurement data are displayed in the six curve graphs in the center of the screen in Figure 14. From the comparison of the tank pressure p_t curve and the output pressure p_o curve, we can see that p_t can be inflated to about 5 kg/cm² ≥ P_tmin = 3.5 kg/cm² each time (steps (2) and (3) in Figure 13). After the shock wave, p_o first appears as steep wave (pulse), and then an output pressure of about 0.5 kg/cm² lasts for 2 (T_d) seconds. During this time, p_t drops to a low point (steps (4) and (5)). At this time, if s_r ≥ S_rmin, we wait for s_r to drop. When s_r < S_rmin, the system inflate p_t again and re-enter the next cycle (steps (6) and (7)). We can see from the speed curve in the screen that the system controls the speed, s_r, of the connecting rod at around 1200 rpm (S_rmin), and the speed, s_r, determines the size of the output voltage, V_p. When the monitoring process is completed, the system automatically saves the set parameters and all measured curve data to the file for subsequent power generation performance analysis.

Figure 15 shows a display screen of the results of a power generation monitoring experiment. This screen displays six curves from top to bottom; they are the curves of pressure (including yellow storage tank pressure p_t and red output pressure p_o), gas flow rate f_g, rotation speed s_r, voltage V_p, current I_p, and power E_p, where E_p = V_p ∙ I_p. The X-axis of each graph is in the same time sequence. Users can simultaneously scroll the X-axis display range of the six graphs through the sliding bar on the upper right side of the screen to observe the power generation performance in each period.

We mark five time points, A, B, C, D, and E, on the X-axis of Figure 15. The A-B period is the power generation period when no load (zero bulbs) is turned on at the power output end, while the B-C, C-D and D-E periods are the power generation periods when one, two, and three light bulbs are turned on respectively. It can be seen from the I_p curve in the figure that the I_p and E_p in the A-B period (zero bulbs) are both zero, while the I_p and E_p in the one-bulb, two-bulb, and two-bulb periods gradually increase, indicating that the greater the load (the greater the number of light bulbs), the larger both the I_p and E_p.

Table 2. The average values of monitoring data in each period when S_rmin = 1200 rpm.

Period	Zero Bulbs	One Bulb	Two Bulbs	Three Bulbs
fs-avg-k (Hz)	0.42	0.54	0.68	0.81
sr-avg-k (rpm)	1262.52	1243.65	1204.34	1170.82
fg-avg-k (L/min)	143.83	176.79	197.15	233.27
Vp-avg-k (V)	28.38	26.79	25.46	24.44
Ip-avg-k (mA)	0	51.33	98.63	143.26
Ep-avg-k (mW)	0	1375.13	2514.68	3501.15

shows the average values of relevant monitoring data in each period, with S_rmin = 1200 rpm, where f_s-avg-k, s_r-avg-k, f_g-avg-k, V_p-avg-k, I_p-avg-k, and E_p-avg-k (k = 0, 1, 2, and 3) are the average values of the shock frequency, rotation speed, flow, voltage, current, and power in the period that k bulbs are turned on. The comparison results in Table 2 show

f_s-avg-0 < f_s-avg-1 < f_s-avg-2 < f_s-avg-3

(24)

s_r-avg-0 > s_r-avg-1 > s_r-avg-2 > s_r-avg-3

(25)

f_g-avg-0 < f_g-avg-1 < f_g-avg-2 < f_g-avg-3

(26)

V_p-avg-0 > V_p-avg-1 > V_p-avg-2 > V_p-avg-3

(27)

I_p-avg-0 < I_p-avg-1 < I_p-avg-2 < I_p-avg-3

(28)

E_p-avg-0 < E_p-avg-1 < E_p-avg-2 < E_p-avg-3

(29)

We also set the control parameter S_rmin to 1500 rpm, keeping P_tmin and T_d unchanged (i.e., P_tmin = 3.5 kg/cm², S_rmin = 1500 rpm, and T_d = 2 s), then re-execute the power generation monitoring experiment and calculate each monitoring data as mentioned above.

Table 3. The average values of monitoring data in each period when S_rmin = 1500 rpm.

Period	Zero Bulbs	One Bulb	Two Bulbs	Three Bulbs
fs-avg-k (Hz)	0.53	0.65	0.79	0.88
sr-avg-k (rpm)	1546.24	1523.75	1508.42	1482.67
fg-avg-k (L/min)	186.64	213.58	238.75	274.89
Vp-avg-k (V)	40.46	38.85	37.78	36.64
Ip-avg-k (mA)	0	74.44	145.24	211.01
Ep-avg-k (mW)	0	2891.99	5487.17	7731.41

shows the average values of relevant monitoring data in each interval when S_rmin = 1500 rpm.

In Table 3, the comparison results of f_s-avg-k, s_r-avg-k, f_g-avg-k, V_p-avg-k, I_p-avg-k, and E_p-avg-k (k = 0, 1, 2, and 3) are the same as Equations (24)–(29).

Based on the calculation and comparison of the above monitoring results, we can analyze the performance of these shock wave-driven power generation experiments as follows:

(1)

When there is no load (the number of bulbs is zero), the output current I_p and power E_p are zero.

(2)

It can be seen from Equation (24) that when the number of light bulbs that are turned on increases, the frequency of the generated shock waves also increases, which means that the greater the load, the greater the aerodynamic force that needs to be supplied.

(3)

Table 2 and Table 3 show that the faster the rotation speed, the higher the voltage generated. Therefore, each average voltage V_p-avg-k generated when S_rmin = 1500 rpm is higher than the corresponding V_p-avg-k generated when S_rmin = 1200 rpm.

(4)

Equations (25) and (27) show that when the rotational speed S_rmin is the same, the greater the number of bulbs, the lower the voltage that can be generated.

(5)

Equation (26) shows that when the number of bulbs increases, to maintain a fixed speed, more high-pressure gas needs to be consumed so that the flow rate will increase significantly, and the greater the number of bulbs, the higher the gas flow rate.

(6)

Equations (28) and (29) indicate that when the number of light bulbs increases, both I_p-avg and E_p-avg become larger. For example, when S_rmin = 1200 rpm, the I_p-avg and E_p-avg generated by turning on one, two, and three bulbs are 51.33, 98.63, and 143.26 (mA) and 1375.13, 2514.68, and 3501.05 (mW), respectively, and their ratios are all about 1:2:3. There is a similar ratio when S_rmin = 1500 rpm.

(7)

When users turn on a light bulb, its average load resistance R_l-avg-1 is calculated as follows:

R_l-avg-1 = V_p-avg-1/I_p-avg-1 = 26.79/0.05133 = 521.92Ω (for S_rmin = 1200 rpm)

R_l-avg-1 = V_p-avg-1/I_p-avg-1 = 38.85/0.07744 = 521.89Ω (for S_rmin = 1500 rpm)

(8)

When turning on two or three bulbs connected in parallel, if R₁, R₂, and R₃ are bulb resistors, R_l2 and R_l3 represent the load resistance of two bulbs and three bulbs connected in parallel. We can express the load resistors R_l2 and R_l3 as Expressions (30) and (31) (since R₁ = R₂ = R₃):

$$\frac{V}{R_{l2}}=\frac{V}{R_1}+\frac{V}{R_2}=\frac{2V}{R_1} \therefore R_{l2}=\frac{R_1}{2}$$

(30)

$$\frac{V}{R_{l3}}=\frac{V}{R_1}+\frac{V}{R_2}+\frac{V}{R_3}=\frac{3V}{R_1} \therefore R_{l3}=\frac{R_1}{3}$$

(31)

The average load resistance R_l-avg-2 and R_l-avg-3 are calculated as follows:

For S_rmin = 1200 rpm,

R_l-avg-2 = V_p-avg-2/I_p-avg-2 = 25.46/0.09863 = 258.14Ω ≈ R_l-avg-1/2 = 260.96Ω

R_l-avg-3 = V_p-avg-3/I_p-avg-3 = 24.44/0.14326 = 170.60Ω ≈ R_l-avg-1/3 = 173.97Ω

For S_rmin = 1500 rpm,

R_l-avg-2 = V_p-avg-2/I_p-avg-2 = 37.78/0.14524 = 260.12Ω ≈ R_l-avg-1/2 = 261.09Ω

R_l-avg-3 = V_p-avg-3/I_p-avg-3 = 36.64/0.21101 = 173.64Ω ≈ R_l-avg-1/3 = 174.06Ω

This calculation result is consistent with the relationship between Equations (30) and (31), showing that the average error of the monitoring results of this experiment is tiny. Therefore, V_p, I_p, and R_l monitored and calculated by the power generation experiments can all comply with the relevant circuit analysis laws for different numbers of parallel light bulb loads.

5. Conclusions

In this paper, we propose the design of a new supersonic shock wave generator as a solution to the problems in traditional shock wave generators. The new shock wave generator mainly comprises a high-pressure storage tank and a balanced valve stem. When the balanced valve stem is moved backward, a gas outlet is created on the high-pressure storage tank to allow a large amount of high-pressure gases to rush out rapidly to generate a shock wave. Then, the balanced valve stem is moved forward to close the gas outlet, and the high-pressure gases are inputted into the high-pressure storage tank once again. Therefore, the balanced valve stem can move backward again, generating another shock wave. In this study, we carried out a CFD numerical simulation of shock wave monitoring. We also developed a shock wave generator with a 2 L gas storage tank volume and a shock wave monitoring system with a 1 M shock tube length to monitor the velocity and pressure of the shock waves generated. The shock wave monitoring experiments carried out by the system show that the new shock wave generator has the following characteristics: (1) saving workforce and material resources; (2) high security; (3) high operation efficiency; (4) repeatable operation; (5) generating supersonic shock waves of Mach 3 to 4; (6) generating high-pressure shock waves of more than 900 kg/cm² (2 L gas storage tank); and (7) the larger the volume of the gas storage tank, the higher the shock wave pressure generated.

Moreover, this research further utilizes the new shock wave generator to develop a shock wave-driven power generation system. This system can repeatedly generate shock waves to drive a Tesla turbine, which rotates a magnetic energy generator to generate electricity. We set the control parameters S_rmin to 1200 and 1500 rpm to conduct shock wave-driven power generation experiments at different rotation speeds. In these experiments, we turned on different numbers of parallel bulb loads and automatically monitored and plotted seven data curves, concerning storage tank pressure p_t, output pressure p_o, rotation speed s_r, gas flow rate f_g, voltage V_p, current I_p, and power E_p. Through observing and calculating these data curves, we can carry out the performance analysis of the power generation experiments. The analysis results show the following: 1. The output voltage, V_p, is proportional to the rotation speed, s_r, so controlling s_r can determine V_p. When there is no load, the average value of s_r increases from 1262.52 rpm to 1546.24 rpm, and the average value of V_p can increase from 28.38 V to 40.46 V. 2. The more light bulbs turned on, the greater the I_p and E_p generated. The ratio of I_p and E_p generated by turning on one, two, or three light bulbs is approximately 1:2:3. 3. The more light bulbs turned on, the greater the required gas flow f_g, and the higher the frequency f_s of the shock wave. 4. When the user turns on three bulbs, S_rmin increases from 1200 rpm to 1500 rpm, and the average value of E_p increases from 3501.15 mW to 7731.45 mW.

This study can verify the feasibility of using supersonic shock waves as a source of aerodynamic force for a power generation system. It will facilitate the research and application of small but high-power aerodynamic power generation systems. In the future, we will further engage in research on the following applications based on the results of this study: 1. using high-pressure shock waves to remove pipeline obstructions; 2. using high-pressure shock waves to break rock formations at the bottom of geothermal wells and increase their productivity; 3. the development of lightweight high-pressure shock waves rock-breaking devices; and 4. high-pressure shock waves emitted radially from the plant roots below the soil surface to increase the aeration of the soil root zone and reduce soil carbon emissions (without damaging the soil surface).

6. Patents

There are seven patents resulting from the work reported in this article. In terms of generator design, we have obtained the patent “Generating device for supersonic shock waves [22]”; in terms of the application of supersonic shock waves, we have obtained the following patents: “Power generation system driven by dual-cycle supersonic shock waves [32]”, “Geothermal well productivity enhancement method and system [36]”, “Portable supersonic shock wave rock crusher [37]”, “Lightweight supersonic shock wave hard ground excavator [38]”, “Pipeline obstruction clearing device using supersonic shock waves [39]” and “Supersonic shock wave soil loosening and hole fertilization device [40]”.