Low-Profile Circularly Polarized HF Helical Phased Array: Design, Analysis, and Experimental Evaluation
Abstract
1. Introduction
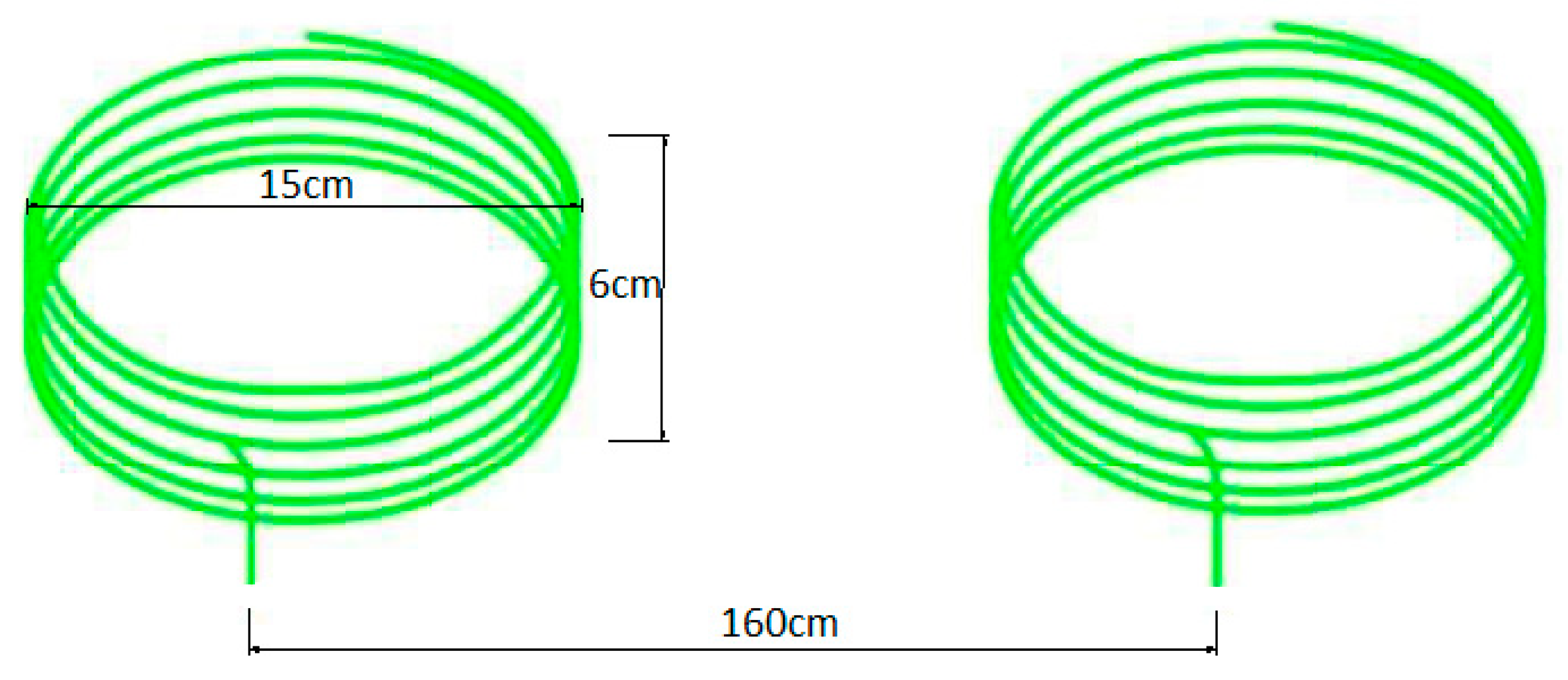
2. The Normal-Mode Helical Antenna Design Considerations
- Cλ: the circumference of the helix in terms of wavelengths.
- Sλ: the spacing between turns in terms of wavelengths.
- A: circle area;
- D: circle diameter;
- S: spacing between the turns of the helix;
- λ: wavelength.
- EΦ = 0 → linear vertical polarization.
- ΕΘ = 0 → linear horizontal polarization.
- EΦ = ΕΘ→ circular polarization.
- R: load resistance;
- Z0: source characteristic impedance;
- X: impedance reactive components.
2.1. LNA Design and Implementation
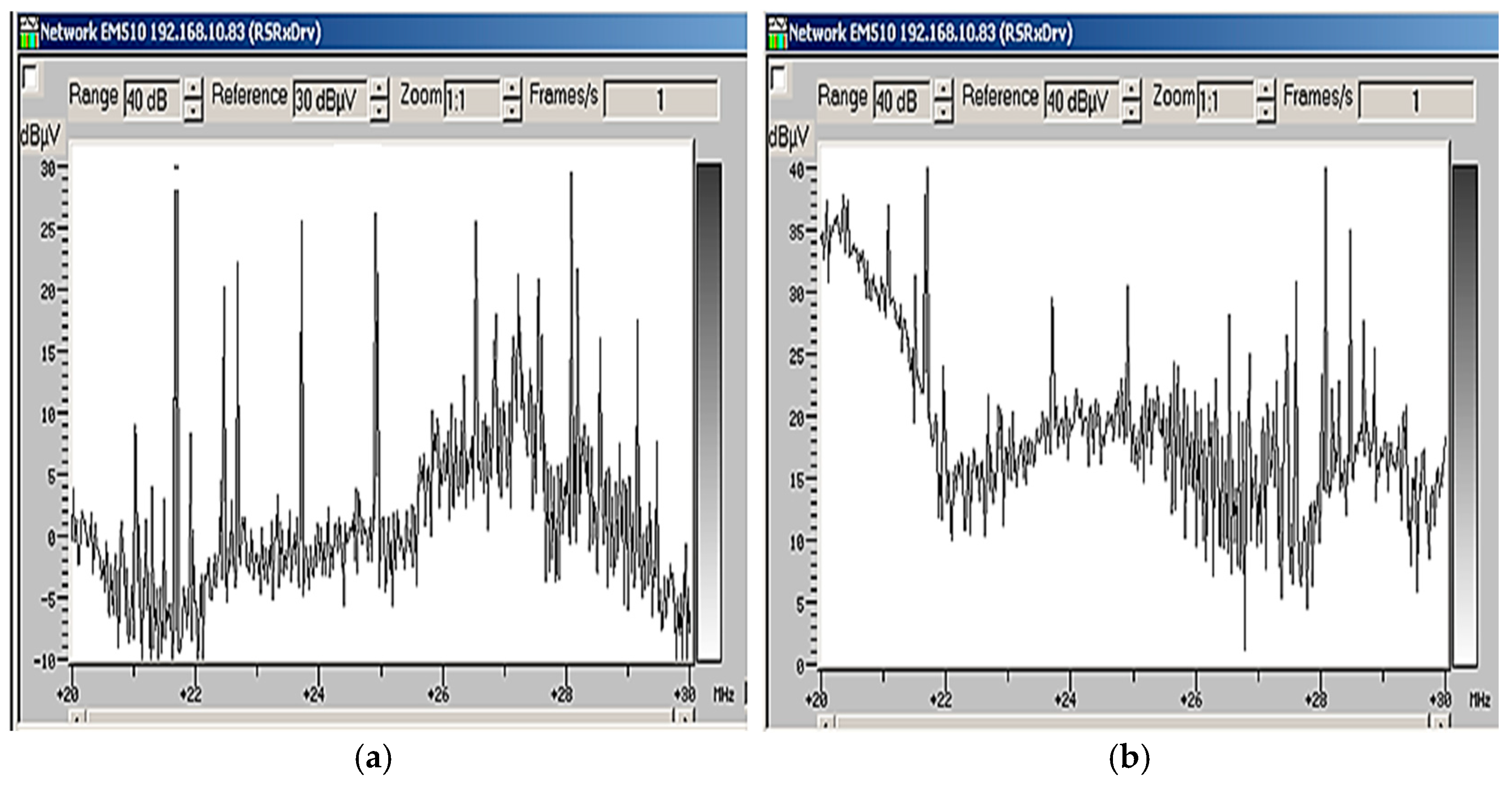
2.2. Testing the Active Helical Antenna under Real Conditions
2.3. Performance Improvement of the Active Helical Antenna over the Half-Wave Dipole
2.4. Testing the NMHA versus a Rohde & Schwarz Dual-Polarization (HE016) Active Antenna
3. Design Principles of the Helical Phased Array
- Ψ: the phase of the array in a given direction;
- Sλ: element spacing;
- Θ: the angle of radiation;
- ΔΦ: phase difference between the two elements;
- λ: wavelength.
- N: the number of elements;
- Ψ: the phase of the array in a given direction.
3.1. Τhe Beamformer Design and Implementation
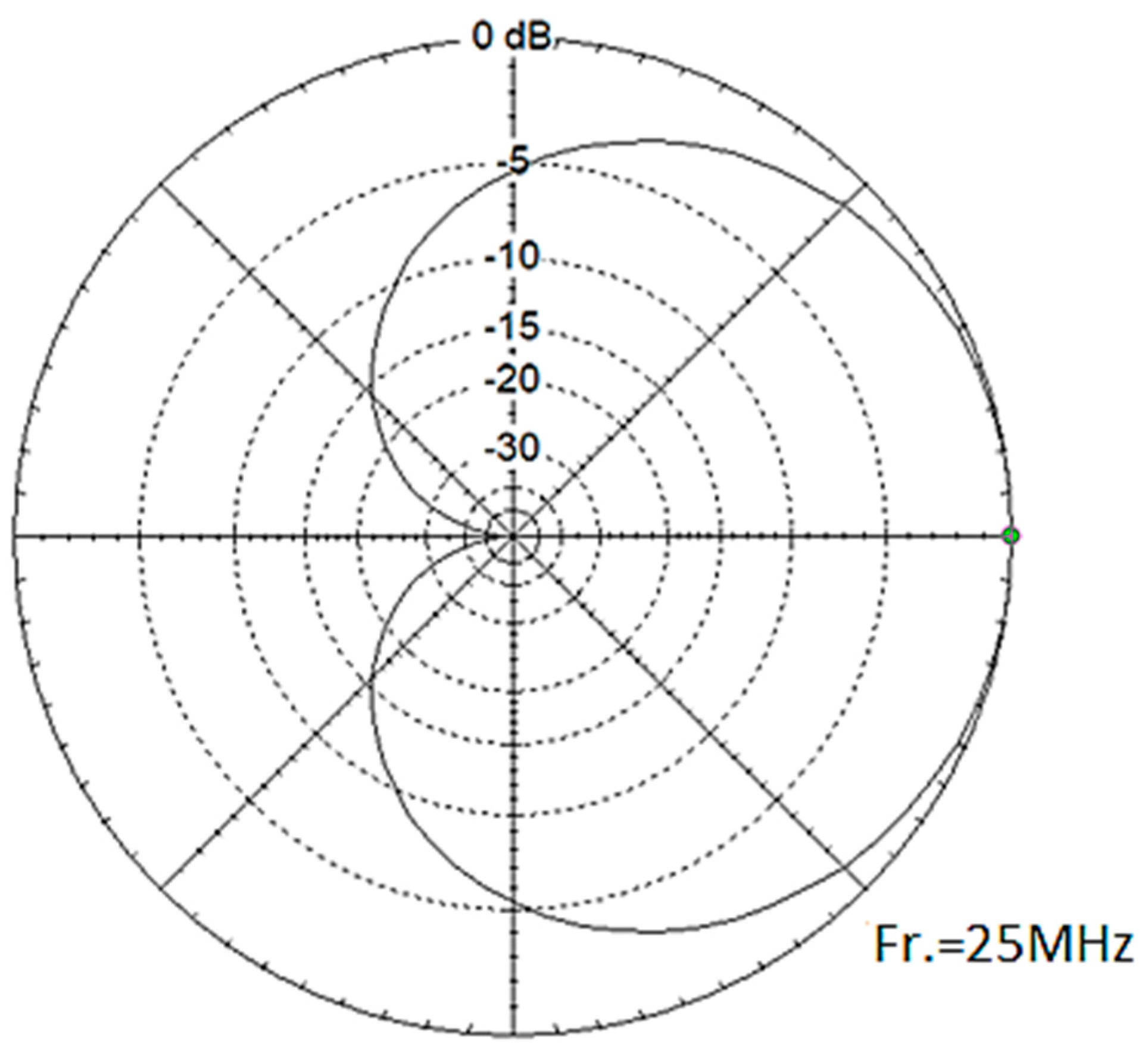
3.2. Beamformer Performance Evaluation
3.3. Final Assessment of the Helical Phased Array
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Constantinides, A.; Haralambous, H. A compact wideband active two-dipole HF phased array. Appl. Sci. 2021, 11, 8952. [Google Scholar] [CrossRef]
- Constantinides, A.; Haralambous, H.; Papadopoulos, H.; Makrominas, M. Models of HF interference over Cyprus. Appl. Sci. 2022, 12, 11808. [Google Scholar] [CrossRef]
- Haralambous, H.; Constantinides, A.; Paul, K.S. HF noise characteristics over Cyprus. Remote Sens. 2022, 14, 6040. [Google Scholar] [CrossRef]
- Taguch, M.; Era, K.; Tanak, K. Two Element Phased Array Dipole Antenna; ACES: Tokyo, Japan, 2007; Volume 22. [Google Scholar]
- Phasing Short HF Vertical Antennas—The Clark County Amateur Radio Association, Springfield, OH. Available online: https://www.w8og.org/short_antenna.html (accessed on 3 April 2024).
- Straw, R.D. The ARRL Antenna Book. 19th ed. ARRL: Newington, CT, USA, 2000. [Google Scholar]
- Fenn, A. Monopole Phased Array Antenna Design, Analysis, and Measurements, YouTube. Available online: https://www.youtube.com/watch?v=4P2mYGAbsJ0 (accessed on 6 April 2024).
- Kraus, J.; Marhefka, R.; Khan, A. Antennas and Wave Propagation; McGraw-Hill: New Delhi, India, 2002. [Google Scholar]
- Lindenmeier, H.; Reiter, L.; Ramadan, A.; Hopf, J.; Lindenmeier, S. A new design principle of active receiving antennas applied with a high impedance amplifier-diversity-module in a compact multi-band-antenna-system on a plastic trunk lid. SAE Tech. Pap. Ser. 2006. [Google Scholar] [CrossRef]
- Zainud-Deen, S.H.; Sharshar, H.A.; Awadalla, K.H. Synthesis of circular polarized normal mode helical antenna. In Proceedings of the IEEE Antennas and Propagation Society International Symposium 1997. Digest, Montreal, QC, Canada, 13–18 July 1997. [Google Scholar] [CrossRef]
- Helical Antenna—Abhinav. (n.d.). Available online: https://astro.abhinav.ac.in/Literature/Antennae/Kraus_Helix_Idea.pdf (accessed on 6 April 2024).
- Balanis, C.A. Antenna Theory: Analysis and Design; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Shin, D.-R.; Lee, G.; Park, W.S. Simplified vector potential and circuit equivalent model for a normal-mode helical antenna. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 1037–1040. [Google Scholar] [CrossRef]
- EZNEC Antenna Software by W7EL. Available online: https://www.eznec.com/ (accessed on 6 April 2024).
- Zainudin, N.; Latef, T.A.; Aridas, N.K.; Yamada, Y.; Kamardin, K.; Rahman, N.H.A. Increase of input resistance of a normal-mode helical antenna (NMHA) in Human body application. Sensors 2020, 20, 958. [Google Scholar] [CrossRef] [PubMed]
- Nanovna. NanoRFE. Available online: https://nanorfe.com/nanovna-v2.html (accessed on 5 October 2023).
- Brown, M. Reflection Coefficient Calculator. 3ROAM. Available online: https://3roam.com/reflection-coefficient-calculator/ (accessed on 7 February 2023).
- Kilambi, S.L.; Da Cunha, M.P. Design and measurements of a small normal mode helical antenna with integrated microstrip structure. In Proceedings of the 2022 Antenna Measurement Techniques Association Symposium (AMTA), Denver, CO, USA, 9–14 October 2022. [Google Scholar] [CrossRef]
- Yamada, Y.; Hong, W.G.; Jung, W.H.; Michishita, N. High gain design of a very small normal mode helical antenna for RFID tags. In Proceedings of the TENCON 2007—2007 IEEE Region 10 Conference, Taipei, Taiwan, 30 October–2 November 2007. [Google Scholar] [CrossRef]
- Frenzel, L. Back to Basics: Impedance Matching (Part 3), Electronic Design. 2024. Available online: https://www.electronicdesign.com/technologies/communications/article/21801154/back-to-basics-impedance-matching-part-3 (accessed on 6 April 2024).
- BF256B.rev2—n-Channel JFET RF Amplifier—Onsemi. (n.d.-a). Available online: https://www.onsemi.com/pdf/datasheet/bf256b-d.pdf (accessed on 6 April 2024).
- P2N2222A Amplifier Transistors—onsemi. (n.d.-c). Available online: https://www.onsemi.com/pdf/datasheet/p2n2222a-d.pdf (accessed on 6 April 2024).
- Multisim Live Online Circuit Simulator (No Date) NI Multisim Live. Available online: https://www.multisim.com/ (accessed on 6 April 2024).
- RF Amplifier Stability Factors and Stabilization Techniques—Technical Articles All about Circuits. Available online: https://www.allaboutcircuits.com/technical-articles/rf-amplifier-stability-tests-and-stabilization-techniques/ (accessed on 6 April 2024).
- Engdahl, S. Electronic Devices; Greenhaven Press: Detroit, MI, USA, 2012. [Google Scholar]
- Rohde & Schwarz GmbH & Co KG. (n.d.). R&S®HE016 Active Antenna System. Rohde & Schwarz. Available online: https://www.rohde-schwarz.com/us/products/aerospace-defense-security/omnidirectional-mobile-and-semi-mobile/rs-he016-active-antenna-system_63493-9365.html (accessed on 7 April 2024).
- EM510 HF Digital Wideband Receiver—AB4OJ. (n.d.-a). Available online: https://www.ab4oj.com/dl/rs/EM510_dat_en.pdf (accessed on 7 April 2024).
- Mailloux, R.J. Phased Array Antenna Handbook; Artech House: Norwood, MA, USA, 2018. [Google Scholar]
- Hansen, R.C. Phased Array Antennas, 2nd ed.; Wiley: Hoboken, NJ, USA, 2009; pp. 1–547. [Google Scholar] [CrossRef]
- Addition of Vectors by Means of Components—Physics. YouTube. 2021. Available online: https://www.youtube.com/watch?v=xS-gdFgZel0 (accessed on 6 April 2024).
- High-Pass Low-Pass Phase Shifters. Available online: https://www.microwaves101.com/encyclopedias/high-pass-low-pass-phase-shifters (accessed on 5 April 2024).
- Plug-in Power Splitter/Combiner PSCQ-2-51W+-Mini-Circuits. (n.d.-e). Available online: https://www.minicircuits.com/pdfs/PSCQ-2-51W+.pdf (accessed on 7 April 2024).
- The Cascode Amplifier: Bipolar Junction Transistors: Electronics Textbook (No Date) All about Circuits. Available online: https://www.allaboutcircuits.com/textbook/semiconductors/chpt-4/cascode-amplifier/ (accessed on 16 April 2024).
- Rohde & Schwarz GmbH & Co KG (No Date) Monitoring Antennas, Monitoring Antennas|Rohde & Schwarz. Available online: https://www.rohde-schwarz.com/products/aerospace-defense-security/monitoring-antennas_229505.html (accessed on 16 April 2024).
- Mostafa, G.; Tsolaki, E.; Haralambous, H. HF Spectral Occupancy Time Series Models over the Eastern Mediterranean Region. IEEE Trans. Electromagn. Compat. 2016, 59, 240–248. [Google Scholar] [CrossRef]


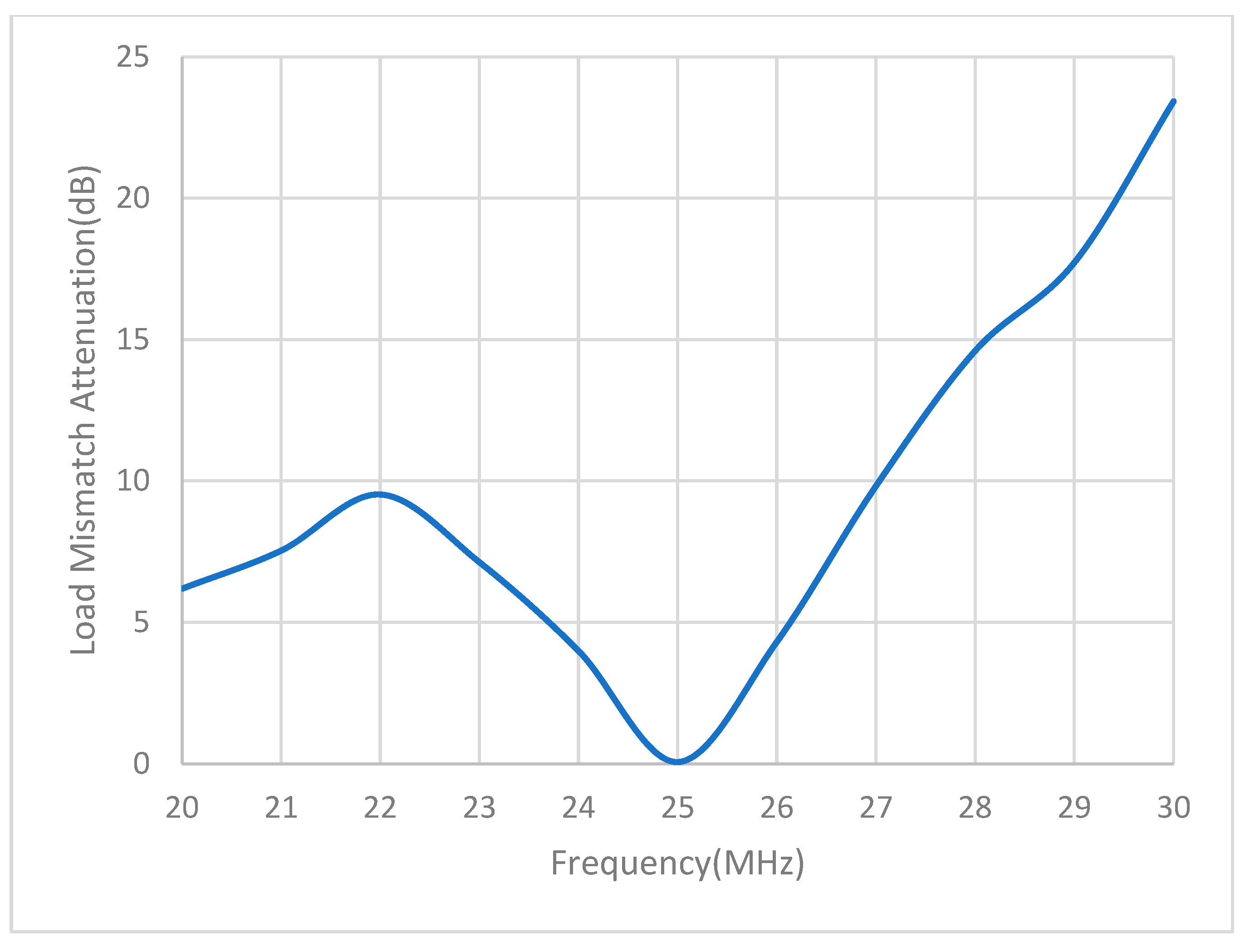
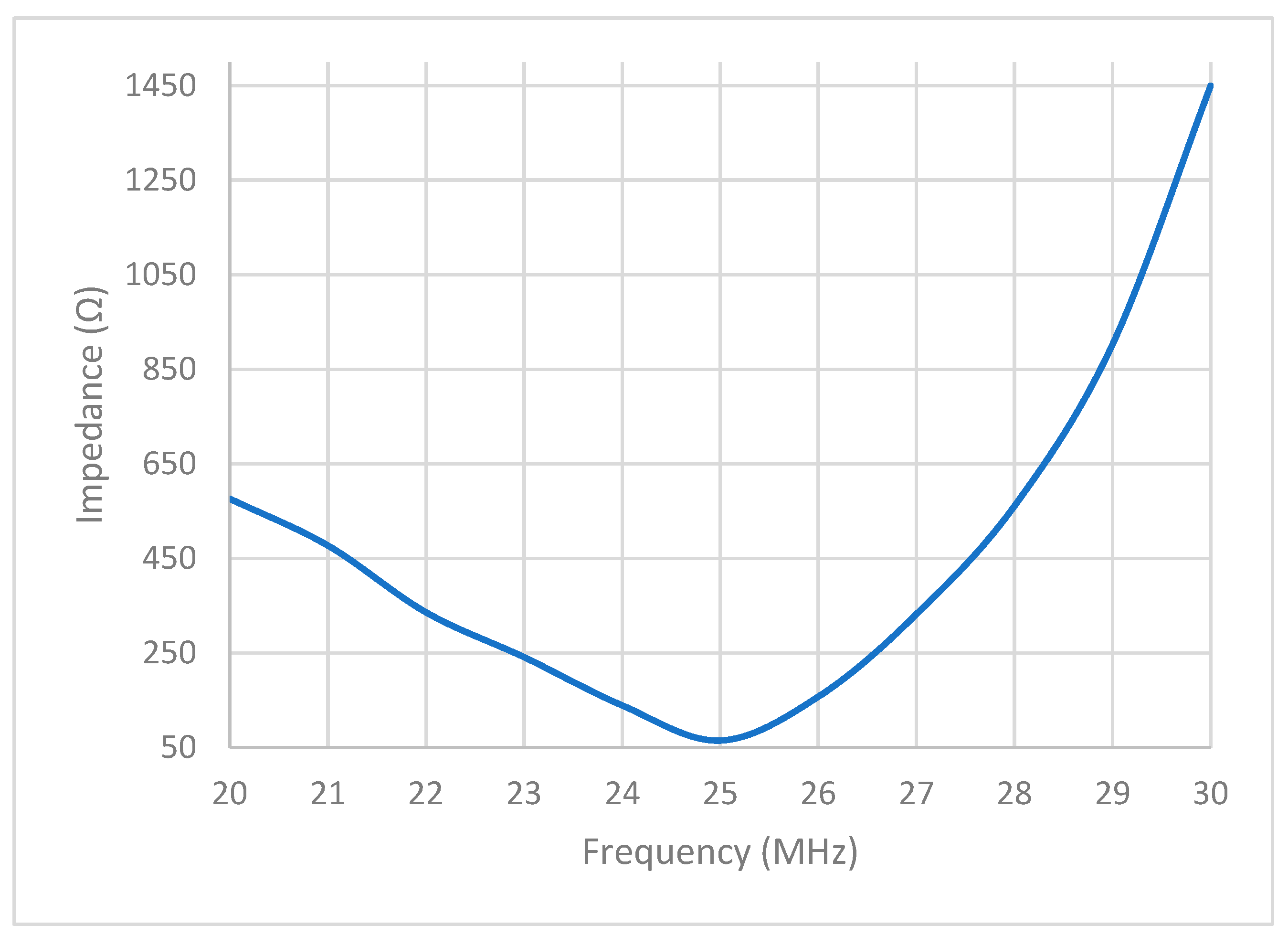

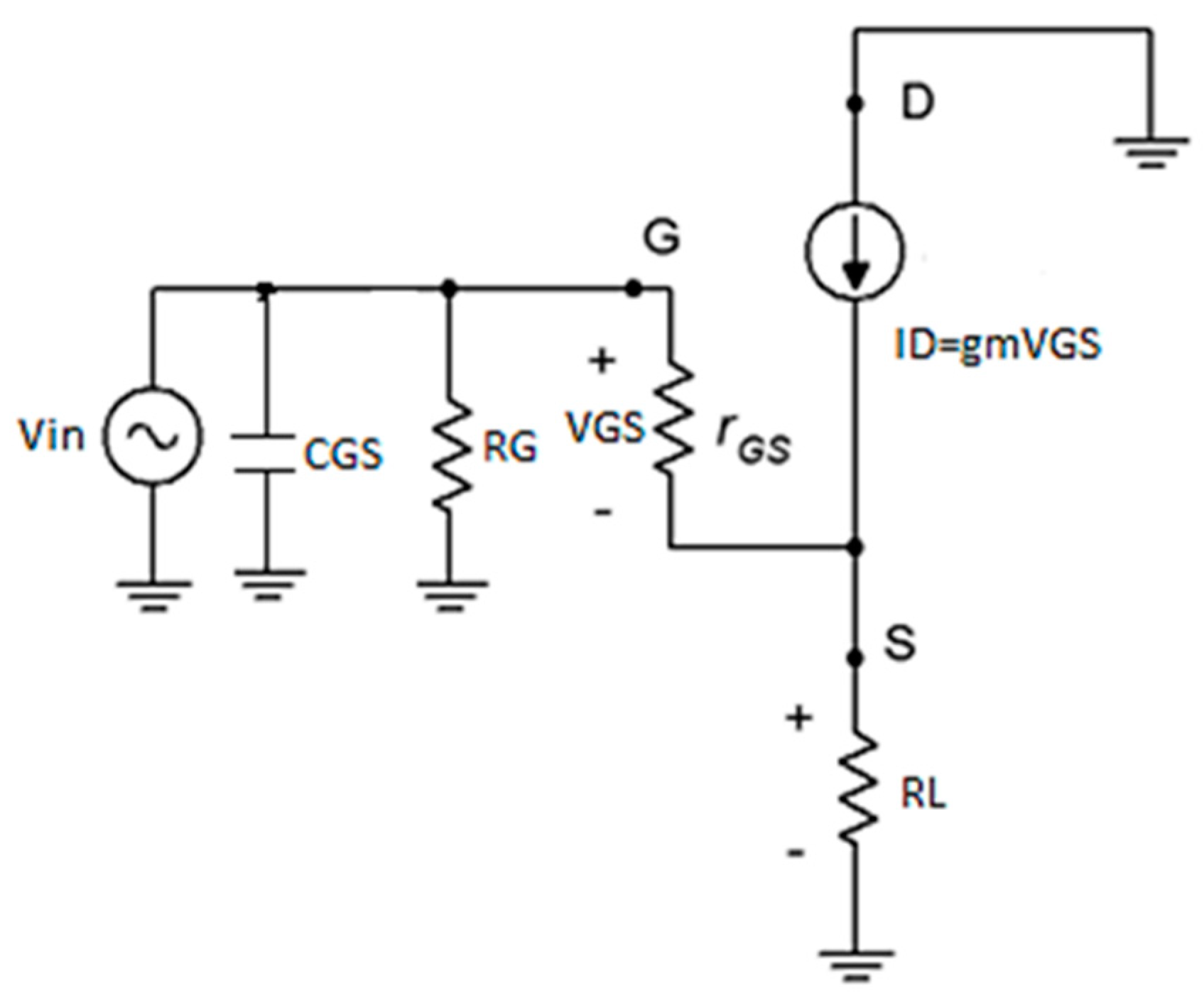
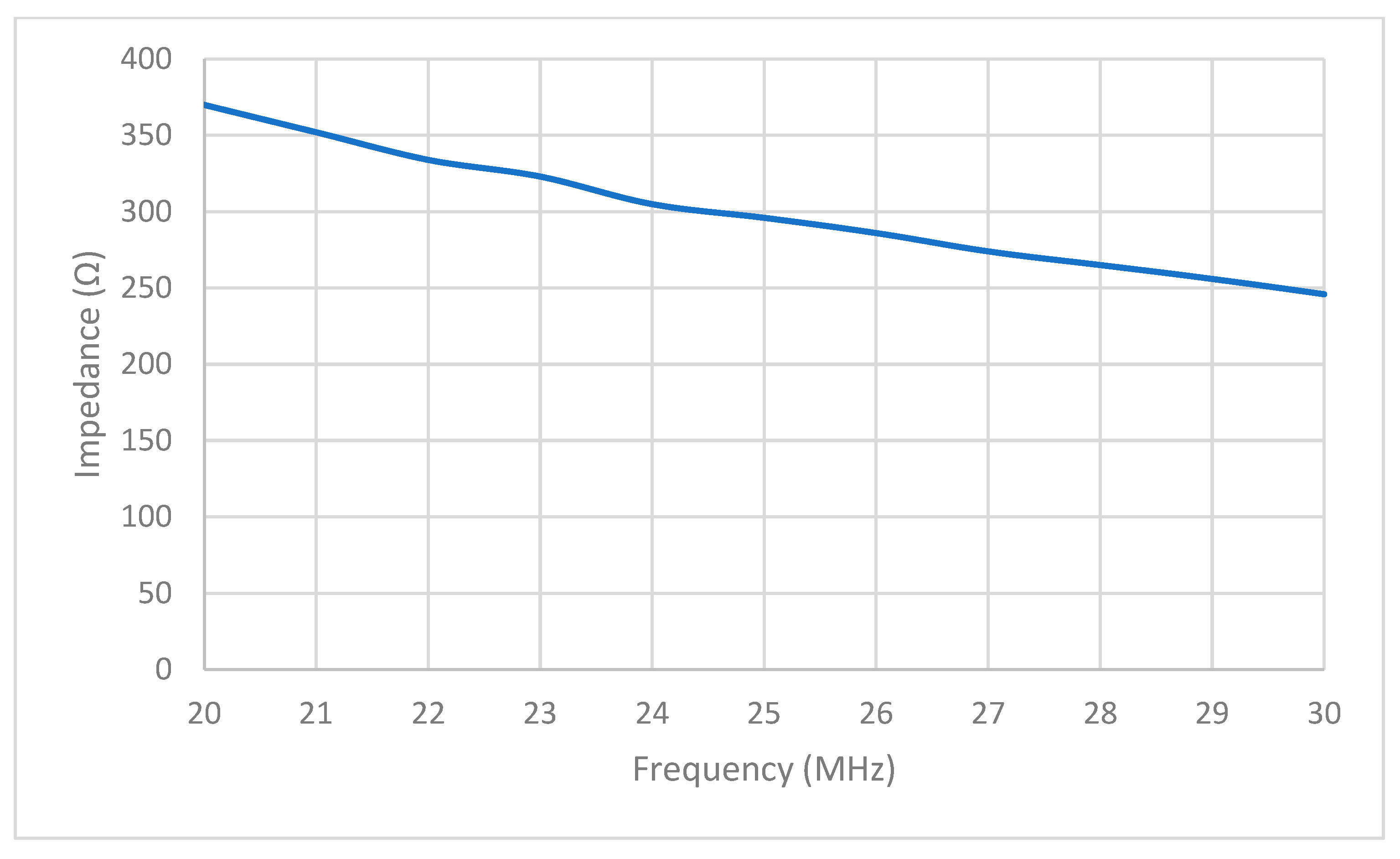
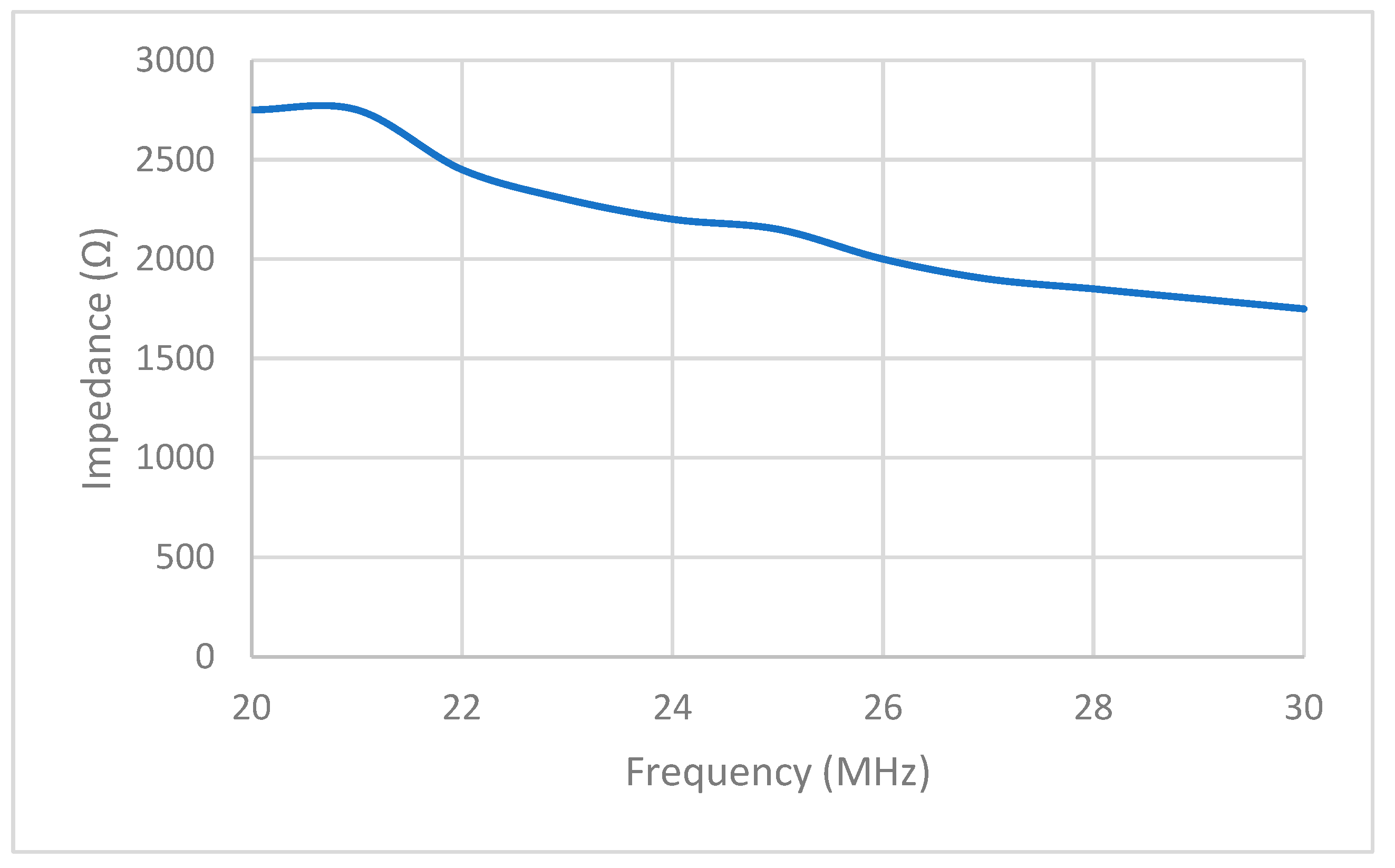






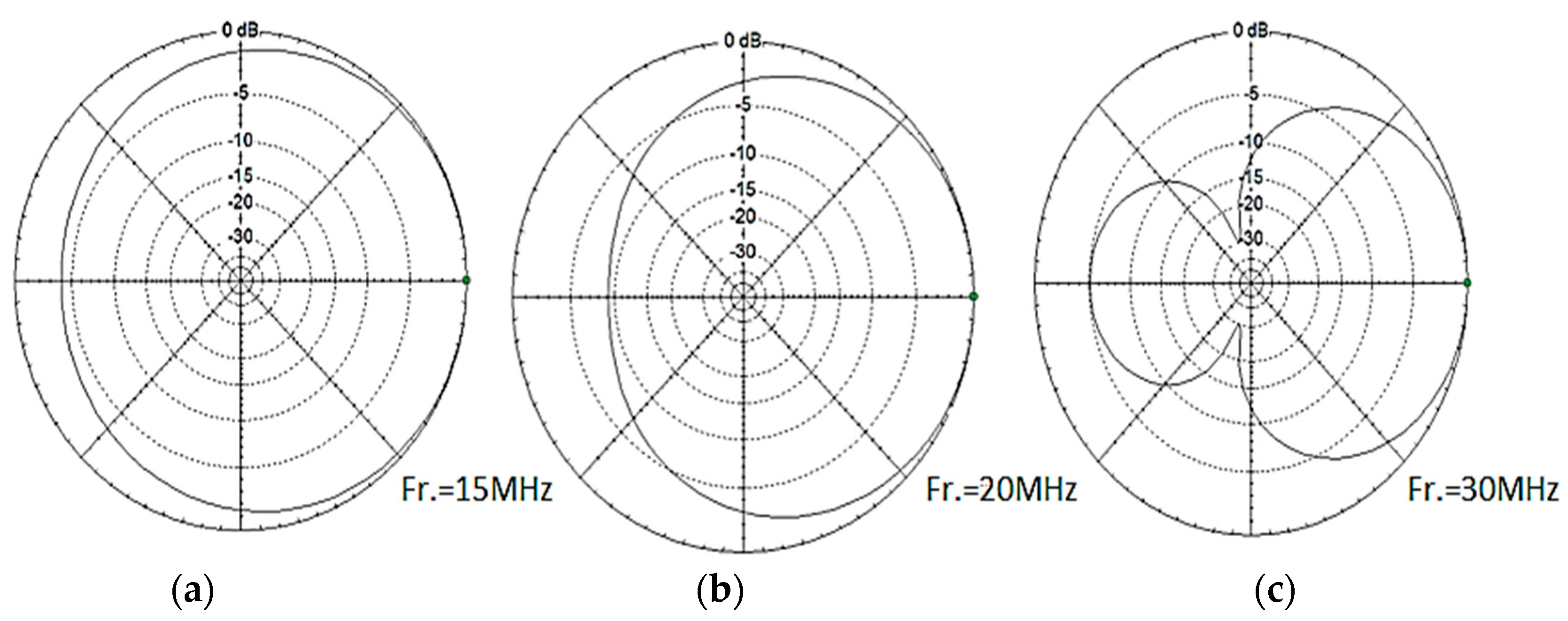
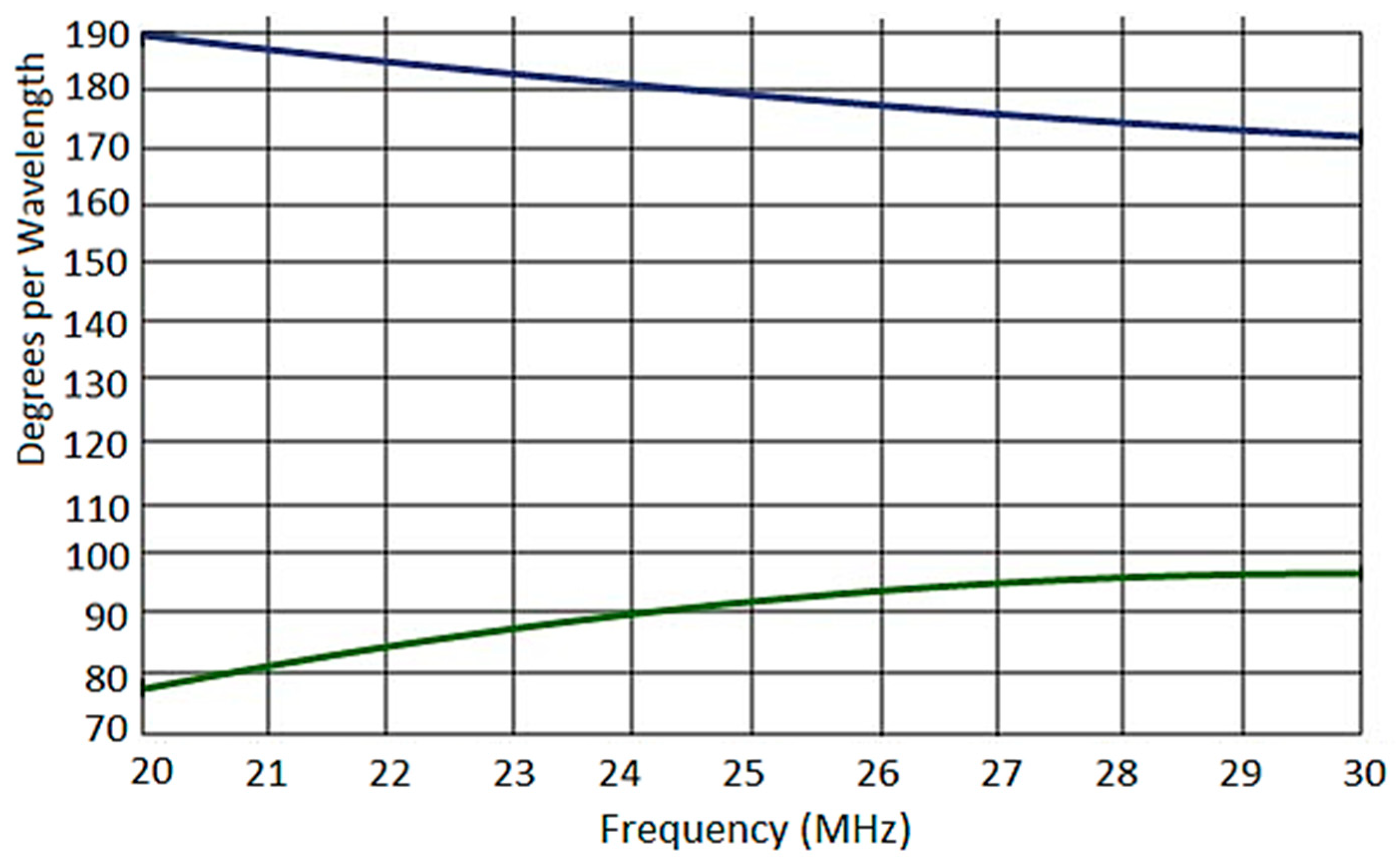

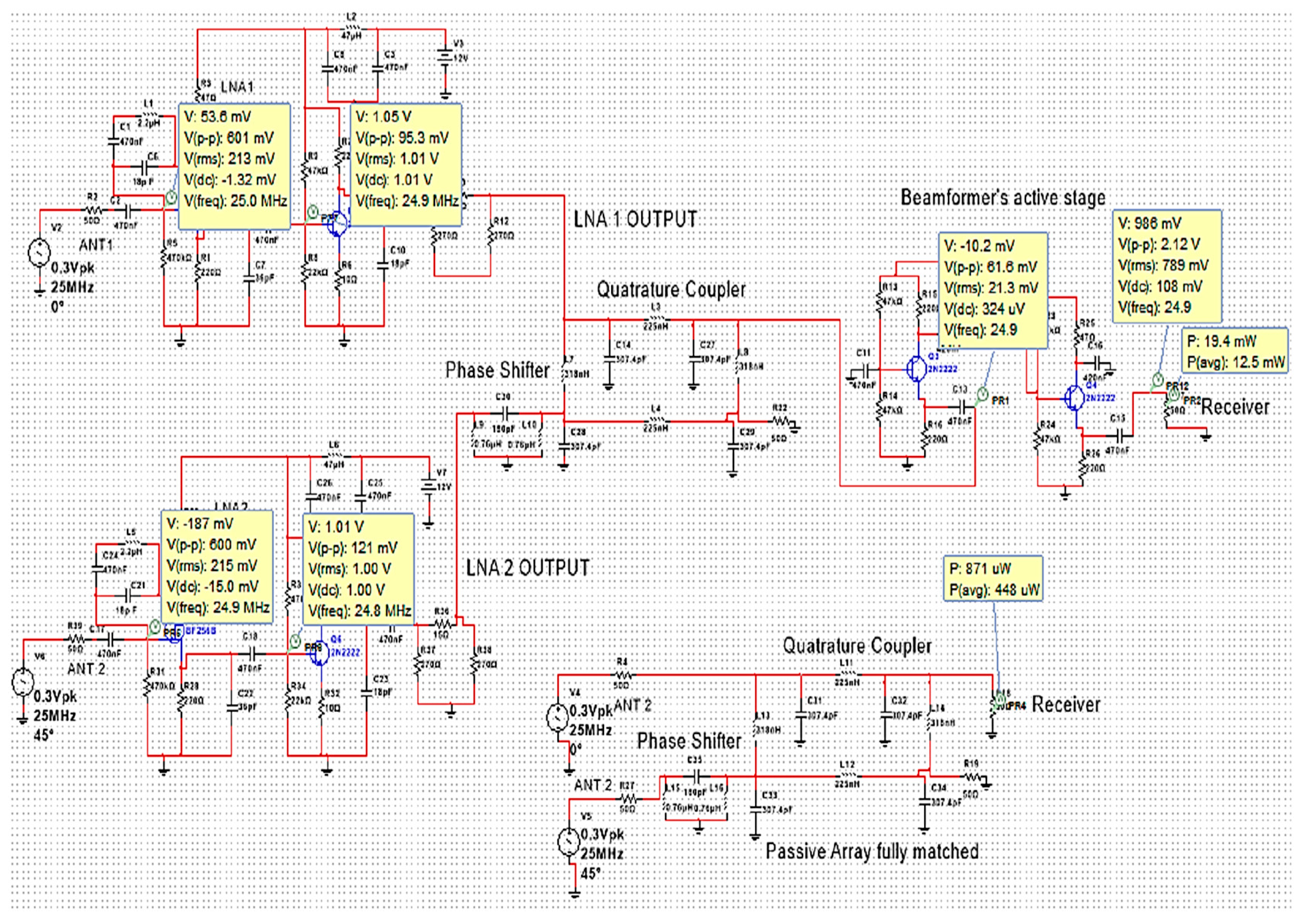
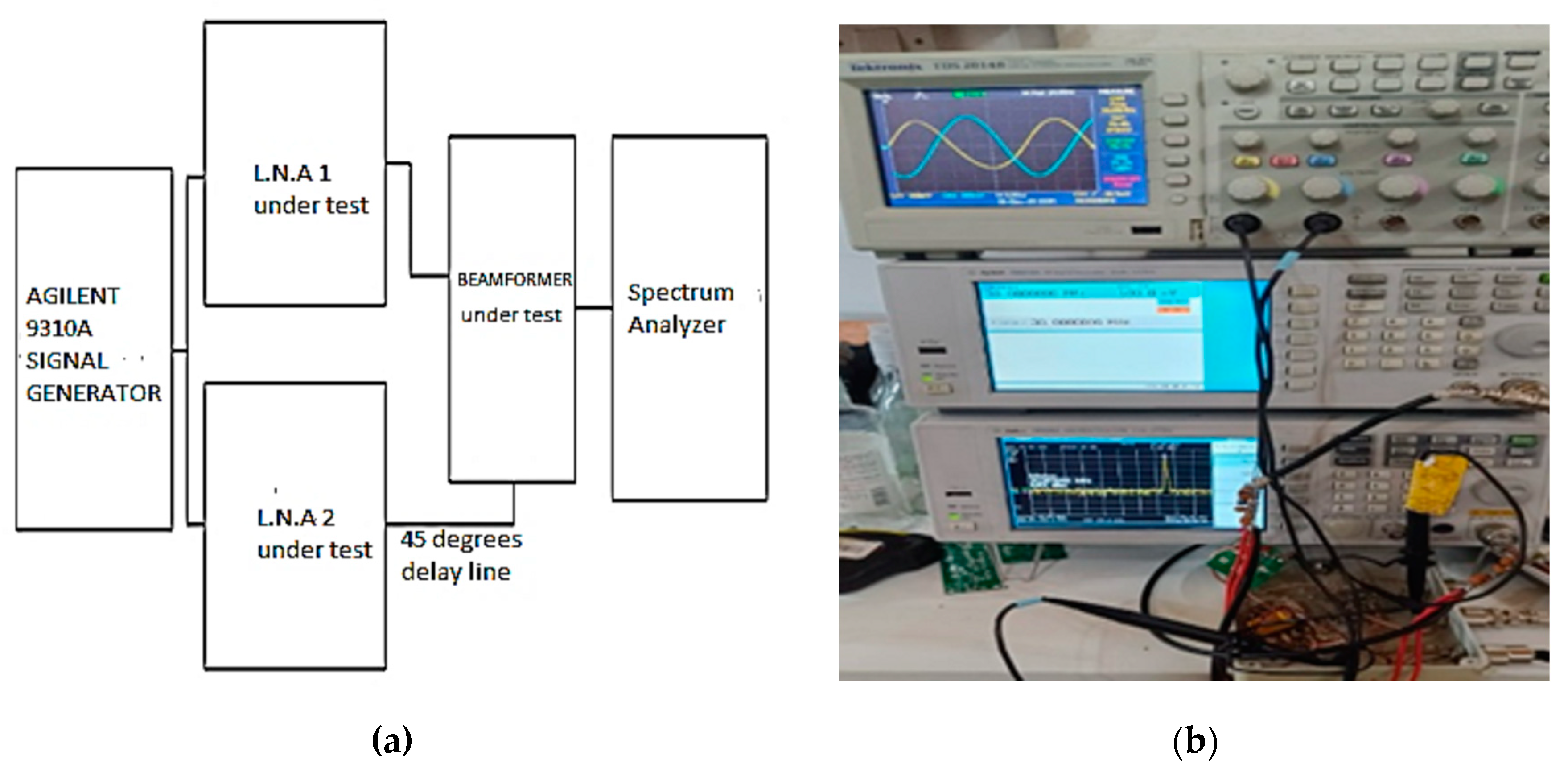

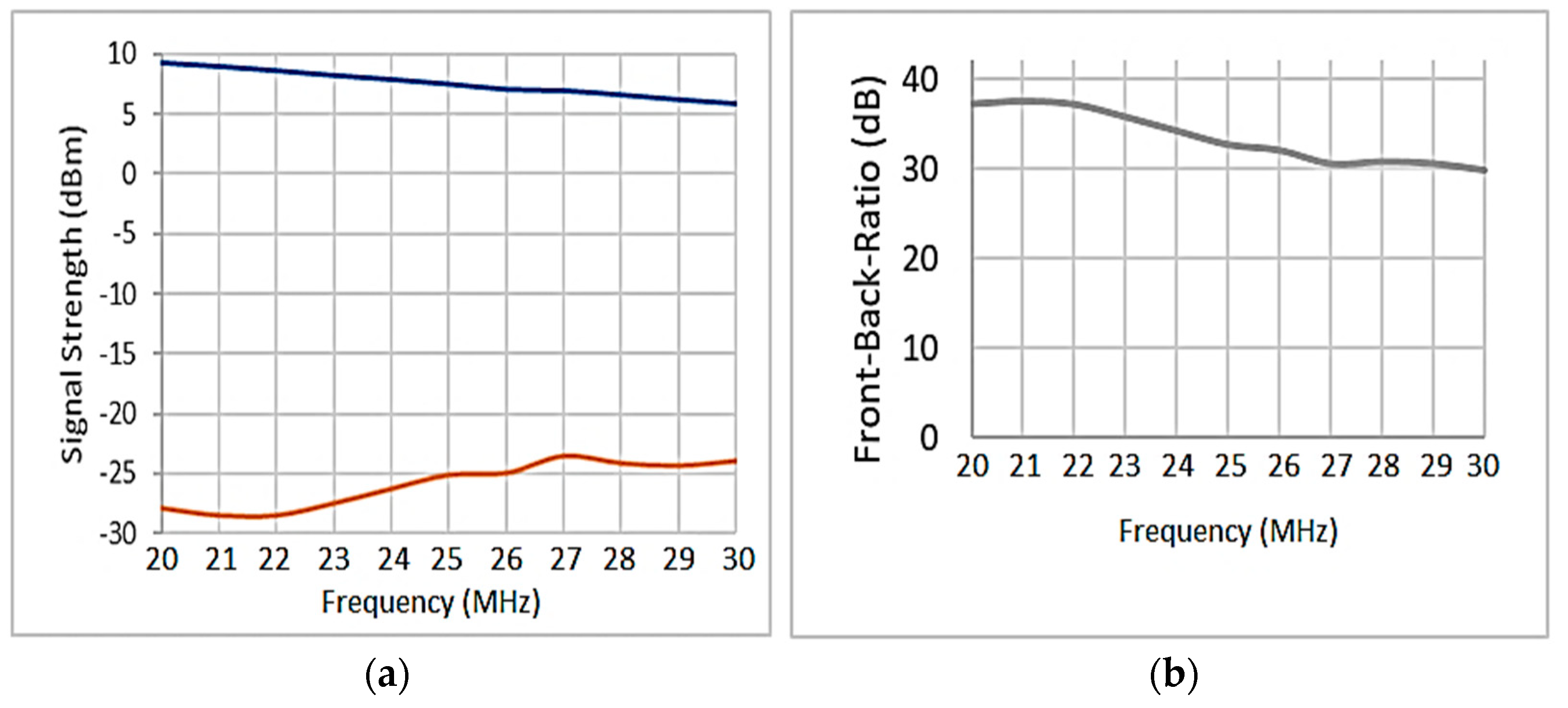

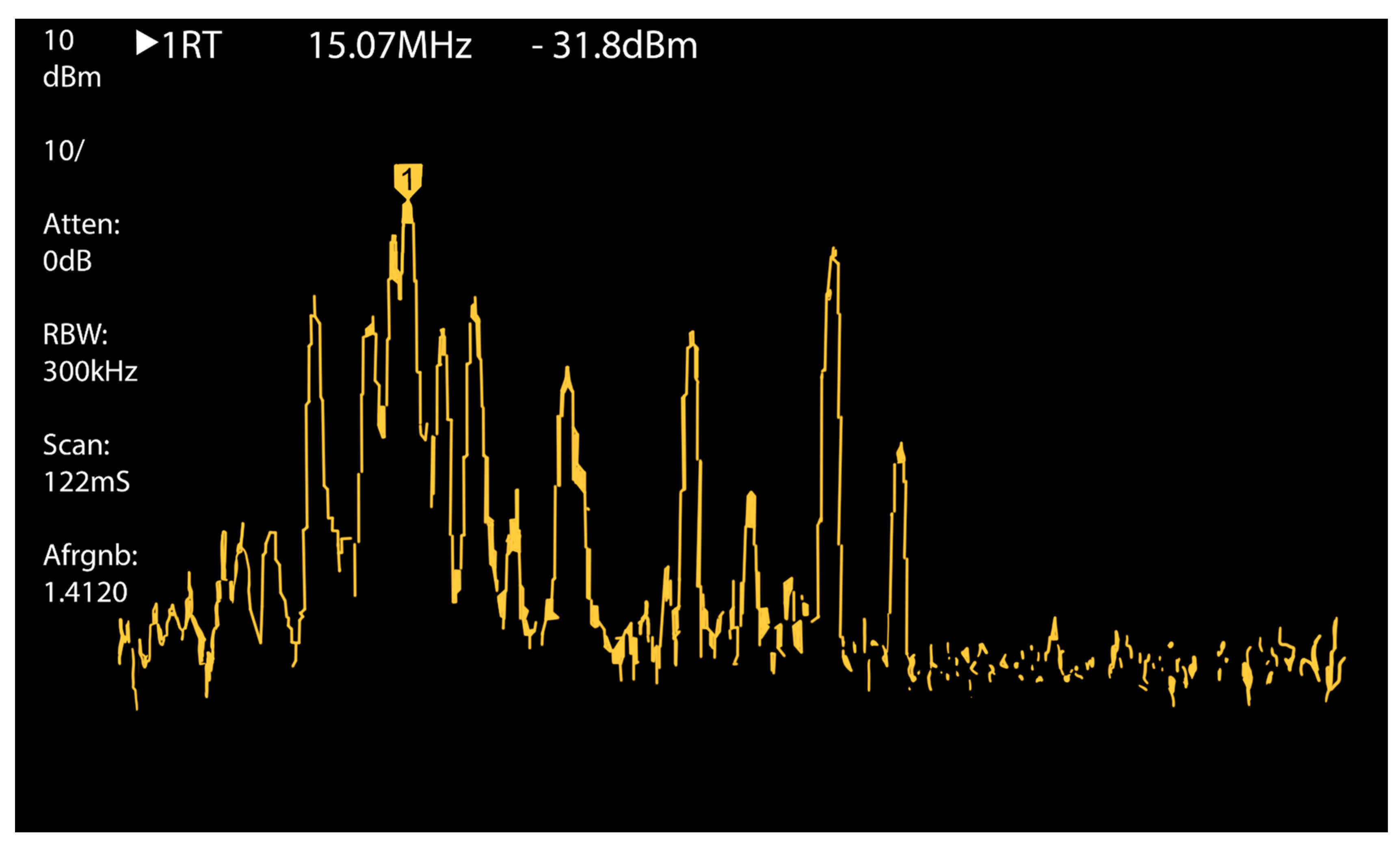
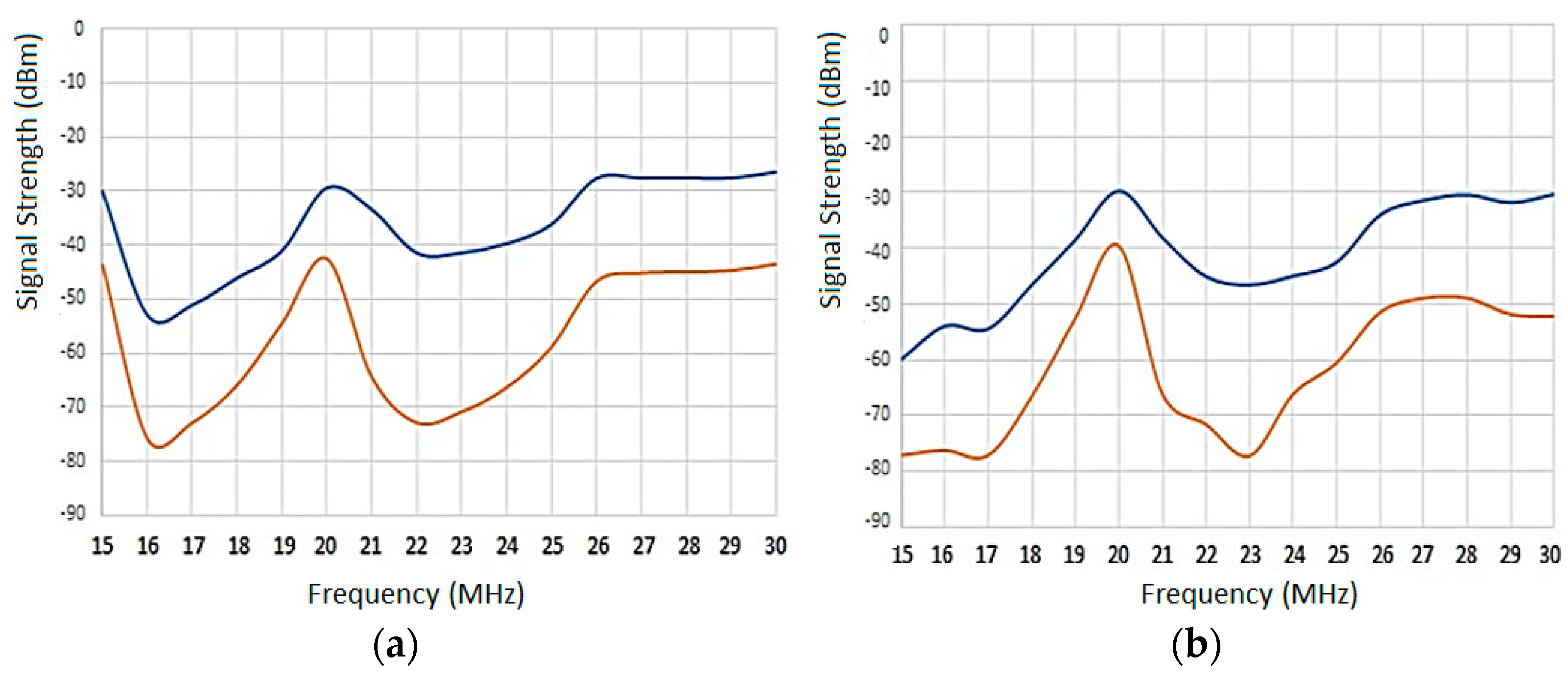

| Frequency (MHz) | Impedance (Ω) |
|---|---|
| 20 | 7.3−368 |
| 21 | 6.9−j392 |
| 22 | 6.3−j337 |
| 23 | 7.0−j322 |
| 24 | 6.9−j322 |
| 25 | 6.9−j294 |
| 26 | 6.0−j285 |
| 27 | 4.8−j274 |
| 28 | 5.5−j263 |
| 29 | 5.8−j255 |
| 30 | 4.8−j245 |
| Frequency (MHz) | LNA Input (mV) | Helical Impedance (Ω) | LNA Output (mV) | LNA Gain (dB) |
|---|---|---|---|---|
| 20 | 600 | 457−j351 | 777 | 2.24 |
| 21 | 600 | 222−j422 | 685 | 1.15 |
| 22 | 600 | 68−j329 | 566 | −0.50 |
| 23 | 600 | 65−j232 | 519 | −1.25 |
| 24 | 600 | 65−j123 | 508 | −1.40 |
| 25 | 600 | 65−j0.96 | 544 | −0.85 |
| 26 | 600 | 62+j145 | 631 | 0.43 |
| 27 | 600 | 61+j326 | 952 | 4.00 |
| 28 | 600 | 56+j559 | 4000 | 16.0 |
| 29 | 600 | 69+j900 | 2610 | 12.0 |
| 30 | 600 | 48+J1450 | 3150 | 14.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Constantinides, A.; Kousioumari, C.; Najat, S.; Haralambous, H. Low-Profile Circularly Polarized HF Helical Phased Array: Design, Analysis, and Experimental Evaluation. Appl. Sci. 2024, 14, 5075. https://doi.org/10.3390/app14125075
Constantinides A, Kousioumari C, Najat S, Haralambous H. Low-Profile Circularly Polarized HF Helical Phased Array: Design, Analysis, and Experimental Evaluation. Applied Sciences. 2024; 14(12):5075. https://doi.org/10.3390/app14125075
Chicago/Turabian StyleConstantinides, Antonios, Charalampos Kousioumari, Saam Najat, and Haris Haralambous. 2024. "Low-Profile Circularly Polarized HF Helical Phased Array: Design, Analysis, and Experimental Evaluation" Applied Sciences 14, no. 12: 5075. https://doi.org/10.3390/app14125075
APA StyleConstantinides, A., Kousioumari, C., Najat, S., & Haralambous, H. (2024). Low-Profile Circularly Polarized HF Helical Phased Array: Design, Analysis, and Experimental Evaluation. Applied Sciences, 14(12), 5075. https://doi.org/10.3390/app14125075






