Research on a Multi-Dimensional Indicator Assessment Model for Evaluating Landslide Risk near Large Alpine Reservoirs
Abstract
:1. Introduction
2. Modeling of a Multi-Dimensional Evaluation Indicator System
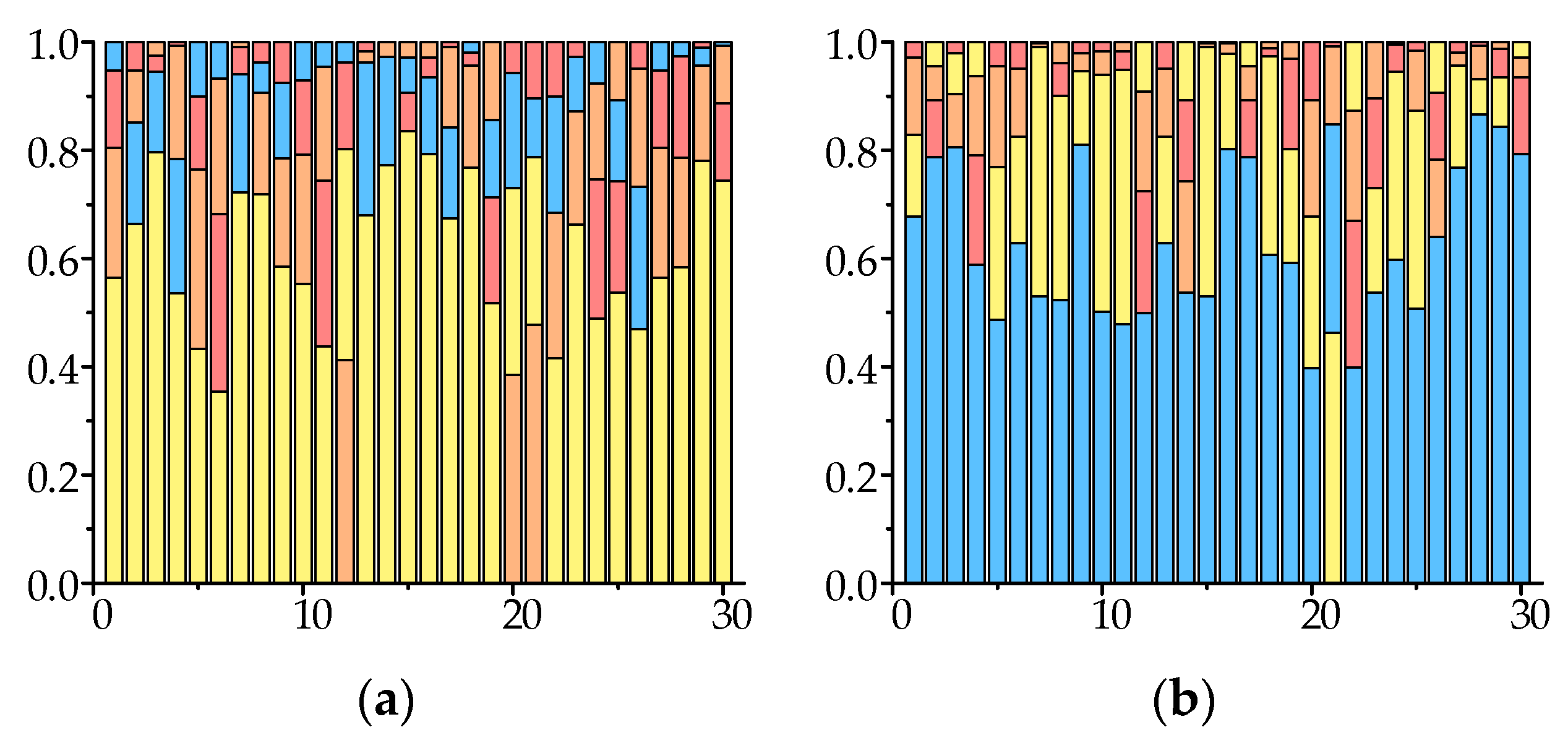
2.1. Basis and Selection of Evaluation Indicators
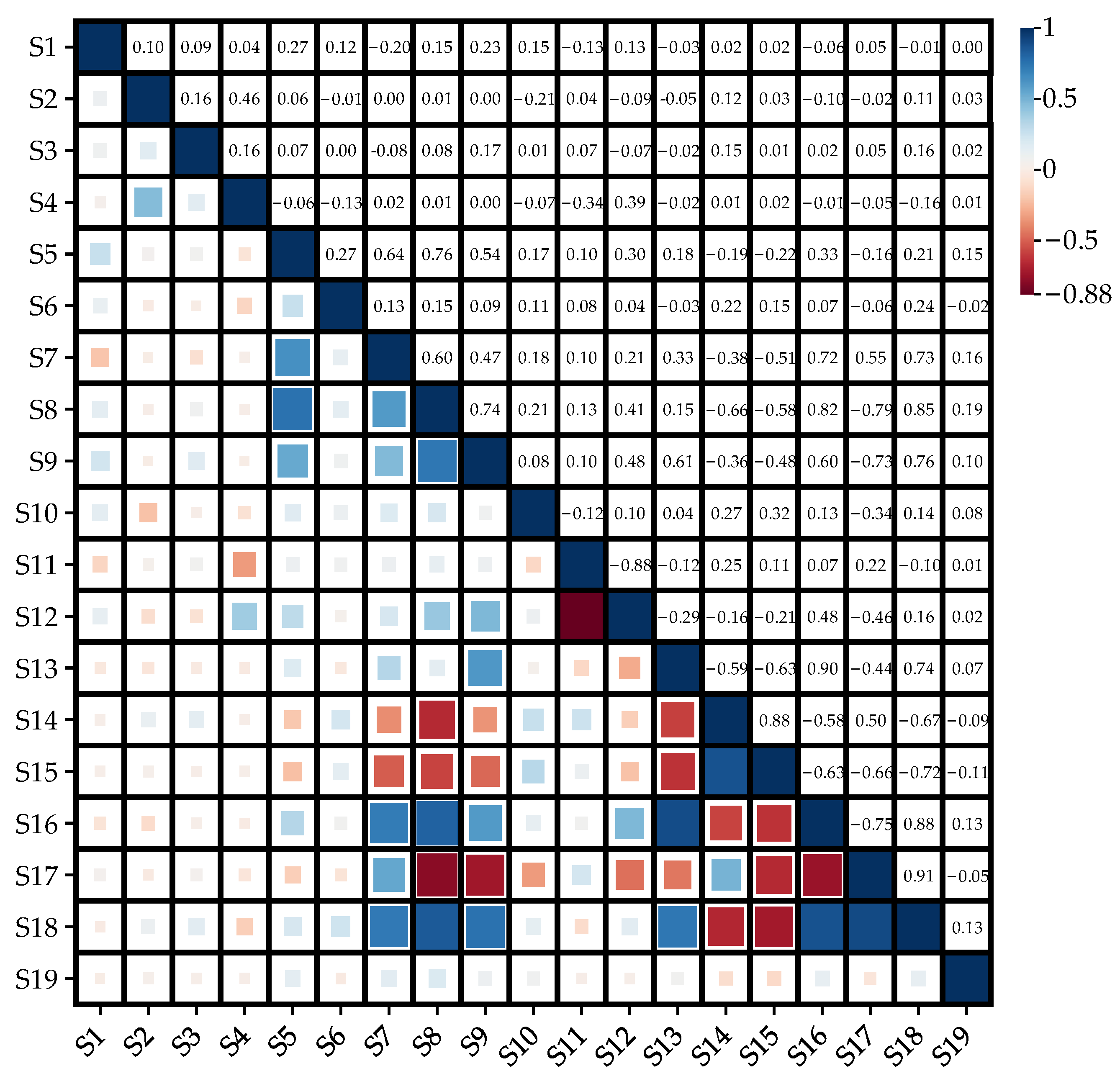
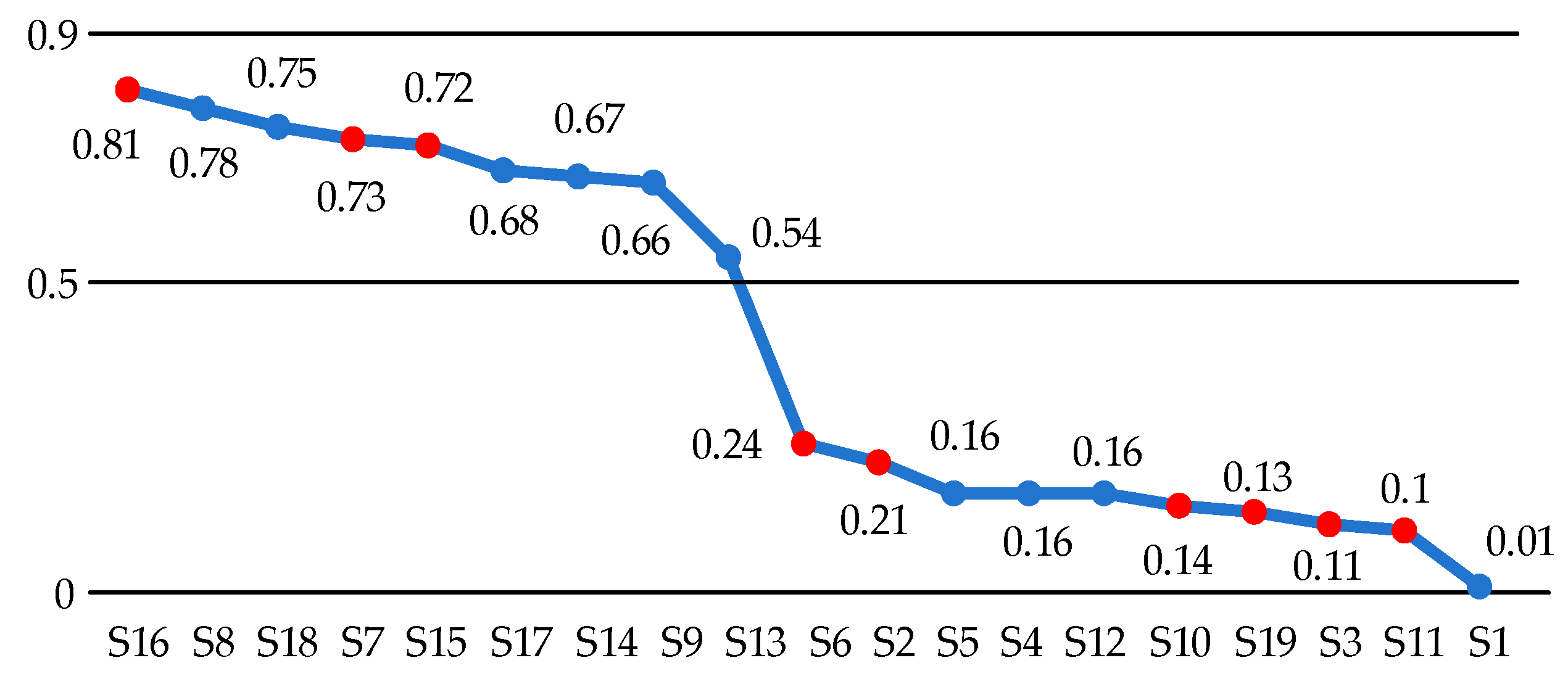
2.2. Methodology for Screening Key Evaluation Indicators
3. Fuzzy-BLS Model for Slope Risk Assessment
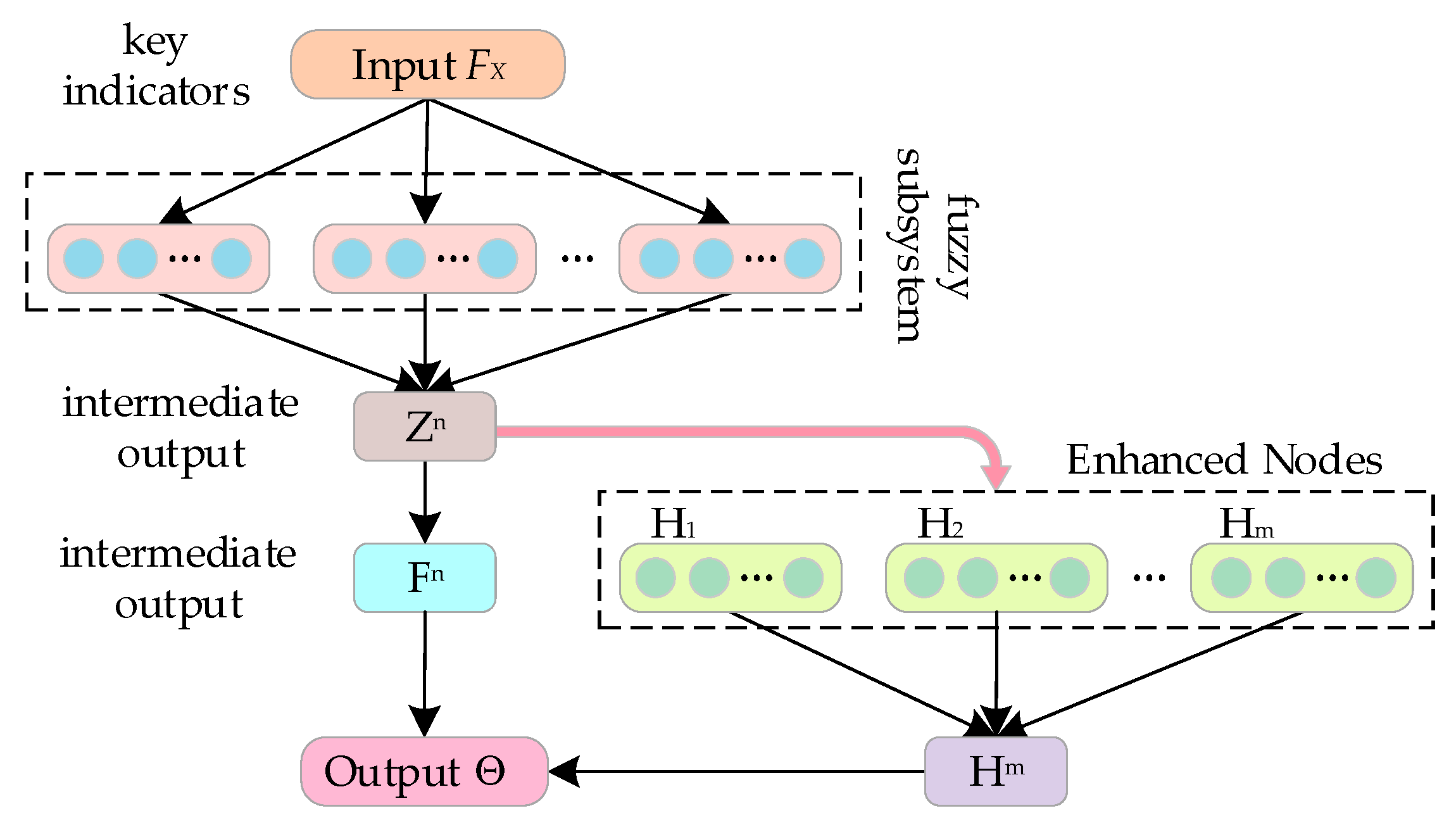
3.1. Fuzzy-BLS Risk Assessment Model Structure
3.2. Risk Assessment Model Training
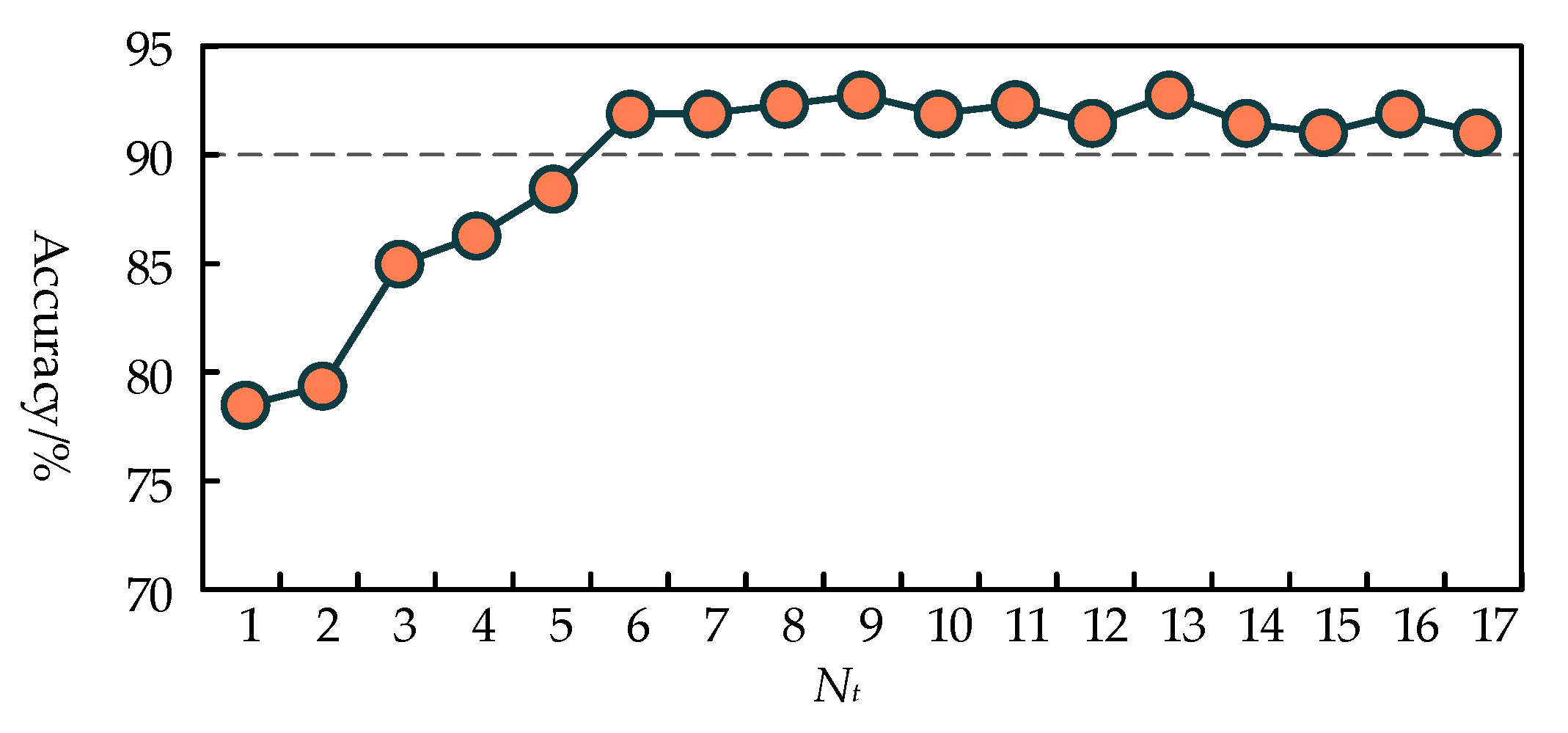
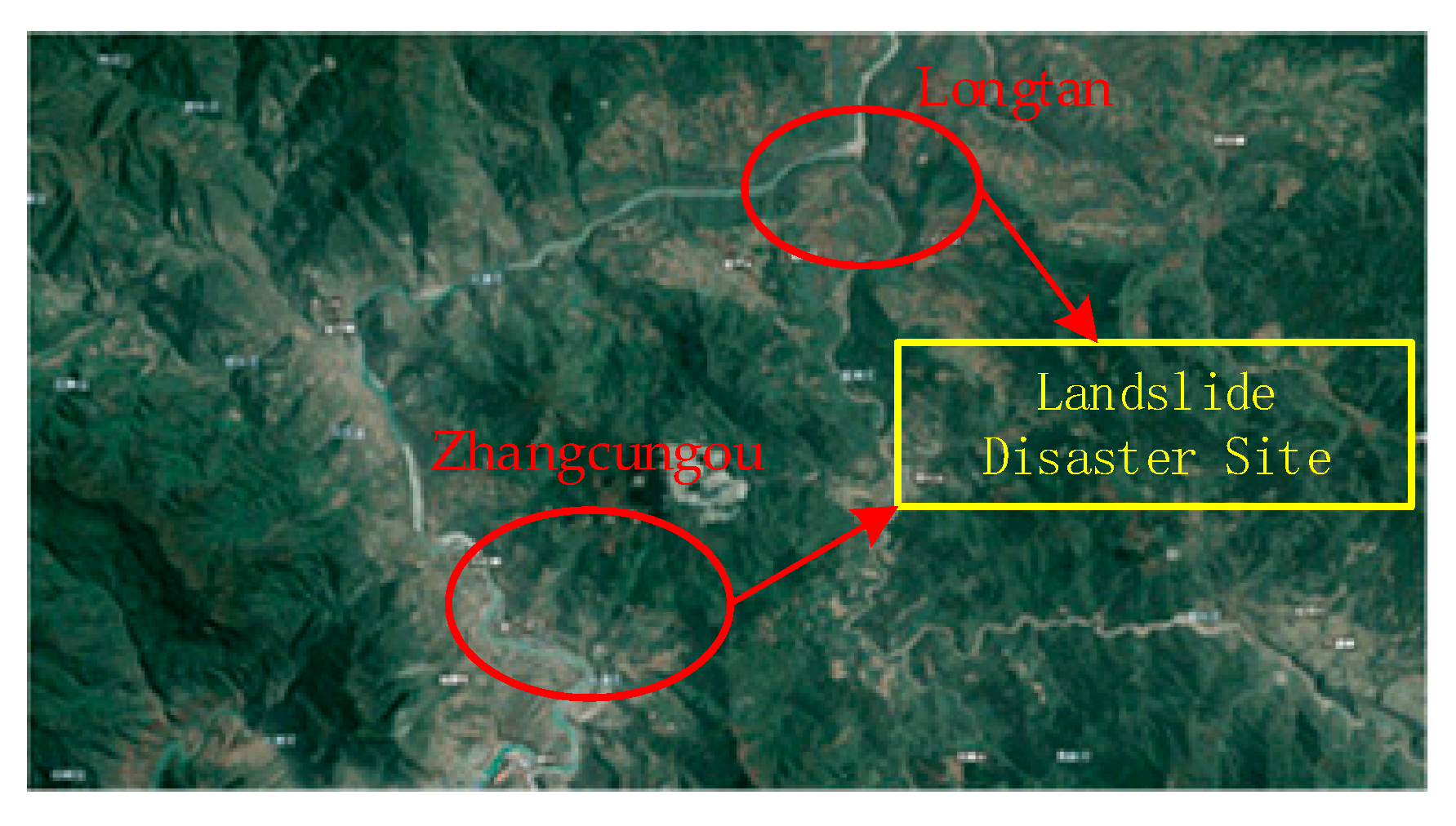
4. Application Testing and Analysis
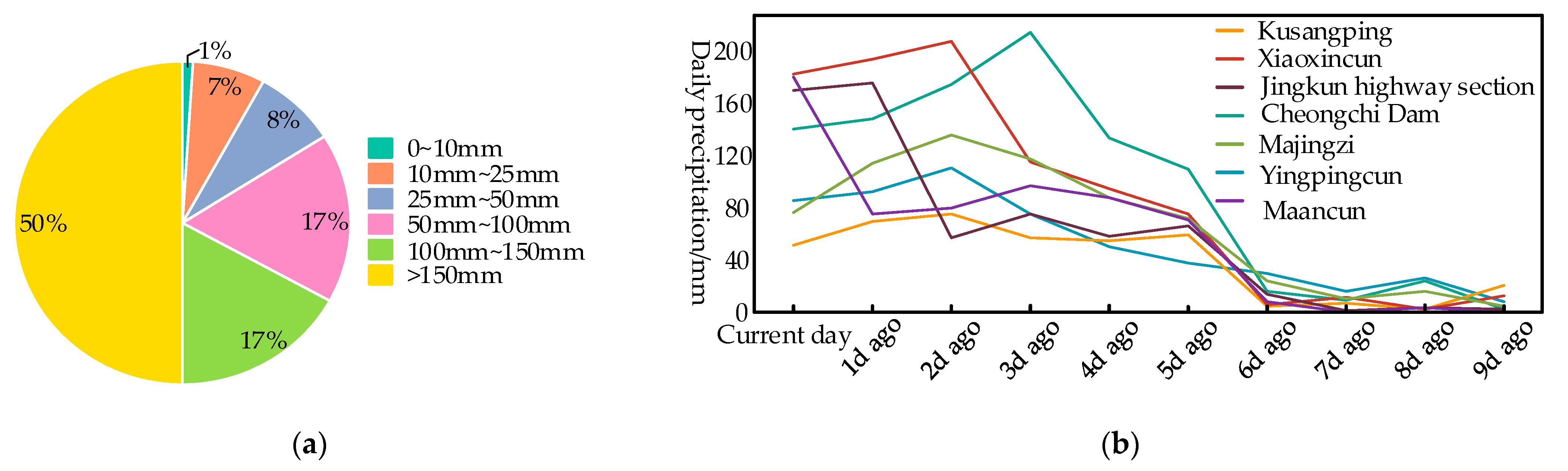
4.1. Access to Evaluation Indicators
4.2. Example Assessment Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, A.; Chi, E.; Ma, J.; Zhong, D. Application of GPS real-time monitoring system in open slope deformation monitoring. Min. Technol. 2020, 20, 140–144. [Google Scholar] [CrossRef]
- Wu, M.; Fang, Y.; Shen, Y.; Dai, K.; Yao, Y.; Chen, J.; Feng, W. Fast Dynamic ldentification of Landslide Hazards in Baihetan Reservoir area based on Short Baseline DInSAR Interferometry. Remote Sens. Technol. Appl. 2023, 38, 1054–1061. [Google Scholar]
- Bi, Z.; Li, S.; Yuan, L.; Lin, Y. Monitoring and analysis of slope deformation in Wudongde Hydropower Station reservoir area based on InSAR. Yangtze River 2024, 55, 143–150. [Google Scholar]
- Gao, B.; He, Y.; Chen, X.; Zheng, X.; Zhang, L.; Zhang, Q.; Lu, J. Landslide risk evaluation in Shenzhen based on stacking ensemble learning and InSAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 1–18. [Google Scholar] [CrossRef]
- He, K.; Chen, X.; Yu, X.; Dong, C.; Zhao, D. Evaluation and prediction of compound geohazards in highly urbanized regions across China’s Greater Bay Area. J. Clean. Prod. 2024, 449, 141641. [Google Scholar] [CrossRef]
- Shan, Y.; Xu, Z.; Zhou, S.; Lu, H.; Yu, W.; Li, Z.; Cao, X.; Li, P.; Li, W. Landslide Hazard Assessment Combined with InSAR Deformation: A Case Study in the Zagunao River Basin, Sichuan Province, Southwestern China. Remote Sens. 2024, 16, 99. [Google Scholar] [CrossRef]
- Gao, Z.; Ding, M.; Huang, T.; Liu, X.; Hao, Z.; Hu, X.; Xi, C. Landslide risk assessment of high-mountain settlements using Gaussian process classification combined with improved weight-based generalized objective function. Int. J. Disaster Risk Reduct. 2022, 67, 102662. [Google Scholar] [CrossRef]
- Chen, C.; Fang, Z. Research on an effective rainfall model for geological disaster early warning in Fujian Province, China. J. Geomech. 2023, 29, 99–110. [Google Scholar] [CrossRef]
- Fan, W.; Wei, X.; Cao, Y.; Zheng, B. Landslide susceptibility assessment using the certainty factor and analytic hierarchy process. J. Mt. Sci. 2017, 14, 906–925. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, G.; Jia, Q. Integration of analytical hierarchy process and landslide susceptibility index based landslide susceptibility assessment of the Pearl river delta area, China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4239–4251. [Google Scholar] [CrossRef]
- Yang, Y.; Guo, Y.; Chen, H.; Tang, H.; Li, M.; Sun, A.; Bian, Y. Application of a Hybrid Model in Landslide Susceptibility Evaluation of the Western Tibet Plateau. Appl. Sci. 2024, 14, 485. [Google Scholar] [CrossRef]
- Li, X.; Cheng, J.; Yu, D. Research on landslide risk assessment based on convolutional neural network. IEEE Geosci. Remote Sens. Lett. 2022, 19, 2505705. [Google Scholar] [CrossRef]
- Geng, W.; Song, Z.; He, C.; Wang, H.; Dong, X. The Impact of Fine-Layering of Tailings Dam on the Variation Pattern of Infiltration Lines. Appl. Sci. 2024, 14, 950. [Google Scholar] [CrossRef]
- Jiang, N.; Li, H.; Li, C.; Xiao, H.; Zhou, J. A fusion method using terrestrial laser scanning and unmanned aerial vehicle photogrammetry for landslide deformation monitoring under complex terrain conditions. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4707214. [Google Scholar] [CrossRef]
- Gao, F.; Gao, X.; Yang, C.; Li, J. Research on the Evolution Network Model of the Landslide Disaster Chain: A Case Study of the Baige Landslide. Appl. Sci. 2024, 14, 499. [Google Scholar] [CrossRef]
- Glueer, F.; Mreyen, A.-S.; Cauchie, L.; Havenith, H.-B.; Bergamo, P.; Halló, M.; Fäh, D. Integrating Seismic Methods for Characterizing and Monitoring Landslides: A Case Study of the Heinzenberg Deep-Seated Gravitational Slope Deformation (Switzerland). Geosciences 2024, 14, 28. [Google Scholar] [CrossRef]
- Li, Q.; Sun, Y.; Wang, S.; Wang, B.; Deng, G.; Zhang, C. Deformation characteristics of active landslides in Xiluodu reservoir area based on InSAR technology. Miner. Explor. 2024, 15, 311–319. [Google Scholar] [CrossRef]
- Wang, R.; Wan, J.; Cheng, R.; Wang, Y.; Wang, Z. Physical and Numerical Simulation of the Mechanism Underpinning Accumulation Layer Deformation, Instability, and Movement Caused by Changing Reservoir Water Levels. Water 2023, 15, 1289. [Google Scholar] [CrossRef]
- Bao, X.; Jiang, Y.; Zhang, L.; Liu, B.; Chen, L.; Zhang, W.; Xie, L.; Liu, X.; Qu, F.; Wu, R. Accurate Prediction of Dissolved Oxygen in Perch Aquaculture Water by DE-GWO-SVR Hybrid Optimization Model. Appl. Sci. 2024, 14, 856. [Google Scholar] [CrossRef]
- Tan, R.; Zhang, W.; Chen, S. Decision-making method based on grey relation analysis and trapezoidal fuzzy neutrosophic numbers under double incomplete information and its application in typhoon disaster assessment. IEEE Access 2019, 8, 3606–3628. [Google Scholar] [CrossRef]
- Feng, S.; Chen, C.L.P. Fuzzy broad learning system: A novel neuro-fuzzy model for regression and classification. IEEE Trans. Cybern. 2018, 50, 414–424. [Google Scholar] [CrossRef] [PubMed]


| Type of Indicator | Number | Indicator | Mathematical Unit | Empirical |
|---|---|---|---|---|
| Terrain morphology | S1 | Aspect | % | 0.05–0.1 |
| S2 | Slope (F1) | % | 0.15–0.25 | |
| S3 | Curvature (F2) | rad/m | 0.1–0.2 | |
| S4 | Elevation | m | 0.05–0.1 | |
| Meteorological condition | S5 | Humidity | % | 0.4–0.5 |
| S6 | Temperature (F3) | °C | 0.25–0.4 | |
| S7 | Daily precipitation (F4) | mm | 0.7–0.8 | |
| S8 | Three-day cumulative precipitation | mm | 0.75–0.85 | |
| S9 | Five-day cumulative precipitation | mm | 0.65–0.8 | |
| Ecological environment | S10 | Vegetation coverage (F5) | % | 0.3–0.4 |
| S11 | Normalized Difference Vegetation Index (F6) | / | 0.2–0.3 | |
| S12 | Normalized Difference Water Index | / | 0.25–0.35 | |
| Soil moisture condition | S13 | Soil bulk density | N/m3 | 0.4–0.6 |
| S14 | Angle of internal soil friction | N/m2 | 0.55–0.65 | |
| S15 | Soil shear strength (F7) | kPa | 0.6–0.7 | |
| S16 | Soil moisture content (F8) | % | 0.8–0.9 | |
| S17 | Porosity ratio | % | 0.65–0.7 | |
| S18 | Topographic Wetness Index | / | 0.75–0.85 | |
| Human activity | S19 | Reservoir water level (F9) | m | 0.15–0.25 |
| External manifestation | S20 | Slope deformation (F10) | mm | 0.9–0.95 |
| Performance | Training Time/s | Training Accuracy | Testing Accuracy | |||||
|---|---|---|---|---|---|---|---|---|
| Proportion | Blanket | Attention Level | Warning Level | Alert Level | Alarm Level | |||
| 6:4 | 5.0207 | 68.75% | 78.75% | 85% | 71.67% | 74.17% | 84.17% | |
| 7:3 | 6.7221 | 76.67% | 83.61% | 90% | 81.11% | 74.44% | 88.89% | |
| 8:2 | 7.4879 | 88.13% | 92.08% | 91.67% | 88.33% | 93.33% | 95% | |
| 9:1 | 10.2057 | 82.22% | 93.33% | 96.67% | 86.67% | 93.33% | 96.67% | |
| 19:1 | 12.0384 | 82.46% | 93.33% | 100% | 80% | 93.33% | 100% | |
| Risk Assessment Models | Testing Accuracy | ||||
|---|---|---|---|---|---|
| Blanket | Attention Level | Warning Level | Alert Level | Alarm Level | |
| Fuzzy-BLS | 92.08% | 91.67% | 88.33% | 93.33% | 95% |
| BLS | 90.83% | 95% | 86.67% | 90% | 91.67% |
| XGBoost | 88.33% | 88.33% | 88.33% | 85% | 91.67% |
| SVM | 79.17% | 78.33% | 73.33% | 81.67% | 83.33% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, H.; Ke, H.; Zhang, X.; Yi, J. Research on a Multi-Dimensional Indicator Assessment Model for Evaluating Landslide Risk near Large Alpine Reservoirs. Appl. Sci. 2024, 14, 5201. https://doi.org/10.3390/app14125201
Hu H, Ke H, Zhang X, Yi J. Research on a Multi-Dimensional Indicator Assessment Model for Evaluating Landslide Risk near Large Alpine Reservoirs. Applied Sciences. 2024; 14(12):5201. https://doi.org/10.3390/app14125201
Chicago/Turabian StyleHu, Hanyin, Hu Ke, Xinyao Zhang, and Jianbo Yi. 2024. "Research on a Multi-Dimensional Indicator Assessment Model for Evaluating Landslide Risk near Large Alpine Reservoirs" Applied Sciences 14, no. 12: 5201. https://doi.org/10.3390/app14125201
APA StyleHu, H., Ke, H., Zhang, X., & Yi, J. (2024). Research on a Multi-Dimensional Indicator Assessment Model for Evaluating Landslide Risk near Large Alpine Reservoirs. Applied Sciences, 14(12), 5201. https://doi.org/10.3390/app14125201





