The Prediction of Incremental Damage on Optics from the Final Optic Assembly in an ICF High-Power Laser Facility
Abstract
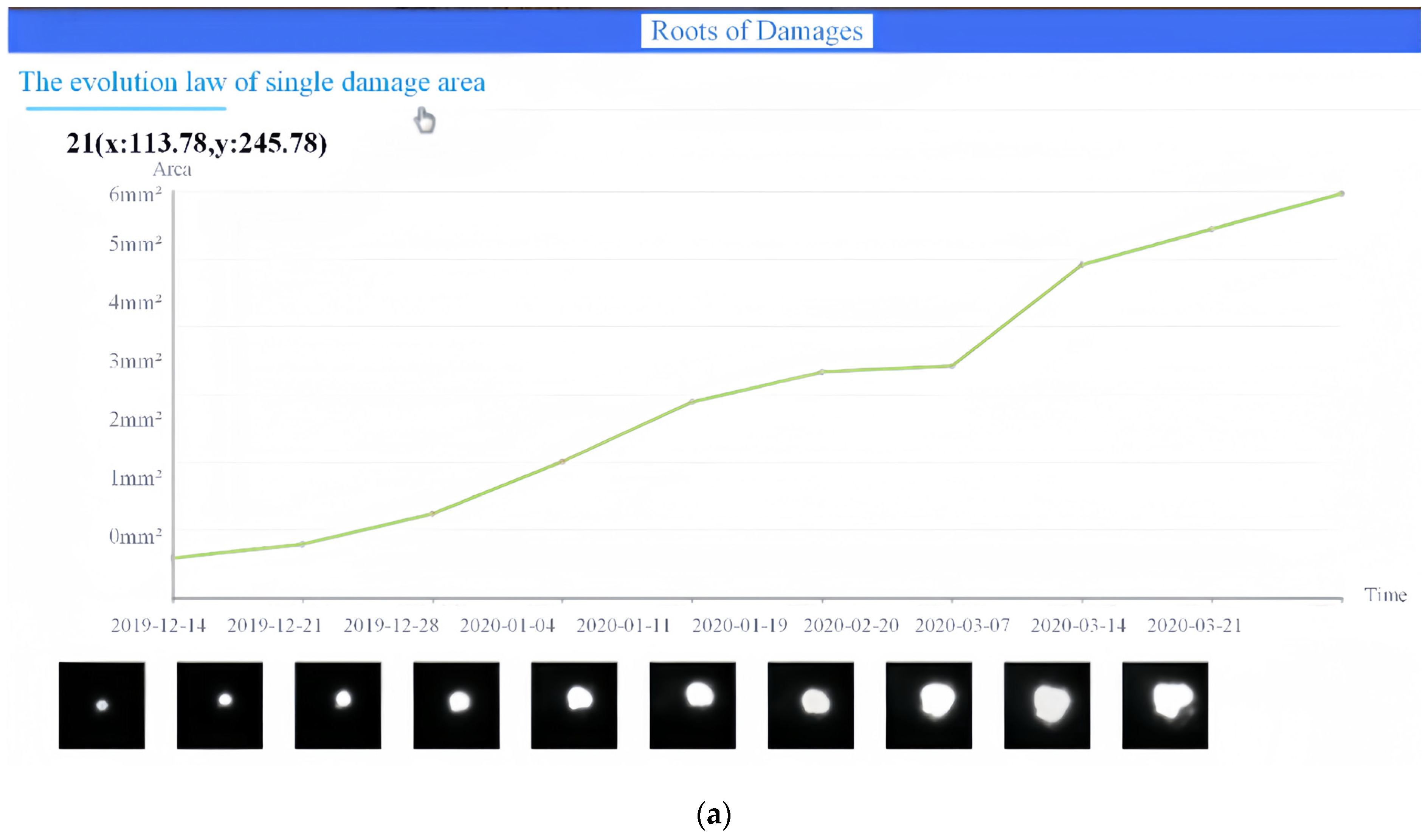
1. Introduction
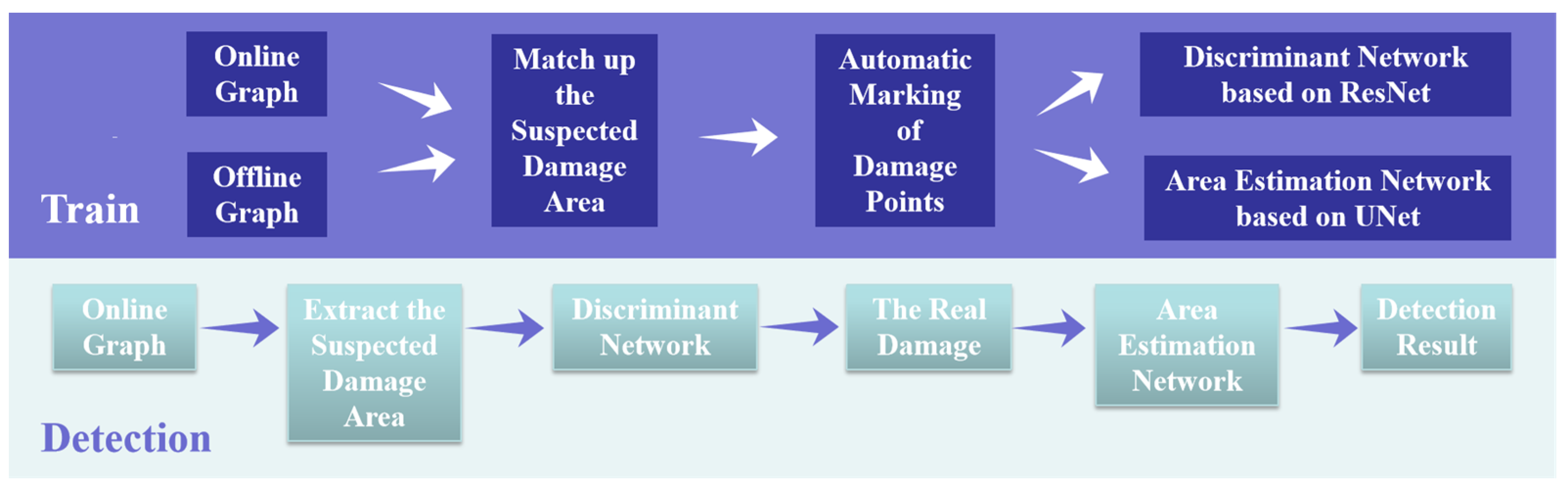
2. Methods
3. Implementation
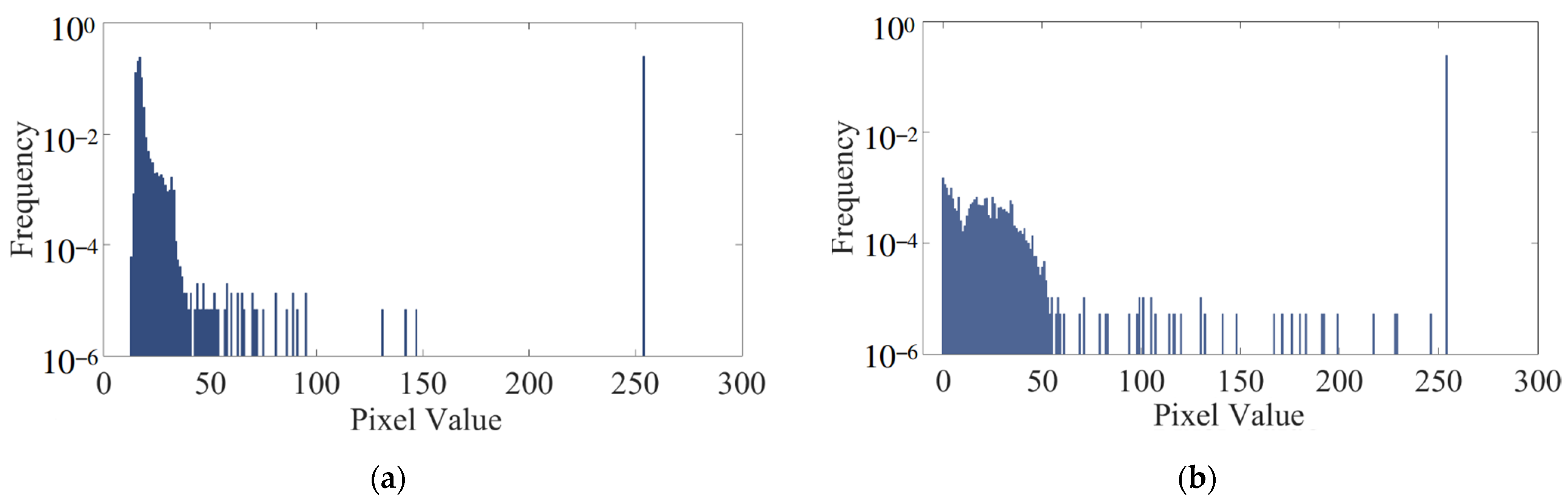
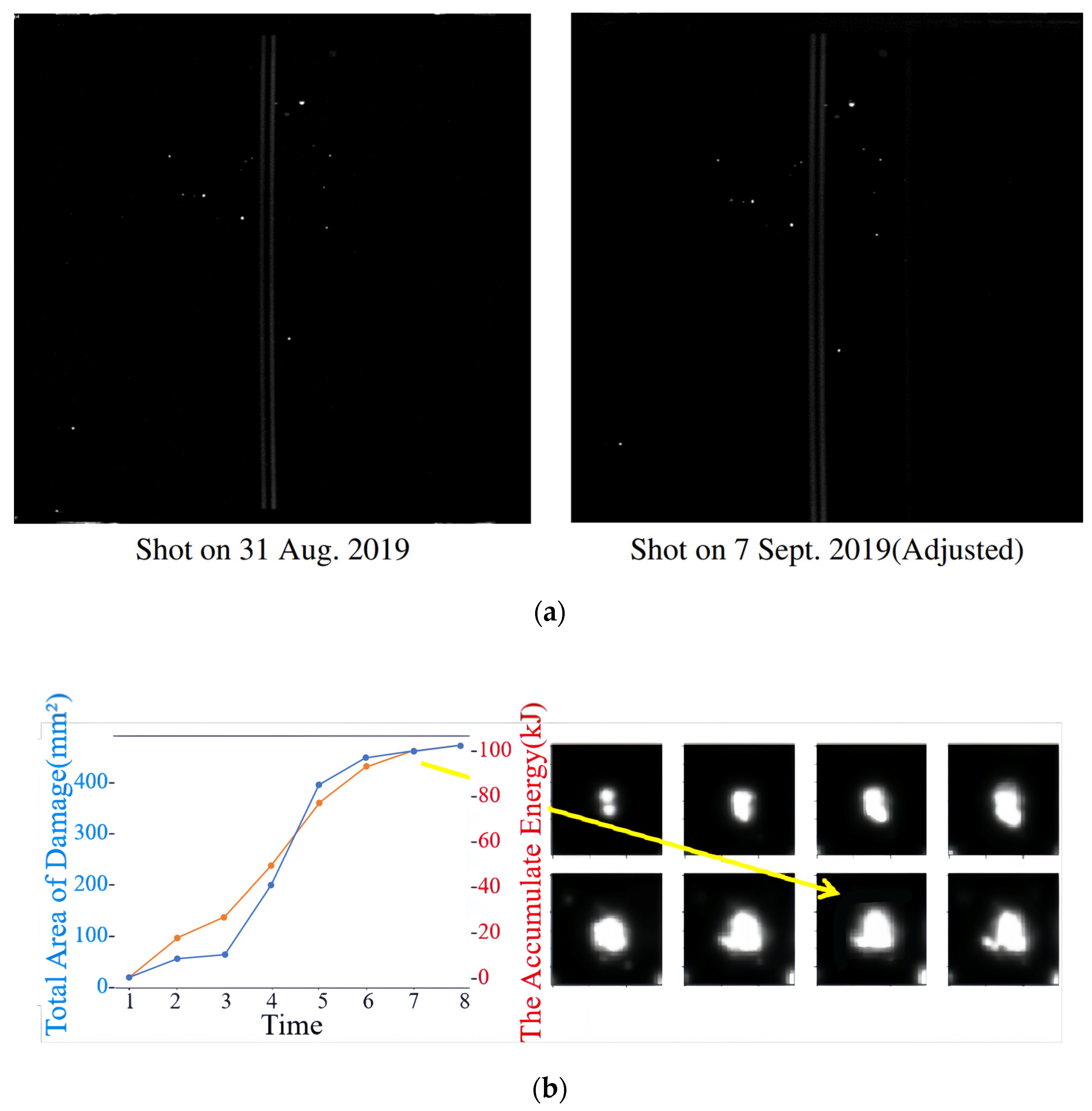
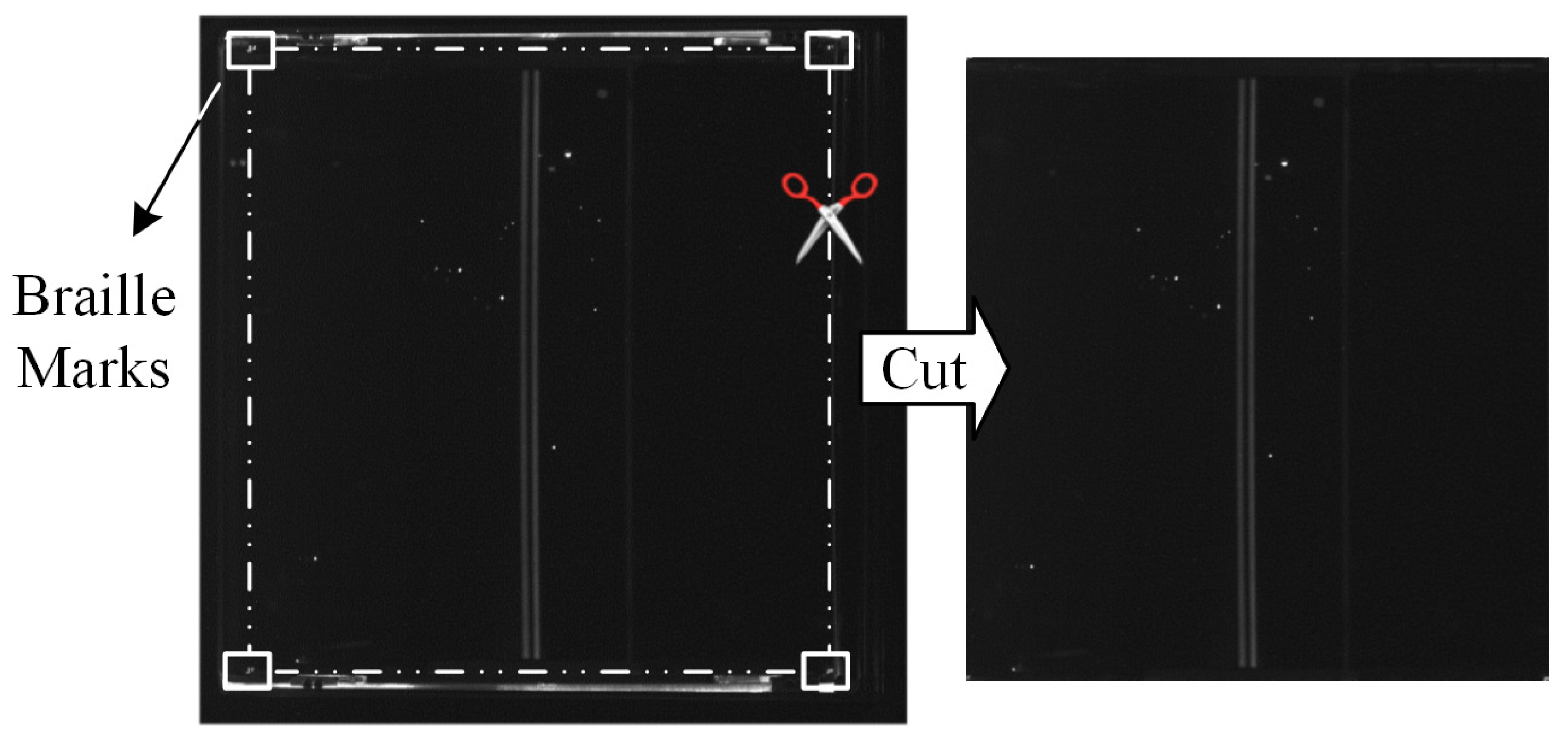
3.1. Data Preprocessing
- (a)
- Image Preprocessing: identical areas marked by braille marks were extracted from all images;
- (b)
- Grayscale Normalization: grayscale distributions within these areas were normalized to ensure consistency across images;
- (c)
- Criterion Selection: the image with the maximum grayscale value (piupper) was selected as the criterion;
- (d)
- Grayscale Adjustment: grayscale intervals of other images were adjusted to match the criterion image;
- (e)
- Coefficient Calculation: each image was assigned its adjustment coefficient (co(i)), likely based on its grayscale values relative to the criterion image;
- (f)
- Adjustment Application: the pixel values of each image were multiplied by their respective adjustment coefficients to achieve uniform brightness values across the image set.
co(i) = piupper(i)/piupper(0) (i∈[1,n])
piadj(i)(j) = piori(i)(j)·co(i) (j∈[1,mi])
r(i, j) = |i − j|
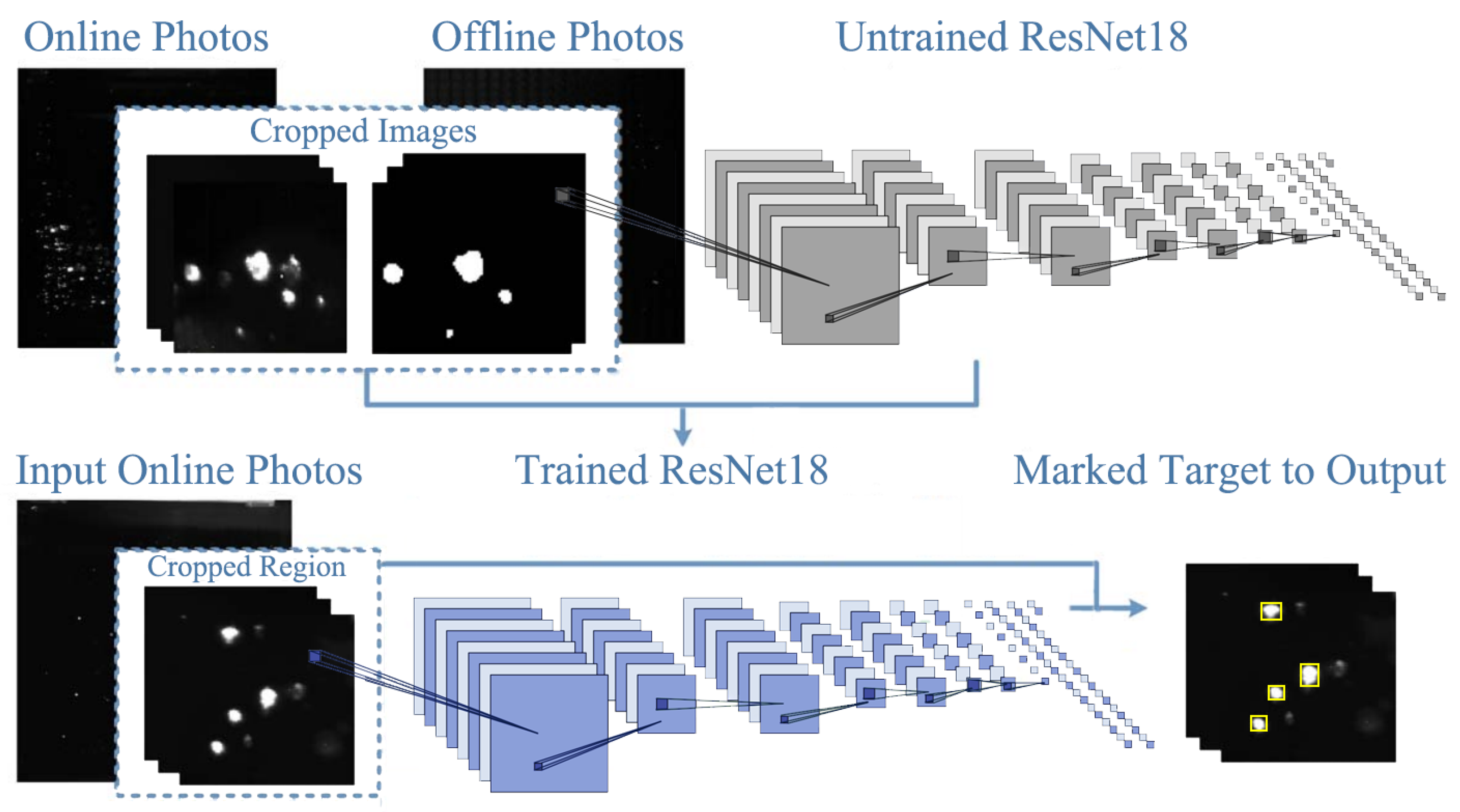
3.2. Algorithm and Model Training
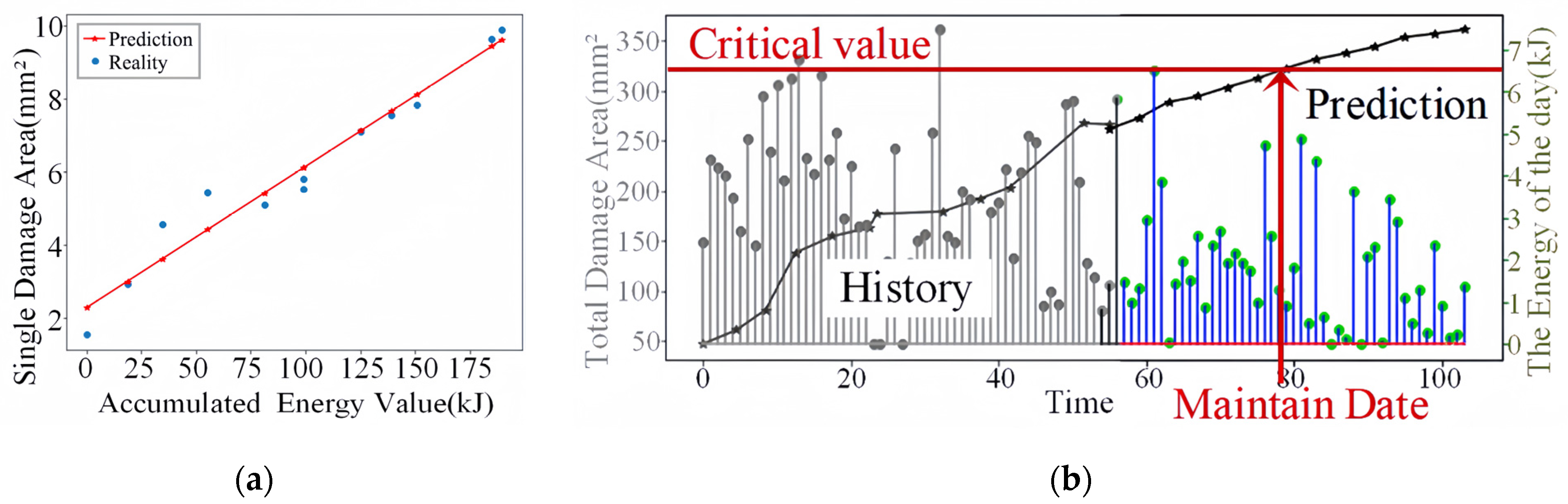
4. Results
R = TP/(TP + FN)
F1 = 2PR/(P + R)
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, G. Overview of the latest progress in laser inertial confinement fusion (ICF). Nucl. Sci. Eng. 1997, 017, 266–269. [Google Scholar]
- Howard Lowdermilk, W. Inertial Confinement Fusion Program at Lawrence Livermore National Laboratory: The National Ignition Facility, Inertial Fusion Energy, 100–1000 TW Lasers, and the Fast Igniter Concept. J. Nonlinear Opt. Phys. Mater. 1997, 06, 507–533. [Google Scholar] [CrossRef]
- Tabak, M.; Hammer, J.; Glinsky, M.E.; Kruer, W.L.; Wilks, S.C.; Woodworth, J.; Campbell, E.M.; Perry, M.D.; Mason, R.J. Ignition and high gain with ultrapowerful lasers. Phys. Plasmas 1998, 1, 1626–1634. [Google Scholar] [CrossRef]
- Hirsch, R.L. Inertial-Electrostatic Confinement of Ionized Fusion Gases. J. Appl. Phys. 1967, 38, 4522–4534. [Google Scholar] [CrossRef]
- Zhu, Q.; Zheng, W.; Wei, X.; Jing, F.; Hu, D.; Zhou, W.; Feng, B.; Wang, J.; Peng, Z.; Liu, L.; et al. Research and construction progress of the SG III laser facility. In Proceedings of the SPIE/SIOM Pacific Rim Laser Damage: Optical Materials for High-Power Lasers, Shanghai, China, 19 May 2013. [Google Scholar]
- Wegner, P.J.; Auerbach, J.M.; Biesiada, T.; Dixit, S.N.; Lawson, J.K.; Menapace, J.A.; Parham, T.G.; Swift, D.W.; Whitman, P.K.; Williams, W.H. NIF final optics system: Frequency conversion and beam conditioning. In Optical Engineering at the Lawrence Livermore National Laboratory II: The National Ignition Facility; SPIE: Bellingham, WA, USA, 2004. [Google Scholar] [CrossRef]
- Spaeth, M.L.; Wegner, P.J.; Suratwala, T.I.; Nostrand, M.C.; Bude, J.D.; Conder, A.D.; Folta, J.A.; Heebner, J.E.; Kegelmeyer, L.M.; MacGowan, B.J.; et al. Optics Recycle Loop Strategy for NIF Operations Above UV Laser-Induced Damage Threshold. Fusion Sci. Technol. 2016, 69, 265–294. [Google Scholar] [CrossRef]
- Baisden, P.A.; Atherton, L.J.; Hawley, R.A.; Land, T.A.; Menapace, J.A.; Miller, P.E.; Runkel, M.J.; Spaeth, M.L.; Stolz, C.J.; Suratwala, T.I.; et al. Large Optics for the National Ignition Facility. Fusion Sci. Technol. 2016, 69, 614–620. [Google Scholar] [CrossRef]
- Liao, Z.M.; Nostrand, M.; Whitman, P.; Bude, J. Analysis of Optics Damage Growth at the National Ignition Facility; SPIE Laser Damage: Boulder, CO, USA, 2015. [Google Scholar]
- Norton, M.A.; Donohue, E.E.; Hollingsworth, W.G.; Feit, M.D.; Rubenchik, A.M.; Hackel, R.P. Growth of laser initiated damage in fused silica at 1053 nm. In Boulder Damage Symposium XXXVI; Proc. SPIE: Boulder, CO, USA, 2005; Volume 5647, pp. 197–205. [Google Scholar]
- Norton, M.A.; Donohue, E.E.; Hollingsworth, W.G.; McElroy, J.N.; Hackel, R.P. Growth of laser-initiated damage in fused silica at 527 nm. In Laser-Induced Damage in Optical Materials; Proc. SPIE: Boulder, CO, USA, 2004; Volume 5273, pp. 236–243. [Google Scholar]
- Norton, M.A.; Hrubesh, L.W.; Wu, Z.; Donohue, E.E.; Feit, M.D.; Kozlowski, M.R.; Milam, D.; Neeb, K.P.; Molander, W.A.; Rubenchik, A.M.; et al. Growth of laser-initiated damage in fused silica at 351 nm. Opt. Eng. 2001, 5273, 468. [Google Scholar]
- Schwartz, S.; Feit, M.D.; Kozlowski, M.R.; Mouser, R.P. Current 3-ω large optic test procedures and data analysis for the quality assurance of national ignition facility optics. In Laser-Induced Damage in Optical Materials; Proc. SPIE—The International Society for Optical Engineering: Boulder, CO, USA, 1999; Volume 3578. [Google Scholar] [CrossRef]
- Sheehan, L.M.; Hendrix, J.L.; Battersby, C.L.; Oberhelman, S. National Ignition Facility small optics laser-induced damage and photometry measurements program. In Spies International Symposium on Optical Science; International Society for Optics and Photonics: Boulder, CO, USA, 1999. [Google Scholar] [CrossRef]
- Nalwa, H.S. Organometallic materials for nonlinear optics. Appl. Organomet. Chem. 1991, 5, 349–377. [Google Scholar] [CrossRef]
- Miller, C.; Kegelmeyer, L.; Nostrand, M.; Raman, R.; Cross, D.; LIao, Z.; Garcha, R.; Carr, W. Method to Characterize Small Damage Sites to Increase the Lifetime of NIF Fused Silica Optics; Lawrence Livermore National Laboratory: Livermore, CA, USA, 2018. Available online: https://www.osti.gov/servlets/purl/1476215 (accessed on 25 August 2022).
- Nostrand, M.C.; Cerjan, C.J.; Johnson, M.A.; Suratwala, T.I.; Weiland, T.L.; Sell, W.D.; Vickers, J.L.; Luthi, R.L.; Stanley, J.R.; Parham, T.G.; et al. Correlation of laser-induced damage to phase objects in bulk fused silica. In Boulder Damage Symposium XXXVI; Proc. SPIE: Boulder, CO, USA, 2005; Volume 5647, pp. 233–246. [Google Scholar]
- Guss, G.M.; Bass, I.L.; Hackel, R.P.; Mailhiot, C.; Demos, S.G. In situ monitoring of surface postprocessing in large-aperture fused silica optics with optical coherence tomography. Appl. Opt. 2008, 47, 4569–4573. [Google Scholar] [CrossRef]
- Raman, R.N.; Matthews, M.J.; Adams, J.J.; Demos, S.G. Monitoring annealing via CO2 laser heating of defect populations on fused silica surfaces using photoluminescence microscopy. Opt. Express 2010, 18, 15207–15215. [Google Scholar] [CrossRef]
- Wu, X.; Sahoo, D.; Hoi, S.C.H. Recent Advances in Deep Learning for Object Detection. Neurocomputing 2020, 396, 39–64. [Google Scholar] [CrossRef]
- Zheng, W. Load Capacity of High Power Laser Device and Related Physical Problems; Science Press: Beijing, China, 2014. [Google Scholar]
- Sasaki, T.; Yokotani, A. Growth of large KDP crystals for laser fusion experiments. J. Cryst. Growth 1990, 99 Pt 2, 820–826. [Google Scholar] [CrossRef]
- Carr, A.; Kegelmeyer, L.; Liao, Z.M.; Abdulla, G.; Cross, D.; Kegelmeyer, W.P.; Ravizza, F.; Carr, C.W. Defect Classification Using Machine Learning; SPIE—The International Society for Optical Engineeringaser: Boulder, CO, USA, 2008. [Google Scholar]
- Abdulla, G.M.; Kegelmeyer, L.M.; Liao, Z.M.; Carr, W. Effective and efficient optics inspection approach using machine learning algorithms. In Laser Damage Symposium XLII: Annual Symposium; SPIE: Boulder, CO, USA, 2010. [Google Scholar]
- Li, L.; Liu, D.; Cao, P.; Xie, S.; Li, Y.; Chen, Y.; Yang, Y. Automated discrimination between digs and dust particles on optical surfaces with dark-field scattering microscopy. Appl. Opt. 2014, 53, 5131–5140. [Google Scholar] [CrossRef] [PubMed]
- Wei, F. Research on Intelligent Detection Method of Weak Feature Damage of Large Aperture Optics. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2019. [Google Scholar]
- Cheng, Y.; Zhao, D.; Wang, Y.; Pei, G. Multi-label learning of kernel extreme learning machine with non-equilibrium label completion. Acta Electron. Sin. 2019, 178, 1–10. [Google Scholar]
- Ongena, J.; Ogawa, Y. Nuclear fusion: Statusreport and future prospects. Energy Policy 2016, 96, 770–778. [Google Scholar] [CrossRef]
- Pryatel, J.A.; Gourdin, W.H. Clean assembly practices to prevent contamination and damage to optics. In Proceedings of the Boulder Damage Symposium XXXVII: Annual Symposium on Optical Materials for High Power Lasers, Boulder, CO, USA, 19 September 2006. [Google Scholar]
- Medel-Vera, C.; Vidal-Estévez, P.; Mädler, T. A convolutional neural network approach to classifying urban spaces using generative tools for data augmentation. Int. J. Archit. Comput. 2024. [Google Scholar] [CrossRef]
- Mennens, J.; Van Tichelen, L.; Francois, G.; Engelen, J.J. Optical recognition of Braille writing using standard equipment. IEEE Trans. Rehabil. Eng. 1994, 2, 207–212. [Google Scholar] [CrossRef]
- Ballard, D.H. Generalizing the hough transform to detect arbitrary shapes. Pattern Recognit. 1981, 13, 111–122. [Google Scholar] [CrossRef]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Bhargavi, K.; Babu, B.S. Application of Convoluted Neural Network and Its Architectures for Fungal Plant Disease Detection; IGI Global: Hershey, PA, USA, 2021. [Google Scholar]
- Bello, I.; Fedus, W.; Du, X.; Cubuk, E.D.; Srinivas, A.; Lin, T.Y.; Shlens, J.; Zoph, B. Revisiting ResNets: Improved Training and Scaling Strategies. Adv. Neural Inf. Process. Syst. 2021, 34, 22614–22627. [Google Scholar] [CrossRef]
- Wang, R.; Zhou, X.; Liu, Y.; Liu, D.; Lu, Y.; Su, M. Identification of the Surface Cracks of Concrete Based on ResNet-18 Depth Residual Network. Appl. Sci. 2024, 14, 3142. [Google Scholar] [CrossRef]
- Khan, B.A.; Jung, J.-W. Semantic Segmentation of Aerial Imagery Using U-Net with Self-Attention and Separable Convolutions. Appl. Sci. 2024, 14, 3712. [Google Scholar] [CrossRef]
- Falk, T.; Mai, D.; Bensch, R.; Cicek, O.; Abdulkadir, A.; Marrakchi, Y.; Bohm, A.; Deubner, J.; Jackel, Z.; Seiwald, K.; et al. U-net: Deep learning for cell counting, detection, and morphometry. Nat. Methods 2018, 16, 67–70. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.W.; Rahman Siddiquee, M.M.; Tajbakhsh, N.; Liang, J.M. UNet++: A Nested U-Net Architecture for Medical Image Segmentation. In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support; Springer International Publishing: Cham, Switzerland, 2018; Volume 11045. [Google Scholar] [CrossRef]
- Lin, T.Y.; Dollar, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature Pyramid Networks for Object Detection. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar] [CrossRef]
- Park, C.; Lee, S.; Han, H. Efficient Shot Detector: Lightweight Network Based on Deep Learning Using Feature Pyramid. Appl. Sci. 2021, 11, 8692. [Google Scholar] [CrossRef]
- Kegelmeyer, L.; Fong, P.; Glenn, S.; Liebman, J.A. Local Area Signal-to-Noise Ratio (LASNR) Algorithm for Image Segmentation; Proc. SPIE—The International Society for Optical Engineering: Boulder, CO, USA, 2007; Volume 6696. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015; Available online: https://arxiv.org/abs/1412.6980 (accessed on 6 September 2022).




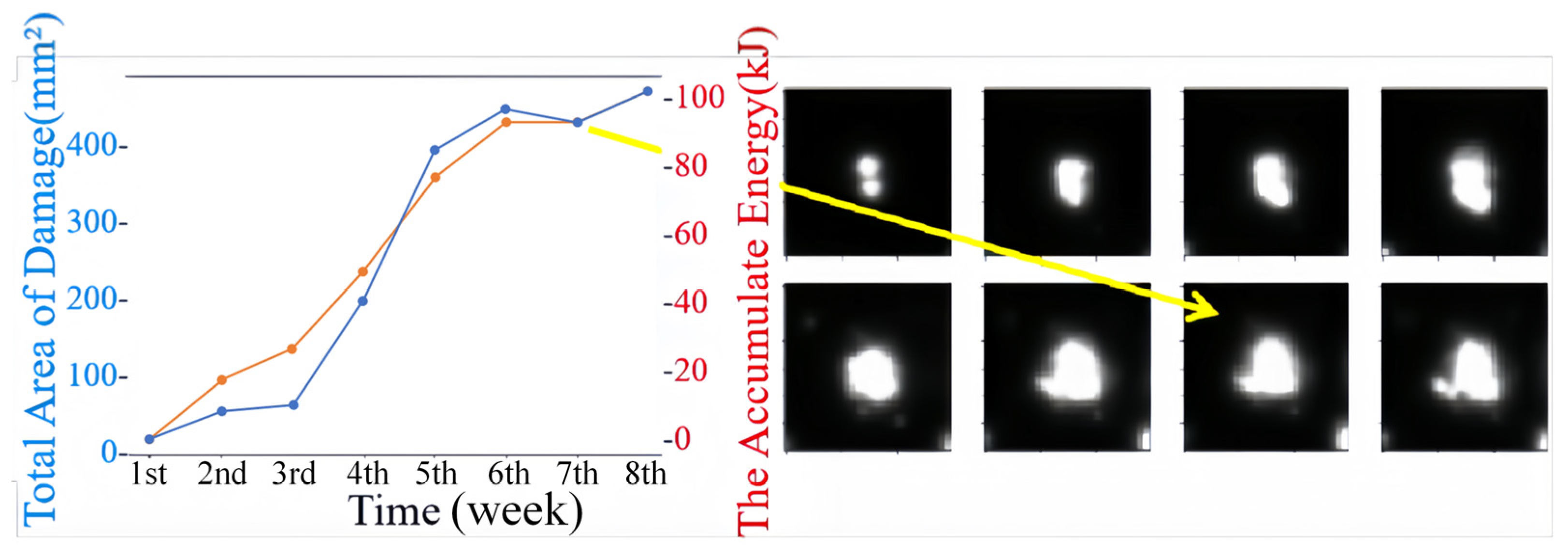





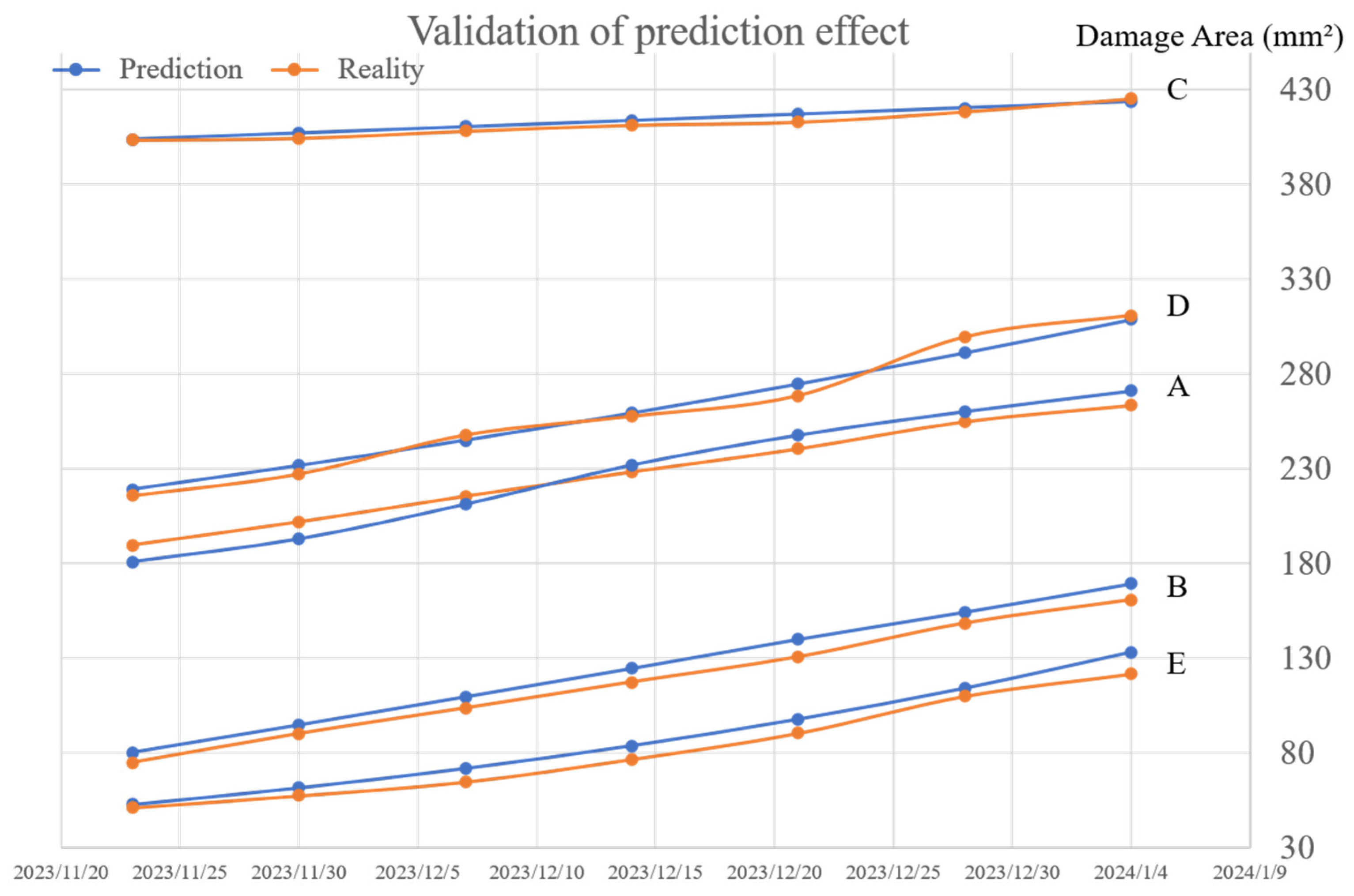


| Object | Date | 11–23 | 11–30 | 12–07 | 12–14 | 12–21 | 12–28 | 01–04 |
|---|---|---|---|---|---|---|---|---|
| Area of Optics A (mm2) | Predicted Value | 189.50 | 201.75 | 215.41 | 228.32 | 240.57 | 254.97 | 263.62 |
| Actual Value | 180.74 | 192.81 | 211.21 | 232.04 | 247.89 | 260.38 | 271.29 | |
| Area of Optics B (mm2) | Predicted Value | 80.07 | 94.54 | 109.41 | 124.41 | 139.81 | 154.2 | 169.17 |
| Actual Value | 74.63 | 89.92 | 103.45 | 117.23 | 130.53 | 148.36 | 160.72 | |
| Area of Optics C (mm2) | Predicted Value | 404.07 | 407.31 | 410.57 | 413.85 | 417.17 | 420.51 | 423.87 |
| Actual Value | 403.54 | 404.46 | 408.22 | 411.38 | 412.98 | 418.44 | 425.34 | |
| Area of Optics D (mm2) | Predicted Value | 179.00 | 191.56 | 204.99 | 219.37 | 234.76 | 251.23 | 268.85 |
| Actual Value | 175.76 | 187.23 | 207.79 | 217.67 | 228.61 | 259.52 | 270.87 | |
| Area of Optics E (mm2) | Predicted Value | 52.64 | 61.43 | 71.69 | 83.67 | 97.64 | 113.95 | 132.98 |
| Actual Value | 50.97 | 57.27 | 64.53 | 76.49 | 90.26 | 109.75 | 121.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, X.; Zhou, W.; Guo, H.; Huang, X.; Zhao, B.; Zhong, W.; Zhu, Q.; Chen, Z. The Prediction of Incremental Damage on Optics from the Final Optic Assembly in an ICF High-Power Laser Facility. Appl. Sci. 2024, 14, 5226. https://doi.org/10.3390/app14125226
Hu X, Zhou W, Guo H, Huang X, Zhao B, Zhong W, Zhu Q, Chen Z. The Prediction of Incremental Damage on Optics from the Final Optic Assembly in an ICF High-Power Laser Facility. Applied Sciences. 2024; 14(12):5226. https://doi.org/10.3390/app14125226
Chicago/Turabian StyleHu, Xueyan, Wei Zhou, Huaiwen Guo, Xiaoxia Huang, Bowang Zhao, Wei Zhong, Qihua Zhu, and Zhifei Chen. 2024. "The Prediction of Incremental Damage on Optics from the Final Optic Assembly in an ICF High-Power Laser Facility" Applied Sciences 14, no. 12: 5226. https://doi.org/10.3390/app14125226
APA StyleHu, X., Zhou, W., Guo, H., Huang, X., Zhao, B., Zhong, W., Zhu, Q., & Chen, Z. (2024). The Prediction of Incremental Damage on Optics from the Final Optic Assembly in an ICF High-Power Laser Facility. Applied Sciences, 14(12), 5226. https://doi.org/10.3390/app14125226







