Collision Study on New Aluminum Alloy W-Beam Guardrail
Abstract
1. Introduction
2. Structure Optimization of W-Beam Guardrail
2.1. Theoretical Analysis
2.2. Mechanism Analysis
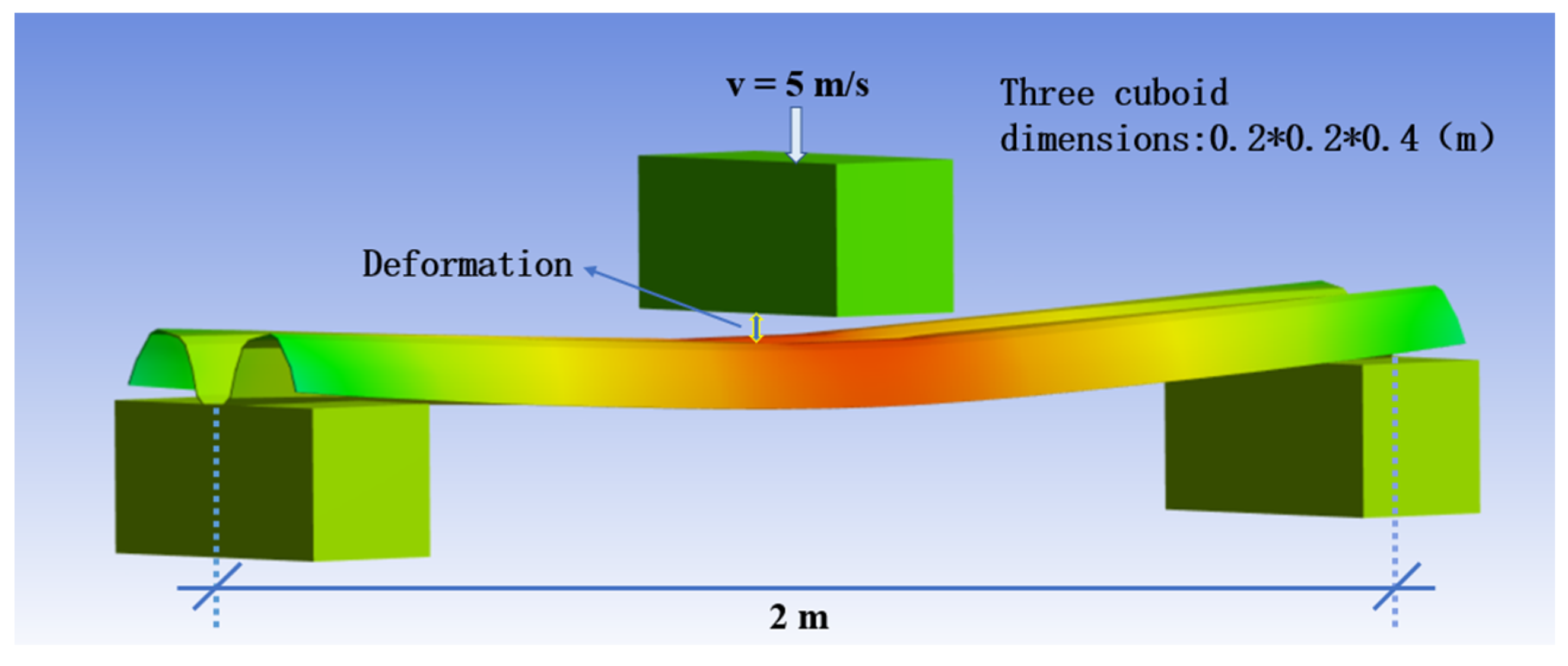
2.3. The Differential Equation for the Wave-Shaped Beam
3. Finite Element Model Construction
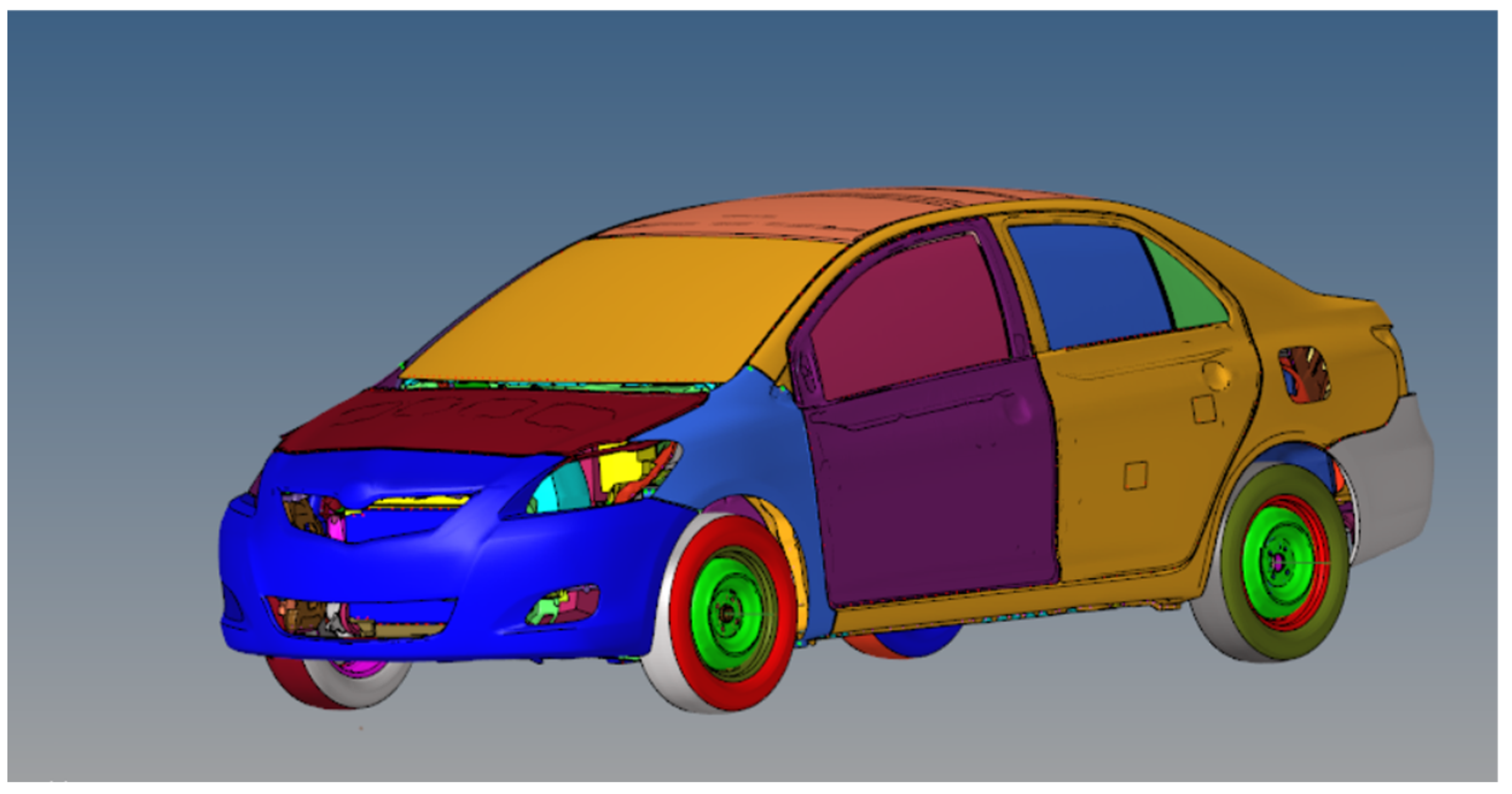
3.1. Finite Element Model of the Vehicle
3.2. Establishment of the Novel W-Beam Guardrail Model
4. Vehicle Collision Conditions and Evaluation Criteria
5. Finite Element Simulation Results
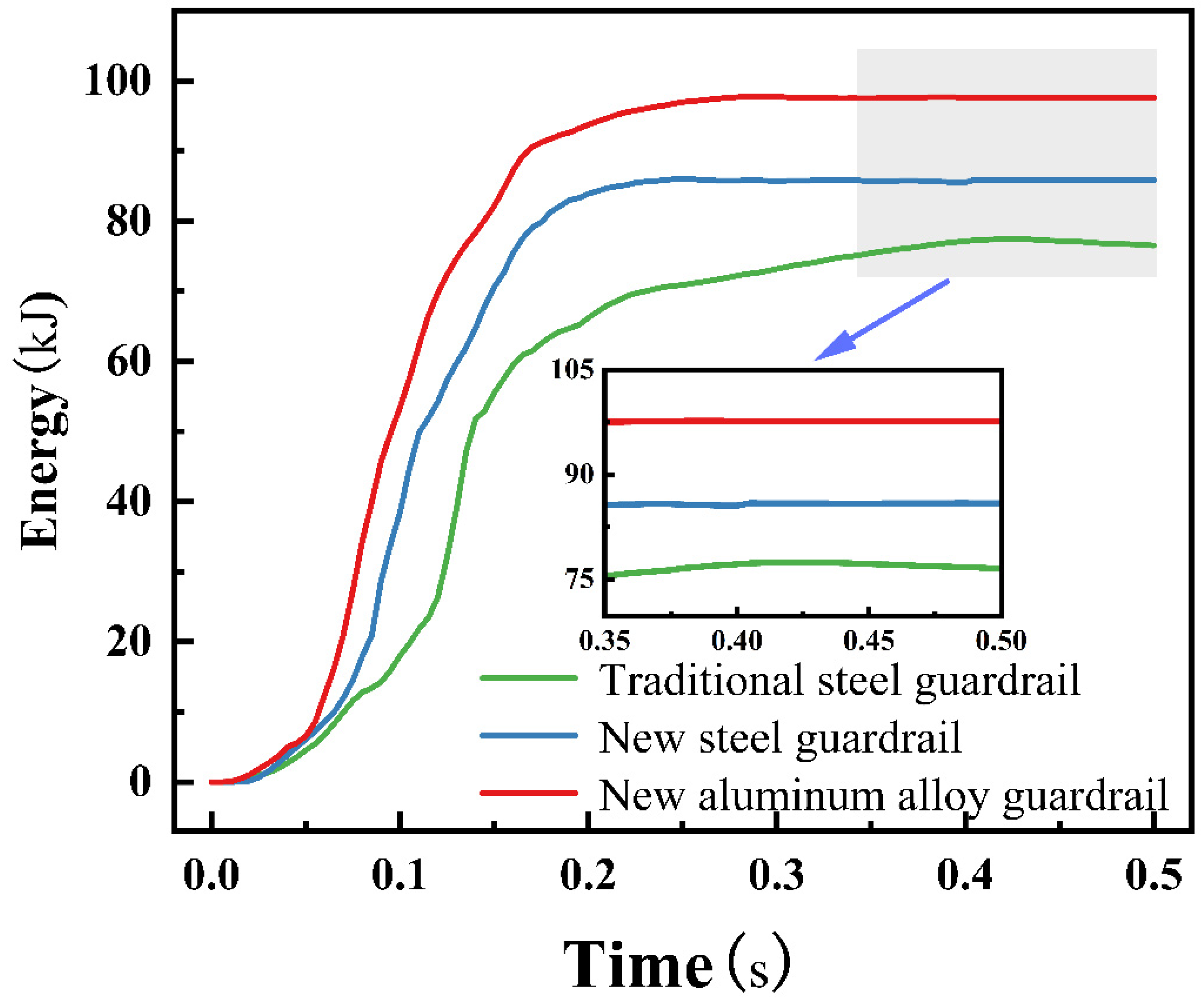
5.1. Guardrail Energy Absorption
5.2. The Maximum Dynamic Deformation of the Guardrail
5.3. Vehicle’s Center of Mass Acceleration
6. Discussion
7. Conclusions
- (1)
- According to theoretical derivation, the collision deformation of waveform beams is inversely proportional to the square root of their bending stiffness. After optimization of the waveform beams, their cross-sectional moment of inertia increased by 28.6%, and the deformation in finite element analysis decreased by 12.8%, confirming the accuracy of this law.
- (2)
- Under the condition of the same guardrail material, compared with the traditional guardrail, the material cost of the new W-beam guardrail increased by 8.1%, while the maximum dynamic deformation decreased by 12.8%, and the energy absorption increased by 11.6%. This reduces the risk of serious injury to occupants when the vehicle runs off the road in severe collisions. This indicates that optimizing the linear shape of the guardrail section to increase its moment of inertia can effectively improve the protective performance of the guardrail. This optimization strategy provides a valuable reference for guardrail design and is expected to promote the improvement of guardrail safety performance in practice.
- (3)
- Compared with the traditional steel guardrail, the new aluminum alloy guardrail re-duces the vehicle’s center of mass acceleration by 33.6% and increases the energy absorption by 26.0% after collision. It exhibits better toughness and energy absorption capacity during a collision, better mitigating the impact force generated by the vehicle collision and providing better protection for occupants.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, W.; Tang, Z.; Lu, F.; Qiao, Y.; Zhang, C. Analysis and Experimental Study on the Guided Wave Phase Characteristics of Highway Guardrail Posts. J. Vib. Shock 2017, 36, 223–228. [Google Scholar]
- Dan, X. Design and Research of Auxiliary Manipulatorfor Highway Guardrail Pile Driver. Master’s Thesis, China University of Mining and Technology, Beijing, China, 2022. [Google Scholar]
- Ji, G. Feasibility Study of Fiberglass Reinforced Composite Materials Applied to Road Guardrails. Urban Roads Bridg. Flood Control 2006, 49–50+7. [Google Scholar] [CrossRef]
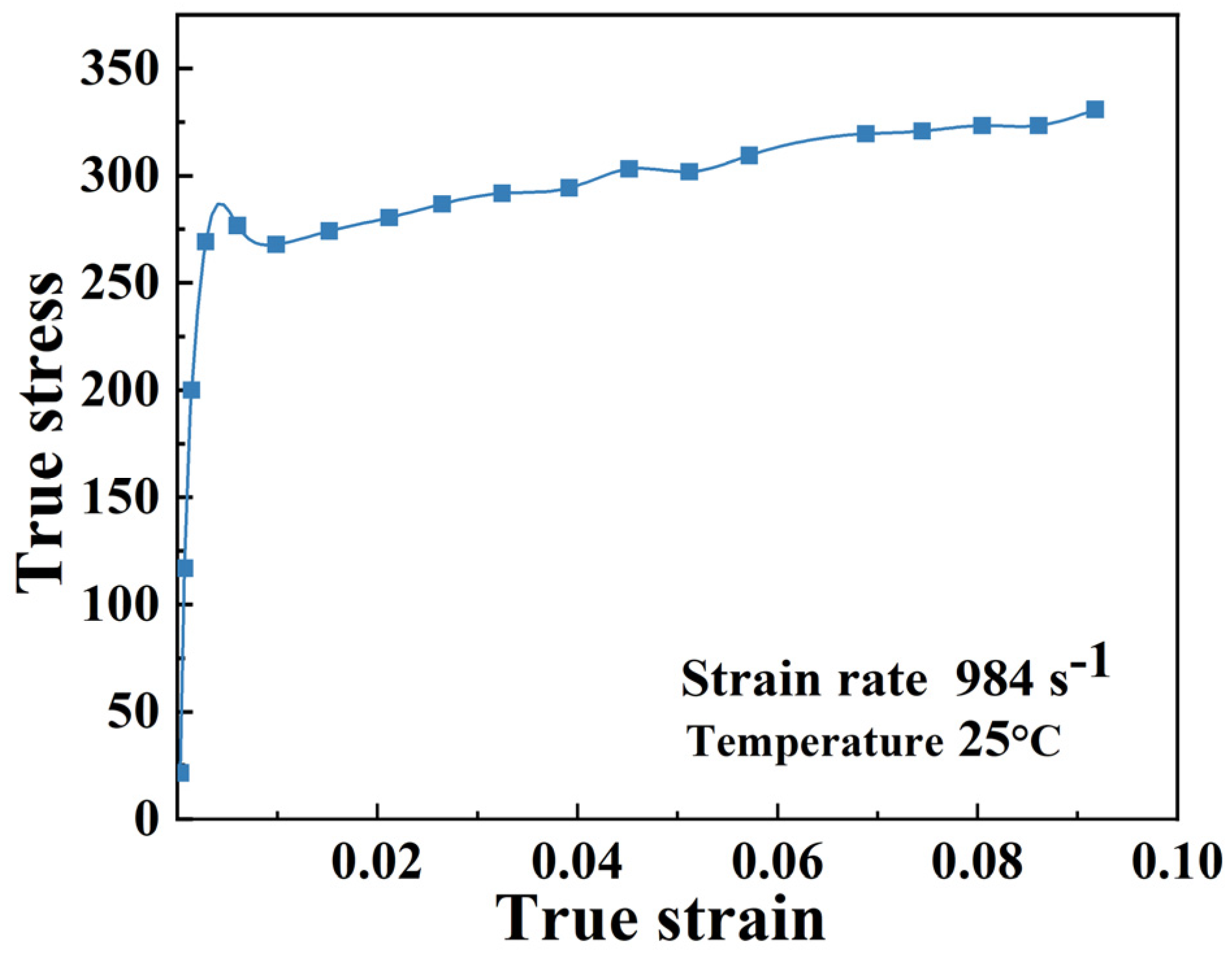
- Fu, X.; Liu, J.; Sun, N.; Sha, H. Experimental and Numerical Simulation of Impact Compression Mechanical Properties of 6061-T6 Aluminum Alloy. J. Disaster Prev. Mitig. Eng. 2023, 43, 1076–1083. [Google Scholar] [CrossRef]
- Manes, A.; Peroni, L.; Scapin, M.; Giglio, M. Analysis of Strain Rate Behavior of an Al 6061 T6 Alloy. Procedia Eng. 2011, 10, 3477–3482. [Google Scholar] [CrossRef]
- Shankar, M.R.; Chandrasekar, S.; Compton, W.D.; King, A.H. Characteristics of Aluminum 6061-T6 Deformed to Large Plastic Strains by Machining. Mater. Sci. Eng. A 2005, 410, 364–368. [Google Scholar] [CrossRef]
- Zhong, Z. Finite Element Method Analysis of Vehicle Durability. Automot. Eng. 1994, 16, 1–6. [Google Scholar]
- Jaber, M.M.; Ali, M.H.; Abd, S.K.; Abosinnee, A.S.; Malik, R.Q. Simulation Research on the Collision between Freight Cars and Expressway Three-Wave Beam Steel Guardrail. Multimed. Tools Appl. 2023, 1–22. [Google Scholar] [CrossRef]
- Sun, S.; Li, H.; Zhu, C.; Mei, K.; Jiang, H.; Sun, Y.; Huang, H. Study on the Anti-Collision Performance of Basalt Fiber Reinforced Polymer Beam–Column Guardrail. Compos. Struct. 2021, 276, 114588. [Google Scholar] [CrossRef]
- Yao, J.; Wang, B.; Hou, Y.; Huang, L. Analysis of Vehicle Collision on an Assembled Anti-Collision Guardrail. Sensors 2021, 21, 5152. [Google Scholar] [CrossRef]
- Yao, J.; Zhang, J.; Huang, L.; Xu, J.; Wang, B. Analysis of Anti-Collision Performance of a New Assembled Rolling Guardrail. In Structures; Elsevier: Amsterdam, The Netherlands, 2023; Volume 47, pp. 246–259. [Google Scholar]
- Liang, J.; Yao, S.; Li, B.; Chen, Y.; Du, Z.; Xu, T. Collision Simulation of Temporary Traffic ProtectionFacilities Based on Finite Element Analysis. Highway 2020, 65, 269–277. [Google Scholar]
- Huang, H.; Mo, J.; Yang, J. The Application of Finite Element Analysis to Guardrail Designand Occupant Protection. Comput. Simul. 2003, 135–139. [Google Scholar]
- Hou, S.; Tan, W.; Zheng, Y.; Han, X.; Li, Q. Optimization Design of Corrugated Beam Guardrail Based on RBF-MQ Surrogate Model and Collision Safety Consideration. Adv. Eng. Softw. 2014, 78, 28–40. [Google Scholar] [CrossRef]
- Yin, H.; Xiao, Y.; Wen, G.; Fang, H. Design Optimization of a New W-Beam Guardrail for Enhanced Highway Safety Performance. Adv. Eng. Softw. 2017, 112, 154–164. [Google Scholar] [CrossRef]
- Yin, H.; Zhang, L.; Liu, Z.; Fan, W.; Wu, X.; Wen, G. Crash Analysis and Evaluation of a New Separate W-Beam Guardrail on Highways Using the Finite Element Method. Eng. Struct. 2023, 278, 115551. [Google Scholar] [CrossRef]
- Triantafyllou, M. Dynamics of Cables and Chains. Shock Vib. Dig. 1987, 19, 3–5. [Google Scholar] [CrossRef]
- Iandiorio, C.; Salvini, P. Elastic-Plastic Analysis with Pre-Integrated Beam Finite Element Based on State Diagrams: Elastic-Perfectly Plastic Flow. Eur. J. Mech.-A/Solids 2023, 97, 104837. [Google Scholar] [CrossRef]
- Bradshaw, R.; Campbell, D.; Gargari, M.; Mirmiran, A.; Tripeny, P. Special Structures: Past, Present, and Future. J. Struct. Eng. 2002, 128, 691–709. [Google Scholar] [CrossRef]
- Arbocz, J.; Starnes, J.H., Jr. Future Directions and Challenges in Shell Stability Analysis. Thin-Walled Struct. 2002, 40, 729–754. [Google Scholar] [CrossRef]
- Lamiel, C.; Hussain, I.; Ogunsakin, O.R.; Zhang, K. MXene in Core–Shell Structures: Research Progress and Future Prospects. J. Mater. Chem. A 2022, 10, 14247–14272. [Google Scholar] [CrossRef]
- JTG D81-2006; Specifications for the Design of Highway Traffic Safety Facilities. Transportation Press: Beijing, China, 2006.
- JTG/T D81-2006; Detailed Rules for Design of Highway Traffic Safety Facilities. Transportation Press: Beijing, China, 2006.
- Dong, S.; Alpdogan, C.; Taciroglu, E. Much Ado about Shear Correction Factors in Timoshenko Beam Theory. Int. J. Solids Struct. 2010, 47, 1651–1665. [Google Scholar] [CrossRef]
- Moon, J.; Lim, N.-H.; Lee, H.-E. Moment Gradient Correction Factor and Inelastic Flexural–Torsional Buckling of I-Girder with Corrugated Steel Webs. Thin-Walled Struct. 2013, 62, 18–27. [Google Scholar] [CrossRef]
- JTG/T D81-2017; Highway Traffic Safety Facility Design Code. Transportation Press: Beijing, China, 2017.
- JTG D81-2017; Highway Traffic Safety Facility Design Specification. Transportation Press: Beijing, China, 2017.
- Noorsumar, G.; Rogovchenko, S.; Robbersmyr, K.G.; Vysochinskiy, D. Mathematical Models for Assessment of Vehicle Crashworthiness: A Review. Int. J. Crashworthiness 2022, 27, 1545–1559. [Google Scholar] [CrossRef]
- Gao, G.; Wang, S. Crashworthiness of Passenger Rail Vehicles: A Review. Int. J. Crashworthiness 2018, 24, 664–676. [Google Scholar] [CrossRef]
- Lee, D.-C.; Han, C.-S. CAE (Computer Aided Engineering) Driven Durability Model Verification for the Automotive Structure Development. Finite Elem. Anal. Des. 2009, 45, 324–332. [Google Scholar] [CrossRef]
- Lee, D.; Woo, Y.; Lee, S.; Han, C. Design Consideration of the Nonlinear Specifications in the Automotive Body. Finite Elem. Anal. Des. 2008, 44, 851–861. [Google Scholar] [CrossRef]
- Yang, R.-J.; Akkerman, A.; Anderson, D.; Faruque, O.; Gu, L. Robustness Optimization for Vehicular Crash Simulations. Comput. Sci. Eng. 2000, 2, 8–13. [Google Scholar] [CrossRef]
- Cui, N. Crash Simulation of Vehicle-Guardrails and Optimization of theRail Post. Master’s Thesis, Dalian University of Technology, Dalian, China, 2018. [Google Scholar]
- Zhang, H.-R.; Zhao, H.; Wang, R.; Liang, X.-X.; Zhu, Y. Coupling Influences of Elevated Temperature and Strain Rate on the Behaviour of 6061-T6 Aluminium Alloy Used as Construction Material. Structures 2022, 40, 596–606. [Google Scholar] [CrossRef]
- JTG/T F83-01-2004; Standard for Evaluation of Safety Performance of Highway Guardrails. Transportation Press: Beijing, China, 2004.
- Soltani, M.; Moghaddam, T.B.; Karim, M.R.; Sulong, N.H.R. The Safety Performance of Guardrail Systems: Review and Analysis of Crash Tests Data. Int. J. Crashworthiness 2013, 18, 530–543. [Google Scholar] [CrossRef]
- Reid, J.D.; Sicking, D.L.; Faller, R.K.; Pfeifer, B.G. Development of a New Guardrail System. Transp. Res. Rec. 1997, 1599, 72–80. [Google Scholar] [CrossRef]
- Ross, H., Jr.; Sicking, D.; Zimmer, R.A.; Michie, J.D. Recommended Procedures for the Safety Performance Evaluation of Highway Features; Transportation Research Board: Washington, DC, USA, 1993. [Google Scholar]


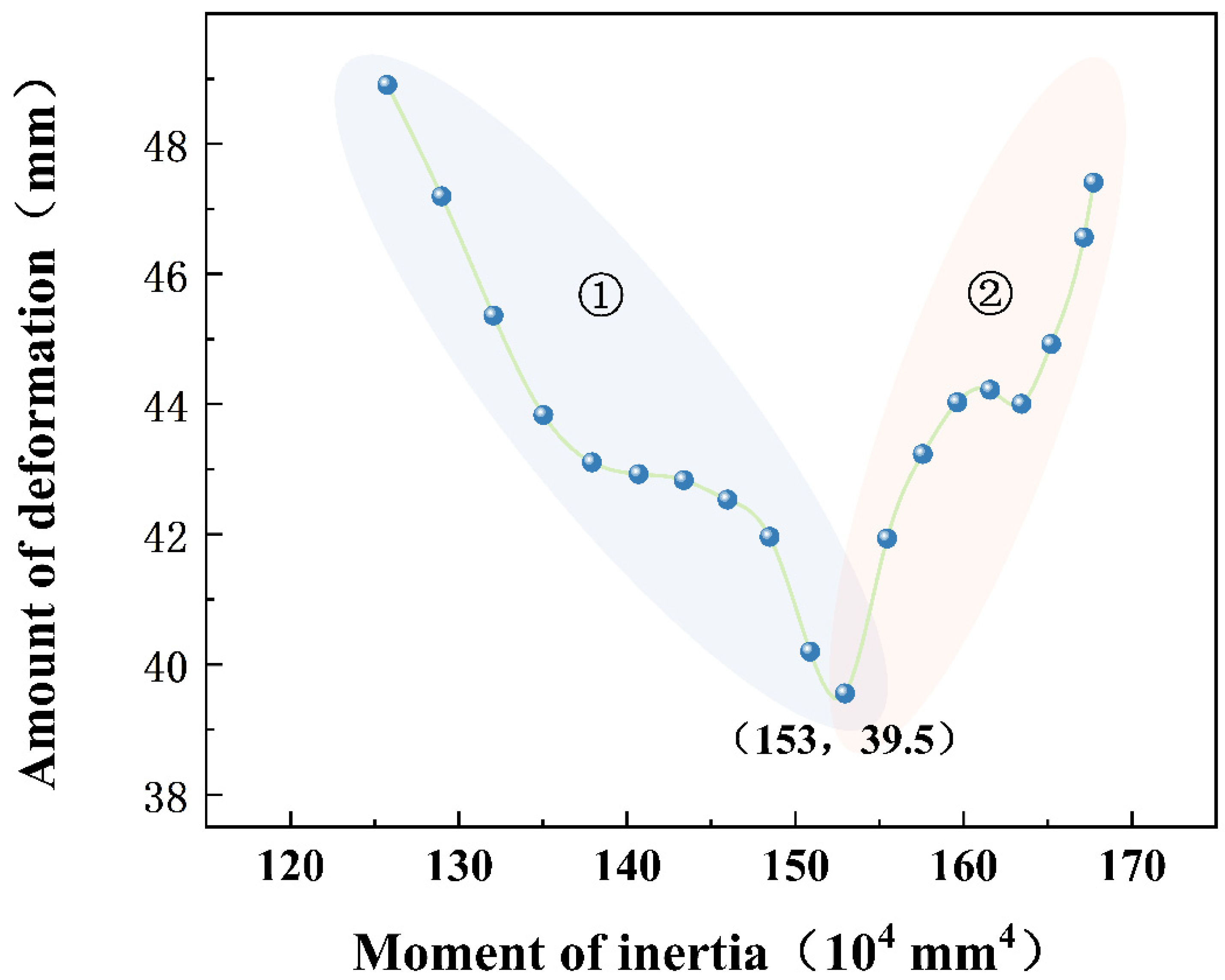



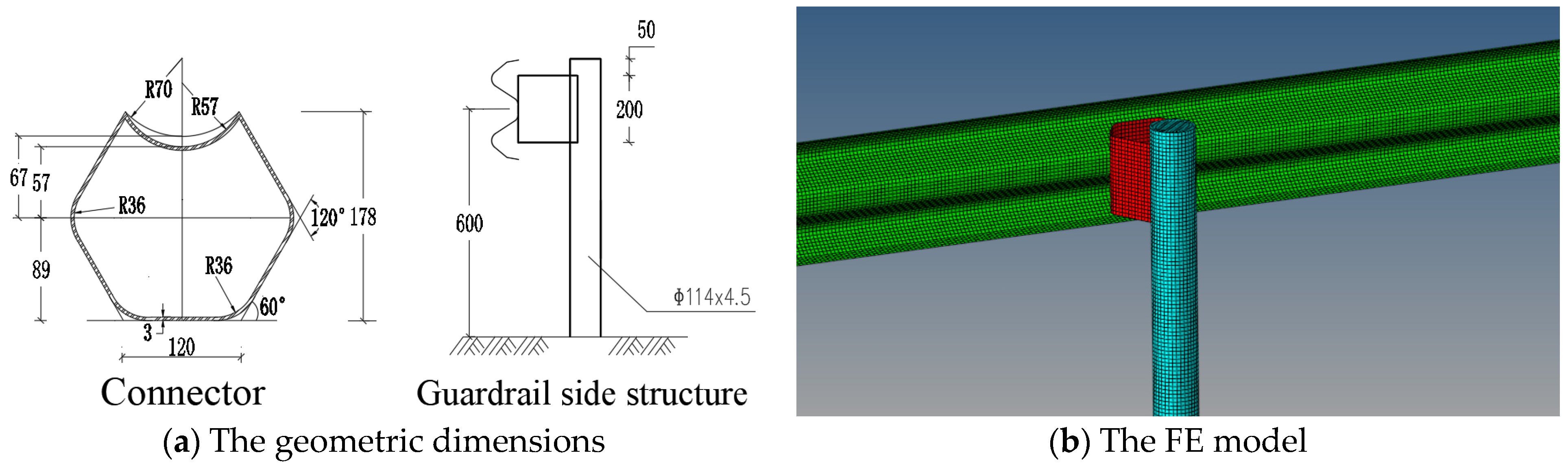



| Type | Area/mm2 | Moment of Inertia/(×104 mm4) |
|---|---|---|
| New guardrail | 1611 | 153 |
| Traditional guardrail | 1491 | 119 |
| Compared | 8.1% | 28.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Huang, X.; Li, R.; Tang, Z.; Li, J.; Chen, D. Collision Study on New Aluminum Alloy W-Beam Guardrail. Appl. Sci. 2024, 14, 5266. https://doi.org/10.3390/app14125266
Wang L, Huang X, Li R, Tang Z, Li J, Chen D. Collision Study on New Aluminum Alloy W-Beam Guardrail. Applied Sciences. 2024; 14(12):5266. https://doi.org/10.3390/app14125266
Chicago/Turabian StyleWang, Liang, Xiaomin Huang, Rui Li, Zhiyi Tang, Jun Li, and Dongyu Chen. 2024. "Collision Study on New Aluminum Alloy W-Beam Guardrail" Applied Sciences 14, no. 12: 5266. https://doi.org/10.3390/app14125266
APA StyleWang, L., Huang, X., Li, R., Tang, Z., Li, J., & Chen, D. (2024). Collision Study on New Aluminum Alloy W-Beam Guardrail. Applied Sciences, 14(12), 5266. https://doi.org/10.3390/app14125266






