Neural Robust Control for a Mobile Agent Leader–Follower System
Abstract
1. Introduction
2. Materials and Methods
2.1. Exact State Feedback Linearization
- , for all and for all x in a neighborhood of .
- The following matrix:is nonsingular at .
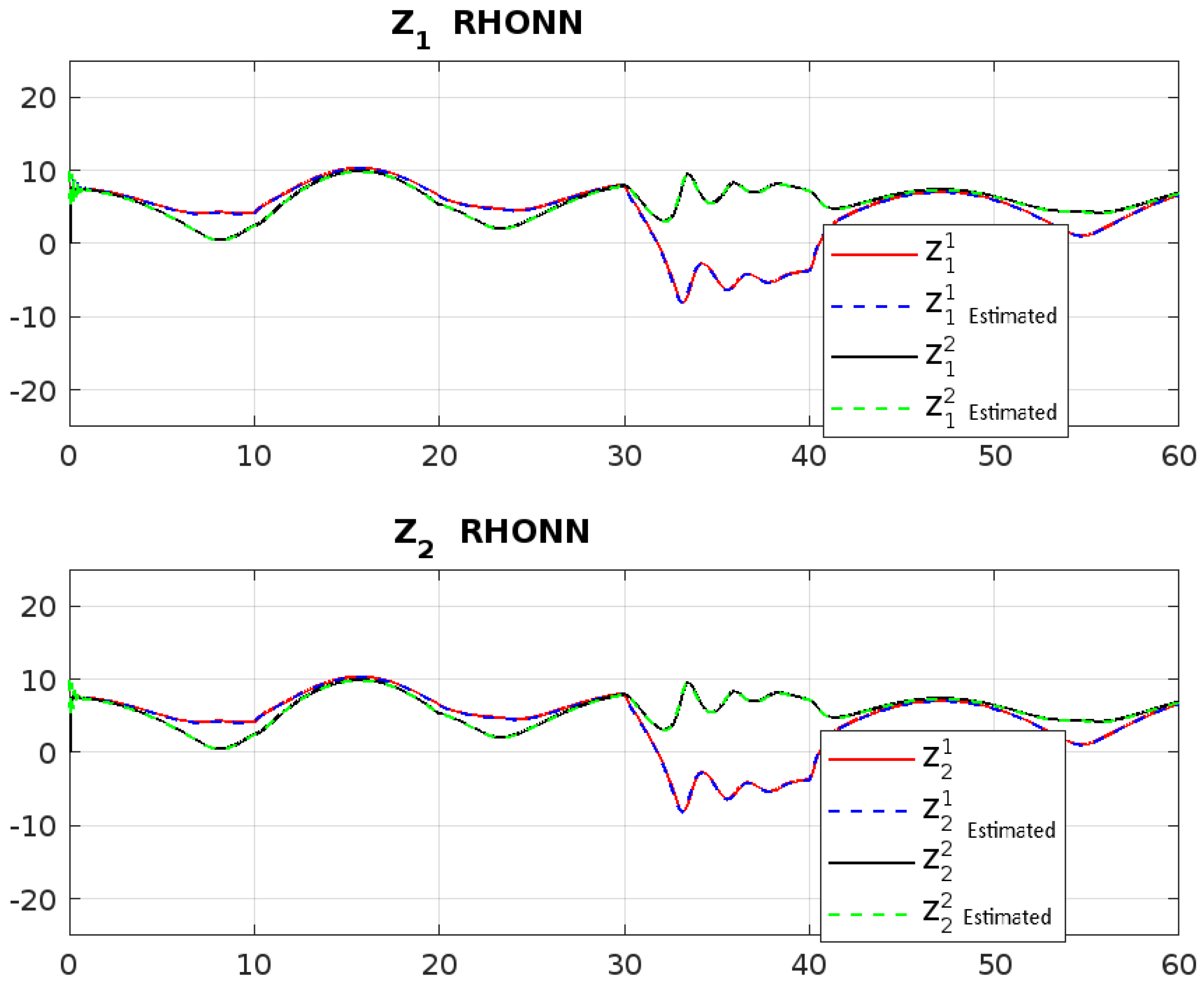
2.2. Recurrent High-Order Neural Networks Estimation
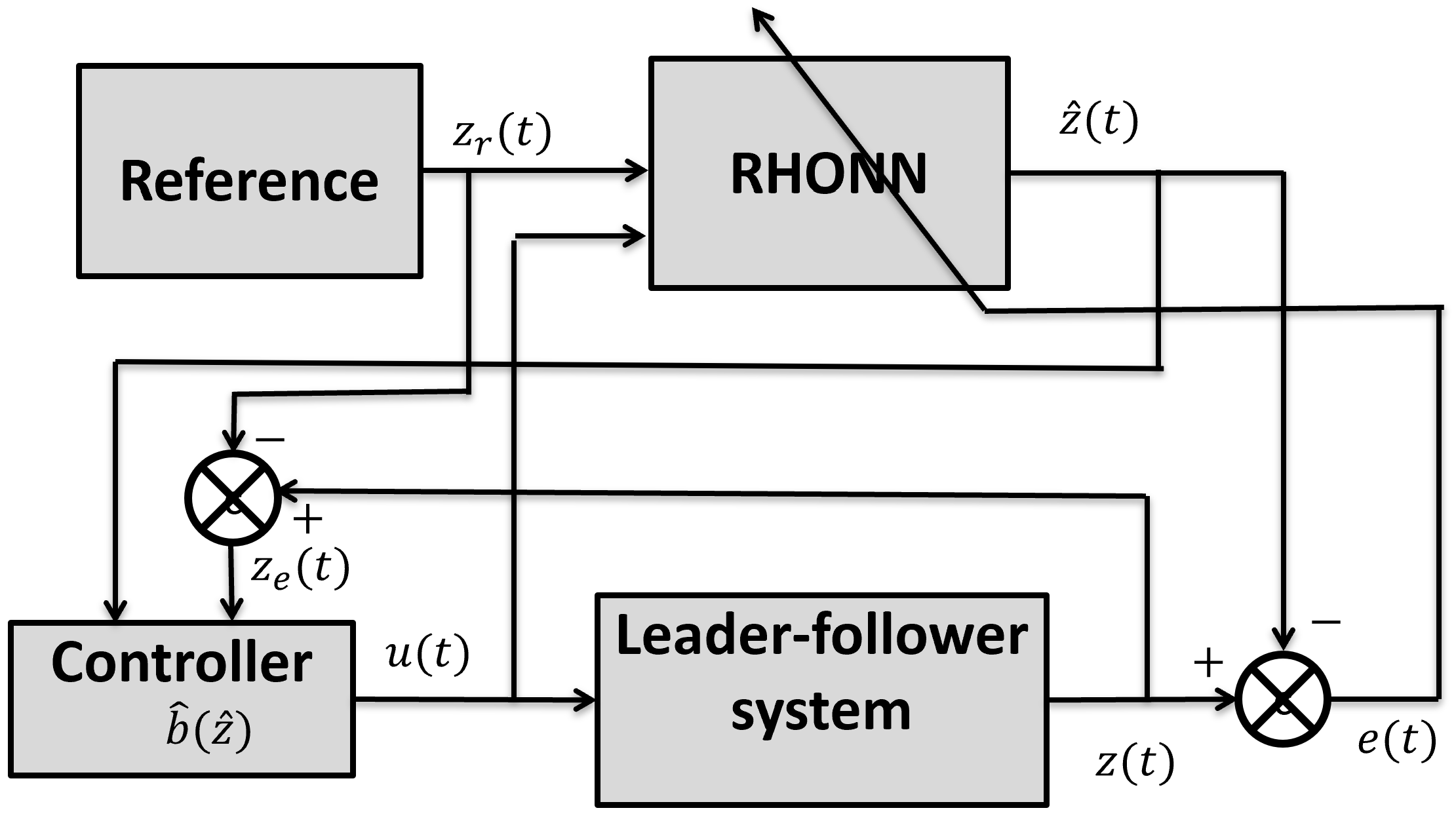
3. Neuro-Robust Control
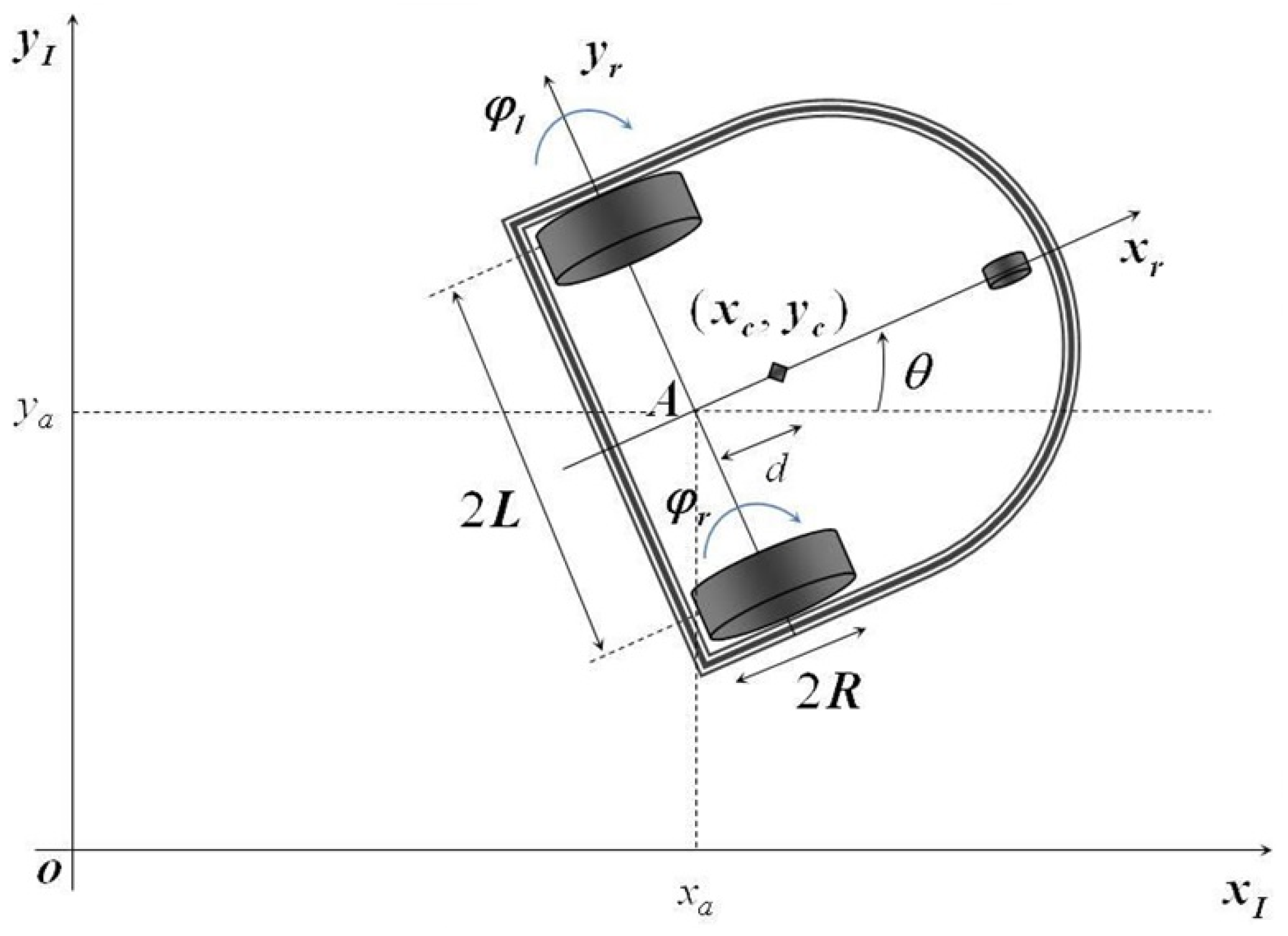
- M is the total mass of the differential mobile robot.
- R is the radius of the wheel.
- d is the distance from the wheel axle center to the center of mass.
- J is the moment of inertia of the differential mobile robot about the vertical axis z through the center of mass.
- L is the distance from the center of the robot to the wheel axis.
- and are the angular velocities of the right and left wheels, respectively.
- and are the desired angular velocities of the right and left wheels, respectively.
3.1. Controller Design
3.2. Stability Analysis
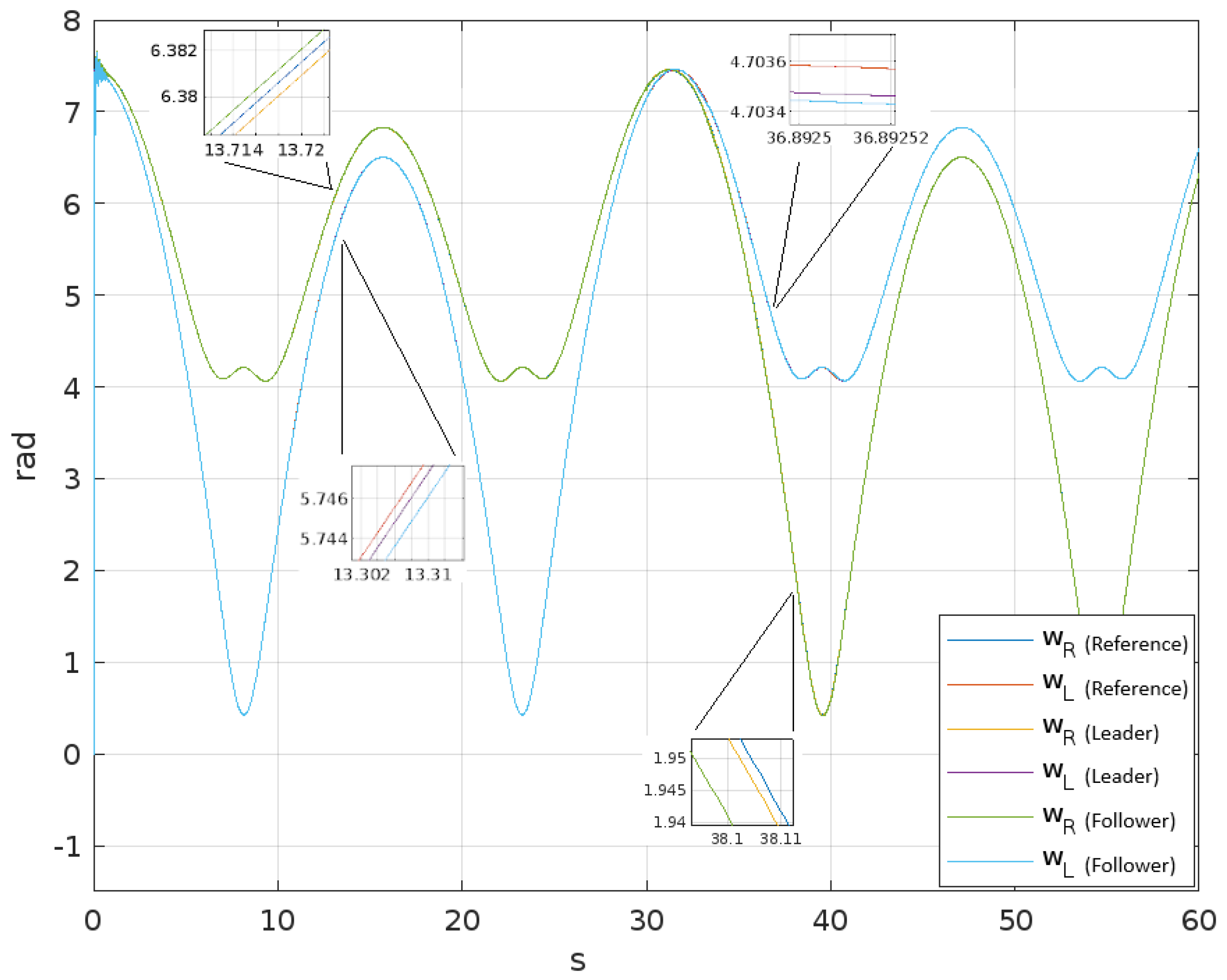
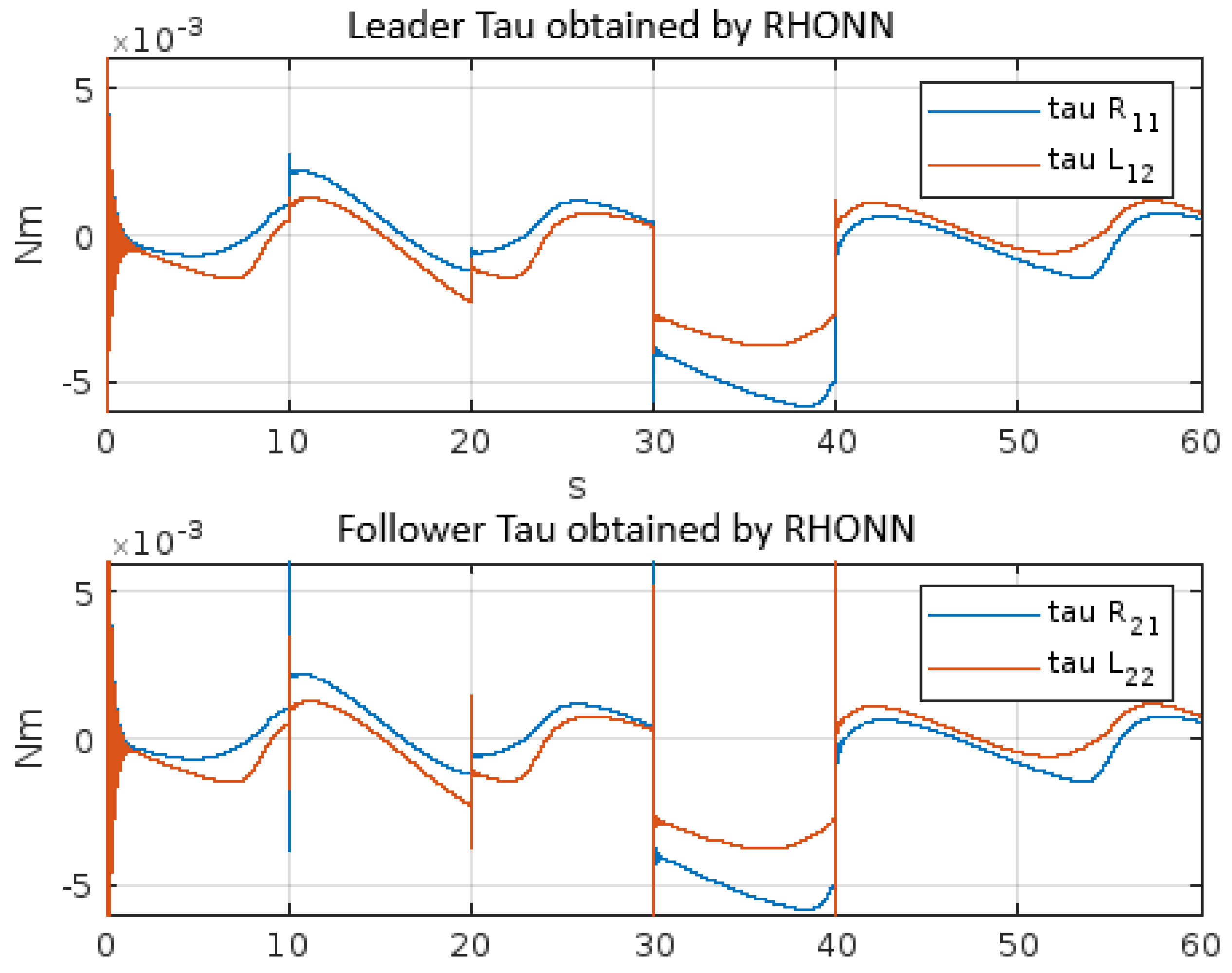
4. Results
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Loganathan, A.; Ahmad, N.S. A systematic review on recent advances in autonomous mobile robot navigation. Eng. Sci. Technol. Int. J. 2023, 40, 101343. [Google Scholar] [CrossRef]
- Alatise, M.B.; Hancke, G.P. A Review on Challenges of Autonomous Mobile Robot and Sensor Fusion Methods. IEEE Access 2020, 8, 39830–39846. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, L.; Hou, Z.; Yu, J.; Tan, M. Optimal formation of multi-robot systems based on recurrent neural network. IEEE Trans. Neuronal Netw. Learn. Syst. 2016, 27, 322–333. [Google Scholar] [CrossRef] [PubMed]
- Lian, K.Y.; Hsu, H.; Tsai, T.S. Leader-Follower mobile robots control based on light source detection. IEEE Sens. J. 2019, 19, 11142–11150. [Google Scholar] [CrossRef]
- Soorki, M.N.; Talebi, H.A.; Nikravesh, S.K.Y. Robust leader-following formation control of multiple mobile robots using Lyapunov redesign. In Proceedings of the IECON 2011—37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, VC, Australia, 7–10 November 2011; pp. 277–282. [Google Scholar]
- Rabani, M.J.; Memon, A.Y. Trajectory tracking and stabilization of nonholonomic wheeled mobile robot using recursive integral backstepping control. Electronics 2021, 10, 1992. [Google Scholar] [CrossRef]
- Hassan, N.; Saleem, A. Neural network-based adaptive controller for trajectory tracking of wheeled mobile robots. IEEE Access 2022, 10, 13582–13597. [Google Scholar] [CrossRef]
- Meng, J.; Liu, A.; Yang, Y.; Wu, Z.; Xu, Q. Two-wheeled robot platform based on PID control. In Proceedings of the 5th International Conference on Information Science and Control Engineering (ICISCE), Zhengzhou, China, 20–22 July 2018; pp. 1011–1014. [Google Scholar]
- Majid, A.; Mohamed, Z.; Basri, M. Velocity control of a unicycle type of mobile robot using optimal PID controller. J. Teknol. Sci. Eng. 2016, 78, 4–7. [Google Scholar] [CrossRef][Green Version]
- Michel, F.; Sanchez, E.N.; Alanis, A.Y.; López-Franco, C. Neural control for a differential drive wheeled Mobile robot integrating stereo vision feedback. Comp. Sist. 2015, 19, 429–443. [Google Scholar]
- Isidori, A. Nonlinear Control System, 3rd ed.; Springer: London, UK, 1995. [Google Scholar]
- Femat, R.; Alavarez, J.; Castillo, B.; González, J. On Robust Chaos suprression in class of nondriven oscillators: Application to the Chua’s circuit. IEEE Trans. Circuits Syst. 1999, 46, 1150–1152. [Google Scholar] [CrossRef]
- Femat, R.; Solis-Perales, G. Robust Synchronization Via Geometrical Control: A General Framework. Lect. Notes Control Inf. Sci. 2008, 378, 99–137. [Google Scholar]
- Rovithakis, G.A.; Christodoulou, M.A. Adaptative Control whit Recurrent High-Order Neural Networks, 1st ed.; Springer: London, UK, 2000. [Google Scholar]
- Arana-Daniel, N.; Alanis, A.Y.; Lopez-Franco, C. Neural Networks for Robotics: An Engineering Perspective; CRC Press, Inc.: Boca Raton, FL, USA, 2018. [Google Scholar]
- Alanis, A.Y.; Arana-Daniel, N.; Lopez-Franco, C. Artificial Neural Networks for Engineering Applications; Academic Press: Cambridge, MA, USA; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Hopfield, J. Neurons with graded response have collective computational properties like those of two-state neurons. Proc. Nat. Acad. Sci. USA 1984, 81, 3088–3092. [Google Scholar] [CrossRef] [PubMed]
- Ricalde, L. Inverse Optimal Adaptive Recurrent Neural Control with Constrained. Ph.D. Thesis, Cinvestav, Guadalajara, Mexico, 2005. Available online: https://repositorio.cinvestav.mx/handle/cinvestav/452 (accessed on 1 May 2024).
- Alanis, A.Y.; Lopez-Franco, M.; Arana-Daniel, N.; Lopez-Franco, C. Discrete-time neural identifier for electrically driven nonholonomic mobile robots. In Proceedings of the 2011 International Joint Conference on Neural Networks, San Jose, CA, USA, 31 July–5 August 2011; pp. 1067–1073. [Google Scholar]
- Jian’an, X.; Mingjun, Z.; Jian, Z. Kinematic model identification of autonomous mobile robot using dynamical recurrent neural networks. In Proceedings of the IEEE International Conference Mechatronics and Automation, Niagara Falls, ON, Canada, 29 July–1 August 2005; Volume 3, pp. 1447–1450. [Google Scholar]
- Wang, S.; Shao, X.; Yang, L.; Liu, N. Deep Learning Aided Dynamic Parameter Identification of 6-DOF Robot Manipulators. IEEE Access 2020, 8, 138102–138116. [Google Scholar] [CrossRef]
- Nicosia, S.; Tomei, P. State observation of elastic joint robots. IFAC Proc. Vol. 1988, 21, 47–52. [Google Scholar] [CrossRef]
- Kim, Y.H.; Lewis, F.L. Neural network output feedback control of robot manipulator. IEEE Trans. Robot. Autom. 1999, 15, 301–309. [Google Scholar] [CrossRef]
- Trujillo, D.; Morales, L.A.; Chávez, D.; Pozo, D.F. Trajectory Tracking Control of a Mobile Robot using Neural Networks. Emerg. Sci. J. 2023, 7, 1843–1862. [Google Scholar] [CrossRef]
- Kosmatopoulus, E.B.; Polycarpou, M.M.; Christodoulou, M.A.; Ioannou, P.A. High order neural network structures for identification of dynamical systems. IEEE Trans. Neural Netw. 1995, 6, 422–435. [Google Scholar] [CrossRef] [PubMed]
- Kosmatopoulus, E.B.; Christodoulou, M.A.; Ioannou, P.A. Dynamical neural networks that ensure exponential identification error convergence. Neural Netw. 1997, 10, 299–314. [Google Scholar] [CrossRef] [PubMed]
- Dhaouadi, R.; Hatab, A. Dynamic modelling of differential-drive mobile robots using lagrange and Newton-Euler methodologies: A unified framework. Adv. Robot. Automat. 2013, 2, 107. [Google Scholar]
- Khalil, H.K. Nonlinear Systems; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Vinod, R.N.; Mathew, T.A. Design, Simulation and implementation of cascaded path tracking controller for a differential drive mobile robot. In Proceedings of the 2015 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Kochi, India, 10–13 August 2015; pp. 1085–1090. [Google Scholar]


| Parameter | Value | |
|---|---|---|
| Nominal | Variation | |
| M | kg | kg |
| d | m | m |
| R | m | m |
| L | m | m |
| J | kg-m | kg-m |
| 0.0172 | 0.0344 | |
| V | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodriguez-Castellanos, D.; Blas-Valdez, M.; Solis-Perales, G.; Perez-Cisneros, M.A. Neural Robust Control for a Mobile Agent Leader–Follower System. Appl. Sci. 2024, 14, 5374. https://doi.org/10.3390/app14135374
Rodriguez-Castellanos D, Blas-Valdez M, Solis-Perales G, Perez-Cisneros MA. Neural Robust Control for a Mobile Agent Leader–Follower System. Applied Sciences. 2024; 14(13):5374. https://doi.org/10.3390/app14135374
Chicago/Turabian StyleRodriguez-Castellanos, David, Marco Blas-Valdez, Gualberto Solis-Perales, and Marco Antonio Perez-Cisneros. 2024. "Neural Robust Control for a Mobile Agent Leader–Follower System" Applied Sciences 14, no. 13: 5374. https://doi.org/10.3390/app14135374
APA StyleRodriguez-Castellanos, D., Blas-Valdez, M., Solis-Perales, G., & Perez-Cisneros, M. A. (2024). Neural Robust Control for a Mobile Agent Leader–Follower System. Applied Sciences, 14(13), 5374. https://doi.org/10.3390/app14135374







