Evaluating Consolidation Centers of an Integrated Transportation Network under the Belt and Road Initiative
Abstract
:1. Introduction
2. Criteria and Procedure for Selecting Consolidation Centers
2.1. Screening Criteria
2.2. Screening Procedure
3. Construction of Integrated Network
3.1. Establishment of the Railway Network
3.2. Establishment of the Highway Network
3.3. Establishment of the Air Network
3.4. Establishment of the Waterway Network
4. Evaluation Indicators
- (1)
- Degree centrality
- (2)
- Betweenness centrality ()
- (3)
- Closeness centrality ()
- (4)
- Eigenvector centrality ()
- (5)
- Clustering coefficient ()
- (6)
- Network constraint coefficient ()
5. The Integrated Evaluation Method
- Step 1:
- Construction of indicator matrix
- Step 2:
- Construction of normalized indicator matrix
- Step 3:
- Construction of indicator weight
- (1)
- Calculate the difference between evaluation indicators
- (2)
- Calculate the conflict between evaluation indicators
- (3)
- Calculate comprehensive information volume
- (4)
- Determine objective weight
- Step 4:
- Calculate the weighted normalization matrix
- Step 5:
- Determine the ideal solutions
- Step 6:
- Calculate the Euclidean distance
- Step 7:
- Grey Relational Analysis (GRA)
- (1)
- Calculate grey relational coefficient
- (2)
- Calculate grey relational degree
- Step 8:
- Dimensionless processing of , ,
- Step 9:
- Calculate the close degree
6. Case Study
6.1. Scoring and Ranking of the Candidate Consolidation Centers for a Single Mode
6.2. Evaluation of the Single Transportation Mode Networks
6.3. Comprehensive Evaluation of the Integrated Transportation Network
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| No. | City | Node City | No. | City | Node City |
|---|---|---|---|---|---|
| 1 | Chongqing | National logistics node city | 23 | Xining | National logistics node city |
| 2 | Wuhan | National logistics node city | 24 | Tianjin | National logistics node city |
| 3 | Zhengzhou | National logistics node city | 25 | Taiyuan | National logistics node city |
| 4 | Suzhou | National logistics node city | 26 | Shenzhen | National logistics node city |
| 5 | Guangzhou | National logistics node city | 27 | Jinan | National logistics node city |
| 6 | Xi’an | National logistics node city | 28 | Shanghai | National logistics node city |
| 7 | Hefei | National logistics node city | 29 | Tangshan | Regional logistics node city |
| 8 | Shenyang | National logistics node city | 30 | Shijiazhuang | National logistics node city |
| 9 | Ningbo | National logistics node city | 31 | Chengdu | National logistics node city |
| 10 | Changsha | National logistics node city | 32 | Yinchuan | National logistics node city |
| 11 | Lianyungang | Regional logistics node city | 33 | Nanning | National logistics node city |
| 12 | Urumqi | National logistics node city | 34 | Hohhot | National logistics node city |
| 13 | Harbin | National logistics node city | 35 | Hangzhou | National logistics node city |
| 14 | Lanzhou | National logistics node city | 36 | Fuzhou | National logistics node city |
| 15 | Qingdao | National logistics node city | 37 | Guiyang | National logistics node city |
| 16 | Kunming | National logistics node city | 38 | Beijing | National logistics node city |
| 17 | Xiamen | National logistics node city | 39 | Xuzhou | Regional logistics node city |
| 18 | Changchun | National logistics node city | 40 | Quanzhou | Regional logistics node city |
| 19 | Nanchang | National logistics node city | 41 | Jiujiang | Regional logistics node city |
| 20 | Dalian | National logistics node city | 42 | Yantai | Regional logistics node city |
| 21 | Dongguan | Regional logistics node city | 43 | Liuzhou | Regional logistics node city |
| 22 | Nanjing | National logistics node city | 44 | Wuxi | Regional logistics node city |
| No. | City | Node City | No. | City | Node City |
|---|---|---|---|---|---|
| 1 | Chongqing | Node city of CR Express | 23 | Xining | Node city of CR Express |
| 2 | Wuhan | Node city of CR Express | 24 | Tianjin | Node city of CR Express |
| 3 | Zhengzhou | Node city of CR Express | 25 | Taiyuan | Node city of CR Express |
| 4 | Suzhou | Node city of CR Express | 26 | Shenzhen | Node city of CR Express |
| 5 | Guangzhou | Node city of CR Express | 27 | Jinan | Node city of CR Express |
| 6 | Xi’an | Node city of CR Express | 28 | Shanghai | Node city of CR Express |
| 7 | Hefei | Node city of CR Express | 29 | Tangshan | Node city of CR Express |
| 8 | Shenyang | Node city of CR Express | 30 | Shijiazhuang | Node city of CR Express |
| 9 | Ningbo | Node city of CR Express | 31 | Chengdu | Node city of CR Express |
| 10 | Changsha | Node city of CR Express | 32 | Yinchuan | Node city of CR Express |
| 11 | Lianyungang | Node city of CR Express | 33 | Nanning | Node city of CR Express |
| 12 | Urumqi | Node city of CR Express | 34 | Hohhot | Node city of CR Express |
| 13 | Harbin | Node city of CR Express | 35 | Hangzhou | Node city of CR Express |
| 14 | Suzhou | Node city of CR Express | 36 | Fuzhou | Node city of CR Express |
| 15 | Qingdao | Node city of CR Express | 37 | Guiyang | Node city of CR Express |
| 16 | Kunming | Node city of CR Express | 38 | Beijing | Node city of CR Express |
| 17 | Xiamen | Node city of CR Express | 39 | Xuzhou | Node city of CR Express |
| 18 | Changchun | Node city of CR Express | 40 | Quanzhou | Node city of CR Express |
| 19 | Nanchang | Node city of CR Express | 41 | Jiujiang | Node city of CR Express |
| 20 | Dalian | Node city of CR Express | 42 | Yantai | Node city of CR Express |
| 21 | Dongguan | Node city of CR Express | 43 | Liuzhou | Node city of CR Express |
| 22 | Nanjing | Node city of CR Express | 44 | Wuxi | Node city of CR Express |
| No. | City | Node Type | No. | City | Node Type |
|---|---|---|---|---|---|
| 1 | Chongqing | Inland river node city | 15 | Tianjin | Coastal node city |
| 2 | Wuhan | Inland river node city | 16 | Shenzhen | Coastal node city |
| 3 | Suzhou | Inland river node city | 17 | Shanghai | Coastal node city |
| 4 | Guangzhou | Coastal node city | 18 | Tangshan | Inland river node city |
| 5 | Hefei | Inland river node city | 19 | Nanning | Inland river node city |
| 6 | Ningbo | Coastal node city | 20 | Hangzhou | Coastal node city |
| 7 | Changsha | Inland river node city | 21 | Fuzhou | Coastal node city |
| 8 | Lianyungang | Coastal node city | 22 | Xuzhou | Inland river node city |
| 9 | Qingdao | Coastal node city | 23 | Quanzhou | Coastal node city |
| 10 | Xiamen | Coastal node city | 24 | Jiujiang | Inland river node city |
| 11 | Nanchang | Inland river node city | 25 | Yantai | Coastal node city |
| 12 | Dalian | Coastal node city | 26 | Liuzhou | Inland river node city |
| 13 | Dongguan | Inland river node city | 27 | Wuxi | Inland river node city |
| 14 | Nanjing | Inland river node city | 28 |
| No. | City | Node Type | No. | City | Node Type |
|---|---|---|---|---|---|
| 1 | Chongqing | Air node city | 21 | Xining | Air node city |
| 2 | Wuhan | Air node city | 22 | Tianjin | Air node city |
| 3 | Zhengzhou | Air node city | 23 | Taiyuan | Air node city |
| 4 | Guangzhou | Air node city | 24 | Shenzhen | Air node city |
| 5 | Xi’an | Air node city | 25 | Jinan | Air node city |
| 6 | Hefei | Air node city | 26 | Shanghai | Air node city |
| 7 | Shenyang | Air node city | 27 | Shijiazhuang | Air node city |
| 8 | Ningbo | Air node city | 28 | Chengdu | Air node city |
| 9 | Changsha | Air node city | 29 | Yinchuan | Air node city |
| 10 | Lianyungang | Air node city | 30 | Nanning | Air node city |
| 11 | Urumqi | Air node city | 31 | Hohhot | Air node city |
| 12 | Harbin | Air node city | 32 | Hangzhou | Air node city |
| 13 | Lanzhou | Air node city | 33 | Fuzhou | Air node city |
| 14 | Qingdao | Air node city | 34 | Guiyang | Air node city |
| 15 | Kunming | Air node city | 35 | Beijing | Air node city |
| 16 | Xiamen | Air node city | 36 | Xuzhou | Air node city |
| 17 | Changchun | Air node city | 37 | Jiujiang | Air node city |
| 18 | Nanchang | Air node city | 38 | Yantai | Air node city |
| 19 | Dalian | Air node city | 39 | Liuzhou | Air node city |
| 20 | Nanjing | Air node city | 40 | Wuxi | Air node city |
| No. | City | Node Type | No. | City | Node Type |
|---|---|---|---|---|---|
| 1 | Chongqing | Municipality | 16 | Xining | Provincial capital |
| 2 | Wuhan | Provincial capital | 17 | Tianjin | Municipality |
| 3 | Zhengzhou | Provincial capital | 18 | Taiyuan | Provincial capital |
| 4 | Guangzhou | Provincial capital | 19 | Jinan | Provincial capital |
| 5 | Xi’an | Provincial capital | 20 | Shanghai | Municipality |
| 6 | Hefei | Provincial capital | 21 | Shijiazhuang | Provincial capital |
| 7 | Shenyang | Provincial capital | 22 | Chengdu | Provincial capital |
| 8 | Changsha | Provincial capital | 23 | Yinchuan | Provincial capital |
| 9 | Urumqi | Provincial capital | 24 | Nanning | Provincial capital |
| 10 | Harbin | Provincial capital | 25 | Hohhot | Provincial capital |
| 11 | Lanzhou | Provincial capital | 26 | Hangzhou | Provincial capital |
| 12 | Kunming | Provincial capital | 27 | Fuzhou | Provincial capital |
| 13 | Changchun | Provincial capital | 28 | Guiyang | Provincial capital |
| 14 | Nanchang | Provincial capital | 29 | Beijing | Municipality |
| 15 | Nanjing | Provincial capital | 30 |
Appendix B
| No. | City | Degree | Degree Centrality | Betweenness Centrality | Closeness Centrality | Eigenvector Centrality | Constraint Coefficient | Clustering Coefficient | Comprehensive Score of Railway Network | Ranking |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Chongqing | 13 | 0.302326 | 0.007049 | 0.573333 | 0.138340 | 0.147733 | 0.589744 | 0.468878 | 26 |
| 2 | Wuhan | 17 | 0.395349 | 0.023898 | 0.623188 | 0.171448 | 0.128758 | 0.514706 | 0.483948 | 13 |
| 3 | Zhengzhou | 26 | 0.604651 | 0.045035 | 0.716667 | 0.247857 | 0.111981 | 0.455385 | 0.495845 | 8 |
| 4 | Suzhou | 16 | 0.372093 | 0.013435 | 0.614286 | 0.166533 | 0.131415 | 0.541667 | 0.481240 | 17 |
| 5 | Guangzhou | 24 | 0.558140 | 0.055312 | 0.693548 | 0.226815 | 0.112617 | 0.445652 | 0.500474 | 6 |
| 6 | Xi’an | 23 | 0.534884 | 0.018487 | 0.682540 | 0.241499 | 0.124304 | 0.561265 | 0.506751 | 3 |
| 7 | Hefei | 14 | 0.325581 | 0.006573 | 0.573333 | 0.152294 | 0.145876 | 0.615385 | 0.477620 | 20 |
| 8 | Shenyang | 15 | 0.348837 | 0.014351 | 0.581081 | 0.135663 | 0.151742 | 0.514286 | 0.480288 | 18 |
| 9 | Ningbo | 15 | 0.348837 | 0.013626 | 0.597222 | 0.156819 | 0.141121 | 0.590476 | 0.483715 | 14 |
| 10 | Changsha | 22 | 0.511628 | 0.028515 | 0.671875 | 0.220099 | 0.126504 | 0.523810 | 0.504486 | 4 |
| 11 | Lianyungang | 9 | 0.209302 | 0.003035 | 0.551282 | 0.099512 | 0.175169 | 0.638889 | 0.454819 | 38 |
| 12 | Urumqi | 26 | 0.604651 | 0.097795 | 0.716667 | 0.237736 | 0.108931 | 0.421538 | 0.507032 | 2 |
| 13 | Harbin | 9 | 0.209302 | 0.009000 | 0.537500 | 0.074581 | 0.171475 | 0.444444 | 0.454941 | 37 |
| 14 | Lanzhou | 16 | 0.372093 | 0.029593 | 0.614286 | 0.150493 | 0.135311 | 0.458333 | 0.475377 | 22 |
| 15 | Qingdao | 23 | 0.534884 | 0.031140 | 0.682540 | 0.224187 | 0.119908 | 0.486166 | 0.499621 | 7 |
| 16 | Kunming | 15 | 0.348837 | 0.011352 | 0.597222 | 0.149395 | 0.145318 | 0.571429 | 0.478006 | 19 |
| 17 | Xiamen | 15 | 0.348837 | 0.016713 | 0.605634 | 0.146181 | 0.125621 | 0.447619 | 0.466563 | 29 |
| 18 | Changchun | 10 | 0.232558 | 0.004698 | 0.544304 | 0.085074 | 0.199911 | 0.622222 | 0.457503 | 35 |
| 19 | Nanchang | 23 | 0.534884 | 0.031356 | 0.682540 | 0.227865 | 0.123532 | 0.513834 | 0.503000 | 5 |
| 20 | Dalian | 8 | 0.186047 | 0.003583 | 0.511905 | 0.065188 | 0.220170 | 0.607143 | 0.458258 | 33 |
| 21 | Dongguan | 3 | 0.069767 | 0.000000 | 0.472527 | 0.036872 | 0.397977 | 1.000000 | 0.450085 | 40 |
| 22 | Nanjing | 20 | 0.465116 | 0.040724 | 0.651515 | 0.184936 | 0.118198 | 0.436842 | 0.492756 | 11 |
| 23 | Xining | 2 | 0.046512 | 0.000000 | 0.430000 | 0.022584 | 0.551827 | 1.000000 | 0.457530 | 34 |
| 24 | Tianjin | 25 | 0.581395 | 0.065271 | 0.704918 | 0.215978 | 0.113469 | 0.403333 | 0.495618 | 9 |
| 25 | Taiyuan | 14 | 0.325581 | 0.004659 | 0.573333 | 0.150739 | 0.150503 | 0.637363 | 0.476714 | 21 |
| 26 | Shenzhen | 17 | 0.395349 | 0.021504 | 0.623188 | 0.169303 | 0.133101 | 0.514706 | 0.484054 | 12 |
| 27 | Jinan | 19 | 0.441860 | 0.032107 | 0.641791 | 0.168003 | 0.122759 | 0.438596 | 0.483260 | 15 |
| 28 | Shanghai | 20 | 0.465116 | 0.032380 | 0.651515 | 0.194503 | 0.115797 | 0.457895 | 0.493701 | 10 |
| 29 | Tangshan | 6 | 0.139535 | 0.000929 | 0.472527 | 0.045667 | 0.269930 | 0.733333 | 0.455568 | 36 |
| 30 | Shijiazhuang | 10 | 0.232558 | 0.001965 | 0.551282 | 0.105552 | 0.175782 | 0.666667 | 0.458857 | 31 |
| 31 | Chengdu | 22 | 0.511628 | 0.016248 | 0.671875 | 0.232521 | 0.129773 | 0.588745 | 0.509849 | 1 |
| 32 | Yinchuan | 3 | 0.069767 | 0.000143 | 0.462366 | 0.030719 | 0.384650 | 0.666667 | 0.432786 | 42 |
| 33 | Nanning | 15 | 0.348837 | 0.006503 | 0.605634 | 0.163758 | 0.154230 | 0.666667 | 0.481669 | 16 |
| 34 | Hohhot | 17 | 0.395349 | 0.044308 | 0.614286 | 0.139838 | 0.114371 | 0.345588 | 0.470704 | 25 |
| 35 | Hangzhou | 12 | 0.279070 | 0.011596 | 0.544304 | 0.103557 | 0.155106 | 0.439394 | 0.466891 | 28 |
| 36 | Fuzhou | 7 | 0.162791 | 0.005679 | 0.511905 | 0.054375 | 0.174249 | 0.238095 | 0.428890 | 43 |
| 37 | Guiyang | 10 | 0.232558 | 0.001753 | 0.524390 | 0.105467 | 0.196212 | 0.755556 | 0.472797 | 23 |
| 38 | Beijing | 15 | 0.348837 | 0.014928 | 0.597222 | 0.143288 | 0.133323 | 0.485714 | 0.471305 | 24 |
| 39 | Xuzhou | 8 | 0.186047 | 0.003215 | 0.524390 | 0.072299 | 0.194695 | 0.535714 | 0.452254 | 39 |
| 40 | Quanzhou | 5 | 0.116279 | 0.002304 | 0.518072 | 0.046195 | 0.260505 | 0.600000 | 0.427987 | 44 |
| 41 | Jiujiang | 5 | 0.116279 | 0.000123 | 0.483146 | 0.052814 | 0.289660 | 0.900000 | 0.458679 | 32 |
| 42 | Yantai | 6 | 0.139535 | 0.000154 | 0.500000 | 0.070883 | 0.242848 | 0.866667 | 0.467560 | 27 |
| 43 | Liuzhou | 8 | 0.186047 | 0.001409 | 0.524390 | 0.090434 | 0.203046 | 0.714286 | 0.461740 | 30 |
| 44 | Wuxi | 6 | 0.139535 | 0.001638 | 0.505882 | 0.049560 | 0.242902 | 0.600000 | 0.440172 | 41 |
| No. | City | Degree | Degree Centrality | Betweenness Centrality | Closeness Centrality | Eigenvector Centrality | Constraint Coefficient | Clustering Coefficient | Comprehensive Score of Air Network | Ranking |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Chongqing | 34 | 0.790698 | 0.022157 | 0.808898 | 0.207518 | 0.107610 | 0.691622 | 0.504407 | 12 |
| 2 | Wuhan | 27 | 0.627907 | 0.013749 | 0.702062 | 0.167107 | 0.111167 | 0.706553 | 0.507661 | 8 |
| 3 | Zhengzhou | 29 | 0.674419 | 0.011407 | 0.729594 | 0.178043 | 0.106081 | 0.677340 | 0.501550 | 14 |
| 4 | Suzhou | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 42 |
| 5 | Guangzhou | 26 | 0.604651 | 0.005700 | 0.689061 | 0.166030 | 0.113788 | 0.756923 | 0.498788 | 19 |
| 6 | Xi’an | 33 | 0.767442 | 0.014321 | 0.791687 | 0.201866 | 0.106578 | 0.687500 | 0.494832 | 23 |
| 7 | Hefei | 22 | 0.511628 | 0.003839 | 0.641540 | 0.143496 | 0.114765 | 0.761905 | 0.484910 | 32 |
| 8 | Shenyang | 26 | 0.604651 | 0.012175 | 0.689061 | 0.163483 | 0.107634 | 0.707692 | 0.500712 | 15 |
| 9 | Ningbo | 18 | 0.418605 | 0.003174 | 0.600150 | 0.118785 | 0.122546 | 0.797386 | 0.482786 | 34 |
| 10 | Changsha | 32 | 0.744186 | 0.025009 | 0.775194 | 0.191227 | 0.102516 | 0.645161 | 0.513417 | 4 |
| 11 | Lianyungang | 9 | 0.209302 | 0.001655 | 0.516796 | 0.053307 | 0.159907 | 0.555556 | 0.457044 | 38 |
| 12 | Urumqi | 22 | 0.511628 | 0.004388 | 0.641540 | 0.141381 | 0.117314 | 0.761905 | 0.489342 | 28 |
| 13 | Harbin | 28 | 0.651163 | 0.005532 | 0.715564 | 0.181860 | 0.112862 | 0.777778 | 0.504578 | 11 |
| 14 | Lanzhou | 26 | 0.604651 | 0.004896 | 0.689061 | 0.169007 | 0.111967 | 0.766154 | 0.497409 | 21 |
| 15 | Qingdao | 30 | 0.697674 | 0.023128 | 0.744186 | 0.184530 | 0.106520 | 0.694253 | 0.525641 | 1 |
| 16 | Kunming | 34 | 0.790698 | 0.024978 | 0.808898 | 0.207101 | 0.106987 | 0.689840 | 0.508767 | 7 |
| 17 | Xiamen | 24 | 0.558140 | 0.003118 | 0.664452 | 0.160177 | 0.116026 | 0.811594 | 0.490206 | 26 |
| 18 | Changchun | 20 | 0.465116 | 0.006532 | 0.620155 | 0.129466 | 0.115638 | 0.747368 | 0.489678 | 27 |
| 19 | Nanchang | 28 | 0.651163 | 0.016774 | 0.715564 | 0.171219 | 0.107440 | 0.687831 | 0.511331 | 6 |
| 20 | Dalian | 31 | 0.720930 | 0.024997 | 0.759374 | 0.186932 | 0.104769 | 0.666667 | 0.520965 | 2 |
| 21 | Dongguan | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 42 |
| 22 | Nanjing | 30 | 0.697674 | 0.014936 | 0.744186 | 0.182812 | 0.104540 | 0.668966 | 0.505921 | 9 |
| 23 | Xining | 10 | 0.232558 | 0.000190 | 0.524075 | 0.068746 | 0.165443 | 0.911111 | 0.482772 | 35 |
| 24 | Tianjin | 27 | 0.627907 | 0.008963 | 0.702062 | 0.170361 | 0.109642 | 0.726496 | 0.499631 | 16 |
| 25 | Taiyuan | 26 | 0.604651 | 0.004522 | 0.689061 | 0.169759 | 0.113734 | 0.781538 | 0.497693 | 20 |
| 26 | Shenzhen | 32 | 0.744186 | 0.020495 | 0.775194 | 0.195552 | 0.108230 | 0.693548 | 0.512061 | 5 |
| 27 | Jinan | 21 | 0.488372 | 0.002576 | 0.630666 | 0.140005 | 0.118750 | 0.809524 | 0.482850 | 33 |
| 28 | Shanghai | 33 | 0.767442 | 0.014887 | 0.791687 | 0.202652 | 0.107103 | 0.696970 | 0.496730 | 22 |
| 29 | Tangshan | 5 | 0.116279 | 0.000215 | 0.471004 | 0.030302 | 0.240696 | 0.600000 | 0.453250 | 41 |
| 30 | Shijiazhuang | 21 | 0.488372 | 0.007760 | 0.630666 | 0.128840 | 0.113221 | 0.685714 | 0.485398 | 30 |
| 31 | Chengdu | 32 | 0.744186 | 0.011791 | 0.775194 | 0.199600 | 0.109484 | 0.721774 | 0.499575 | 17 |
| 32 | Yinchuan | 20 | 0.465116 | 0.002538 | 0.620155 | 0.132878 | 0.123724 | 0.826316 | 0.485644 | 29 |
| 33 | Nanning | 25 | 0.581395 | 0.003217 | 0.676533 | 0.166405 | 0.117022 | 0.820000 | 0.494052 | 24 |
| 34 | Hohhot | 21 | 0.488372 | 0.001475 | 0.630666 | 0.144287 | 0.122168 | 0.871429 | 0.485132 | 31 |
| 35 | Hangzhou | 30 | 0.697674 | 0.014640 | 0.744186 | 0.182050 | 0.105157 | 0.668966 | 0.505550 | 10 |
| 36 | Fuzhou | 19 | 0.441860 | 0.004997 | 0.600150 | 0.123659 | 0.124252 | 0.795322 | 0.499014 | 18 |
| 37 | Guiyang | 27 | 0.627907 | 0.004663 | 0.702062 | 0.176297 | 0.116645 | 0.800570 | 0.504032 | 13 |
| 38 | Beijing | 32 | 0.744186 | 0.029049 | 0.775194 | 0.188191 | 0.103704 | 0.637097 | 0.520587 | 3 |
| 39 | Xuzhou | 7 | 0.162791 | 0.000610 | 0.509716 | 0.042801 | 0.199387 | 0.714286 | 0.456481 | 39 |
| 40 | Quanzhou | 13 | 0.302326 | 0.000670 | 0.547196 | 0.089531 | 0.137968 | 0.820513 | 0.476879 | 36 |
| 41 | Jiujiang | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 42 |
| 42 | Yantai | 21 | 0.488372 | 0.007319 | 0.630666 | 0.133342 | 0.117115 | 0.747619 | 0.492713 | 25 |
| 43 | Liuzhou | 4 | 0.093023 | 0.000000 | 0.471004 | 0.029524 | 0.299941 | 1.000000 | 0.473039 | 37 |
| 44 | Wuxi | 5 | 0.116279 | 0.000123 | 0.489596 | 0.032621 | 0.249509 | 0.800000 | 0.455676 | 40 |
| No. | City | Degree | Degree Centrality | Betweenness Centrality | Closeness Centrality | Eigenvector Centrality | Constraint Coefficient | Clustering Coefficient | Comprehensive Score of Highway Network | Ranking |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Chongqing | 6 | 0.139535 | 0.058190 | 0.320494 | 0.334837 | 0.321927 | 0.466667 | 0.551215 | 3 |
| 2 | Wuhan | 8 | 0.186047 | 0.130688 | 0.369579 | 0.364111 | 0.191493 | 0.178571 | 0.563992 | 2 |
| 3 | Zhengzhou | 4 | 0.093023 | 0.031241 | 0.323018 | 0.186243 | 0.283203 | 0.166667 | 0.480866 | 22 |
| 4 | Suzhou | 2 | 0.046512 | 0.002178 | 0.284884 | 0.044002 | 0.500000 | 0.000000 | 0.427225 | 43 |
| 5 | Guangzhou | 6 | 0.139535 | 0.162912 | 0.366279 | 0.116712 | 0.166667 | 0.000000 | 0.510489 | 11 |
| 6 | Xi’an | 8 | 0.186047 | 0.107286 | 0.341860 | 0.369397 | 0.242148 | 0.285714 | 0.571843 | 1 |
| 7 | Hefei | 5 | 0.116279 | 0.074074 | 0.347655 | 0.212818 | 0.221250 | 0.100000 | 0.496015 | 15 |
| 8 | Shenyang | 2 | 0.046512 | 0.088594 | 0.181519 | 0.000994 | 0.500000 | 0.000000 | 0.475598 | 27 |
| 9 | Ningbo | 3 | 0.069767 | 0.008576 | 0.293023 | 0.082429 | 0.413580 | 0.333333 | 0.455729 | 31 |
| 10 | Changsha | 2 | 0.046512 | 0.006943 | 0.318010 | 0.094605 | 0.500000 | 0.000000 | 0.434066 | 40 |
| 11 | Lianyungang | 5 | 0.116279 | 0.104133 | 0.330833 | 0.106715 | 0.232044 | 0.100000 | 0.500935 | 14 |
| 12 | Urumqi | 2 | 0.046512 | 0.011350 | 0.262970 | 0.046462 | 0.500000 | 0.000000 | 0.437345 | 38 |
| 13 | Harbin | 1 | 0.023256 | 0.000000 | 0.134063 | 0.000040 | 1.000000 | 0.000000 | 0.477364 | 25 |
| 14 | Lanzhou | 5 | 0.116279 | 0.074518 | 0.293023 | 0.183821 | 0.261528 | 0.200000 | 0.515617 | 9 |
| 15 | Qingdao | 3 | 0.069767 | 0.062685 | 0.299440 | 0.042882 | 0.333333 | 0.000000 | 0.45468 | 32 |
| 16 | Kunming | 6 | 0.139535 | 0.060330 | 0.303876 | 0.241649 | 0.267230 | 0.266667 | 0.530426 | 5 |
| 17 | Xiamen | 3 | 0.069767 | 0.008712 | 0.282919 | 0.071386 | 0.333333 | 0.000000 | 0.430196 | 42 |
| 18 | Changchun | 2 | 0.046512 | 0.045404 | 0.154805 | 0.000203 | 0.500000 | 0.000000 | 0.464427 | 30 |
| 19 | Nanchang | 4 | 0.093023 | 0.015110 | 0.295131 | 0.129352 | 0.307726 | 0.166667 | 0.464533 | 29 |
| 20 | Dalian | 2 | 0.046512 | 0.129568 | 0.217054 | 0.004848 | 0.500000 | 0.000000 | 0.493271 | 16 |
| 21 | Dongguan | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 44 |
| 22 | Nanjing | 5 | 0.116279 | 0.055260 | 0.339035 | 0.136403 | 0.263600 | 0.200000 | 0.483643 | 21 |
| 23 | Xining | 1 | 0.023256 | 0.000000 | 0.226648 | 0.036168 | 1.000000 | 0.000000 | 0.477001 | 26 |
| 24 | Tianjin | 6 | 0.139535 | 0.186401 | 0.333522 | 0.072444 | 0.213611 | 0.066667 | 0.542425 | 4 |
| 25 | Taiyuan | 4 | 0.093023 | 0.029904 | 0.323018 | 0.143596 | 0.301758 | 0.166667 | 0.472072 | 28 |
| 26 | Shenzhen | 3 | 0.069767 | 0.040947 | 0.318010 | 0.066540 | 0.333333 | 0.000000 | 0.449829 | 36 |
| 27 | Jinan | 5 | 0.116279 | 0.099076 | 0.339035 | 0.087577 | 0.200000 | 0.000000 | 0.478785 | 24 |
| 28 | Shanghai | 6 | 0.139535 | 0.114235 | 0.356724 | 0.173884 | 0.250556 | 0.200000 | 0.51856 | 8 |
| 29 | Tangshan | 2 | 0.046512 | 0.000000 | 0.282919 | 0.028432 | 0.700278 | 1.000000 | 0.48791 | 18 |
| 30 | Shijiazhuang | 4 | 0.093023 | 0.028380 | 0.310782 | 0.096308 | 0.250000 | 0.000000 | 0.449369 | 37 |
| 31 | Chengdu | 5 | 0.116279 | 0.018644 | 0.313155 | 0.304616 | 0.375972 | 0.600000 | 0.524607 | 6 |
| 32 | Yinchuan | 4 | 0.093023 | 0.030564 | 0.308446 | 0.147397 | 0.352109 | 0.333333 | 0.485985 | 19 |
| 33 | Nanning | 4 | 0.093023 | 0.073643 | 0.315564 | 0.128803 | 0.295139 | 0.166667 | 0.493179 | 17 |
| 34 | Hohhot | 3 | 0.069767 | 0.048209 | 0.290945 | 0.052321 | 0.333333 | 0.000000 | 0.453534 | 34 |
| 35 | Hangzhou | 6 | 0.139535 | 0.067050 | 0.320494 | 0.150083 | 0.255509 | 0.200000 | 0.50741 | 12 |
| 36 | Fuzhou | 4 | 0.093023 | 0.030408 | 0.297270 | 0.094970 | 0.250000 | 0.000000 | 0.453631 | 33 |
| 37 | Guiyang | 6 | 0.139535 | 0.041596 | 0.308446 | 0.238201 | 0.267230 | 0.266667 | 0.522408 | 7 |
| 38 | Beijing | 5 | 0.116279 | 0.121983 | 0.341860 | 0.072057 | 0.264444 | 0.100000 | 0.504772 | 13 |
| 39 | Xuzhou | 4 | 0.093023 | 0.034448 | 0.323018 | 0.116747 | 0.250000 | 0.000000 | 0.452537 | 35 |
| 40 | Quanzhou | 3 | 0.069767 | 0.011185 | 0.277184 | 0.058074 | 0.333333 | 0.000000 | 0.430582 | 41 |
| 41 | Jiujiang | 4 | 0.093023 | 0.029674 | 0.308446 | 0.174168 | 0.307726 | 0.166667 | 0.484654 | 20 |
| 42 | Yantai | 3 | 0.069767 | 0.170007 | 0.266385 | 0.023646 | 0.333333 | 0.000000 | 0.511687 | 10 |
| 43 | Liuzhou | 1 | 0.023256 | 0.000000 | 0.233087 | 0.047546 | 1.000000 | 0.000000 | 0.480385 | 23 |
| 44 | Wuxi | 3 | 0.069767 | 0.025539 | 0.303876 | 0.049751 | 0.333333 | 0.000000 | 0.437343 | 39 |
| No. | City | Degree | Degree Centrality | Betweenness Centrality | Closeness Centrality | Eigenvector Centrality | Constraint Coefficient | Clustering Coefficient | Comprehensive Score of Water Network | Ranking |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Chongqing | 6 | 0.230769 | 0.001055 | 0.509804 | 0.121452 | 0.335575 | 0.866667 | 0.515338 | 13 |
| 2 | Wuhan | 8 | 0.307692 | 0.008615 | 0.530612 | 0.133928 | 0.354590 | 0.607143 | 0.500424 | 23 |
| 3 | Zhengzhou | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0 | 28 |
| 4 | Suzhou | 20 | 0.769231 | 0.218469 | 0.787879 | 0.320946 | 0.180992 | 0.326316 | 0.532996 | 5 |
| 5 | Guangzhou | 17 | 0.653846 | 0.252188 | 0.742857 | 0.297861 | 0.185935 | 0.404412 | 0.547004 | 1 |
| 6 | Xi’an | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0 | 28 |
| 7 | Hefei | 8 | 0.307692 | 0.012659 | 0.577778 | 0.179610 | 0.258644 | 0.714286 | 0.505258 | 21 |
| 8 | Shenyang | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0 | 28 |
| 9 | Ningbo | 13 | 0.500000 | 0.024375 | 0.650000 | 0.288151 | 0.198567 | 0.666667 | 0.527235 | 7 |
| 10 | Changsha | 2 | 0.076923 | 0.000000 | 0.472727 | 0.059531 | 0.548331 | 1.000000 | 0.511659 | 15 |
| 11 | Lianyungang | 9 | 0.346154 | 0.014349 | 0.590909 | 0.206743 | 0.227639 | 0.694444 | 0.505318 | 20 |
| 12 | Urumqi | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0 | 28 |
| 13 | Harbin | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0 | 28 |
| 14 | Lanzhou | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0 | 28 |
| 15 | Qingdao | 11 | 0.423077 | 0.033293 | 0.619048 | 0.232660 | 0.353492 | 0.636364 | 0.538485 | 3 |
| 16 | Kunming | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0 | 28 |
| 17 | Xiamen | 11 | 0.423077 | 0.013371 | 0.619048 | 0.247289 | 0.263967 | 0.709091 | 0.524528 | 10 |
| 18 | Changchun | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0 | 28 |
| 19 | Nanchang | 4 | 0.153846 | 0.000000 | 0.490566 | 0.074821 | 0.440707 | 1.000000 | 0.522685 | 11 |
| 20 | Dalian | 11 | 0.423077 | 0.011388 | 0.619048 | 0.245856 | 0.235484 | 0.727273 | 0.518903 | 12 |
| 21 | Dongguan | 2 | 0.076923 | 0.000000 | 0.448276 | 0.048422 | 0.564354 | 1.000000 | 0.509409 | 18 |
| 22 | Nanjing | 12 | 0.461538 | 0.038400 | 0.604651 | 0.226923 | 0.288540 | 0.515152 | 0.529569 | 6 |
| 23 | Xining | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0 | 28 |
| 24 | Tianjin | 15 | 0.576923 | 0.054679 | 0.684211 | 0.302066 | 0.213960 | 0.542857 | 0.537336 | 4 |
| 25 | Taiyuan | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0 | 28 |
| 26 | Shenzhen | 9 | 0.346154 | 0.001166 | 0.590909 | 0.225655 | 0.252924 | 0.916667 | 0.524569 | 9 |
| 27 | Jinan | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0 | 28 |
| 28 | Shanghai | 18 | 0.692308 | 0.116558 | 0.742857 | 0.331277 | 0.227944 | 0.424837 | 0.542556 | 2 |
| 29 | Tangshan | 5 | 0.192308 | 0.002897 | 0.541667 | 0.126045 | 0.298255 | 0.800000 | 0.504278 | 22 |
| 30 | Shijiazhuang | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0 | 28 |
| 31 | Chengdu | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0 | 28 |
| 32 | Yinchuan | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0 | 28 |
| 33 | Nanning | 2 | 0.076923 | 0.076923 | 0.448276 | 0.027415 | 0.719672 | 0.000000 | 0.446181 | 27 |
| 34 | Hohhot | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0 | 28 |
| 35 | Hangzhou | 3 | 0.115385 | 0.000000 | 0.490566 | 0.087101 | 0.397655 | 1.000000 | 0.514296 | 14 |
| 36 | Fuzhou | 8 | 0.307692 | 0.000342 | 0.577778 | 0.206196 | 0.261719 | 0.964286 | 0.524839 | 8 |
| 37 | Guiyang | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0 | 28 |
| 38 | Beijing | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0 | 28 |
| 39 | Xuzhou | 6 | 0.230769 | 0.007238 | 0.520000 | 0.117471 | 0.339870 | 0.533333 | 0.487505 | 24 |
| 40 | Quanzhou | 3 | 0.115385 | 0.000000 | 0.520000 | 0.079051 | 0.397919 | 1.000000 | 0.510794 | 16 |
| 41 | Jiujiang | 7 | 0.269231 | 0.005593 | 0.530612 | 0.137952 | 0.382926 | 0.714286 | 0.507533 | 19 |
| 42 | Yantai | 6 | 0.230769 | 0.002154 | 0.509804 | 0.128808 | 0.305361 | 0.800000 | 0.510318 | 17 |
| 43 | Liuzhou | 1 | 0.038462 | 0.000000 | 0.313253 | 0.002502 | 1.000000 | 0.000000 | 0.447931 | 26 |
| 44 | Wuxi | 3 | 0.115385 | 0.002747 | 0.520000 | 0.067202 | 0.420811 | 0.666667 | 0.482609 | 25 |
References
- Ministry of Commerce People’s Republic of China (MCPRC). Available online: http://tradeinservices.mofcom.gov.cn/article/ydyl/sedly/ysfw/202301/144654.html (accessed on 10 January 2023).
- Yidaiyilu.gov.cn. Available online: https://www.yidaiyilu.gov.cn/xwzx/gnxw/281310.htm (accessed on 10 January 2023).
- Ma, Y.T.; Shi, X.L.; Qiu, Y. Hierarchical Multimodal Hub Location with Time Restriction for China Railway (CR) Express Network. IEEE Access 2020, 8, 61395–61404. [Google Scholar] [CrossRef]
- Wei, H.R.; Wu, F. Formation of Coordinated Alliance for China Railway Express Platforms Considering Logistics Cost Sharing. Transp. Res. Rec. 2023, 3, 6489296. [Google Scholar] [CrossRef]
- Chen, G.; Cheung, W.; Chu, S.C.; Xu, L. Transshipment hub selection from a shipper’s and freight forwarder’s perspective. Expert Syst. Appl. 2017, 83, 396–404. [Google Scholar] [CrossRef]
- Zhang, X.F.; Lu, J.; Peng, Y. Decision framework for location and selection of container multimodal hubs: A case in China under the Belt and Road Initiative. J. Ind. Manag. Optim. 2022, 5, 2163–2190. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, W.; Lee, P.T.W. Importance rankings of nodes in the China Railway Express network under the Belt and Road Initiative. Transp. Res. Part A 2020, 139, 134–147. [Google Scholar] [CrossRef]
- Li, C.Z.; Wang, J.; Wang, H.J.; Jin, X.; Du, L.J. Intermodal transportation hub location optimization with governments subsidies under the Belt and Road Initiative. Ocean Coast. Manag. 2023, 231, 106414. [Google Scholar] [CrossRef]
- Wan, C.; Zhao, Y.; Zhang, D.; Yip, T.L. Identifying important ports in maritime container shipping networks along the Maritime Silk Road. Ocean Coast. Manag. 2021, 211, 105738. [Google Scholar] [CrossRef]
- Lee, P.T.W.; Hu, Z.H.; Lee, S.; Feng, X.; Notteboom, T. Strategic locations for logistics distribution centers along the Belt and Road: Explorative analysis and research agenda. Transp. Policy 2022, 116, 24–47. [Google Scholar] [CrossRef]
- Li, D.Q.; Zhao, L.J.; Wang, C.; Sun, W.J.; Xue, J. Selection of China’s imported grain distribution centers in the context of the Belt and Road initiative. Transp. Res. Part E 2018, 120, 16–34. [Google Scholar] [CrossRef]
- Aljohani, K.; Thompson, R.G. A multi-criteria spatial evaluation framework to optimise the siting of freight consolidation facilities in inner-city areas. Transp. Res. Part A Policy Pract. 2020, 138, 51–69. [Google Scholar] [CrossRef]
- Muerza, V.; Milenkovic, M.; Larrodé, E.; Bojovic, N. Selection of an international distribution center location: A comparison between stand-alone ANP and DEMATEL-ANP applications. Res. Transp. Bus. Manag. 2024, 56, 101135. [Google Scholar] [CrossRef]
- Civil Aviation Administration of China (CAAC). Available online: http://www.caac.gov.cn/XXGK/XXGK/ZCFBJD/202205/t20220506_213121.html (accessed on 8 May 2023).
- Zhou, Y.M.; Kundu, T.; Goh, M.; Sheu, J.B. Multimodal transportation network centrality analysis for Belt and Road Initiative. Transp. Res. Part E Logist. Transp. Rev. 2021, 149, 102292. [Google Scholar] [CrossRef]
- Derudder, B.; Liu, X.; Kunaka, C. Connectivity along Overland Corridors of the Belt and Road Initiative; World Bank: Washington, DC, USA, 2018. [Google Scholar]
- An, F.; Gao, X.Y.; Guan, J.H.; Jiang, M.H.; Liu, Q. Detecting the significant nodes in two-layer flow networks: An interlayer non-failure cascading effect perspective. Eur. Phys. J. Spec. Top. 2019, 228, 2475–2490. [Google Scholar] [CrossRef]
- Wang, L.; Zheng, S.; Wang, Y.; Wang, L. Identification of critical nodes in multimodal transportation network. Phys. A-Stat. Mech. Its Appl. 2021, 580, 126170. [Google Scholar] [CrossRef]
- Li, Z.; Tang, J.; Zhao, C.; Gao, F. Improved centrality measure based on the adapted PageRank algorithm for urban transportation multiplex networks. Chaos Solitons Fractals 2023, 167, 112998. [Google Scholar] [CrossRef]
- Meng, Y.; Tian, X.; Li, Z.; Zhou, W.; Zhou, Z.; Zhong, M. Exploring node importance evolution of weighted complex networks in urban rail transit. Phys. A-Stat. Mech. Its Appl. 2020, 558, 124925. [Google Scholar] [CrossRef]
- De Bona, A.A.; de Oliveira Rosa, M.; Fonseca, K.V.O.; Lüders, R. A reduced model for complex network analysis of public transportation systems. Phys. A-Stat. Mech. Its Appl. 2021, 567, 125715. [Google Scholar] [CrossRef]
- Wang, L.N.; Wang, K.; Shen, J.L. Weighted complex networks in urban public transportation: Modeling and testing. Phys. A-Stat. Mech. Its Appl. 2020, 545, 123498. [Google Scholar] [CrossRef]
- Sun, W.; Zhao, L.; Wang, C.; Li, D.; Xue, J. Selection of consolidation centers for China Railway Express. Int. J. Logist. Res. Appl. 2020, 23, 417–442. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, Y.; Du, L.; Goerlandt, F.; Sui, Z.; Wen, Y. A rule-based maritime traffic situation complex network approach for enhancing situation awareness of vessel traffic service operators. Ocean Eng. 2023, 284, 115203. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, B. Study on node importance evaluation of the high-speed passenger traffic complex network based on the Structural Hole Theory. Open Phys. 2017, 15, 1–11. [Google Scholar] [CrossRef]
- Belkoura, S.; Cook, A.; Peña, J.M.; Zanin, M. On the multi-dimensionality and sampling of air transport networks. Transp. Res. Part E Logist. Transp. Rev. 2016, 94, 95–109. [Google Scholar] [CrossRef]
- Zhao, L.; Zhao, Y.; Hu, Q.; Li, H.; Stoeter, J. Evaluation of consolidation center cargo capacity and locations for China railway express. Transp. Res. Part E 2018, 117, 58–81. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, T.; Xiao, X.; Zhang, Q.; Guo, H. Research on the Measurement of Logistics Capability of Core Cities along “the Belt and Road” in China. Adv. Math. Phys. 2022, 2022, 2223212. [Google Scholar] [CrossRef]
- Feng, F.L.; Cai, M.X.; Jia, J. Key node identification of China Railway Express transportation network based on multilayer complex network. J. Transp. Syst. Eng. Inf. Technol. 2022, 12, 191–200. [Google Scholar]
- Yin, C.; Zhang, Z.; Zhang, X.; Chen, J.; Tao, X.; Yang, L. Hub seaport multimodal freight transport network design: Perspective of regional integration development. Ocean Coast. Manag. 2023, 242, 106675. [Google Scholar] [CrossRef]
- Van Heeswijk, W.; Larsen, R.; Larsen, A. An urban consolidation center in the city of Copenhagen: A simulation study. Int. J. Sustain. Transp. 2019, 9, 675–691. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhao, L.; Wang, G.; Li, H.; Hu, Q. Selection of consolidation center locations for China railway express to reduce greenhouse gas emission. J. Clean. Prod. 2021, 305, 126872. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Q.P.; Karimi, H. Seeking the Important Nodes of Complex Networks in Product R&D Team Based on Fuzzy AHP and TOPSIS. Math. Probl. Eng. 2013, 2013, 327592. [Google Scholar]
- National Development and Reform Commission (NDRC). China National Highway Network Planning 2013–2030. Available online: http://csl.chinawuliu.com.cn/upload/files/635349288757214896.pdf (accessed on 8 June 2023).
- Wasserman, S.; Faust, K. Social Network Analysis: Method and Applications; Cambridge University Press: New York, NY, USA, 1994. [Google Scholar]
- Burt, R.S. Structural holes and good ideas. Am. J. Sociol. 2004, 110, 349–399. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining Objective Weights in Multiple Criteria Problems: The CRITIC Method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Croux, C.; Dehon, C. Influence functions of the Spearman and Kendall correlation measures. Stat. Methods Appl. 2010, 19, 497–515. [Google Scholar] [CrossRef]
- Liu, D.; Liu, C.; Fu, Q.; Li, T.; Imran, K.M.; Cui, S.; Abrar, F.M. ELM evaluation model of regional groundwater quality based on the crow search algorithm. Ecol. Indic. 2017, 81, 302–314. [Google Scholar] [CrossRef]
- National Bureau of Statistic (NBS). Available online: http://www.stats.gov.cn/xxgk/sjfb/zxfb2020/202302/t20230228_1919001.html (accessed on 20 July 2023).
- Civil Aviation Administration of China (CAAC). Catalogue of Domestic Airlines Implementing Market Adjusted Prices [EB/OL]. Available online: http://www.caac.gov.cn/XXGK/XXGK/ZFGW/201911/P020191206554926012537.pdf (accessed on 20 July 2023).
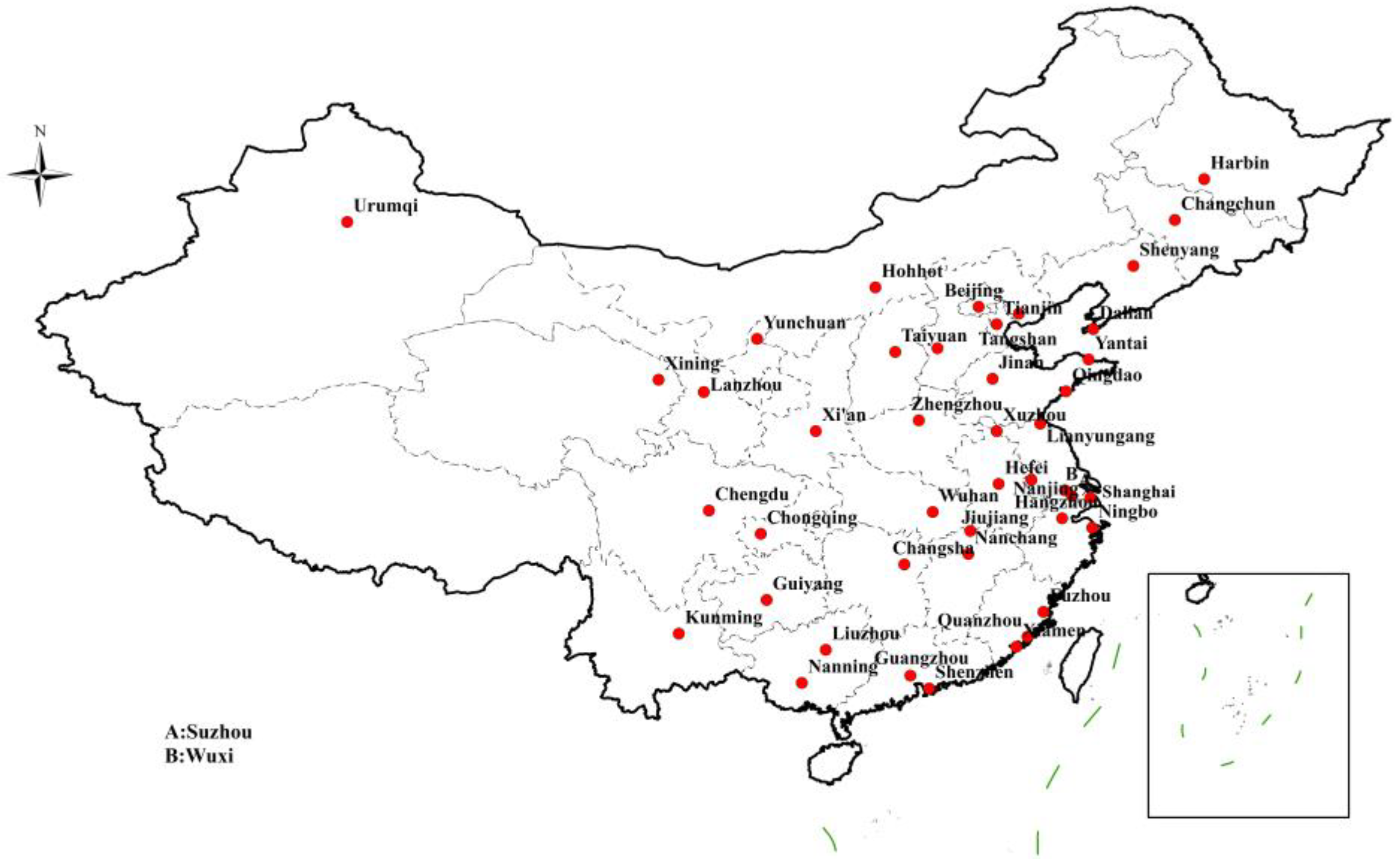

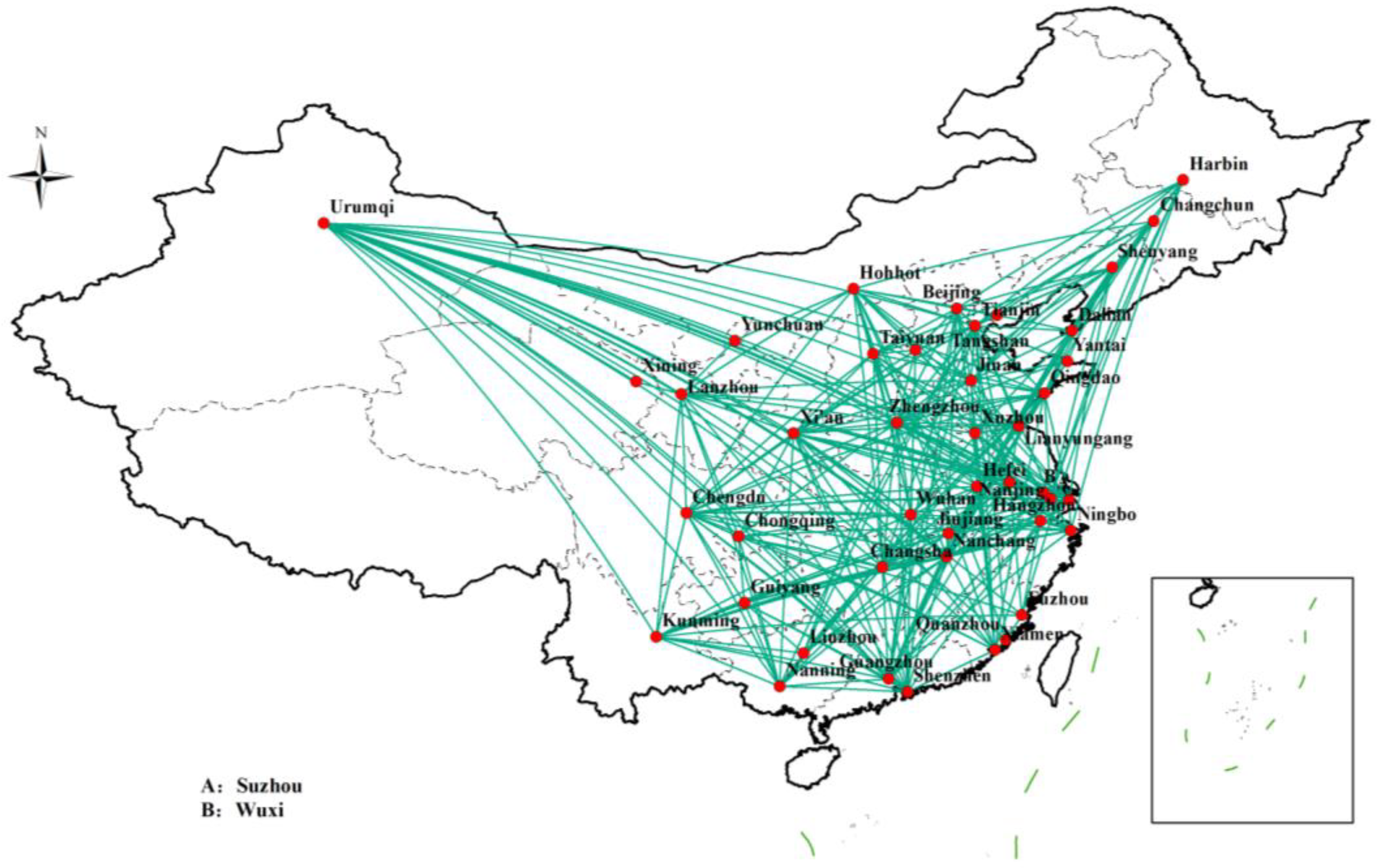

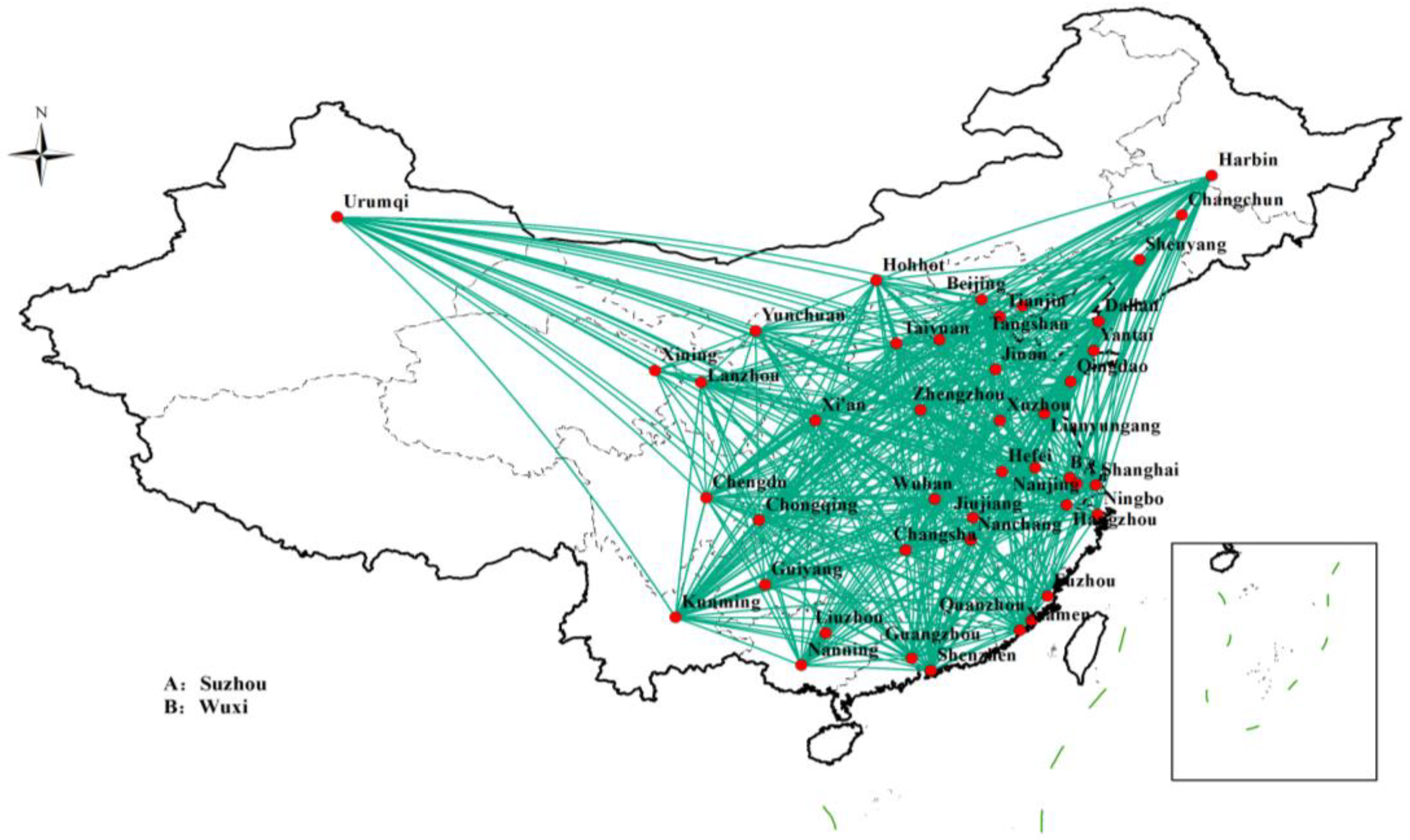
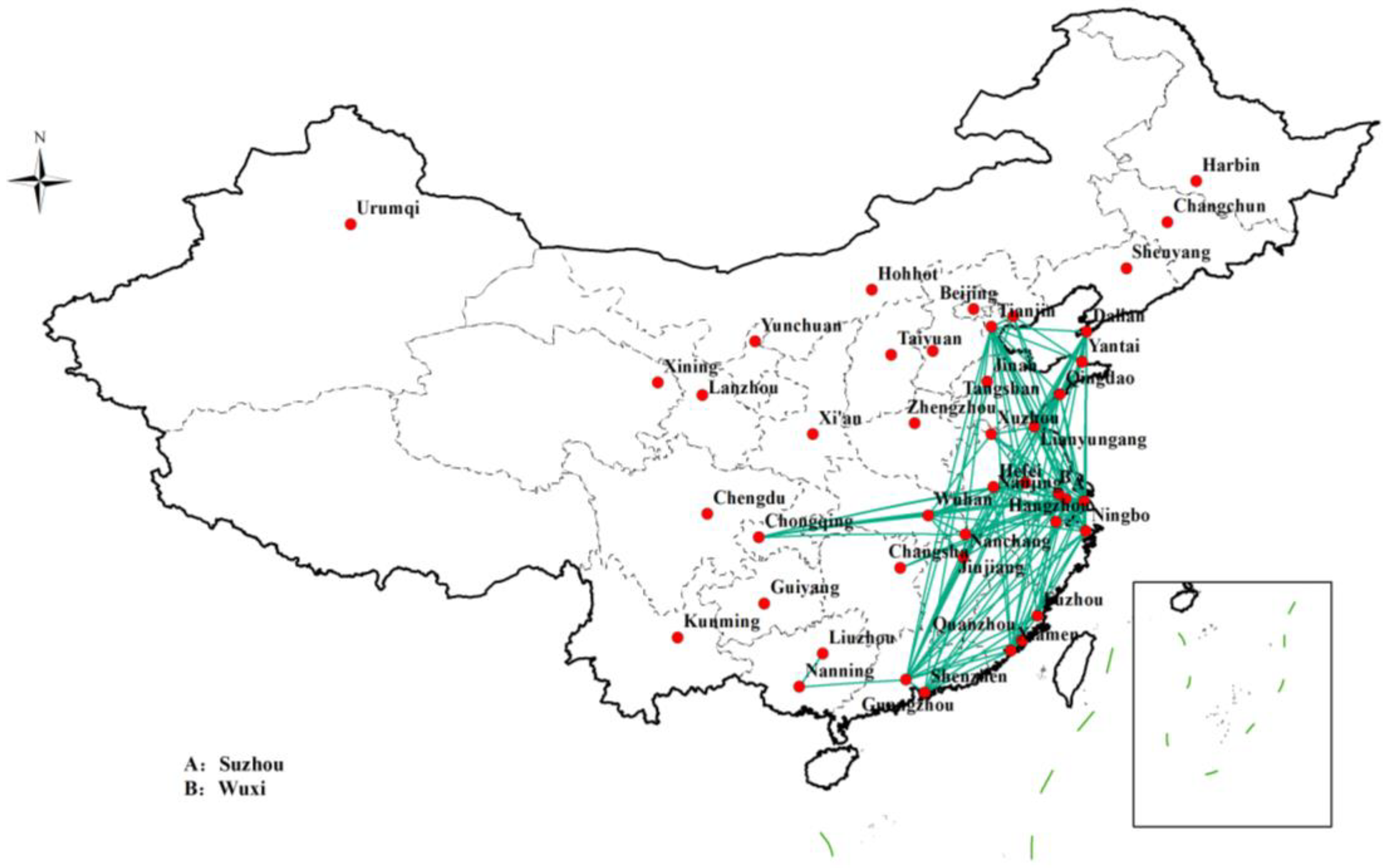
| Number | City | Number | City | Number | City | Number | City |
|---|---|---|---|---|---|---|---|
| 1 | Chongqing | 12 | Urumqi | 23 | Xining | 34 | Hohhot |
| 2 | Wuhan | 13 | Harbin | 24 | Tianjin | 35 | Hangzhou |
| 3 | Zhengzhou | 14 | Lanzhou | 25 | Taiyuan | 36 | Fuzhou |
| 4 | Suzhou | 15 | Qingdao | 26 | Shenzhen | 37 | Guiyang |
| 5 | Guangzhou | 16 | Kunming | 27 | Jinan | 38 | Beijing |
| 6 | Xi’an | 17 | Xiamen | 28 | Shanghai | 39 | Xuzhou |
| 7 | Hefei | 18 | Changchun | 29 | Tangshan | 40 | Quanzhou |
| 8 | Shenyang | 19 | Nanchang | 30 | Shijiazhuang | 41 | Jiujiang |
| 9 | Ningbo | 20 | Dalian | 31 | Chengdu | 42 | Yantai |
| 10 | Changsha | 21 | Dongguan | 32 | Yinchuan | 43 | Liuzhou |
| 11 | Lianyungang | 22 | Nanjing | 33 | Nanning | 44 | Wuxi |
| Weight | Degree Centrality | Betweenness Centrality | Closeness Centrality | Eigenvector Centrality | Constraint Coefficient | Clustering Coefficient | |
|---|---|---|---|---|---|---|---|
| Mode | |||||||
| Railway | 0.1939 | 0.1363 | 0.2029 | 0.1994 | 0.1335 | 0.1339 | |
| Highway | 0.1533 | 0.1979 | 0.1713 | 0.1681 | 0.1811 | 0.1283 | |
| Air | 0.1746 | 0.1750 | 0.2092 | 0.1765 | 0.1489 | 0.1158 | |
| Water | 0.1639 | 0.1504 | 0.1613 | 0.1771 | 0.1561 | 0.1911 | |
| Number | City | Ranking | |||||
|---|---|---|---|---|---|---|---|
| 1 | Chongqing | 0.468878 | 0.504407 | 0.551215 | 0.515338 | 0.537127 | 2 |
| 2 | Wuhan | 0.483948 | 0.507661 | 0.563992 | 0.500424 | 0.545447 | 1 |
| 3 | Zhengzhou | 0.495845 | 0.50155 | 0.480866 | 0 | 0.401084 | 34 |
| 4 | Suzhou | 0.481240 | 0 | 0.427225 | 0.532996 | 0.450306 | 24 |
| 5 | Guangzhou | 0.500474 | 0.498788 | 0.510489 | 0.547004 | 0.515681 | 5 |
| 6 | Xi’an | 0.506751 | 0.494832 | 0.571843 | 0 | 0.468879 | 19 |
| 7 | Hefei | 0.47762 | 0.48491 | 0.496015 | 0.505258 | 0.495783 | 9 |
| 8 | Shenyang | 0.480288 | 0.500712 | 0.475598 | 0 | 0.395705 | 37 |
| 9 | Ningbo | 0.483715 | 0.482786 | 0.455729 | 0.527235 | 0.470540 | 18 |
| 10 | Changsha | 0.504486 | 0.513417 | 0.434066 | 0.511659 | 0.454045 | 23 |
| 11 | Lianyungang | 0.454819 | 0.457044 | 0.500935 | 0.505318 | 0.497178 | 8 |
| 12 | Urumqi | 0.507032 | 0.489342 | 0.437345 | 0 | 0.370250 | 44 |
| 13 | Harbin | 0.454941 | 0.504578 | 0.477364 | 0 | 0.394531 | 38 |
| 14 | Lanzhou | 0.475377 | 0.497409 | 0.515617 | 0 | 0.424580 | 32 |
| 15 | Qingdao | 0.499621 | 0.525641 | 0.454680 | 0.538485 | 0.473226 | 16 |
| 16 | Kunming | 0.478006 | 0.508767 | 0.530426 | 0 | 0.435700 | 28 |
| 17 | Xiamen | 0.466563 | 0.490206 | 0.430196 | 0.524528 | 0.449684 | 25 |
| 18 | Changchun | 0.457503 | 0.489678 | 0.464427 | 0 | 0.385290 | 41 |
| 19 | Nanchang | 0.503 | 0.511331 | 0.464533 | 0.522685 | 0.478111 | 15 |
| 20 | Dalian | 0.458258 | 0.520965 | 0.493271 | 0.518903 | 0.494194 | 10 |
| 21 | Dongguan | 0.450085 | 0 | 0.416530 | 0.509409 | 0.435441 | 29 |
| 22 | Nanjing | 0.492756 | 0.505921 | 0.483643 | 0.529569 | 0.492293 | 11 |
| 23 | Xining | 0.45753 | 0.482772 | 0.477001 | 0 | 0.394515 | 39 |
| 24 | Tianjin | 0.495618 | 0.499631 | 0.542425 | 0.537336 | 0.537000 | 3 |
| 25 | Taiyuan | 0.476714 | 0.497693 | 0.472072 | 0 | 0.392770 | 40 |
| 26 | Shenzhen | 0.484054 | 0.512061 | 0.449829 | 0.524569 | 0.465798 | 20 |
| 27 | Jinan | 0.48326 | 0.48285 | 0.478785 | 0 | 0.398330 | 36 |
| 28 | Shanghai | 0.493701 | 0.49673 | 0.518560 | 0.542556 | 0.520190 | 4 |
| 29 | Tangshan | 0.455568 | 0.45325 | 0.487910 | 0.504278 | 0.487521 | 12 |
| 30 | Shijiazhuang | 0.458857 | 0.485398 | 0.449369 | 0 | 0.374376 | 43 |
| 31 | Chengdu | 0.509849 | 0.499575 | 0.524607 | 0 | 0.434533 | 30 |
| 32 | Yinchuan | 0.432786 | 0.485644 | 0.485985 | 0 | 0.398694 | 35 |
| 33 | Nanning | 0.481669 | 0.494052 | 0.493179 | 0.446181 | 0.484117 | 14 |
| 34 | Hohhot | 0.470704 | 0.485132 | 0.453534 | 0 | 0.378585 | 42 |
| 35 | Hangzhou | 0.466891 | 0.50555 | 0.507410 | 0.514296 | 0.504626 | 7 |
| 36 | Fuzhou | 0.42889 | 0.499014 | 0.453631 | 0.524839 | 0.463257 | 21 |
| 37 | Guiyang | 0.472797 | 0.504032 | 0.522408 | 0 | 0.429311 | 31 |
| 38 | Beijing | 0.471305 | 0.520587 | 0.504772 | 0 | 0.416231 | 33 |
| 39 | Xuzhou | 0.452254 | 0.456481 | 0.452537 | 0.487505 | 0.458418 | 22 |
| 40 | Quanzhou | 0.427987 | 0.476879 | 0.430582 | 0.510794 | 0.443887 | 27 |
| 41 | Jiujiang | 0.458679 | 0 | 0.484654 | 0.507533 | 0.485931 | 13 |
| 42 | Yantai | 0.46756 | 0.492713 | 0.511687 | 0.510318 | 0.507155 | 6 |
| 43 | Liuzhou | 0.46174 | 0.473039 | 0.480385 | 0.447931 | 0.473085 | 17 |
| 44 | Wuxi | 0.440172 | 0.455676 | 0.437343 | 0.482609 | 0.445269 | 26 |
| Number | City | GRA–TOPSIS | TOPSIS | ||
|---|---|---|---|---|---|
| Value | Ranking | Value | Ranking | ||
| 1 | Chongqing | 0.537127 | 2 | 0.457012 | 3 |
| 2 | Wuhan | 0.545447 | 1 | 0.486452 | 1 |
| 3 | Zhengzhou | 0.401084 | 34 | 0.27509 | 37 |
| 4 | Suzhou | 0.450306 | 24 | 0.306019 | 29 |
| 5 | Guangzhou | 0.515681 | 5 | 0.453044 | 4 |
| 6 | Xi’an | 0.468879 | 19 | 0.428785 | 6 |
| 7 | Hefei | 0.495783 | 9 | 0.380365 | 11 |
| 8 | Shenyang | 0.395705 | 37 | 0.303452 | 30 |
| 9 | Ningbo | 0.47054 | 18 | 0.320886 | 24 |
| 10 | Changsha | 0.454045 | 23 | 0.306945 | 28 |
| 11 | Lianyungang | 0.497178 | 8 | 0.374032 | 13 |
| 12 | Urumqi | 0.37025 | 44 | 0.23912 | 42 |
| 13 | Harbin | 0.394531 | 38 | 0.32307 | 22 |
| 14 | Lanzhou | 0.42458 | 32 | 0.319028 | 25 |
| 15 | Qingdao | 0.473226 | 16 | 0.321006 | 23 |
| 16 | Kunming | 0.4357 | 28 | 0.343287 | 17 |
| 17 | Xiamen | 0.449684 | 25 | 0.284713 | 35 |
| 18 | Changchun | 0.38529 | 41 | 0.275626 | 36 |
| 19 | Nanchang | 0.478111 | 15 | 0.329265 | 20 |
| 20 | Dalian | 0.494194 | 10 | 0.40438 | 8 |
| 21 | Dongguan | 0.435441 | 29 | 0.350229 | 16 |
| 22 | Nanjing | 0.492293 | 11 | 0.356334 | 15 |
| 23 | Xining | 0.394515 | 39 | 0.319023 | 26 |
| 24 | Tianjin | 0.537 | 3 | 0.465946 | 2 |
| 25 | Taiyuan | 0.39277 | 40 | 0.252404 | 41 |
| 26 | Shenzhen | 0.465798 | 20 | 0.299306 | 31 |
| 27 | Jinan | 0.39833 | 36 | 0.290313 | 33 |
| 28 | Shanghai | 0.52019 | 4 | 0.437888 | 5 |
| 29 | Tangshan | 0.487521 | 12 | 0.386399 | 9 |
| 30 | Shijiazhuang | 0.374376 | 43 | 0.219985 | 44 |
| 31 | Chengdu | 0.434533 | 30 | 0.361857 | 14 |
| 32 | Yinchuan | 0.398694 | 35 | 0.271357 | 39 |
| 33 | Nanning | 0.484117 | 14 | 0.340074 | 18 |
| 34 | Hohhot | 0.378585 | 42 | 0.225792 | 43 |
| 35 | Hangzhou | 0.504626 | 7 | 0.381728 | 10 |
| 36 | Fuzhou | 0.463257 | 21 | 0.29892 | 32 |
| 37 | Guiyang | 0.429311 | 31 | 0.32843 | 21 |
| 38 | Beijing | 0.416231 | 33 | 0.314666 | 27 |
| 39 | Xuzhou | 0.458418 | 22 | 0.286317 | 34 |
| 40 | Quanzhou | 0.443887 | 27 | 0.274308 | 38 |
| 41 | Jiujiang | 0.485931 | 13 | 0.337719 | 19 |
| 42 | Yantai | 0.507155 | 6 | 0.419587 | 7 |
| 43 | Liuzhou | 0.473085 | 17 | 0.378515 | 12 |
| 44 | Wuxi | 0.445269 | 26 | 0.260848 | 40 |
| Method | GRA-TOPSIS | TOPSIS |
|---|---|---|
| KTC | 1 | 0.661734 |
| Method | GRA-TOPSIS | TOPSIS |
|---|---|---|
| Distinction degree | 1.075746 | 1.075126 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Q.; Wang, G.; Xiao, Y. Evaluating Consolidation Centers of an Integrated Transportation Network under the Belt and Road Initiative. Appl. Sci. 2024, 14, 5637. https://doi.org/10.3390/app14135637
Yu Q, Wang G, Xiao Y. Evaluating Consolidation Centers of an Integrated Transportation Network under the Belt and Road Initiative. Applied Sciences. 2024; 14(13):5637. https://doi.org/10.3390/app14135637
Chicago/Turabian StyleYu, Qin, Guangmin Wang, and Yun Xiao. 2024. "Evaluating Consolidation Centers of an Integrated Transportation Network under the Belt and Road Initiative" Applied Sciences 14, no. 13: 5637. https://doi.org/10.3390/app14135637
APA StyleYu, Q., Wang, G., & Xiao, Y. (2024). Evaluating Consolidation Centers of an Integrated Transportation Network under the Belt and Road Initiative. Applied Sciences, 14(13), 5637. https://doi.org/10.3390/app14135637





