Study on the Influence of Some Ventilation Parameters on Dust Dispersion in Heading Face Coal Mine Using CFD Numerical Model
Abstract
:1. Introduction
2. Modeling Geometry and Meshing
3. Numerical Model
3.1. Mathematical Model
3.2. The Setting of the Simulation Parameters and Boundary Conditions
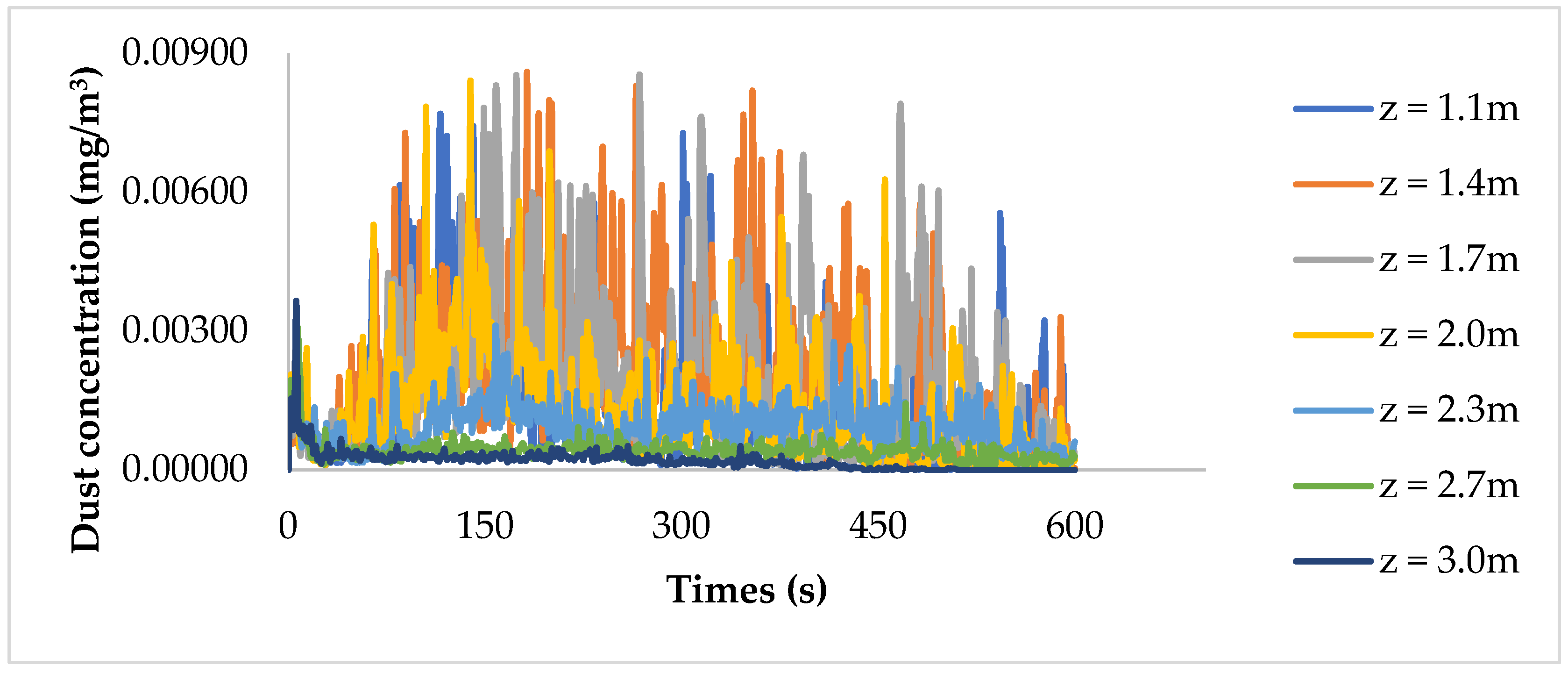
4. Results and Discussion
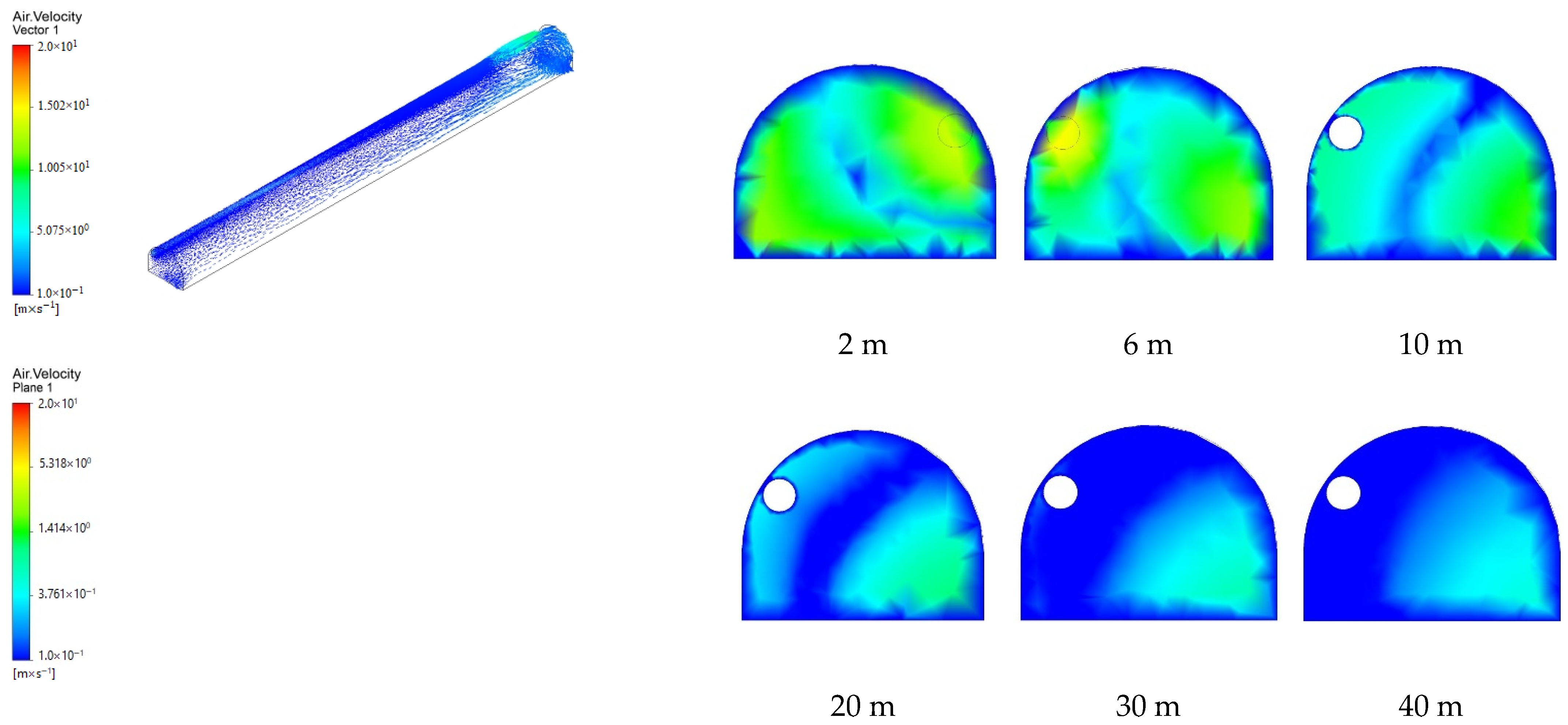
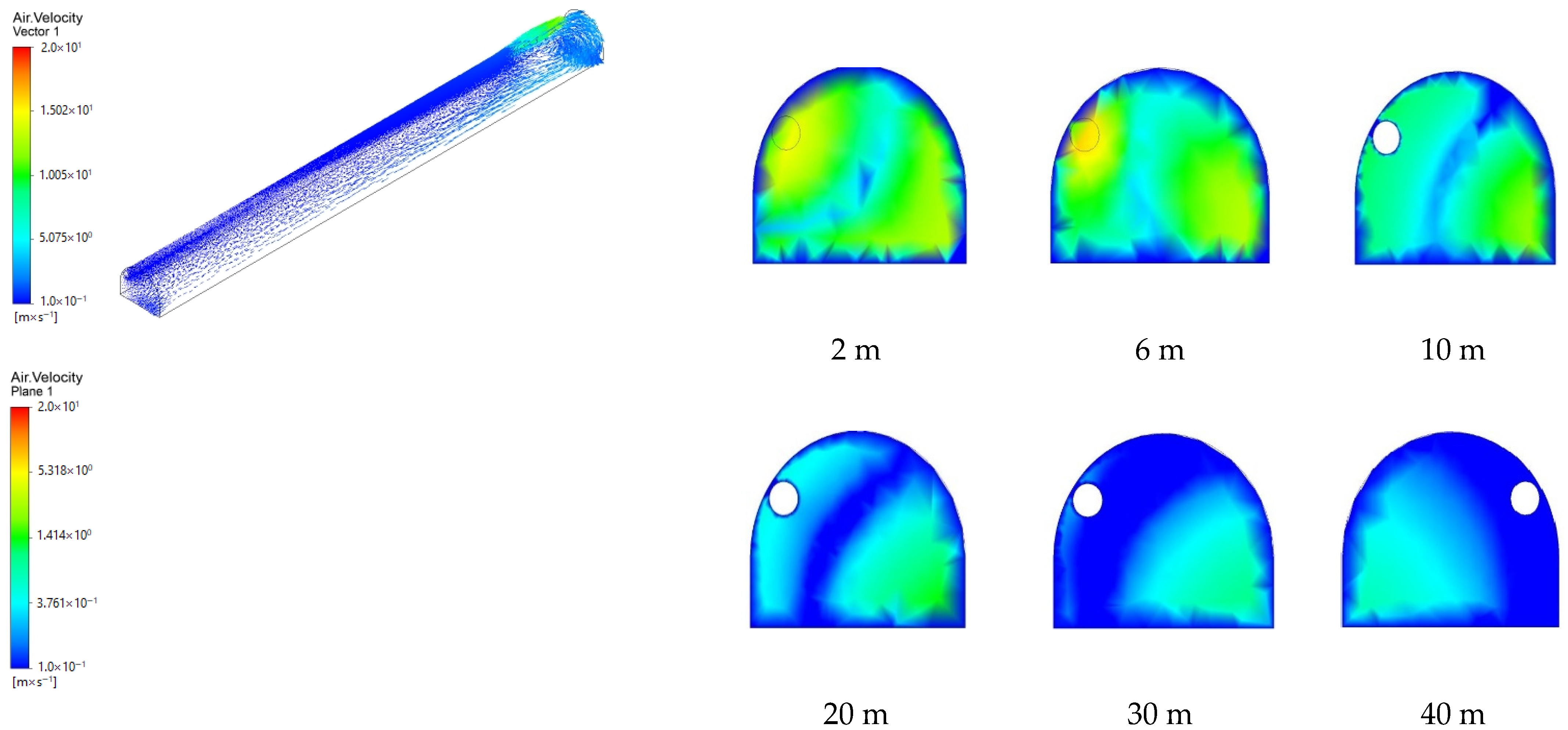
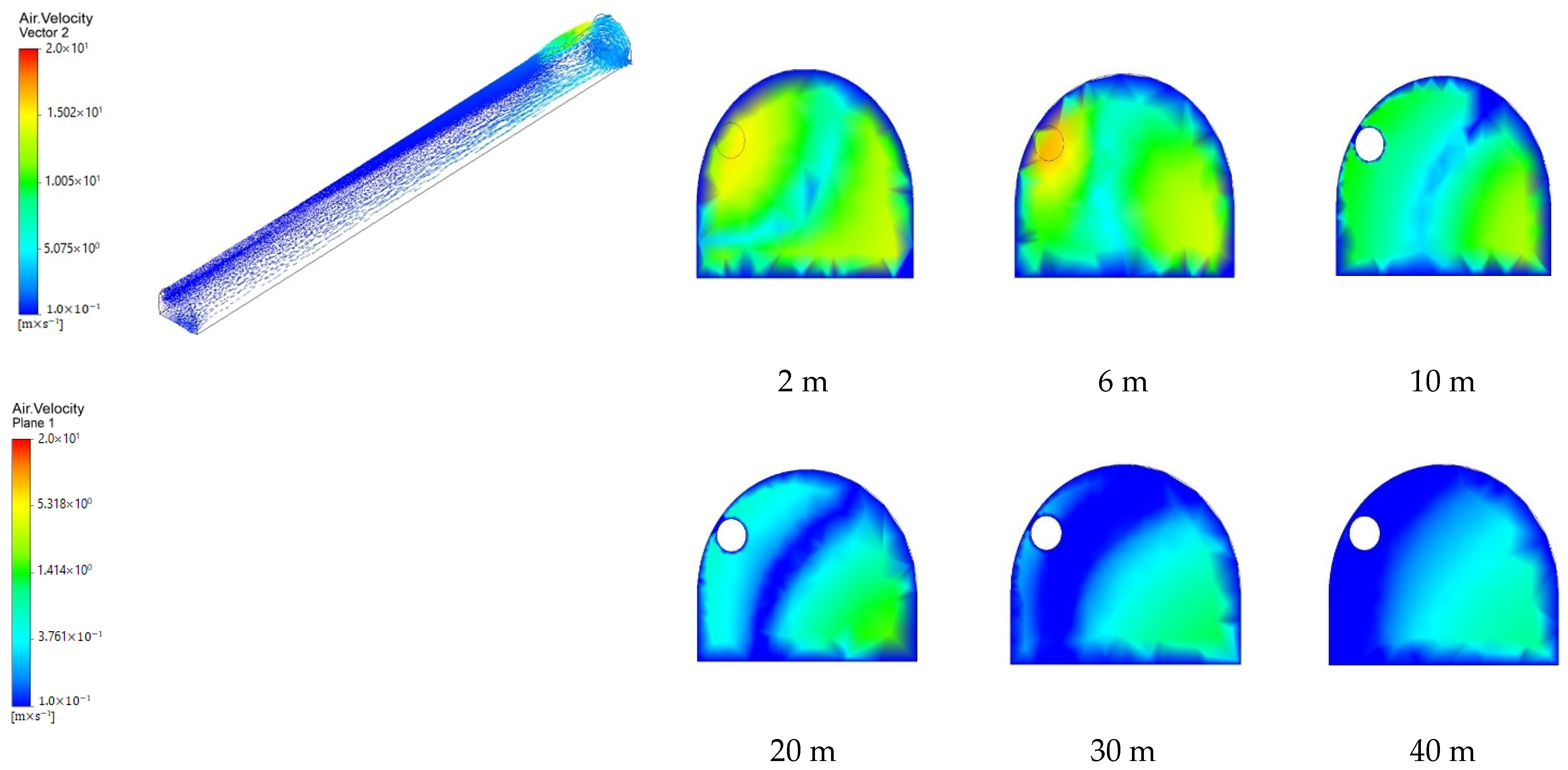
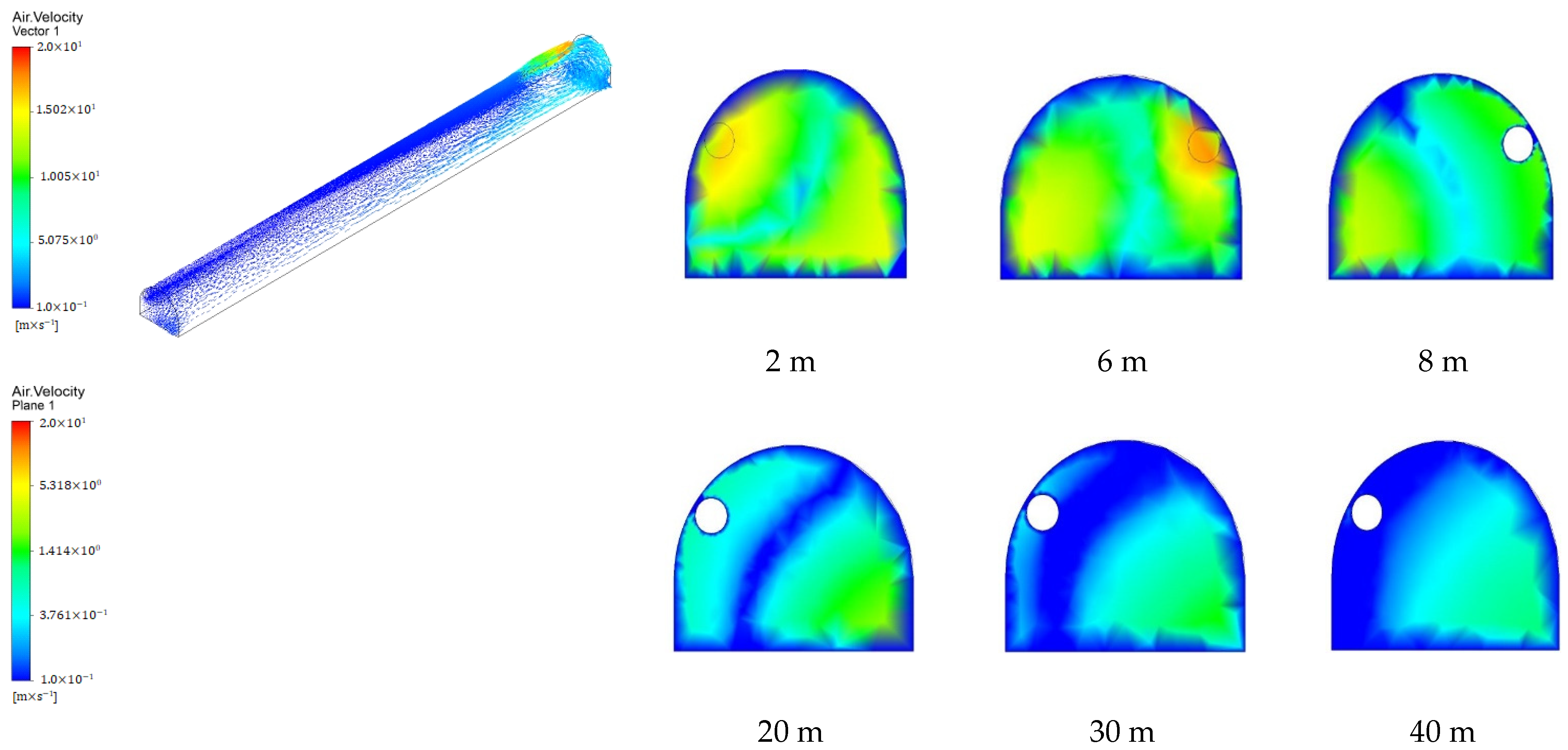
4.1. Analysis of Gas Flow Distribution at Different Wind Speeds
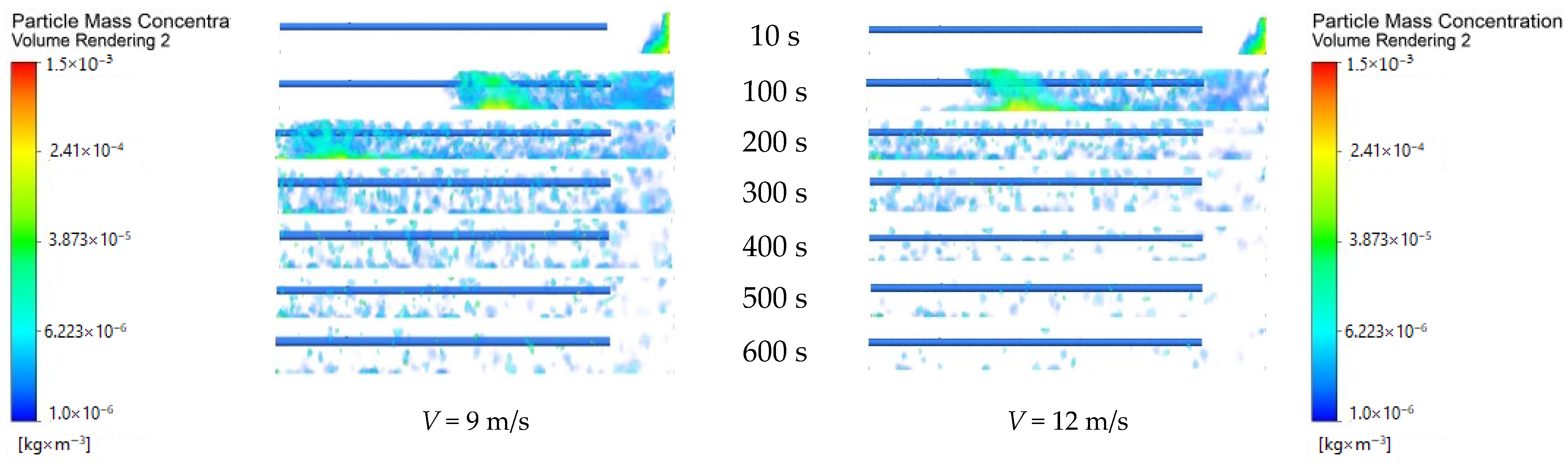
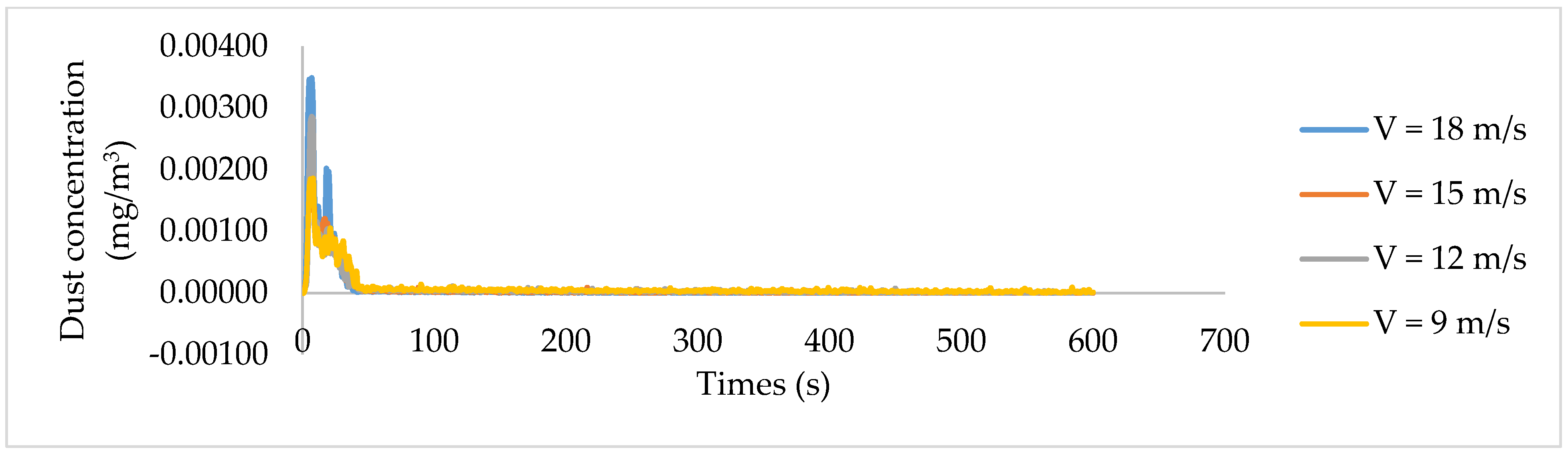
4.2. Influence of Wind Velocity on Dust Distribution in the Heading Face
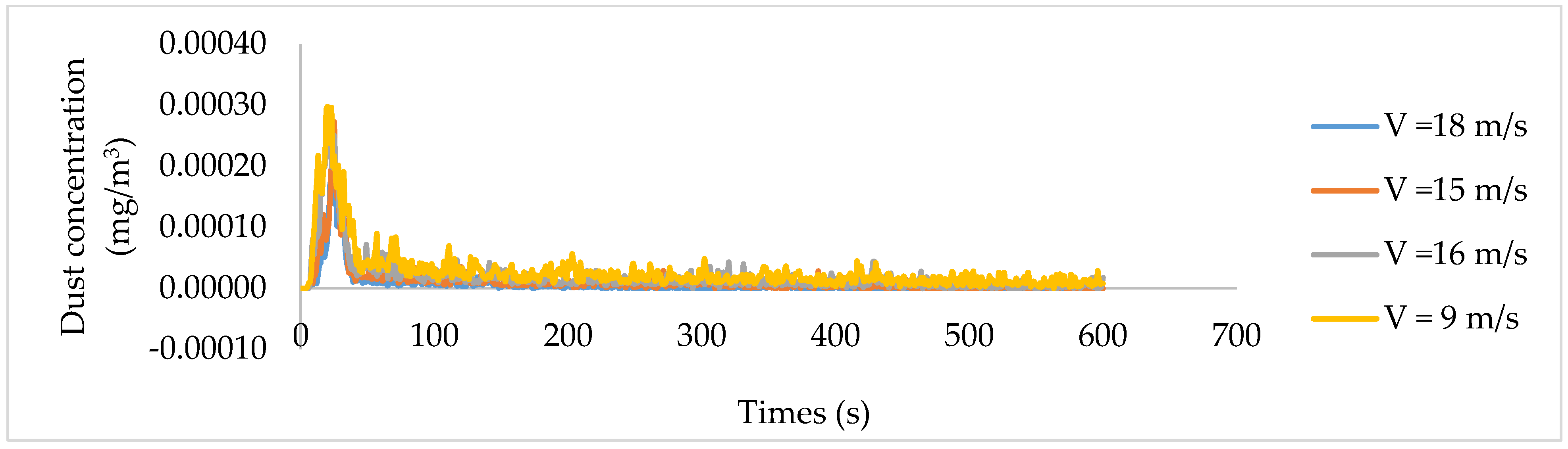
4.3. Influence of Ventilation Duct Position on Dust Dispersion
4.4. Model Validation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| L | the length of roadway (m) |
| y | the height of the roadway (m) |
| b | the width of the roadway (m) |
| ϕduct | air duct diameter (m) |
| hduct | air duct height (m) |
| V | wind velocities using (m/s) |
| t | represents time (s) |
| ρ | is the air density (kg/m3) |
| Ti,j | is the Reynolds stress tensor |
| ցj | is the acceleration of gravity (kg/m2) |
| xi and xj | are the coordinates in the X, Y directions. |
| ui and uj | are the velocities in the X, Y directions (m/s). |
| Fi | is the particle flow resistance (N) |
| k | is the turbulent kinetic energy (m2/s2) |
| μ | the laminar viscosity coefficient |
| Gk | is the rate of turbulent energy production caused by the mean velocity gradient, kg/(s3.m) |
| μt | is the viscosity coefficient for turbulent flow, Pa.s |
| ε | is the dissipation velocity of the turbulent kinetic energy, m2/s3 |
| C1ε, C2ε, Cμ, σk, and σε | are empirical constants. |
| FD(u−up) | is the drag force on the particle per unit mass (N) |
| CD | is the drag force coefficent. |
| u | is the fluid phase velocity (m/s) |
| up | is the particle velocity (m/s) |
| ρp | is the particle density (kg/m3) |
| dp | is the particle diameter (m) |
| τp | is the relaxation time of the particle (s) |
| is the average velocity (m/s) | |
| u′(t) | is the pulsation velocity (m/s) |
| F | is normal contact force between particles |
| Y* | is the equivalent Young’s modulus |
| M | is the particle mass |
| R∗ | is the equivalent radius |
| δij | is the normal overlap |
| Sn, ij | is the normal stiffness |
| Vn | is the normal component of the relative velocity |
| Ft, ij | is denotes the tangential force |
| δt,ij | is the tangential overlap |
| St,ij | is the tangential stiffness |
| μs | is the coefficient of static friction |
| G* | is the shear modulus. |
| Lij | is the distance from the center of particle i to the contact plane with particle j |
| nij | is the represents the normal unit vector between two contacted particles |
| ωij | is the angular velocity vector of the object at the contact point |
References
- Thao, L.V. Study on Dust Control in Stone Furnaces of Underground Coal Mines; Scientific Research Project, Ministry of Industry: Hanoi, Vietnam, 1995. (In Vietnamese)
- Manh, L.V. Study on the Impact and Measures to Reduce Dust Effects on Workers in Underground Coal Mines in Quang Ninh Province. Ph.D. Thesis, University of Mining and Geology, Hanoi, Vietnam, 2018. (In Vietnamese). [Google Scholar]
- Quang, N.V.; Thinh, N.V. Study on Solutions to Reduce Dust Concentration and Improve Climatic Conditions in Mining Faces of Nui Beo Coal Mine. Ind. Min. J. 2019, 2, 60–64. (In Vietnamese) [Google Scholar]
- Geng, F.; Zhou, F.B.; Luo, G. Research Status and Method Progress of Dust Prevention and Control Technology for Fully Mechanized Heading Face in Coal Mine. Min. Saf. Environ. Prot. 2014, 41, 85–89. (In Chinese) [Google Scholar]
- Zhang, L.; Zhou, G.; Ma, Y.; Jing, B.; Sun, B.; Han, F.; He, M.; Chen, X. Numerical analysis on spatial distribution for concentration and particle size of particulate pollutants in dust environment at fully mechanized coal mining face. Powder Technol. 2021, 383, 143–158. [Google Scholar] [CrossRef]
- Kanaoka, C.; Furuuchi, M.; Inaba, J.; Ohmata, K.; Myojo, T. Flow and dust concentration near working face of a tunnel under construction. Doboku Gakkai Ronbunshu 2002, 714, 43–52. [Google Scholar] [CrossRef] [PubMed]
- Rao, S.; Baafi, E.Y.; Aziz, N.I.; Singh, R.N. Three dimensional numerical modeling of air velocity and dust control techniques in a langwall face. In Proceedings of the 6th US Mine Ventilation Symposium, Salt Lake City, UT, USA, 21–23 June 1993. [Google Scholar]
- Jiang, W.; Xu, X.; Wen, Z.; Wei, L. Applying the similarity theory to model dust dispersion during coal-mine tunneling. Process Saf. Environ. Prot. 2021, 148, 415–427. [Google Scholar] [CrossRef]
- Cashdollar, K.L.; Zlochower, I.A. Explosion temperatures and pressures of metals and other elemental dust clouds. J. Loss Prev. Process Ind. 2007, 20, 337–348. [Google Scholar] [CrossRef]
- Li, Q.; Wang, K.; Zheng, Y.; Mei, X.; Lin, B. Explosion severity of micro-sized aluminum dust and its flame propagation properties in 20L spherical vessel. Powder Technol. 2016, 301, 1299–1308. [Google Scholar] [CrossRef]
- Castellanos, D.; Carreto-Vazquez, V.H.; Mashuga, C.V.; Trottier, R.; Mejia, A.F.; Mannan, M.S. The effect of particle size polydispersity on the explosibility characteristics of aluminum dust. Powder Technol. 2014, 254, 331–337. [Google Scholar] [CrossRef]
- Hu, S.; Liao, Q.; Feng, G.; Huang, Y.; Shao, H.; Gao, Y.; Hu, F. Influences of ventilation velocity on dust dispersion in coal roadways. Powder Technol. 2020, 360, 683–694. [Google Scholar] [CrossRef]
- Zhang, G.; Zhou, G.; Song, S.; Zhang, L.; Sun, B. CFD investigation on dust dispersion pollution of down/upwind coal cutting and relevant countermeasures for spraying dustfall in fully mechanized mining face. Adv. Powder Technol. 2020, 31, 3177–3190. [Google Scholar] [CrossRef]
- Zhanyou, S.; Feng, L.; Bo, Q.; Xiaohong, P. Numerical simulation study of dust concentration distribution regularity in cavern stope. Saf. Sci. 2012, 50, 857–860. [Google Scholar]
- Patankar, N.A.; Joseph, D.D. Modeling and numerical simulation of particulate flows by the Eulerian-Lagrangian approach. Int. J. Multiph. Flow 2001, 27, 1659–1684. [Google Scholar] [CrossRef]
- Zhang, J.J. Gas-Solid Two-Phase Flow Simulation of Dust Migration and Deposition in Fully Mechanized Excavation Face. Master’s Thesis, University of Mining and Technology, Xuzhou, China, 2015. (In Chinese). [Google Scholar]
- Zhou, G.; Liu, Y.; Liu, Z.; Zhang, Y.; Zhu, Y.; Sun, B.; Ma, Y. Study on the characteristics of compound dust source pollution and foam dust suppression technology in coal mine anchor excavation production. Process Saf. Environ. Prot. 2024, 186, 593–611. [Google Scholar] [CrossRef]
- Shi, J.; Zhang, W.; Guo, S.; An, H. Numerical Modelling of Blasting Dust Concentration and Particle Size Distribution during Tunnel Construction by Drilling and Blasting. Metals 2022, 12, 547. [Google Scholar] [CrossRef]
- Liu, H.; Wu, X.; Mao, S.; Li, M.; Yue, J. A Time Varying Ventilation and Dust Control Strategy Based on the Temporospatial Characteristics of Dust Dispersion. Minerals 2017, 7, 59. [Google Scholar] [CrossRef]
- Yu, H.; Cheng, W.; Xie, Y.; Peng, H. Micro-scale pollution mechanism of dust diffusion in a blasting driving face based on CFD-DEM coupled model. Environ. Sci. Pollut. Res. 2018, 25, 21768–21788. [Google Scholar] [CrossRef] [PubMed]
- Feng, G.; Liao, Q.; Hu, S. Numerical Simulation of Particulate Matter 2.5 Distribution in a Roadway. Sci. Rep. 2018, 8, 13220. [Google Scholar] [CrossRef] [PubMed]
- Mine Rescue Center. Gas Analysis Results of Vietnam National Coal and Mineral Industries Group; Mine Rescue Center: Quang Ninh, Vietnam, 2024. (In Vietnamese)
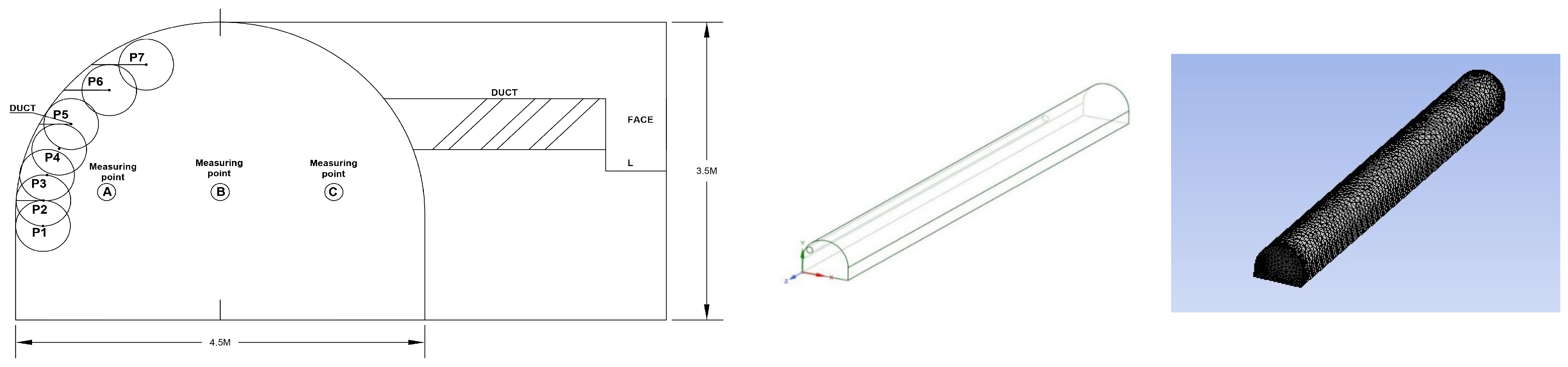






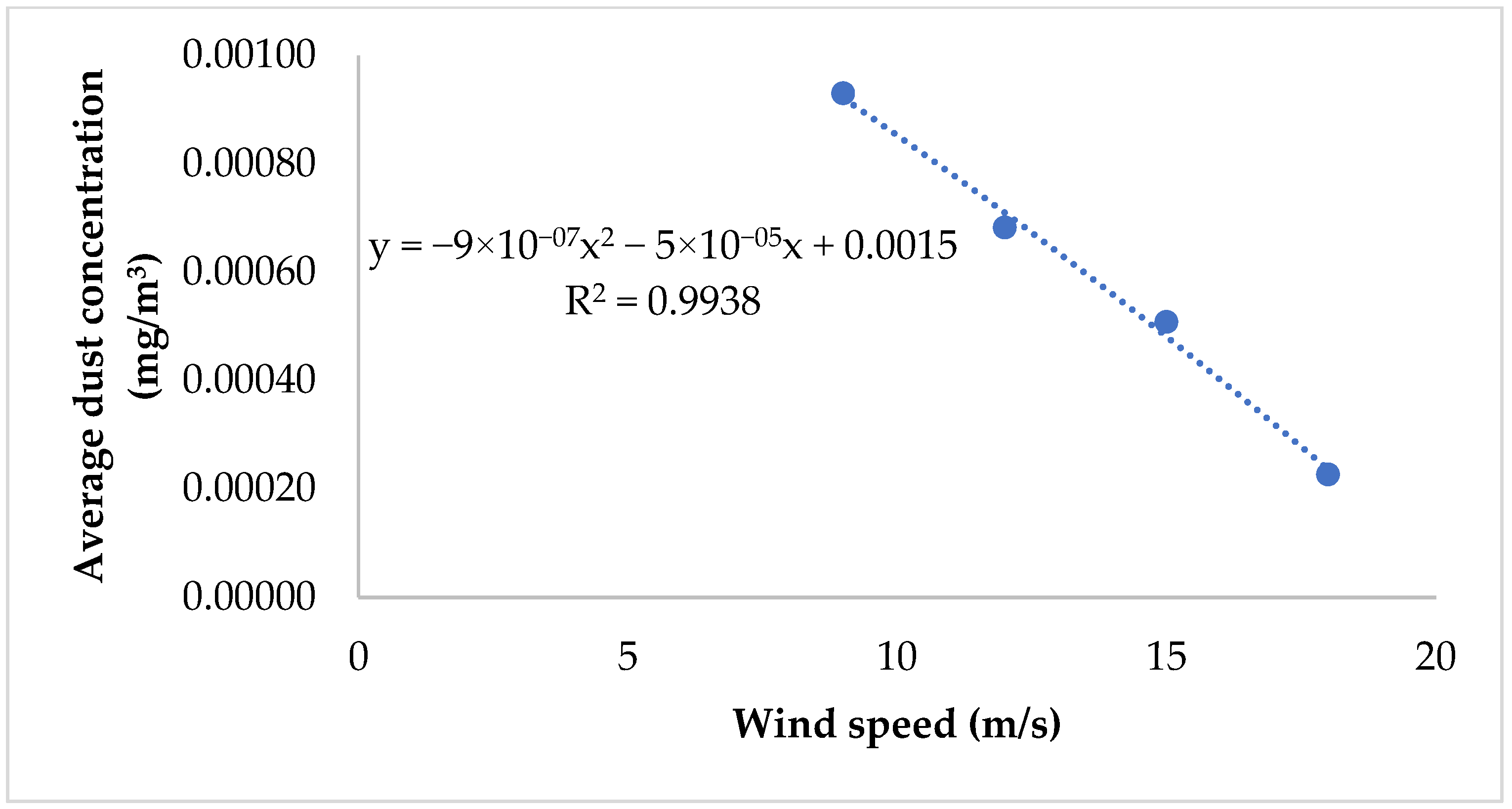
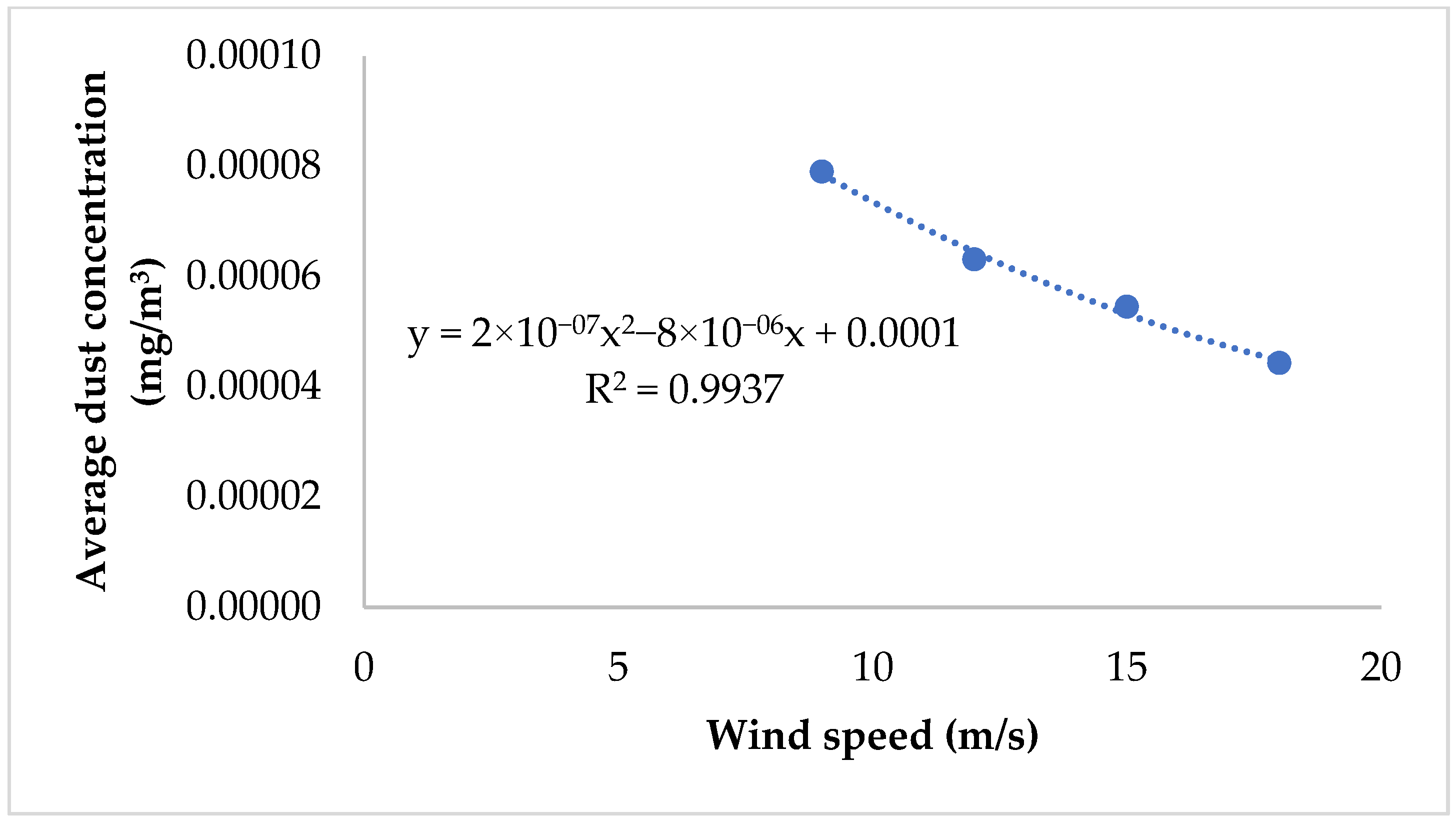



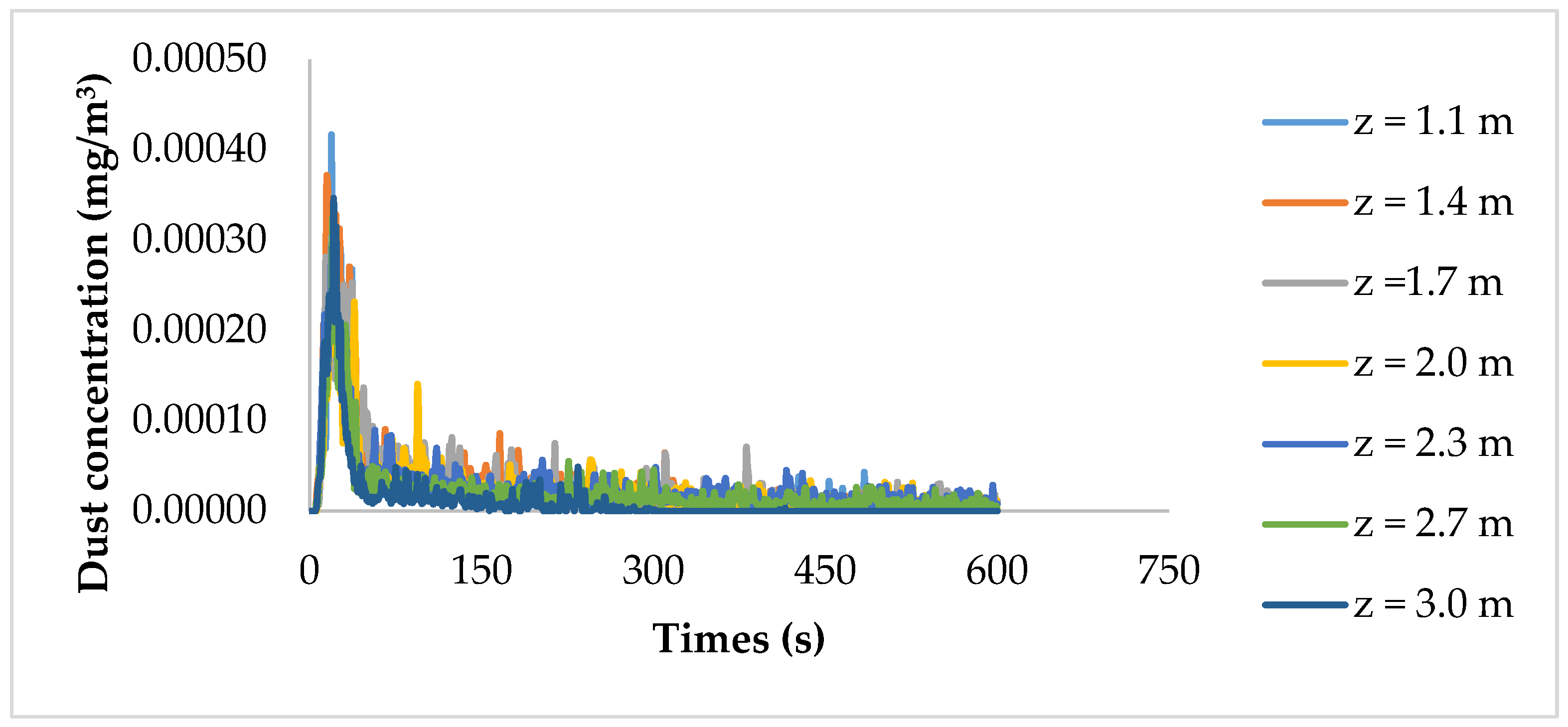
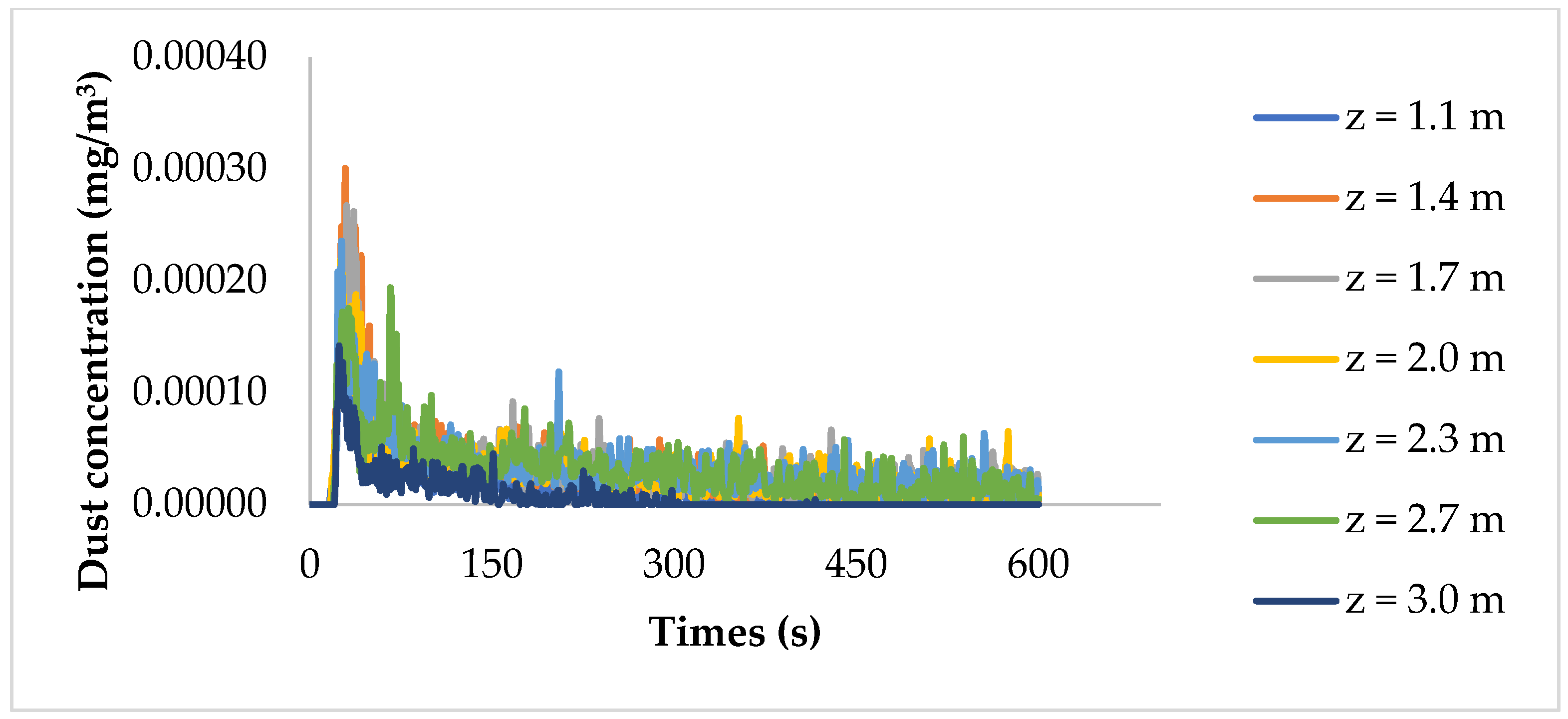

| Parameter Name | Parameter Setting | Parameter Name | Parameter Setting |
|---|---|---|---|
| Solver | Pressure-based solver | Min. particle diameter | 1 × 10−6 (m) |
| Viscous model | k—epsilon model | Max. particle diameter | 0.0001 (m) |
| Inlet boundary type | Velocity inlet | Median diameter | 1.5 × 10−5 (m) |
| Inlet velocity | 9 m/s; 12 m/s; 15 m/s; 18 m/s | Distribution index | 3.5 |
| Outlet boundary type | Pressure outlet | Mass flow rate | 0.0012 kg/s |
| Material | Coal—hv | Height of the air duct | 1.1 m, 1.4 m, 1.7 m, 2.3 m, 2.7 m, 3.0 m |
| Diameter distribution | Rosin–Rammler | Injection type | Surface |
| Number of timesteps for transient simulation | 600 s | Material | Coal—HV |
| Drag law | Spherical | Physical models; Saffman Lift force | DEM Collisiom |
| DPM-boundary type | Reflect | Discrete Phase model | Interaction: interaction with continuous phase; particle treatment: unsteady particle tracking; Stochastic tracking: discrete random walk model |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, Q.V.; Nguyen, T.V.; Nguyen, P.D. Study on the Influence of Some Ventilation Parameters on Dust Dispersion in Heading Face Coal Mine Using CFD Numerical Model. Appl. Sci. 2024, 14, 5643. https://doi.org/10.3390/app14135643
Nguyen QV, Nguyen TV, Nguyen PD. Study on the Influence of Some Ventilation Parameters on Dust Dispersion in Heading Face Coal Mine Using CFD Numerical Model. Applied Sciences. 2024; 14(13):5643. https://doi.org/10.3390/app14135643
Chicago/Turabian StyleNguyen, Quang Van, Thinh Van Nguyen, and Phong Duyen Nguyen. 2024. "Study on the Influence of Some Ventilation Parameters on Dust Dispersion in Heading Face Coal Mine Using CFD Numerical Model" Applied Sciences 14, no. 13: 5643. https://doi.org/10.3390/app14135643
APA StyleNguyen, Q. V., Nguyen, T. V., & Nguyen, P. D. (2024). Study on the Influence of Some Ventilation Parameters on Dust Dispersion in Heading Face Coal Mine Using CFD Numerical Model. Applied Sciences, 14(13), 5643. https://doi.org/10.3390/app14135643








