Performance Analysis of a Cognitive RIS-NOMA in Wireless Sensor Network

Abstract

The reconfigurable intelligent surfaces (RIS) represent a transformative technology in wireless communication, offering a novel approach to managing and enhancing radio signal propagation. By dynamically adjusting their electromagnetic properties, RIS can significantly improve the performance and efficiency of 5G and beyond communication systems. In this paper, we study a cognitive RIS-aided non-orthogonal multiple access (NOMA) network that serves multiple users and improves spectrum efficiency. Our analysis assumes a secondary network operates under multi-primary user constraints and interference from the primary source. We derive approximation closed-form formulas for outage probability (OP), and system throughput. To obtain further insights, an asymptotic expression for OP is computed by taking into account two power configurations at the source. Additionally, numerical results show the effects of important factors on performance, confirming the accuracy of the theoretical derivation. According to the simulation results, performance by the system under consideration might be improved considerably by combining a RIS and NOMA, particularly when compared to an orthogonal multiple access scheme.

1. Introduction

Massive machine-type communications (mMTC), enhanced mobile broadband (eMBB), and ultra-reliable low-latency communications (URLLCs) are some of the critical performance criteria that next-generation communication networks such as fifth-generation (5G) and sixth-generation (6G) are required to achieve. In order to increase spectral efficiency while lowering hardware costs and power consumption, researchers are focusing on solutions that go beyond the network, such as using a reconfigurable intelligent surface (RIS), also known as an intelligent reflecting surface (IRS) [1,2,3,4,5]. It has been demonstrated that an RIS increases network capacity and provides end-to-end performance that is on par with standard relaying systems [6,7]. In [8], the authors demonstrated a less complex active RIS compared with fully connected active RIS architectures and then provided the flexibility to position the RIS at any location, with more increase in performance than passive RIS. The vast majority of RIS implementations consist of arrays of two-dimensional metasurfaces. One may modify the signal’s propagation properties by expertly adjusting each element’s phase shift [9]. When RIS is used in place of communication auxiliary technologies like amplifying and forwarding relays, less energy is used [10]. The RIS enables IoT performance increases in connection, power, and coverage far less costly since it can be simply implanted into the inside of buildings and onto the surface of huge vehicles without requiring changes to the device’s hardware and software [11]. In the meantime, RIS can cover a wide area while using little power [12].

Non-orthogonal multiple access (NOMA) is a technique that facilitates several linked devices and improves spectral efficiency. Multiple user equipments (UEs) can use the same resource without being constrained by conventional orthogonal multiple access (OMA) techniques thanks to the utilization of successive interference cancelation (SIC) at the receiver and superposition coding at the transmitter to cancel out intra-NOMA user interference [13,14,15,16,17]. Performance benefits are higher with NOMA than with OMA approaches because it enables UEs with poor channel conditions (far) to serve UEs with good channel conditions (near) at a single access point [18,19,20]. In addition, to increase spectrum efficiency, cognitive radio (CR) offers secondary users (SU) access to a licensed spectrum of the primary user (PU) [21]. It has drawn notice for helping new applications, especially when incorporating NOMA with CR, which may satisfy the high throughput, enormous connection, and low-latency needs of the 5G network [22,23,24]. The goal of cognitive NOMA is to offer more thoughtful spectrum sharing [25]. There are three operating paradigms for CR networks: the interweave mode, the overlay mode, and the underlay mode. Since the frame structure in overlay and underlay modes simply consists of data transmission, PU and SU networks can coexist at the same frequency band [26].

1.1. Related Work

This section provides a brief summary of the combination of the RIS in a NOMA [10,27,28,29,30,31,32,33,34] or CR network [35,36,37,38,39,40,41] or RIS-NOMA-CR [42,43]. By making use of the fixed reflecting components in [10], the system total rate of IRS-NOMA was increased for multi-antenna situations. In [27], the authors developed a distributed and iterative approach for optimizing the phase shift matrix and power allocation in the RIS-NOMA-assisted simultaneous wireless information and power transfer (SWIPT) network. In [28], the developers used active/passive RIS to aid in uplink communication, allowing the adoption of NOMA schemes amongst users with similar transmission power. In [29], a combination of user clustering and RIS allocation techniques was developed to secure the NOMA scheme’s execution while optimizing the system’s sum rate. The performance of the RIS-powered NOMA network was studied in [30], which looked at energy efficiency (EE) in both delay-restricted and delay-tolerant modes. The authors in [31] developed the IRS-NOMA system throughput maximization by considering the reflection coefficients and the decoding order. In order to get over the hardware constraints, a straightforward IRS-NOMA transmission scheme was created in [32], where the outage probability for a single user is calculated using on-off control. In [33], the authors derived the closed-form formulas of the RIS-NOMA outage probability under Nakagami-m fading channels based on the passive beamforming weights. In order to improve the coverage of both uplink and downlink NOMA networks, the RIS was implemented [34], demonstrating the advantages of RIS over FD relaying.

In multiple-input multiple-output (MIMO) CR systems, the authors in [35] used a RIS to help the SUs transmit data. To increase the maximum SU rate that could be achieved, the authors of [36] incorporated multiple RISs to downlink multiple-input single-output CR systems. A simultaneous transmit precoding and reflect beamforming design for RIS-assisted downlink MIMO CR networks was created in [37]. The authors of [38] investigated resilient beamforming design based on both bounded and statistical channel state information (CSI) error models for PU-related channels in RIS-aided CR systems. In order to maximize the secrecy rate for safety purposes, a novel numerical solution has been suggested of a RIS-assisted spectrum sharing underlay CR wiretap channel [39]. In [40], the authors jointly designed the passive beamforming at the RIS and the transmit beamforming at the multi-antenna cognitive base station, resulting in a secrecy EE maximization technique. The authors of [41] focused their attention on potential improvements to the resource allocation architecture for RIS-assisted full-duplex CR systems. In [42], the performance of the RIS-assisted CR-NOMA system was examined, and a deep learning (DL) framework for ergodic capacity prediction was created. The authors in [43] studied the RIS-assisted non-terrestrial under CR and NOMA. Furthermore, the outage performance of secondary users is derived under perfect/imperfect SIC and interference from PN.

1.2. Motivation and Contribution

Based on RIS, NOMA, and CR advances, this paper proposes a cognitive RIS-aided NOMA communications network to improve spectrum efficiency and to overcome severe fading/obstacles. Different from the work in [42], we study a cognitive RIS-aided NOMA network with multiple UEs to improve efficient spectrum utilization. In addition, interference from the primary network (PN) with UEs of a secondary network (SN) is investigated to reflect real-world conditions. The main contributions of this work are as follows.

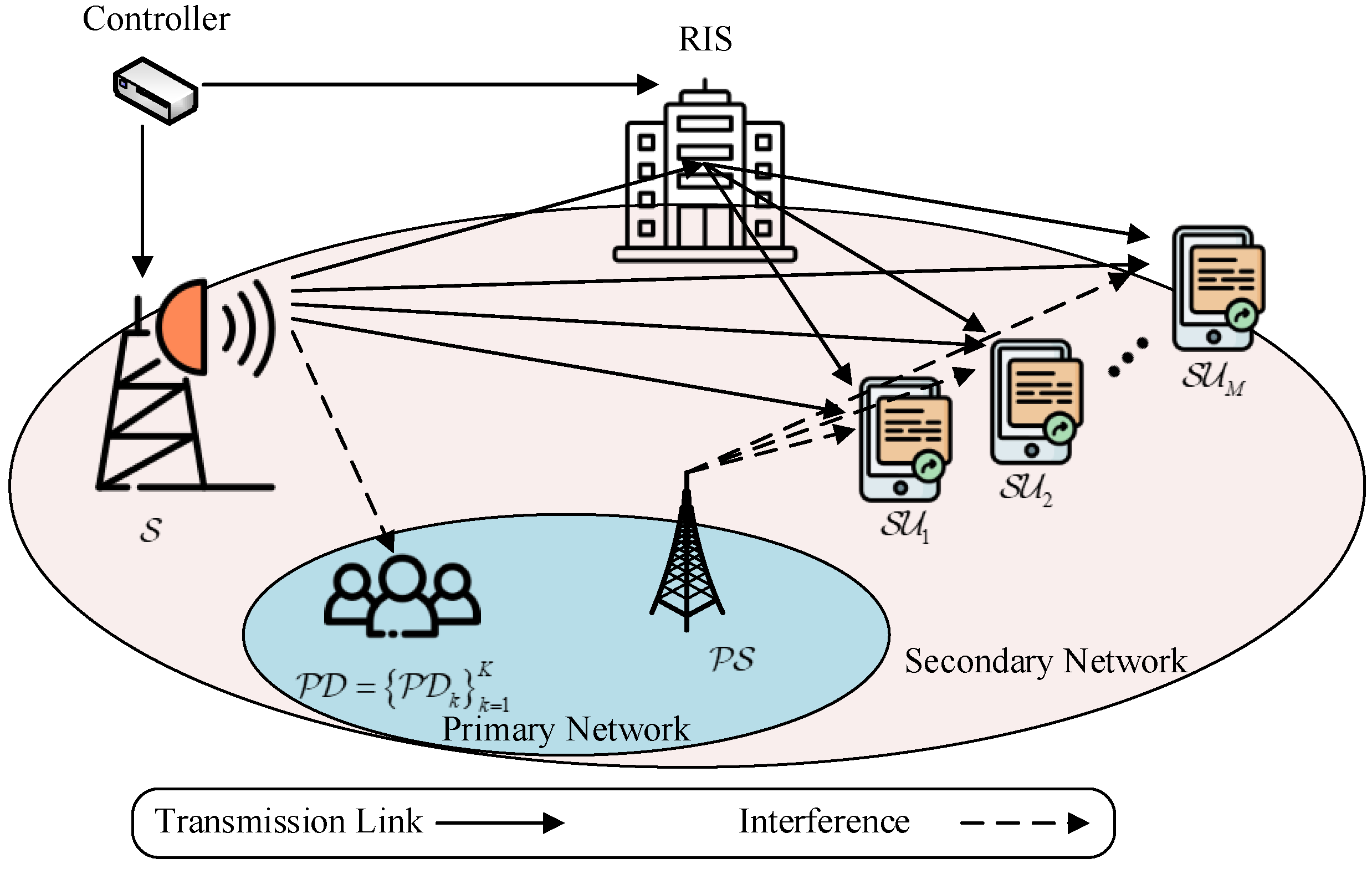
• First, we propose a novel, cognitive RIS-aided NOMA network where a secondary source serves multiple SNs despite interference from the PN.
• Secondly, we analyze the performance of the suggested system in terms of outage probability and system throughput. The approximate closed-form analytical and asymptotic expressions for OP are obtained, providing helpful insights into the proposed system’s configuration.
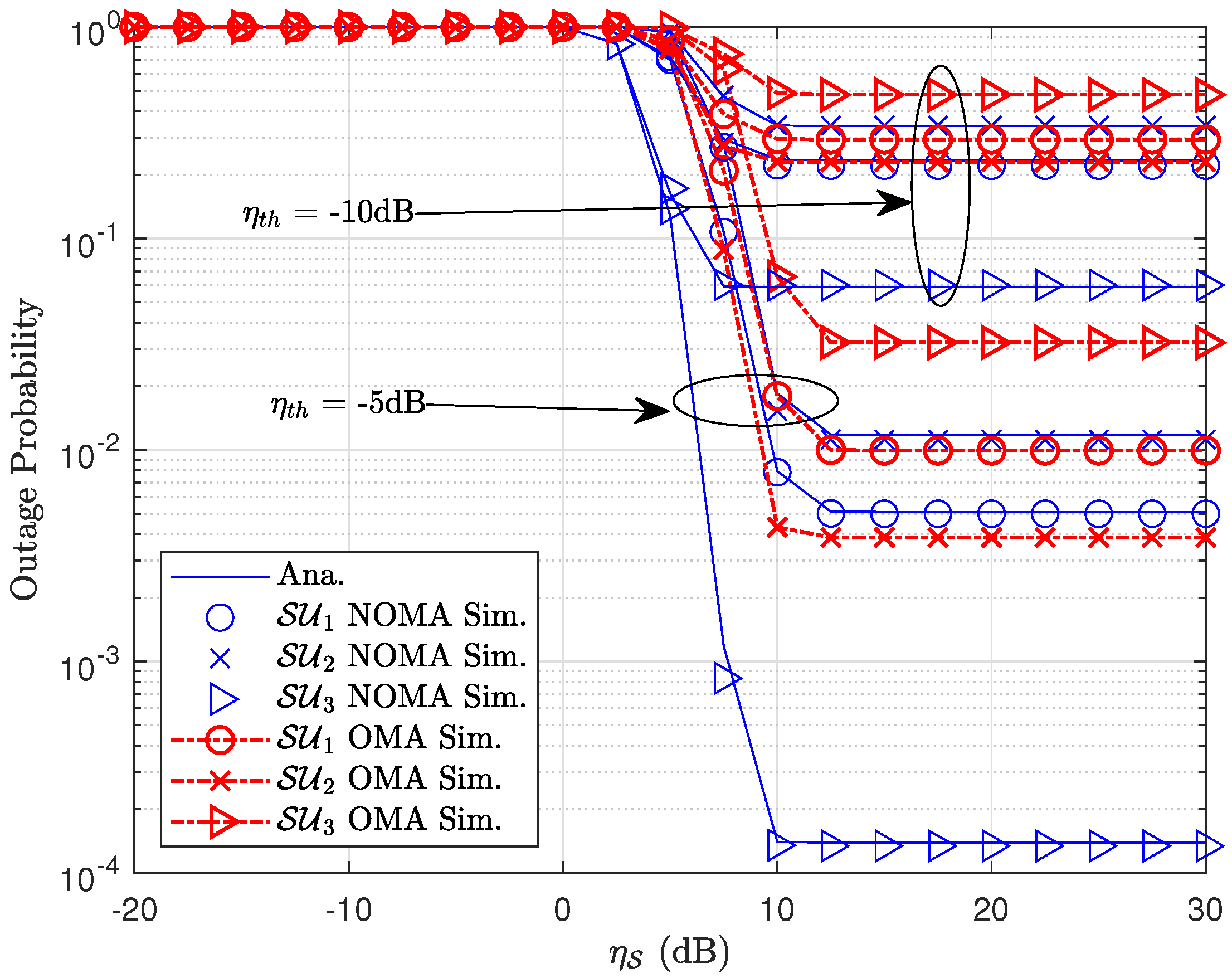
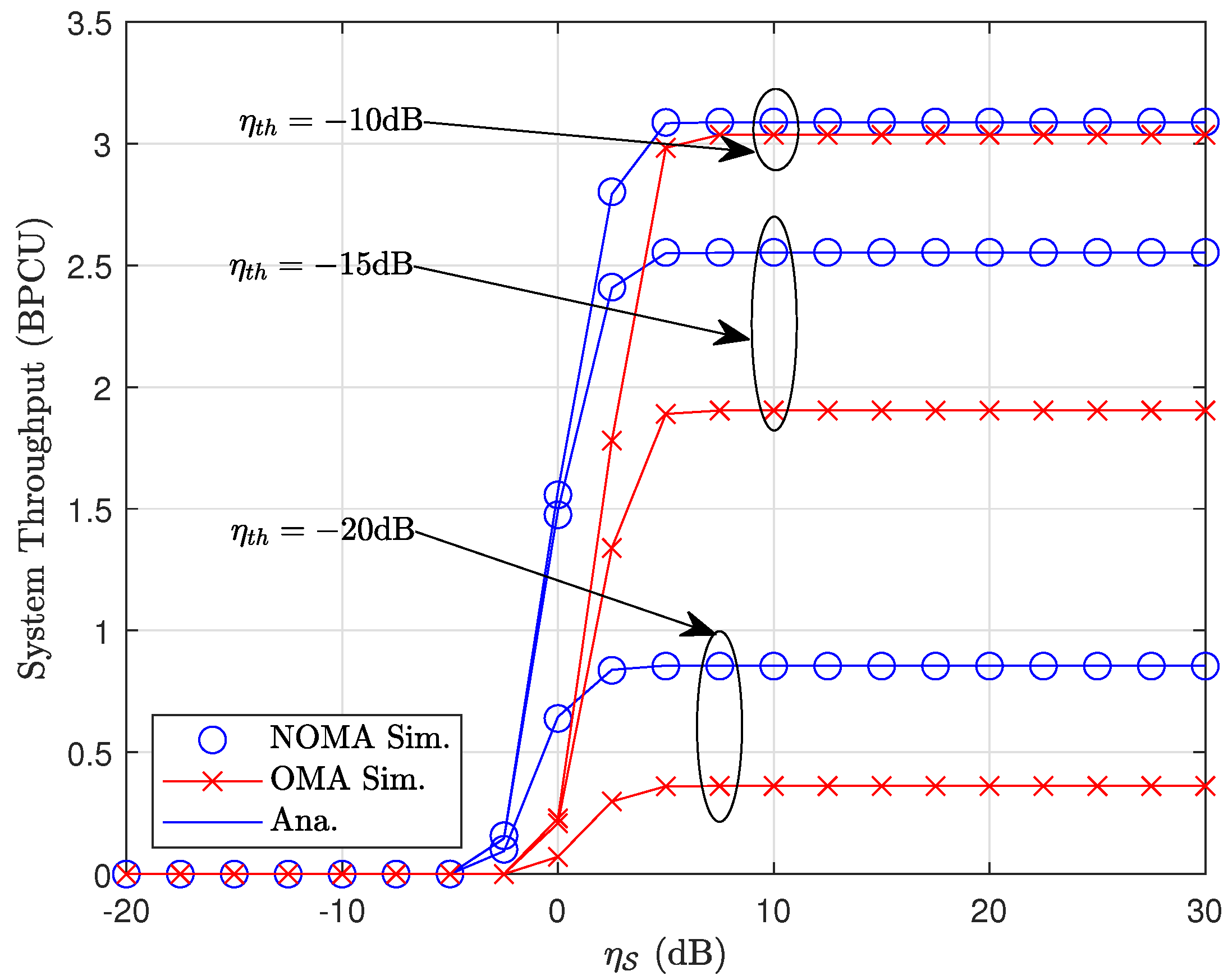
• Finally, we present a Monte Carlo simulation to validate the accuracy of the theoretical analysis, then we show the discussions about the impacts of (i) the number of reflective elements of the RIS, (ii) the number of PUs, and (iii) the interference from the primary source on the SN. We also present a comparison of the OP and system throughput between the cognitive NOMA system assisted by the RIS and its OMA equivalent.

The remainder of this work is structured as follows. Section 2 describes the proposed system model. The channel model and performance analyses of the proposed system are in Section 3. The numerical results from analysis of our suggested system are provided in Section 4. Finally, conclusions are in Section 5.

2. The System Model

In this paper, we consider the cognitive RIS-aided NOMA communications network shown in Figure 1, which operates over the spectrum of a primary network where a secondary source ($\mathcal{S}$) and M secondary user ${\left\{{\mathcal{SU}}_m\right\}}_{m=1}^M$ are assisted by a RIS ($\mathcal{R}$) with N reflective elements, the K primary user ${\left\{{\mathcal{PD}}_k\right\}}_{k=1}^K$ is in the area of interest of a primary source ($\mathcal{PS}$). Furthermore, all PN and SN nodes are equipped with a single antenna. We designate $h_{{\mathcal{SR}}_n},n\in \{1,\dots ,N\}$ as the channel from $\mathcal{S}$ to n-th reflective elements of $\mathcal{R}$, while $h_{{\mathcal{R}}_n{\mathcal{U}}_m}$ denotes the channel from the n-th reflective elements of $\mathcal{R}$ to ${\mathcal{SU}}_m$; $h_{{\mathcal{SU}}_m}$ denotes the channel from $\mathcal{S}$ to ${\mathcal{SU}}_m$, $h_{{\mathcal{SD}}_k}$ denotes the channel from $\mathcal{S}$ to ${\mathcal{PD}}_k$, $h_{{\mathcal{PU}}_m}$ denotes the channel from $\mathcal{PS}$ to ${\mathcal{SU}}_m$. In our paper, the CSI of $\mathcal{PS}$ is not available in SN [44]. Moreover, all primary transmitter interference signals are treated as AWGN with $\mathcal{CN}(0,\zeta {\sigma }^2)$, where $\zeta$ denotes the scaling coefficient. All channels follow Rayleigh fading. Without loss generality, the channel from $\mathcal{S}$ to M SU and the cascade channel from $\mathcal{S}$ to $\mathcal{R}$ and $\mathcal{R}$ to M SU are ordered as ${\left|{\mathbf{h}}_{{\mathcal{RU}}_1}^H\Theta {\mathbf{h}}_{\mathcal{SR}}+h_{{\mathcal{SU}}_1}\right|}^2⩽\cdots ⩽{\left|{\mathbf{h}}_{{\mathcal{RU}}_M}^H\Theta {\mathbf{h}}_{\mathcal{SR}}+h_{{\mathcal{SU}}_M}\right|}^2$ [33], where ${\mathbf{h}}_{{\mathcal{SR}}_n}=[h_{{\mathcal{SR}}_1},\dots ,h_{{\mathcal{SR}}_N}]$, ${\mathbf{h}}_{{\mathcal{RU}}_1}=[h_{{\mathcal{R}}_1{\mathcal{U}}_1},\dots ,h_{{\mathcal{R}}_N{\mathcal{U}}_1}]$, and $\Theta =\mathrm{diag}\left({\alpha }_1{e}^{j{\theta }_1},\dots ,{\alpha }_N{e}^{j{\theta }_N}\right)$, with ${\alpha }_n=1,\forall n$ and ${\theta }_n\in [0,2\pi )$ being the amplitude coefficient and the phase shift, respectively, of the n-th reflective elements of $\mathcal{R}$.

In the CR model, $\mathcal{S}$ must dynamically modify its transmit power in accordance with the maximum allowable interference level, $P_{th}$, in order to prevent the interference that an SU transmission causes for the PU. As a result, transmit power at $\mathcal{S}$ according to [42], is

$$\begin{array}{c}\hfill P_{\mathcal{S}}=min\left({\overline{P}}_{\mathcal{S}},\frac{P_{th}}{\underset{k=1,\dots ,K}{max}{\left|h_{{\mathcal{SD}}_k}\right|}^2}\right)\end{array}$$

(1)

where ${\overline{P}}_{\mathcal{S}}$ denotes the maximum transmit power at S. Next, $\mathcal{S}$ sends superposed signals to the M SU assisted by the RIS. Thus, the received signal at ${\mathcal{SU}}_m$ is

$$\begin{array}{c}\hfill y_{{\mathcal{SU}}_m}=\left({\mathbf{h}}_{{\mathcal{RU}}_m}^H\Theta {\mathbf{h}}_{\mathcal{SR}}+h_{{\mathcal{SU}}_m}\right)\sum _{i=0}^M\sqrt{P_{\mathcal{S}}{\beta }_i}{x}_i+h_{{\mathcal{PU}}_m}+n_{{\mathcal{SU}}_m}\end{array}$$

(2)

where ${\beta }_i$ denotes the power allocation with ${\beta }_1⩾\dots ⩾{\beta }_M$, and ${\displaystyle \sum _{i=0}^M}{\beta }_i=1$, with $x_i$ denoting the message of i-th $\mathcal{SU}$, and $n_{{\mathcal{SU}}_m}$ denoting AWGN with $\mathcal{CN}(0,{\sigma }^2)$.

Following NOMA procedures [30], the signal-to-interference plus noise ratio (SINR) at the m-th SU to detect information of p-th SU ($m>p$) is given by

$$\begin{array}{c}\hfill {\mathrm{SINR}}_{m\to p}=\frac{{\mathcal{G}}_m^2{P}_{\mathcal{S}}{\beta }_p}{{\mathcal{G}}_m^2{P}_{\mathcal{S}}{\sum }_{i=p+1}^M{\beta }_i+\zeta {\sigma }^2+{\sigma }^2}\end{array}$$

(3)

where ${\mathcal{G}}_m=|G_m+h_{{\mathcal{SU}}_m}|$, and $G_m=\left|{\sum }_{n=1}^N{h}_{{\mathcal{SR}}_n}{h}_{{\mathcal{R}}_n{\mathcal{U}}_m}{e}^{j{\theta }_n}\right|$. For the case of perfect CSI as explained in [45], we can obtain $G_m={\sum }_{n=1}^N|h_{{\mathcal{SR}}_n}\left|\right|h_{{\mathcal{R}}_n{\mathcal{U}}_m}|={\sum }_{n=1}^N{G}_{m,n}$. After eliminating previous user signals with SIC, the SINR at ${\mathcal{SU}}_M$ to decode its own information is

$$\begin{array}{c}\hfill {\mathrm{SINR}}_M=\frac{{\mathcal{G}}_M^2{P}_{\mathcal{S}}{\beta }_M}{\zeta {\sigma }^2+{\sigma }^2}\end{array}$$

(4)

3. Performance Analysis

3.1. The Channel Model

In this section, we calculate new channel statistics for the cognitive RIS-aided NOMA network utilized to evaluate OP and asymptotic OP.

Lemma 1.

The corresponding PDF and CDF of the m-th ordered ${\mathcal{G}}_m^2$ is given by

$$\begin{array}{cc}\hfill f_{{\mathcal{G}}_m^2}\left(x\right)& =\sum _{a=0}^{M-m}{\Delta }_M{\left(-1\right)}^a{f}_{{\overline{\mathcal{G}}}_m^2}\left(x\right){\left[F_{{\overline{\mathcal{G}}}_m^2}\left(x\right)\right]}^{m+a-1}\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill F_{{\mathcal{G}}_m^2}\left(x\right)& =\sum _{a=0}^{M-m}\frac{{\Delta }_M{\left(-1\right)}^a}{m+a}{\left[F_{{\overline{\mathcal{G}}}_m^2}\left(x\right)\right]}^{m+a}\hfill \end{array}$$

(6)

where ${\Delta }_M=\frac{M!}{\left(m-1\right)!\left(M-m-a\right)!a!}$.

Proof of Lemma 1. 

Following Rayleigh fading, the PDF and CDF, respectively, of $|h_j|$, where $j\in \{{\mathcal{SR}}_n,{\mathcal{R}}_n{\mathcal{U}}_m,{\mathcal{SU}}_m,{\mathcal{SD}}_k\}$, are

$$f_{|h_j|}\left(x\right)=\frac{2x}{{\Omega }_j}{e}^{-\frac{x^2}{{\Omega }_j}},F_{|h_j|}\left(x\right)=1-e^{-\frac{x^2}{{\Omega }_j}}.$$

(7)

where ${\Omega }_j$ denotes the average power of channel. Furthermore, the k-th moment of $|h_j|$ is obtained with

$${\mu }_{h_j}\left(k\right)=\underset{0}{\overset{\infty }{\int }}{x}^k{f}_{\left|h_j\right|}\left(x\right)dx={\left(\sqrt{{\Omega }_j}\right)}^k\Gamma \left(\frac{k}{2}+1\right)$$

(8)

Then, the PDF expression for $G_{m,n}$ can can be calculated as follows:

$$\begin{array}{cc}\hfill f_{G_{m,n}}\left(x\right)& =\underset{0}{\overset{\infty }{\int }}\frac{1}{\gamma }{f}_{\left|h_{{\mathcal{R}}_n{\mathcal{U}}_m}\right|}\left(\frac{x}{\gamma }\right)f_{\left|h_{{\mathcal{SR}}_n}\right|}\left(\gamma \right)d\gamma \hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & =\frac{4x}{{\Omega }_{{\mathcal{R}}_n{\mathcal{U}}_m}{\Omega }_{{\mathcal{SR}}_n}}\underset{0}{\overset{\infty }{\int }}\frac{1}{\gamma }{e}^{-\frac{x^2}{{\Omega }_{{\mathcal{R}}_n{\mathcal{U}}_m}{\gamma }^2}}{e}^{-\frac{{\gamma }^2}{{\Omega }_{{\mathcal{SR}}_n}}}d\gamma .\hfill \end{array}$$

(10)

Using [Equation 3.471.9] in [46], the exact PDF of $G_{m,n}$ is

$$\begin{array}{c}\hfill f_{G_{m,n}}\left(x\right)=\frac{4x}{{\Omega }_{{\mathcal{R}}_n{\mathcal{U}}_m}{\Omega }_{{\mathcal{SR}}_n}}{K}_0\left(\sqrt{\frac{4x^2}{{\Omega }_{{\mathcal{R}}_n{\mathcal{U}}_m}{\Omega }_{{\mathcal{SR}}_n}}}\right)\end{array}$$

(11)

where $K_0\left(x\right)$ denotes the zero-th order modified Bessel function of the second kind [46]. With the help of the PDF of $G_{m,n}$ and [Equation 6.561.16] in [46], the k-th moment of $G_{m,n}$ is derived as

$$\begin{array}{c}\hfill {\mu }_{G_{m,n}}\left(k\right)=\underset{0}{\overset{\infty }{\int }}{x}^k{f}_{G_{m,n}}\left(x\right)dx={\left({\Omega }_{{\mathcal{R}}_n{\mathcal{U}}_m}{\Omega }_{{\mathcal{SR}}_n}\right)}^{\frac{k}{2}}\Gamma {\left(\frac{k}{2}+1\right)}^2\end{array}$$

(12)

With the help of the multinomial expansion [47], the k-th moment of $G_m$ can be expressed as

$$\begin{array}{cc}\hfill {\mu }_{G_m}\left(k\right)& =\sum _{k_1=0}^k\sum _{k_2=0}^{k_1}\cdots \sum _{k_{N-1}}^{k_{N-2}}\left(\begin{array}{c}k\\ k_1\end{array}\right)\left(\begin{array}{c}{k}_1\\ k_2\end{array}\right)\cdots \left(\begin{array}{c}{k}_{N-2}\\ k_{N-1}\end{array}\right)\hfill \\ \hfill & \times {\mu }_{G_{m,1}}\left(k-k_1\right){\mu }_{G_{m,2}}\left(k_1-k_2\right)\cdots {\mu }_{G_{m,N}}\left(k_{N-1}\right)\hfill \end{array}$$

(13)

Based on the independence of $G_m$ and $h_{{\mathcal{SU}}_m}$, with the help of [Equation (1.111)] in [46], the k-th moment of unordered ${\overline{\mathcal{G}}}_m^2$ can be expressed as

$$\begin{array}{c}\hfill {\mu }_{{\overline{\mathcal{G}}}_m^2}\left(k\right)=\sum _{q=0}^{2k}\left(\begin{array}{c}2k\\ q\end{array}\right){\mu }_{G_m}\left(q\right){\mu }_{h_{{\mathcal{SU}}_m}}\left(2k-q\right)\end{array}$$

(14)

Furthermore, we can approximate the unordered ${\overline{\mathcal{G}}}_m^2$ as a Gamma distribution based on the k-th moment of the unordered ${\overline{\mathcal{G}}}_m^2$ with the shape $k_m$ and the scale parameter $w_m$, and it can be expressed as

$$\begin{array}{cc}\hfill k_m& =\frac{{\left(E\left[{\overline{\mathcal{G}}}_m^2\right]\right)}^2}{Var\left[{\overline{\overline{\mathcal{G}}}}_m^2\right]}=\frac{{\left({\mu }_{{\overline{\mathcal{G}}}_m^2}\left(1\right)\right)}^2}{{\mu }_{{\overline{\mathcal{G}}}_m^2}\left(2\right)-{\mu }_{{\mathcal{G}}_m^2}\left(1\right)}\hfill \\ \hfill w_m& =\frac{Var\left[{\overline{\mathcal{G}}}_m^2\right]}{E\left[{\overline{\mathcal{G}}}_m^2\right]}=\frac{{\mu }_{{\overline{\mathcal{G}}}_m^2}\left(2\right)-{\mu }_{{\overline{\mathcal{G}}}_m^2}\left(1\right)}{{\mu }_{{\overline{\mathcal{G}}}_m^2}\left(1\right)}\hfill \end{array}$$

(15)

Next, the PDF and CDF of the unordered ${\overline{\mathcal{G}}}_m^2$ are given, respectively, as

$$\begin{array}{cc}\hfill f_{{\overline{\mathcal{G}}}_m^2}\left(x\right)& =\frac{x^{k_m-1}}{{\left(w_m\right)}^{k_m}\Gamma \left(k_m\right)}{e}^{-\frac{x}{w_m}}\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill F_{{\overline{\mathcal{G}}}_m^2}\left(x\right)& =\frac{1}{\Gamma \left(k_m\right)}\gamma \left(k_m,\frac{x}{w_m}\right)\hfill \end{array}$$

(17)

where $\gamma (.,.)$ denotes the incomplete Gamma function. Furthermore, the corresponding PDF and CDF of the m-th ordered ${\mathcal{G}}_m^2$ are given, respectively, as (5) and (6), and the proof is completed. □

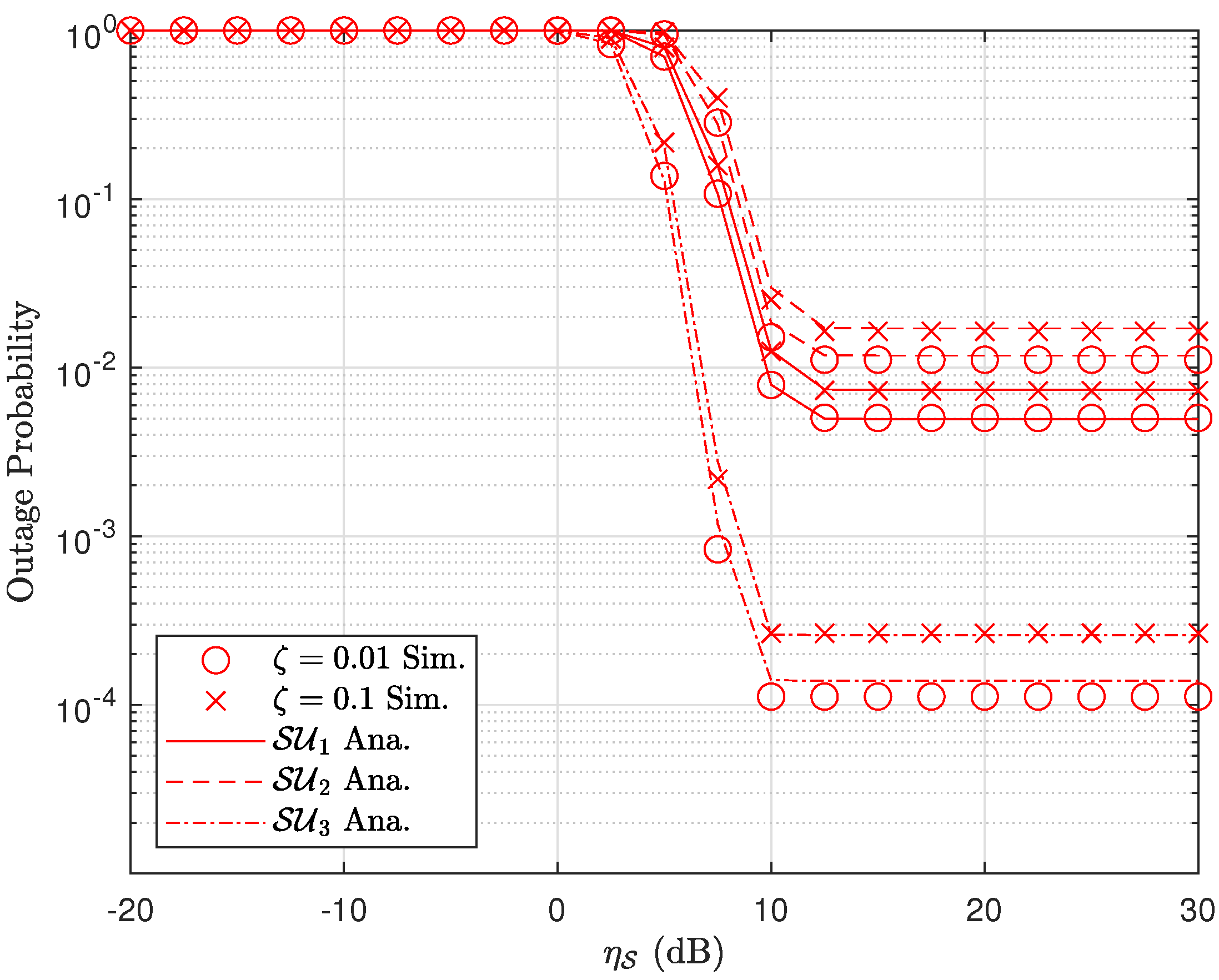
3.2. Outage Probability Analysis

Before the m-th SU decodes its own signal, the SIC is executed at that SU by identifying and canceling the information of the p-th SU ($m⩾p$). An outage occurs if the m-th SU is unable to identify the information of the p-th SU, as indicated by

$$\begin{array}{c}\hfill E_{m,p}=\left\{\frac{{\mathcal{G}}_m^2{P}_{\mathcal{S}}{\beta }_p}{{\mathcal{G}}_m^2{P}_{\mathcal{S}}{\sum }_{i=p+1}^M{\beta }_i+\zeta {\sigma }^2+{\sigma }^2}>{\gamma }_p\right\}\end{array}$$

(18)

where ${\gamma }_p=2^{R_p}-1$, $R_p$ denotes the target rate of m-th SU to detect $x_p$. Then, the outage probability of m-th SU is given by

$$\begin{array}{c}\hfill {\mathcal{P}}_m=1-Pr\left[E_{m,1}\cap E_{m,2}\cap \dots \cap E_{m,m}\right]\end{array}$$

(19)

Theorem 1.

The approximate expression OP of m-th SU is given by

$$\begin{array}{cc}\hfill {\mathcal{P}}_m& \approx \sum _{l=0}^K\sum _{a=0}^{M-m}\left(\begin{array}{c}K\\ l\end{array}\right)\frac{{\Delta }_M{\left(-1\right)}^{l+a}{e}^{-\frac{l{\eta }_{th}}{{\Omega }_{\mathcal{SD}}{\eta }_{\mathcal{S}}}}}{m+a}{\left[\frac{1}{\Gamma \left(k_m\right)}\gamma \left(k_m,\frac{{\vartheta }_m^{*}}{{\eta }_{\mathcal{S}}{w}_m}\right)\right]}^{m+a}\hfill \\ \hfill & +\frac{K{\pi }^2}{{\Omega }_{\mathcal{SD}}4I}\sum _{l=0}^{K-1}\sum _{a=0}^{M-m}\left(\begin{array}{c}K-1\\ l\end{array}\right)\frac{{\Delta }_M{\left(-1\right)}^{l+a}}{\left(m+a\right)}\hfill \\ \hfill & \times \sum _{c=1}^I\sqrt{1-{\phi }_c^2}{sec}^2\left(\frac{({\phi }_c+1)\pi }{4}\right){\left[\frac{1}{\Gamma \left(k_m\right)}\gamma \left(k_m,\frac{{\vartheta }_m^{*}{\varpi }_c}{w_m{\eta }_{th}}\right)\right]}^{m+a}{e}^{-\frac{l+1}{{\Omega }_{SD}}{\varpi }_c}\hfill \end{array}$$

(20)

Proof of Theorem 1. 

With the help of (1) and (18), the OP in (19) can be rewritten as

$$\begin{array}{cc}\hfill {\mathcal{P}}_m& =Pr\left[{\mathcal{G}}_m^2<\frac{{\vartheta }_m^{*}}{{\eta }_{\mathcal{S}}},Z_{\mathcal{SD}}<\frac{{\eta }_{th}}{{\eta }_{\mathcal{S}}}\right]+Pr\left[{\mathcal{G}}_m^2<\frac{{\vartheta }_m^{*}{Z}_{\mathcal{SD}}}{{\eta }_{th}},Z_{\mathcal{SD}}>\frac{{\eta }_{th}}{{\eta }_{\mathcal{S}}}\right]\hfill \\ \hfill & =\underset{I_1}{\underbrace{\underset{0}{\overset{\frac{{\eta }_{th}}{{\eta }_{\mathcal{S}}}}{\int }}{f}_{Z_{\mathcal{SD}}}\left(y\right)\underset{0}{\overset{\frac{{\vartheta }_m^{*}}{{\eta }_{\mathcal{S}}}}{\int }}{f}_{{\mathcal{G}}_m^2}\left(x\right)dxdy}}+\underset{I_2}{\underbrace{\underset{\frac{{\eta }_{th}}{{\eta }_{\mathcal{S}}}}{\overset{\infty }{\int }}{f}_{Z_{\mathcal{SD}}}\left(y\right)\underset{0}{\overset{\frac{{\vartheta }_m^{*}y}{{\eta }_{th}}}{\int }}{f}_{{\mathcal{G}}_m^2}\left(x\right)dxdy}}\hfill \end{array}$$

(21)

where ${\eta }_{\mathcal{S}}=\frac{{\overline{P}}_{\mathcal{S}}}{{\sigma }^2}$, ${\eta }_{th}=\frac{P_{th}}{{\sigma }^2}$, ${\vartheta }_m^{*}=max\left({\vartheta }_1,\dots ,{\vartheta }_m\right)$, ${\vartheta }_m=\frac{{\gamma }_m(\zeta +1)}{\left({\beta }_m-{\gamma }_m{\displaystyle \sum _{i=m+1}^M}{\beta }_i\right)}$, ${\vartheta }_M=\frac{{\gamma }_M(\zeta +1)}{{\beta }_M}$, and $Z_{\mathcal{SD}}=\underset{k=1,\dots ,K}{max}{\left|h_{{\mathcal{SD}}_k}\right|}^2$. Based on [Equations (19) and (20)] in [48], the PDF and CDF of $Z_{\mathcal{SD}}$ are expressed, respectively, as

$$\begin{array}{cc}\hfill f_{Z_{\mathcal{SD}}}\left(x\right)& =\sum _{l=0}^{K-1}\left(\begin{array}{c}K-1\\ l\end{array}\right)\frac{{\left(-1\right)}^{l}K}{{\Omega }_{\mathcal{SD}}}{e}^{-\frac{l+1}{{\Omega }_{\mathcal{SD}}}x}\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill F_{Z_{\mathcal{SD}}}\left(x\right)& =\sum _{l=0}^K\left(\begin{array}{c}K\\ l\end{array}\right){\left(-1\right)}^l{e}^{-\frac{l}{{\Omega }_{\mathcal{SD}}}x}\hfill \end{array}$$

(23)

Furthermore, the term $I_1$ can be obtained as

$$\begin{array}{cc}\hfill I_1& =F_{Z_{\mathcal{SD}}}\left(\frac{{\eta }_{th}}{{\eta }_{\mathcal{S}}}\right)F_{{\mathcal{G}}_m^2}\left(\frac{{\vartheta }_m^{*}}{{\eta }_{\mathcal{S}}}\right)\hfill \\ \hfill & =\sum _{l=0}^K\sum _{a=0}^{M-m}\left(\begin{array}{c}K\\ l\end{array}\right)\frac{{\Delta }_M{\left(-1\right)}^{l+a}{e}^{-\frac{l{\eta }_{th}}{{\Omega }_{\mathcal{SD}}{\eta }_{\mathcal{S}}}}}{m+a}{\left[\frac{1}{\Gamma \left(k_m\right)}\gamma \left(k_m,\frac{{\vartheta }_m^{*}}{{\eta }_{\mathcal{S}}{w}_m}\right)\right]}^{m+a}\hfill \end{array}$$

(24)

Next, the term $I_2$ in (21) is calculated as

$$\begin{array}{cc}\hfill I_2& =\underset{\frac{{\eta }_{th}}{{\eta }_{\mathcal{S}}}}{\overset{\infty }{\int }}{f}_{Z_{\mathcal{SD}}}\left(y\right)F_{{\mathcal{G}}_m^2}\left(\frac{{\vartheta }_m^{*}y}{{\eta }_{th}}\right)dy\hfill \\ \hfill & =\sum _{l=0}^{K-1}\sum _{a=0}^{M-m}\left(\begin{array}{c}K-1\\ l\end{array}\right)\frac{K{\Delta }_M{\left(-1\right)}^{l+a}}{\left(m+a\right){\Omega }_{\mathcal{SD}}}\underset{\frac{{\eta }_{th}}{{\eta }_{\mathcal{S}}}}{\overset{\infty }{\int }}{\left[\frac{1}{\Gamma \left(k_m\right)}\gamma \left(k_m,\frac{{\vartheta }_m^{*}}{w_m{\eta }_{th}}y\right)\right]}^{m+a}{e}^{-\frac{l+1}{{\Omega }_{SD}}y}dy\hfill \end{array}$$

(25)

Moreover, the integral in (25) is difficult to solve in closed form. Therefore, by applying the Gaussian–Chebyshev quadrature method [49], $I_2$ can be approximated as

$$\begin{array}{cc}\hfill I_2& \approx \frac{K{\pi }^2}{{\Omega }_{\mathcal{SD}}4I}\sum _{l=0}^{K-1}\sum _{a=0}^{M-m}\left(\begin{array}{c}K-1\\ l\end{array}\right)\frac{{\Delta }_M{\left(-1\right)}^{l+a}}{\left(m+a\right)}\hfill \\ \hfill & \times \sum _{c=1}^I\sqrt{1-{\phi }_c^2}{sec}^2\left(\frac{({\phi }_c+1)\pi }{4}\right){\left[\frac{1}{\Gamma \left(k_m\right)}\gamma \left(k_m,\frac{{\vartheta }_m^{*}{\varpi }_c}{w_m{\eta }_{th}}\right)\right]}^{m+a}{e}^{-\frac{l+1}{{\Omega }_{SD}}{\varpi }_c}\hfill \end{array}$$

(26)

where ${\phi }_c=cos\left(\frac{2c-1}{2I}\pi \right)$ and ${\varpi }_c=tan\left(\frac{({\phi }_c+1)\pi }{4}\right)+\frac{{\eta }_{th}}{{\eta }_{\mathcal{S}}}$. By substituting (24) and (26) into (21), (20) can be obtained. This proof is completed. □

3.3. Outage Probability Floor Analysis

In a CR system, the OP floor implies that even if the average SNR keeps rising, the OP cannot drop below a specific bound. In real-world networks, PNs are arranged in one of two ways: $\left(i\right)$ farthest from the SNs ($P_{th}\gg {\overline{P}}_{\mathcal{S}}$) and $\left(ii\right)$ closest to the SNs (${\overline{P}}_{\mathcal{S}}\gg P_{th}$). Consequently, more information about the system architecture may be obtained from the performance floor analysis assessed for a user’s OP.

Theorem 2.

The asymptotic expression for the OP floor of the m-th SU when $P_{th}\gg {\overline{P}}_{\mathcal{S}}$ and ${\overline{P}}_{\mathcal{S}}\gg P_{th}$, respectively, are given as

$$\begin{array}{c}\hfill {\mathcal{P}}_m^{\infty }\approx \sum _{a=0}^{M-m}\frac{{\Delta }_M{\left(-1\right)}^a}{m+a}{\left[\frac{1}{\Gamma \left(k_m\right)}\gamma \left(k_m,\frac{{\vartheta }_m^{*}}{{\eta }_{\mathcal{S}}{w}_m}\right)\right]}^{m+a}\end{array}$$

(27)

and

$$\begin{array}{cc}\hfill {\mathcal{P}}_m^{\infty }& \approx \frac{K{\pi }^2}{{\Omega }_{\mathcal{SD}}4I}\sum _{l=0}^{K-1}\sum _{a=0}^{M-m}\left(\begin{array}{c}K-1\\ l\end{array}\right)\frac{{\Delta }_M{\left(-1\right)}^{l+a}}{\left(m+a\right)}\hfill \\ \hfill & \times \sum _{c=1}^I\sqrt{1-{\phi }_c^2}{sec}^2\left(\frac{({\phi }_c+1)\pi }{4}\right){\left[\frac{1}{\Gamma \left(k_m\right)}\gamma \left(k_m,\frac{{\vartheta }_m^{*}{\overline{\varpi }}_c}{w_m{\eta }_{th}}\right)\right]}^{m+a}{e}^{-\frac{l+1}{{\Omega }_{SD}}{\overline{\varpi }}_c}\hfill \end{array}$$

(28)

where ${\overline{\varpi }}_c=tan\left(\frac{({\phi }_c+1)\pi }{4}\right)$.

Proof of Theorem 2. 

To calculate the asymptotic expression for the OP of m-th users. The term ${\mathcal{P}}_m^{\infty }$ in (21) can be calculated as

$$\begin{array}{cc}\hfill {\mathcal{P}}_m^{\infty }& =\left\{\begin{array}{c}{F}_{{\mathcal{G}}_m^2}\left(\frac{{\vartheta }_m^{*}}{{\eta }_{\mathcal{S}}}\right),P_{th}\gg {\overline{P}}_{\mathcal{S}}\hfill \\ \underset{0}{\overset{\infty }{\int }}{f}_{Z_{\mathcal{SD}}}\left(y\right)F_{{\mathcal{G}}_m^2}\left(\frac{{\vartheta }_m^{*}y}{{\eta }_{th}}\right)dy,P_{th}\ll {\overline{P}}_{\mathcal{S}}\hfill \end{array}\right.\hfill \end{array}$$

(29)

With the help (6), (22), and applying similarly the Gaussian–Chebyshev quadrature method, (28) can be obtained. The proof is completed. □

3.4. Throughput Analysis

In this subsection, we derive and analyze the throughput of the proposed system configuration. Throughput is defined by evaluating the outage probability, ${\mathcal{P}}_m$, at a fixed-source transmission rate, i.e., R (bits/sec/Hz) in the delay-limited transmission mode. Based on the attainable OP, the system throughput may be represented as follows:

$$\begin{array}{c}\hfill {\mathcal{T}}_{system}=\sum _{m=1}^M{R}_m(1-{\mathcal{P}}_m)\end{array}$$

(30)

4. Numerical Result and Discussion

For the analyses in this section, the main parameters are listed in

Table 1. Table of the main parameter.

Parameter	Value
Number of secondary users	$M=3$
Number of primary users	$K=3$
Number of reflective elements	$N=20$
Power allocation	${\beta }_1=0.5$, ${\beta }_2=0.3$ and ${\beta }_3=0.2$
Scaling coefficient	$\zeta =0.01$
Target rate	$R_1=0.6$, $R_2=0.9$, $R_3=1.6$ [BPCU]
Maximum interference level	${\eta }_{th}=-10$ [dB]
Pass loss exponent	$\ell =2$
Distance	$d_{\mathcal{SR}}=d_{\mathcal{SD}}=d_{{\mathcal{RU}}_3}=10$ [m], $d_{{\mathcal{RU}}_1}=20$ [m], $d_{{\mathcal{RU}}_2}=15$ [m], $d_{{\mathcal{SU}}_1}=30$ [m], $d_{{\mathcal{SU}}_2}=25$ [m], and $d_{{\mathcal{SU}}_3}=20$ [m]

—${\Omega }_j=d_j^{\ell }$, in which ℓ denotes the pass loss exponent and BPCU denotes the bit per channel use. In all figures, Sim. and Ana. are the abbreviations of Simulation and Analytical, respectively. For simulation, we apply the Monte Carlo method with a ${10}^6$ trial to clarify the accuracy of our analysis.

Figure 2 plots the outage probability of three users versus ${\eta }_{\mathcal{S}}$ in dB from varying N. We can see that over the whole range of ${\eta }_{\mathcal{S}}$, outage probability curves and analytical results accord exceptionally well based on a Monte Carlo simulation. It can be seen that when ${\eta }_S$ is from −20 to 0 dB and the number of reflective elements N is 15, the OP almost reaches 1. It leads to the system not being able to operate and presents operational challenges. But when we increase ${\eta }_S$ as well as N, the OP will be decreased, specifically when ${\eta }_S$ is larger than 5 dB and N = 20. Therefore, in reality, choosing the parameters to configure the system to operate well also plays a very important role. Furthermore, the asymptotic findings produced in (27) and (28) are extremely constrained, with the theoretical analysis at a high ${\eta }_{\mathcal{S}}$ confirming the accuracy of our developed analysis approach. In addition, observe that outage performance improved when increasing the transmit power but did not change with a high ${\eta }_{\mathcal{S}}$. The fact that OP depends on more factors than only transmitting ${\eta }_{\mathcal{S}}$ can be explained. Specifically, we can see in (1) that the transmission power of ${\eta }_{\mathcal{S}}$ in the SN is limited by ${\eta }_{th}$ in the PN. Another observation is that outage performance was better when increasing the number of RIS reflective elements. This is because applying an RIS to a NOMA network offers an additional level of flexibility to improve performance for users.

Figure 3 plots the outage probability of three users versus ${\eta }_{\mathcal{S}}$ in dB when varying ${\eta }_{th}$. Observe that the outage performance improved when increasing ${\eta }_{th}$. Furthermore, we can see that the outage performance for three users from RIS-NOMA was superior to RIS-OMA. Figure 4 and Figure 5 plot outage probability versus ${\eta }_{\mathcal{S}}$ in dB when varying the number of primary users K and when varying interference $\zeta$, respectively. We can see in Figure 4 that when increasing K, outage performance for secondary users was reduced regardless of the increase in transmit power. Figure 5 shows that when increasing interference, $\zeta$ outage performance for users was reduced but not significantly. That is because of interference with the secondary network from the source in the primary network.

Figure 6 plots system throughput versus ${\eta }_{\mathcal{S}}$ in dB when varying the number of reflective elements N. As in Figure 2, the outage probability of users is reduced when increasing ${\eta }_{\mathcal{S}}$ and the number of reflective elements N. That leads to an increase in system throughput, as shown in Figure 6. On the other hand, system throughput improved when increasing the value of ${\eta }_{th}$, as shown in Figure 7. Furthermore, system throughput for RIS-NOMA outperformed RIS-OMA. In addition, RIS-NOMA and RIS-OMA converged to the throughput ceiling in the high ${\eta }_{\mathcal{S}}$ regime.

5. Conclusions

In this paper, we studied the performance of a cognitive RIS-NOMA network in terms of outage probability and throughput. In particular, we derived the closed-form expression for outage probability throughput. Furthermore, the asymptotic expression of outage probability is shown to give more insight into the proposed system. Numerical results showed validation of the derived expression and the impacts of the main parameters in the proposed system by conducting a Monte Carlo simulation. Furthermore, the results show that outage performance and throughput from RIS-NOMA were superior to those of RIS-OMA. Most articles in the literature presume possession of perfect CSI in RIS-NOMA to easily analyze the user selection procedure. The CSI for user selection may be out of date for a variety of reasons, including feedback latency, movement, etc. Furthermore, with widespread frequency reuse in wireless networks, RIS-NOMA is susceptible to co-channel interference (CCI). These issues require more effort in future work.