Multi-Objective Ship Route Optimisation Using Estimation of Distribution Algorithm
Abstract
:1. Introduction
- A 3D-graph-based design space and the computational topology it generates for dynamic programming (DP)-based local search (Section 4.1);
- An (inspired by the estimation of distribution algorithm) adaptive Markov chain-based path generator directing the global search process (Section 4.2);
- The dp-based local search algorithm, significantly boosting—thanks to its exploitation capabilities—the global search process (Section 4.3);
- The meta-heuristic algorithm combining the above elements to create an effective framework for (simulation based) multi-objective optimal path planning in non-stationary environments (Section 4.4);
- Experimental results showing the high effectiveness of the proposed algorithm in finding very good quality and diversified approximations of the set of Pareto optimal solutions (Section 5).
2. Related Research
2.1. Methods for Ship Routing Problem
2.2. Estimation of Distribution Algorithms
| Method | Problem Features | Algorithm Features | |||||
|---|---|---|---|---|---|---|---|
| Combinatorial Optimisation | Multi-Objective Problem | Non-Stationary Problem | (Explicit) Probability Distribution Based | Local Search | Deterministic Local Search (with Tabu List) | ||
| Our method | YES | YES | YES | YES | YES | YES | |
| [2,4,12,13,14,15,19,20,21,22] | YES | NO | NO | NO | NO | NO | |
| [3,5,16,17,18,23,24,25,26,27,28] | YES | YES | NO | NO | NO | NO | |
| [18] | YES | YES | YES | NO | NO | NO | |
| [39,40,41,42,44] | NO | YES | NO | YES | NO | NO | |
| [43] | NO | YES | YES | YES | NO | NO | |
| [45,46] | YES | NO | NO | YES | NO | NO | |
| [47,48,49] | YES | NO | NO | YES | YES | NO | |
3. Problem Formulation
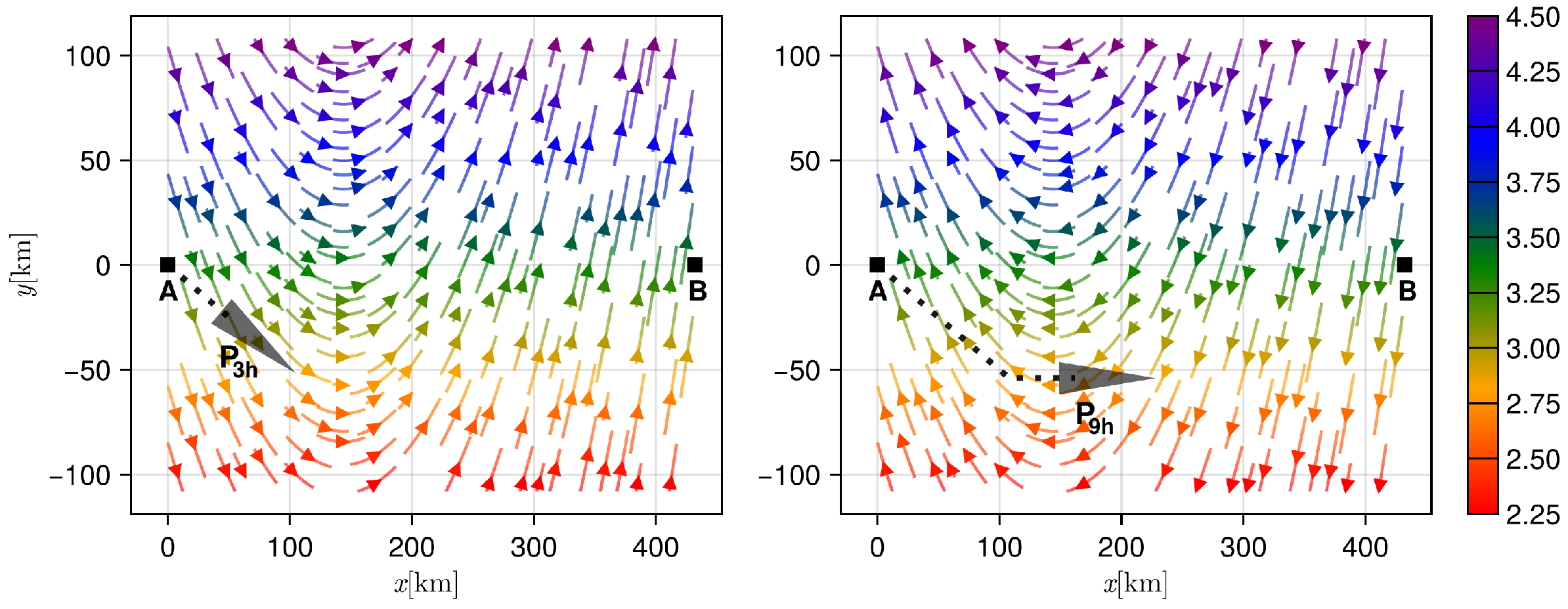
- With the (tidal) stream (a horizontal flow of water caused by the rise and fall of the tide) given by the following velocity vector field:
- From point A to B, along the path/route:
- Under a specific control input (that corresponds to path ):
4. Proposed Solution
- Transformation of the continuous optimisation problem into a (discrete) search problem over a specially constructed graph;
- Application of the proposed optimal path search algorithm to find a good approximation of the set of Pareto optimal control input sequences:
- A 3D-graph-based solution (design) space and the computational topology it generates (for dynamic programming (dp)-based local search);
- Adaptive Markov chain-based path generator (directing the search process);
- The search process augmented by the dp-based pruned local search.
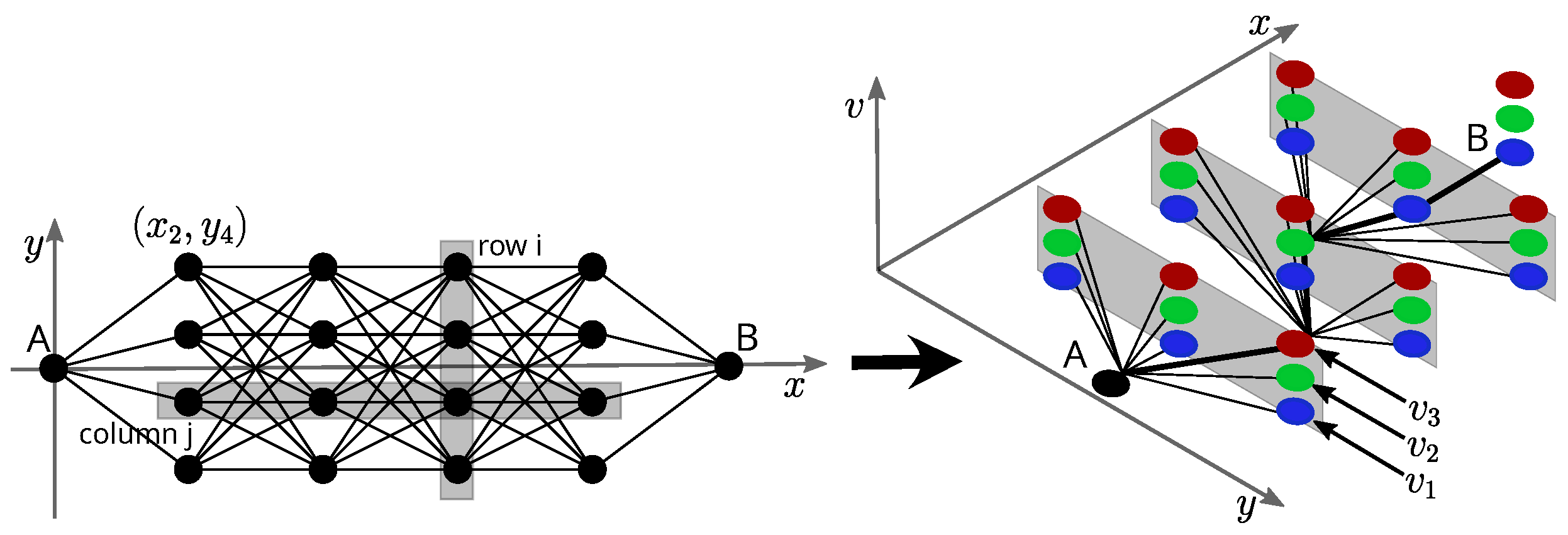
4.1. The Solution (Design) Space Representation
- Has nodes;
- Has edges;
- Represents different control input sequences. (trajectories).
4.2. Path Generator
- At each node, the predecessor selection problem is two-dimensional (c and v are to be chosen) and discrete; hence, the corresponding joint probability distributions are represented as 2D-frequency tables ();
- The prior (initial) distributions are not uniform—they form a “gable roof shape” (with the marginal distribution of v being uniform, and the marginal distribution of c being triangular);
- Drawing is performed from the joint distribution, i.e., with a single draw, we obtain a pair of values ;
- Distribution adaptation is performed in two steps: first, the value corresponding to is increased by a predefined constant, i.e., , then, the distribution is “smoothed” locally (e.g., by weighted averaging).
4.3. dp-Based Pruned Local Search
4.4. The Search Algorithm
| Algorithm 1: Multi-objective ship route optimisation using estimation of distribution algorithm (EDA) with dp-based pruned local search. |
Input:
Output: —(good) approximation of the set of Pareto optimal control input sequences (see Equation (5)) |
 |
5. Results and Discussion
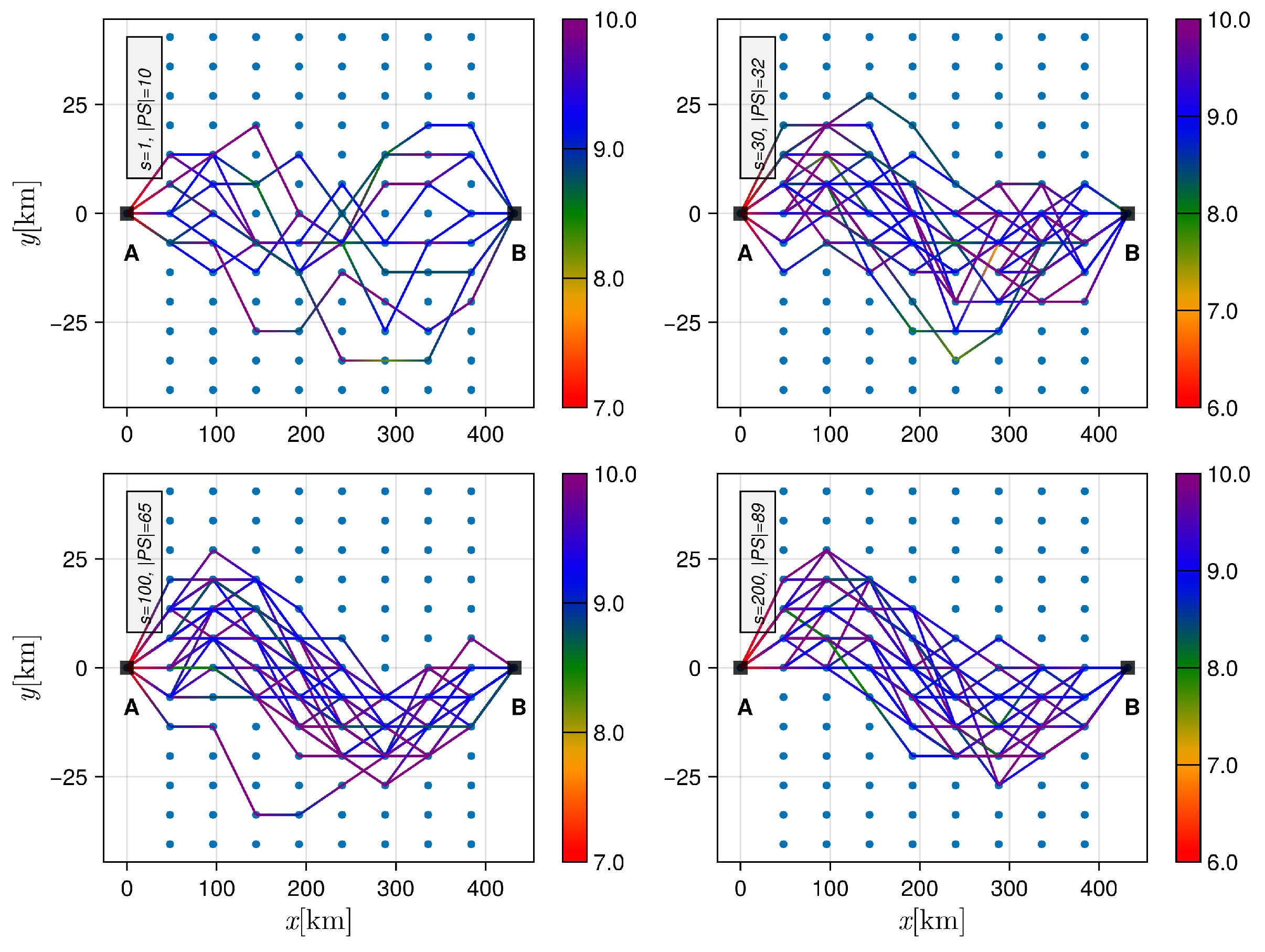
5.1. Pareto Set Evolution (the Design Space Perspective)

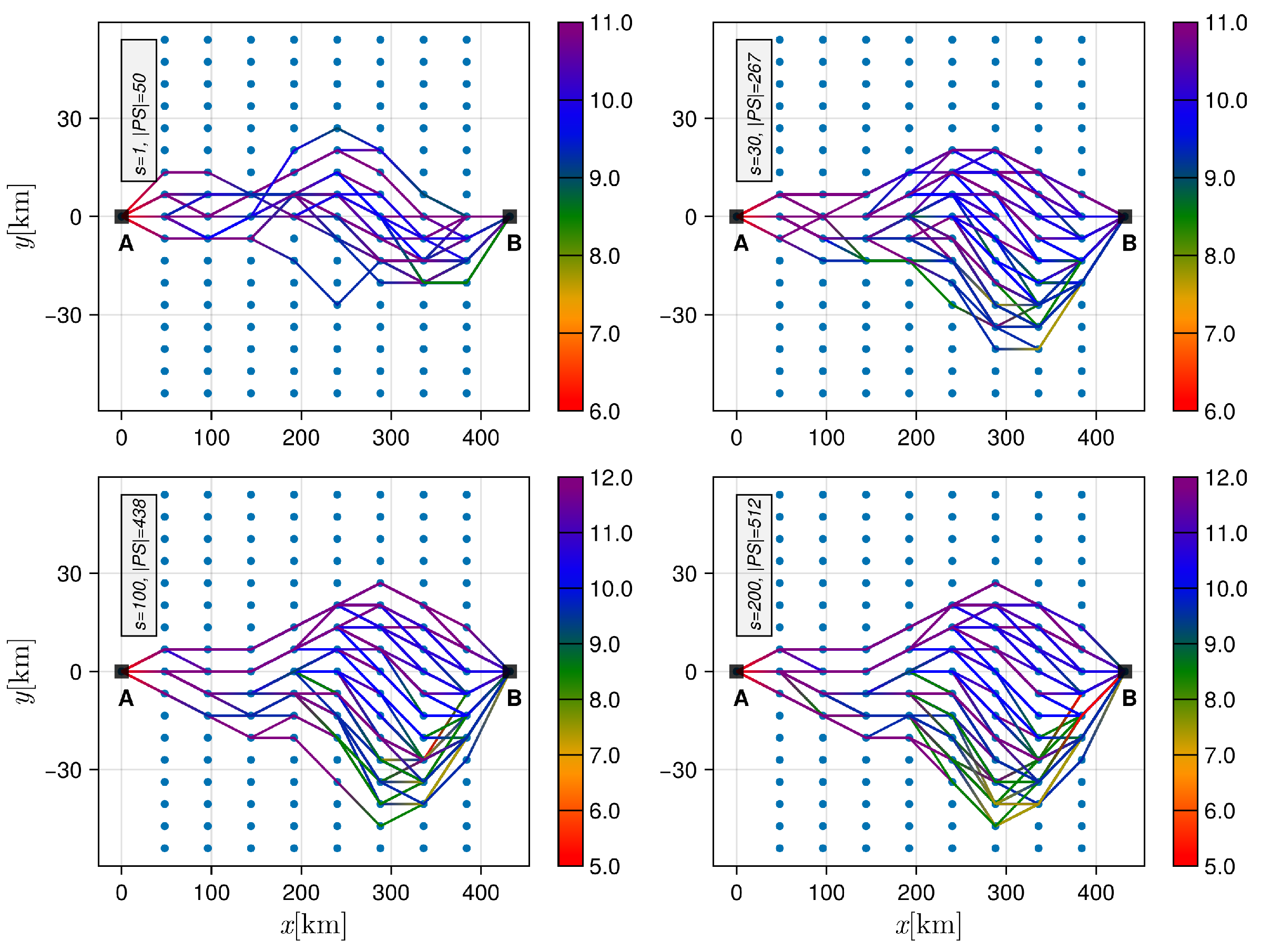
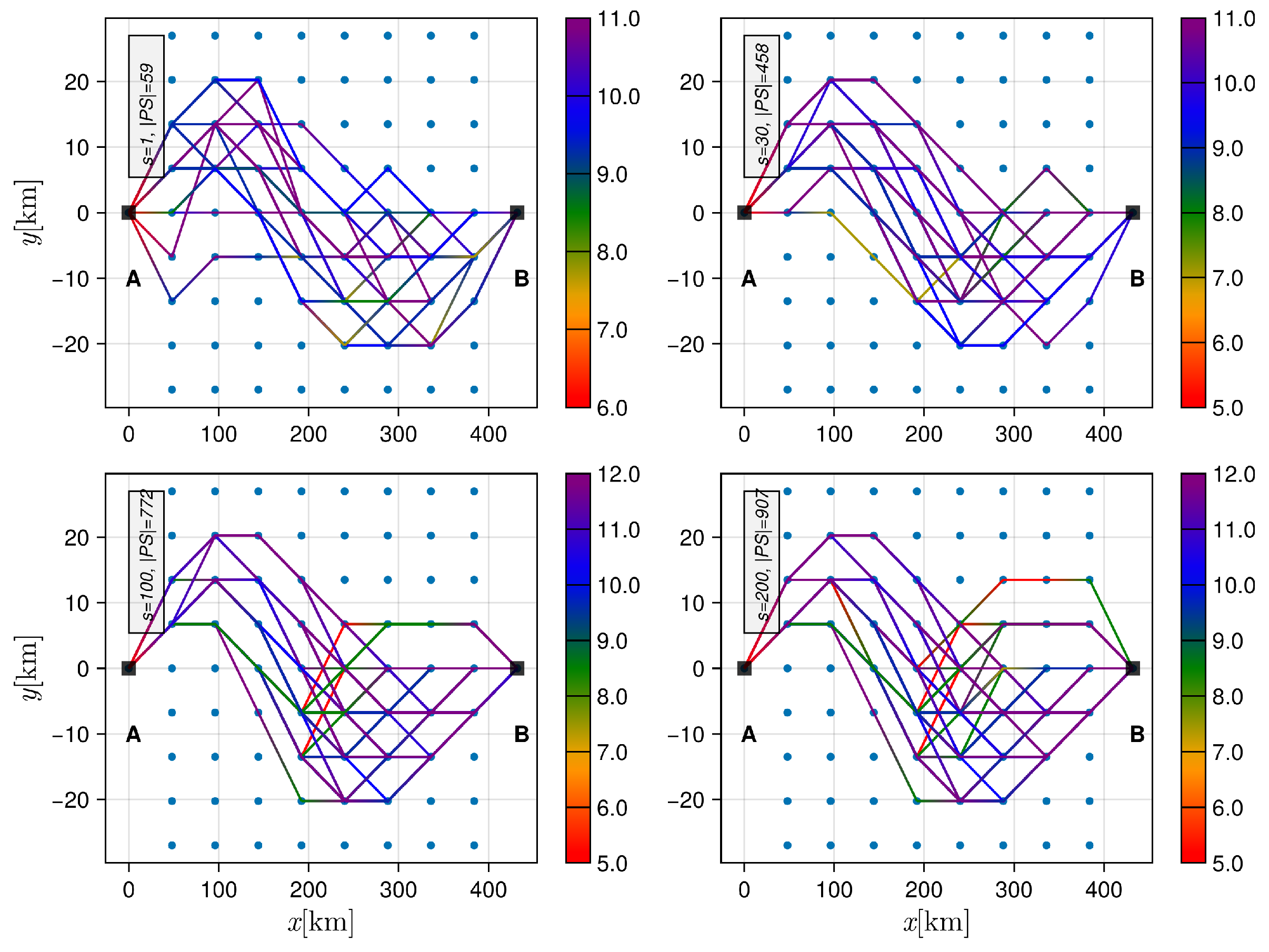
5.2. Pareto Front Evolution (The Criterion Space Perspective)
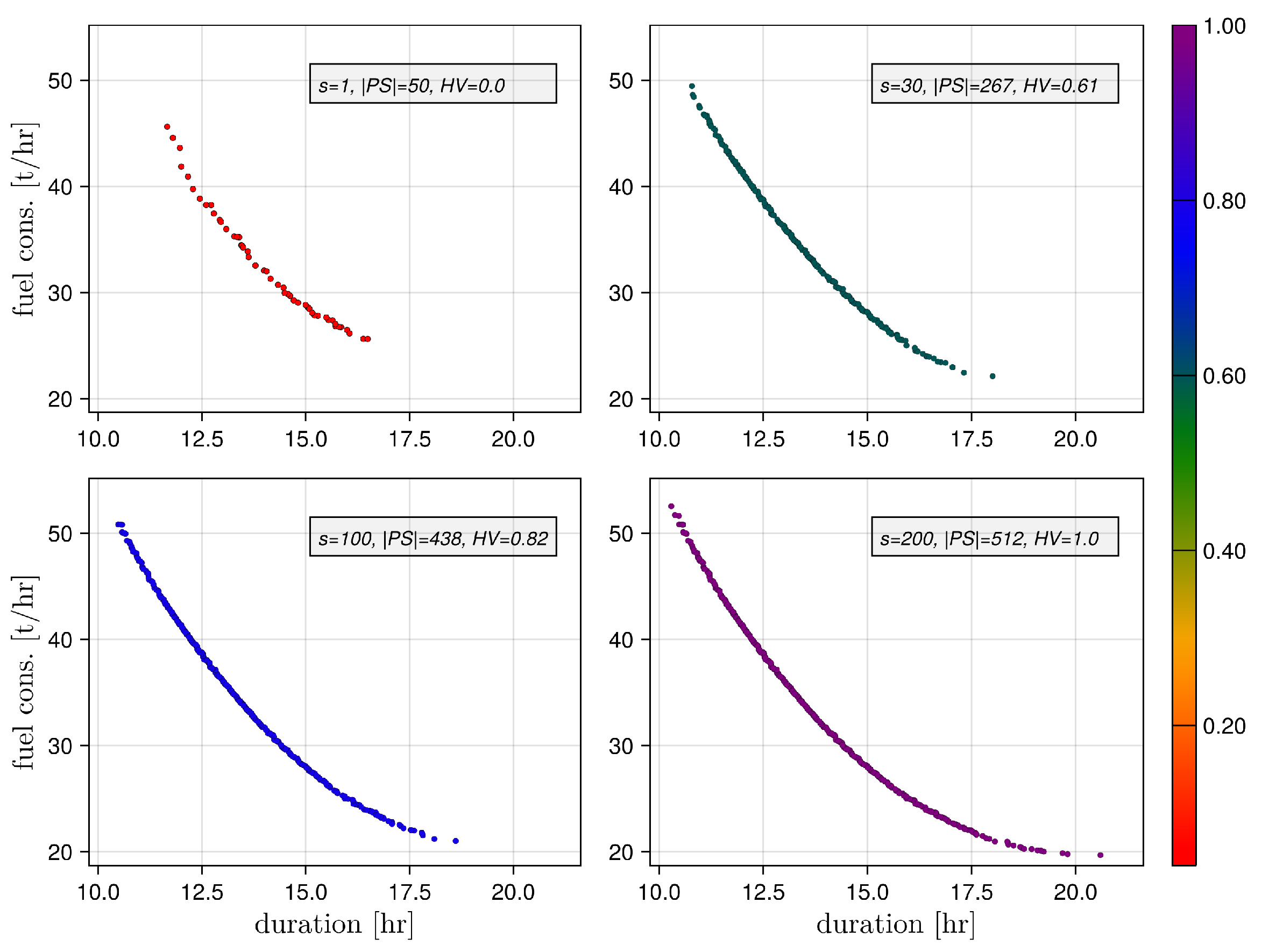
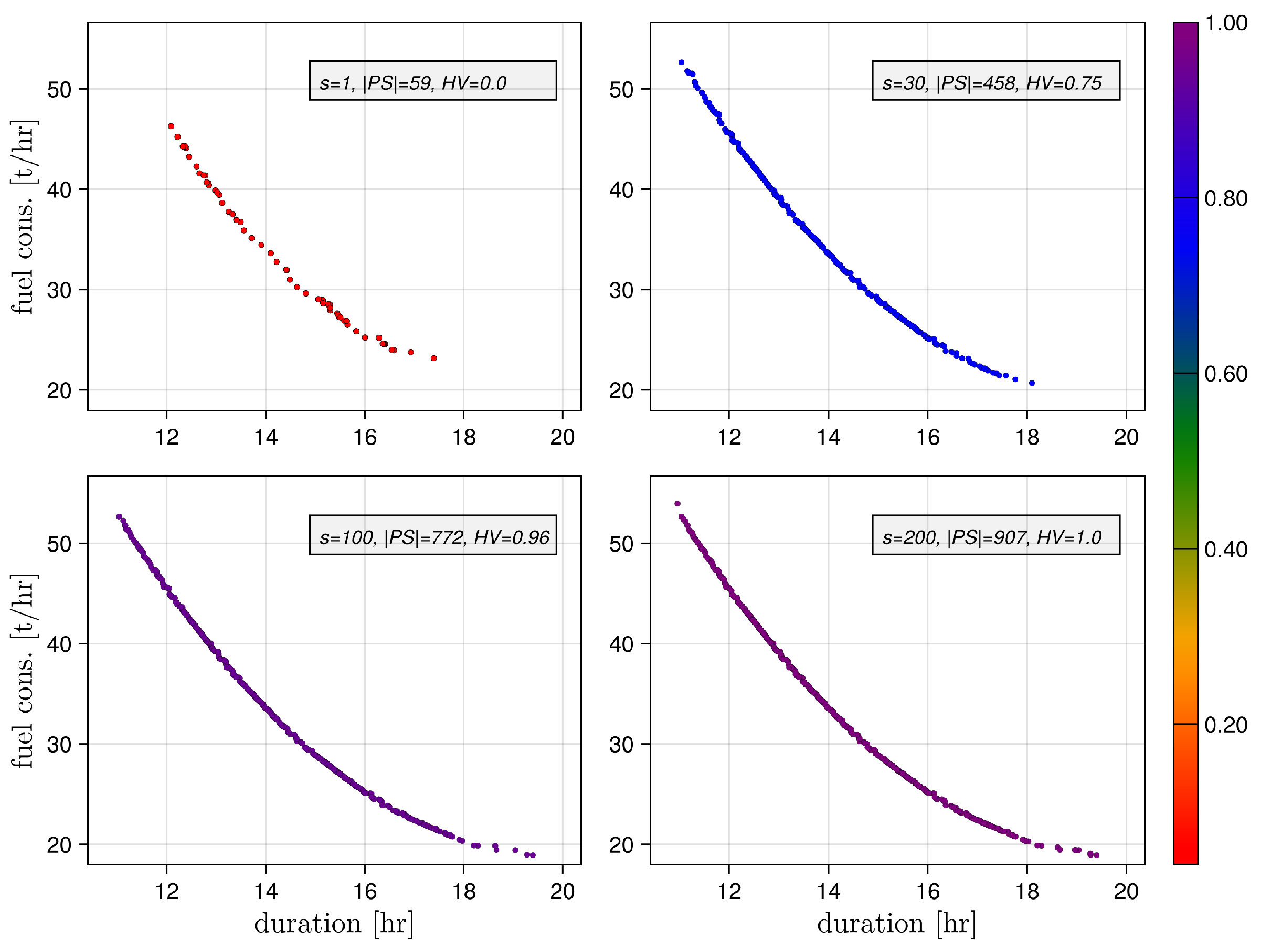
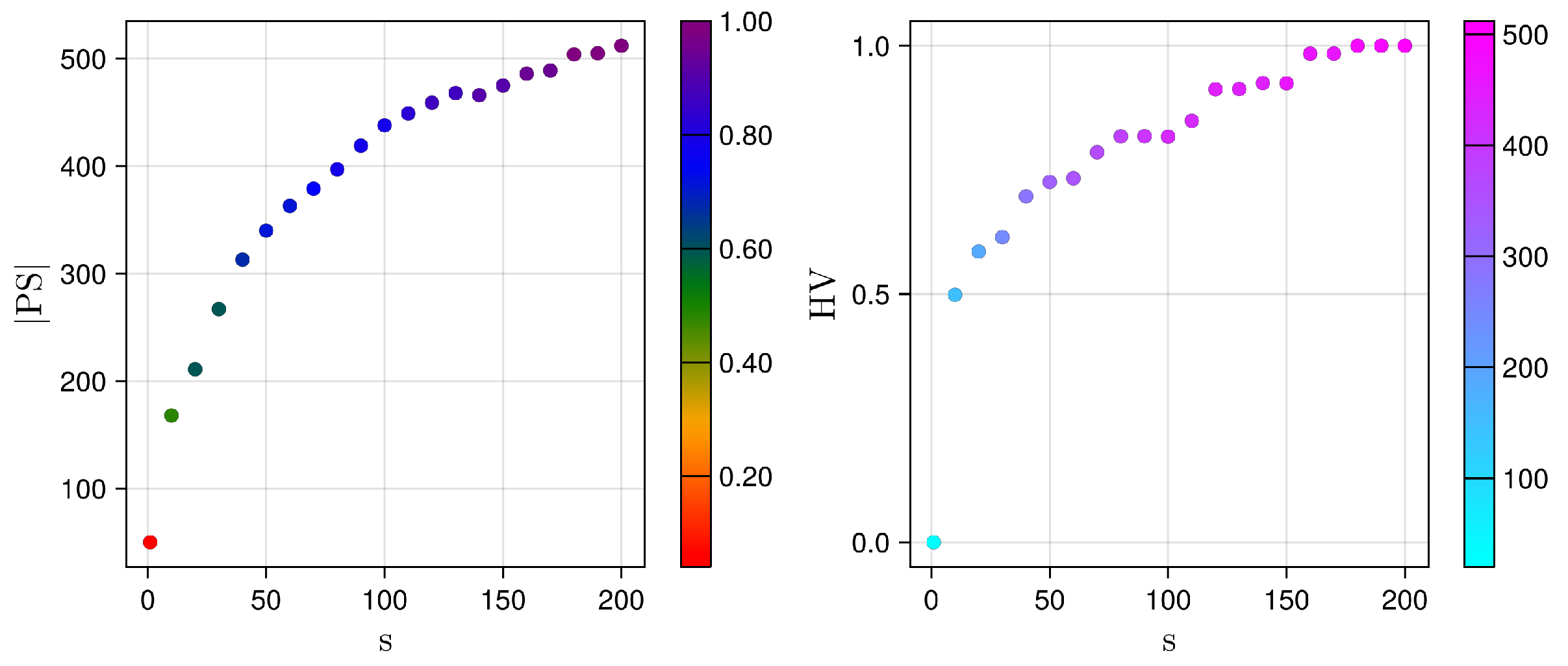
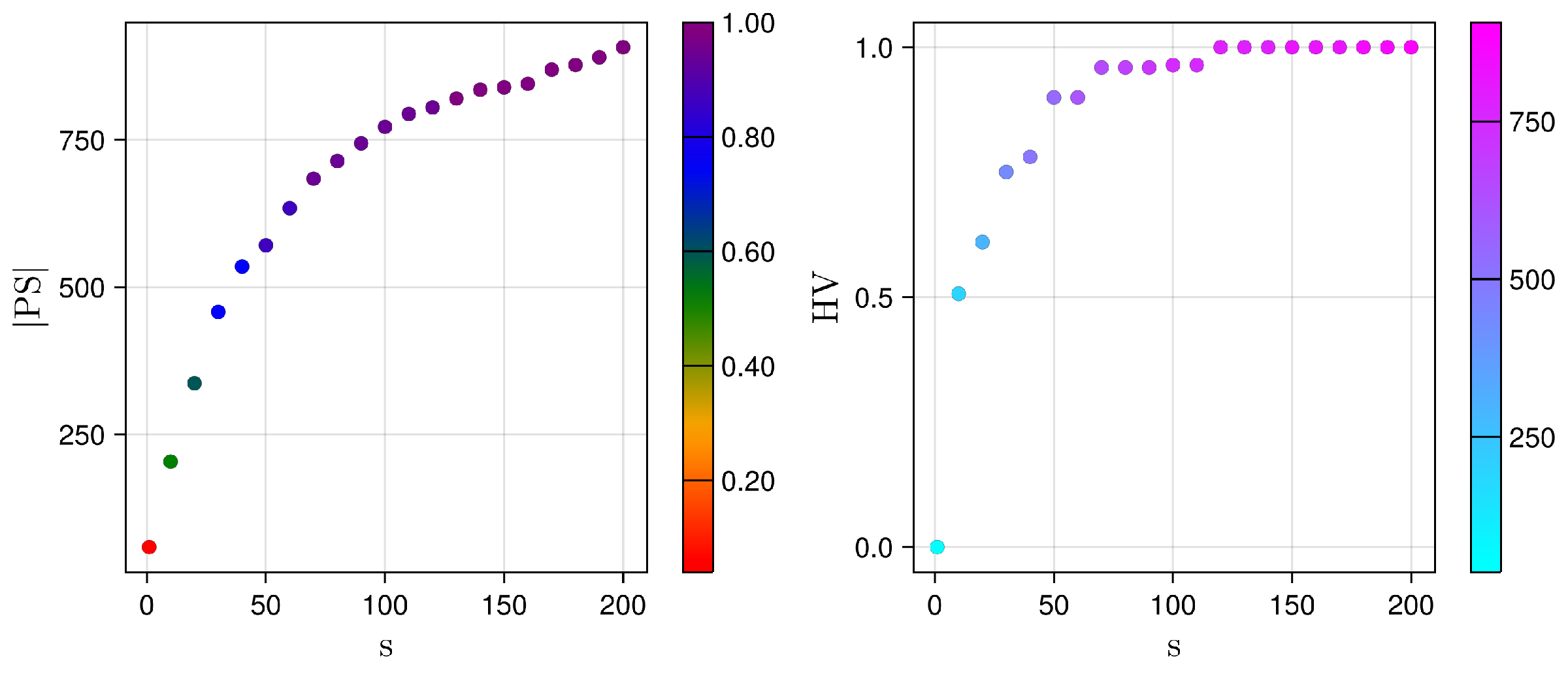
5.3. Pareto Front Quality: The Impact of the Local Search


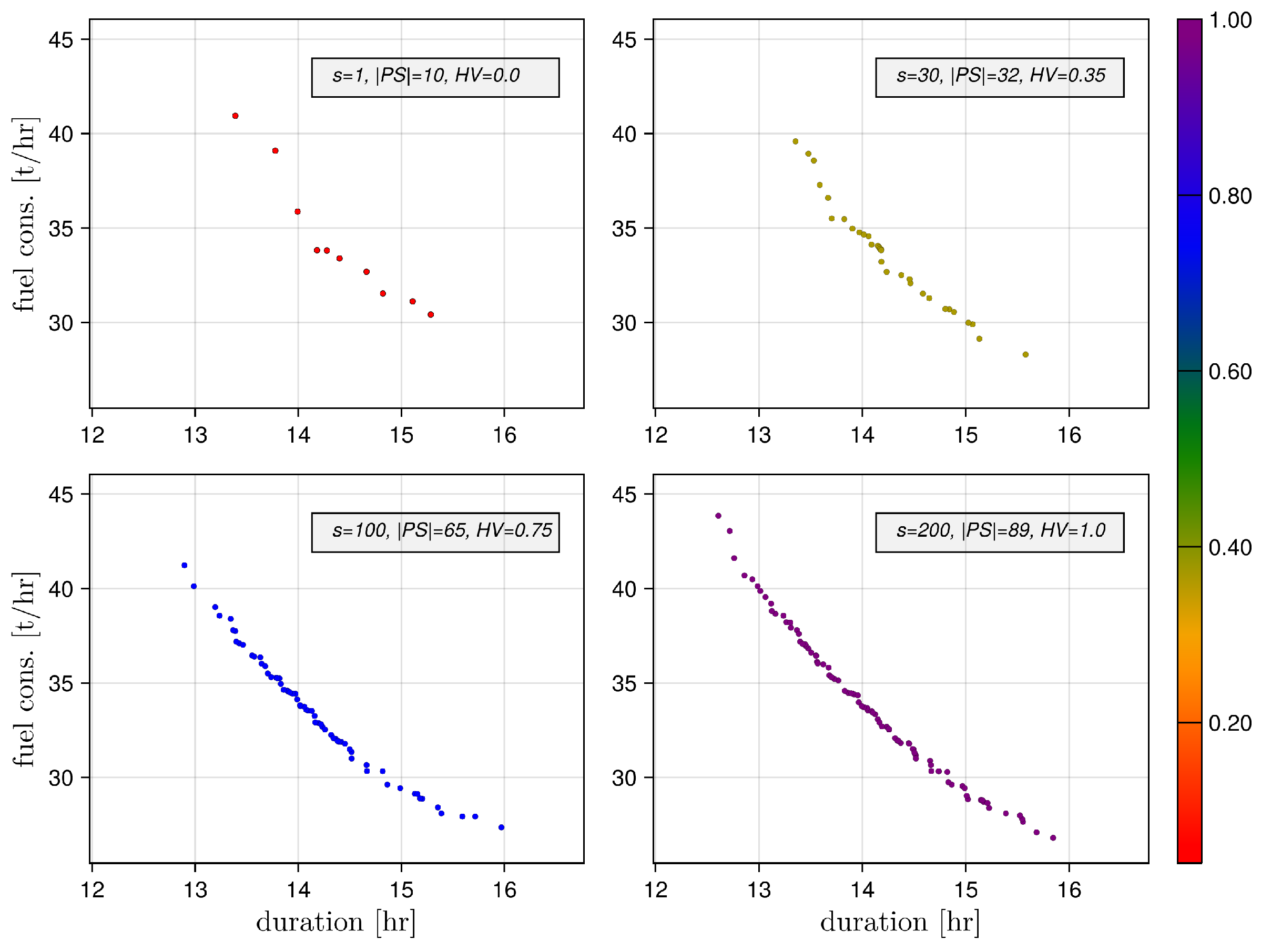
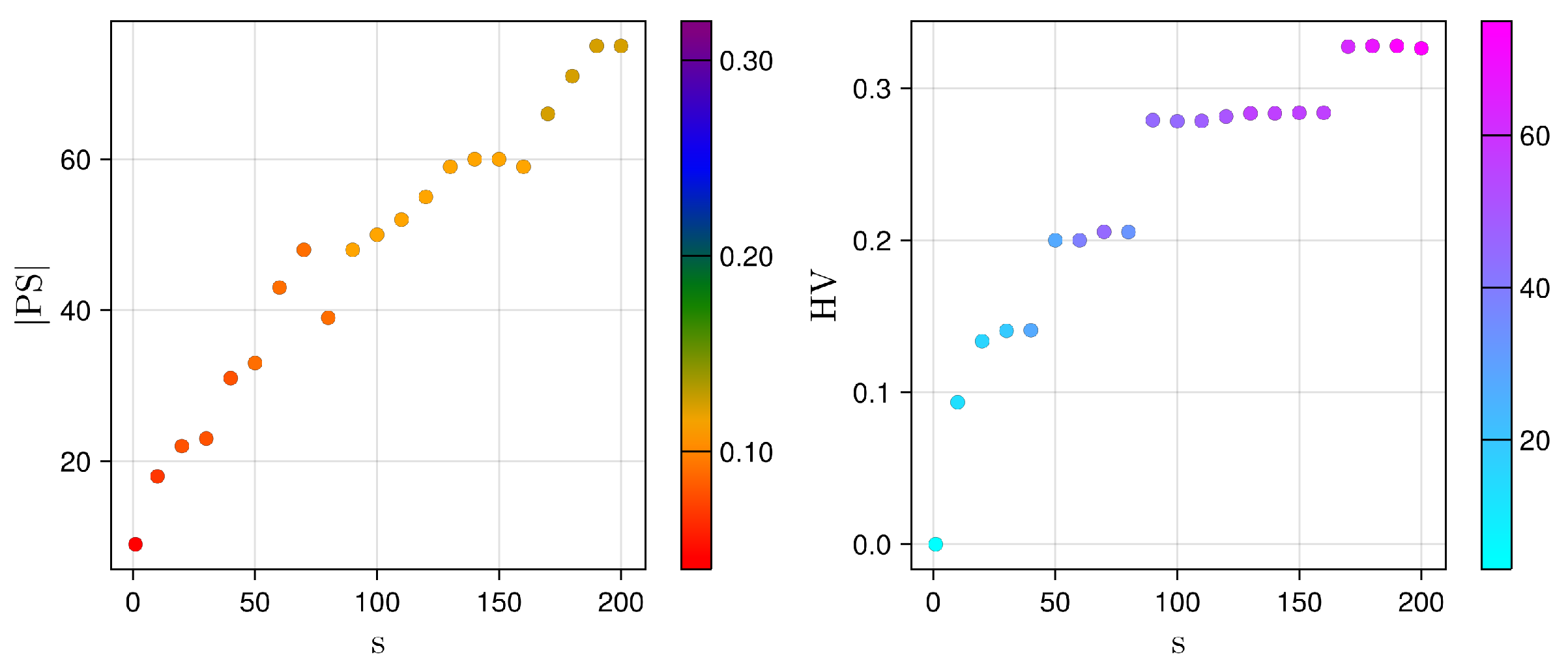
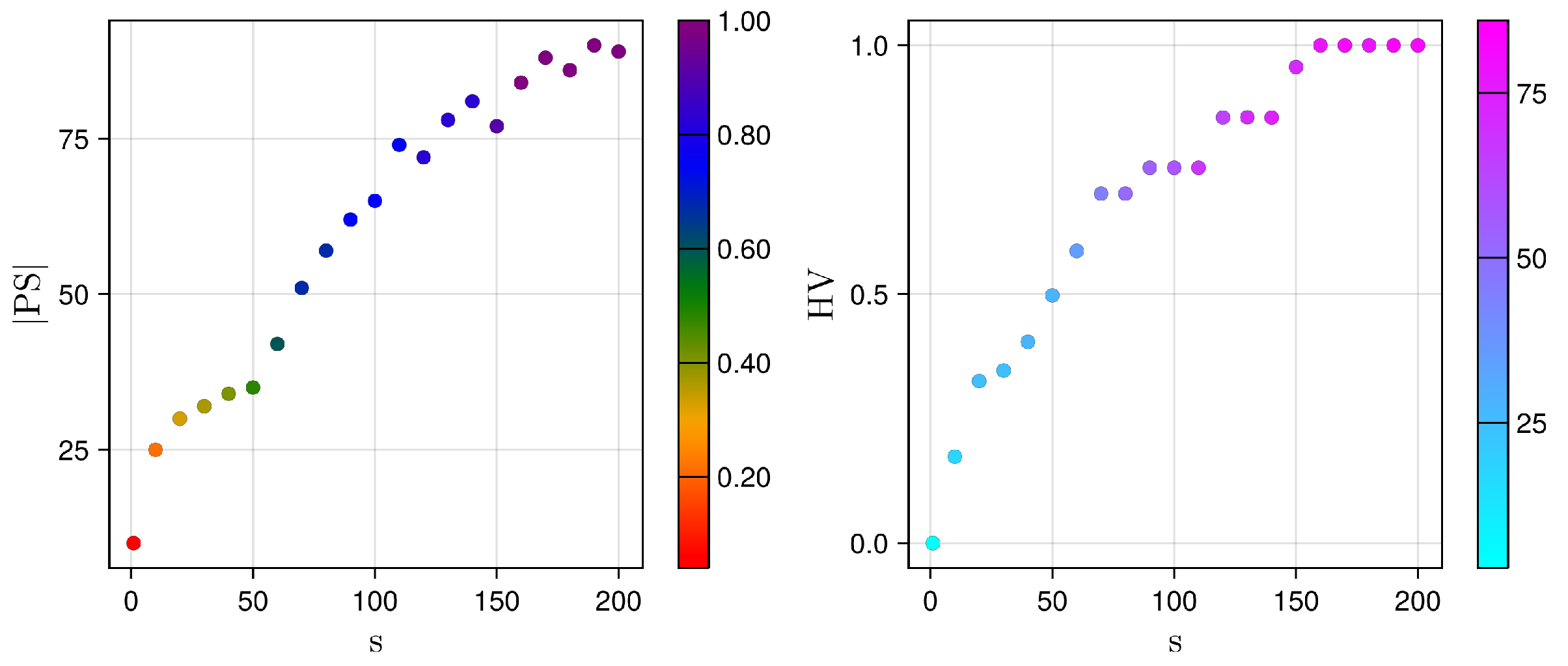
5.4. Summary of the Results
6. Conclusions
- Verification of the proposed algorithm with a more accurate ship simulator (based on ship dynamics);
- Verification of other (selected) existing meta-heuristics as the global search process engines;
- The search algorithm hyper-parameters tuning, combined with sensitivity analysis;
- The parallelisation of the algorithm;
- The use of other types of surrogate models.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. The Simulation Model
- Without loss of generality (the simulator—independently of its complexity—is treated by the optimisation algorithm as a black-box), we define only the kinematic model of a ship, which describes the motion of the ship without consideration of forces (an example of a more complex model can be found, for instance, in [50]).
- The optimisation problem under consideration (see Section 3) has two objectives: the passage time and the corresponding fuel consumption are to be minimised. They are defined in the following way:
- (a)
- Passage time (duration), calculated as a sum of passage times for each linear path segment, r:
- (b)
- Fuel consumption (total), as above—accumulated over all segments:
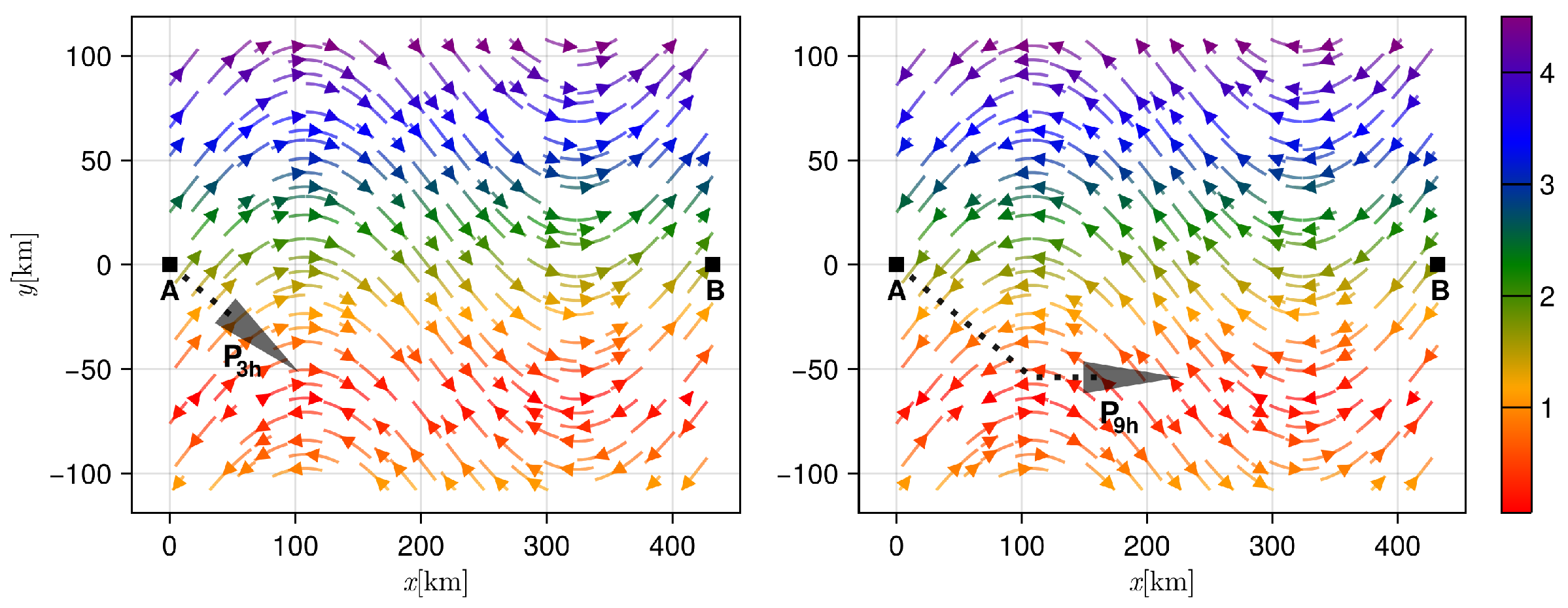
where () is the number of segments forming a single ab-path, is the length of the r-th segment, is the number of subsegments used to approximate the integral , is the absolute speed (SOG—Speed Over the Ground) of the ship (along the r-th linear segment), and is the speed of the ship relative to the water (STW—Speed Through Water). - The ship absolute speed (SOG) depends on the tidal stream (typically given in the form of a vector field), which in the simulations is assumed to be as follows (see Figure 1 and Figure 4):where:
- (a)
- (b)
Finally, the ship absolute speed (along the given path segment ) is defined as follows:where is the angle (slope) of and - In addition, we assume the following:
- (a)
- Each ab-path is a continuous piecewise-linear function (formed by the sequence of the corresponding graph edges).
- (b)
- Each control input sequence is a piecewise-constant function (constant along each linear path segment).
References
- United Nations Conference on Trade and Development (UNCTAD). Review of Maritime Transport; UNCTAD: Geneva, Switzerland, 2022. [Google Scholar]
- Shao, W.; Zhou, P.; Thong, S.K. Development of a novel forward dynamic programming method for weather routing. J. Mar. Sci. Technol. 2012, 17, 239–251. [Google Scholar] [CrossRef]
- Szlapczynska, J.; Szlapczynski, R. Preference-based evolutionary multi-objective optimization in ship weather routing. Appl. Soft Comput. 2019, 84, 105742. [Google Scholar] [CrossRef]
- Du, W.; Li, Y.; Zhang, G.; Wang, C.; Zhu, B.; Qiao, J. Energy saving method for ship weather routing optimization. Ocean Eng. 2022, 258, 111771. [Google Scholar] [CrossRef]
- Gunawan; Utomo, A.; Pambudi, G.; Hamada, K.; Yanuar. Optimization of Shipping Routes for Container Ships from Indonesia to the Asia-Pacific Using Heuristic Algorithms. J. Mar. Sci. Eng. 2023, 11, 1360. [Google Scholar] [CrossRef]
- Chung, S.H. Applications of smart technologies in logistics and transport: A review. Transp. Res. Part E Logist. Transp. Rev. 2021, 153, 102455. [Google Scholar] [CrossRef]
- Khan, W.A.; Chung, S.; Awan, M.U.; Wen, X. Machine learning facilitated business intelligence (Part II): Neural networks optimization techniques and applications. Ind. Manag. Data Syst. 2020, 120, 128–163. [Google Scholar] [CrossRef]
- Orosa, J.A.; Pérez-Canosa, J.M.; Pérez-Castelo, F.J.; Durán-Grados, V. Research on the Improvement of Safety Navigation Based on the Shipmaster’s Control of Ship Navigational Parameters When Sailing in Different Sea State Conditions. Appl. Sci. 2023, 13, 4486. [Google Scholar] [CrossRef]
- Du, W.; Li, Y.; Zhang, G.; Wang, C.; Chen, P.; Qiao, J. Estimation of ship routes considering weather and constraints. Ocean Eng. 2021, 228, 108695. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, X.; Wang, G.; Wang, Q.; Feng, K. Weather Route Optimization Method of Unmanned Ship Based on Continuous Dynamic Optimal Control. Sustainability 2022, 14, 2165. [Google Scholar] [CrossRef]
- Wang, H.; Mao, W.; Eriksson, L. A Three-Dimensional Dijkstra’s algorithm for multi-objective ship voyage optimization. Ocean Eng. 2019, 186, 106131. [Google Scholar] [CrossRef]
- Hagiwara, H.; Spaans, J.A. Practical Weather Routing of Sail-assisted Motor Vessels. J. Navig. 1987, 40, 96–119. [Google Scholar] [CrossRef]
- Spaans, J.A.; Stoter, P.H. New developments in ship weather routing. Navigation 1995, 43, 95–106. [Google Scholar]
- Bijlsma, S.J. On the Applications of Optimal Control Theory and Dynamic Programming in Ship Routing. Navigation 2002, 49, 71–80. [Google Scholar] [CrossRef]
- Padhy, C.; Sen, D.; Bhaskaran, P. Application of wave model for weather routing of ships in the North Indian Ocean. Nat. Hazards 2008, 44, 373–385. [Google Scholar] [CrossRef]
- Szlapczynska, J.; Smierzchalski, R. Multicriteria Optimisation in Weather Routing. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2009, 3, 393–400. [Google Scholar] [CrossRef]
- Maki, A.; Akimoto, Y.; Nagata, Y.; Kobayashi, S.; Kobayashi, E.; Shiotani, S.; Ohsawa, T.; Umeda, N. A new weather-routing system that accounts for ship stability based on a real-coded genetic algorithm. J. Mar. Sci. Technol. 2011, 16, 311–322. [Google Scholar] [CrossRef]
- Lin, Y.H.; Fang, M.C.; Yeung, R.W. The optimization of ship weather-routing algorithm based on the composite influence of multi-dynamic elements. Appl. Ocean Res. 2013, 43, 184–194. [Google Scholar] [CrossRef]
- Kytariolou, A.; Themelis, N. Optimized Route Planning under the Effect of Hull and Propeller Fouling and Considering Ocean Currents. J. Mar. Sci. Eng. 2023, 11, 828. [Google Scholar] [CrossRef]
- Zis, T.P.; Psaraftis, H.N.; Ding, L. Ship weather routing: A taxonomy and survey. Ocean Eng. 2020, 213, 107697. [Google Scholar] [CrossRef]
- Li, Y.; Cui, J.; Zhang, X.; Yang, X. A Ship Route Planning Method under the Sailing Time Constraint. J. Mar. Sci. Eng. 2023, 11, 1242. [Google Scholar] [CrossRef]
- Jia, H.; Yang, Y.; An, J.; Fu, R. A Ship Trajectory Prediction Model Based on Attention-BILSTM Optimized by the Whale Optimization Algorithm. Appl. Sci. 2023, 13, 4907. [Google Scholar] [CrossRef]
- Mao, W.; Rychlik, I.; Wallin, J.; Storhaug, G. Statistical models for the speed prediction of a container ship. Ocean Eng. 2016, 126, 152–162. [Google Scholar] [CrossRef]
- Veneti, A.; Makrygiorgos, A.; Konstantopoulos, C.; Pantziou, G.; Vetsikas, I.A. Minimizing the fuel consumption and the risk in maritime transportation: A bi-objective weather routing approach. Comput. Oper. Res. 2017, 88, 220–236. [Google Scholar] [CrossRef]
- Szlapczynska, J. Multiobjective Approach to Weather Routing. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2007, 1, 273–278. [Google Scholar]
- Hinnenthal, J.; Clauss, G. Robust Pareto-optimum routing of ships utilising deterministic and ensemble weather forecasts. Ships Offshore Struct. 2010, 5, 105–114. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, Y.; Zhang, Z.; Wang, H. Multicriteria Ship Route Planning Method Based on Improved Particle Swarm Optimization—Genetic Algorithm. J. Mar. Sci. Eng. 2021, 9, 357. [Google Scholar] [CrossRef]
- Zhao, S.; Zhao, S. Ship Global Traveling Path Optimization via a Novel Non-Dominated Sorting Genetic Algorithm. J. Mar. Sci. Eng. 2024, 12, 485. [Google Scholar] [CrossRef]
- Larrañaga, P.; Lozano, J.A. (Eds.) Estimation of Distribution Algorithms: A New Tool for Evolutionary Computation, 2nd ed.; Springer: New York, NY, USA, 2012. [Google Scholar]
- Li, Y.; Yang, Q.; Gao, X.D.; Lu, Z.Y.; Zhang, J. A layered learning estimation of distribution algorithm. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Boston, MA, USA, 9–13 July 2022; pp. 399–402. [Google Scholar] [CrossRef]
- Ceberio, J.; Irurozki, E.; Mendiburu, A.; Lozano, J.A. A review on estimation of distribution algorithms in permutation-based combinatorial optimization problems. Prog. Artif. Intell. 2012, 1, 103–117. [Google Scholar] [CrossRef]
- Krejca, M.S. Theoretical Analyses of Univariate Estimation-of-Distribution Algorithms. Ph.D. Thesis, University of Potsdam, Potsdam, Germany, 2019. [Google Scholar] [CrossRef]
- Yang, Q.; Chen, W.N.; Zhang, J. Probabilistic Multimodal Optimization. In Metaheuristics for Finding Multiple Solutions; Preuss, M., Epitropakis, M.G., Li, X., Fieldsend, J.E., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 191–228. [Google Scholar] [CrossRef]
- Grahl, J.; Bosman, P.A.; Rothlauf, F. The correlation-triggered adaptive variance scaling IDEA. In Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation, New York, NY, USA, 8–12 July 2006; pp. 397–404. [Google Scholar] [CrossRef]
- Bosman, P.A.N.; Grahl, J.; Rothlauf, F. SDR: A better trigger for adaptive variance scaling in normal EDAs. In Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation, New York, NY, USA, 7–11 July 2007; pp. 492–499. [Google Scholar] [CrossRef]
- Cai, Y.; Sun, X.; Xu, H.; Jia, P. Cross entropy and adaptive variance scaling in continuous EDA. In Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation, New York, NY, USA, 7–11 July 2007; pp. 609–616. [Google Scholar] [CrossRef]
- Yang, P.; Tang, K.; Lu, X. Improving Estimation of Distribution Algorithm on Multimodal Problems by Detecting Promising Areas. IEEE Trans. Cybern. 2015, 45, 1438–1449. [Google Scholar] [CrossRef]
- Huang, S.; Jiang, H. Multimodal estimation of distribution algorithm based on cooperative clustering strategy. In Proceedings of the 2018 Chinese Control And Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 5297–5302. [Google Scholar] [CrossRef]
- Khan, N. Bayesian Optimization Algorithms for Multiobjective and Hierarchically Difficult Problems. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Urbana, IL, USA, 2003. [Google Scholar]
- Laumanns, M.; Ocenasek, J. Bayesian optimization algorithms for multi-objective optimization. In Proceedings of the 7th International Conference on Parallel Problem Solving from Nature, Granada, Spain, 7–11 September 2002; Springer: Berlin/Heidelberg, Germany, 2002; pp. 298–307. [Google Scholar]
- Pelikan, M.; Sastry, K.; Goldberg, D.E. Multiobjective Estimation of Distribution Algorithms. In Scalable Optimization via Probabilistic Modeling; Pelikan, M., Sastry, K., CantúPaz, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 223–248. [Google Scholar] [CrossRef]
- Karshenas, H.; Santana, R.; Bielza, C.; Larrañaga, P. Multiobjective Estimation of Distribution Algorithm Based on Joint Modeling of Objectives and Variables. IEEE Trans. Evol. Comput. 2014, 18, 519–542. [Google Scholar] [CrossRef]
- Jiang, M.; Qiu, L.; Huang, Z.; Yen, G.G. Dynamic Multi-Objective Estimation of Distribution Algorithm Based on Domain Adaptation and Nonparametric Estimation. Inf. Sci. 2018, 435, 203–223. [Google Scholar] [CrossRef]
- Botello-Aceves, S.; Hernandez-Aguirre, A.; Valdez, S.I. The Directed Multi-Objective Estimation Distribution Algorithm (D-MOEDA). Math. Comput. Simul. 2023, 214, 334–351. [Google Scholar] [CrossRef]
- Yang, P.; Tang, K.; Lozano, J.A. Estimation of Distribution Algorithms based Unmanned Aerial Vehicle path planner using a new coordinate system. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; pp. 1469–1476. [Google Scholar] [CrossRef]
- Shirazi, A. Adaptive Estimation of Distribution Algorithms for Low-Thrust Trajectory Optimization. J. Spacecr. Rocket. 2023, 60, 1–12. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, J.; Tsang, E.; Ford, J. Estimation of Distribution Algorithm with 2-opt Local Search for the Quadratic Assignment Problem. In Towards a New Evolutionary Computation: Advances in the Estimation of Distribution Algorithms; Lozano, J.A., Larrañaga, P., Inza, I., Bengoetxea, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 281–292. [Google Scholar] [CrossRef]
- Jarboui, B.; Eddaly, M.; Siarry, P. An estimation of distribution algorithm for minimizing the total flowtime in permutation flowshop scheduling problems. Comput. Oper. Res. 2009, 36, 2638–2646. [Google Scholar] [CrossRef]
- Du, Y.; Li, J.Q.; Luo, C.; Meng, L.L. A hybrid estimation of distribution algorithm for distributed flexible job shop scheduling with crane transportations. Swarm Evol. Comput. 2021, 62, 100861. [Google Scholar] [CrossRef]
- Dębski, R.; Dreżewski, R. Surrogate-Assisted Ship Route Optimisation. In Proceedings of the International Conference on Computational Science, Prague, Czech Republic, 3–5 July 2023; Springer: Cham, Switzerland, 2023; pp. 395–409. [Google Scholar] [CrossRef]
- Bezanson, J.; Edelman, A.; Karpinski, S.; Shah, V.B. Julia: A fresh approach to numerical computing. SIAM Rev. 2017, 59, 65–98. [Google Scholar] [CrossRef]
- Audet, C.; Bigeon, J.; Cartier, D.; Le Digabel, S.; Salomon, L. Performance indicators in multiobjective optimization. Eur. J. Oper. Res. 2021, 292, 397–422. [Google Scholar] [CrossRef]
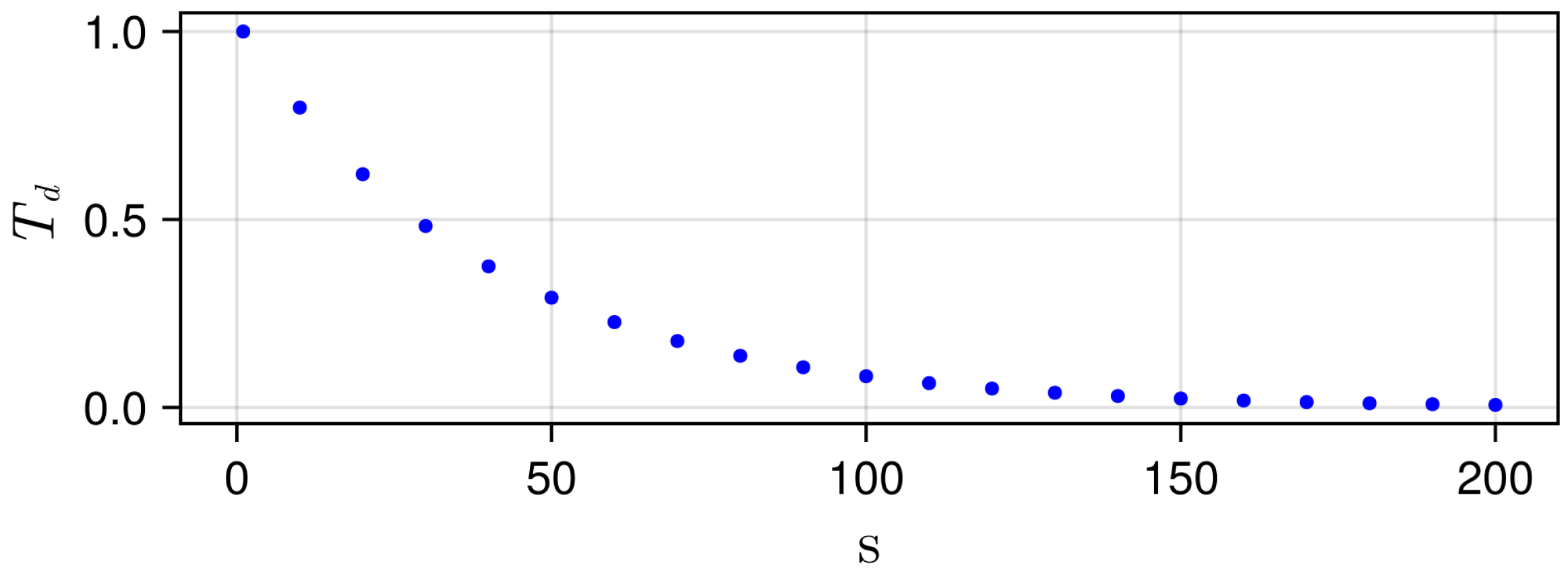
| Problem | EDA Only (E) | EDA + Local Search () | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 76 | 0.326 | 12.11 | 27.71 | 31.86 | 512 | 1 | 10.31 | 20.68 | 27.84 | 574 | 207 | 15 | 25 | 13 | |||
| 89 | 0.345 | 12.47 | 26.43 | 31.28 | 907 | 1 | 10.43 | 19.77 | 27.10 | 919 | 190 | 16 | 25 | 13 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dębski, R.; Dreżewski, R. Multi-Objective Ship Route Optimisation Using Estimation of Distribution Algorithm. Appl. Sci. 2024, 14, 5919. https://doi.org/10.3390/app14135919
Dębski R, Dreżewski R. Multi-Objective Ship Route Optimisation Using Estimation of Distribution Algorithm. Applied Sciences. 2024; 14(13):5919. https://doi.org/10.3390/app14135919
Chicago/Turabian StyleDębski, Roman, and Rafał Dreżewski. 2024. "Multi-Objective Ship Route Optimisation Using Estimation of Distribution Algorithm" Applied Sciences 14, no. 13: 5919. https://doi.org/10.3390/app14135919
APA StyleDębski, R., & Dreżewski, R. (2024). Multi-Objective Ship Route Optimisation Using Estimation of Distribution Algorithm. Applied Sciences, 14(13), 5919. https://doi.org/10.3390/app14135919







