Fuzzy Classification of the Maturity of the Orange (Citrus × sinensis) Using the Citrus Color Index (CCI)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Samples
2.2. Refractometer
2.3. Fruit Penetrometer
2.4. General Structure of Computer Vision System
2.5. Image Acquisition, Capture, and Segmentation
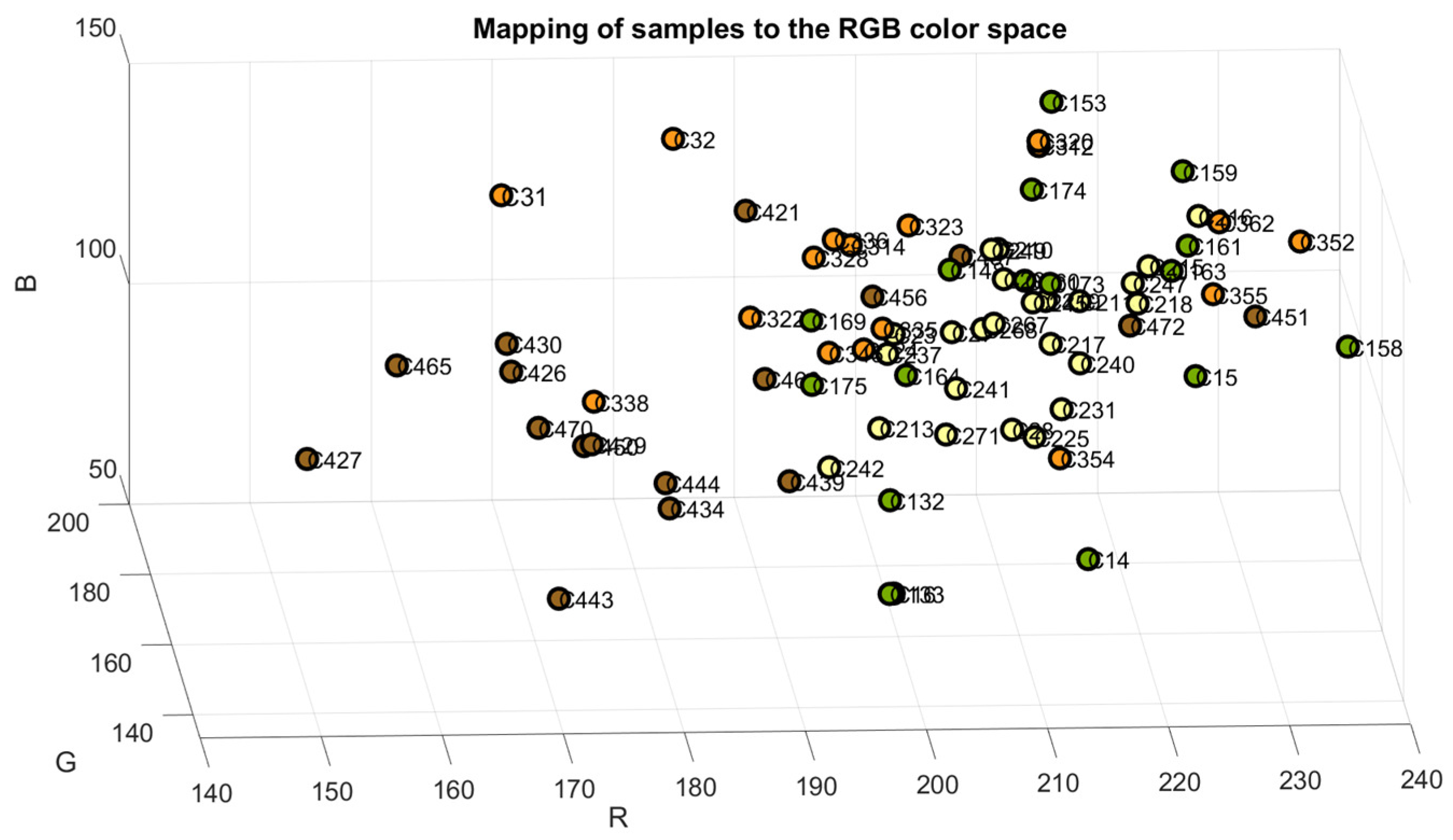
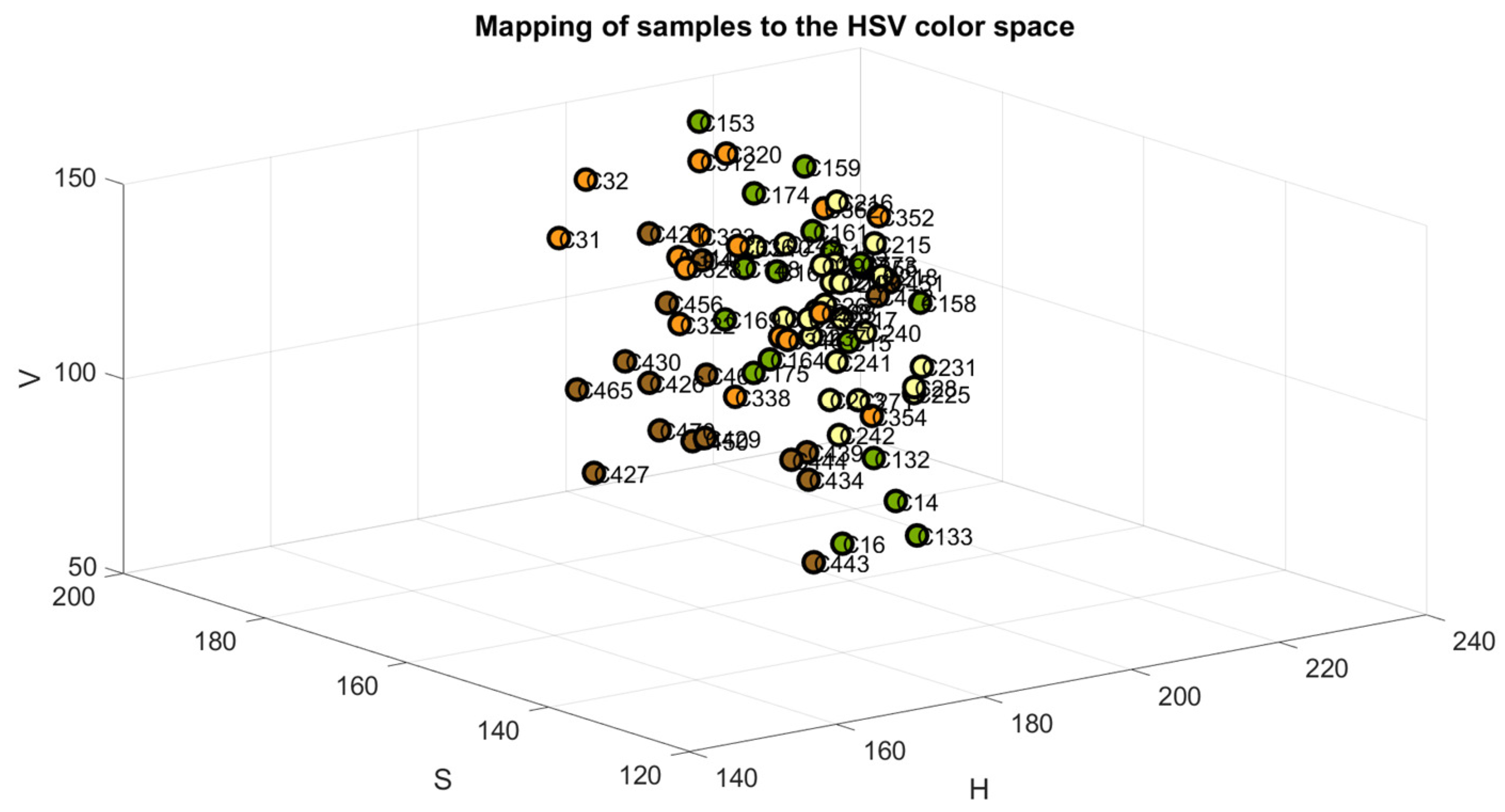
2.6. Citrus Color Index (CII) Extraction
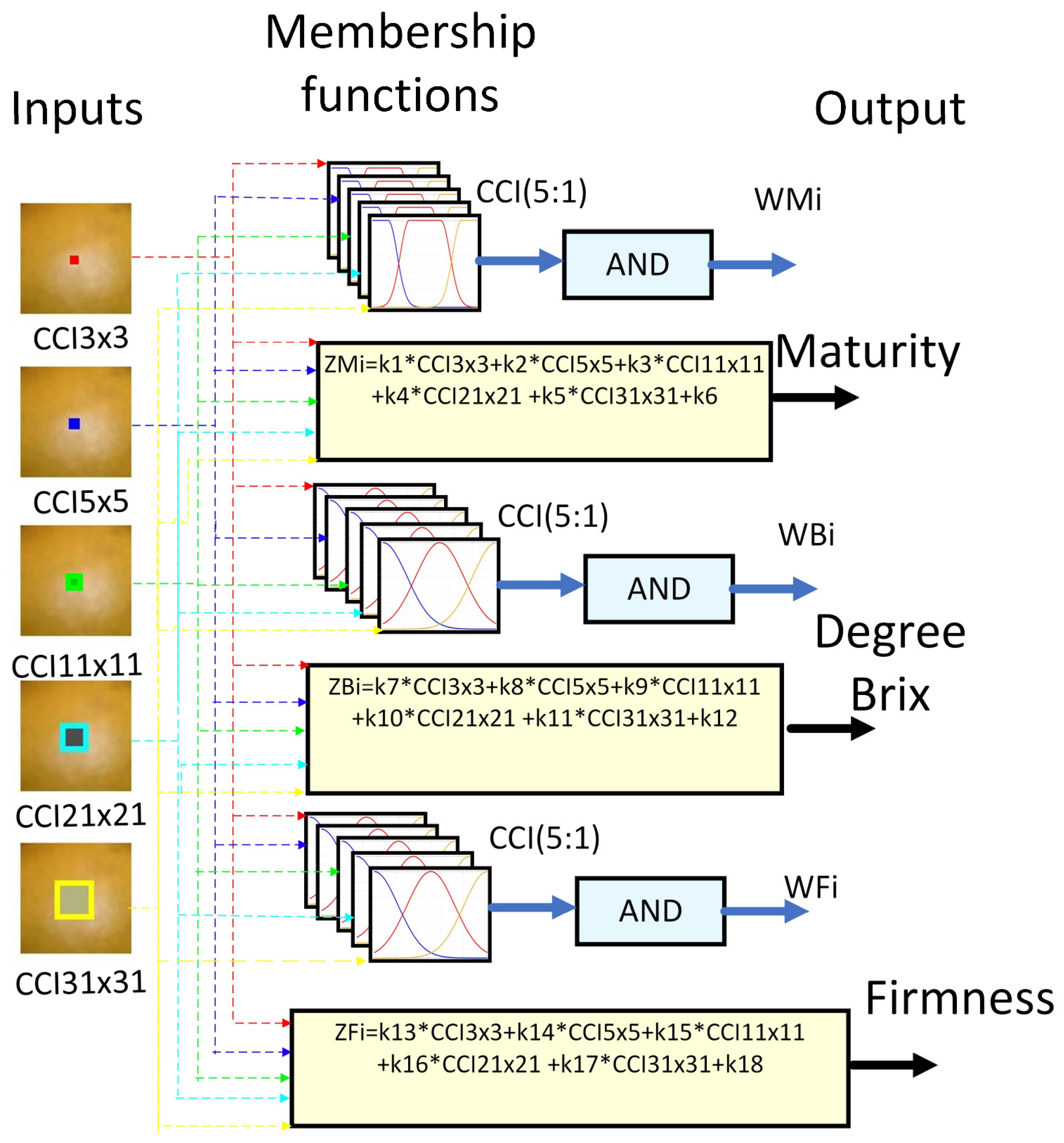
2.7. Fuzzy Estimator
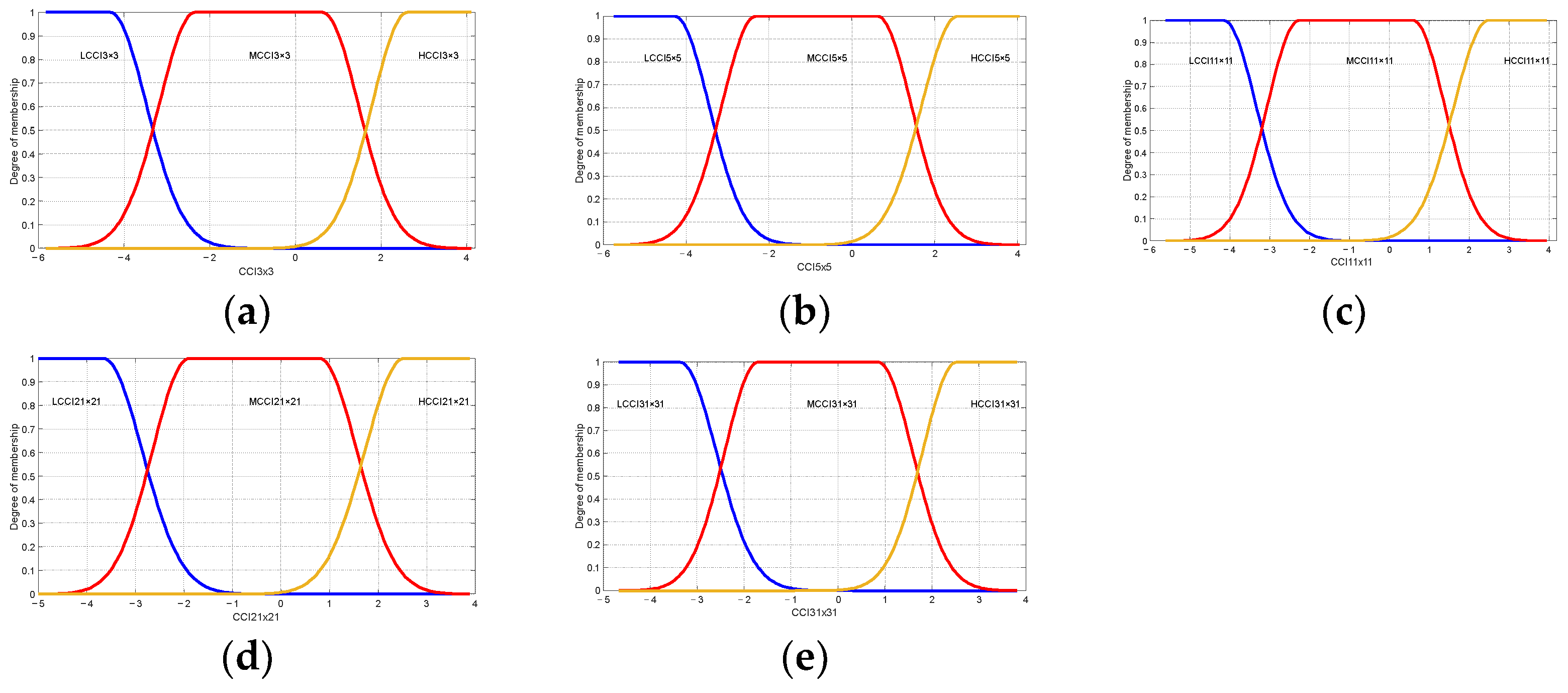
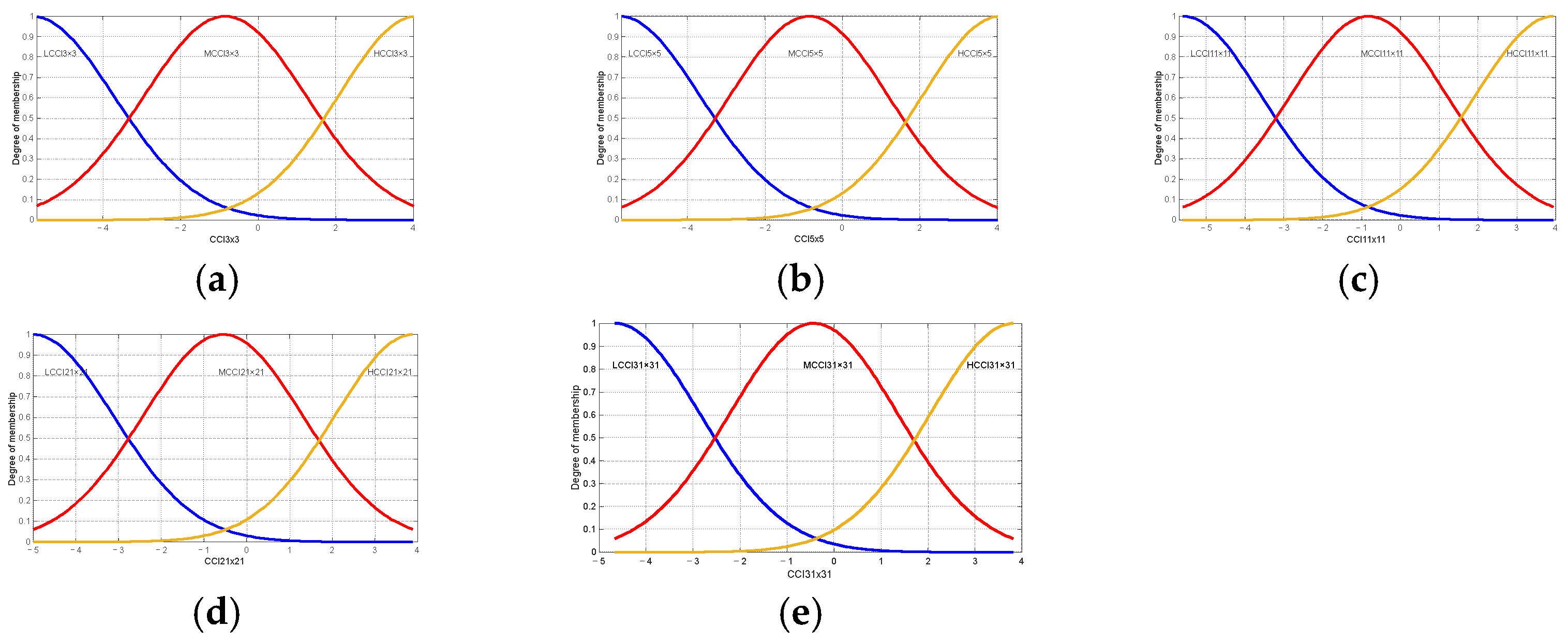
2.8. Fuzzification
- Inference
- If (CCI 3 × 3 is LCCI 3 × 3) and (CCI 5 × 5 is LCCI 5 × 5) and (CCI 11 × 11 is LCCI 11 × 11) and (CCI 21 × 21 is LCCI 21 × 21) and (CCI 31 × 31 is LCCI 31 × 31) then (Maturity is WMi).
- If (CCI 3 × 3 is LCCI 3 × 3) and (CCI 5 × 5 is LCCI 5 × 5) and (CCI 11 × 11 is LCCI 11 × 11) and (CCI 21 × 21 is LCCI 21 × 21) and (CCI 31 × 31 is LCCI 31 × 31) then (Brix is WBi).
- If (CCI 3 × 3 is LCCI 3 × 3) and (CCI 5 × 5 is LCCI 5 × 5) and (CCI 11 × 11 is LCCI 11 × 11) and (CCI 21 × 21 is LCCI 21 × 21) and (CCI 31 × 31 is LCCI 31 × 31) then (Firmness is WFi).
2.9. Defuzzification
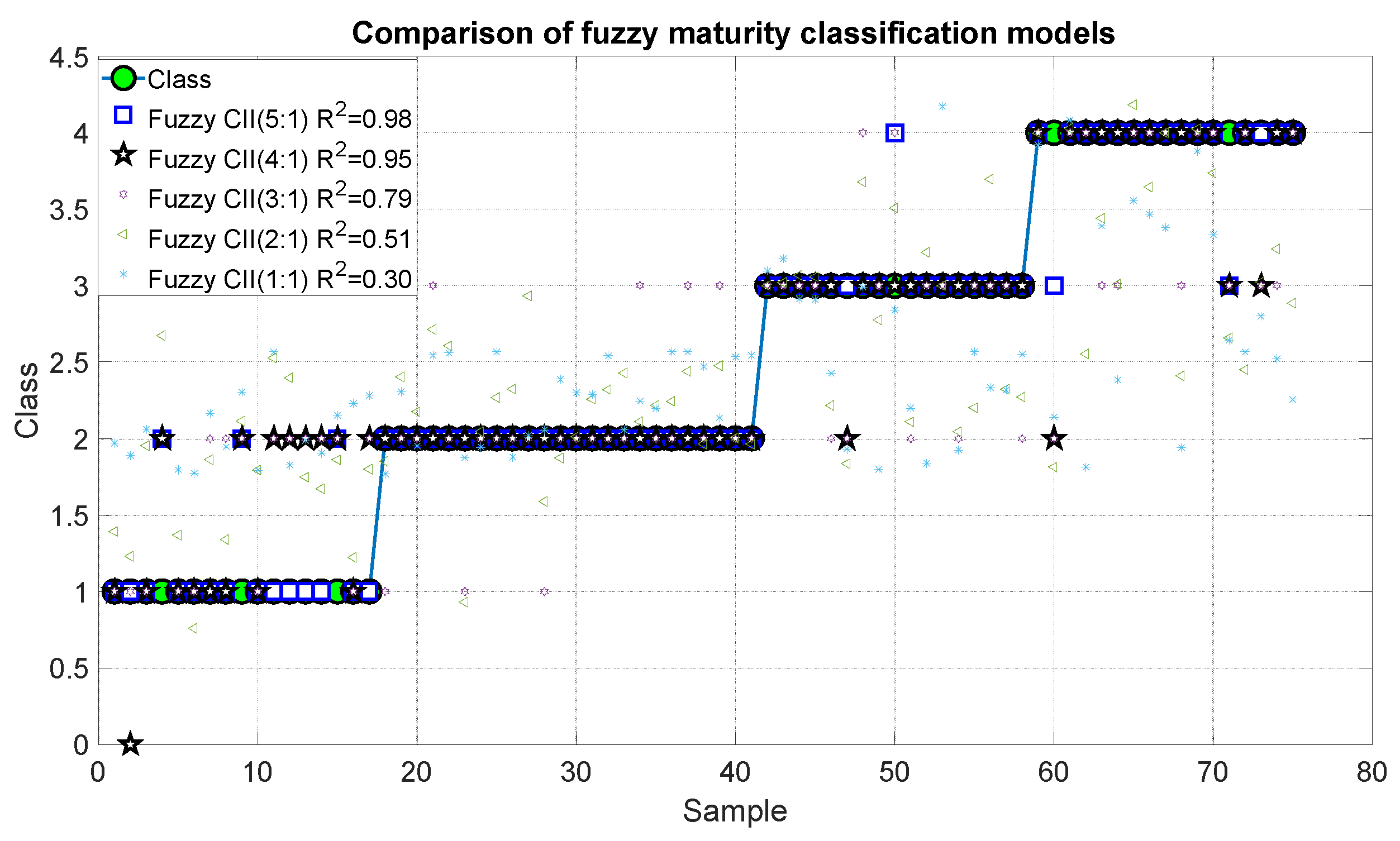
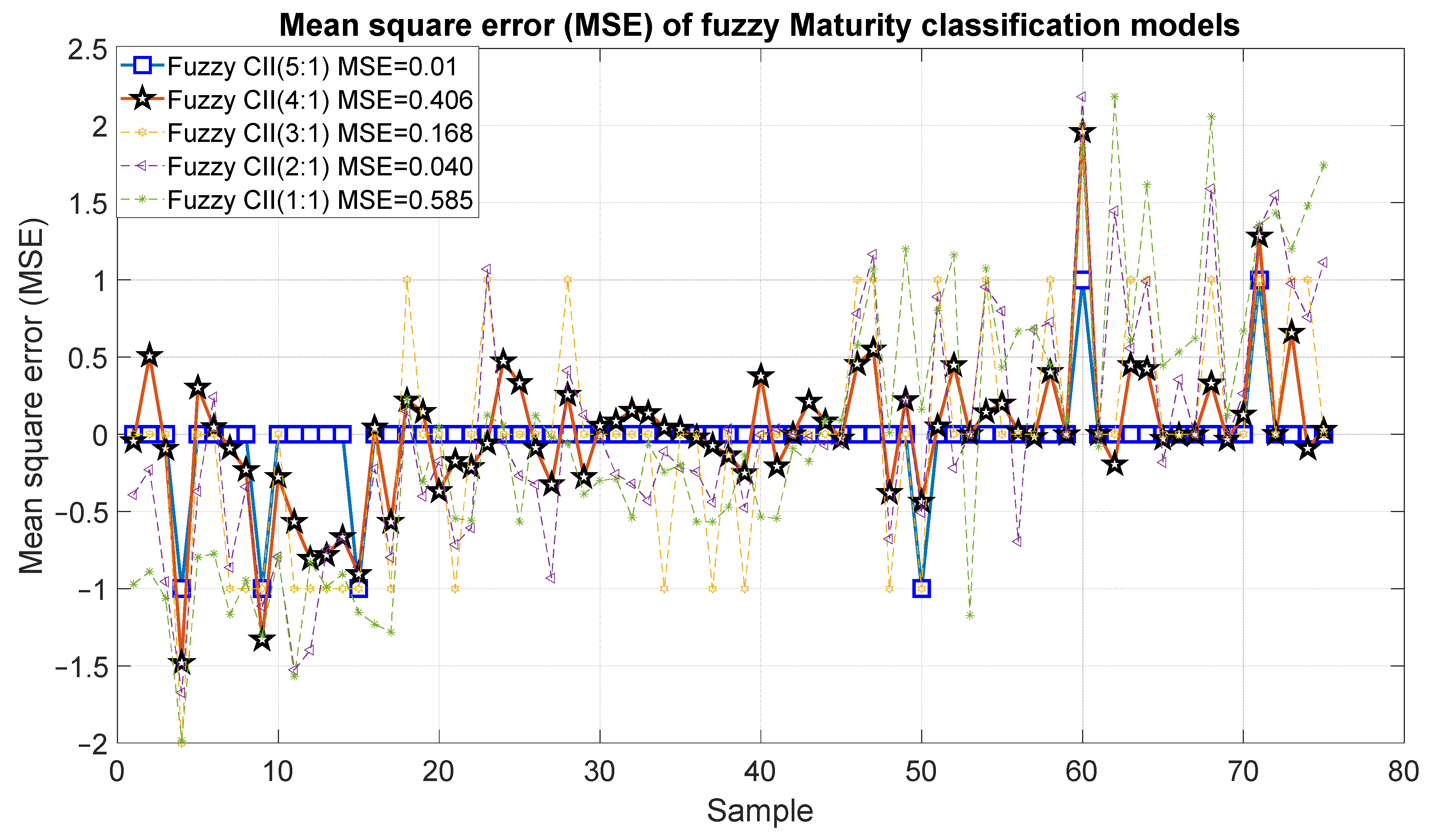
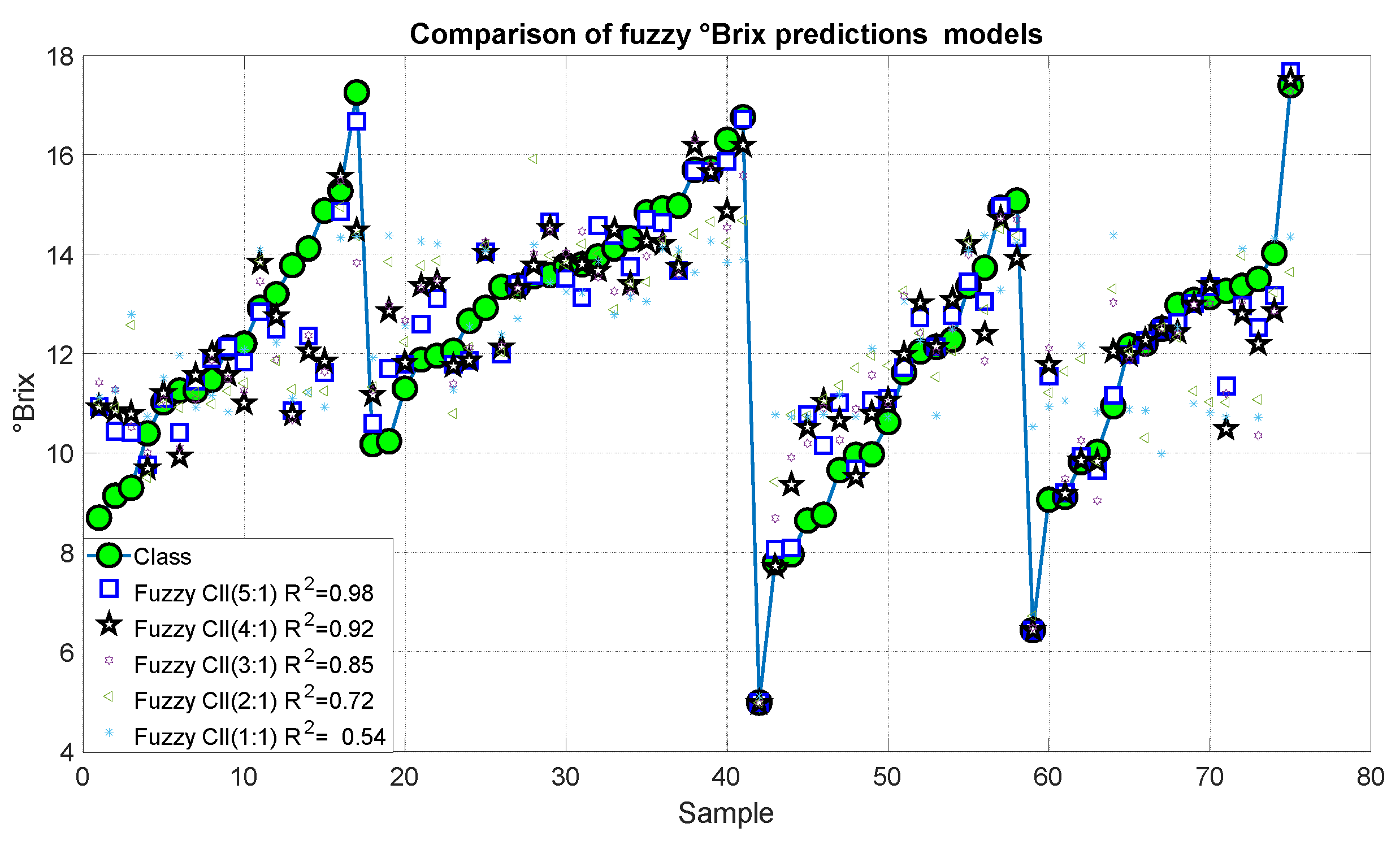
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Available online: https://www.fao.org/faostat/en/#home (accessed on 4 March 2024).
- Teixeira, F.; dos Santos, B.A.; Nunes, G.; Soares, J.M.; Amaral, L.A.D.; de Souza, G.H.O.; de Resende, J.T.V.; Menegassi, B.; Rafacho, B.P.M.; Schwarz, K.; et al. Addition of Orange Peel in Orange Jam: Evaluation of Sensory, Physicochemical, and Nutritional Characteristics. Molecules 2020, 25, 1670. [Google Scholar] [CrossRef]
- Mak, K.K.; Tan, J.J.; Marappan, P.; Balijepalli, M.K.; Choudhury, H.; Ramamurthy, S.; Pichika, M.R. Galangin’s Potential as a Functional Food Ingredient. J. Funct. Foods 2018, 46, 490–503. [Google Scholar] [CrossRef]
- de Castro, L.A.; Lizi, J.M.; das Chagas, E.G.L.; de Carvalho, R.A.; Vanin, F.M. From Orange Juice By-Product in the Food Industry to a Functional Ingredient: Application in the Circular Economy. Foods 2020, 9, 593. [Google Scholar] [CrossRef] [PubMed]
- Mahajan, M.; Sadana, R. Citrus Based Food Products and Their Shelf Life. In vBook Recent Advances in Citrus Fruits, 1st ed.; Singh, S., Punia, S., Eds.; Recent Advances in Citrus Fruits; Springer: Cham, Switzerland; Berlin/Heidelberg, Germany, 2023; pp. 367–393. [Google Scholar]
- Mahajan, M.; Sadana, R.; Ayala, J.R.; Montero, G.; Coronado, M.A.; García, C.; Curiel-Alvarez, M.A.; León, J.A.; Sagaste, C.A.; Montes, D.G. Characterization of Orange Peel Waste and Valorization to Obtain Reducing Sugars. Molecules 2021, 26, 1348. [Google Scholar] [CrossRef]
- Escobedo-Avellaneda, Z.; Gutiérrez-Uribe, J.; Valdez-Fragoso, A.; Torres, J.A.; Welti-Chanes, J. Phytochemicals and antioxidant activity of juice, flavedo, albedo and comminuted orange. J. Funct. Foods 2014, 6, 470–481. [Google Scholar] [CrossRef]
- Chen, X.; Tait, A.R.; Kitts, D.D. Flavonoid composition of orange peel and its association with antioxidant and anti-inflammatory activities. Food Chem. 2017, 218, 15–21. [Google Scholar] [CrossRef] [PubMed]
- Kowalska, M.; Konopska, J.; Feszterová, M.; Zbikowska, A.; Kowalska, B. Quality Assessment of Natural Juices and Consumer Preferences in the Range of Citrus Fruit Juices. Appl. Sci. 2023, 13, 765. [Google Scholar] [CrossRef]
- Yang, C.; Chen, H.; Chen, H.; Zhong, B.; Luo, X.; Chun, J. Antioxidant and Anticancer Activities of Essential Oil from Gannan Navel Orange Peel. Molecule 2017, 22, 1391. [Google Scholar] [CrossRef]
- Al-Dairi, M.; Pathare, P.B.; Al-Mahdouri, A. Effect of storage conditions on postharvest quality of tomatoes: A case study at market-level. J. Agric. Marine Sci. 2021, 26, 13–20. [Google Scholar]
- Campbell, B.L.; Nelson, R.G.; Ebel, C.E.; Dozier, W.A.; Adrian, J.L.; Hockema, B.R. Fruit quality characteristics that affect consumer preferences for satsuma mandarins. HortScience 2004, 39, 1664–4669. [Google Scholar] [CrossRef]
- Barrett, D.M.; Beaulieu, J.C.; Shewfelt, R.; Barrett, D.M.; Beaulieu, J.C.; Color, R.S.; Barrett, D.M.; Beaulieu, J.C.; Shewfelt, R.O.B. Color, Flavor, Texture, and Nutritional Quality of Fresh-Cut Fruits and Vegetables: Desirable Levels, Instrumental and Sensory Measurement, and the Effects of Processing Nutritional Quality of Fresh-Cut Fruits and Vegetables: Desirable Levels, Instrumenta. Crit. Rev. Food Sci. Nutr. 2010, 50, 369–389. [Google Scholar] [CrossRef]
- Pathare, P.B.; Opara, U.L.; Al-Said, F.A. Colour measurement and analysis in fresh and processed foods: A review. Food Bioprocess Technol. 2013, 6, 36–60. [Google Scholar] [CrossRef]
- Fashi, M.; Naderloo, L.; Javadikia, H. The relationship between the appearance of pomegranate fruit and color and size of arils based on image processing. Postharvest Biol. Technol. 2019, 154, 52–57. [Google Scholar] [CrossRef]
- Castro, W.; Oblitas, J.; De-La-Torre, M.; Cotrina, C.; Bazán, K.; Avila-George, H. Classification of Cape Gooseberry Fruit According to its Level of Ripeness Using Machine Learning Techniques and Different Color Spaces. IEEE Access 2019, 7, 27389–27400. [Google Scholar] [CrossRef]
- Mariod, A.A. Effect of essential oils on organoleptic (smell, taste, and texture) properties of food. In Essential Oils in Food Preservation, Flavor and Safety, 1st ed.; Preedy, V.R., Ed.; Academic Press: London, UK, 2016; pp. 131–137. [Google Scholar]
- Choi, K.-O.; Hur, Y.Y.; Park, S.J.; Lee, D.H.; Kim, S.J.; Im, D. Relationships between Instrumental and Sensory Quality Indices of Shine Muscat Grapes with Different Harvesting Times. Foods 2022, 11, 2482. [Google Scholar] [CrossRef]
- Cui, J.; Zhao, C.; Feng, L.; Han, Y.; Du, H.; Xiao, H.; Zheng, J. Pectins from fruits: Relationships between extraction methods, structural characteristics, and functional properties. Trends Food Sci. Technol. 2021, 110, 39–54. [Google Scholar] [CrossRef]
- Saini, R.K.; Ranjit, A.; Sharma, K.; Prasad, P.; Shang, X.; Gowda, K.G.M.; Keum, Y.-S. Bioactive Compounds of Citrus Fruits: A Review of Composition and Health Benefits of Carotenoids, Flavonoids, Limonoids, and Terpenes. Antioxidants 2022, 11, 239. [Google Scholar] [CrossRef]
- Villaseñor-Aguilar, M.-J.; Padilla-Medina, J.-A.; Prado-Olivarez, J.; Botello-Álvarez, J.-E.; Bravo-Sánchez, M.-G.; Barranco-Gutiérrez, A.-I. Low-Cost Sensor for Lycopene Content Measurement in Tomato Based on Raspberry Pi 4. Plants 2023, 12, 2683. [Google Scholar] [CrossRef]
- Feng, L.; Xu, Y.; Xiao, Y.; Song, J.; Li, D.; Zhang, Z.; Liu, C.; Chunju, L.; Jiang, N.; Zhang, M.; et al. Effects of pre-drying treatments combined with explosion puffing drying on the physicochemical properties, antioxidant activities and flavor characteristics of apples. Food Chem. 2021, 338, 128015. [Google Scholar] [CrossRef]
- Harker, F.R.; Gunson, F.A.; Jaeger, S.R. The case for fruit quality: An interpretive review of consumer attitudes, and preferences for apples. Postharvest Biol. Technol. 2003, 28, 333–347. [Google Scholar] [CrossRef]
- Ali, M.M.; Anwar, R.; Yousef, A.F.; Li, B.; Luvisi, A.; De Bellis, L.; Aprile, A.; Chen, F. Influence of Bagging on the Development and Quality of Fruits. Plants 2021, 10, 358. [Google Scholar] [CrossRef]
- Jaywant, S.A.; Singh, H.; Arif, K.M. Sensors and Instruments for Brix Measurement: A Review. Sensors 2022, 22, 2290. [Google Scholar] [CrossRef]
- Pupin, A.M.; Dennis, M.J.; Toledo, M.C.F. HPLC analysis of carotenoids in orange juice. Food Chem. 1999, 64, 269–275. [Google Scholar] [CrossRef]
- Omoba, O.S.; Obafaye, R.O.; Salawu, S.O.; Boligon, A.A.; Athayde, M.L. HPLC-DAD Phenolic Characterization and Antioxidant Activities of Ripe and Unripe Sweet Orange Peels. Antioxidants 2015, 4, 498–512. [Google Scholar] [CrossRef]
- Sabzi, S.; Javadikia, H.; Arribas, J.I. A three-variety automatic and non-intrusive computer vision system for the estimation of orange fruit pH value. Measurement 2020, 152, 107298. [Google Scholar] [CrossRef]
- Padda, M.S.; do Amarante, C.V.; Garcia, R.M.; Slaughter, D.C.; Mitcham, E.J. Methods to analyze physico-chemical changes during mango ripening: A multivariate approach. Postharvest Biol. Technol. 2011, 62, 267–274. [Google Scholar] [CrossRef]
- Wagare, D.S.; Shirsath, S.E.; Shaikh, M.; Netankar, P. Sustainable solvents in chemical synthesis: A review. Environ. Chem. Lett. 2021, 19, 3263–3282. [Google Scholar] [CrossRef]
- Wu, C.; Xiao, H.J.; Wang, S.W.; Tang, M.S.; Tang, Z.L.; Xia, W.; Li, W.F.; Cao, Z.; He, W.M. Natural deep eutectic solvent-catalyzed selenocyanation of activated alkynes via an intermolecular H-bonding activation process. ACS Sustain. Chem. Eng. 2019, 7, 2169–2175. [Google Scholar] [CrossRef]
- Villaseñor-Aguilar, M.J.; Botello-Álvarez, J.E.; Pérez-Pinal, F.J.; Cano-Lara, M.; León-Galván, M.F.; Bravo-Sánchez, M.G.; Barranco-Gutierrez, A.I. Fuzzy classification of the maturity of the tomato using a vision system. J. Sens. 2019, 2019, 3175848. [Google Scholar] [CrossRef]
- Constante, P.; Gordon, A.; Chang, O.; Pruna, E.; Acuna, F.; Escobar, I. Artificial Vision Techniques to Optimize Strawberrys Industrial Classification. IEEE Lat. Am. Trans. 2016, 14, 2576–2581. [Google Scholar] [CrossRef]
- Villaseñor-Aguilar, M.-J.; Bravo-Sánchez, M.-G.; Padilla-Medina, J.-A.; Vázquez-Vera, J.L.; Guevara-González, R.-G.; García-Rodríguez, F.-J.; Barranco-Gutiérrez, A.-I. A Maturity Estimation of Bell Pepper (Capsicum annuum L.) by Artificial Vision System for Quality Control. Appl. Sci. 2020, 10, 5097. [Google Scholar] [CrossRef]
- Al-Sammarraie, M.A.J.; Gierz, Ł.; Przybył, K.; Koszela, K.; Szychta, M.; Brzykcy, J.; Baranowska, H.M. Predicting Fruit’s Sweetness Using Artificial Intelligence—Case Study: Orange. Appl. Sci. 2022, 12, 8233. [Google Scholar] [CrossRef]
- Muhammad Zahir, S.A.; Yahaya, O.K.; Omar, A.F. Correlating the natural color of tropical fruit juice with its pH. Color Res. Appl. 2021, 46, 467–476. [Google Scholar] [CrossRef]
- Wu, D.; Sun, D.W. Colour measurements by computer vision for food quality control—A review. Trends Food Sci. Technol. 2013, 29, 5–20. [Google Scholar] [CrossRef]
- Tarancón, P.; Cebrián, B.; Fernández-Serrano, P.; Besada, C. Relation between Rind Pigmentation and Internal Quality of Blood Orange ‘Sanguinelli’: Physicochemical and Sensory Studies. Horticulturae 2022, 8, 448. [Google Scholar] [CrossRef]
- Habibi, F.; Guillén, F.; Serrano, M.; Valero, D. Physicochemical Changes, Peel Colour, and Juice Attributes of Blood Orange Cultivars Stored at Different Temperatures. Horticulturae 2021, 7, 320. [Google Scholar] [CrossRef]
- Dongare, M.; Buchade, P.; Shaligram, A. Refractive index based optical Brix measurement technique with equilateral angle prism for sugar and Allied Industries. Optik 2015, 126, 2383–2385. [Google Scholar] [CrossRef]
- Ugwu, K.; Mbajiorgu, C.; Okonkwo, W.; Ani, A. Design, fabrication and performance evaluation of a portable hand-held refractometer.Niger. J. Technol. 2018, 37, 537–542. [Google Scholar]
- Altemimi, A.B.; Al-Hilphy, A.R.S.; Abedelmaksoud, T.G.; Aboud, S.A.; Badwaik, L.S.; G, L.; Noore, S.; Pratap-Singh, A. Infrared Radiation Favorably Influences the Quality Characteristics of Key Lime Juice. Appl. Sci. 2021, 11, 2842. [Google Scholar] [CrossRef]
- Rungpichayapichet, P.; Nagle, M.; Yuwanbun, P.; Khuwijitjaru, P.; Mahayothee, B.; Müller, J. Prediction mapping of physicochemical properties in mango by hyperspectral imaging. Biosyst. Eng. 2017, 159, 109–120. [Google Scholar] [CrossRef]
- Cevher, E.Y.; Yıldırım, D. Using Artificial Neural Network Application in Modeling the Mechanical Properties of Loading Position and Storage Duration of Pear Fruit. Processes 2022, 10, 2245. [Google Scholar] [CrossRef]
- Domingues, A.R.; Marcolini, C.D.M.; Gonçalves, C.H.d.S.; Gonçalves, L.S.A.; Roberto, S.R.; Carlos, E.F. Fruit Ripening Development of Valencia Orange Trees Grafted on Different ‘Trifoliata’ Hybrid Rootstocks. Horticulturae 2021, 7, 3. [Google Scholar] [CrossRef]
- Wan, P.; Toudeshki, A.; Tan, H.; Ehsani, R. A methodology for fresh tomato maturity detection using computer vision. Comput. Electron. Agric. 2018, 146, 43–50. [Google Scholar] [CrossRef]
- Konar, A. Computational Intelligence: Principles, Techniques and Applications; Springer: Berlin/Heidelberg, Germany, 2005; ISBN 3-540-20898-4. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Li, P.; Li, S.; Du, G.; Jiang, L.; Liu, X.; Ding, S.; Shan, Y. A simple and nondestructive approach for the analysis of soluble solid content in citrus by using portable visible to near-infrared spectroscopy. Food Sci. Nutr. 2020, 8, 2543–2552. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Jin, G.; Jiang, X.; Yi, S.; Tian, X. Non-destructive determination of soluble solids content using a multi-region combination model in hybrid citrus. Infrared Phys. Technol. 2020, 104, 103138. [Google Scholar] [CrossRef]
- Olmo, M.; Nadas, A.; García, J.M. Nondestructive Methods to Evaluate Maturity Level of Oranges. Sens. Nutr. Qual. Food Nondestruct. 2000, 65, 365–369. [Google Scholar] [CrossRef]











| ROI (Pixels) | CCI | |||
|---|---|---|---|---|
Class 1 | Class 2 | Class 3 | Class 4 | |
| 3 × 3 | −3.25 | 0.406 | 2.59 | 3.68 |
| 5 × 5 | −3.30 | 0.461 | 2.58 | 3.67 |
| 11 × 11 | −3.32 | 0.534 | 2.62 | 3.83 |
| 21 × 21 | −3.22 | 0.6109 | 2.71 | 3.76 |
| 31 × 31 | −3.20 | 0.6250 | 2.745 | 3.79 |
| Input | Number of MF | Epochs | MSE | |
|---|---|---|---|---|
| ROI of CII | Triangle | |||
| Model 1 | 3 × 3 | 3 | 10 | 0.766 |
| Model 2 | 3 × 3, 5 × 5 | 6 | 10 | 0.705 |
| Model 3 | 3 × 3, 5 × 5, 11 × 11 | 9 | 10 | 0.623 |
| Model 4 | 3 × 3, 5 × 5, 11 × 11, 21 × 21 | 12 | 10 | 0.613 |
| Model 5 | 3 × 3, 5 × 5, 11 × 11, 21 × 21, 31 × 31 | 15 | 10 | 0.172 |
| Input | Number of MF | Epochs | MSE | |
|---|---|---|---|---|
| ROI of CII | Triangle | |||
| Model 6 | 3 × 3 | 3 | 10 | 1.738 |
| Model 7 | 3 × 3, 5 × 5 | 6 | 10 | 1.416 |
| Model 8 | 3 × 3, 5 × 5, 11 × 11 | 9 | 10 | 1.109 |
| Model 9 | 3 × 3, 5 × 5, 11 × 11, 21 × 21 | 12 | 10 | 0.582 |
| Model 10 | 3 × 3, 5 × 5, 11 × 11, 21 × 21, 31 × 31 | 15 | 10 | 0.293 |
| Input | Number of MF | Epochs | MSE | |
|---|---|---|---|---|
| ROI of CII | Triangle | |||
| Model 11 | 3 × 3 | 3 | 10 | 1.207 |
| Model 12 | 3 × 3, 5 × 5 | 6 | 10 | 1.021 |
| Model 13 | 3 × 3, 5 × 5, 11 × 11 | 9 | 10 | 0.888 |
| Model 14 | 3 × 3, 5 × 5, 11 × 11, 21 × 21 | 12 | 10 | 0.602 |
| Model 15 | 3 × 3, 5 × 5, 11 × 11, 21 × 21, 31 × 31 | 15 | 10 | 0.381 |
| MF | MSE | Coefficient of Determination (R²) | ||||
|---|---|---|---|---|---|---|
| Maturity | Degree Brix | Firmness | Maturity | Degree Brix | Firmness | |
| Trimf | 0.172 | 0.293 | 0.381 | 0.96 | 0.9881 | 0.91 |
| Trampmf | 0.405 | 0.872 | 0.614 | 0.80 | 0.89 | 0.81 |
| Gbellmf | 0.118 | 0.340 | 0.283 | 0.98 | 0.98 | 0.96 |
| Gaussmf | 0.132 | 0.289 | 0.319 | 0.97 | 0.98 | 0.95 |
| Gauss2mf | 0.100 | 0.423 | 0.250 | 0.98 | 0.97 | 0.97 |
| Gaussian2mf | ||
|---|---|---|
| Low | Medium | High |
| LCCI 3 × 3 = (0.842, −7.306, 0.845, −4.329) | MCCI 3 × 3 = (0.842, −2.344, 0.876, 0.647) | HCCI 3 × 3 = (0.846, 2.613, 0.842, 5.594) |
| LCCI 5 × 5 = (0.83, −7.219, 0.833, −4.278) | MCCI 5 × 5 = (0.832, −2.318, 0.827, 0.625) | HCCI 5 × 5 = (0.831, 2.583, 0.832, 5.522) |
| LCCI 11 × 11 = (0.810, −7.033, 0.810, −4.171) | MCCI 11 × 11 = (0.810, −2.262, 0.815, 0.607) | HCCI 11 × 11 = (0.805, 2.512, 0.810, 5.370) |
| LCCI 21 × 21 = (0.755, −6.347, 0.758, −3.677) | MCCI 21 × 21 = (0.755, −1.898, 0.829, 0.796) | HCCI 21 × 21 = (0.759, 2.548, 0.755, 5.221) |
| LCCI 31 × 31 = (0.720, −5.941, 0.720, −3.396) | MCCI 31 × 31 = (0.720, −1.700, 0.759, 0.861) | HCCI 31 × 31 = (0.725, 2.542, 0.720, 5.084) |
| Gaussian | ||
|---|---|---|
| Low | Medium | High |
| LCCI 3 × 3 = (2.108, −5.817) | MCCI 3 × 3 = (2.106, −0.844) | HCCI 3 × 3 = (2.084, 4.127) |
| LCCI 5 × 5 = (2.081, −5.748) | MCCI 5 × 5 = (2.058, −0.851) | HCCI 5 × 5 = (2.058, 4.068) |
| LCCI 11 × 11 = (2.026, −5.602) | MCCI 11 × 11 = (1.998, −0.827) | HCCI 11 × 11 = (1.997, 3.967) |
| LCCI 21 × 21 = (1.889, −5.012) | MCCI 21 × 21 = (1.892, −0.541) | HCCI 21 × 21 = (1.869, 3.914) |
| LCCI 31 × 31 = (1.801, −4.668) | MCCI 31 × 31 = (1.833, −0.395) | HCCI 31 × 31 = (1.778, 3.840) |
| Gaussian2mf | ||
|---|---|---|
| Low | Medium | High |
| LCCI 3 × 3 = (0.842, −7.306, 0.842, −4.329) | MCCI 3 × 3 = (0.842, −2.344, 0.822, 0.645) | HCCI 3 × 3 = (0.807, 2.654, 0.842, 5.594) |
| LCCI 5 × 5 = (0.832, −7.219, 0.832, −4.278) | MCCI 5 × 5 = (0.832, −2.318, 0.870, 0.644) | HCCI 5 × 5 = (0.831, 2.597, 0.832, 5.522) |
| LCCI 11 × 11 = (0.810, −7.033, 0.813, −4.170) | MCCI 11 × 11 = (0.810, −2.262, 0.908, 0.660) | HCCI 11 × 11 = (0.807, 2.490, 0.810, 5.370) |
| LCCI 21 × 21 = (0.755, −6.347, 0.774, −3.671) | MCCI 21 × 21 = (0.755, −1.898, 0.878, 0.821) | HCCI 21 × 21 = (0.764, 2.55, 0.755, 5.221) |
| LCCI 31 × 31 = (0.720, −5.941, 0.722, −3.395) | MCCI 31 × 31 = (0.720, −1.700, 0.720, 0.869) | HCCI 31 × 31 = (0.687, 2.558, 0.720, 5.084755) |
| Models | Technique | Input | Output | R2 | Error Mean Square (MSE) |
|---|---|---|---|---|---|
| Model 5 | Fuzzy | CCI(3 × 3), CCI(5 × 5), CCI(11 × 11), CCI(21 × 21), CCI(31 × 31) | Maturity | 0.98 | 0.01 |
| Model 10 | Fuzzy | CCI(3 × 3), CCI(5 × 5), CCI(11 × 11), CCI(21 × 21), CCI(31 × 31) | °Brix | 0.98 | 0.082 |
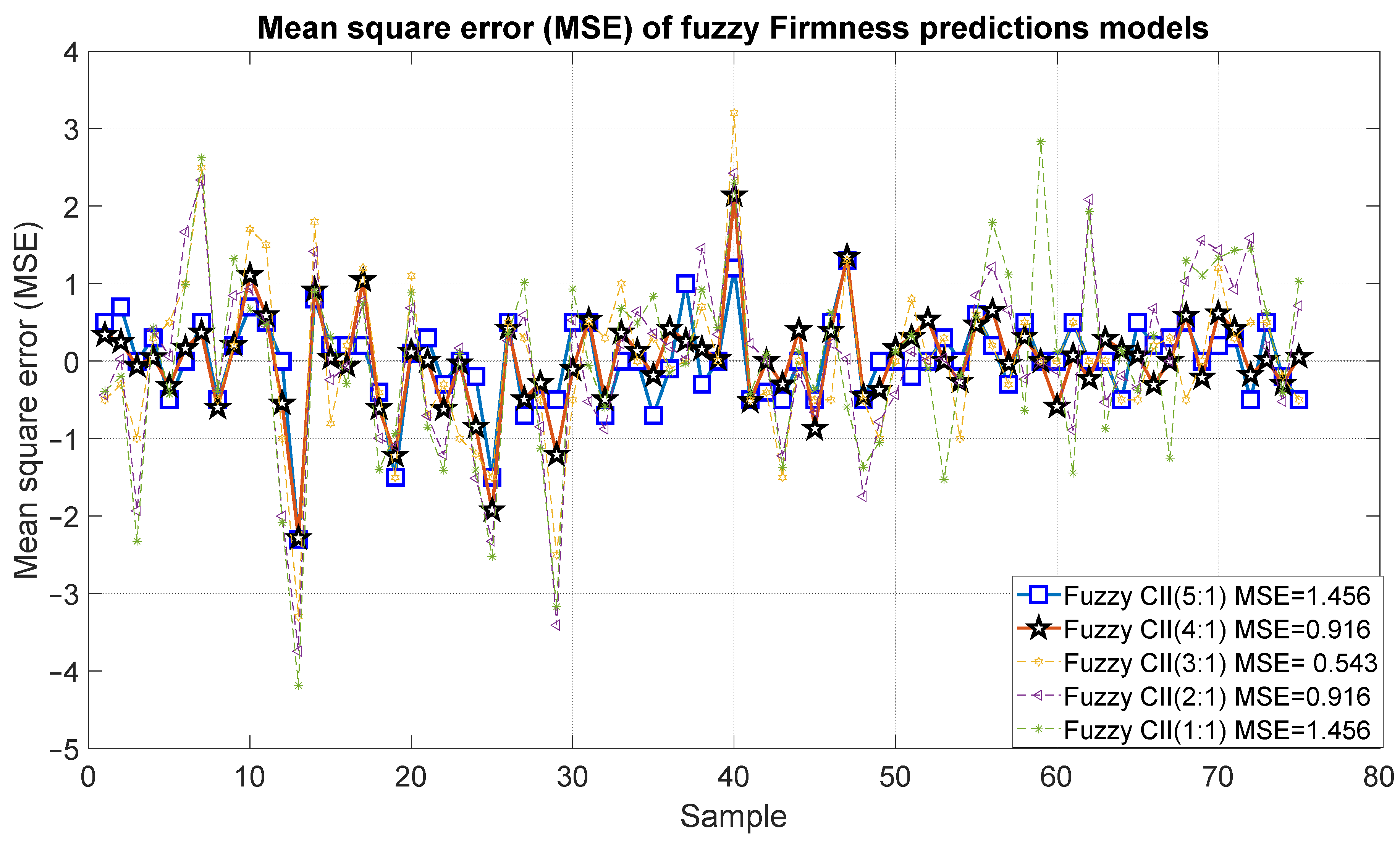
| Model 15 | Fuzzy | CCI(3 × 3), CCI(5 × 5), CCI(11 × 11), CCI(21 × 21), and CCI(31 × 31) | Firmness | 0.95 | 1.456 |
| Villaseñor-Aguilar et al. (2020) [34] | Artificial neuronal network fuzzy | GAROI, YAROI, OAROI, and RARO | Maturity °Brix Maturity °Brix | 1 0.6327 0.88 0.891 | 0 0.3888 - 0.484 |
| Li et al. (2020) [49] | SNV-VABPLS | Spectra | Total soluble solids (TSS) | 0.82 | 0.5764 |
| Li et al. (2020) [50] | Multi-region combination models | Spectra | Total soluble solids (TSS) | 0.8687 | 0.3445 |
| Olmo et al. (2000) [51] | Linear regression | Weight losses | Firmness | 0.95 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villaseñor-Aguilar, M.J.; Cano-Lara, M.; Lopez, A.R.; Rostro-Gonzalez, H.; Padilla-Medina, J.A.; Barranco-Gutiérrez, A.I. Fuzzy Classification of the Maturity of the Orange (Citrus × sinensis) Using the Citrus Color Index (CCI). Appl. Sci. 2024, 14, 5953. https://doi.org/10.3390/app14135953
Villaseñor-Aguilar MJ, Cano-Lara M, Lopez AR, Rostro-Gonzalez H, Padilla-Medina JA, Barranco-Gutiérrez AI. Fuzzy Classification of the Maturity of the Orange (Citrus × sinensis) Using the Citrus Color Index (CCI). Applied Sciences. 2024; 14(13):5953. https://doi.org/10.3390/app14135953
Chicago/Turabian StyleVillaseñor-Aguilar, Marcos J., Miroslava Cano-Lara, Adolfo R. Lopez, Horacio Rostro-Gonzalez, José Alfredo Padilla-Medina, and Alejandro Israel Barranco-Gutiérrez. 2024. "Fuzzy Classification of the Maturity of the Orange (Citrus × sinensis) Using the Citrus Color Index (CCI)" Applied Sciences 14, no. 13: 5953. https://doi.org/10.3390/app14135953
APA StyleVillaseñor-Aguilar, M. J., Cano-Lara, M., Lopez, A. R., Rostro-Gonzalez, H., Padilla-Medina, J. A., & Barranco-Gutiérrez, A. I. (2024). Fuzzy Classification of the Maturity of the Orange (Citrus × sinensis) Using the Citrus Color Index (CCI). Applied Sciences, 14(13), 5953. https://doi.org/10.3390/app14135953








