Electromagnetic Optimization of a High-Speed Interior Permanent Magnet Motor Considering Rotor Stress
Abstract
1. Introduction
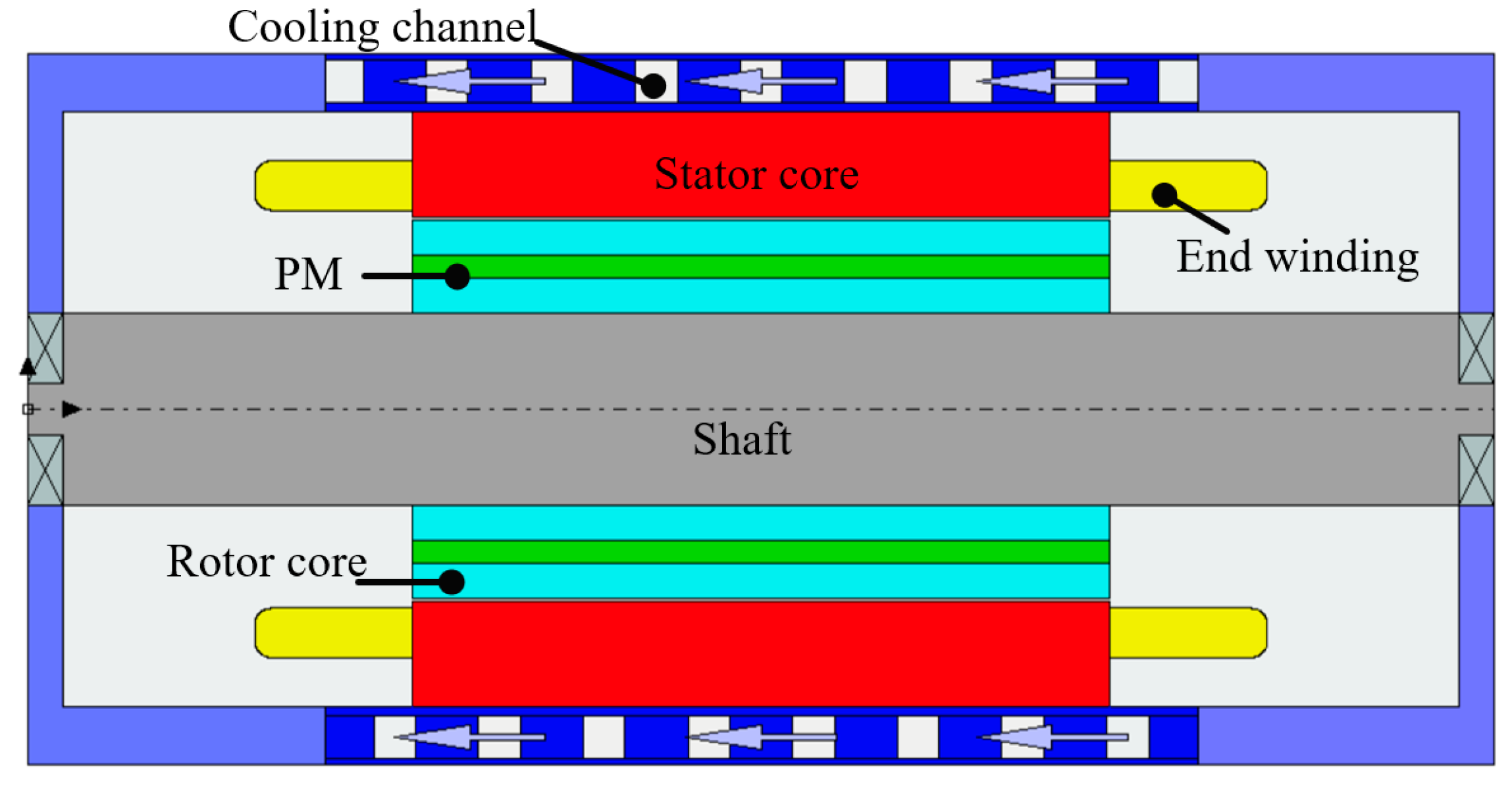
2. Motor Structure and Initial Design Parameters
3. Analysis of Rotor Parameter Influence on Electromagnetic and Mechanical Stress Performance
3.1. Pre-Treatment of Finite-Element Model
3.1.1. Calculation Process of Rotor Stress
3.1.2. Calculation Process of Electromagnetic Characteristics
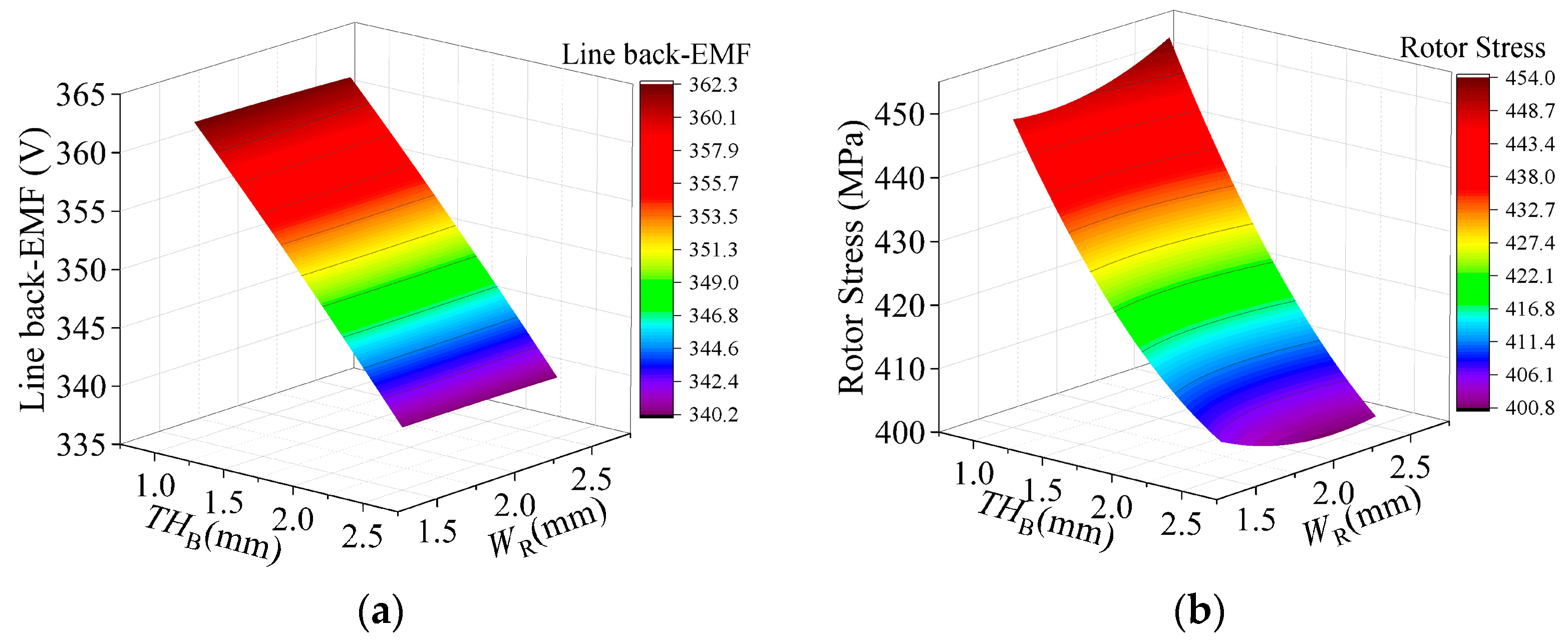
3.2. Influence of Magnetic Bridge and Stiffeners Thickness
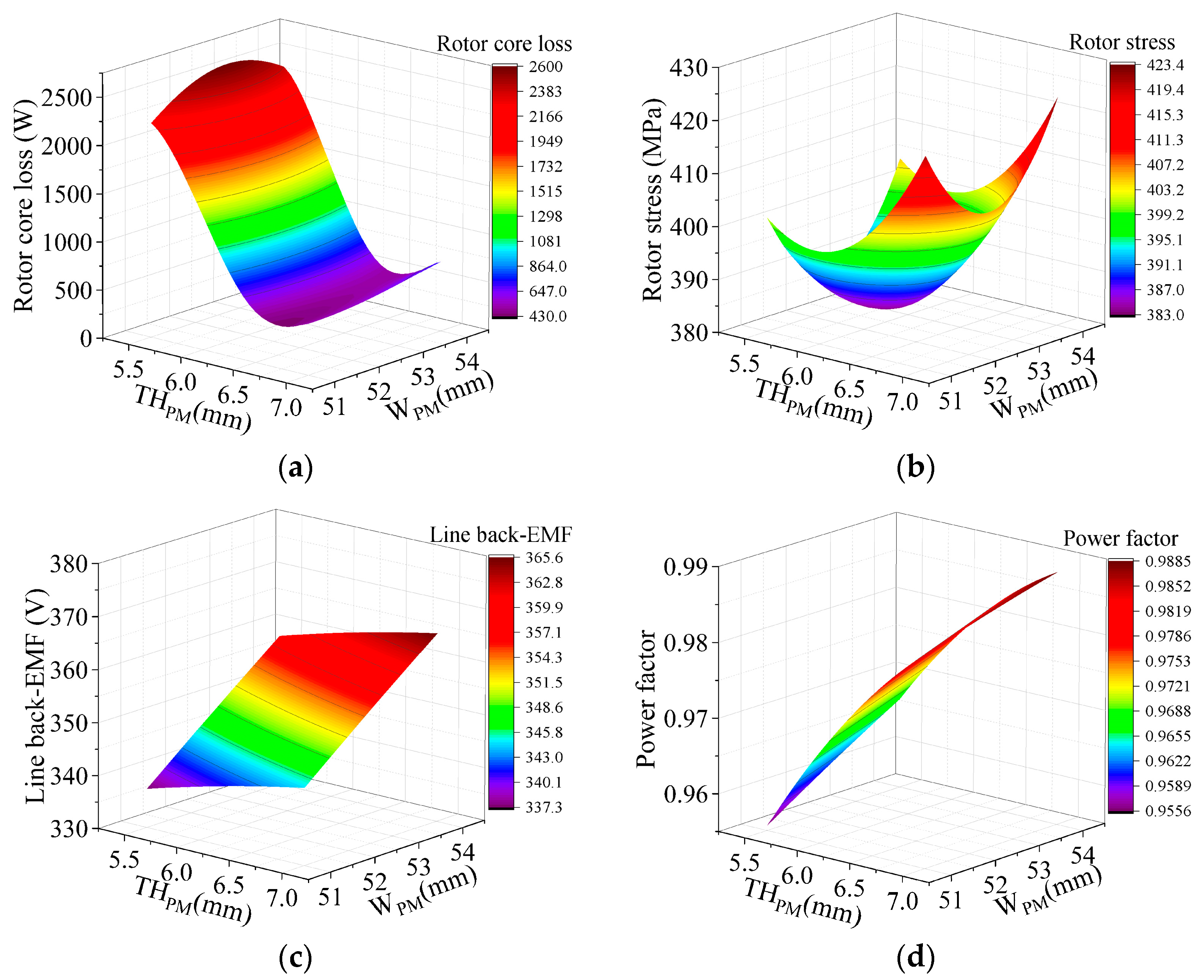
4. Sensitive Analysis of Rotor Parameters
4.1. Rotor Optimize Parameters
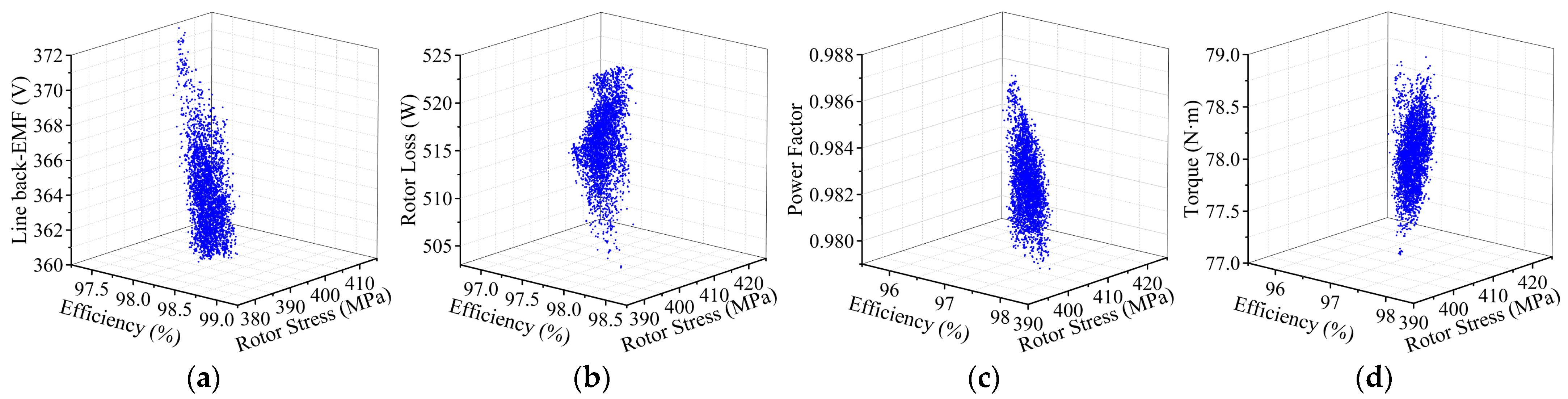
4.2. Response Surface Analysis
4.3. Sensitivity Analysis
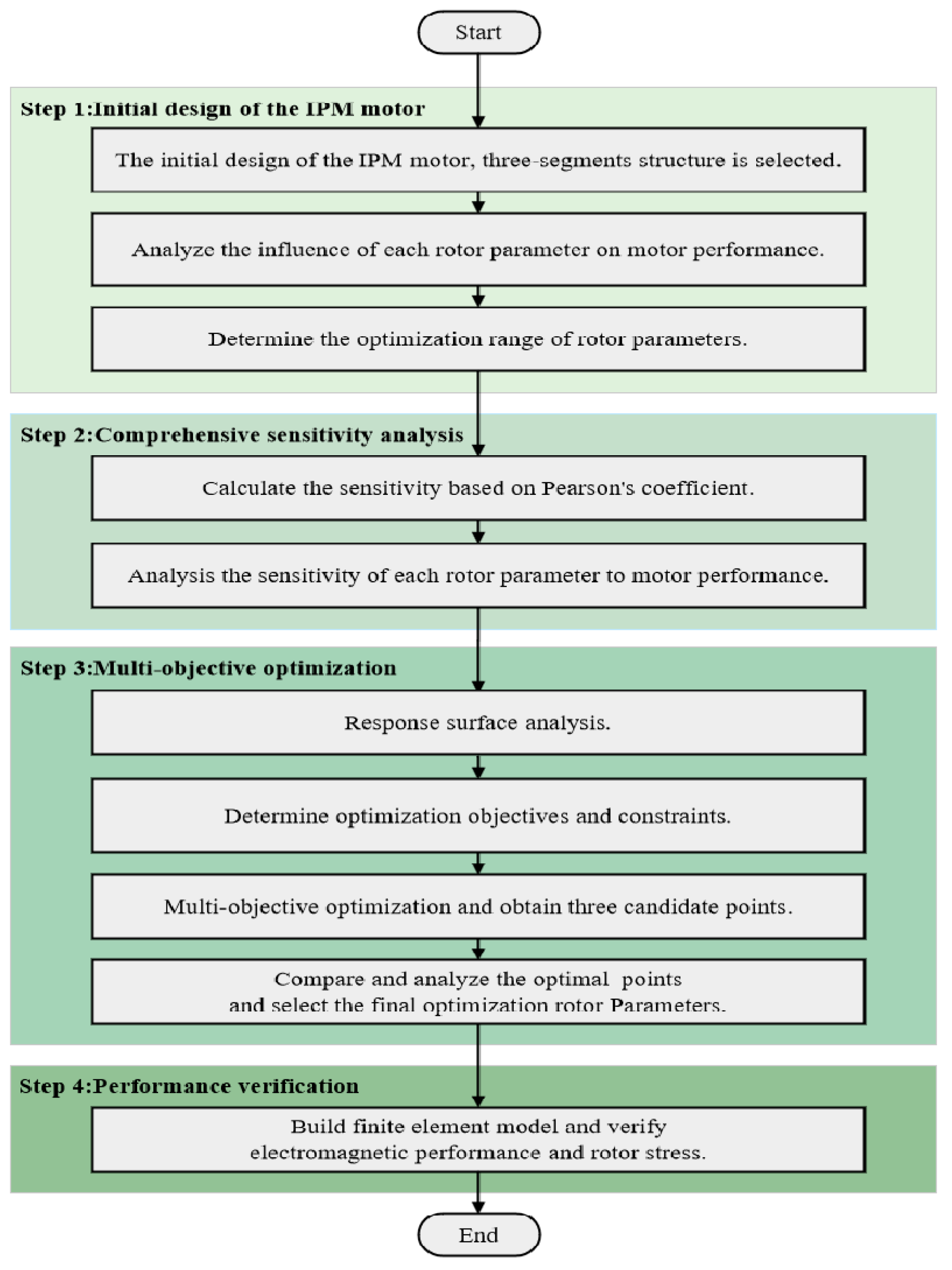
5. Comprehensive Optimization
5.1. Optimization Process
5.2. Optimization Objectives and Constraints
5.3. Optimization Results
6. Performance Comparison
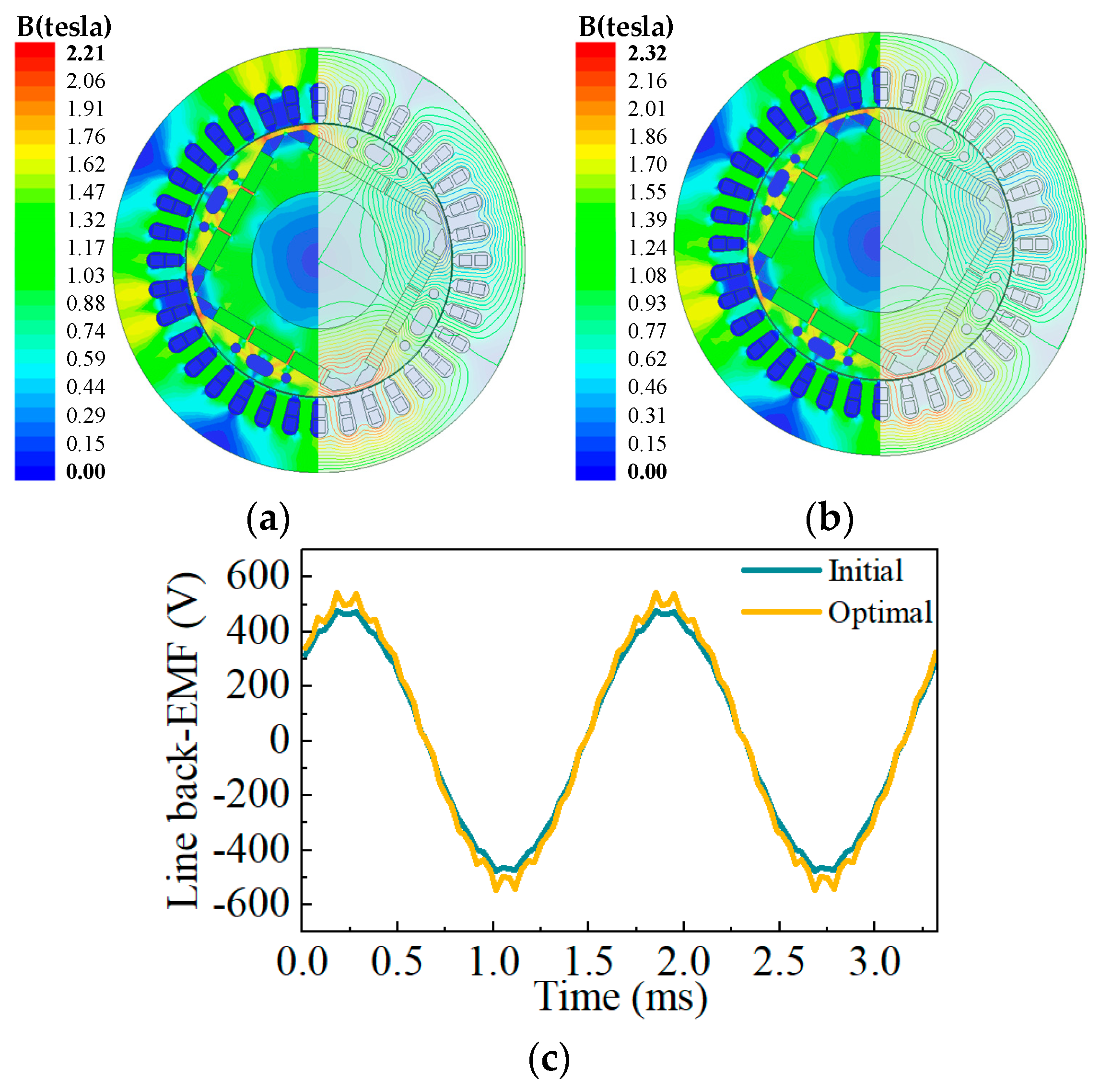
6.1. Comparison of Electromagnetic Performances
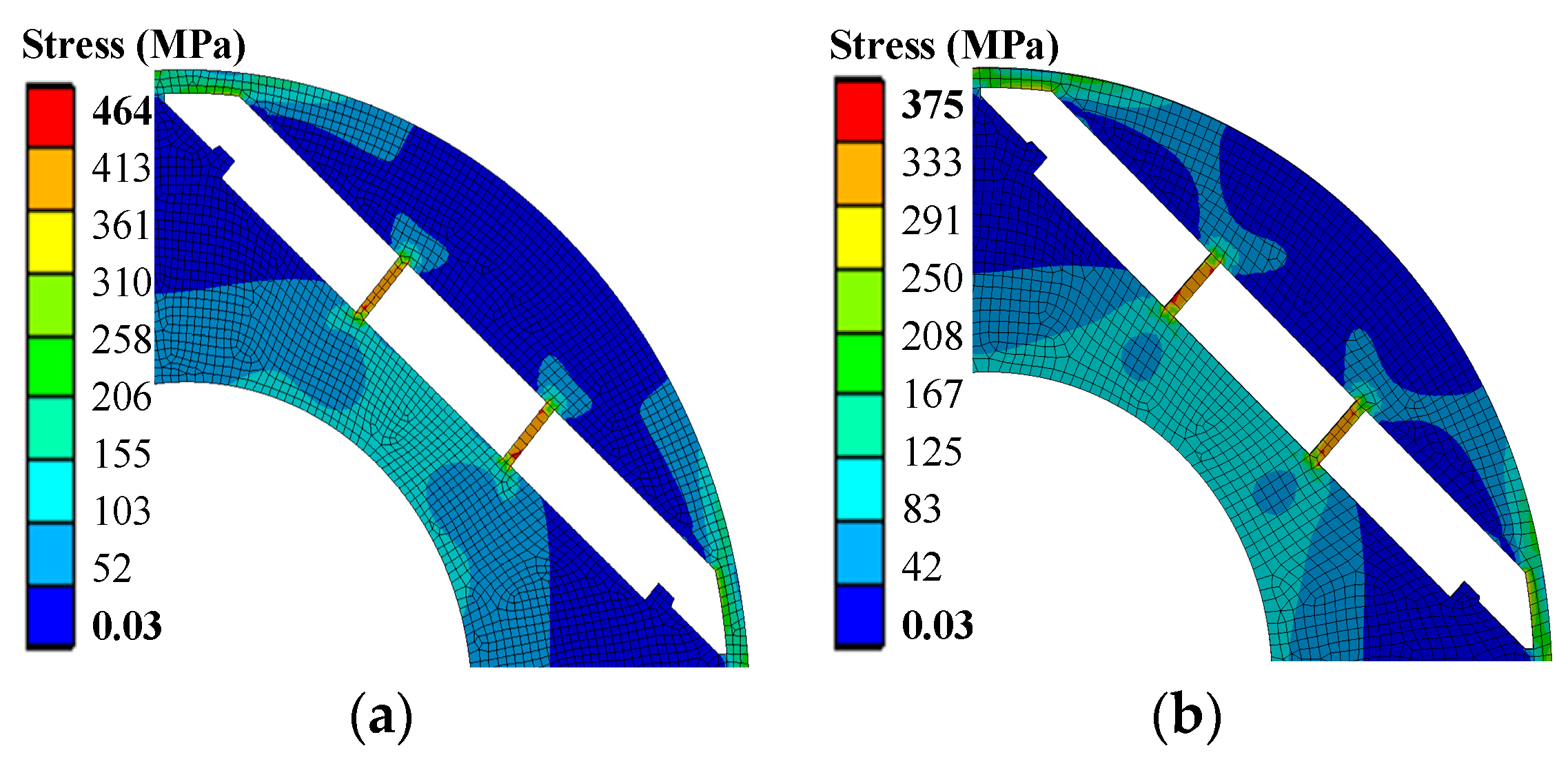
6.2. Comparison of Rotor Stress
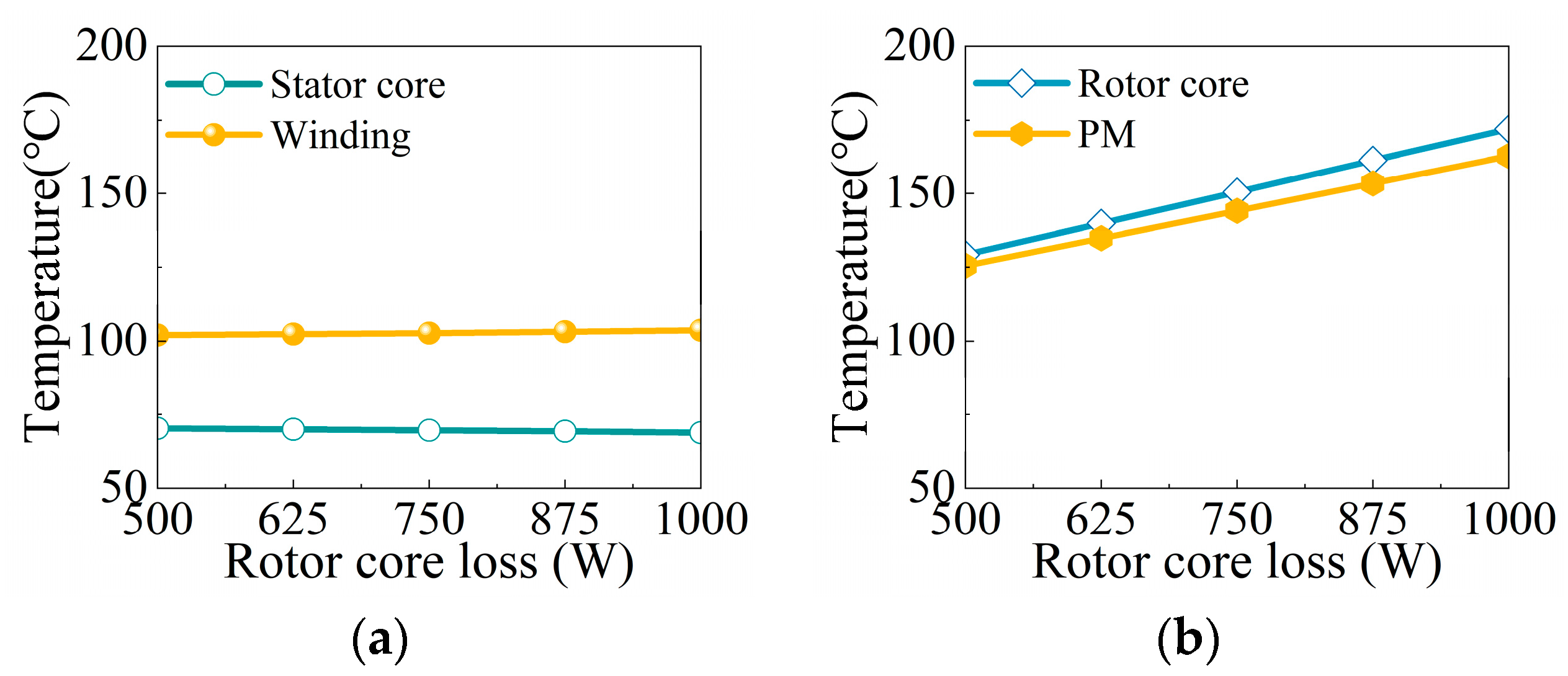
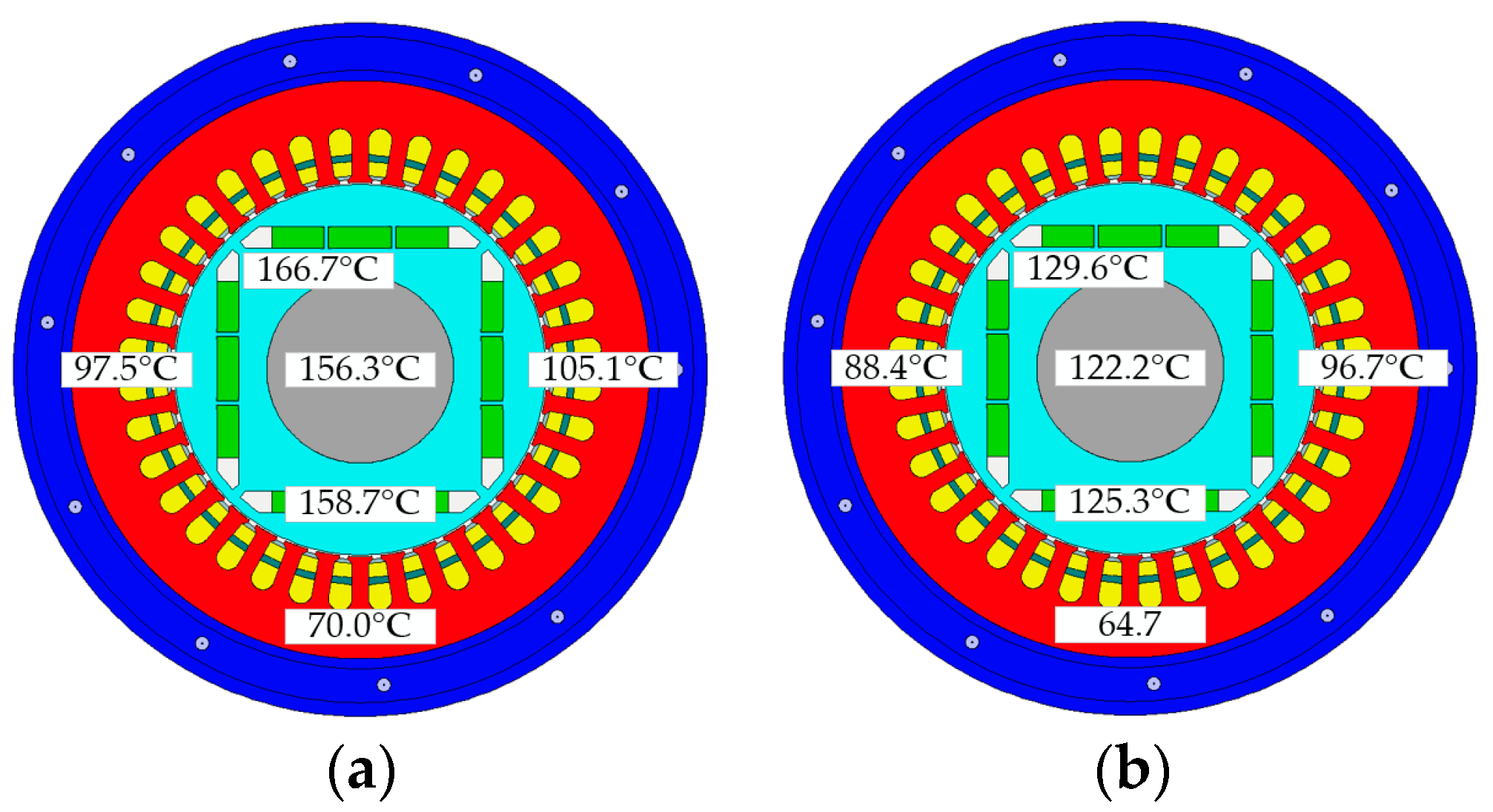
6.3. Comparison of Temperature Distribution
7. Prototype and Experiment
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, F.; Wang, X.H.; Xing, Z.Z.; Ren, J.; Li, X. Analysis and research on no-load air gap magnetic field and system multiobjective optimization of interior PM motor. IEEE Trans. Ind. Electron. 2022, 69, 10915–10925. [Google Scholar] [CrossRef]
- Li, L.N.; Zhu, G.J. Electromagnetic-Thermal-Stress Efforts of Stator-Casing Grease Buffers for Permanent Magnet Driving Motors. IEEE Trans. Ind. Appl. 2024, 60, 1268–1276. [Google Scholar] [CrossRef]
- Du, G.H.; Huang, N.; He, H.C.; Lei, G.; Zhu, J.G. Parameter design for a high-speed permanent magnet machine under multiphysics constraints. IEEE Trans. Energy Convers. 2020, 35, 2025–2035. [Google Scholar] [CrossRef]
- Qin, X.F.; Yao, L.; Wan, W.J.; Shi, D.; Wang, Y.C.; Shen, J.X. Investigation of bessel functions in analytical modeling of rotor eddy current losses in PM machine rotor with copper shield. IEEE Trans. Magn. 2023, 59, 8100609. [Google Scholar] [CrossRef]
- Du, G.H.; Li, N.M.; Zhou, Q.X.; Gao, W.T.; Wang, L.; Pu, T. Multi-physics comparison of surface-mounted and interior permanent magnet synchronous motor for high-speed applications. Machines 2022, 10, 700. [Google Scholar] [CrossRef]
- Wang, J.; Geng, W.W.; Li, Q.; Li, L.; Zhang, Z.R. A new flux-concentrating rotor of permanent magnet motor for electric vehicle application. IEEE Trans. Ind. Electron. 2022, 69, 10882–10892. [Google Scholar] [CrossRef]
- Peng, C.; Wang, D.H.; Feng, Z.K.; Wang, B.D. A new segmented rotor to mitigate torque ripple and electromagnetic vibration of interior permanent magnet machine. IEEE Trans. Ind. Electron. 2022, 69, 1367–1377. [Google Scholar] [CrossRef]
- Yang, Y.Y.; Castano, S.; Yang, R.; Kasprzak, M.; Bilgin, B. Design and comparison of interior permanent magnet motor topologies for traction applications. IEEE Trans. Transp. Electrific. 2017, 3, 86–97. [Google Scholar] [CrossRef]
- Abdelrahman, A.; Sahu, A.; Emery, N.; Al-Ani, D.; Bilgin, B. Multi-physics design platform for a high power density multi-phase IPM traction motor: Analysis and simulation. In Proceedings of the 2022 IEEE Transportation Electrification Conference & Expo (ITEC), Anaheim, CA, USA, 15–17 June 2022; pp. 92–96. [Google Scholar]
- Xu, Y.M.; Ai, M.M.; Xu, Z.Y.; Liu, W.H.; Wang, Y.D. Research on interior permanent magnet synchronous motor based on performance matching of electric bus. IEEE Trans. Appl. Supercond. 2021, 31, 5204304. [Google Scholar] [CrossRef]
- Chai, F.; Li, Y.; Liang, P.X.; Pei, Y. Calculation of the maximum mechanical stress on the rotor of interior permanent-magnet synchronous motors. IEEE Trans. Ind. Electron. 2016, 63, 3420–3432. [Google Scholar] [CrossRef]
- Li, Y.; Pei, Y.L.; Liang, P.X.; Chai, F. Analysis of the rotor mechanical strength of interior permanent magnet synchronous in-wheel motor with high speed and large torque. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014; pp. 1–5. [Google Scholar]
- Jung, J.W.; Lee, B.H.; Kim, D.J.; Hong, J.P.; Kim, J.Y.; Leon, S.M.; Song, D.H. Mechanical stress reduction of rotor core of interior permanent magnet synchronous motor. IEEE Trans. Magn. 2012, 48, 911–914. [Google Scholar] [CrossRef]
- Rao, J.; Qu, R.H.; Ma, J.; Xu, W. Investigate the influence of magnetic bridge design on mechanical strength and electromagnetic characteristics in high speed IPM machines. In Proceedings of the 2014 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22–25 October 2014; pp. 22–27. [Google Scholar]
- Chu, G.Y.; Dutta, R.; Rahman, M.F.; Lovatt, H.; Sarlioglu, B. Analytical calculation of maximum mechanical stress on the rotor of interior permanent-magnet synchronous machines. IEEE Trans. Ind. Appl. 2020, 56, 1321–1331. [Google Scholar] [CrossRef]
- Du, G.H.; Huang, N.; Zhao, Y.Y.; Lei, G.; Zhu, J.G. Comprehensive sensitivity analysis and multiphysics optimization of the rotor for a high speed permanent magnet machine. IEEE Trans. Energy Convers. 2021, 36, 358–367. [Google Scholar] [CrossRef]
- Jung, Y.-H.; Park, M.-R.; Kim, K.-O.; Chin, J.-W.; Hong, J.-P.; Lim, M.-S. Design of high-speed multilayer IPMSM using ferrite PM for EV traction considering mechanical and electrical characteristics. IEEE Trans. Ind. Appl. 2021, 57, 327–339. [Google Scholar] [CrossRef]
- Lin, R.; Sudhoff, S.D.; Nascimento, V.C.D. A multi-physics design method for V-shape interior permanent-magnet machines based on multi-objective optimization. IEEE Trans. Energy Convers. 2020, 35, 651–661. [Google Scholar] [CrossRef]
- Praslicka, B.; Ma, C.; Taran, N. A computationally efficient high-fidelity multi-physics design optimization of traction motors for drive cycle loss minimization. IEEE Trans. Ind. Appl. 2023, 59, 1351–1360. [Google Scholar] [CrossRef]
- Liu, F.; Wang, X.H. Design and multiobjective optimization of dual-circulation cooling system considering electro-thermal coupling for IPMSM. IEEE Trans. Transp. Electrific. 2023, 9, 3072–3084. [Google Scholar] [CrossRef]
- Sun, X.D.; Shi, Z.; Lei, G.; Guo, Y.G.; Zhu, J.G. Multi-objective design optimization of an IPMSM based on multilevel strategy. IEEE Trans. Ind. Electron. 2021, 68, 139–148. [Google Scholar] [CrossRef]
- Tahkola, M.; Keränen, J.; Sedov, D.; Far, M.F.; Kortelainen, J. Surrogate modeling of electrical machine torque using artificial neural networks. IEEE Access 2020, 8, 220027–220045. [Google Scholar] [CrossRef]
- Li, Z.; Che, S.; Zhao, H.; Zhang, L.C.; Wang, P.J.; Du, S.H.; Zhang, H.J.; Feng, Y.F.; Sun, H.X. Loss analysis of high-speed permanent magnet motor based on energy saving and emission reduction. Energy Rep. 2023, 9, 2379–2394. [Google Scholar] [CrossRef]
- Chen, H.; Lee, C.H.T. Parametric sensitivity analysis and design optimization of an interior permanent magnet synchronous motor. IEEE Access 2019, 7, 159918–159929. [Google Scholar] [CrossRef]
- Geng, W.W.; Wang, J.; Li, L.; Guo, J. Design and multiobjective optimization of a new flux-concentrating rotor combining halbach PM array and spoke-type IPM machine. IEEE Trans. Mechatron. 2023, 28, 257–266. [Google Scholar] [CrossRef]
- Lim, D.K.; Yi, K.P.; Jung, S.Y.; Jung, H.K.; Ro, J.S. Optimal design of an interior permanent magnet synchronous motor by using a new surrogate-assisted multi-objective optimization. IEEE Trans. Magn. 2015, 51, 8207504. [Google Scholar]
- Praslicka, B.; Taran, N.; Ma, C. An ultra-fast method for analyzing IPM motors at multiple operating points using surrogate models. In Proceedings of the 2022 IEEE Transportation Electrification Conference & Expo (ITEC), Anaheim, CA, USA, 15–17 June 2022; pp. 868–873. [Google Scholar]
- Ahn, J.H.; Han, C.; Kim, C.W.; Choi, J.Y. Rotor design of high-speed permanent magnet synchronous motors considering rotor magnet and sleeve materials. IEEE Trans. Appl. Supercond. 2018, 28, 5201504. [Google Scholar] [CrossRef]
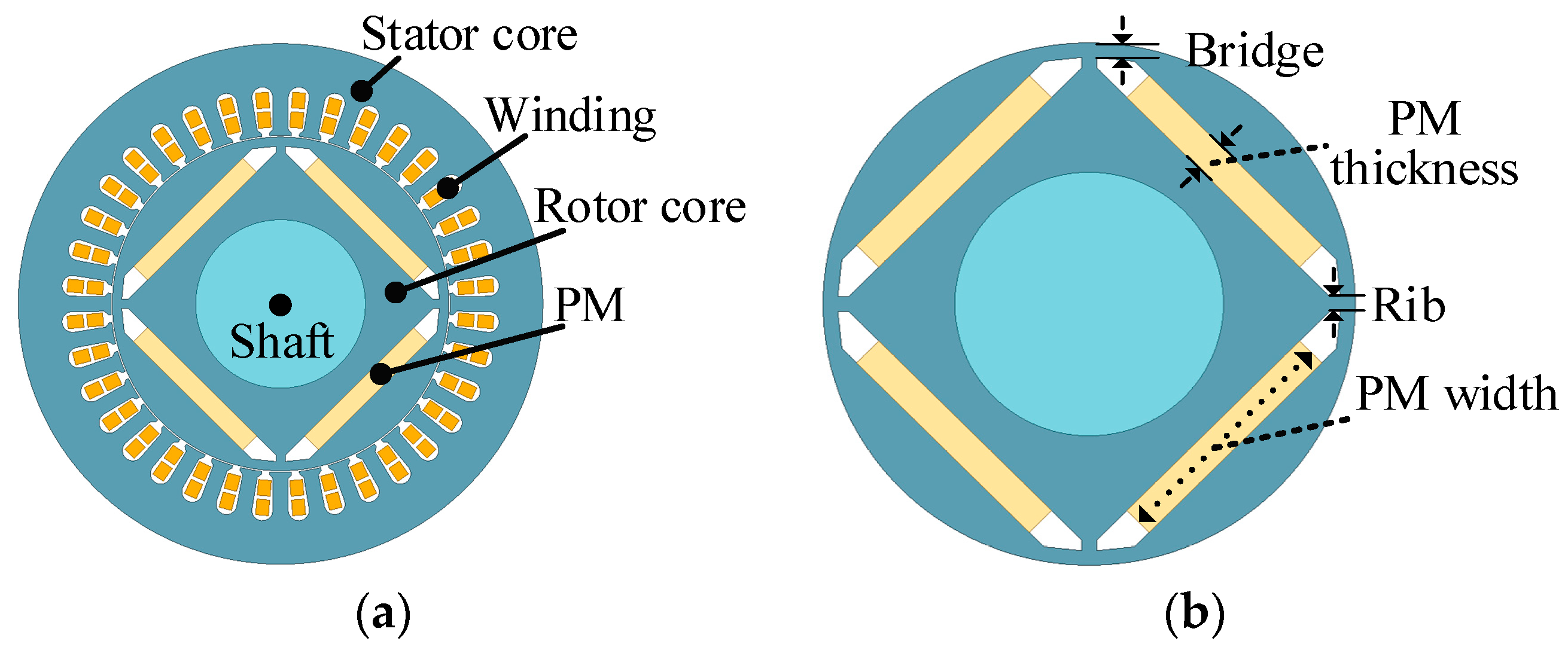
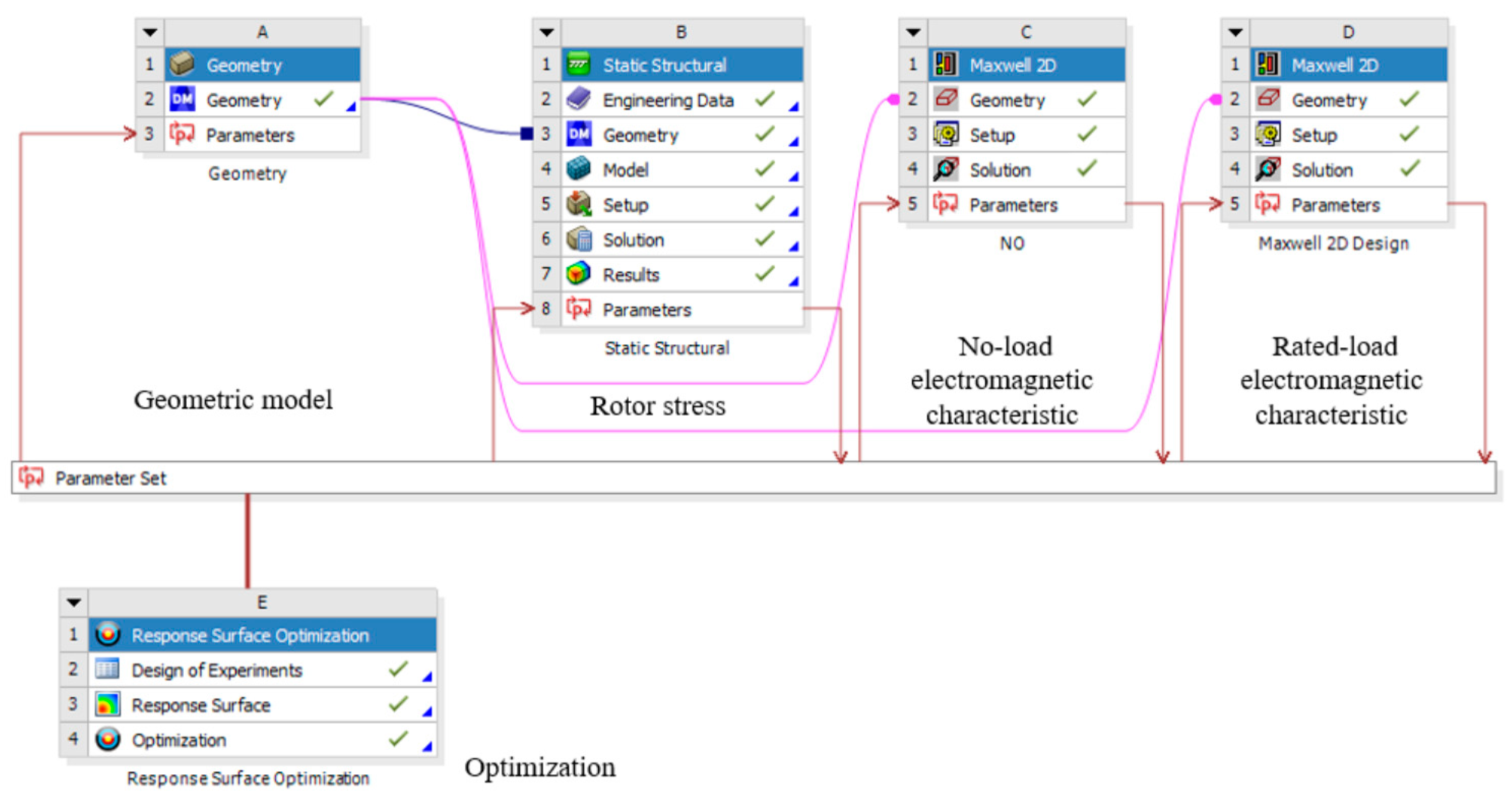




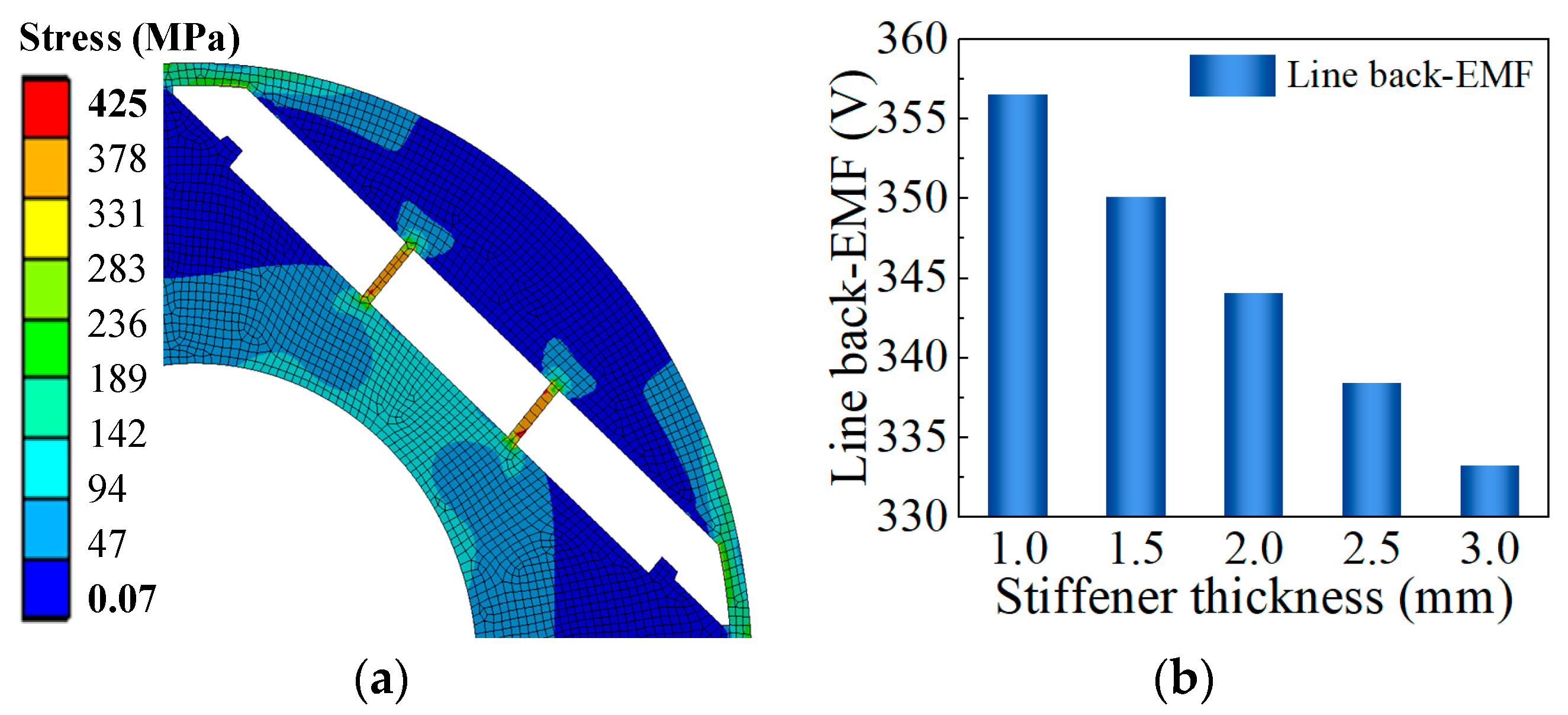


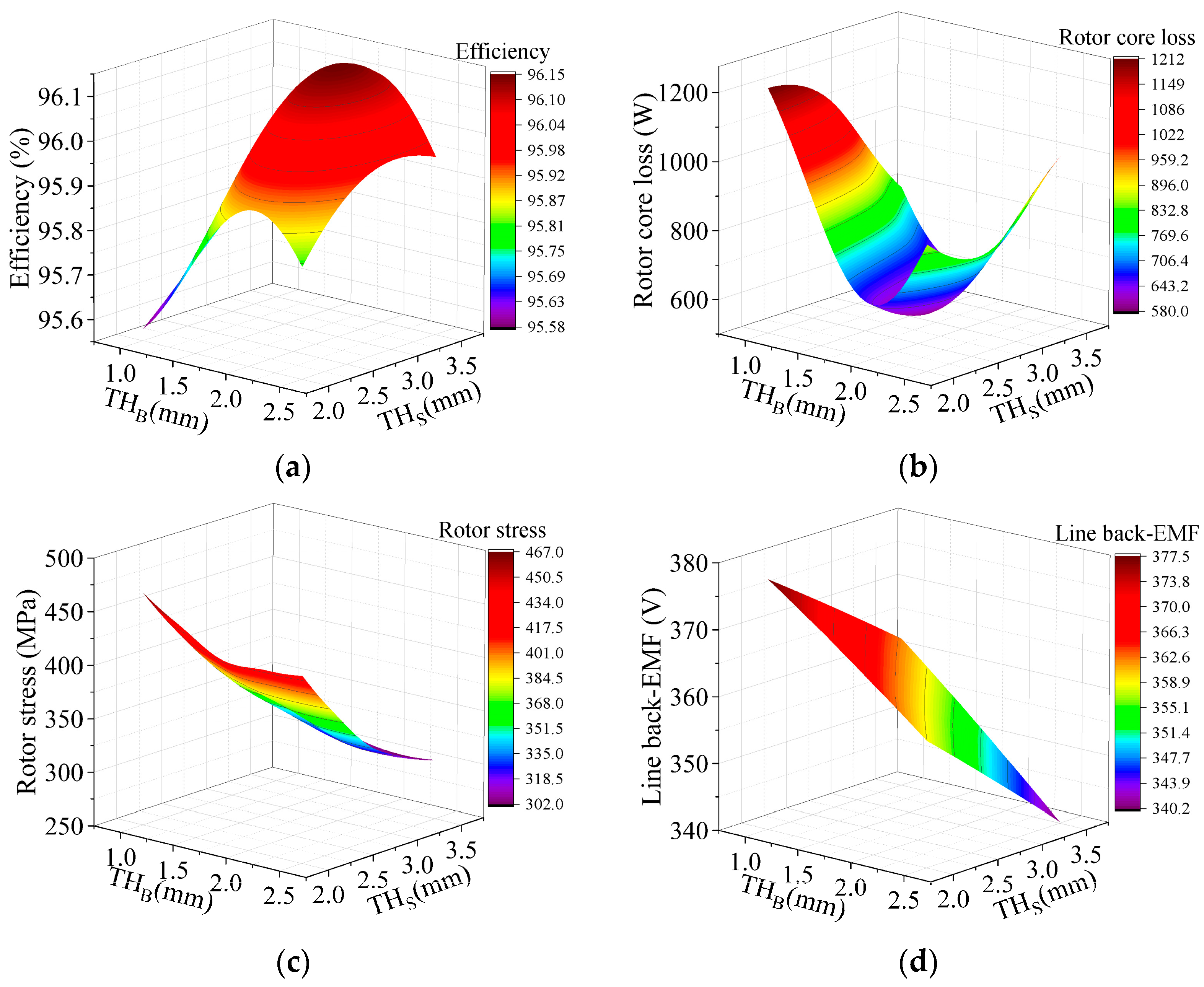



| Parameters | Value |
|---|---|
| Rated power (kW) | 140 |
| Rated speed (rpm) | 18,000 |
| Rated voltage (V) | 380 |
| Stator outer diameter (mm) | 170 |
| Stator inner diameter (mm) | 110 |
| Air-gap length (mm) | 0.5 |
| Axial length (mm) | 200 |
| Surface speed (m/s) | 103 |
| Slot fill factor | 75% |
| Symbol | Paraments | Value |
|---|---|---|
| THB | Bridge thickness (mm) | 2 |
| WR | Rib width (mm) | 2 |
| THS | Stiffener thickness (mm) | 2 |
| THPM | PM thickness (mm) | 6 |
| WPM | PM width (mm) | 50 |
| Material Property | Rotor Core | PM |
|---|---|---|
| Name | DW310-35 | N38UH |
| Density (kg/m3) | 7850 | 7400 |
| Elastic modulus (GPa) | 200 | 160 |
| Poisson’s ratio | 0.3 | 0.24 |
| Coefficient of thermal expansion (10−6/K) | 11 | 8 |
| Yield strength (MPa) | 480 | 75 |
| Resistivity at 20 °C | 4.4 × 10−7 | 1.8 × 10−6 |
| Loss coefficient (Kh/alpha/Kexc) | 0.00393/5/0.00166 | - |
| Remanence Br at 100 °C (Tesla) | - | 1.139 |
| Coercive force Hc at 100 °C (A/m) | −9.1 × 105 |
| Symbol | Paraments | Range |
|---|---|---|
| THB | Bridge thickness (mm) | [1.0, 2.5] |
| WR | Rib width (mm) | [1.5, 2.5] |
| THS | Stiffener thickness (mm) | [2.0, 3.5] |
| THPM | PM thickness (mm) | [5.5, 7.0] |
| WPM | PM width (mm) | [51, 54] |
| Parameters | Candidate 1 | Candidate 2 | Candidate 3 | |
|---|---|---|---|---|
| Design parameters | Bridge thickness THB (mm) | 1.68 | 1.66 | 1.67 |
| Rib width WR (mm) | 2.14 | 2.17 | 2.13 | |
| Stiffener thickness THS (mm) | 2.41 | 2.39 | 2.40 | |
| PM thickness THPM (mm) | 6.57 | 6.61 | 6.64 | |
| PM width WPM (mm) | 52.84 | 52.71 | 52.77 | |
| Performance | Efficiency (%) | 96.32 | 96.33 | 96.35 |
| Rotor core loss (W) | 546.8 | 541.2 | 533.0 | |
| Rotor stress (MPa) | 373.8 | 378.1 | 374.9 | |
| Back-EMF (V) | 366.2 | 366.1 | 366.3 | |
| Torque (N·m) | 78.34 | 78.40 | 78.41 | |
| Power factor | 0.9720 | 0.9721 | 0.9725 |
| Paraments | Initial | Optimized |
|---|---|---|
| Bridge thickness (mm) | 2 | 1.7 |
| Rib width (mm) | 2 | 2.1 |
| Stiffener thickness (mm) | 2 | 2.4 |
| PM thickness (mm) | 6 | 6.6 |
| PM width (mm) | 50 | 52.7 |
| Paraments | Initial | Optimized |
|---|---|---|
| Efficiency (%) | 95.96 | 96.34 |
| Line back-EMF (V) | 345 | 366.5 |
| Torque (N·m) | 76.2 | 78.3 |
| Rotor core loss (W) | 893 | 538 |
| Stator core loss (W) | 3091 | 2891 |
| Power factor | 0.963 | 0.972 |
| Rotor stress (MPa) | 464 | 373 |
| Stress safety factor | 1.03 | 1.29 |
| Stator temperature (°C) | 97.5 | 88.4 |
| Winding temperature (°C) | 105.1 | 96.7 |
| PM temperature (°C) | 158.7 | 125.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, F.; Li, N.; Du, G.; Huang, M.; Kang, Z. Electromagnetic Optimization of a High-Speed Interior Permanent Magnet Motor Considering Rotor Stress. Appl. Sci. 2024, 14, 6033. https://doi.org/10.3390/app14146033
Yang F, Li N, Du G, Huang M, Kang Z. Electromagnetic Optimization of a High-Speed Interior Permanent Magnet Motor Considering Rotor Stress. Applied Sciences. 2024; 14(14):6033. https://doi.org/10.3390/app14146033
Chicago/Turabian StyleYang, Fang, Niumei Li, Guanghui Du, Ming Huang, and Zhen Kang. 2024. "Electromagnetic Optimization of a High-Speed Interior Permanent Magnet Motor Considering Rotor Stress" Applied Sciences 14, no. 14: 6033. https://doi.org/10.3390/app14146033
APA StyleYang, F., Li, N., Du, G., Huang, M., & Kang, Z. (2024). Electromagnetic Optimization of a High-Speed Interior Permanent Magnet Motor Considering Rotor Stress. Applied Sciences, 14(14), 6033. https://doi.org/10.3390/app14146033






