Effects of Age and Sex on the Kinematics of the Sprinting Technique in the Maximum Velocity Phase
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Experimental Procedure
2.3. Data Analysis
- SL: the horizontal distance between the touchdown points of the feet recorded for two consecutive supports;
- Touchdown distance (STD): the horizontal distance between the toe of the support foot and the BCM projection at touchdown;
- Take-off distance (STO): the horizontal distance between the toes of the support foot and the BCM projection at take-off;
- Horizontal BCM take-off velocity (VxTO): the horizontal velocity of BCM at take-off;
- Vertical BCM take-off velocity (VyTO): the vertical velocity of BCM at take-off;
- Angle of take-off (AngPr): the Arc-tangent of the vertical/horizontal BCM take-off velocity;
- Horizontal ankle touchdown velocity (VXankle): the horizontal velocity of the ankle at touchdown;
- BCM height: the height of the BCM at touchdown (HTD), maximum lowering of the BCM (HAM), and take-off (HTO);
- Knee joint angle: The angle formed between the thigh and the shank at touchdown (θkneeTD), maximum knee amortization (θkneeAM), and take-off (θkneeTO). The minimum swing leg’s knee angle at the support phase was also calculated (θkneeMIN);
- Ankle joint angle: the angle formed between the shank and the foot at touchdown (θankleTD) and take-off (θkneeTO);
- Knee joint angular velocity (ωKNEE): the angular velocity of the swing leg’s knee joint at take-off;
- Ankle joint angular velocity (ωANKLE): the angular velocity of the support leg’s ankle joint at touchdown;
- Thigh inclination (φTHIGH): the angle formed by the horizontal axis and the thigh of the swing leg at take-off;
- Leg inclination: the angle formed by the horizontal axis and the line passing from the support leg’s ankle and hip at touchdown (φlegTD) and take-off (φlegTO).
2.4. Statistical Analysis
3. Results
4. Discussion
Limitations of This Study
5. Conclusions and Practical Applications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ross, A.; Leveritt, M.; Riek, S. Neural influences on sprint running: Training adaptations and acute responses. Sports Med. 2001, 31, 409–425. [Google Scholar] [CrossRef] [PubMed]
- Cardoso, P.; Tavares, F.; Loureiro, N.; Ferreira, R.; Araújo, J.P.; Reis, J.; Vaz, J.R. In-situ acceleration-speed profile of an elite soccer academy: A cross-sectional study. J. Sports Sci. 2023, 41, 1868–1874. [Google Scholar] [CrossRef] [PubMed]
- King, M.; Brown, M.; Cox, J.; McLellan, R.; Towlson, C.; Barrett, S. Talent identification in soccer: The influence of technical, physical and maturity-related characteristics on a national selection process. PLoS ONE 2024, 19, e0298359. [Google Scholar] [CrossRef] [PubMed]
- De Lacey, J.; Brughelli, M.E.; McGuigan, M.R.; Hansen, K.T. Strength, speed and power characteristics of elite rugby league players. J. Strength Cond. Res. 2014, 28, 2372–2375. [Google Scholar] [CrossRef] [PubMed]
- Djaoui, L.; Chamari, K.; Owen, A.L.; Dellal, A. Maximal Sprinting Speed of Elite Soccer Players During Training and Matches. J. Strength Cond. Res. 2017, 31, 1509–1517. [Google Scholar] [CrossRef] [PubMed]
- Joseph, J.; McIntyre, F.; Joyce, C.; Scanlan, A.; Cripps, A. A comparison of multidimensional qualities discriminant of selection in elite adolescent Australian basketball athletes. PLoS ONE 2021, 16, e0256032. [Google Scholar] [CrossRef]
- Tsoukos, A.; Drikos, S.; Brown, L.E.; Sotiropoulos, K.; Veligekas, P.; Bogdanis, G.C. Upper and Lower Body Power Are Strong Predictors for Selection of Male Junior National Volleyball Team Players. J. Strength Cond. Res. 2019, 33, 2760–2767. [Google Scholar] [CrossRef] [PubMed]
- Ae, M.; Ito, A.; Suzuki, M. The men’s 100 metres. N. Stud. Athl. 1992, 7, 47–52. [Google Scholar]
- Dal Pupo, J.; da Rocha, C.I., Jr.; Mota, C.B. Concentrações de lactato sangüíneo e o comportamento cinemático de corredores mirins em provas de 50 e 100m rasos. Rev. Bras. Cineantropom. Desempenho Hum. 2008, 10, 393–398. [Google Scholar] [CrossRef]
- Delecluse, C.; Van Coppenolle, H.; Willems, R.; Diels, M.; Goris, M.; Van Leempurte, M.; Vuylsteke, M. Analysis of 100 meter sprint performance as a multi-dimensional skill. J. Hum. Mov. Stud. 1995, 28, 87–101. [Google Scholar]
- Ferro, A.; Rivera, A.; Pagola, I.; Ferreruela, M.; Martin, A.; Rocandio, V. Biomechanical analysis of the 7th World Championships in Athletics Seville 1999. N. Stud. Athl. 2001, 16, 25–60. [Google Scholar]
- Gajer, B.; Thepaut-Mathieu, C.; Lehenaff, D. Evolution of stride and amplitude during course of the 100 m event in athletics. N. Stud. Athl. 1999, 14, 43–50. [Google Scholar]
- Graubner, R.; Nixdorf, E. Biomechanical analysis of the sprint and hurdles events at the 2009 IAAF World Championships in Athletics. N. Stud. Athl. 2011, 26, 17–53. [Google Scholar]
- Kersting, U.G. Biomechanical analysis of the sprinting events. In Biomechanical Research Project Athens 1997—Final Report; Brüggemann, G.P., Koszewski, D., Müller, H., Eds.; Meyer & Meyer Sport: Oxford, UK, 1999; pp. 12–61. [Google Scholar]
- Letzelter, S. The development of velocity and acceleration in sprints: A comparison of elite and juvenile female sprinters. N. Stud. Athl. 2006, 21, 15–22. [Google Scholar]
- Mackala, K. Optimisation of performance through kinematic analysis of the different phases of the 100 metres. N. Stud. Athl. 2007, 22, 7–16. [Google Scholar]
- Moravec, P.; Ruzicka, J.; Susanka, P.; Dostal, E.; Kodejs, M.; Nosek, M. The 1987 International Athletic Foundation/IAAF Scientific Project Report: Time analysis of Ihe 100 Metres events at the II World Championships in Athletics. N. Stud. Athl. 1988, 3, 61–96. [Google Scholar]
- Colyer, S.L.; Nagahara, R.; Salo, A.I.T. Kinetic demands of sprinting shift across the acceleration phase: Novel analysis of entire force waveforms. Scand. J. Med. Sci. Sports 2018, 28, 1784–1792. [Google Scholar] [CrossRef]
- Hay, J.G. The Biomechanics of Sports Techniques, 3rd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1985. [Google Scholar]
- Babic, V.; Coh, M.; Dizdar, D. Differences in kinematic parameters of athletes of different running quality. Biol. Sport 2011, 28, 115–121. [Google Scholar] [CrossRef]
- Mann, R.V.; Herman, J. Kinematic analysis of Olympic sprint performance: Men’s 200 meters. Int. J. Sports Biomech. 1985, 1, 151–162. [Google Scholar] [CrossRef]
- Mero, A.; Komi, P.V. Force-, EMG-, and elasticity-velocity relationships at submaximal, maximal and supramaximal running speeds in sprinters. Eur. J. Appl. Physiol. 1986, 55, 553–561. [Google Scholar] [CrossRef]
- Nummela, A.; Stray-Gundersen, J.; Rusko, H. Effects of fatigue on stride characteristics during a short-term maximal run. J. Appl. Biomech. 1996, 12, 151–160. [Google Scholar] [CrossRef]
- Vardaxis, V.; Hoshizaki, T.B. Power patterns of the leg during the recovery phase of the sprinting stride for advanced and intermediate sprinters. Int. J. Sport Biomech. 1989, 5, 332–349. [Google Scholar] [CrossRef]
- Coh, M.; Bracic, M.; Smajlovic, N. Methodical aspects of maximum speed development. Sport Sci. 2010, 3, 11–14. [Google Scholar]
- Kumar, H. Age changes in the speed of running during 30 meter sprint running. J. Exerc. Sci. Physiother. 2006, 2, 92–95. [Google Scholar]
- Loko, J.; Aule, R.; Sikkut, T.; Ereline, J.; Viru, A. Age differences in growth and physical abilities in trained and untrained girls 10–17 years of age. Am. J. Hum. Biol. 2003, 15, 72–77. [Google Scholar] [CrossRef] [PubMed]
- Milanese, C.; Bortolami, O.; Bertucco, M.; Verlato, G.; Zancanaro, C. Anthropometry and motor fitness in children aged 6–12 years. J. Hum. Sport Exerc. 2010, 5, 265–279. [Google Scholar] [CrossRef]
- Papaiakovou, G.; Giannakos, A.; Michailidis, C.; Patikas, D.; Bassa, E.; Kalopisis, V.; Anthrakidis, N.; Kotzamanidis, C. The effect of chronological age and gender on the development of sprint performance during childhood and puberty. J. Strength Cond. Res. 2009, 23, 2568–2573. [Google Scholar] [CrossRef]
- Rumpf, M.C.; Cronin, J.B.; Oliver, J.L.; Hughes, M. Assessing Youth Sprint Ability—Methodological Issues, Reliability and Performance Data. Ped. Exerc. Sci. 2011, 23, 442–467. [Google Scholar] [CrossRef] [PubMed]
- Vanderka, M.; Kampmiller, T. Ontogenetic development of kinematic parameters of the running stride. Sport Sci. Rev. 2011, 10, 5–24. [Google Scholar] [CrossRef]
- Malina, R.M.; Bouchard, C.; Bar-Or, O. Growth, Maturation, and Physical Activity; Human Kinetics: Champaign, IL, USA, 2004. [Google Scholar]
- Viru, A.; Loko, J.; Harro, M.; Volver, A.; Laaneots, L.; Viru, M. Critical periods in the development of performance capacity during childhood and adolescence. Eur. J. Phys. Educ. 1999, 4, 75–119. [Google Scholar] [CrossRef]
- Branta, C.; Haubenstricker, J.; Seefeldt, V. Age changes in motor skills during childhood and adolescence. Exerc. Sport Sci. Rev. 1984, 12, 467–520. [Google Scholar] [CrossRef]
- Shephard, R.J.; Lavallee, H. Changes of physical performance as indicators of the response to enhanced physical education. J. Sport Med. Phys. Fitness 1994, 34, 323–335. [Google Scholar]
- Loko, J.; Aule, R.; Sikkut, T. Dynamics of Estonian adolescents physical abilities. Acta Academ. Olymp. Est. 1994, 2, 102–114. [Google Scholar]
- Keller, B.A. Development of fitness in children: The influence of gender and physical activity. Am. J. Lifestyle Med. 2008, 2, 58–74. [Google Scholar] [CrossRef]
- Whithall, J. Development of locomotor co-ordination and control in children. In Development of Movement Coordination in Children: Applications in the Field of Ergonomics, Health Sciences and Sport; Savelsberg, G.P.J., Davids, K., Van der Kamp, J., Eds.; Routledge: London, UK, 2003; pp. 251–270. [Google Scholar]
- Sokołowski, B.; Chrzanowska, M. Development of selected motor skills in boys and girls in relation to their rate of maturation—A longitudinal study. Hum. Mov. 2012, 13, 132–138. [Google Scholar] [CrossRef]
- Nagahara, R.; Takai, Y.; Haramura, M.; Mizutani, M.; Matsuo, A.; Kanehisa, H.; Fukunaga, T. Age-Related Differences in Spatiotemporal Variables and Ground Reaction Forces During Sprinting in Boys. Pediatr. Exerc. Sci. 2018, 30, 335–344. [Google Scholar] [CrossRef] [PubMed]
- Coh, M.; Babic, V.; Mackała, K. Biomechanical, neuro-muscular and methodical aspects of running speed development. J. Hum. Kin. 2010, 26, 73–81. [Google Scholar] [CrossRef]
- Coh, M.; Skof, B.; Kugovnik, O.; Dolenec, A.; Kampmiller, T.; Laczo, E.; Šelinger, P. Kinematic and dynamic characteristics of maximal speed in young sprinters. Kinesiol. Slov. 1995, 2, 5–10. [Google Scholar]
- Kampmiller, T.; Vanderka, M.; Selinger, P.; Selingerova, M.; Cierna, D. Kinematic parameters of the running stride in 7- to 18-year-old youth. Kinesiol. Slov. 2011, 17, 63–75. [Google Scholar]
- Coh, M.; Babic, V. Biodynamic characteristics of maximum speed development. Facta Univers. Phys. Educ. Sport 2010, 8, 141–148. [Google Scholar]
- Meyers, R.W.; Oliver, J.L.; Hughes, M.G.; Cronin, J.B.; Lloyd, R.S. Maximal sprint speed in boys of increasing maturity. Pediatr. Exerc. Sci. 2015, 27, 85–94. [Google Scholar] [CrossRef] [PubMed]
- Chatzilazaridis, I.; Panoutsakopoulos, V.; Papaiakovou, G. Stride characteristics progress in a 40-m sprinting test executed by male preadolescent, adolescent and adult athletes. J. Biol. Exerc. 2012, 8, 58–77. [Google Scholar] [CrossRef]
- Kotzamanidis, C. The effect of sprint training on running performance and vertical jumping in pre-adolescent boys. J. Hum. Mov. Stud. 2003, 44, 225–240. [Google Scholar]
- Hunter, J.P.; Marshall, R.N.; McNair, P.J. Interaction of step length and step rate during sprint running. Med. Sci. Sport Exerc. 2004, 36, 261–271. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Zhou, H.; Quan, W.; Jiang, X.; Liang, M.; Li, S.; Ugbolue, U.C.; Baker, J.S.; Gusztav, F.; Ma, X.; et al. A new method proposed for realizing human gait pattern recognition: Inspirations for the application of sports and clinical gait analysis. Gait Posture 2024, 107, 293–305. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Quan, W.; Zhou, H.; Sun, D.; Baker, J.S.; Gu, Y. Explaining the differences of gait patterns between high and low-mileage runners with machine learning. Sci. Rep. 2022, 12, 2981. [Google Scholar] [CrossRef] [PubMed]
- Weyand, P.G.; Sternlight, D.B.; Bellizzi, M.J.; Wright, S. Faster top running speeds are achieved with greater ground forces not more rapid leg movements. J. Appl. Physiol. 2000, 89, 1991–1999. [Google Scholar] [CrossRef]
- Weyand, P.G.; Sandell, R.F.; Prime, D.N.; Bundle, M.W. The biological limits to running speed are imposed from the ground up. J. Appl. Physiol. 2010, 108, 950–961. [Google Scholar] [CrossRef]
- Wisløff, U.; Castagna, C.; Helgerud, J.; Jones, R.; Hoff, J. Strong correlation of maximal squat strength with sprint performance and vertical jump height in elite soccer players. Br. J. Sport Med. 2004, 38, 285–288. [Google Scholar] [CrossRef]
- Schepens, B.; Willems, P.A.; Cavagna, G.A. The mechanics of running in children. J. Physiol. 1998, 509 Pt 3, 927–940. [Google Scholar] [CrossRef]
- Rumpf, M.C.; Cronin, J.B.; Oliver, J.; Hughes, M. Kinematics and Kinetics of Maximum Running Speed in Youth Across Maturity. Pediatr. Exerc. Sci. 2015, 27, 277–284. [Google Scholar] [CrossRef]
- Nagahara, R.; Haramura, M.; Takai, Y.; Oliver, J.L.; Wichitaksorn, N.; Sommerfield, L.M.; Cronin, J.B. Age-related differences in kinematics and kinetics of sprinting in young female. Scand. J. Med. Sci. Sports 2019, 29, 800–807. [Google Scholar] [CrossRef] [PubMed]
- Rumpf, M.C.; Cronin, J.B.; Oliver, J.L.; Hughes, M. Vertical and leg stiffness and stretch-shortening cycle changes across maturation during maximal sprint running. Hum. Mov. Sci. 2013, 32, 668–676. [Google Scholar] [CrossRef] [PubMed]
- Tanner, J.M. Normal growth and techniques of growth assessment. Clin. Endocrinol. Metabol. 1986, 15, 411–451. [Google Scholar] [CrossRef] [PubMed]
- Kotzamandis, C. The acute and long-term effect of training on running velocity. Inq. Sport Phys. Educ. 2007, 5, 179–186. [Google Scholar]
- Babic, V.; Blazevic, I.; Vlasic, J. Characteristics of sprinting in pre-school and junior elementary school children. Hrvat. Športskomed. Vjesn. 2010, 25, 3–8. [Google Scholar]
- Kollias, I.A. Sources of error and their elimination in the use of DLT with the basic recording tools for the analysis of human body in motion. Exerc. Societ. J. Sport Sci. 1997, 18, 9–26. [Google Scholar]
- Plagenhoef, S.; Evans, F.G.; Abdelnour, T. Anatomical data for analyzing human motion. Res. Q. Exerc. Sport 1983, 54, 169–178. [Google Scholar] [CrossRef]
- Winter, D.A.; Sidwall, H.D.; Hobson, D.A. Measurement and reduction of noise in kinematics of locomotion. J. Biomech. 1974, 7, 157–159. [Google Scholar] [CrossRef] [PubMed]
- Babic, V.; Harasin, D.; Dizdar, D. Relations of the variables of power and morphological characteristics to the kinematic indicators of maximal speed running. Kinesiology 2007, 39, 28–39. [Google Scholar]
- Hoshikawa, Y.; Muramatsu, M.; Iida, T.; Uchiyama, A.; Nakajima, Y.; Kanehisa, H.; Fukunaga, T. Influence of the psoas major and thigh muscularity on 100-m times in junior sprinters. Med. Sci. Sports Exerc. 2006, 38, 2138–2143. [Google Scholar] [CrossRef]
- Chow, J.W. Maximum speed of female high school runners. Int. J. Sport Biomech. 1987, 3, 110–127. [Google Scholar] [CrossRef]
- Lazaridis, S.N.; Bassa, E.I.; Patikas, D.; Hatzikotoulas, K.; Lazaridis, F.K.; Kotzamanidis, C.M. Biomechanical comparison in different jumping tasks between untrained boys and men. Pediatr. Exerc. Sci. 2013, 25, 101–113. [Google Scholar] [CrossRef] [PubMed]
- Katsikari, K.; Bassa, E.; Skoufas, D.; Lazaridis, S.; Kotzamanidis, C.; Patikas, D.A. Kinetic and Kinematic Changes in Vertical Jump in Prepubescent Girls After 10 Weeks of Plyometric Training. Pediatr. Exerc. Sci. 2020, 32, 81–88. [Google Scholar] [CrossRef] [PubMed]
- Coh, M.; Jost, B.; Stuhec, S. Kinematic and dynamic structure of the sprinting stride of top female sprinters. Biol. Sport 1998, 15, 237–243. [Google Scholar]
- Vonstein, W. Some reflections on maximum speed sprinting technique. N. Stud. Athl. 1996, 11, 161–165. [Google Scholar]
- Kellis, E. Quantification of quadriceps and hamstring antagonist activity. Sports Med. 1998, 25, 37–62. [Google Scholar] [CrossRef]
- Bassa, E.; Patikas, D.; Kotzamanidis, C. Activation of Antagonist Knee Muscles during Isokinetic Efforts in Prepubertal and Adult Males. Pediatr. Exerc. Sci. 2005, 17, 171–181. [Google Scholar] [CrossRef]
- O’Brien, T.D.; Reeves, N.D.; Baltzopoulos, V.; Jones, D.A.; Maganaris, C.N. Strong relationships exist between muscle volume, joint power and whole-body external mechanical power in adults and children. Exp. Physiol. 2009, 94, 731–738. [Google Scholar] [CrossRef]
- Falk, B.; Usselman, C.; Dotan, R.; Brunton, L.; Klentrou, P.; Shaw, J.; Gabriel, D. Child-adult differences in muscle strength and activation pattern during isometric elbow flexion and extension. Appl. Physiol. Nutr. Metab. 2009, 34, 609–615. [Google Scholar] [CrossRef]
- Grosset, J.F.; Mora, I.; Lambertz, D.; Pérot, C. Voluntary activation of the triceps surae in prepubertal children. J. Electromyogr. Kinesiol. 2008, 18, 455–465. [Google Scholar] [CrossRef] [PubMed]
- Frost, G.; Dowling, J.; Dyson, K.; Bar-Or, O. Cocontraction in three age groups of children during treadmill locomotion. J. Electromyogr. Kinesiol. 1997, 7, 179–186. [Google Scholar] [CrossRef] [PubMed]
- Ford, K.R.; van den Bogert, J.; Myer, G.D.; Shapiro, R.; Hewett, T.E. The effects of age and skill level on knee musculature co-contraction during functional activities: A systematic review. Br. J. Sports Med. 2008, 42, 561–566. [Google Scholar] [CrossRef] [PubMed]
- Kubo, K.; Teshima, T.; Hirose, N.; Tsunoda, N. Growth changes in morphological and mechanical properties of human patellar tendon in vivo. J. Appl. Biomech. 2014, 30, 415–422. [Google Scholar] [CrossRef]
- Kavvoura, A.; Zaras, N.; Stasinaki, A.-N.; Arnaoutis, G.; Methenitis, S.; Terzis, G. The Importance of Lean Body Mass for the Rate of Force Development in Taekwondo Athletes and Track and Field Throwers. J. Funct. Morphol. Kinesiol. 2018, 3, 43. [Google Scholar] [CrossRef]
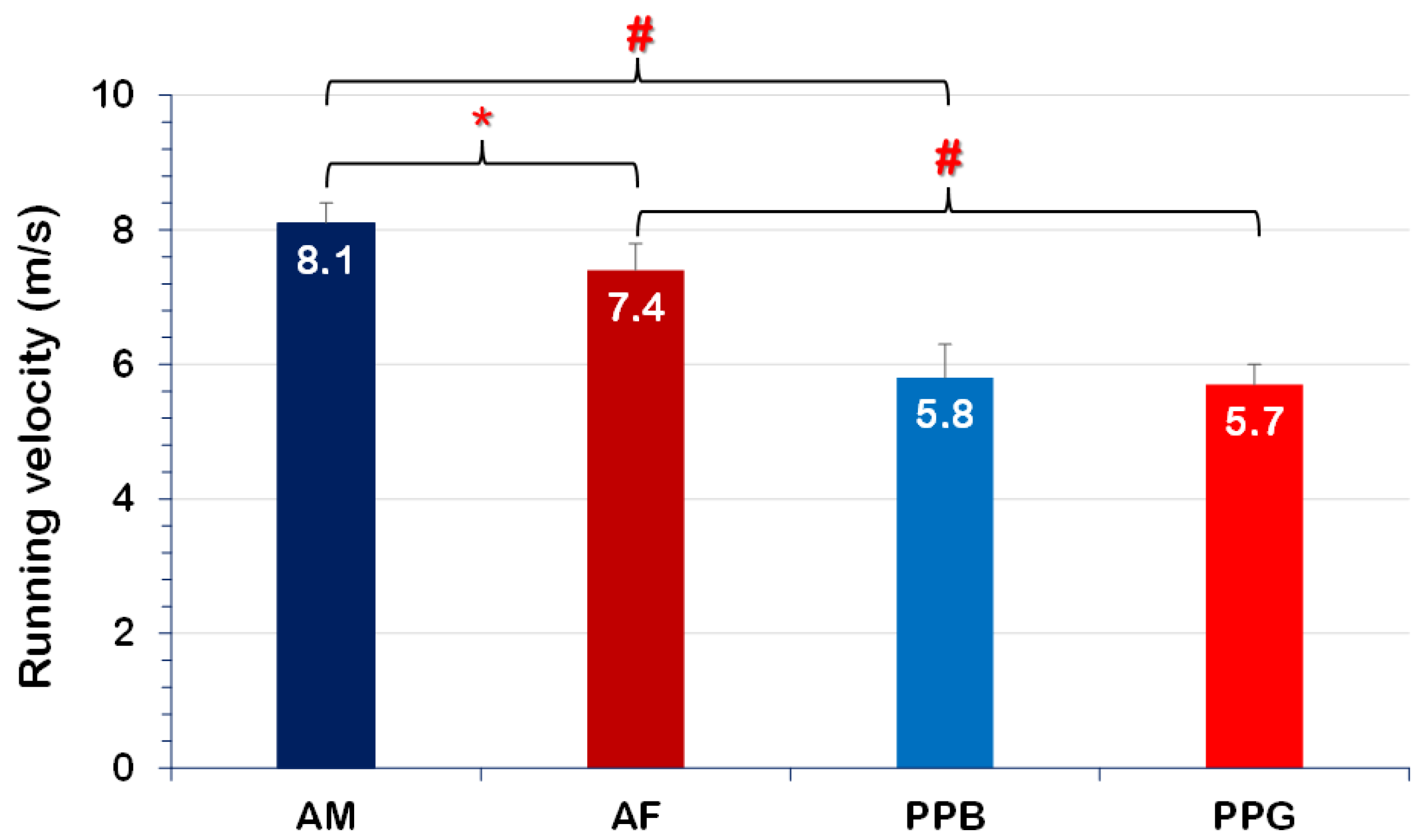
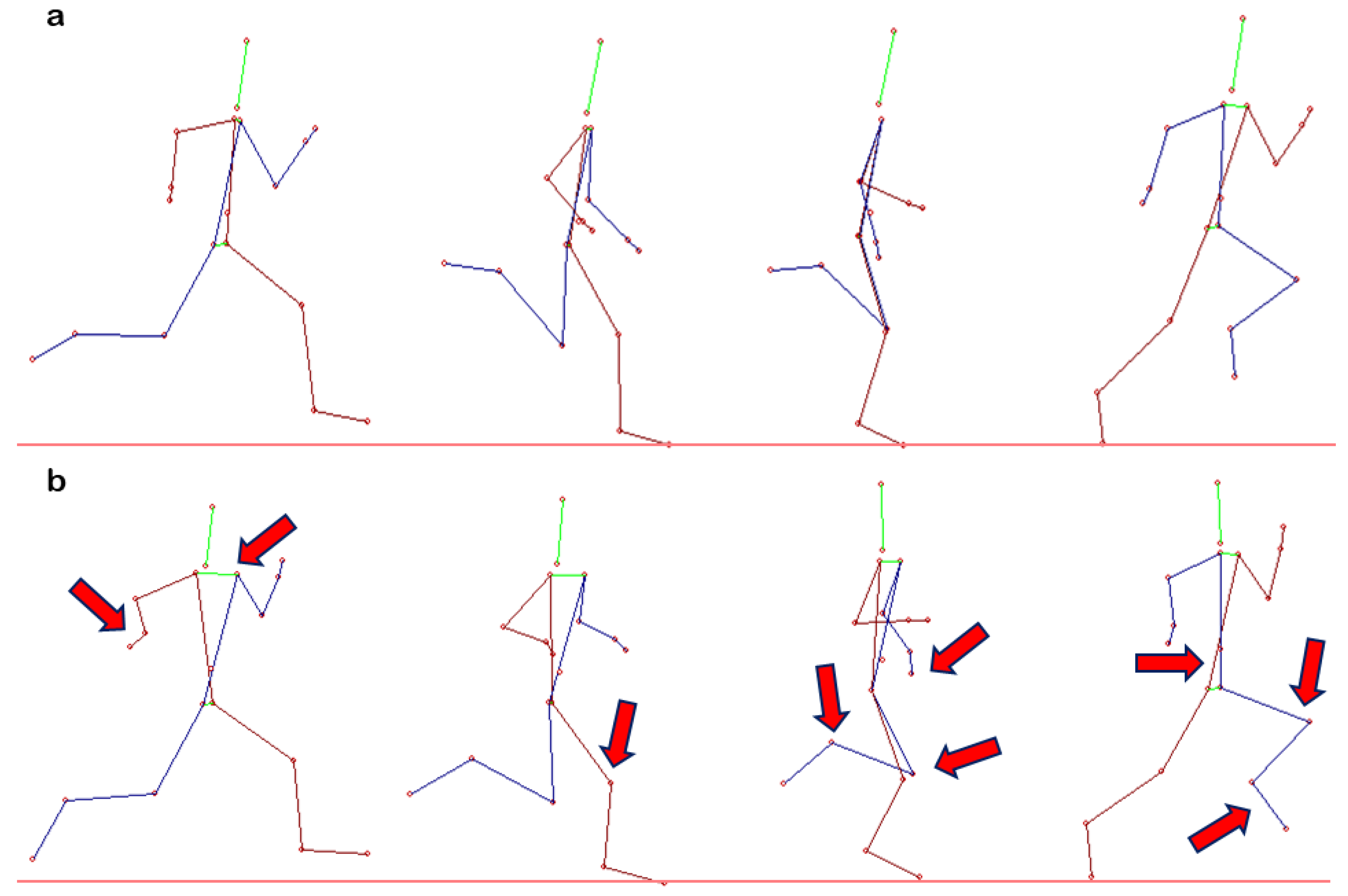

| Group | n | Age (yrs) | Body Height (m) | Body Mass (kg) | Training Experience (yrs) | Sprint Performance (s) |
|---|---|---|---|---|---|---|
| AM | 14 | 21.4 ± 3.7 | 1.75 ± 0.06 | 68.0 ± 8.4 | 11.1 ± 3.1 | 10.9 ± 0.3 a |
| AF | 8 | 21.1 ± 2.6 | 1.68 ± 0.03 | 58.9 ± 4.7 | 10.6 ± 2.1 | 12.4 ± 0.3 a |
| PPB | 10 | 10.8 ± 1.0 | 1.49 ± 0.09 | 40.3 ± 8.3 | 2.8 ± 0.9 | 8.6 ± 0.7 b |
| PPG | 10 | 11.2 ± 0.8 | 1.53 ± 0.08 | 44.5 ± 8.5 | 3.1 ± 0.9 | 8.7 ± 0.4 b |
| Parameter | AM (n = 14) | AF (n = 8) | PPB (n = 10) | PPG (n = 10) |
|---|---|---|---|---|
| Step length (SL, m) | 2.08 ± 0.15 | 1.95 ± 0.12 | 1.56 ± 0.17 # | 1.55 ± 0.07 # |
| Step length (SL, %body height) | 118.3 ± 5.8 | 115.7 ± 7.1 | 104.4 ± 8.0 # | 101.6 ± 3.9 # |
| Step frequency (SF, Hz) | 4.54 ± 0.27 | 4.01 ± 0.23 * | 4.03 ± 0.41 # | 3.90 ± 0.34 |
| Contact time (TC, s) | 0.10 ± 0.01 | 0.11 ± 0.02 * | 0.13 ± 0.02 # | 0.14 ± 0.02 # |
| Contact time (TC, % step time) | 43.0 ± 2.1 | 45.6 ± 6.1 | 53.2 ± 4.0 # | 54.2 ± 4.1 # |
| Flight time (Tf, s) | 0.13 ± 0.01 | 0.14 ± 0.02 | 0.12 ± 0.01 | 0.12 ± 0.01 |
| Horizontal BCM take-off velocity (VxTO, m/s) | 9.57 ± 0.57 | 7.82 ± 0.65 * | 6.36 ± 0.66 # | 6.26 ± 0.49 # |
| Vertical BCM take-off velocity (VyTO, m/s) | 0.59 ± 0.14 | 0.62 ± 0.13 | 0.50 ± 0.10 | 0.46 ± 0.12 # |
| Angle of projection (AngPr, deg) | 3.5 ± 0.8 | 4.6 ± 1.2 * | 4.5 ± 0.9 # | 4.2 ± 1.2 |
| Touchdown distance (STD, m) | 0.35 ± 0.03 | 0.39 ± 0.04 * | 0.35 ± 0.04 | 0.36 ± 0.04 |
| Touchdown distance (STD, %body height) | 20.1 ± 1.6 | 22.8 ± 2.5 * | 23.8 ± 2.5 # | 23.9 ± 2.5 |
| Take-off distance (STO, m) | 0.52 ± 0.05 | 0.49 ± 0.07 | 0.46 ± 0.05 | 0.45 ± 0.02 |
| Take-off distance (STO, %body height) | 29.8 ± 2.6 | 30.7 ± 3.7 | 30.6 ± 2.4 # | 29.4 ± 1.8 |
| BCM height at touchdown (HTD, %body height) | 54.7 ± 2.1 | 53.5 ± 1.4 | 53.9 ± 1.4 | 54.2 ± 1.3 |
| Minimum BCM height (HAM, %body height) | 53.6 ± 2.2 | 52.5 ± 1.3 | 52.1 ± 1.3 # | 52.4 ± 1.3 |
| Lowering of BCM during support phase (ΔHAM, m) | −0.02 ± 0.01 | −0.02 ± 0.01 | −0.03 ± 0.01 # | −0.03 ± 0.01 # |
| BCM height at take-off (HTO, %body height) | 56.2 ± 2.3 | 55.4 ± 0.8 | 55.8 ± 1.1 | 55.7 ± 0.9 |
| Sex | Age | Interaction | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | F | p | ηp2 | F | p | ηp2 | F | p | ηp2 |
| Step length (SL, m) | 2.404 | 0.130 | 0.061 | 111.041 | <0.001 # | 0.755 | 1.802 | 0.188 | 0.046 |
| Step length (SL, %body height) | 1.719 | 0.198 | 0.046 | 45.637 | <0.001 # | 0.559 | 0.001 | 0.971 | 0.000 |
| Step frequency (SF, Hz) | 7.130 | 0.011 * | 0.165 | 11.740 | 0.002 # | 0.246 | 2.030 | 0.163 | 0.053 |
| Contact time (TC, s) | 8.204 | 0.007 * | 0.178 | 51.074 | <0.001 # | 0.573 | 1.708 | 0.199 | 0.043 |
| Contact time (TC, % step time) | 2.025 | 0.163 | 0.051 | 54.307 | <0.001 # | 0.588 | 0.366 | 0.549 | 0.010 |
| Flight time (Tf, s) | 0.070 | 0.792 | 0.002 | 5.583 | 0.024 # | 0.134 | 0.000 | 0.995 | 0.000 |
| Horizontal BCM take-off velocity (VxTO, m/s) | 23.789 | <0.001 * | 0.391 | 158.841 | <0.001 # | 0.811 | 18.822 | <0.001 † | 0.337 |
| Vertical BCM take-off velocity (VyTO, m/s) | 0.006 | 0.939 | 0.000 | 9.408 | 0.004 # | 0.203 | 1.043 | 0.314 | 0.027 |
| Angle of projection (AngPr, deg) | 1.663 | 0.205 | 0.043 | 1.116 | 0.298 | 0.029 | 4.981 | 0.032 † | 0.119 |
| Touchdown distance (STD, m) | 4.216 | 0.047 * | 0.102 | 1.073 | 0.307 | 0.028 | 1.429 | 0.240 | 0.037 |
| Touchdown distance (STD, %body height) | 3.759 | 0.060 | 0.095 | 10.788 | 0.002 # | 0.231 | 3.261 | 0.079 | 0.083 |
| Take-off distance (STO, m) | 1.401 | 0.244 | 0.036 | 11.991 | 0.001 # | 0.245 | 0.393 | 0.534 | 0.011 |
| Take-off distance (STO, %body height) | 0.025 | 0.875 | 0.001 | 0.099 | 0.754 | 0.003 | 1.598 | 0.214 | 0.042 |
| BCM height at touchdown (HTD, %body height) | 0.802 | 0.376 | 0.022 | 0.004 | 0.950 | 0.000 | 1.841 | 0.183 | 0.049 |
| Minimum BCM height (HAM, %body height) | 0.521 | 0.475 | 0.014 | 2.230 | 0.144 | 0.058 | 1.632 | 0.210 | 0.043 |
| Lowering of BCM during support phase (ΔHAM, m) | 0.223 | 0.639 | 0.006 | 9.733 | 0.003 # | 0.208 | 0.223 | 0.639 | 0.006 |
| BCM height at take-off (HTO, %body height) | 0.828 | 0.369 | 0.022 | 0.028 | 0.868 | 0.001 | 0.462 | 0.501 | 0.013 |
| Parameter | AM (n = 14) | AF (n = 8) | PPB (n = 10) | PPG (n = 10) |
|---|---|---|---|---|
| Knee angle at touchdown (θkneeTD, deg) | 148.9 ± 7.6 | 148.7 ± 6.7 | 149.0 ± 5.1 | 144.0 ± 6.9 |
| Minimum knee angle during support phase (θkneeAM, deg) | 145.4 ± 7.1 | 139.1 ± 5.5 | 143.9 ± 5.0 | 134.3 ± 6.7 |
| Knee flexion at the breaking phase (ΔkneeAM, deg) | −3.5 ± 2.0 | −9.6 ± 6.2 * | −5.2 ± 2.4 | −8.1 ± 3.8 |
| Knee angle at take-off (θkneeTO, deg) | 153.7 ± 0.6 | 154.2 ± 5.2 | 157.5 ± 5.6 | 158.0 ± 5.5 |
| Ankle horizontal velocity at touchdown (Vxankle, m/s) | 1.95 ± 0.46 | 1.66 ± 0.40 | 2.45 ± 0.40 | 2.71 ± 1.20 # |
| Ankle horizontal velocity at touchdown (relative to VxTD, m/s) | −7.40 ± 0.74 | −6.18 ± 0.43 | −3.69 ± 0.60 # | −3.35 ± 1.08 # |
| Ankle angular velocity at touchdown (ωknee, rad/sec) | −5.4 ± 1.4 | −6.1 ± 2.5 * | −2.5 ± 2.8# | −3.5 ± 2.1 * |
| Ankle angle at touchdown (θankleTD, deg) | 103.6 ± 5.4 | 109.1 ± 6.0 * | 104.9 ± 4.4 | 106.1 ± 7.8 |
| Ankle angle at take-off (θankleTO, deg) | 123.2 ± 4.3 | 131.4 ± 4.1 * | 125.9 ± 6.4 | 128.8 ± 5.2 |
| Ankle joint range of motion during support (ΔankleTO, deg) | 19.6 ± 5.3 | 22.3 ± 6.1 | 21.0 ± 8.0 | 22.7 ± 6.1 |
| Minimum swing leg’s knee angle during support (θkneeMIN, deg) | 35.5 ± 5.9 | 33.9 ± 5.1 | 46.8 ± 14.6 | 39.9 ± 8.2 |
| Maximum swing leg’s knee angular velocity (ωkneeS, rad/s) | 16.8 ± 2.5 | 16.7 ± 2.0 | 13.2 ± 1.5 | 12.8 ± 2.5 |
| Swing leg’s knee angle at take-off (θkneeS, deg) | 69.0 ± 7.4 | 76.5 ± 12.2 * | 78.1 ± 14.4 | 71.3 ± 5.9 |
| Swing leg’s ankle angle at take-off (θankleS, deg) | 109.7 ± 6.7 | 118.7 ± 10.8 * | 108.5 ± 7.5 | 107.0 ± 7.8 |
| Swing leg’s thigh inclination at take-off (φthighTO, deg) | −15.1 ± 7.2 | −18.5 ± 7.0 * | −26.7 ± 5.6 | −23.4 ± 7.7 |
| Support leg inclination at touchdown (φlegTD, deg) | 78.0 ± 4.0 | 75.7 ± 4.9 | 75.2 ± 3.9 | 74.2 ± 3.7 |
| Support leg inclination at take-off (φlegTO, deg) | 51.9 ± 3.6 | 54.7 ± 2.3 | 51.9 ± 4.0 | 52.4 ± 3.8 |
| Sex | Age | Interaction | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | F | p | ηp2 | F | p | ηp2 | F | p | ηp2 |
| Knee angle at touchdown (θkneeTD, deg) | 1.476 | 0.232 | 0.038 | 1.005 | 0.323 | 0.026 | 1.261 | 0.269 | 0.033 |
| Minimum knee angle during support phase (θkneeAM, deg) | 15.051 | <0.001 * | 0.295 | 2.402 | 0.130 | 0.063 | 0.675 | 0.417 | 0.018 |
| Knee flexion at the breaking phase (ΔkneeAM, deg) | 15.382 | <0.001 * | 0.294 | 0.019 | 0.892 | 0.001 | 1.973 | 0.168 | 0.051 |
| Knee angle at take-off (θkneeTO, deg) | 0.087 | 0.770 | 0.002 | 5.051 | 0.031 # | 0.120 | 0.000 | 0.998 | 0.000 |
| Ankle horizontal velocity at touchdown (Vxankle, m/s) | 0.005 | 0.944 | 0.000 | 11.989 | 0.001 # | 0.245 | 1.537 | 0.223 | 0.040 |
| Ankle horizontal velocity at touchdown (relative to VxTD, m/s) | 9.779 | 0.003 * | 0.209 | 174.317 | <0.001 # | 0.825 | 3.163 | 0.084 | 0.079 |
| Ankle angular velocity at touchdown (ωknee, rad/s) | 1.739 | 0.195 | 0.045 | 15.494 | <0.001 # | 0.295 | 0.049 | 0.825 | 0.001 |
| Ankle angle at touchdown (θankleTD, deg) | 2.966 | 0.093 | 0.074 | 0.196 | 0.661 | 0.005 | 1.204 | 0.280 | 0.032 |
| Ankle angle at take-off (θankleTO, deg) | 11.643 | 0.002 * | 0.239 | 0.000 | 0.999 | 0.000 | 2.626 | 0.114 | 0.066 |
| Ankle joint range of motion during support (ΔankleTO, deg) | 1.233 | 0.274 | 0.032 | 0.173 | 0.680 | 0.005 | 0.070 | 0.792 | 0.002 |
| Minimum swing leg’s knee angle during support (θkneeMIN, deg) | 2.086 | 0.157 | 0.053 | 8.435 | 0.006 # | 0.186 | 0.819 | 0.371 | 0.022 |
| Maximum swing leg’s knee angular velocity (ωkneeS, rad/s) | 0.134 | 0.716 | 0.004 | 25.982 | <0.001 # | 0.419 | 0.165 | 0.800 | 0.002 |
| Swing leg’s knee angle at take-off (θkneeS, deg) | 0.010 | 0.921 | 0.000 | 0.347 | 0.560 | 0.009 | 4.861 | 0.034 † | 0.116 |
| Swing leg’s ankle angle at take-off (θankleS, deg) | 2.038 | 0.016 | 0.055 | 6.038 | 0.019 # | 0.147 | 4.017 | 0.053 | 0.103 |
| Swing leg’s thigh inclination at take-off (φthighTO, deg) | 0.000 | 0.990 | 0.000 | 12.972 | <0.001 # | 0.265 | 2.123 | 0.154 | 0.056 |
| Support leg inclination at touchdown (φlegTD, deg) | 1.914 | 0.175 | 0.050 | 0.864 | 0.359 | 0.023 | 0.932 | 0.341 | 0.025 |
| Support leg inclination at take-off (φlegTO, deg) | 1.567 | 0.219 | 0.042 | 2.568 | 0.118 | 0.067 | 0.251 | 0.620 | 0.007 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chatzilazaridis, I.; Panoutsakopoulos, V.; Bassa, E.; Kotzamanidou, M.C.; Papaiakovou, G.I. Effects of Age and Sex on the Kinematics of the Sprinting Technique in the Maximum Velocity Phase. Appl. Sci. 2024, 14, 6057. https://doi.org/10.3390/app14146057
Chatzilazaridis I, Panoutsakopoulos V, Bassa E, Kotzamanidou MC, Papaiakovou GI. Effects of Age and Sex on the Kinematics of the Sprinting Technique in the Maximum Velocity Phase. Applied Sciences. 2024; 14(14):6057. https://doi.org/10.3390/app14146057
Chicago/Turabian StyleChatzilazaridis, Ioannis, Vassilios Panoutsakopoulos, Eleni Bassa, Mariana C. Kotzamanidou, and Georgios I. Papaiakovou. 2024. "Effects of Age and Sex on the Kinematics of the Sprinting Technique in the Maximum Velocity Phase" Applied Sciences 14, no. 14: 6057. https://doi.org/10.3390/app14146057
APA StyleChatzilazaridis, I., Panoutsakopoulos, V., Bassa, E., Kotzamanidou, M. C., & Papaiakovou, G. I. (2024). Effects of Age and Sex on the Kinematics of the Sprinting Technique in the Maximum Velocity Phase. Applied Sciences, 14(14), 6057. https://doi.org/10.3390/app14146057








