Acceleration of Service Life Testing by Using Weibull Distribution on Fiber Optical Connectors
Abstract
1. Introduction
2. Theoretical Background
2.1. Fiber Optical Connector Measurements
2.2. Proportional Hazard Models
2.3. Weibull Statistics Analysis
2.4. Weibull Stress Random Analysis
2.5. Vibration Analysis
3. Validation of the Procedure
3.1. Numerical Validation
3.2. Acceleration Coefficients Estimation
3.3. Accelerated Vibration
4. Results
5. Discussion
6. Conclusions
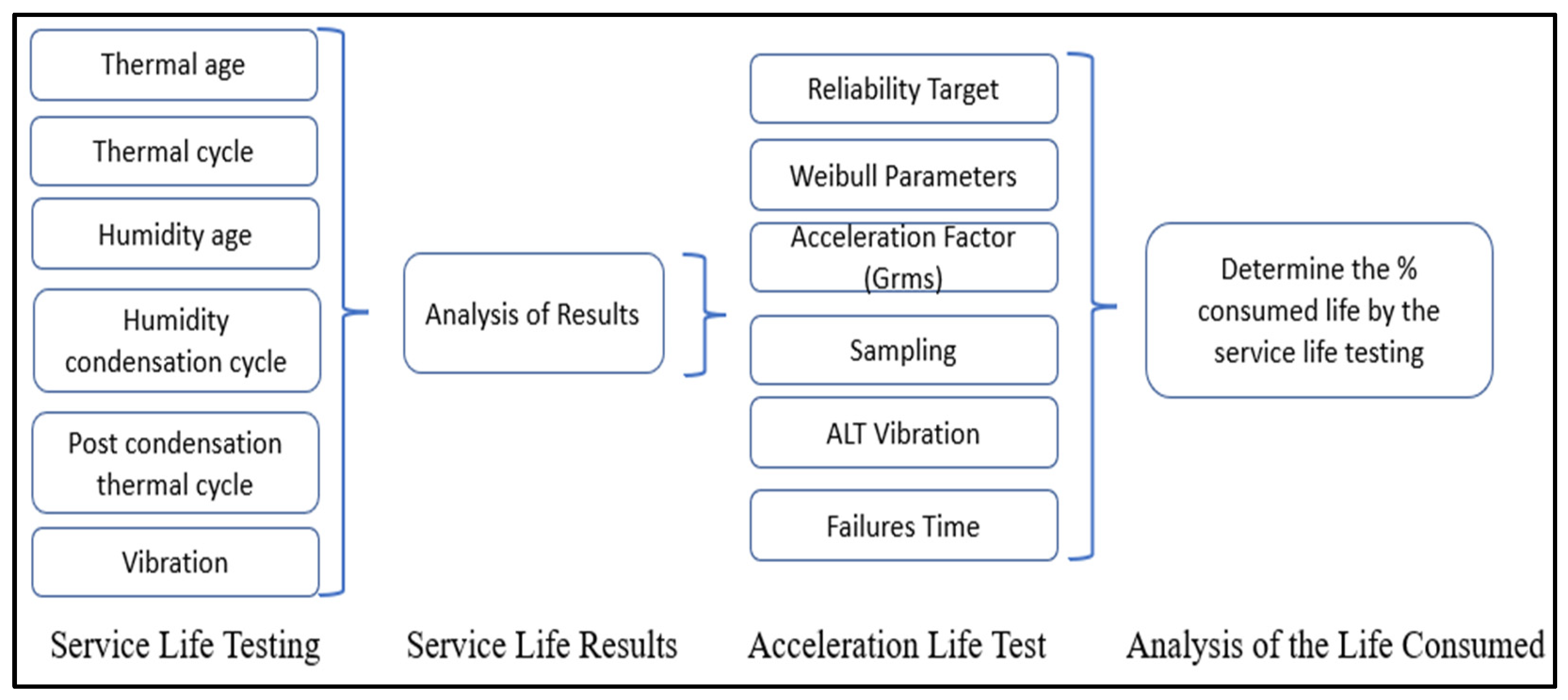
- A vibration ALT was developed using the probabilistic Weibull distribution and acceleration coefficients to estimate the reliability of the fiber optic connectors. According to the samples tested, the reliability R(t) was 0.970.
- The reliability was determined by the fiber optical connector failure times obtained from the insertion loss measurements performed during testing. The measurements were performed using Agilent N7745A equipment with an 8-channel optical multiport power meter, with a speed measurement data acquisition and transfer of 5 kHz per channel and with event detection in a wavelength range from 1310 to 1550 nm, as shown in Figure 1.
- This investigation can be applied to fiber optical connectors used in the telecommunications industry to assist in real and practical reliability analysis. An experiment by using the service life testing program from GR-326 was performed and its reliability R(t) = 0.694 was determined.
- By using the relation of the scale Weibull parameter data from each experiment, (1) service life testing program, and (2) vibration ALT, the percentage of the product’s service life consumed was obtained.
- Finally, to determine the reliability and the remaining life of a product, we recommend, based on the statistical Weibull analysis conducted, performing the service life tests, because each test of the service life consumes a percentage of the product’s life.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vacca, H.; Rodríguez, J.A.; Ruiz, D. Measurement and interpretation of vibrations produced by the traffic in Bogota D.C. Rev. Ing. Cons. 2011, 26, 60–80. [Google Scholar]
- Barraza-Contreras, J.M.; Piña-Monarrez, M.R.; Torres-Villaseñor, R.C. Vibration Fatigue Life Reliability Cable Trough Assessment by Using Weibull Distribution. App. Sci. 2023, 13, 4403. [Google Scholar] [CrossRef]
- Thomes, W.J.; Laroccaa, F.V.; Switzera, R.C.; Ott, M.N.; Chuskaa, R.F.; Macmurphya, S.L. Vibration Performance Comparison Study on Current Fiber Optic Connector Technologies. NASA 2019, 11, 6729. [Google Scholar]
- Patkó, G.; Takács, G.; Barna, B.; Demeter, P.; Hegedűs, G.; Barak, A.; Simon, G.; Szilágyi, A. A Process for Establishing the Remanent Lifetime of Rolling Element Bearings. In Proceedings of the XXIV microCAD International Scientific Conference, University of Miskolc, Miskolc, Hungary, 18–20 March 2010. [Google Scholar]
- Hiu, R.; O’Sullivan, M. Fiber-Optic Measurement Techniques, 2nd ed.; Academic Press: London, UK, 2023; pp. 61–64. [Google Scholar]
- Bagdonavicius, V.; Nikulin, M. Accelerated Life Models, 1st ed.; Champman & HALL/CRC: Boca Raton, FL, USA, 2002; pp. 29–32. [Google Scholar] [CrossRef]
- Berghmans, F.; Eve, S.; Held, M. An introduction to reliability of optical components and fiber optic sensors. In NATO Science for Peace and Security Series B: Physics and Biophysics; Bock, W.J., Gannot, I., Tanev, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 73–100. [Google Scholar] [CrossRef]
- Piña-Monarrez, M.R.; Baro-Tijerina, M.; Ortiz-Yañez, J.F. Weibull stress method to determine the minimum required strength to improve the actual reliability. Qual. Reliab. Eng. Int. 2023, 39, 2230–2243. [Google Scholar] [CrossRef]
- Piña-Monarrez, M.R. Weibull analysis for normal/accelerated and fatigue random vibration test. Qual. Reliab. Eng. Int. 2019, 35, 2408–2428. [Google Scholar] [CrossRef]
- Marin, E.B.; Tran, H.V.; Kobyakov, A. Mechanical performance of physical-contact, multi-fiber optical connectors: Finite element analysis and semi-analytical model. Opt. Fiber Technol. 2016, 30, 48–64. [Google Scholar] [CrossRef]
- Bartos, J.; Thomas, M.; Roter, M. Risk assessment of new programs as a basis for reliability planning. In Proceedings of the 2017 Annual Reliability and Maintainability Symposium, Orlando, FL, USA, 23–26 January 2017. [Google Scholar] [CrossRef]
- El Abdi, R.; Rujinski, A.D.; Poulain, M.; Severin, I. Damage of Optical Fibers Under Wet Environments. Exp. Mech. 2010, 50, 1225–1234. [Google Scholar] [CrossRef]
- Annovazzi-Lodi, V.; Donati, S.; Merlo, S.; Zapelloni, G. Statistical Analysis of Fiber Failures Under Bending-Stress Fatigue. J. Light. Technol. 1997, 15, 288–293. [Google Scholar] [CrossRef]
- Telcordia. Generic Requirements for Singlemode Optical Connectors and Jumper Assemblies GR-326, 4th ed.; Telcordia: Piscataway, NJ, USA, 2010; pp. 6.1–6.2. [Google Scholar]
- Angeli, A.; Cornelis, B.; Troncossi, M. Synthesis of Sine-on-Random vibration profiles for accelerated life tests based on fatigue damage spectrum equivalence. Mech. Syst. Signal Process. 2018, 103, 340–351. [Google Scholar] [CrossRef]
- Hoss, R.J.; Lacy, E.A. Fiber Optics, 2nd ed.; Prentice Hall PTR: Hoboken, NJ, USA, 1993; pp. 241–243. [Google Scholar]
- Unión Internacional de Telecomunicaciones. Empalmes de Fibra Óptica; Recomendación UIT-T L.12; UIT-T: Ginebra, Suiza, 2001; pp. 14–19. [Google Scholar]
- Optical Society of America. Fiber Optics Handbook. Fiber, Devices and Systems for Optical Communications, 1st ed.; McGraw-Hill: New York, NY, USA, 2002; pp. 4.55–4.56. [Google Scholar] [CrossRef]
- McCool, J.I. Using the Weibull Distribution: Reliability, Modeling, and Inference, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012; pp. 49–51. [Google Scholar]
- Zhang, Q.; Hua, C.; Xu, G. A mixture Weibull proportional hazard model for mechanical system failure prediction utilising lifetime and monitoring data. Mech. Syst. Signal Process 2014, 43, 103–112. [Google Scholar] [CrossRef]
- Carroll, K.J. On the use and utility of the Weibull model in the analysis of survival data. Control. Clin. Trials 2003, 24, 682–701. [Google Scholar] [CrossRef]
- Barraza-Contreras, J.M.; Piña-Monarrez, M.R.; Torres-Villaseñor, R.C. Reliability by Using Weibull Distribution Based on Vibration Fatigue Damage. App. Sci. 2023, 13, 10291. [Google Scholar] [CrossRef]
- Weibull, W. A Statistical Theory of the Strength of Materials; Generalstabens Litografiska Anstalts Förlag: Stockholm, Sweden, 1939. [Google Scholar]
- Piña-Monarrez, M.R. Weibull stress distribution for static mechanical stress and its stress/strength analysis. Qual. Reliab. Eng. Int. 2018, 34, 229–244. [Google Scholar] [CrossRef]
- Mischke, C.R. A distribution-Independent Plotting Rule for Ordered Failures. J. Mech. Des. 1979, 104, 593–597. [Google Scholar] [CrossRef]
- Edson, L. The GMW3172 Users Guide; The Electrical Validation Engineers Handbook Series; Electrical Component Testing. 2015. Available online: https://kolegite.com/EE_library/books_and_lectures/%D0%9A%D0%B0%D1%87%D0%B5%D1%81%D1%82%D0%B2%D0%BE%20%D0%B8%20%D0%BD%D0%B0%D0%B4%D0%B5%D0%B6%D0%B4%D0%BD%D0%BE%D1%81%D1%82%20%D0%BD%D0%B0%20%D0%B5%D0%BB%D0%B5%D0%BA%D1%82%D1%80%D0%BE%D0%BD%D0%BD%D0%B0%D1%82%D0%B0%20%D0%B0%D0%BF%D0%B0%D1%80%D0%B0%D1%82%D1%83%D1%80%D0%B0/Handbook_testing.pdf (accessed on 24 June 2022).
- Serway, R.A.; Jewett, J.W. Física para Ciencias e Ingeniería, 10th ed.; Cengage: Mexico City, Mexico, 2019; pp. 404–406. [Google Scholar]
- Gutierrez-Wing, E.S.; Vélez-Castan, G.; Szwedowicz-Wasik, D.; Bedolla-Hernández, J.; Cortés-Garcia, C. Identification of Close Vibration Modes of a Quasi-Axisymmetric Structure: Complementary Study. Ing. Investig. Tecnol. 2013, XIV, 207–222. [Google Scholar]
- Barraza-Contreras, J.M.; Piña-Monarrez, M.R.; Rodríguez-Borbón, M.I. Método Weibull para la Reducción de Tiempo de Prueba Ambiental para Divisor Óptico. Rev. Cienc. Tecnológicas 2019, 2, 137–143. [Google Scholar] [CrossRef]
- General Motors Company; Worldwide Engineering Standards. Test Procedure GMW8758 Calibrated Accelerated Life Testing (CALT); GMW: Detroit, MI, USA, 2011; pp. 2–3. [Google Scholar]



| Failure Times in Vibration Service Life Test | |||
|---|---|---|---|
| Sample ID | Failure Time (h) | Insertion Loss Requirement (dB) | Insertion Loss Result (dB) |
| 1 | 4.670 | 0.400 | 0.501 |
| 2 | 5.000 | 0.400 | 0.576 |
| 3 | 5.500 | 0.400 | 0.485 |
| 4 | 5.830 | 0.400 | 0.566 |
| 5 | 12.289 | 0.400 | 0.464 |
| 6 | 13.861 | 0.400 | 0.561 |
| fi (Hz) | PSDi (G2/Hz) | dB | Oct | m (dB/Oct) | Area | Grms |
|---|---|---|---|---|---|---|
| 10 | 0.004 | 0.000 | 0.000 | 0.000 | 0.040 | |
| 20 | 0.02 | 6.990 | 1.000 | 6.990 | 0.108 | |
| 30 | 0.06 | 4.771 | 0.585 | 8.156 | 0.377 | |
| 40 | 0.14 | 3.680 | 0.415 | 8.866 | 0.963 | |
| 50 | 0.30 | 3.310 | 0.322 | 10.282 | 2.129 | |
| 55 | 0.4 | 1.249 | 0.138 | 9.086 | 1.742 | |
| 5.320 | 2.306 |
| fi (Hz) | PSDi (G2/Hz) | dB | Oct | m (dB/Oct) | Area | Grms |
|---|---|---|---|---|---|---|
| 16.599 | 0.004 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 33.197 | 0.020 | 6.990 | 1.000 | 6.990 | 0.180 | |
| 49.796 | 0.060 | 4.771 | 0.585 | 8.156 | 0.626 | |
| 66.394 | 0.140 | 3.680 | 0.415 | 8.866 | 1.599 | |
| 82.993 | 0.300 | 3.310 | 0.322 | 10.282 | 3.534 | |
| 91.292 | 0.400 | 1.249 | 0.138 | 9.086 | 2.891 | |
| 8.833 | 2.972 |
| Sample ID | Failure Time (H) | Requirement (dB) | Result (dB) |
|---|---|---|---|
| 1 (service life survived) | 4.00 | 0.400 | 0.464 |
| 2 (service life survived) | 5.00 | 0.400 | 0.561 |
| 1 (new Sample without service life) | 66.00 | 0.400 | 0.876 |
| 2 (new Sample without service life) | 63.00 | 0.400 | 0.509 |
| Samples ID | Failure Time (h) Deaccelerated |
|---|---|
| 1 (service life survived) | 6.639 |
| 2 (service life survived) | 8.299 |
| 1 (new Sample without service life) | 109.550 |
| 2 (new Sample without service life) | 104.571 |
| ni | Yi Equation (12) | µy Equation (13) | R(t) Equation (14) | toi Equation (15) | σ2i Equation (16) | σ1i Equation (17) |
|---|---|---|---|---|---|---|
| 1 | −2.156 | −0.359 | 0.891 | 0.312 | 2.509 | 25.803 |
| 2 | −1.175 | −0.196 | 0.734 | 0.523 | 4.262 | 15.188 |
| −1.008 | −0.544 | 0.694 | 0.580 | 4.670 | 13.861 | |
| 3 | −0.602 | −0.100 | 0.578 | 0.722 | 5.812 | 11.138 |
| 4 | −0.147 | −0.025 | 0.422 | 0.924 | 7.429 | 8.712 |
| 5 | 0.282 | 0.047 | 0.266 | 1.165 | 9.370 | 6.908 |
| 6 | 0.794 | 0.132 | 0.109 | 1.536 | 12.361 | 5.237 |
| ni | Yi Equation (12) | µy Equation (13) | R(t) Equation (20) | toi Equation (15) | σ2i Equation (16) | σ1i Equation (17) |
|---|---|---|---|---|---|---|
| −3.504 | −1.402 | 0.970 | 0.246 | 6.639 | 109.550 | |
| 1 | −1.753 | −0.438 | 0.841 | 0.496 | 13.377 | 54.371 |
| 2 | −0.717 | −0.179 | 0.614 | 0.751 | 20.247 | 35.922 |
| 3 | −0.050 | −0.013 | 0.386 | 0.980 | 26.432 | 27.516 |
| 4 | 0.609 | 0.152 | 0.159 | 1.276 | 34.405 | 21.139 |
| Weibull | Service Life Testing | Vibration ALT |
|---|---|---|
| 1.850 | 2.500 | |
| 8.045 | 26.967 | |
| −0.501 | −0.617 | |
| 2.085 | 3.295 | |
| 0.694 | 0.970 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barraza-Contreras, J.M.; Piña-Monarrez, M.R.; Hernández-Ramos, M.M.; Monclova-Quintana, O.; Ramos-Lozano, S. Acceleration of Service Life Testing by Using Weibull Distribution on Fiber Optical Connectors. Appl. Sci. 2024, 14, 6198. https://doi.org/10.3390/app14146198
Barraza-Contreras JM, Piña-Monarrez MR, Hernández-Ramos MM, Monclova-Quintana O, Ramos-Lozano S. Acceleration of Service Life Testing by Using Weibull Distribution on Fiber Optical Connectors. Applied Sciences. 2024; 14(14):6198. https://doi.org/10.3390/app14146198
Chicago/Turabian StyleBarraza-Contreras, Jesús M., Manuel R. Piña-Monarrez, María M. Hernández-Ramos, Osvaldo Monclova-Quintana, and Secundino Ramos-Lozano. 2024. "Acceleration of Service Life Testing by Using Weibull Distribution on Fiber Optical Connectors" Applied Sciences 14, no. 14: 6198. https://doi.org/10.3390/app14146198
APA StyleBarraza-Contreras, J. M., Piña-Monarrez, M. R., Hernández-Ramos, M. M., Monclova-Quintana, O., & Ramos-Lozano, S. (2024). Acceleration of Service Life Testing by Using Weibull Distribution on Fiber Optical Connectors. Applied Sciences, 14(14), 6198. https://doi.org/10.3390/app14146198







