Calculation Model for the Exit Decision Sight Distance of Right-Turn Ramps on the Left at Interchange
Abstract
:1. Introduction
2. Data Collection and Analysis
2.1. Data Collection
2.2. Data Analysis
- Datasets in which trajectories began and ended nearby, including those encompassing road markings within the detection range, were discarded.
- Iteration through each frame of the vehicle trajectory was conducted to eliminate data points with x-coordinates that were less than their predecessors.
- Vehicle trajectory data located on the paved shoulder were excluded.
2.2.1. Vehicle Speed
2.2.2. Time Headway
2.2.3. Lane-Change Behavior
3. Driver Behavior Simulation
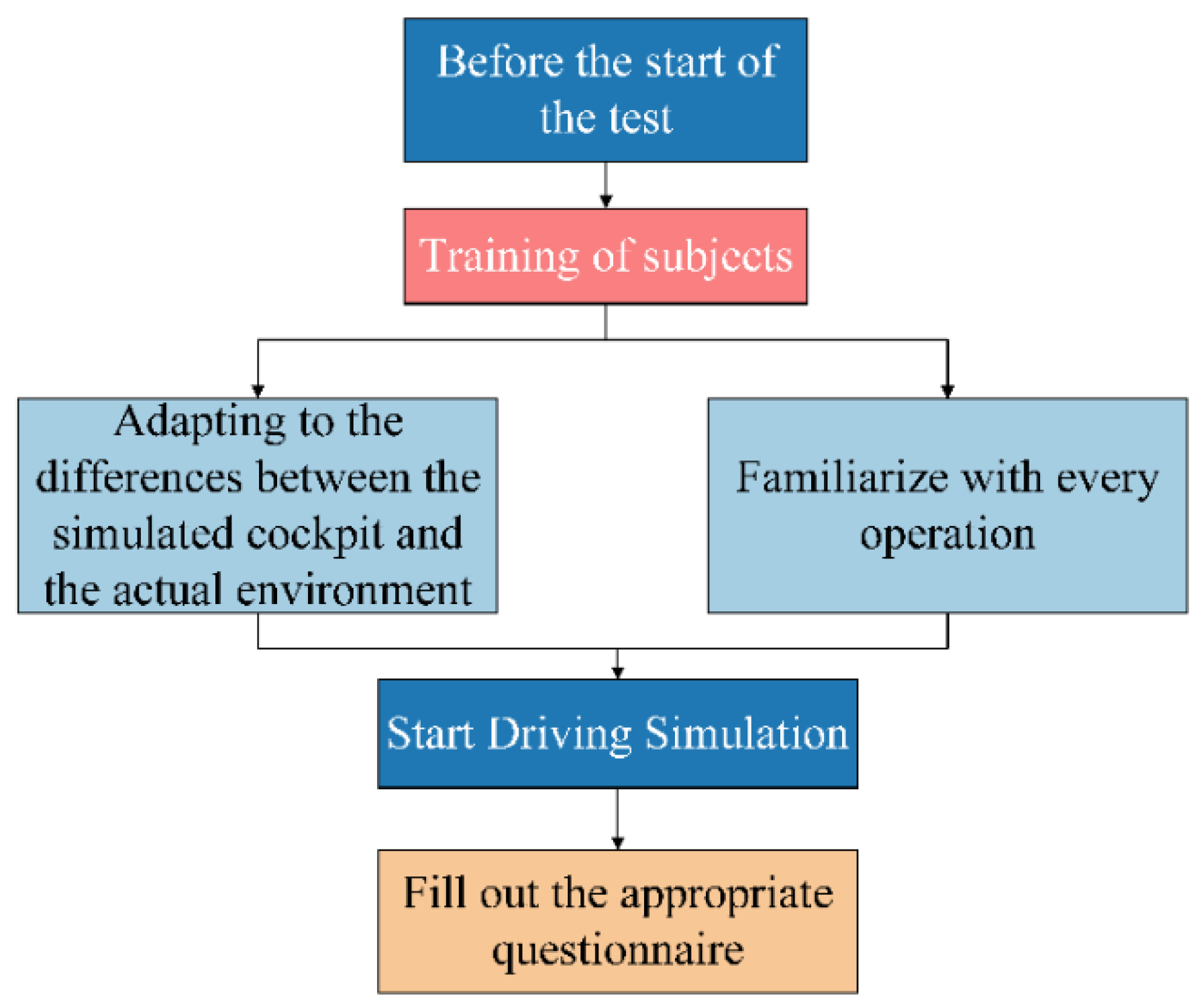
3.1. Determination of Test Apparatus and Personnel
- Subjects were required to be in a normal physiological condition before commencing the test.
- Prior simulated driving training was mandatory to ensure complete familiarity with and mastery of the simulated cockpit operation. This training aimed to facilitate adaptation to the differences between a simulated driving environment and that of a real vehicle.
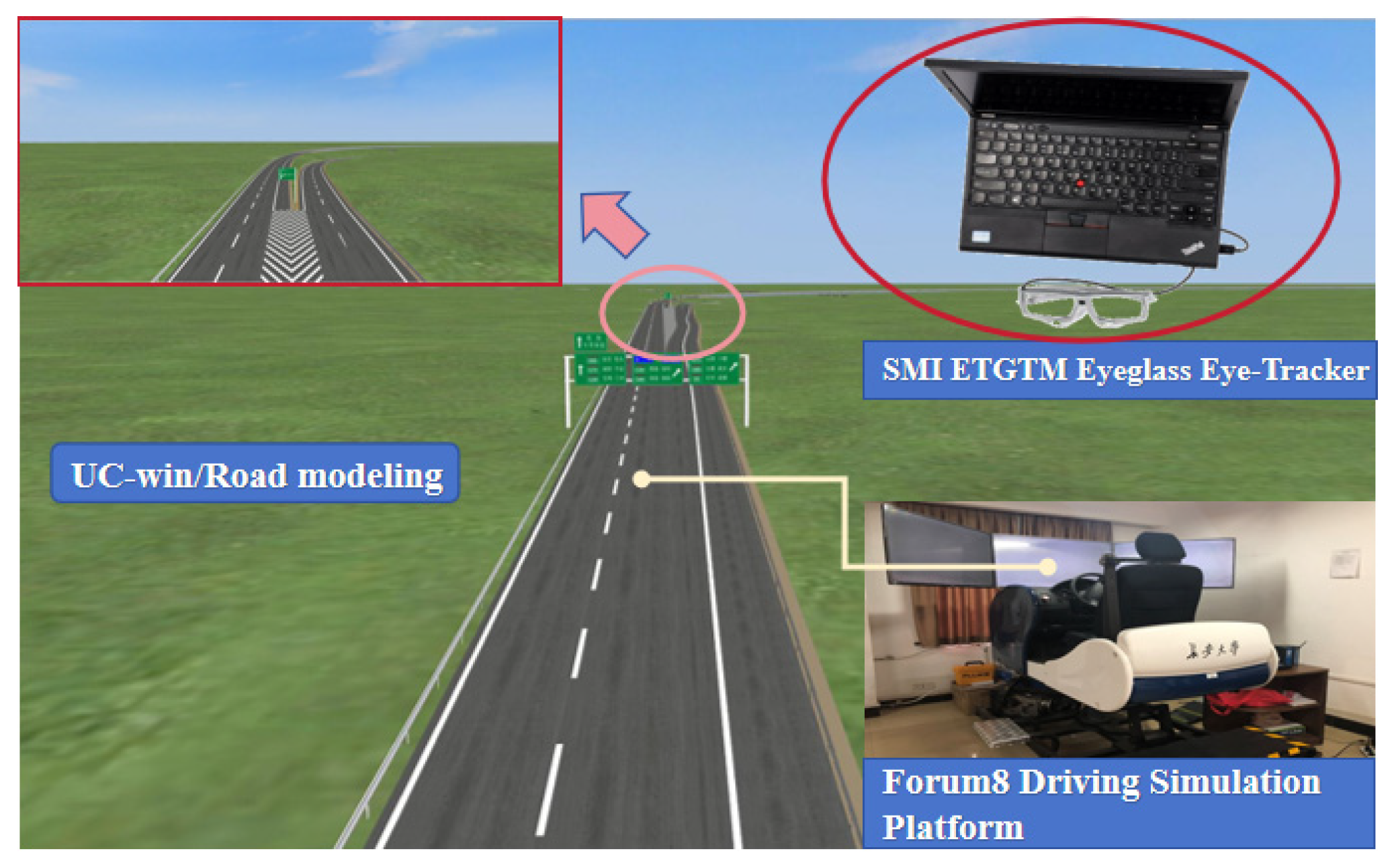
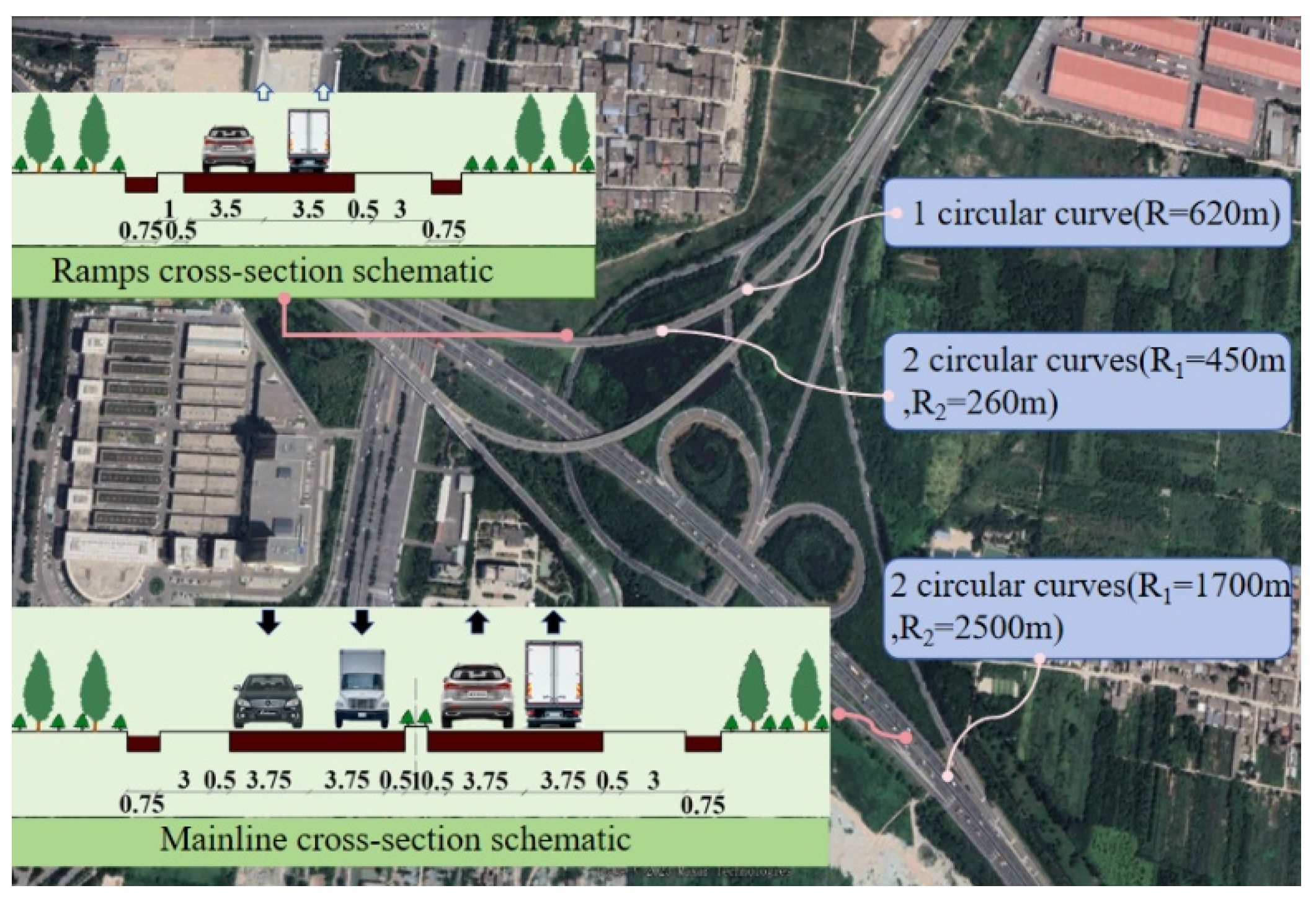
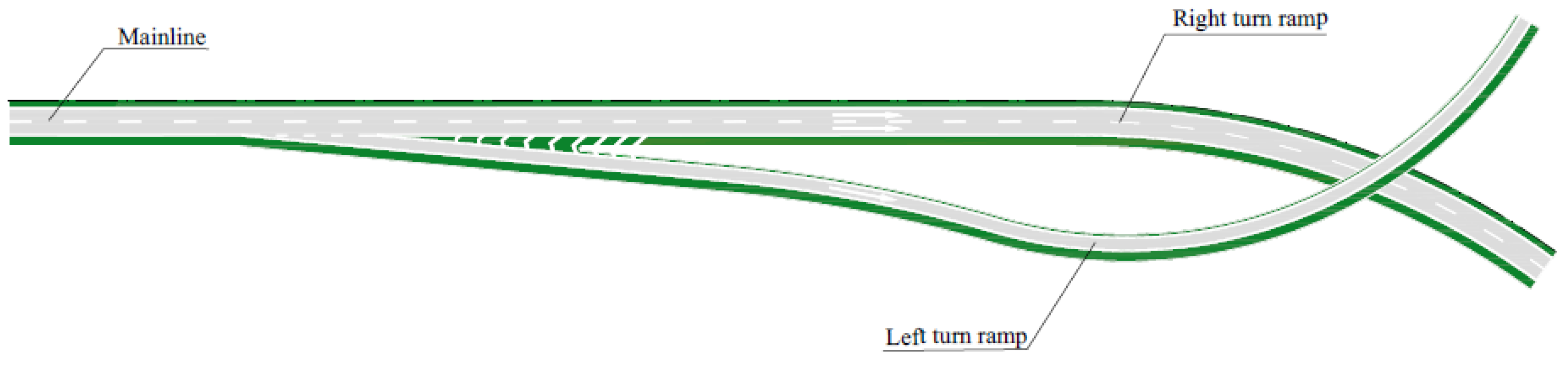
3.2. Scene Modeling and Test Procedure
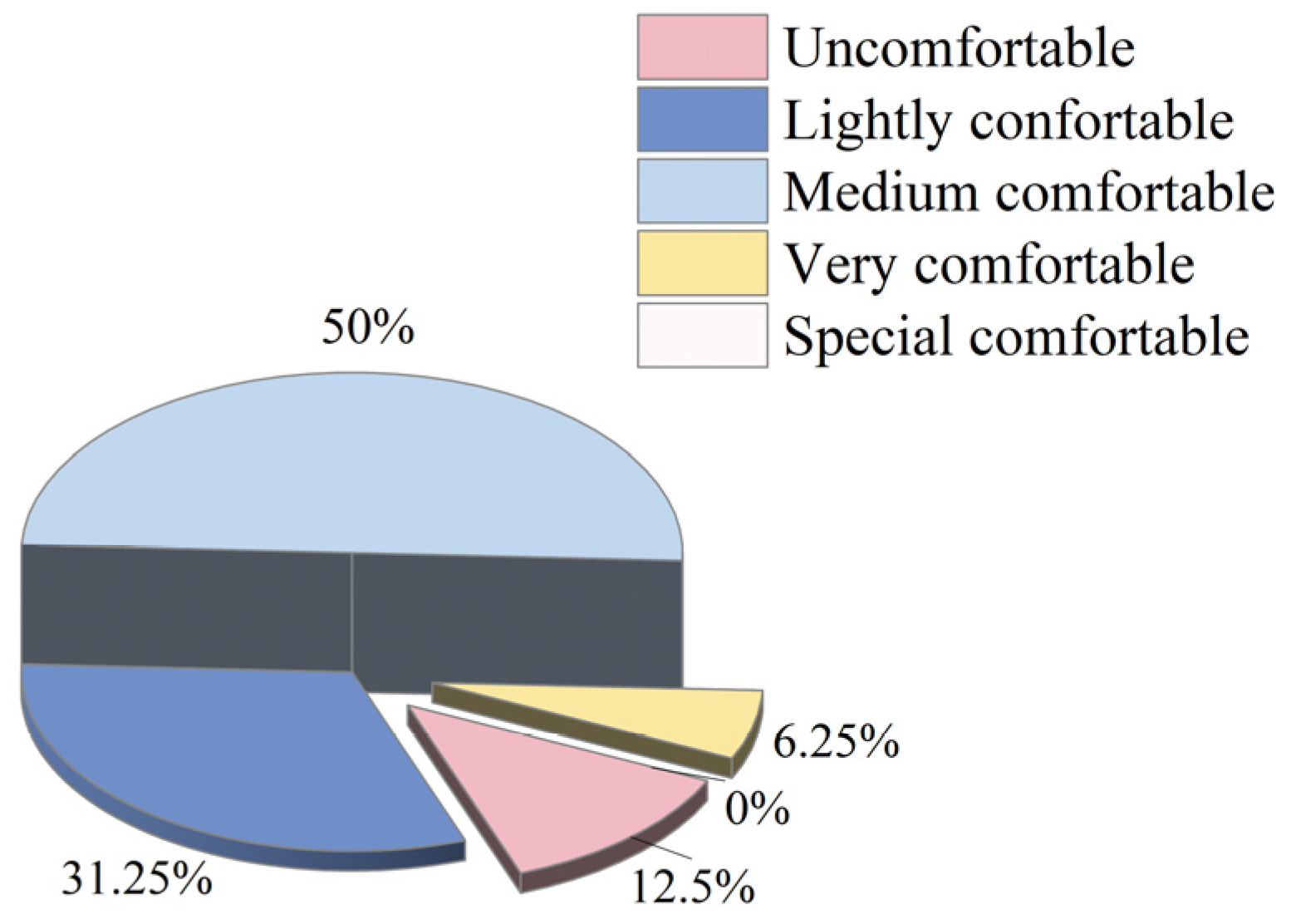
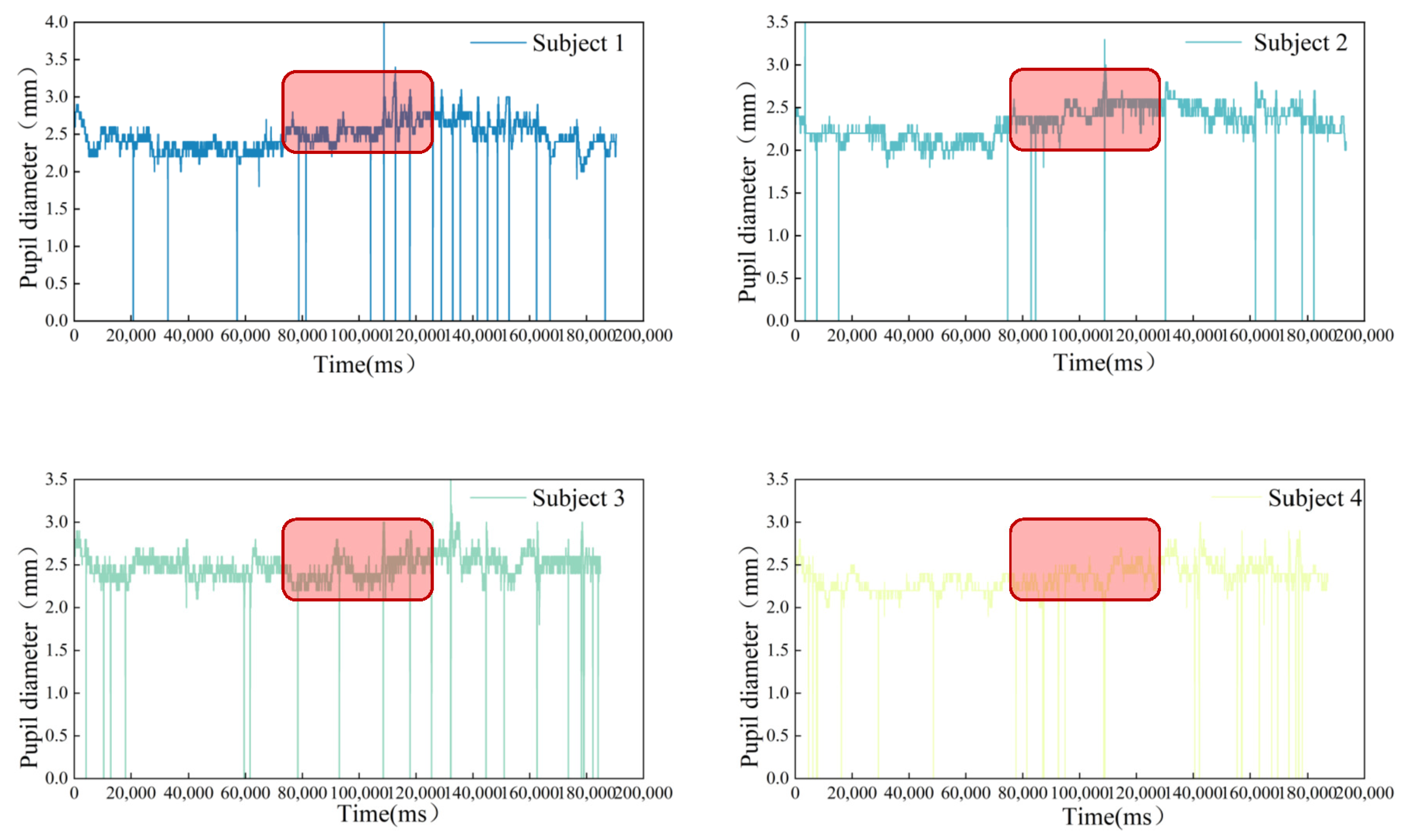
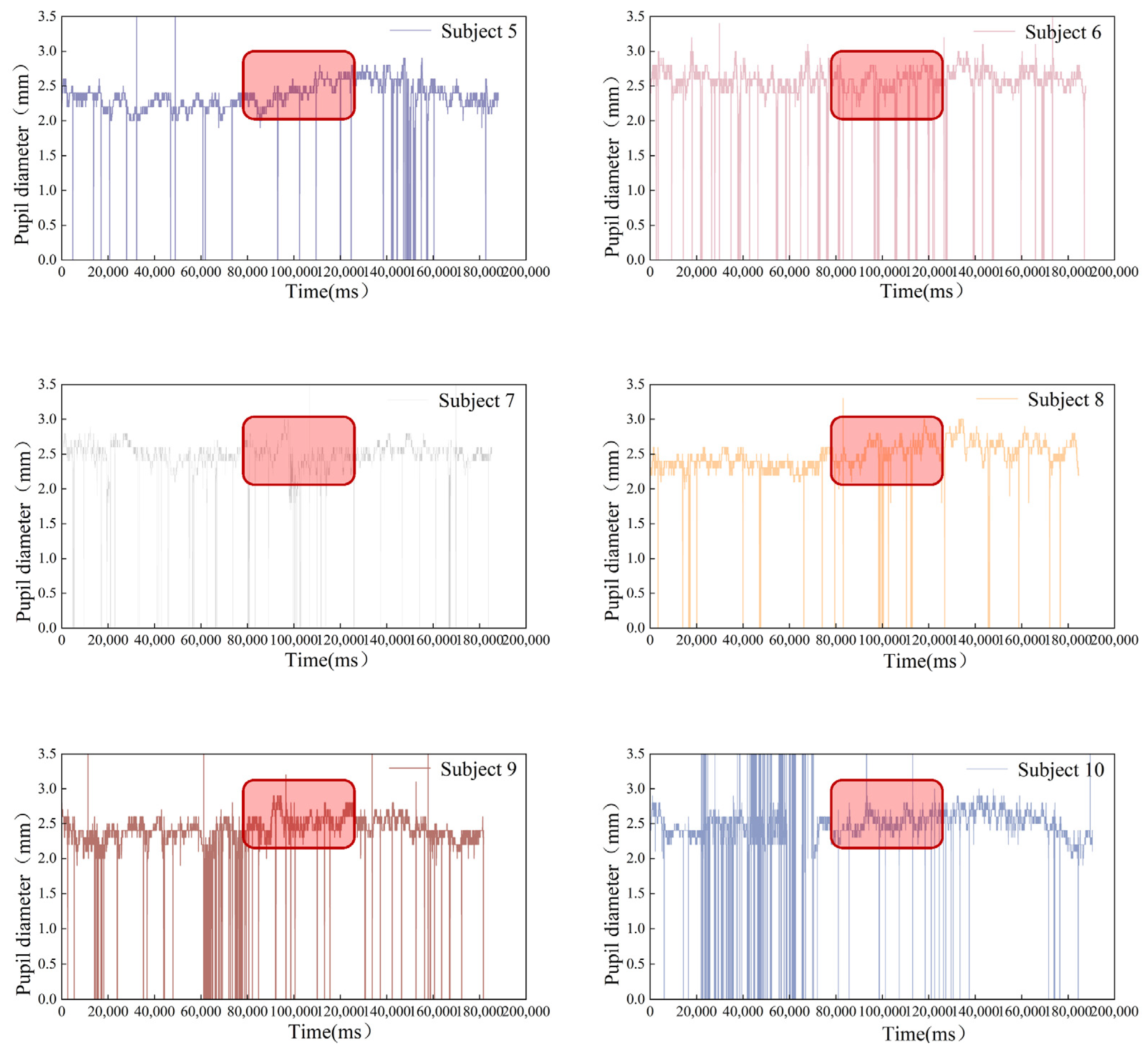
3.3. Driver Accuracy and Comfort
3.4. Driver Workload Measurement and Results
- Subjective Measurement
- The weightings assigned to the three load dimensions—mental demand, time demand, and effort, are notably substantial, indicating elevated demands on drivers’ cognitive faculties, decision-making skills, and attentiveness caused by RTRL. Simultaneously, ensuring optimal driving efficiency within RTRL necessitates the application of relevant design parameters and signage placement, enabling drivers to have sufficient reaction time for operations.
- The majority of subjects exhibit higher workload values, confirming the escalated complexity involved in the driving task within RTRL.
- 2.
- Task Performance Measures
- 3.
- Physiological Measurements
4. Calculation and Results
4.1. Calculation Model
4.2. Decision Distance S1
4.3. Queuing Distance S2
4.4. Execution of Lane-Change Distance S3
5. Conclusions
- Utilizing UAV aerial photography combined with the YOLOv3 target detection algorithm, Kalman filtering, and the Frenet coordinate transformation method, microscopic lane-changing trajectory data is obtained. This data analysis sheds light on the travel speed, headway, and lane-changing behaviors within the left exit section of the right-turn ramp.
- Employing the modified hyperbolic tangent function lane-change trajectory model, Python calculations yield a 97.18% goodness of fit for the right lane change, affirming the accuracy of this model in depicting vehicle driving characteristics. Furthermore, the vehicle’s headway adheres to the 2-stage Erlang distribution, determining the waiting time.
- Simulated driving tests conducted using UC-win/Road simulation software, Forum8 driving simulation platform, and SMI ETGTM spectacle-type eye-tracking device analyze driver accuracy, workload, and traffic and visual behavior characteristics within the left-handed section of the right-turn on-ramp at the interchange.
- A formulated model for calculating the decision sight distance within the left-placed right-turn ramp section of the interchange is presented. This model segments the decision distance, queuing distance, and execution lane-changing distance, elucidating the underlying principles for calculating the decision sight distance. Sequential calibration of the relevant model parameters based on the measured data and driver behavior simulation experiments yields recommended decision sight distance values corresponding to different mainline design velocities.
- Chinese specified sight distance values appear smaller than the recommended value, raising concerns regarding the potential insufficiency of the decision sight distance when adopting the Route Specification’s special value due to the distinctive nature of the right-turn ramp left placement.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| RTRL | right-turn ramps on the left |
| UAV | unmanned aerial vehicles |
| LCR | lane change to the right side |
References
- Wang, X.; Lin, R.; Ye, W.; Ma, Z. Are Expensive Expressways in China Attractive to Businesses? Evidence From the Location Selections of Manufacturing Enterprises. Transp. Res. Rec. J. Transp. Res. Board 2023, 2677, 567–578. [Google Scholar] [CrossRef]
- Abatan, A.; Savolainen, P.T. Safety Analysis of Interchange Functional Areas. Transp. Res. Rec. J. Transp. Res. Board 2018, 2672, 120–130. [Google Scholar] [CrossRef]
- Heddebaut, O.; Di Ciommo, F. City-hubs for smarter cities. The case of Lille “EuraFlandres” interchange. Eur. Transp. Res. Rev. 2017, 10, 10. [Google Scholar] [CrossRef]
- Wu, Z.Y.; Fu, Q. Research on Fiber Micro-Surfacing Mixture Design and Pavement Performance in Interchange’s Connections. In Proceedings of the 5th International Conference on Civil Engineering and Transportation, Guangzhou, China, 28–29 November 2015; pp. 167–174. [Google Scholar]
- Lan, C.J.; Li, J.; Chimba, E.D. Statistical Evaluation of Motorcycle Crash Injury Severities by Using Multinomial Models. In Proceedings of the Transportation Research Board of the National Academies, Washington, DC, USA, 22–26 June 2006. [Google Scholar]
- McCartt, A.T.; Northrup, V.S.; Retting, R.A. Types and characteristics of ramp-related motor vehicle crashes on urban interstate roadways in Northern Virginia. J. Saf. Res. 2004, 35, 107–114. [Google Scholar] [CrossRef]
- Hongchao, L.; Shisheng, L.; Zhongxiang, F.; Kun, W.; Yewei, L. Driving anger in China: A case study on professional drivers. Transp. Res. Part F Traffic Psychol. 2016, 42, 255–266. [Google Scholar]
- Xu, S.X.; Liu, T.L.; Huang, H.J.; Liu, R. Mode choice and railway subsidy in a congested monocentric city with endogenous population distribution. Transp. Res. Part A Policy Pract. 2018, 116, 413–433. [Google Scholar] [CrossRef]
- Chen, F.; Chen, S. Injury severities of truck drivers in single- and multi-vehicle accidents on rural highways. Accid. Anal. Prev. 2011, 43, 1677–1688. [Google Scholar] [CrossRef]
- Chen, F.; Peng, H.; Ma, X.; Liang, J.; Hao, W.; Pan, X. Examining the safety of trucks under crosswind at bridge-tunnel section: A driving simulator study. Tunn. Undergr. Space Technol. 2019, 92, 103034. [Google Scholar] [CrossRef]
- Feng, Z.; Yang, M.; Ma, C.; Kang, J.; Yewei, L.; Huang, W.; Huang, Z.; Zhan, J.; Zhou, M. Driving anger and its relationships with type A behavior patterns and trait anger: Differences between professional and non-professional drivers. PLoS ONE 2017, 12, e0189793. [Google Scholar] [CrossRef]
- Guerrieri, M.; Mauro, R.; Tollazzi, T.J.T.E.P.A.S. Turbo-Roundabout: Case Study of Driver Behavior and Kinematic Parameters of Light and Heavy Vehicles. J. Transp. Eng. Part A Syst. 2019, 145. [Google Scholar] [CrossRef]
- Wang, C.; Lu, L.; Lu, J.; Wang, T. Selection for optimal exit ramp type on Florida’s freeways based on operational analysis. Adv. Mech. Eng. 2016, 8, 1–8. [Google Scholar] [CrossRef]
- Kayes, M.I.; Sandt, A.; Al-Deek, H.; Uddin, N.; Rogers, J.H.; Carrick, G. Modeling Wrong-Way Driving Entries at Limited Access Facility Exit Ramps in Florida. Transp. Res. Rec. J. Transp. Res. Board 2019, 2673, 567–576. [Google Scholar] [CrossRef]
- Atiquzzaman, M.; Zhou, H. Modeling the Risk of Wrong-Way Driving Entry at the Exit Ramp Terminals of Full Diamond Interchanges. Transp. Res. Rec. J. Transp. Res. Board 2018, 2672, 35–47. [Google Scholar] [CrossRef]
- Wu, P.; Meng, X.; Song, L. Identification and spatiotemporal evolution analysis of high-risk crash spots in urban roads at the microzone-level: Using the space-time cube method. J. Transp. Saf. Secur. 2022, 14, 1510–1530. [Google Scholar] [CrossRef]
- Wang, T.; Wang, C.; Qian, Z. Development of a new conflict-based safety metric for freeway exit ramps. Adv. Mech. Eng. 2017, 9, 1687814017723286. [Google Scholar] [CrossRef]
- Li, Z.; Wang, W.; Liu, P.; Bai, L.; Du, M. Analysis of Crash Risks by Collision Type at Freeway Diverge Area Using Multivariate Modeling Technique. J. Transp. Eng. 2015, 141, 04015002. [Google Scholar] [CrossRef]
- Chen, H.; Liu, P.; Lu, J.J.; Behzadi, B.J.A.A. Evaluating the safety impacts of the number and arrangement of lanes on freeway exit ramps. Accid. Anal. Prev. 2009, 41, 543–551. [Google Scholar] [CrossRef]
- Zahabi, M.; Machado, P.; Lau, M.Y.; Deng, Y.; Pankok, C.; Hummer, J.; Rasdorf, W.; Kaber, D.B. Driver performance and attention allocation in use of logo signs on freeway exit ramps—ScienceDirect. Appl. Ergon. 2017, 65, 70–80. [Google Scholar] [CrossRef]
- Bassan, S. Decision Sight Distance Review and Evaluation. Traffic Eng. Control. 2011, 52, 23–26. [Google Scholar]
- Ho, G.; Rozental, J.J.; Majstorović, S. Decision Sight Distance for Freeway Exit Ramps—A Road Safety Perspective. Eng. Environ. Sci. 2016. [Google Scholar]
- Liu, B.S.; Tseng, H.Y.; Pan, C.H.; Chia, T.C. Association of vehicle types and traffic conditions on driving speed at the freeway exit ramp. In Proceedings of the 38th International Conference on Computers & Industrial Engineering, Beijing, China, 31 October–2 November 2008. [Google Scholar]
- Lyu, N.; Cao, Y.; Wu, C.; Xu, J.; Xie, L. The effect of gender, occupation and experience on behavior while driving on a freeway deceleration lane based on field operational test data. Accid. Anal. Prev. 2018, 121, 82–93. [Google Scholar] [CrossRef] [PubMed]
- Calvi, A.; Bella, F.; D’Amico, F. Evaluating the effects of the number of exit lanes on the diverging driver performance. J. Transp. Saf. Secur. 2018, 10, 105–123. [Google Scholar] [CrossRef]
- Lasky, T.A.; Yen, K.; Ravani, B. Evaluating Wrong-Way Driving Incidents at Highway Exit Ramps and the Effect of Mitigation. J. Transp. Eng. Part A Syst. 2021, 147, 04021086. [Google Scholar] [CrossRef]
- Wei, M.; Teng, D.; Wu, S. Trajectory planning and optimization algorithm for automated driving based on Frenet coordinate system. Control. Decis. 2021, 36, 815–824. [Google Scholar]
- Wu, S.B.; Zou, Y.J.; Wu, L.T.; Zhang, Y. Application of Bayesian model averaging for modeling time headway distribution. Phys. A—Stat. Mech. Its Appl. 2023, 620, 128747. [Google Scholar] [CrossRef]
- Pan, B.; Wang, C.; Wang, Q.; Ma, Z.; Xie, Z. A Study of Length of Auxiliary Lanes for Two-Lane Expressway Exits Based on Microscopic Lane Change. J. Tongji Univ. Nat. Sci. 2022, 50, 1647–1657. [Google Scholar]
- Li, L.; Liu, Y.; Wang, J.; Deng, W.; Oh, H. Human dynamics based driver model for autonomous car. Intell. Transp. Syst. 2016, 10, 545–554. [Google Scholar] [CrossRef]
- Piranveyseh, P.; Kazemi, R.; Soltanzadeh, A.; Smith, A. A field study of mental workload: Conventional bus drivers versus bus rapid transit drivers. Ergonomics 2022, 65, 804–814. [Google Scholar] [CrossRef] [PubMed]
- Evans, J.L.; Elefteriadou, L.; Gautam, N. Probability of breakdown at freeway merges using Markov chains. Transp. Res. Part B Methodol. 2001, 35, 237–254. [Google Scholar] [CrossRef]
- Pan, B.; Zhou, X.; Zhou, T.; Zhao, Y.; Yang, C. Decision Sight Distance Calculation Model of Expressway Interchange Exit. J. Tongji Univ. Nat. Sci. 2020, 48, 1312. [Google Scholar]
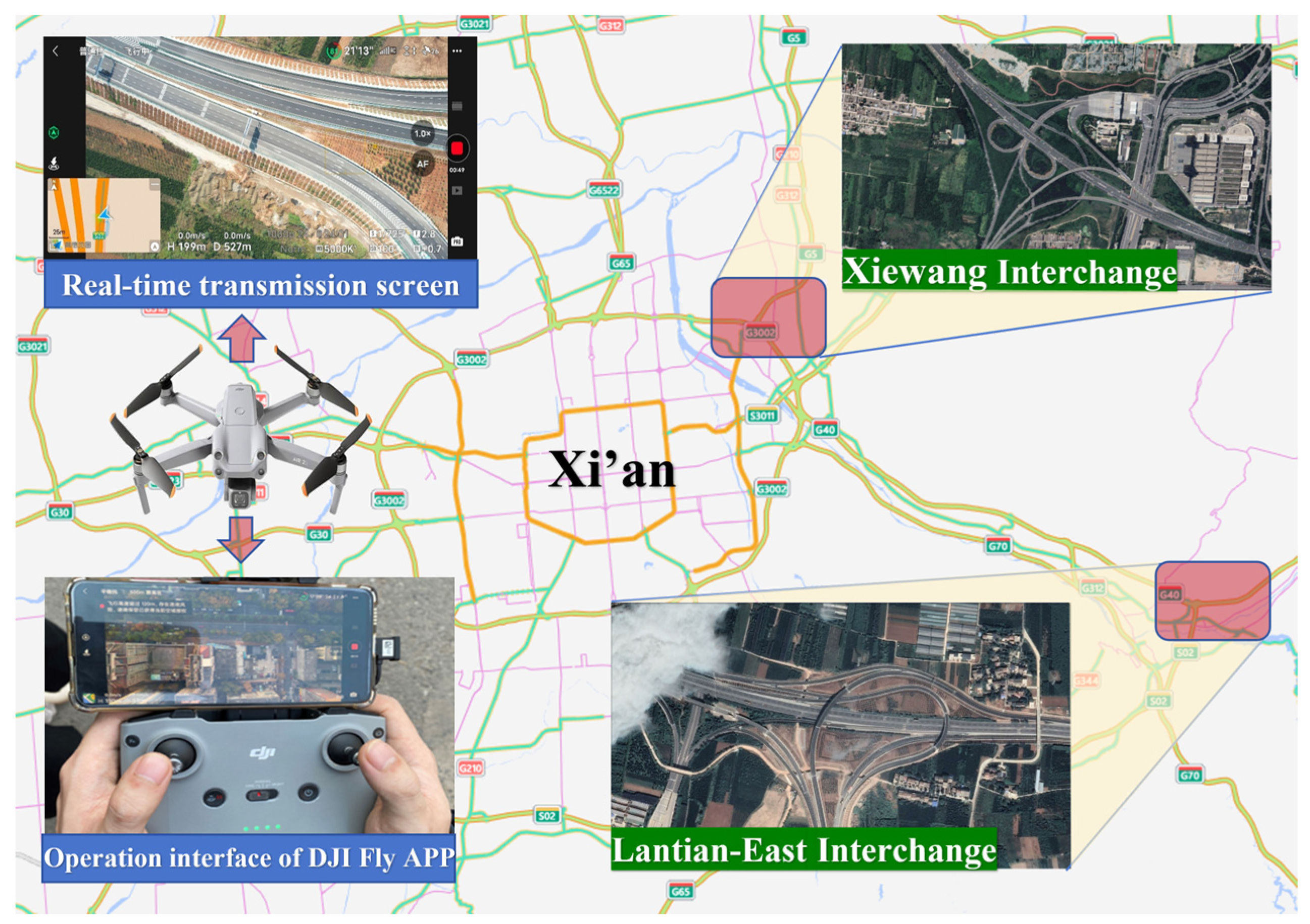

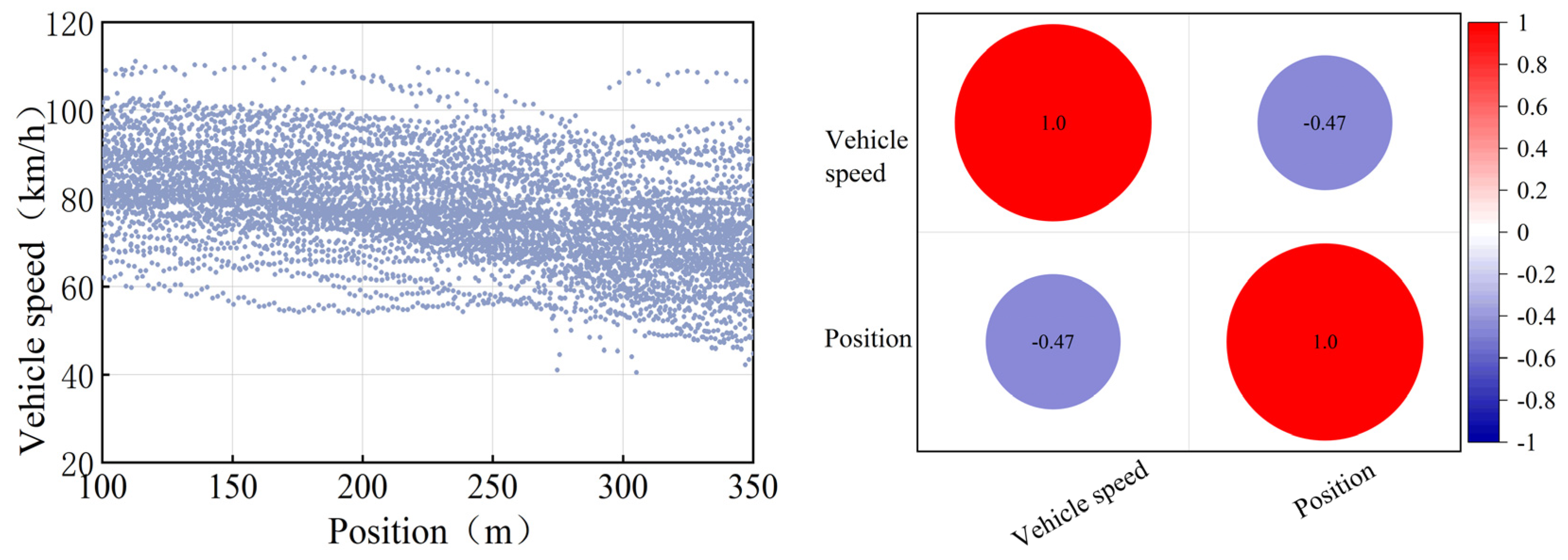
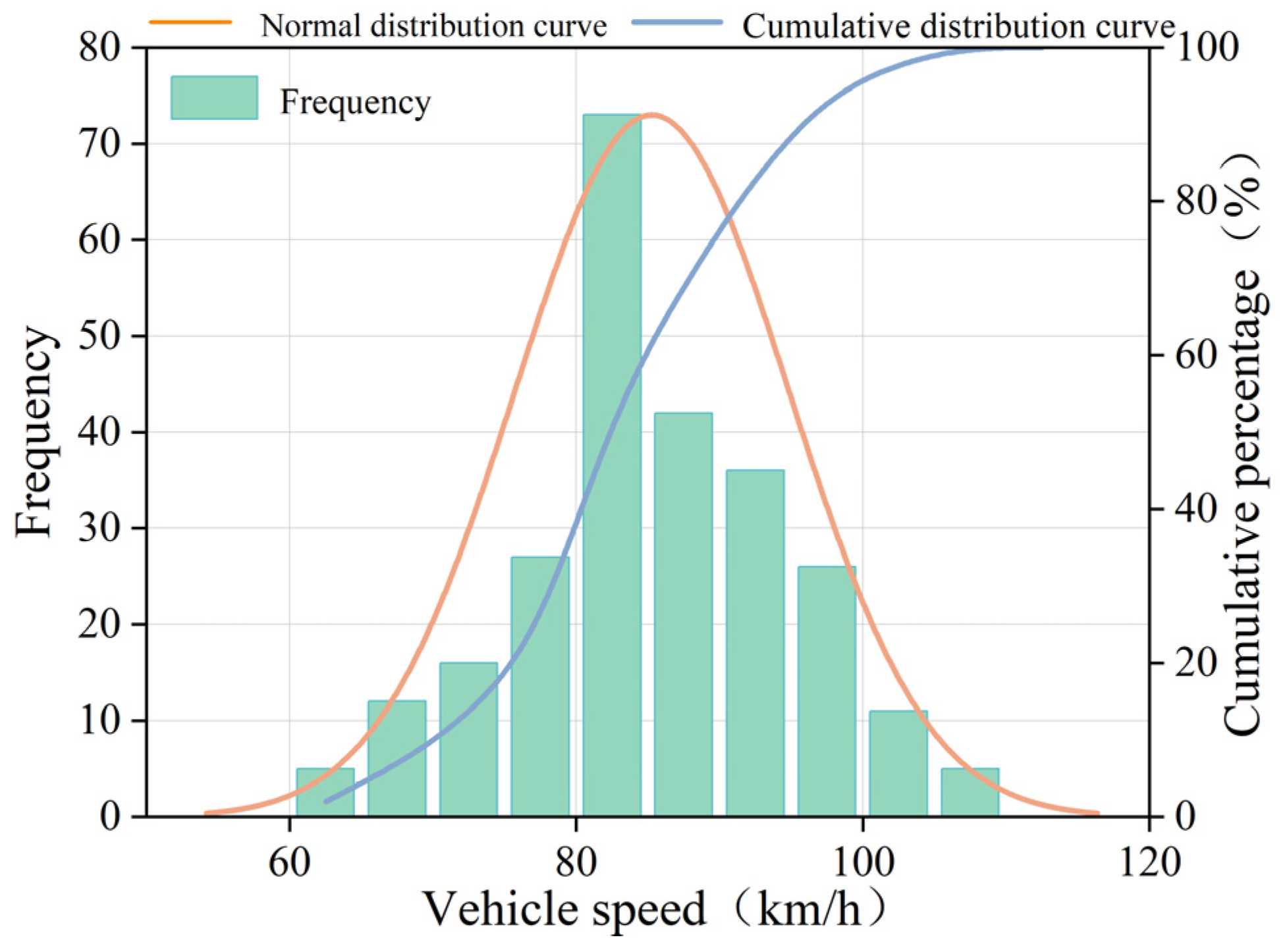
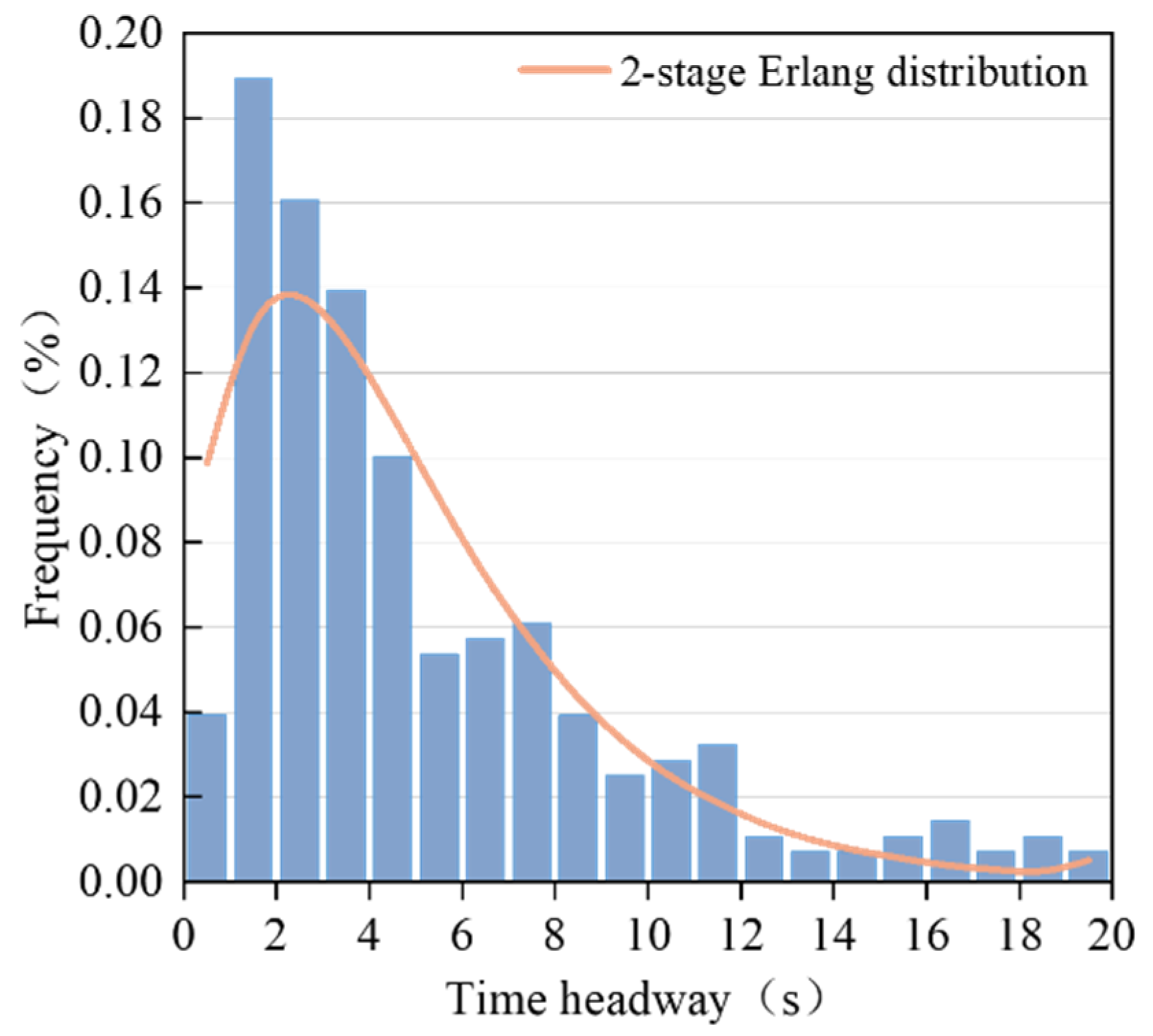




| Name of Interchange | Mainline Design Vehicle Speed (km/h) | Mainline Curb Lane Limited Vehicle Speed (km/h) | Average Vehicle Passing Vehicle Speed (km/h) | (km/h) |
|---|---|---|---|---|
| Interchange X | 120 | 100 | 85.3 | 93.0 |
| Interchange L | 100 | 80 | 68.2 | 82.0 |
| Name of Interchange | Distribution Type | g | α | DF | Conclusion | |||
|---|---|---|---|---|---|---|---|---|
| Interchange X | 2-stage Erlang distribution | 19.432 | 14 | 0.05 | 11 | 19.675 | Y | acceptance |
| 3-stage Erlang distribution | 58.971 | 12 | 0.05 | 9 | 16.919 | N | rejection | |
| Negative exponential distribution | 18.489 | 15 | 0.05 | 12 | 21.026 | Y | acceptance | |
| Interchange L | 2-stage Erlang distribution | 20.667 | 15 | 0.05 | 12 | 21.026 | Y | acceptance |
| 3-stage Erlang distribution | 19.333 | 17 | 0.05 | 14 | 23.685 | Y | acceptance | |
| Negative exponential distribution | 37.512 | 11 | 0.05 | 8 | 15.507 | N | rejection |
| Serial Number | Gender | Age (Years) | Driving Experience (Years) |
|---|---|---|---|
| 1 | Male | 32 | 9 |
| 2 | Male | 35 | 8 |
| 3 | Male | 28 | 5 |
| 4 | Male | 27 | 4 |
| 5 | Male | 26 | 4 |
| 6 | Male | 26 | 3 |
| 7 | Male | 25 | 3 |
| 8 | Male | 25 | 3 |
| 9 | Male | 25 | 2 |
| 10 | Male | 24 | 1 |
| 11 | Male | 24 | 1 |
| 12 | Male | 23 | 1 |
| 13 | Female | 28 | 5 |
| 14 | Female | 26 | 3 |
| 15 | Female | 25 | 3 |
| 16 | Female | 23 | 2 |
| Participant | |||||||
|---|---|---|---|---|---|---|---|
| Physical Need | Spiritual Needs | Time Requirement | Operational Performance | Effort | Frustration Level | ||
| 1 | 20/0 | 60/2 | 80/5 | 80/4 | 70/3 | 30/1 | 72 |
| 2 | 10/0 | 75/4 | 75/5 | 50/3 | 25/2 | 25/1 | 60 |
| 3 | 15/0 | 55/4 | 50/3 | 80/5 | 40/2 | 20/1 | 58 |
| 4 | 30/0 | 85/5 | 65/4 | 35/1 | 65/3 | 60/2 | 69 |
| 5 | 10/1 | 40/2 | 40/3 | 70/5 | 45/4 | 10/0 | 49 |
| 6 | 30/0 | 65/4 | 65/3 | 50/1 | 70/5 | 50/2 | 64 |
| 7 | 35/1 | 75/5 | 65/4 | 60/2 | 65/3 | 50/1 | 69 |
| 8 | 15/1 | 50/3 | 40/2 | 90/5 | 55/4 | 10/0 | 61 |
| 9 | 20/0 | 60/3 | 65/4 | 70/5 | 55/2 | 30/1 | 62 |
| 10 | 10/1 | 35/3 | 35/2 | 95/5 | 40/4 | 10/0 | 55 |
| 11 | 25/0 | 75/4 | 75/5 | 50/1 | 75/3 | 60/2 | 71 |
| 12 | 40/1 | 80/4 | 80/5 | 80/3 | 55/2 | 30/0 | 74 |
| 13 | 25/0 | 60/3 | 65/5 | 55/2 | 60/4 | 45/1 | 60 |
| 14 | 15/0 | 55/2 | 65/4 | 65/3 | 70/5 | 30/1 | 63 |
| 15 | 20/0 | 70/3 | 70/4 | 70/2 | 75/5 | 35/1 | 69 |
| 16 | 10/0 | 65/3 | 70/4 | 75/5 | 65/2 | 40/1 | 68 |
| Parameters | Freeway | ||
|---|---|---|---|
| (km/h) | 120 | 100 | 80 |
| (m) | 106.7 | 88.9 | 71.1 |
| (pcu/h/ln) | 1650 | 1600 | 1500 |
| (pcu/s) | 0.458 | 0.444 | 0.417 |
| Widths of Traveled-way (m) | 3.75 | 3.75 | 3.75 |
| (s) | 3.75 | 3.75 | 3.75 |
| Vehicle speed in the diversion area (km/h) | 95 | 85 | 75 |
| (km/h) | 107.5 | 92.5 | 77.5 |
| (s) | 7.56 | 6.79 | 5.50 |
| (m) | 225.8 | 174.5 | 118.4 |
| 0.10 | 0.12 | 0.13 | |
| (km/h) | 95 | 85 | 75 |
| (m/s2) | 0.588 | 0.784 | 0.882 |
| (m/s3) | 0.6 | 0.6 | 0.6 |
| 3.5 | 3.5 | 3.5 | |
| (m) | 173.6 | 155.3 | 137.1 |
| Recommended values for decision sight distance (m) | 510 | 420 | 330 |
| Design Specification for Freeway Alignment decision sight distance (m) | 460 (350) | 380 (290) | 300 (230) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Z.; Zhang, J.; Pan, B.; Wu, S.; Yang, H. Calculation Model for the Exit Decision Sight Distance of Right-Turn Ramps on the Left at Interchange. Appl. Sci. 2024, 14, 6205. https://doi.org/10.3390/app14146205
Fu Z, Zhang J, Pan B, Wu S, Yang H. Calculation Model for the Exit Decision Sight Distance of Right-Turn Ramps on the Left at Interchange. Applied Sciences. 2024; 14(14):6205. https://doi.org/10.3390/app14146205
Chicago/Turabian StyleFu, Zhipeng, Jiale Zhang, Binghong Pan, Shangen Wu, and Hang Yang. 2024. "Calculation Model for the Exit Decision Sight Distance of Right-Turn Ramps on the Left at Interchange" Applied Sciences 14, no. 14: 6205. https://doi.org/10.3390/app14146205
APA StyleFu, Z., Zhang, J., Pan, B., Wu, S., & Yang, H. (2024). Calculation Model for the Exit Decision Sight Distance of Right-Turn Ramps on the Left at Interchange. Applied Sciences, 14(14), 6205. https://doi.org/10.3390/app14146205






