A Novel Method of Time-Varying Formation Control Based on a Directed Graph for Multiple Autonomous Underwater Vehicles
Abstract
1. Introduction
2. Background Description
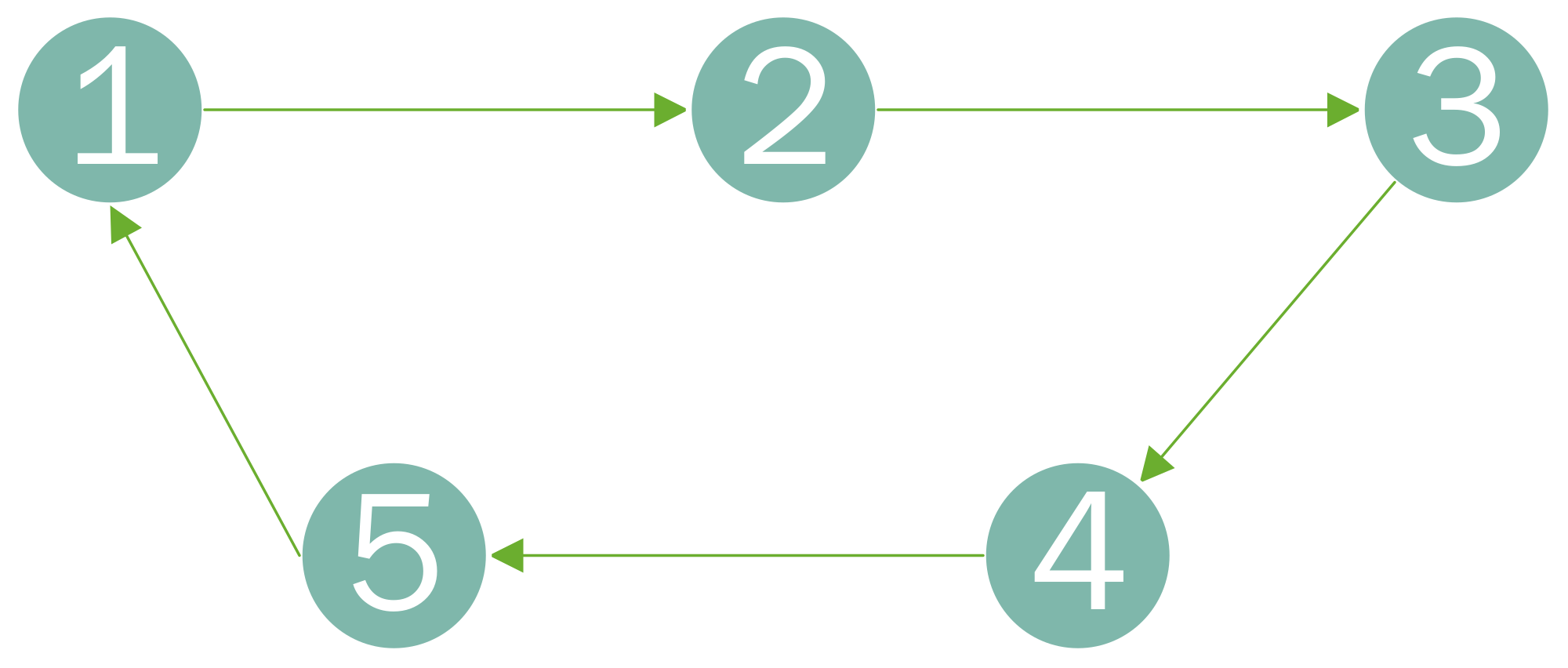
2.1. Basic Concepts
- (1)
- has at least one zero eigenvalue, and is the associated eigenvector; that is, ;
- (2)
- If has a spanning tree, then is a simple eigenvalue of , and all the other eigenvalues have positive real parts;
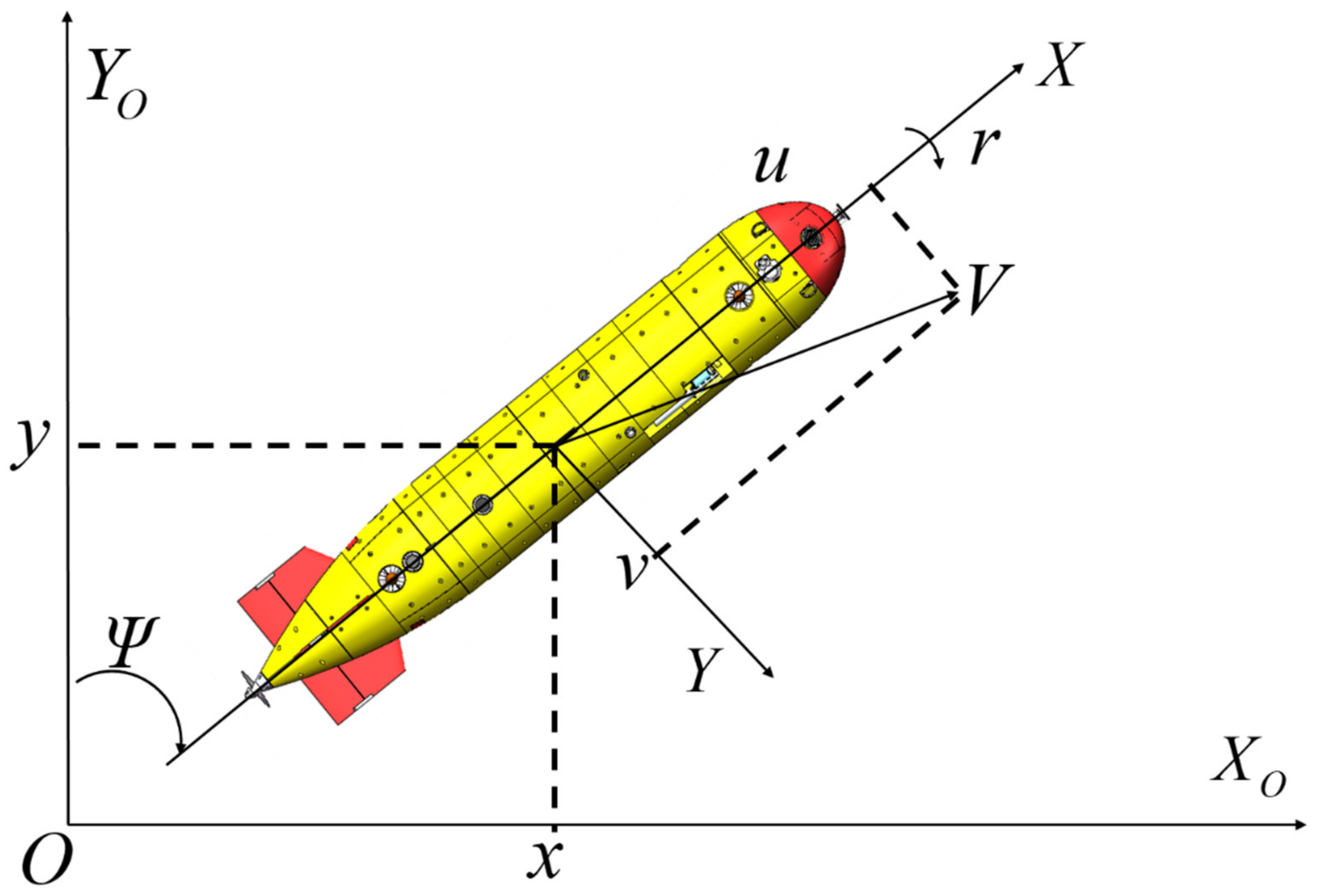
2.2. Mathematical Model of the AUV
- When the time-varying formation is established.
- If the system obtains the time-varying formation, what is the protocol in Equation (17)?
3. Theoretical Analysis
3.1. Formation Analysis
- (1)
- (2)
- if and , then:
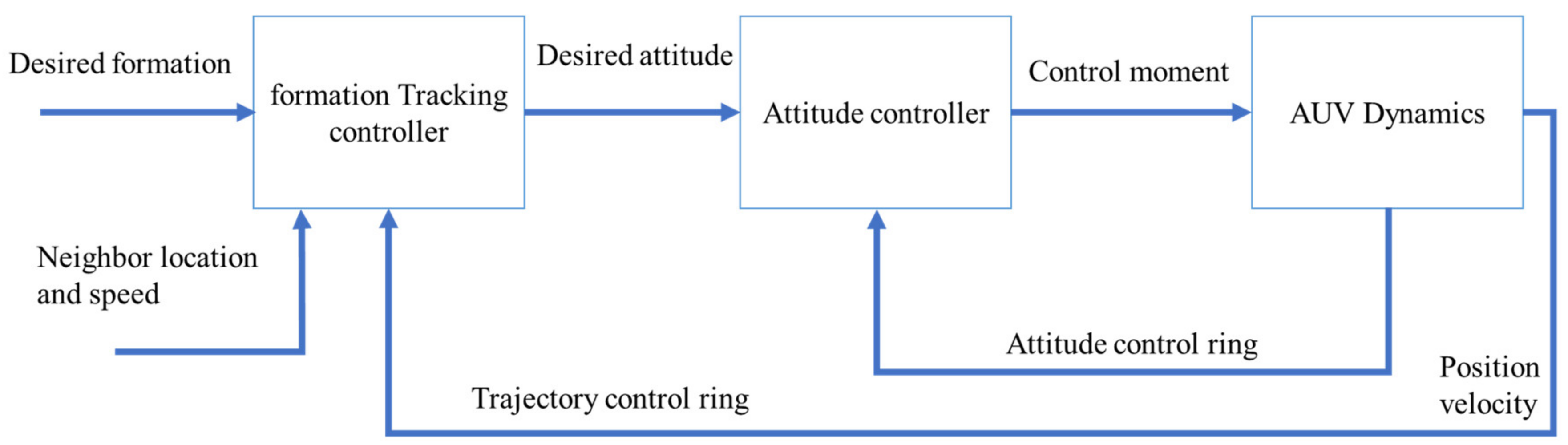
3.2. Protocol Design
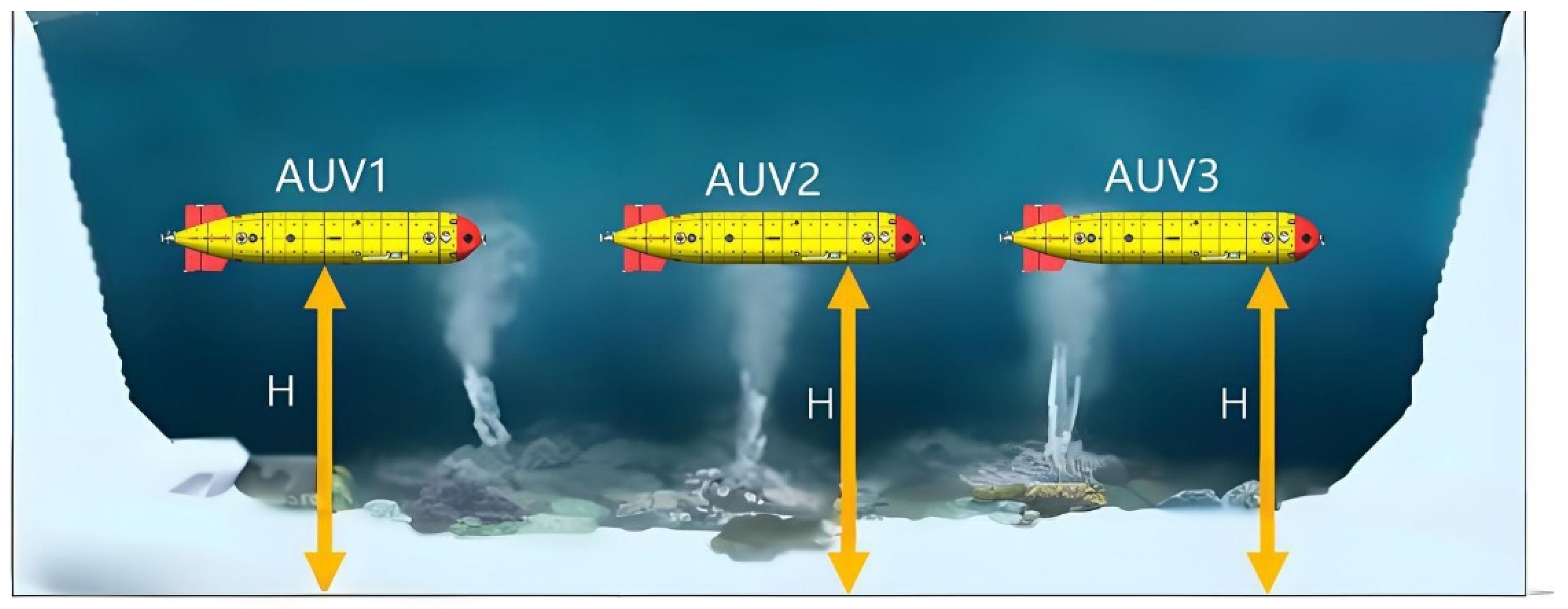
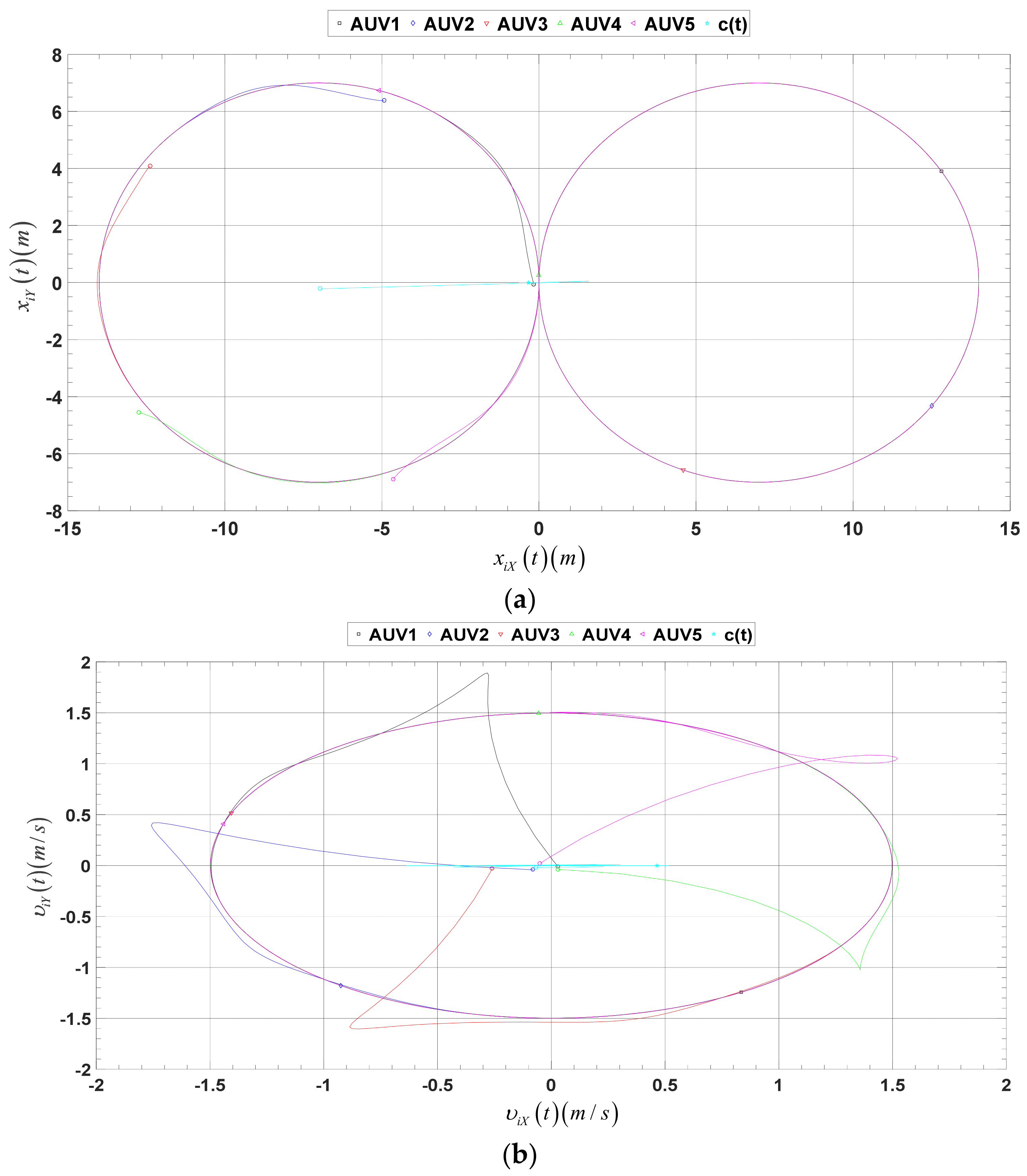
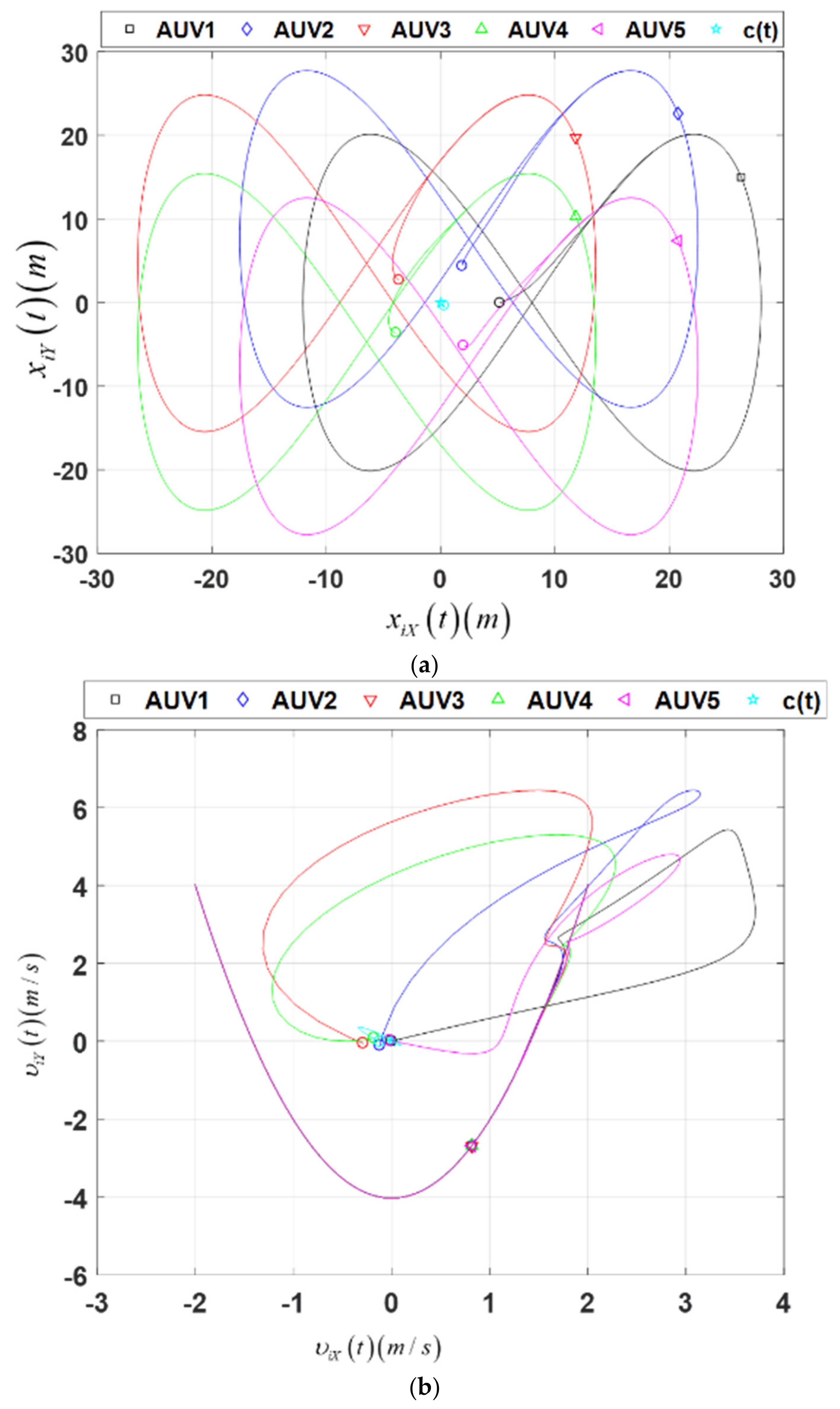
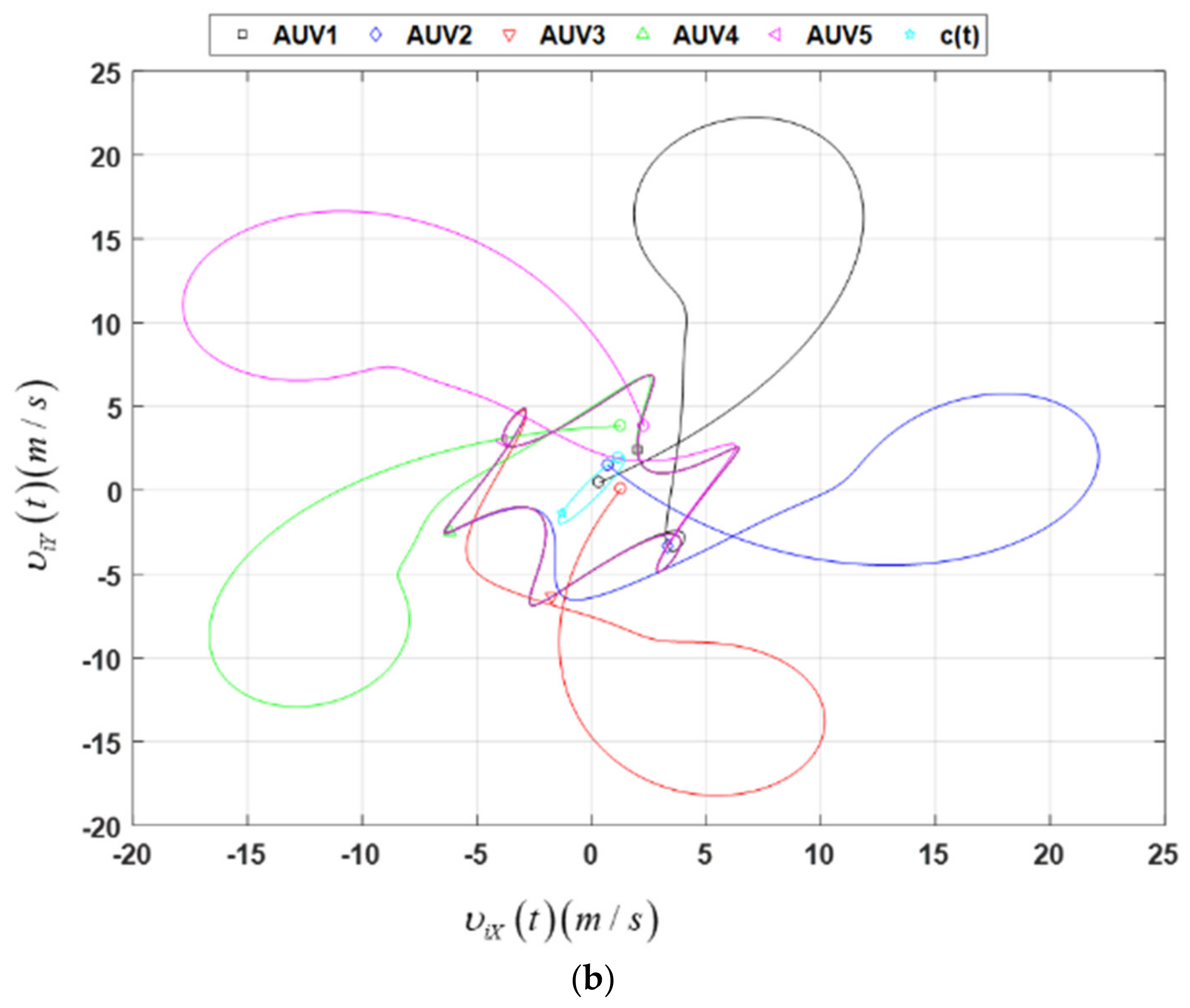
4. Simulation
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Weitz, L.A.; Hurtado, J.E.; Sinclair, A.J. Decentralized cooperative-control design for multivehicle formations. J. Guid. Control Dyn. 2008, 31, 970–979. [Google Scholar] [CrossRef]
- Yang, S.; Chen, J.; Liu, F. Observer-based consensus control of multi-agent systems with input delay. In Proceedings of the 2018 IEEE 4th International Conference on Control Science and Systems Engineering (ICCSSE), Wuhan, China, 21–23 August 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 533–537. [Google Scholar]
- Cai, W.; Liu, Z.; Zhang, M.; Lv, S.; Wang, C. Cooperative formation control for multiple AUVs with intermittent underwater acoustic communication in IoUT. IEEE Internet Things J. 2023, 10, 15301–15313. [Google Scholar] [CrossRef]
- Li, J.; Zhang, H.; Chen, T.; Wang, J. AUV formation coordination control based on transformed topology under time-varying delay and communication interruption. J. Mar. Sci. Eng. 2022, 10, 950. [Google Scholar] [CrossRef]
- Okamoto, A.; Kim, K.; Sasano, M.; Sato, T.; Inaba, S.; Kondo, S.; Matsumoto, H.; Murashima, T.; Shimura, T.; Fujiwara, T.; et al. Development of a basic formation control system for heterogeneous autonomous marine vehicles and its sea trials in suruga bay. In Proceedings of the 2023 IEEE Underwater Technology (UT), Tokyo, Japan, 6–9 March 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–10. [Google Scholar]
- Yan, Z.; Pan, X.; Yang, Z.; Yue, L. Formation control of leader-following multi-uuvs with uncertain factors and time-varying delays. IEEE Access 2019, 7, 118792–118805. [Google Scholar] [CrossRef]
- Yan, Z.; Yang, Z.; Pan, X.; Zhou, J.; Wu, D. Virtual leader based path tracking control for multi-uuv considering sampled-data delays and packet losses. Ocean Eng. 2020, 216, 108065. [Google Scholar] [CrossRef]
- Suryendu, C.; Subudhi, B. Formation control of multiple autonomous underwater vehicles under communication delays. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 3182–3186. [Google Scholar] [CrossRef]
- Li, J.; Tian, Z.; Zhang, H. Discrete-time AUV formation control with leader-following consensus under time-varying delays. Ocean Eng. 2023, 286, 115678. [Google Scholar] [CrossRef]
- Zhang, N.; Niu, W.; Li, T. Consistency control of multi—Agent system based on unknown input observer. IFAC-PapersOnLine 2018, 51, 566–571. [Google Scholar] [CrossRef]
- Shao, G.; Wan, L.; Xu, H. Multi-AUV control method based on inverse optimal control of integrated obstacle avoidance algorithm. Appl. Sci. 2023, 13, 12198. [Google Scholar] [CrossRef]
- Zhang, M.; Yan, Z.; Zhou, J.; Yue, L. Distributed dual closed-loop model predictive formation control for collision-free multi-AUV system subject to compound disturbances. J. Mar. Sci. Eng. 2023, 11, 1897. [Google Scholar] [CrossRef]
- Xu, B.; Wang, Z.; Li, W.; Yu, Q. Distributed robust model predictive control-based formation-containment tracking control for autonomous underwater vehicles. Ocean Eng. 2023, 283, 115210. [Google Scholar] [CrossRef]
- Arcos-Legarda, J.; Gutiérrez, Á. Robust model predictive control based on active disturbance rejection control for a robotic autonomous underwater vehicle. J. Mar. Sci. Eng. 2023, 11, 929. [Google Scholar] [CrossRef]
- Pang, W.; Zhu, D.; Chu, Z.; Chen, Q. Distributed adaptive formation reconfiguration control for multiple AUVs based on affine transformation in three-dimensional ocean environments. IEEE Trans. Veh. Technol. 2023, 72, 7338–7350. [Google Scholar] [CrossRef]
- Zhang, P.; de Queiroz, M.; Cai, X. Three-dimensional dynamic formation control of multi-agent systems using rigid graphs. J. Dyn. Syst. Meas. Contr. 2015, 137, 111006. [Google Scholar] [CrossRef]
- Cai, X.; Queiroz, M.d. Adaptive rigidity-based formation control for multirobotic vehicles with dynamics. IEEE Trans. Control Syst. Technol. 2015, 23, 389–396. [Google Scholar] [CrossRef]
- Oh, K.-K.; Ahn, H.-S. Distance-based undirected formations of single-integrator and double-integrator modeled agents in n-dimensional space. Int. J. Robust Nonlinear Control 2013, 24, 1809–1820. [Google Scholar] [CrossRef]
- Ramazani, S.; Selmic, R.; de Queiroz, M. Rigidity-based multiagent layered formation control. IEEE Trans. Cybern. 2017, 47, 1902–1913. [Google Scholar] [CrossRef]
- Yan, Z.; Yue, L.; Zhou, J.; Pan, X.; Zhang, C. Formation coordination control of leaderless multi-AUV system with double independent communication topology and nonconvex control input constraints. J. Mar. Sci. Eng. 2023, 11, 107. [Google Scholar] [CrossRef]
- Yu, W.; DiMassa, D.D. Formation control of networked autonomous underwater vehicles with obstacle avoidance. In Proceedings of the OCEANS 2022, Hampton Roads, VA, USA, 17–20 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–7. [Google Scholar]
- Gao, Z.; Guo, G. Fixed-time leader-follower formation control of autonomous underwater vehicles with event-triggered intermittent communications. IEEE Access 2018, 6, 27902–27911. [Google Scholar] [CrossRef]
- Xia, G.; Zhang, Y.; Zhang, W.; Chen, X.; Yang, H. Dual closed-loop robust adaptive fast integral terminal sliding mode formation finite-time control for multi-underactuated AUV system in three dimensional space. Ocean Eng. 2021, 233, 108903. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, C.; Zhang, K.; Cai, S. Research on guaranteed cost formation tracking control of multi-auv with virtual leader. In Proceedings of the OCEANS 2023—Limerick, Limerick, Ireland, 5–8 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Li, J.; Tian, Z.; Zhang, G.; Li, W. Multi-AUV formation predictive control based on CNN-LSTM under communication constraints. J. Mar. Sci. Eng. 2023, 11, 873. [Google Scholar] [CrossRef]
- Li, J.; Tian, Z.; Zhang, H.; Li, W. Robust finite-time control of a multi-AUV formation based on prescribed performance. J. Mar. Sci. Eng. 2023, 11, 897. [Google Scholar] [CrossRef]
- Zuo, Z. Non-singular fixed-time terminal sliding mode control of non-linear systems. IET Control Theory Appl. 2015, 9, 545–552. [Google Scholar] [CrossRef]
- Zuo, Z. Nonsingular fixed-time consensus tracking for second-order multi-agent networks. Automatica 2015, 54, 305–309. [Google Scholar] [CrossRef]
- Ni, J.; Liu, L.; Liu, C.; Hu, X.; Li, S. Fast fixed-time nonsingular terminal sliding mode control and its application to chaos suppression in power system. IEEE Trans. Circuits Syst. II Express Briefs 2017, 64, 151–155. [Google Scholar] [CrossRef]
- Ni, J.; Liu, L.; Liu, C.; Liu, J. Fixed-time leader-following consensus for second-order multiagent systems with input delay. IEEE Trans. Ind. Electron. 2017, 64, 8635–8646. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Bao, H.; Zhap, G. Nonsingular terminal sliding mode based impact angle constraint guidance law with fixed-time convergence. Control Decis. 2020, 35, 474–482. [Google Scholar] [CrossRef]
- Wang, C.; Wen, G.; Peng, Z.; Zhang, X. Integral sliding-mode fixed-time consensus tracking for second-order non-linear and time delay multi-agent systems. J. Frankl. Inst. 2019, 356, 3692–3710. [Google Scholar] [CrossRef]
- Jenabzadeh, A.; Safarinejadian, B. Distributed estimation and control for nonlinear multi-agent systems in the presence of input delay or external disturbances. ISA Trans. 2020, 98, 198–206. [Google Scholar] [CrossRef]
- Wang, C.; Tnunay, H.; Zuo, Z.; Lennox, B.; Ding, Z. Fixed-time formation control of multirobot systems: Design and experiments. IEEE Trans. Ind. Electron. 2019, 66, 6292–6301. [Google Scholar] [CrossRef]
- Mehra, S.; Sahoo, S.R. Trajectory tracking with input delay in multi-agent system: Double integrator case. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 387–393. [Google Scholar]
- Wu, C.; Karimi, H.R.; Shan, L.; Dai, Y. Data-driven iterative learning cooperative trajectory tracking control for multiple autonomous underwater vehicles with input saturation constraints. J. Field Robot. 2024. Early View. [Google Scholar] [CrossRef]
- Fay, K.; Giordano, M.; Soto, A.; Clark, C.M.; Spurgeon, E.; Anderson, J.; Lowe, C. Multi-Robot Expansive Planning and Trajectory Evaluation for Tracking and Localization of Marine Life. In Proceedings of the 38th ACM/SIGAPP Symposium on Applied Computing, Tallinn, Estonia, 27–31 March 2023. [Google Scholar] [CrossRef]
- Lins De Oliveira, É.; Maia Matarazzo Orsino, R.; Crisol Donha, D. Formation-Kee and Cooperative Control of AUVs Based on the Udwadia-Kalaba Equation. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Boston, MA, USA, 20–23 August 2023; American Society of Mechanical Engineers: New York, NY, USA, 2023; Volume 87387. [Google Scholar] [CrossRef]
- Chen, B.; Hu, J.; Ghosh, B.K. Finite-time tracking control of heterogeneous multi-AUV systems with partial measurements and intermittent communication. Sci. China Inf. Sci. 2024, 67, 152202. [Google Scholar] [CrossRef]
- Mokhtari, M.; Taghizadeh, M.; Mazare, M. Distributed Consensus and Formation Control of Multi-AUV Systems under Actuator Faults and Switching Topology. Eur. J. Control. 2024, 79, 101006. [Google Scholar] [CrossRef]
- Godsil, C.; Royle, G. Algebraic Graph Theory; Springer: New York, NY, USA, 2001. [Google Scholar] [CrossRef]
- Wei, R.; Beard, R.W. Consensus seeking in multiagent systems under dynamically changing interaction topologies. IEEE Trans. Autom. Control 2005, 50, 655–661. [Google Scholar] [CrossRef]
- Zahreddine, Z.; El-Shehawey, E.F. On the stability of a system of differential equations with complex coefficients. Indian J. Pure Appl. Math. 1988, 19, 963–972. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, G.; Wan, L.; Xu, H. A Novel Method of Time-Varying Formation Control Based on a Directed Graph for Multiple Autonomous Underwater Vehicles. Appl. Sci. 2024, 14, 6377. https://doi.org/10.3390/app14146377
Shao G, Wan L, Xu H. A Novel Method of Time-Varying Formation Control Based on a Directed Graph for Multiple Autonomous Underwater Vehicles. Applied Sciences. 2024; 14(14):6377. https://doi.org/10.3390/app14146377
Chicago/Turabian StyleShao, Gang, Lei Wan, and Huixi Xu. 2024. "A Novel Method of Time-Varying Formation Control Based on a Directed Graph for Multiple Autonomous Underwater Vehicles" Applied Sciences 14, no. 14: 6377. https://doi.org/10.3390/app14146377
APA StyleShao, G., Wan, L., & Xu, H. (2024). A Novel Method of Time-Varying Formation Control Based on a Directed Graph for Multiple Autonomous Underwater Vehicles. Applied Sciences, 14(14), 6377. https://doi.org/10.3390/app14146377





