BESO and SESO: Comparative Analysis of Spatial Structures Considering Self-Weight and Structural Reliability
Abstract
:1. Introduction
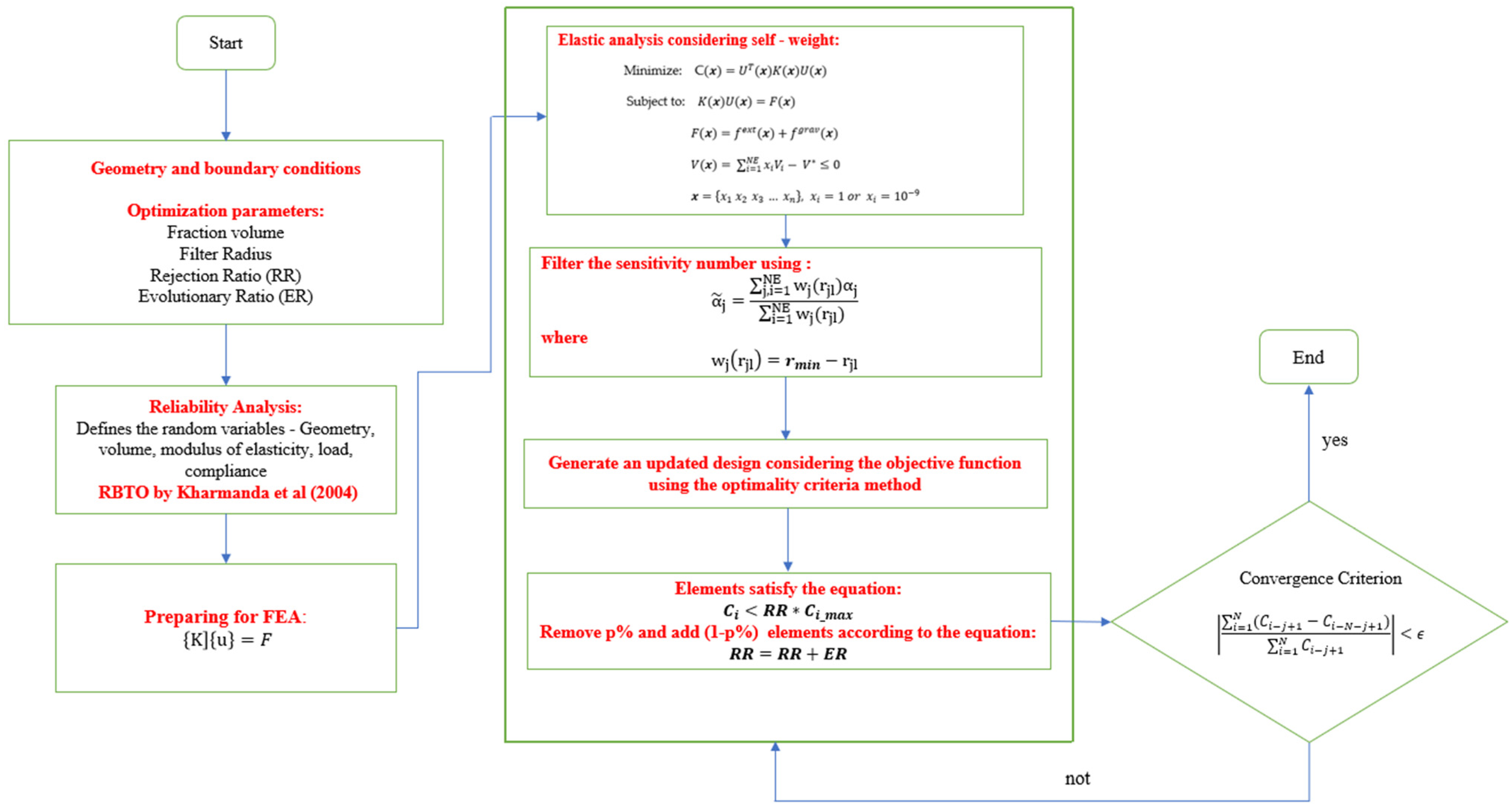
2. SESO—Subject to Self-Weight Loads
Formulation for Self-Weight Structure
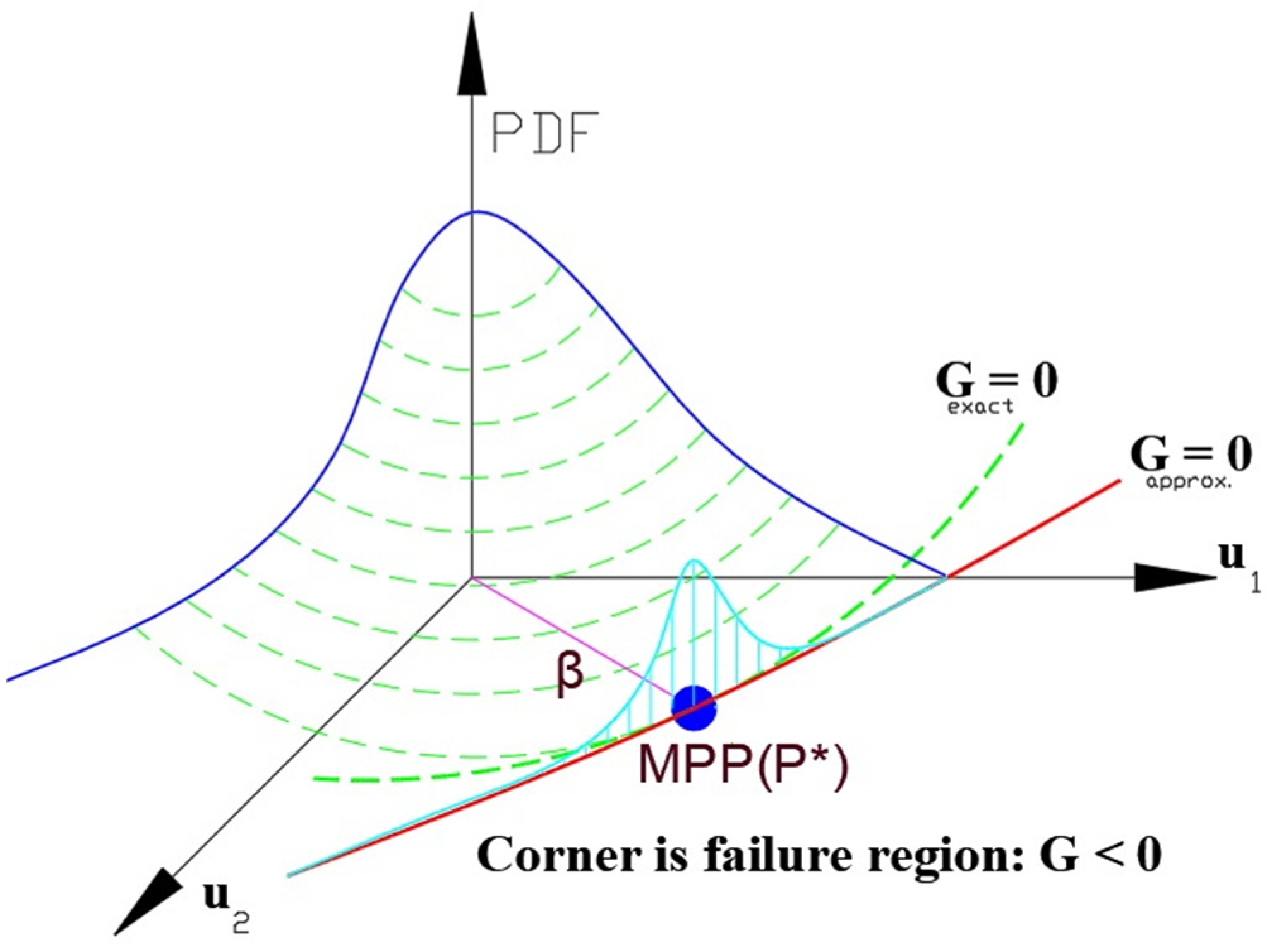
3. Reliability Analysis
3.1. Formulation of the RBTO
3.2. Formulation of the RBTO Problem Considering the Self-Weight
3.3. Sensitivity Analysis and Principal Stress for Determining Tensile and Compression Regions
3.3.1. Tensile and Compressive State
- (1)
- If this indicates that the mean stress is positive, suggesting a predominantly tensile state.
- (2)
- If this indicates that the mean stress is negative, suggesting a predominantly compressive state.
3.3.2. Derivative Sign Analysis: Sensitivity Analysis
4. Numerical Examples
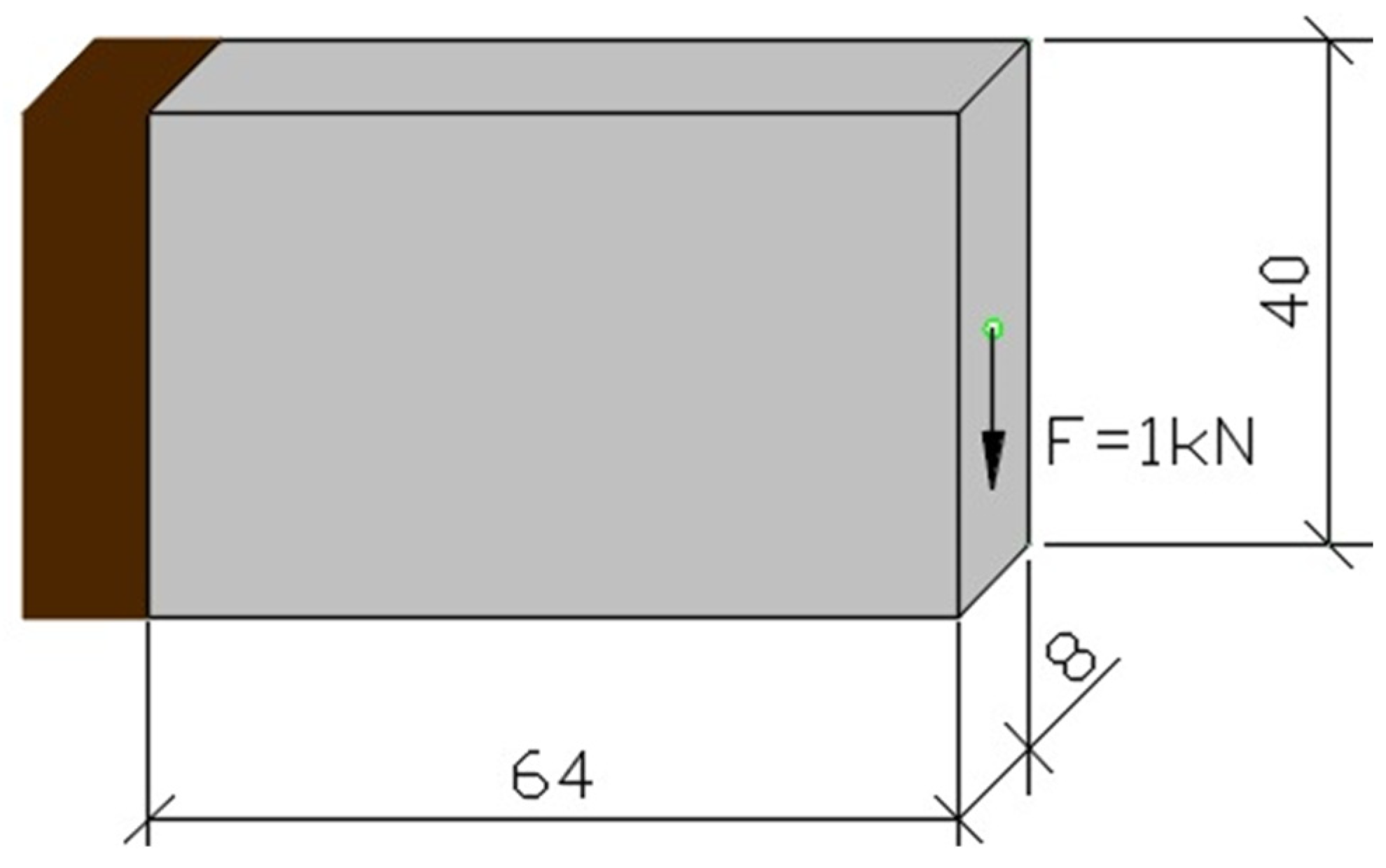
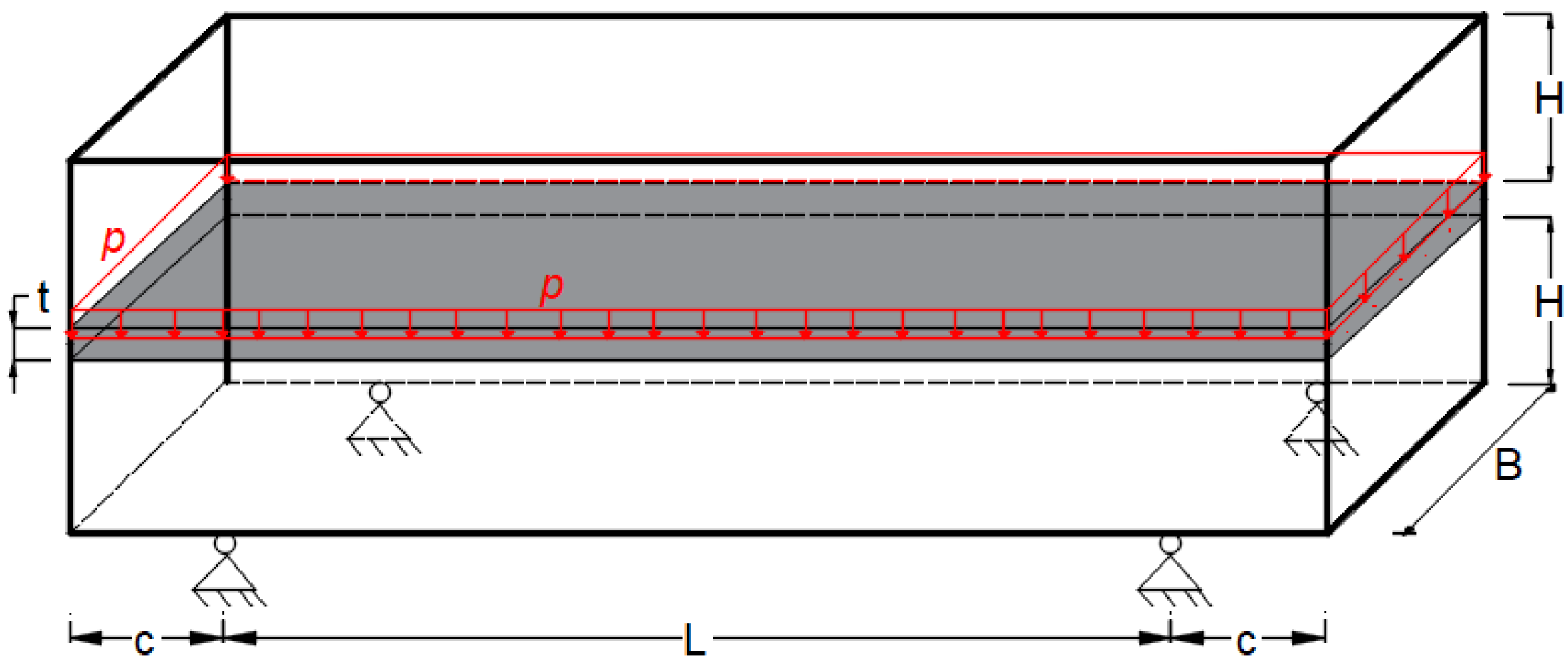
4.1. Cantilever Beam
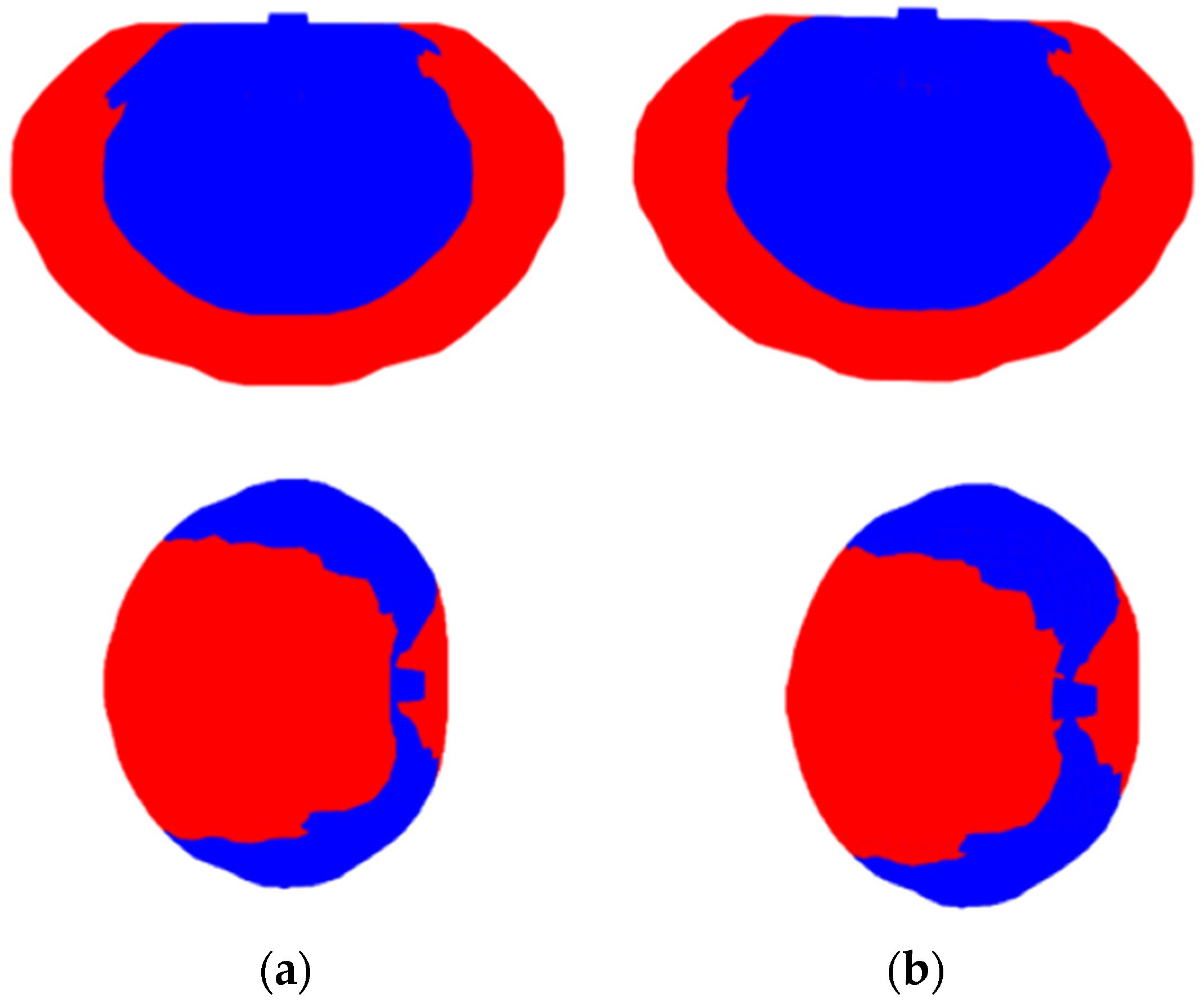
4.2. Example 2—Application of BESO and SESO to the Design of an Apple
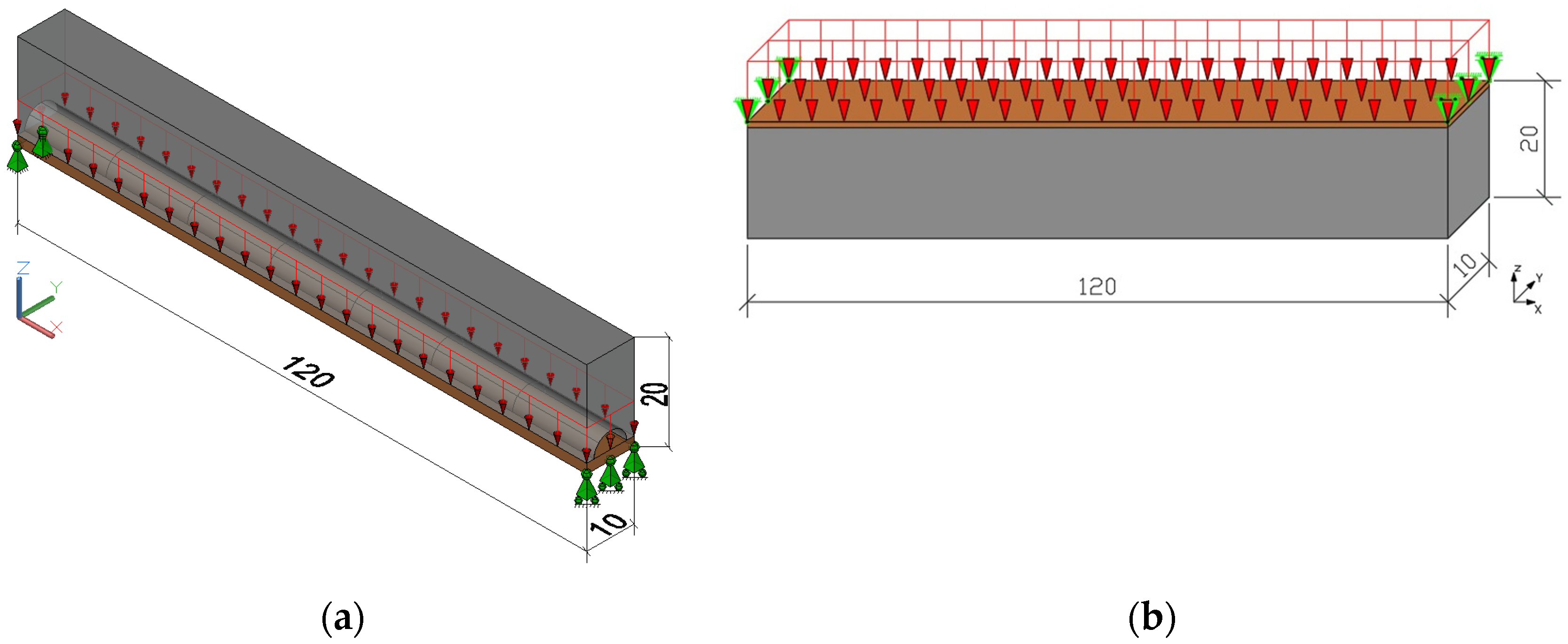
4.3. Example 3—Deterministic Analysis: Bridge Topology Optimization
4.4. Example 4—Reliability-Based Topology Optimization without Considering Self-Weight
4.5. Example 5—Reliability-Based Topology Optimization Considering Self-Weight
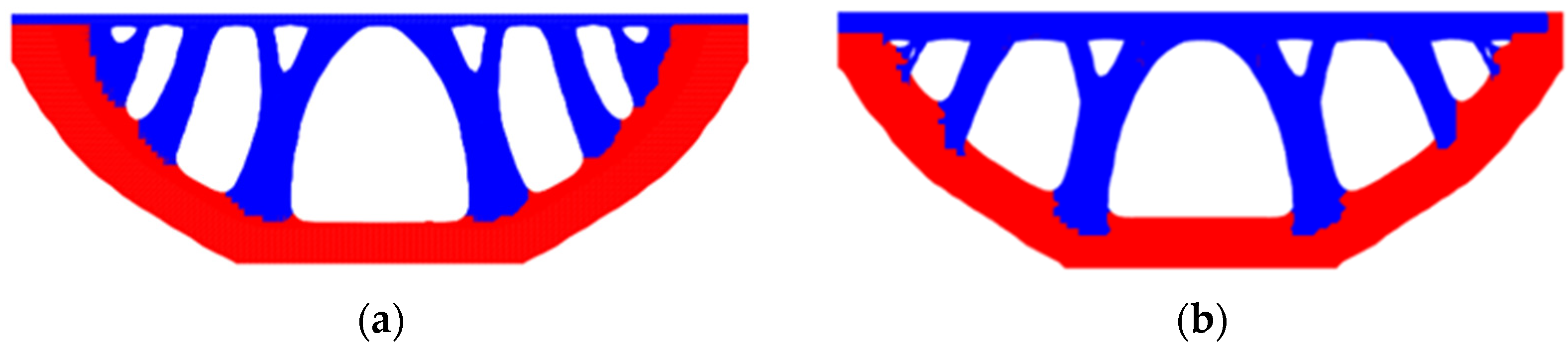
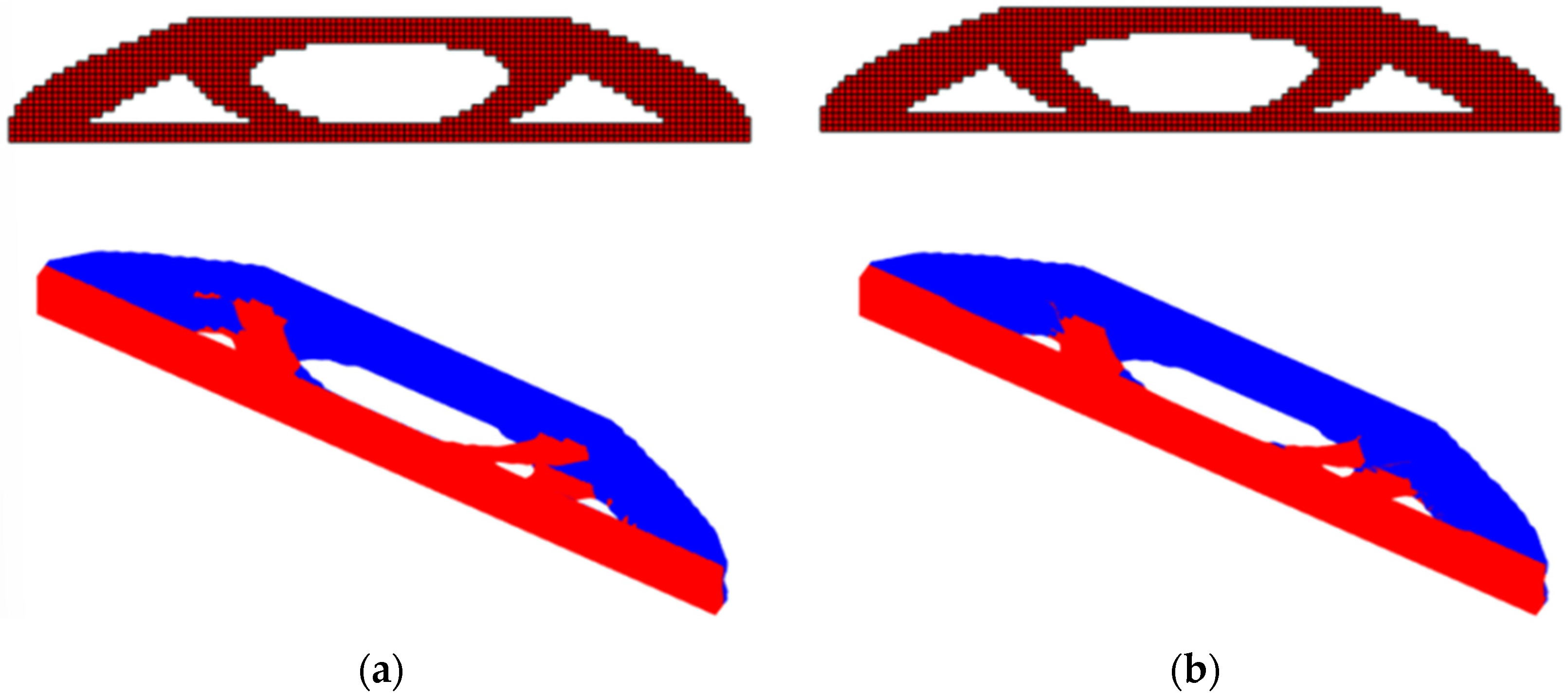
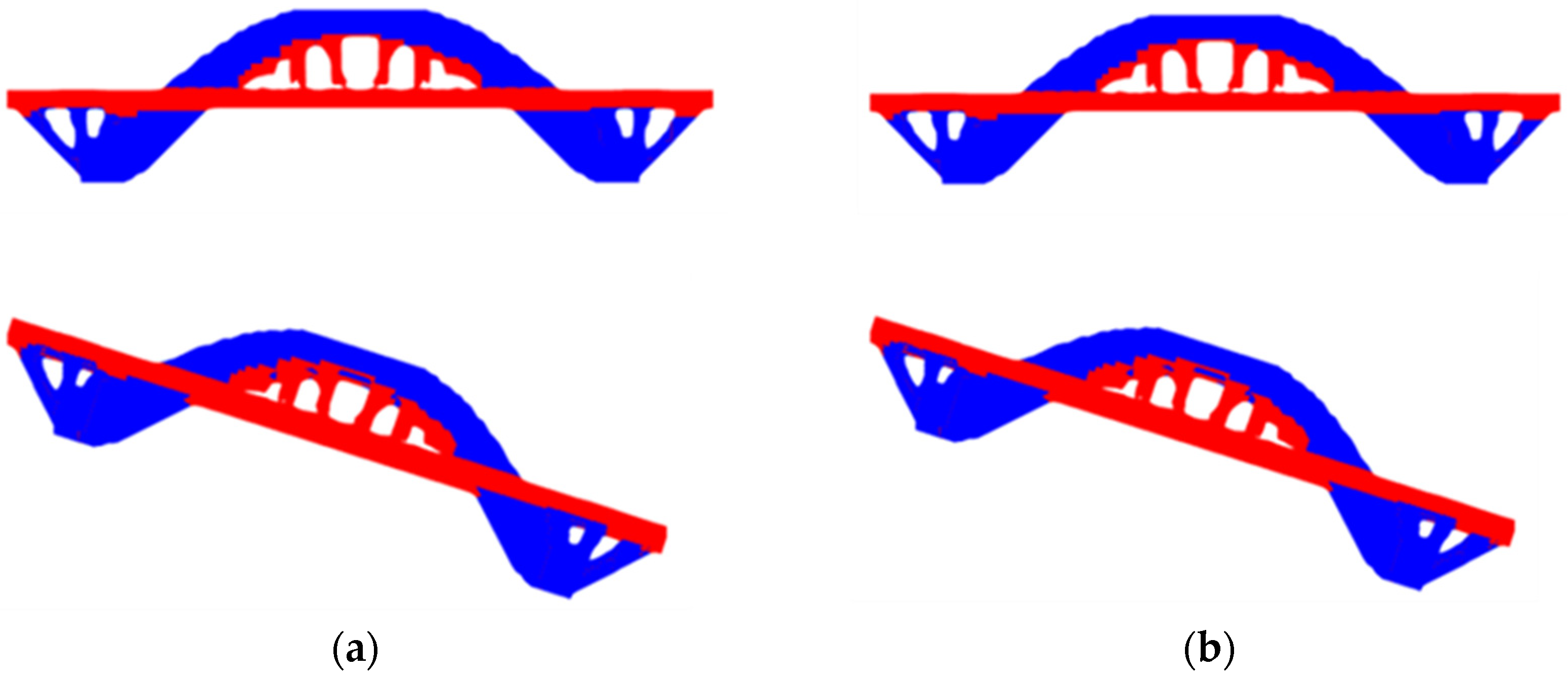
4.6. Example 6—Reliability Analysis—Effects of Boundary Conditions and Self-Weight on Bridge Topology
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Svanberg, K. Method of moving asymptotes—A new method for structural optimization. Int. J. Num. Meth. Eng. 1987, 24, 359–373. [Google Scholar] [CrossRef]
- Bendsøe, M.P. Optimal shape design as a material distribution problem. Struct. Optim. 1989, 1, 193–202. [Google Scholar] [CrossRef]
- Zhou, M.; Rozvany, G.I.N. The COC algorithm, Part II: Topological, geometrical and generalized shape optimization. Comp. Meth. Appl. Mech. Engrg. 1991, 89, 309–330. [Google Scholar] [CrossRef]
- Eschenauer, H.A.; Kobelev, V.V.; Schumacher, A. Bubble method for topology and shape optimization of structures. Struct. Optim. 1994, 8, 42–51. [Google Scholar] [CrossRef]
- Allaire, G.; Jouve, F.; Toader, A.-M. A level set method for shape optimization. C. R. Acad. Sci. Paris Série I 2002, 334, 1125–1130. [Google Scholar] [CrossRef]
- Wang, M.Y.; Wang, X.; Guo, D. A level set method for structural topology optimization. Comput. Methods Appl. Mech. Engrg. 2003, 192, 227–246. [Google Scholar] [CrossRef]
- Xia, Q.; Shi, T. Topology optimization of compliant mechanism and its support through a level set method. Comput. Methods Appl. Mech. Eng. 2016, 305, 359–375. [Google Scholar] [CrossRef]
- Xie, Y.M.; Steven, G.P. Um procedimento evolucionário simples para otimização estrutural. Comput. Estrut. 1993, 49, 885–896. [Google Scholar] [CrossRef]
- Xie, Y.M.; Steven, G.P. Evolutionary Structural Optimization; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar] [CrossRef]
- Querin, O.M.; Steven, G.P.; Xie, Y.M. Evolutionary structural optimisation (ESO) using a bidirectional algorithm. Eng. Comput. 1998, 15, 1031–1048. [Google Scholar] [CrossRef]
- Yang, X.Y.; Xie, Y.M.; Steven, G.P.; Querin, O.M. Topology optimization for frequencies using an evolutionary method. J. Struct. Eng. 1999, 125, 1432–1438. [Google Scholar] [CrossRef]
- Querin, O.M.; Young, V.; Steven, G.P.; Xie, Y.M. Computational efficiency and validation of bi-directional evolutionary structural optimisation. Comput. Methods Appl. Mech. Eng. 2000, 189, 559–573. [Google Scholar] [CrossRef]
- Huang, X.; Xie, Y.M.; Burry, M.C. Advantages of bi-directional evolutionary structural optimization (BESO) over evolutionary structural optimization (ESO). Adv. Struct. Eng. 2007, 10, 727–737. [Google Scholar] [CrossRef]
- Almeida, V.S.; Simonetti, H.L.; Neto, L.O. Comparative analysis of strut-and-tie models using Smooth Evolutionary Structural Optimization. Eng. Struct. 2013, 56, 1665–1675. [Google Scholar] [CrossRef]
- Simonetti, H.L.; Almeida, V.S.; de Oliveira Neto, L. A smooth evolutionary structural optimization procedure applied to plane stress problem. Eng. Struct. 2014, 75, 248–258. [Google Scholar] [CrossRef]
- Shobeiri, V.; Ahmadi-Nedushan, B. Bi-directional evolutionary structural optimization for strut-and-tie modelling of three-dimensional structural concrete. Eng. Optim. 2017, 49, 2055–2078. [Google Scholar] [CrossRef]
- Shobeiri, V. Determination of strut-and-tie models for structural concrete under dynamic loads. Can. J. Civ. Eng. 2019, 46, 1090–1102. [Google Scholar] [CrossRef]
- Huang, X.; Zuo, Z.H.; Xie, Y.M. Evolutionary topological optimization of vibrating continuum structures for natural frequencies. Comput. Struct. 2010, 88, 357–364. [Google Scholar] [CrossRef]
- Zuo, Z.H.; Xie, Y.M. A simple and compact Python code for complex 3D topology optimization. Adv. Eng. Softw. 2015, 85, 1–11. [Google Scholar] [CrossRef]
- Bi, M.; Tran, P.; Xie, Y.M. Topology optimization of 3D continuum structures under geometric self-supporting constraint. Addit. Manuf. 2020, 36, 101422. [Google Scholar] [CrossRef]
- Habashneh, M.; Movahedi Rad, M. Reliability based geometrically nonlinear bi-directional evolutionary structural optimization of elasto-plastic material. Sci. Rep. 2022, 12, 5989. [Google Scholar] [CrossRef]
- Eom, Y.S.; Yoo, K.S.; Park, J.Y.; Han, S.Y. Reliability-based topology optimization using a standard response surface method for three-dimensional structures. Struct. Multidiscip. Optim. 2011, 43, 287–295. [Google Scholar] [CrossRef]
- Simonetti, H.L.; Almeida, V.S.; de Assis das Neves, F.; Del Duca Almeida, V.; de Oliveira Neto, L. Reliability-Based Topology Optimization: An Extension of the SESO and SERA Methods for Three-Dimensional Structures. Appl. Sci. 2022, 12, 4220. [Google Scholar] [CrossRef]
- Simonetti, H.L.; Almeida, V.S.; Neves FdAd Almeida, V.D.D.; Cutrim, M.D.S. 3D Structural Topology Optimization Using ESO, SESO and SERA: Comparison and an Extension to Flexible Mechanisms. Appl. Sci. 2023, 13, 6215. [Google Scholar] [CrossRef]
- Liu, K.; Tovar, A. An efficient 3D topology optimization code written in Matlab. Struct. Multidiscip. Optim. 2014, 50, 1175–1196. [Google Scholar] [CrossRef]
- Han, Y.; Xu, B.; Wang, Q.; Liu, Y. Bi-directional evolutionary topology optimization of continuum structures subjected to inertial loads. Adv. Eng. Softw. 2021, 155, 102897. [Google Scholar] [CrossRef]
- Meng, D.; Yang, H.; Yang, S.H.; Zhang, Y.; Jesus, A.M.; Correia, J.; Fazeres-Ferradosa, T.; Macek, W.; Branco, R.; Zhu, S. Kriging-assisted hybrid reliability design and optimization of offshore wind turbine support structure based on a portfolio allocation strategy. Ocean. Eng. 2024, 295, 116842. [Google Scholar] [CrossRef]
- Meng, D.; Yang, S.; Yang, H.; De Jesus, A.M.; Correia, J.; Zhu, S.P. Intelligent-inspired framework for fatigue reliability evaluation of offshore wind turbine support structures under hybrid uncertainty. Ocean. Eng. 2024, 307, 118213. [Google Scholar] [CrossRef]
- Yang, S.; Meng, D.; Wang, H.; Yang, C. A novel learning function for adaptive surrogate-model-based reliability evaluation. Philos. Trans. R. Soc. A 2024, 382, 20220395. [Google Scholar] [CrossRef]
- Kharmanda, G.; Olhoff, N.; Mohamed, A.; Lemaire, M. Reliability-based topology optimization. Struct. Multidiscip. Optim. 2004, 26, 295–307. [Google Scholar] [CrossRef]
- Li, Y.; Yuan, P.F.; Xie, Y.M. A strategy for improving the safety and strength of topologically optimized multi-material structures. Acta Mech. Sin. 2023, 39, 422134. [Google Scholar] [CrossRef]
- Jain, N.; Saxena, R. Effect of self-weight on topological optimization of static loading structures. Alex. Eng. J. 2018, 57, 527–535. [Google Scholar] [CrossRef]







| Distribution Parameter | Distribution Type | Mean () | Standard Deviation () |
|---|---|---|---|
| nelx (mm) | Normal | 120 | 0.1 |
| nely (mm) | Normal | 20 | 0.1 |
| nelz (mm) | Normal | 10 | 0.1 |
| E (GPa) | Normal | 1 | 0.1 |
| Constant | 0.30 | 0 | |
| F (1000 N/m2) | Normal | 1 | 0.1 |
| Volume (mm3) | Normal | 0.30 | 0.1 |
| Compliance (N.mm) | Normal | 4.82 × 106 | 0.1 |
| Opt. Techniques | RBTO-BESO | RBTO-SESO | Time RBTO-BESO (Hours)/Compliance/Iteration FORM | Time RBTO-SESO (Hours)/Compliance/Iteration FORM |
|---|---|---|---|---|
 |  | Time = 2.22 | Time = 1.86 | |
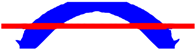 | 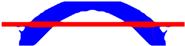 | Time = 1.62 | Time = 1.33 | |
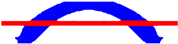 | 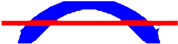 | Time = 1.37 | Time = 1.19 | |
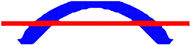 | 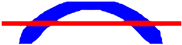 | Time = 1.56 | Time = 1.24 | |
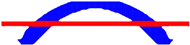 | 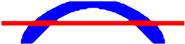 | Time = 1.58 | Time = 1.25 | |
 | 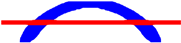 | Time = 1.83 | Time = 1.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simonetti, H.L.; Almeida, V.S.; Neves, F.d.A.d.; Azar, S.Z.; Silva, M.M.d. BESO and SESO: Comparative Analysis of Spatial Structures Considering Self-Weight and Structural Reliability. Appl. Sci. 2024, 14, 6465. https://doi.org/10.3390/app14156465
Simonetti HL, Almeida VS, Neves FdAd, Azar SZ, Silva MMd. BESO and SESO: Comparative Analysis of Spatial Structures Considering Self-Weight and Structural Reliability. Applied Sciences. 2024; 14(15):6465. https://doi.org/10.3390/app14156465
Chicago/Turabian StyleSimonetti, Hélio Luiz, Valério S. Almeida, Francisco de Assis das Neves, Sina Zhian Azar, and Márcio Maciel da Silva. 2024. "BESO and SESO: Comparative Analysis of Spatial Structures Considering Self-Weight and Structural Reliability" Applied Sciences 14, no. 15: 6465. https://doi.org/10.3390/app14156465






