A Review of Foot–Terrain Interaction Mechanics for Heavy-Duty Legged Robots
Abstract
1. Introduction
2. Supporting Feet of Heavy-Duty Legged Robots
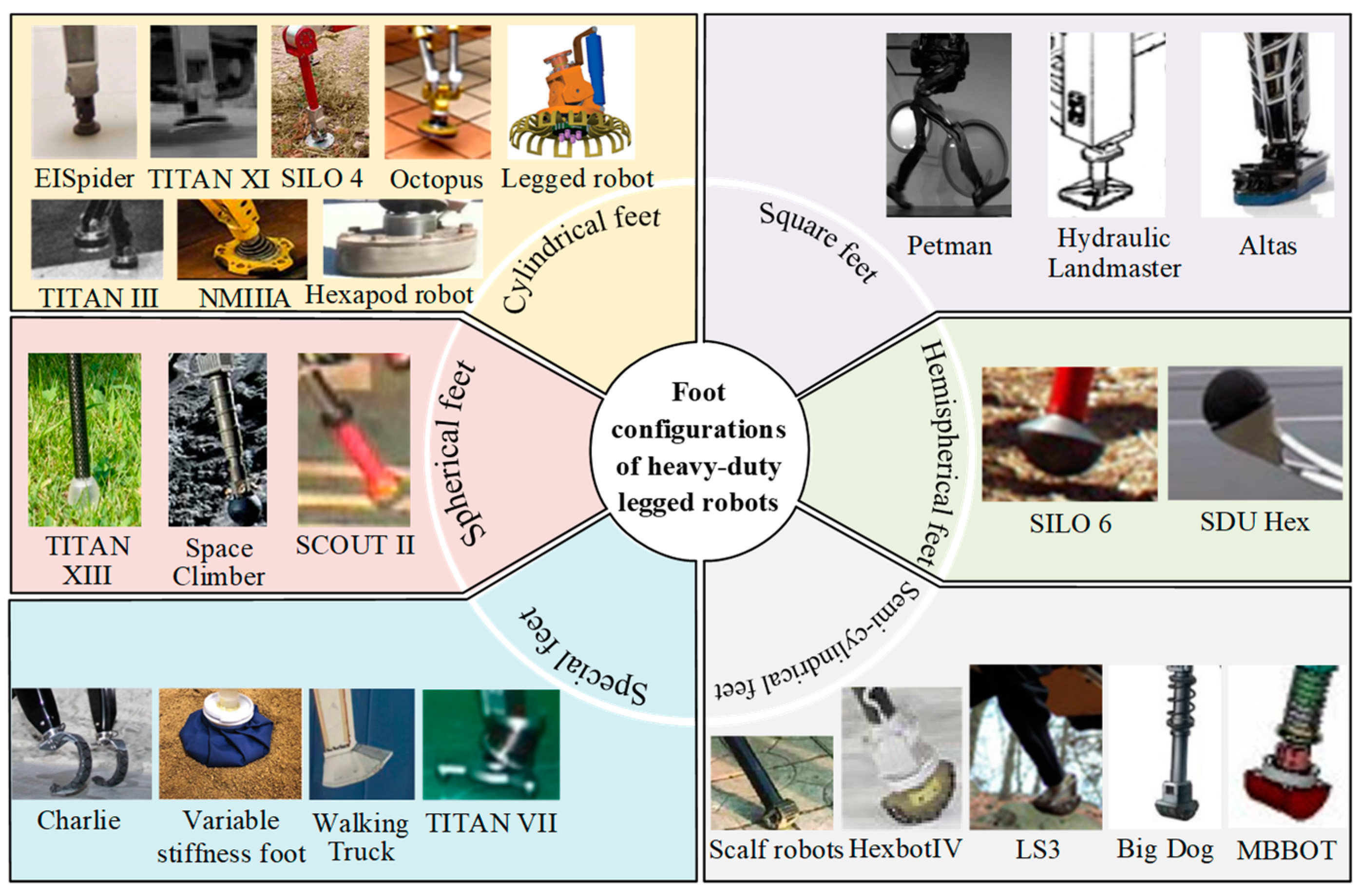
2.1. Supporting Foot Configurations of Heavy-Duty Legged Robots
2.1.1. Feet with Passive Adaptive Joints
Cylindrical Supporting Foot Configurations
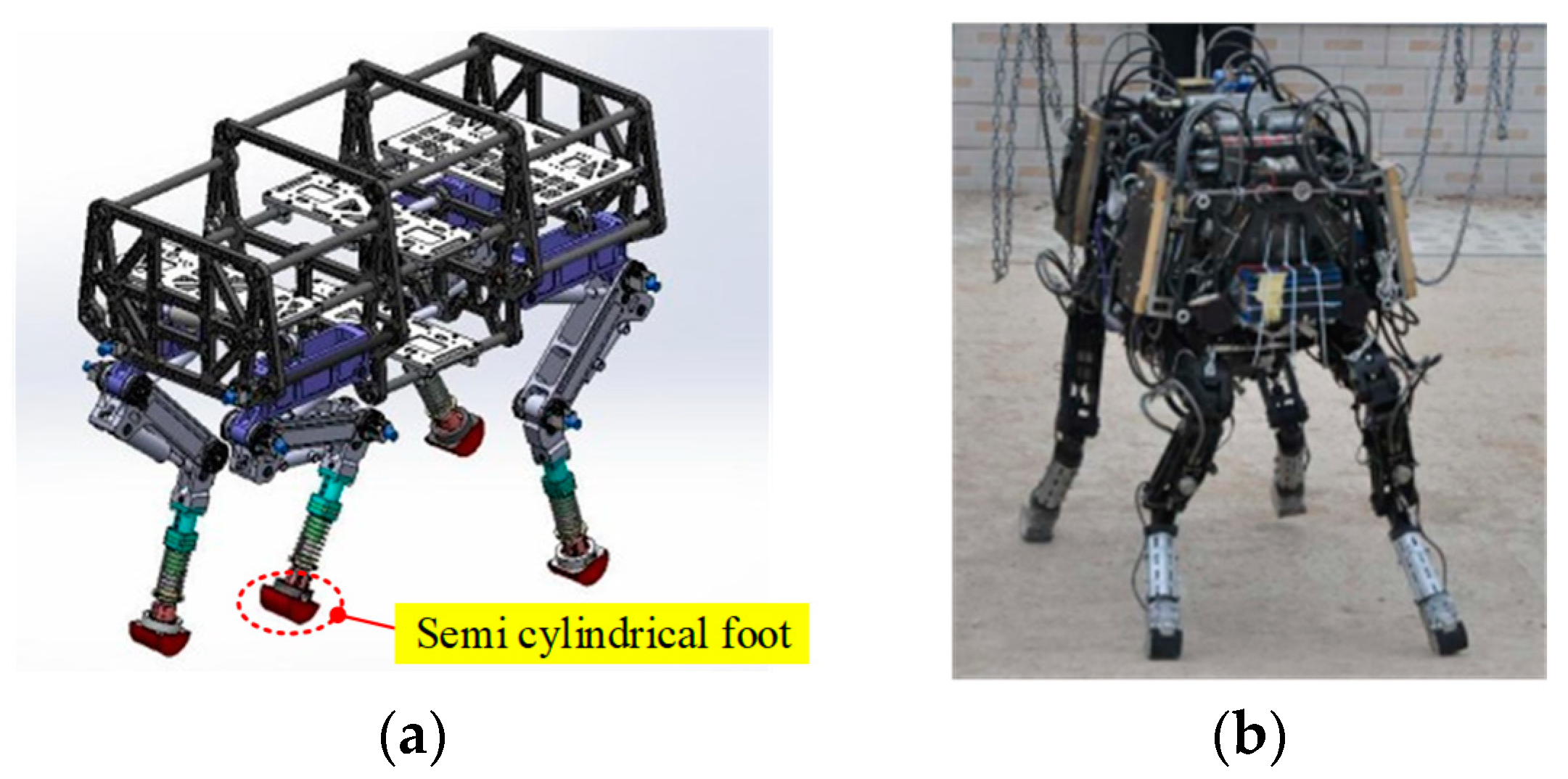
Semi-Cylindrical Supporting Foot Configurations
Spherical Supporting Foot Configurations
Hemispherical Supporting Foot Configurations
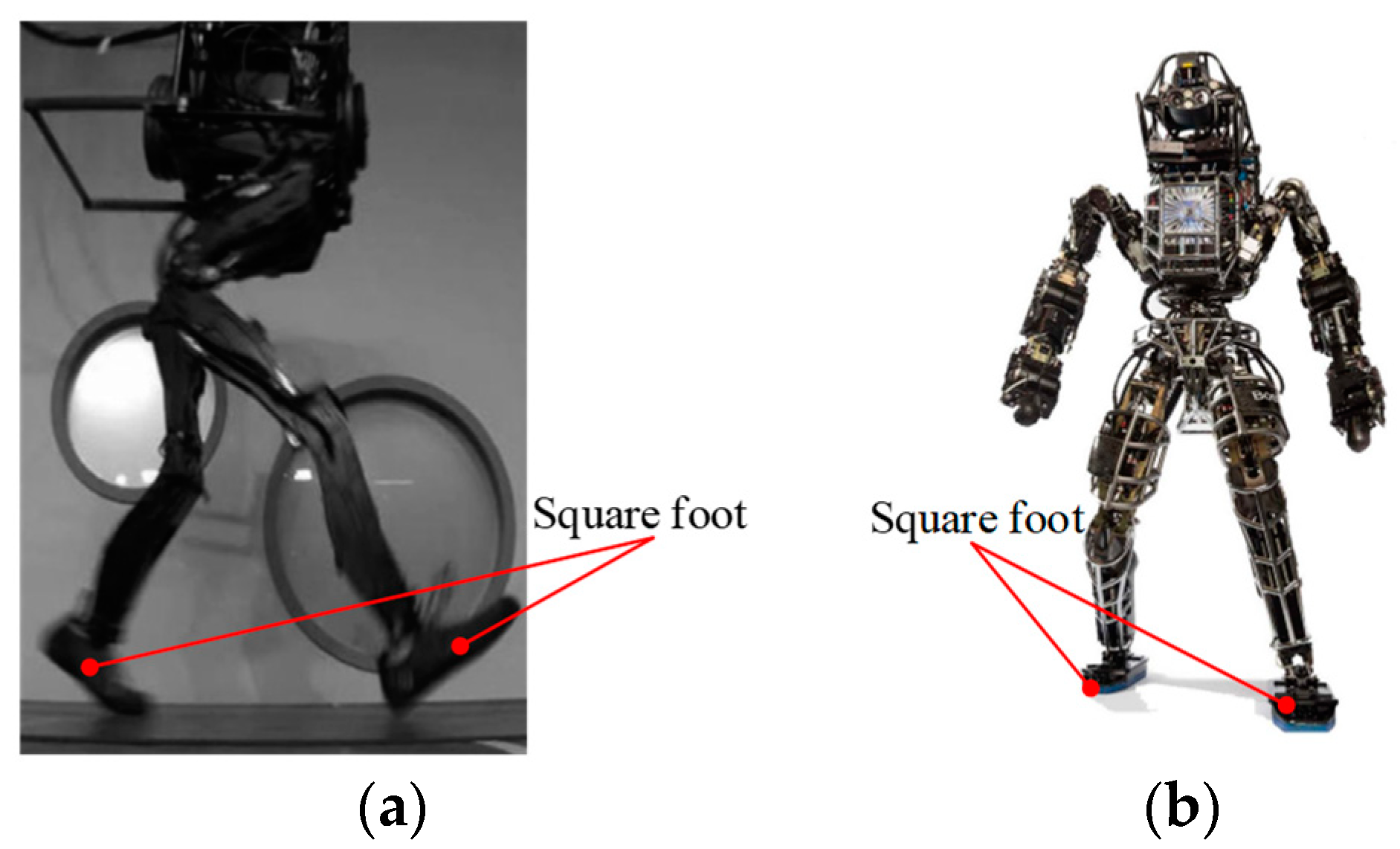
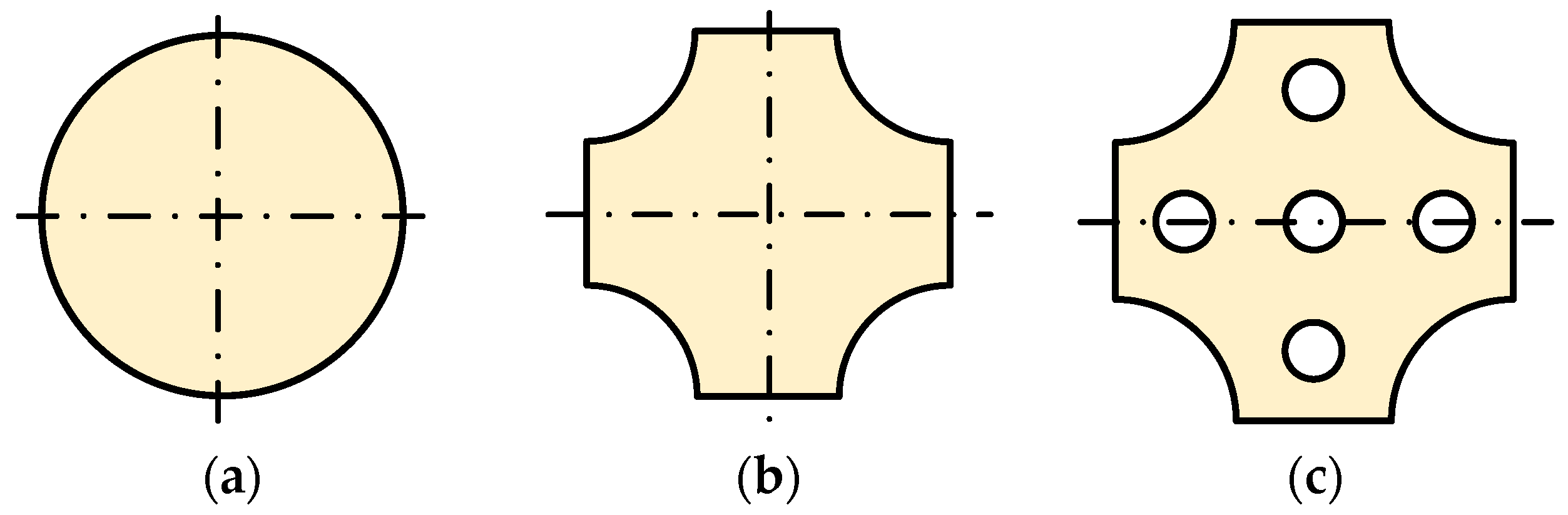
Square Supporting Foot Configurations
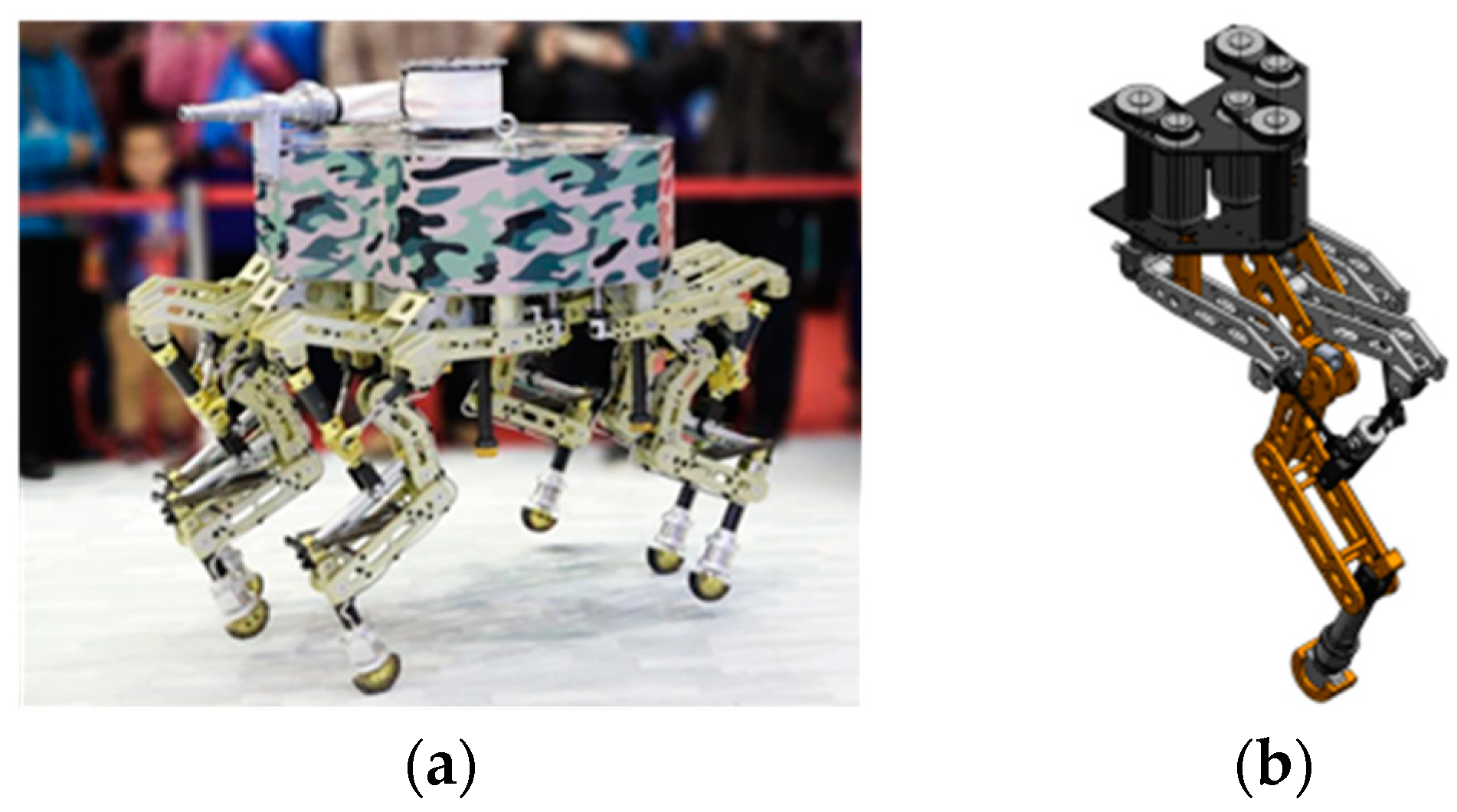
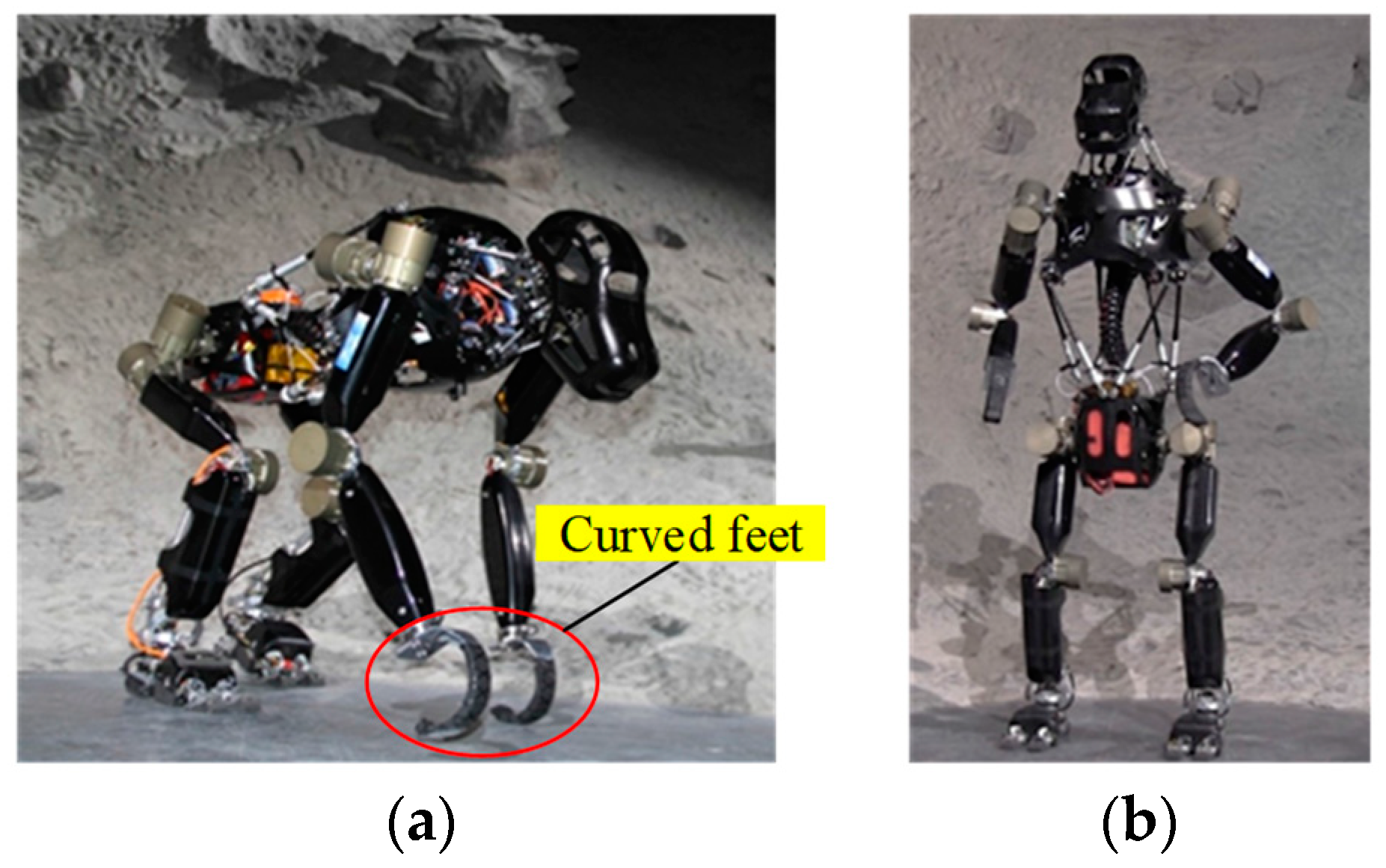
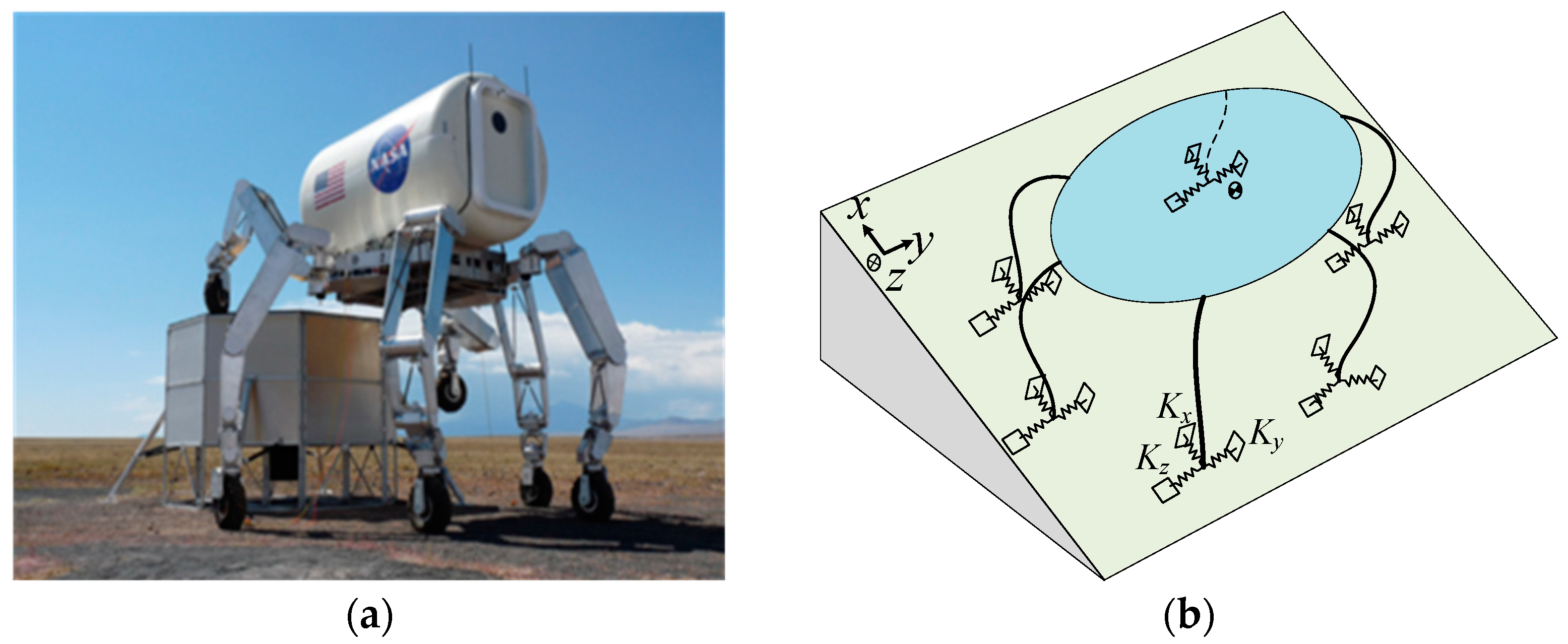
Special Supporting Foot Configurations
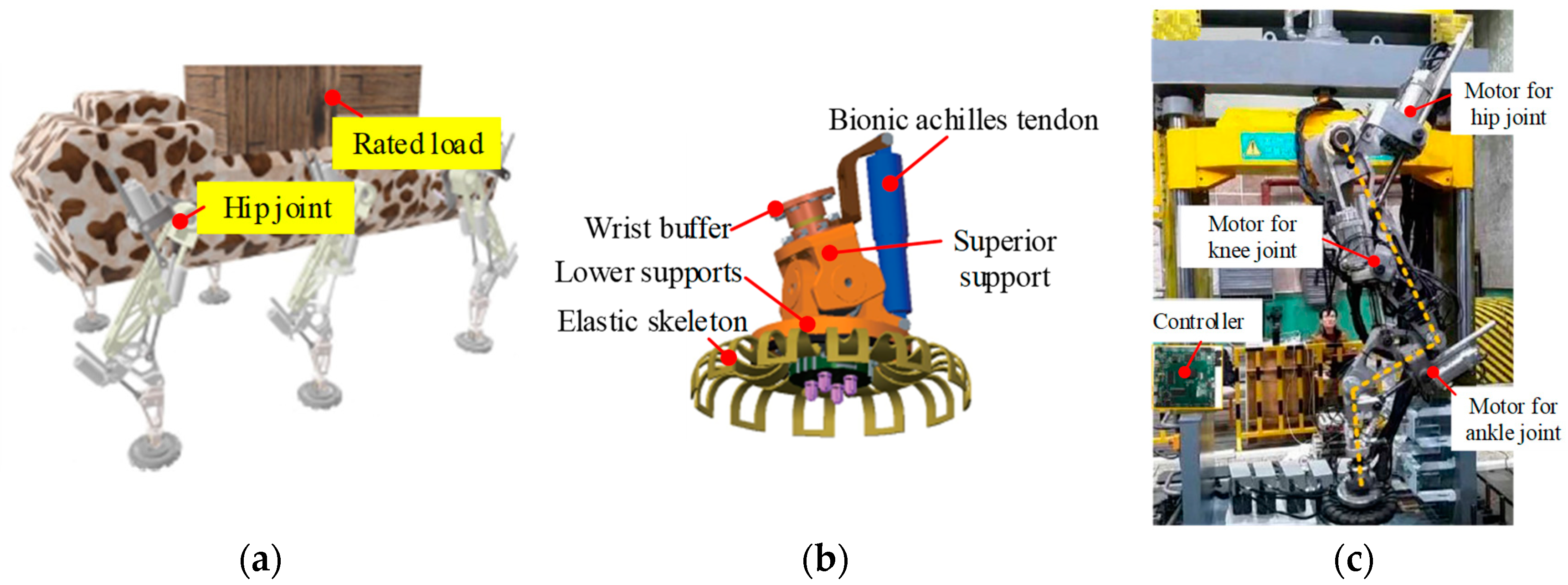
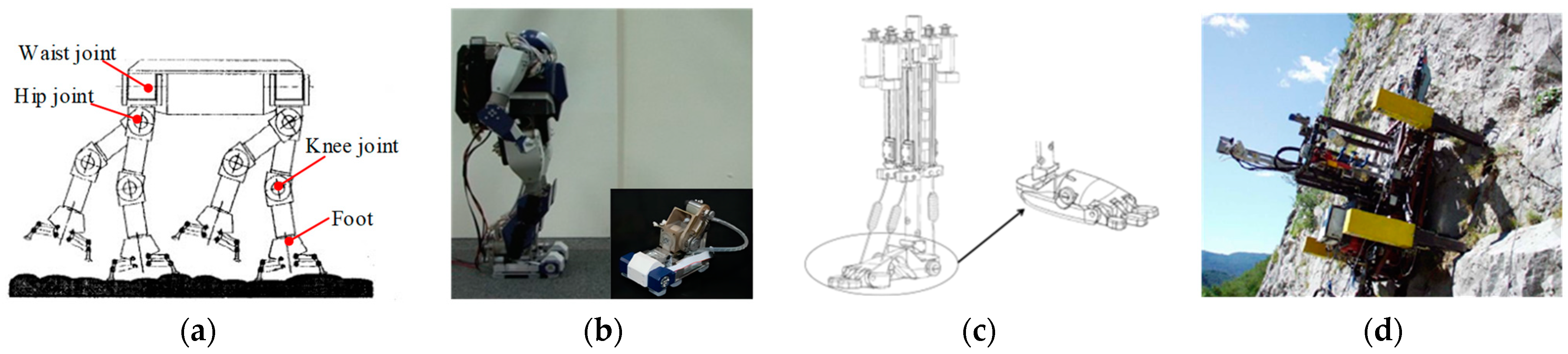
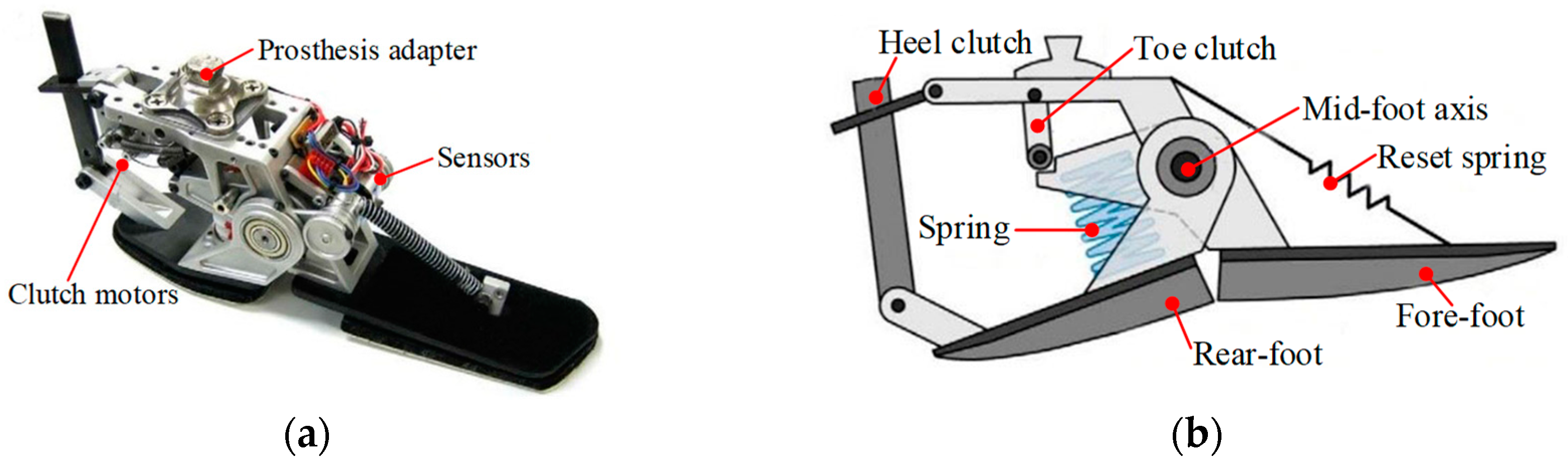
2.1.2. Feet with Active Driving Joints
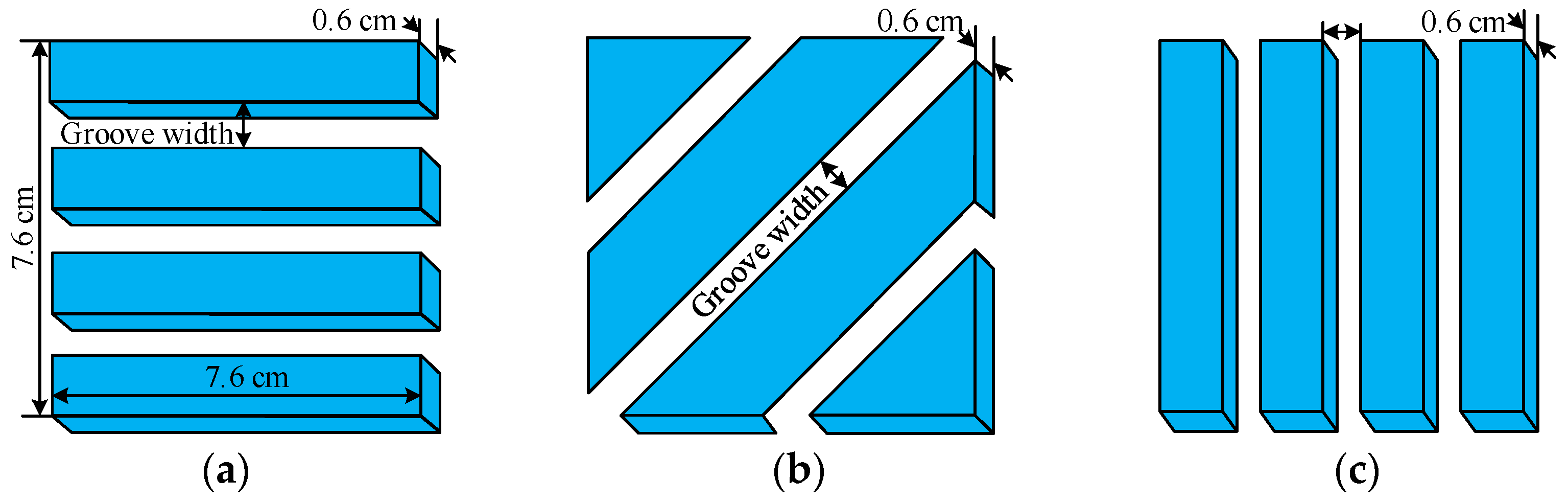
2.2. Plantar Patterns of Supporting Foot of Legged Robots
3. Dynamics Analysis of Robot
3.1. Models of Pressure–Sinkage for Mobile Robot
3.1.1. Models for Pressure–Sinkage at Zero Slip Conditions
A Theoretical Exploration of the Wheeled Robots
A Theoretical Exploration of the Wheel-Legged Composite Robots
A Theoretical Exploration of the Legged Robots
3.1.2. Models for Pressure–Sinkage at Non-Zero Slip Conditions
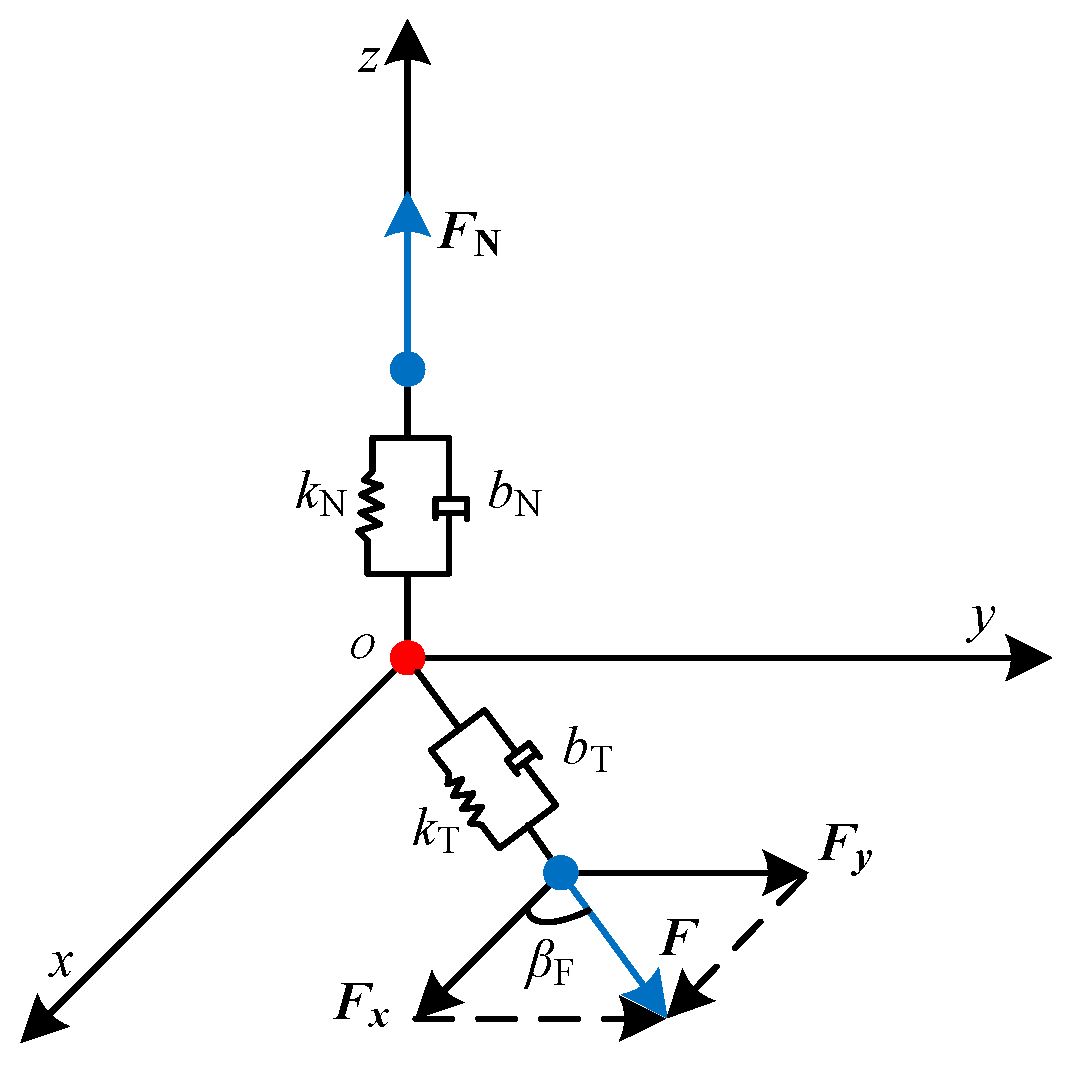
3.2. Tangential Force Models
4. Further Research
4.1. Configuration Research of Biomimetic Supporting Feet
4.1.1. Application of Bionic Technology in Supporting Feet Design
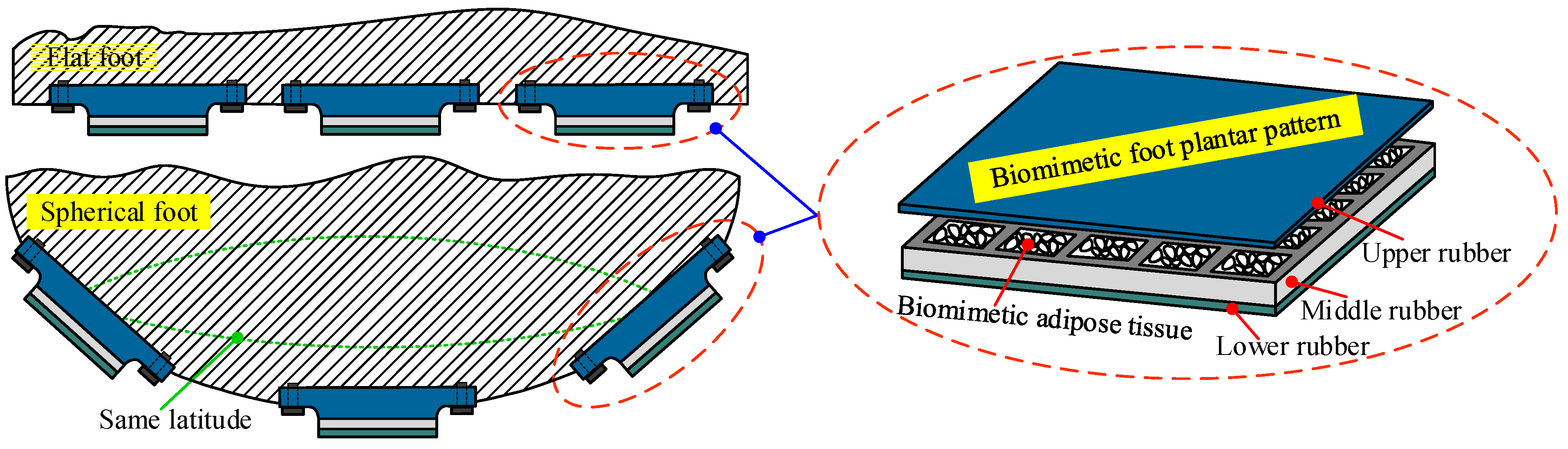
4.1.2. Design and Distribution of Plantar Patterns of Supporting Feet
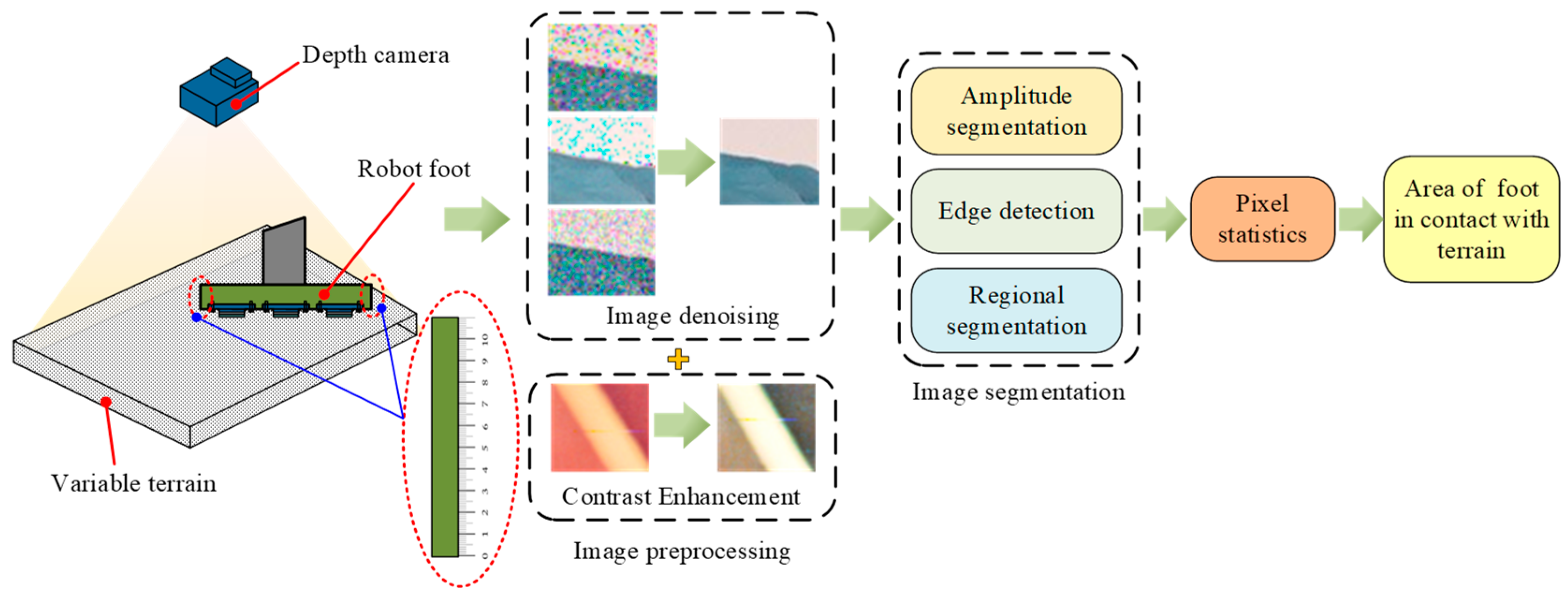
4.2. Study of Effective Contact Area between Irregular Foot and Dynamic Deformable Terrain
4.3. Mechanical Behavior Modeling of Interaction between Supporting Feet and Extreme/Dynamic Environments
4.3.1. Construction of Nonlinear Tangential Force Mathematical Model
4.3.2. Construction of Resultant Force Mathematical Model
4.4. Parameterization Research of Soil Characteristics in Extreme/Dynamic Environments
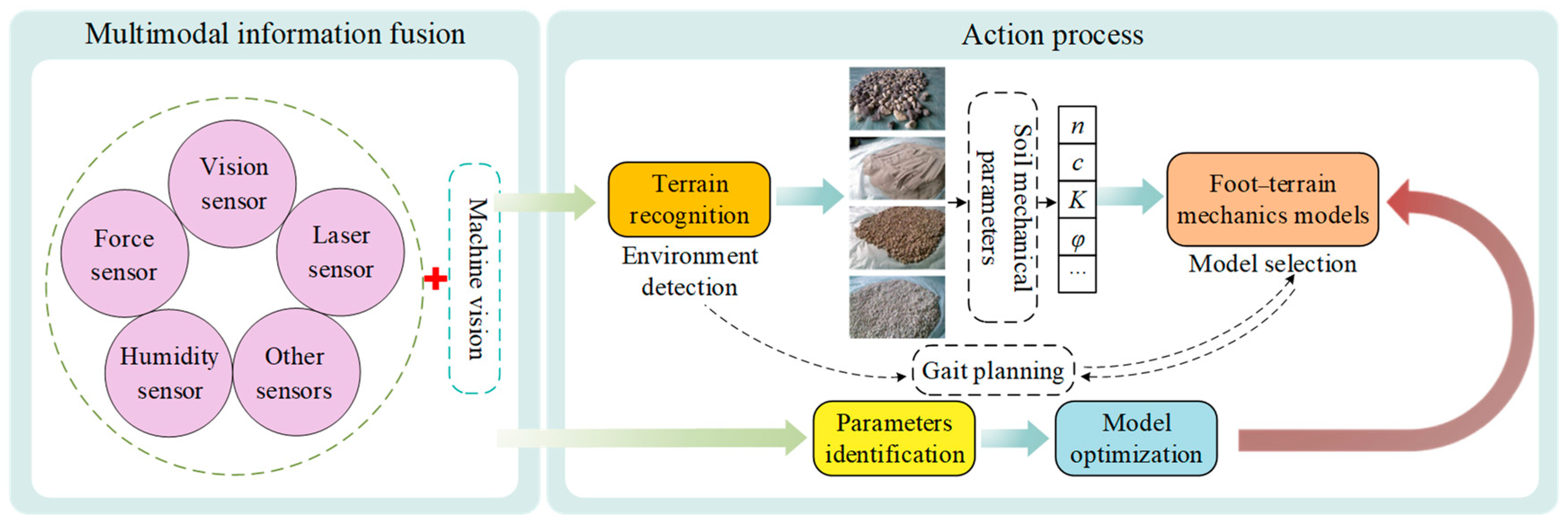
4.5. Cross-Application of Multimodal Information Fusion and Foot–Terrain Interaction Mechanics
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | Contact area | δ | Sum of foot and terrain deformations |
| B | Geometric parameter of plate | λN | Dimensionless function |
| b | Smaller dimension of contact patch | vT | Tangential sliding velocity |
| CN | Normal damping coefficient | δT | Terrain deformation |
| CT | Tangential damping coefficient | δF | Feet deformation |
| Cm | Model parameter | μ | Coefficient of friction |
| Cf | Shape coefficient of contact surface | FN | Normal support force |
| c | Soil stickiness | FT | Tangential driving force |
| α | Dimensionless geometric constant | Hp | Propagation depth of soil deformation |
| β | Dimensionless geometric constant | hgr | Grouser height |
| i | Slip ratio | N1, N2 | Model parameter |
| j | Soil shear displacement | p | Pressure |
| k | Sinkage modulus | p0 | Bearing capacity |
| kN | Equivalent stiffness coefficient | s | Shearing displacement |
| kFN | Stiffness coefficient of foot | s0 | Model parameter |
| kTN | Stiffness coefficient of terrain | sm | Model parameter |
| kc | Sinkage modulus | v | Poisson’s ratio |
| kΦ | Sinkage modulus | vs | Solid volume |
| kS | Stiffness modulus of terrain | vr | Pore volume |
| k1 | Model parameter | w | Dimensionless coefficient |
| k2 | Model parameter | z | Sinkage |
| m | Exponent of damping term | zo | Static sinkage |
| mF | Mass of foot | zj | Dynamic sinkage |
| n | Model parameter | ρ | Bulk density |
| n1, n2 | Indicators of stiffness terms |
References
- Zhuang, H.; Gao, H.; Deng, Z.; Ding, L.; Liu, Z. A review of heavy-duty legged robots. Sci. China Technol. Sci. 2014, 57, 298–314. [Google Scholar] [CrossRef]
- Biswal, P.; Mohanty, P.K. Development of quadruped walking robots: A review. Ain Shams Eng. J. 2021, 12, 2017–2031. [Google Scholar] [CrossRef]
- Maity, A.; Majumder, S.; Ghosh, S. An experimental hyper redundant serpentine robot. In Proceedings of the 2010 IEEE International Conference on Systems, Man and Cybernetics—SMC, Istanbul, Turkey, 10–13 October 2010; pp. 3180–3185. [Google Scholar] [CrossRef]
- Joshi, V.A.; Banavar, R.N.; Hippalgaonkar, R. Design and analysis of a spherical mobile robot. Mech. Mach. Theory 2010, 45, 130–136. [Google Scholar] [CrossRef]
- Bartsch, S.; Manz, M.; Kampmann, P.; Dettmann, A.; Hanff, H.; Langosz, M.; von Szadkowski, K.; Hilljegerdes, J.; Simnofske, M.; Kloss, P.; et al. Development and Control of the Multi-Legged Robot MANTIS. In Proceedings of the ISR 2016: 47st International Symposium on Robotics, Munich, Germany, 21–22 June 2016; pp. 1–8. [Google Scholar]
- Cobano, J.; Ponticelli, R.; de Santos, P.G. Mobile robotic system for detection and location of antipersonnel land mines: Field tests. Ind. Robot. Int. J. Robot. Res. Appl. 2008, 35, 520–527. [Google Scholar] [CrossRef]
- Carbone, G.; Ceccarelli, M. Legged Robotic Systems; Intech Open Access Publisher: London, UK, 2005. [Google Scholar]
- Zhang, Q.; Zhao, W.; Chu, S.; Wang, L.; Fu, J.; Yang, J.; Gao, B. Research Progress of Nuclear Emergency Response Robot. IOP Conf. Ser. Mater. Sci. Eng. 2018, 452, 042102. [Google Scholar] [CrossRef]
- Zhuang, H.C.; Wang, N.; Gao, H.B.; Deng, Z.Q. Autonomous fault-tolerant gait planning research for electrically driven large-load-ratio six-legged robot. In Proceedings of the 12th International Conference on Intelligent Robotics and Applications (ICIRA 2019), Shenyang, China, 8–11 August 2019; pp. 231–244. [Google Scholar] [CrossRef]
- Zhuang, H.-C.; Gao, H.-B.; Deng, Z.-Q. Gait Planning Research for an Electrically Driven Large-Load-Ratio Six-Legged Robot. Appl. Sci. 2017, 7, 296. [Google Scholar] [CrossRef]
- Zhuang, H.-C.; Gao, H.-B.; Deng, Z.-Q. Analysis Method of Articulated Torque of Heavy-Duty Six-Legged Robot under Its Quadrangular Gait. Appl. Sci. 2016, 6, 323. [Google Scholar] [CrossRef]
- Bloesch, M.; Gehring, C.; Fankhauser, P.; Hutter, M.; Hoepflinger, M.A.; Siegwart, R. State estimation for legged robots on unstable and slippery terrain. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2013), Tokyo, Japan, 3–7 November 2013; pp. 6058–6064. [Google Scholar] [CrossRef]
- Voloshina, A.S.; Kuo, A.D.; Ferris, D.P.; Remy, D.C. A model-based analysis of the mechanical cost of walking on uneven terrain. bioRxiv 2020. [Google Scholar] [CrossRef]
- Zhuang, H.; Xia, Y.; Wang, N.; Li, W.; Dong, L.; Li, B. Interactive method research of dual mode information coordination integration for astronaut gesture and eye movement signals based on hybrid model. Sci. China Technol. Sci. 2023, 66, 1717–1733. [Google Scholar] [CrossRef] [PubMed]
- Saraiva, L.; da Silva, M.R.; Marques, F.; da Silva, M.T.; Flores, P. A review on foot-ground contact modeling strategies for human motion analysis. Mech. Mach. Theory 2022, 177, 105046. [Google Scholar] [CrossRef]
- Hodoshima, R.; Doi, T.; Fukuda, Y.; Hirose, S.; Okamoto, T.; Mori, J. Development of a Quadruped Walking Robot TITAN XI for Steep Slope Operation—Step Over Gait to Avoid Concrete Frames on Steep Slopes. J. Robot. Mechatron. 2007, 19, 13–26. [Google Scholar] [CrossRef]
- Hirose, S.; Yokota, S.; Torii, A.; Ogata, M.; Suganuma, S.; Takita, K.; Kato, K. Quadruped Walking Robot Centered Demining System—Development of TITAN-IX and its Operation. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 1284–1290. [Google Scholar] [CrossRef]
- Hirose, S.; Fukuda, Y.; Kikuchi, H. The gait control system of a quadruped walking vehicle. Adv. Robot. 1986, 1, 289–323. [Google Scholar] [CrossRef]
- Irawan, A.; Nonami, K. Compliant Walking Control for Hydraulic Driven Hexapod Robot on Rough Terrain. J. Robot. Mechatronics 2011, 23, 149–162. [Google Scholar] [CrossRef]
- Bares, J.E.; Wettergreen, D.S. Dante II: Technical Description, Results, and Lessons Learned. Int. J. Robot. Res. 1999, 18, 621–649. [Google Scholar] [CrossRef]
- A Galvez, J.; Estremera, J.; de Santos, P.G. A new legged-robot configuration for research in force distribution. Mechatronics 2003, 13, 907–932. [Google Scholar] [CrossRef]
- Zhuang, H.C. Electrically Driven Large-Load-Ratio Six-Legged Robot Structural Design and Its Mobile Characteristics Research. Ph.D. Dissertation, Harbin Institute of Technology, Harbin, China, 2014. (In Chinese). [Google Scholar]
- Zhuang, H.; Wang, N.; Gao, H.; Deng, Z. Quickly Obtaining Range of Articulated Rotating Speed for Electrically Driven Large-Load-Ratio Six-Legged Robot Based on Maximum Walking Speed Method. IEEE Access 2019, 7, 29453–29470. [Google Scholar] [CrossRef]
- Liu, Y.; Ding, L.; Gao, H.; Liu, G.; Deng, Z.; Yu, H. Efficient force distribution algorithm for hexapod robot walking on uneven terrain. In Proceedings of the 2016 IEEE International Conference on Robotics and Biomimetics (ROBIO), Qingdao, China, 3–7 December 2016; pp. 432–437. [Google Scholar] [CrossRef]
- Xu, P.; Ding, L.; Li, Z.; Yang, H.; Wang, Z.; Gao, H.; Zhou, R.; Su, Y.; Deng, Z.; Huang, Y. Learning physical characteristics like animals for legged robots. Natl. Sci. Rev. 2023, 10, nwad045. [Google Scholar] [CrossRef]
- Pan, Y.; Gao, F. A new six-parallel-legged walking robot for drilling holes on the fuselage. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2014, 228, 753–764. [Google Scholar] [CrossRef]
- Yang, P.; Gao, F. Kinematical Model and Topology Patterns of a New 6-Parallel-Legged Walking Robot. In Proceedings of the ASME 2012 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Volume 4: 36th Mechanisms and Robotics Conference, Parts A and B, Chicago, IL, USA, 12–15 August 2012; pp. 1197–1205. [Google Scholar] [CrossRef]
- Pan, Y.; Gao, F. Payload capability analysis of a new kind of parallel leg hexapod walking robot. In Proceedings of the 2013 International Conference on Advanced Mechatronic Systems (ICAMechS), Luoyang, China, 25–27 September 2013; pp. 541–544. [Google Scholar] [CrossRef]
- Yang, P.; Gao, F. Leg kinematic analysis and prototype experiments of walking-operating multifunctional hexapod robot. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013, 228, 2217–2232. [Google Scholar] [CrossRef]
- Zhang, H.Y. Analysis of the Structure and Stability of a Large and Highly Adaptable Hexapod Robot. Master’s Thesis, Jilin University, Changchun, China, 2021. (In Chinese). [Google Scholar]
- Zhai, C. Research on Motion Trajectory Planning of Heavy-Load Hydraulic Driven Hexapod Robots. Master’s Thesis, Jilin University, Changchun, China, 2023. (In Chinese). [Google Scholar]
- Gao, J. Leg Mechanism Design and Simulation Analysis for a Heavy-Duty Hydraulic Hexapod Robot. Master’s Thesis, Jilin University, Changchun, China, 2017. (In Chinese). [Google Scholar]
- Xu, Z.; Yi, H.; Liu, D.; Zhang, R.; Luo, X. Design a Hybrid Energy-Supply for the Electrically Driven Heavy-Duty Hexapod Vehicle. J. Bionic Eng. 2023, 20, 1434–1448. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, X.; Liu, Y.; Wang, L.; Zhou, L.; Yi, H.; Bao, C. Design and Implementation of a Novel Robot Foot with High-adaptability and High-adhesion for Heavy-load Walking Robots. In Proceedings of the 2019 IEEE 9th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Suzhou, China, 29 July–2 August 2019; pp. 1509–1514. [Google Scholar] [CrossRef]
- Raibert, M.; Blankespoor, K.; Nelson, G.; Playter, R. BigDog, the rough-terrain quadruped robot. IFAC Proc. Vol. 2008, 41, 10822–10825. [Google Scholar] [CrossRef]
- Wooden, D.; Malchano, M.; Blankespoor, K.; Howardy, A.; Rizzi, A.A.; Raibert, M. Autonomous navigation for BigDog. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation (ICRA 2010), Anchorage, AK, USA, 3–7 May 2010; pp. 4736–4741. [Google Scholar] [CrossRef]
- Meng, X.; Wang, S.; Cao, Z.; Zhang, L. A review of quadruped robots and environment perception. In Proceedings of the IEEE 35th Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 6350–6356. [Google Scholar] [CrossRef]
- Zang, H.; Zhao, D.; Shen, L. Theoretical Study of Global Scale Analysis Method for Agile Bionic Leg Mechanism. Robotica 2020, 38, 427–441. [Google Scholar] [CrossRef]
- Han, B.; Yi, H.; Xu, Z.; Yang, X.; Luo, X. 3D-SLIP model based dynamic stability strategy for legged robots with impact disturbance rejection. Sci. Rep. 2022, 12, 5892. [Google Scholar] [CrossRef]
- Zhong, J.F. Design, Control of Hydraulical Actuators for Quadruped Legged Robot. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2014. (In Chinese). [Google Scholar]
- Cheng, P. Research, Design of Control System for Bionic Quadruped Robot. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2014. (In Chinese). [Google Scholar]
- Qi, C.; Gao, F.; Sun, Q.; Chen, X.; Xu, Y.; Zhao, X. A foot force sensing approach for a legged walking robot using the motor current. In Proceedings of the 2015 IEEE International Conference on Robotics and Biomimetics (ROBIO), Zhuhai, China, 6–9 December 2015; pp. 1078–1083. [Google Scholar] [CrossRef]
- Sun, Q.; Gao, F.; Chen, X. Towards dynamic alternating tripod trotting of a pony-sized hexapod robot for disaster rescuing based on multi-modal impedance control. Robotica 2018, 36, 1048–1076. [Google Scholar] [CrossRef]
- Qiao, S. Design, Dynamic Gait Control of the Rescue Hexapod Robot with Erect Posture and Parallel Mechanism Leg. Ph.D. Dissertation, Shanghai Jiaotong University, Shanghai, China, 2018. (In Chinese). [Google Scholar]
- Michael, K. Meet Boston Dynamics’ LS3—The Latest Robotic War Machine; University of Wollongong: Wollongong, NSW, Australia, 2012. [Google Scholar]
- Rong, X.; Li, Y.; Ruan, J.; Li, B. Design and simulation for a hydraulic actuated quadruped robot. J. Mech. Sci. Technol. 2012, 26, 1171–1177. [Google Scholar] [CrossRef]
- Chen, T.; Rong, X.; Li, Y.; Ding, C.; Chai, H.; Zhou, L. A compliant control method for robust trot motion of hydraulic actuated quadruped robot. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418813235. [Google Scholar] [CrossRef]
- Yang, K.; Zhou, L.; Rong, X.; Li, Y. Onboard hydraulic system controller design for quadruped robot driven by gasoline engine. Mechatronics 2018, 52, 36–48. [Google Scholar] [CrossRef]
- Bartsch, S.; Birnschein, T.; Cordes, F.; Kuehn, D.; Kampmann, P.; Hilljegerdes, J.; Planthaber, S.; Roemmermann, M.; Kirchner, F. Spaceclimber: Development of a six-legged climbing robot for space exploration. In Proceedings of the ISR 2010 (41st International Symposium on Robotics) and ROBOTIK 2010 (6th German Conference on Robotics), Munich, Germany, 7–9 June 2010; pp. 1–8. [Google Scholar]
- Bartsch, S.; Birnschein, T.; Römmermann, M.; Hilljegerdes, J.; Kühn, D.; Kirchner, F. Development of the six-legged walking and climbing robot SpaceClimber. J. Field Robot. 2012, 29, 506–532. [Google Scholar] [CrossRef]
- Kitano, S.; Hirose, S.; Horigome, A.; Endo, G. TITAN-XIII: Sprawling-type quadruped robot with ability of fast and energy-efficient walking. ROBOMECH J. 2016, 3, 8. [Google Scholar] [CrossRef]
- Ohtsuka, S.; Endo, G.; Fukushima, E.F.; Hirose, S. Development of terrain adaptive sole for multi-legged walking robot. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2010), Taipei, Taiwan, 18–22 October 2010; pp. 5354–5359. [Google Scholar] [CrossRef]
- Talebi, S.; Poulakakis, I.; Papadopoulos, E.; Buehler, M. Quadruped robot running with a bounding gait. In Experimental Robotics VII; Springer: Berlin/Heidelberg, Germany, 2001; pp. 281–289. [Google Scholar] [CrossRef]
- de Santos, P.G.; Cobano, J.; Garcia, E.; Estremera, J.; Armada, M. A six-legged robot-based system for humanitarian demining missions. Mechatronics 2007, 17, 417–430. [Google Scholar] [CrossRef]
- Chen, T.; Li, Y.; Rong, X.; Zhang, G.; Chai, H.; Bi, J.; Wang, Q. Design and Control of a Novel Leg-Arm Multiplexing Mobile Operational Hexapod Robot. IEEE Robot. Autom. Lett. 2022, 7, 382–389. [Google Scholar] [CrossRef]
- Nelson, G.; Saunders, A.; Neville, N.; Swilling, B.; Bondaryk, J.; Billings, D.; Lee, C.; Playter, R.; Raibert, M. PETMAN: A Humanoid Robot for Testing Chemical Protective Clothing. J. Robot. Soc. Jpn. 2012, 30, 372–377. [Google Scholar] [CrossRef]
- Kuindersma, S.; Deits, R.; Fallon, M.; Valenzuela, A.; Dai, H.; Permenter, F.; Koolen, T.; Marion, P.; Tedrake, R. Optimization-based locomotion planning, estimation, and control design for the atlas humanoid robot. Auton. Robot. 2016, 40, 429–455. [Google Scholar] [CrossRef]
- Kuehn, D.; Schilling, M.; Stark, T.; Zenzes, M.; Kirchner, F. System Design and Testing of the Hominid Robot Charlie. J. Field Robot. 2017, 34, 666–703. [Google Scholar] [CrossRef]
- Fondahl, K.; Kuehn, D.; Beinersdorf, F.; Bernhard, F.; Grimminger, F.; Schilling, M.; Stark, T.; Kirchner, F. An adaptive sensor foot for a bipedal and quadrupedal robot. In Proceedings of the 2012 4th IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob 2012), Rome, Italy, 24–27 June 2012; pp. 270–275. [Google Scholar] [CrossRef]
- Mosher, R. Test and evaluation of a versatile walking truck. In Proceedings of the Off-Road Mobility Research Symposium, Washington, DC, USA, 1968; pp. 359–379. [Google Scholar]
- Hirose, S.; Yoneda, K.; Tsukagoshi, H. TITAN VII: Quadruped walking and manipulating robot on a steep slope. In Proceedings of the International Conference on Robotics and Automation, Albuquerque, NM, USA, 25 April 1987; pp. 494–500. [Google Scholar] [CrossRef]
- He, G.; Xu, J.; Jiang, J.; Cao, Z.; Zhu, D. Soil arching effect analysis and structure optimization of a robot foot sinking in soft soil. Adv. Mech. Eng. 2017, 9, 1687814017727940. [Google Scholar] [CrossRef]
- He, G.; Cao, Z.; Li, Q.; Zhu, D.; Aimin, J. Influence of hexapod robot foot shape on sinking considering multibody dynamics. J. Mech. Sci. Technol. 2020, 34, 3823–3831. [Google Scholar] [CrossRef]
- Chopra, S.; Tolley, M.T.; Gravish, N. Granular Jamming Feet Enable Improved Foot-Ground Interactions for Robot Mobility on Deformable Ground. IEEE Robot. Autom. Lett. 2020, 5, 3975–3981. [Google Scholar] [CrossRef]
- Hong, Y.; Yi, S.; Ryu, S.; Lee, C. Design and experimental test of a new robot foot for a quadrupedal jointed-leg type walking robot. In Proceedings of the 5th IEEE International Workshop on Robot and Human Communication. RO-MAN’96 TSUKUBA, Tsukuba, Japan, 11–14 November 1996; pp. 317–322. [Google Scholar] [CrossRef]
- Yamamoto, K.; Sugihara, T.; Nakamura, Y. Toe joint mechanism using parallel four-bar linkage enabling humanlike multiple support at toe pad and toe tip. In Proceedings of the 2007 7th IEEE-RAS International Conference on Humanoid Robots (Humanoids 2007), Pittsburgh, PA, USA, 29 November–1 December 2007; pp. 410–415. [Google Scholar] [CrossRef]
- Borovac, B.; Slavnic, S. Design of Multi-segment Humanoid Robot Foot. In Proceedings of the Research and Education in Robotics—EUROBOT 2008: International Conference, Heidelberg, Germany, 22–24 May 2008; pp. 12–18. [Google Scholar] [CrossRef]
- Nabulsi, S.; Sarria, J.F.; Montes, H.; Armada, M.A. High-Resolution Indirect Feet–Ground Interaction Measurement for Hydraulic-Legged Robots. IEEE Trans. Instrum. Meas. 2009, 58, 3396–3404. [Google Scholar] [CrossRef]
- Collins, S.H.; Kuo, A.D. Recycling Energy to Restore Impaired Ankle Function during Human Walking. PLoS ONE 2010, 5, e9307. [Google Scholar] [CrossRef]
- Song, Y. The Analysis and Test of the Robot Foot-Ground Adhesion Properties. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2014. (In Chinese). [Google Scholar]
- Zou, Y.Y. Landing Point Planning and Foot Pattern Design of Hexapod Robot. Master’s Thesis, Dalian University of Technology, Dalian, China, 2019. (In Chinese). [Google Scholar]
- Li, J. The Design and Research of Heavy-Duty Robot High Adaptability Foot. Master’s Thesis, Dalian University of Technology, Dalian, China, 2016. (In Chinese). [Google Scholar]
- Li, K.W.; Wu, H.H.; Lin, Y.-C. The effect of shoe sole tread groove depth on the friction coefficient with different tread groove widths, floors and contaminants. Appl. Ergon. 2006, 37, 743–748. [Google Scholar] [CrossRef]
- Li, K.W.; Chen, C.J.; Lin, C.-H.; Hsu, Y.W. Relationship between measured friction coefficients and two tread groove design parameters for footwear pads. Tsinghua Sci. Technol. 2006, 11, 712–719. [Google Scholar] [CrossRef]
- Li, K.W.; Chen, C.J. Effects of tread groove orientation and width of the footwear pads on measured friction coefficients. Saf. Sci. 2005, 43, 391–405. [Google Scholar] [CrossRef]
- Irani, R.; Bauer, R.; Warkentin, A. A dynamic terramechanic model for small lightweight vehicles with rigid wheels and grousers operating in sandy soil. J. Terramechanics 2011, 48, 307–318. [Google Scholar] [CrossRef]
- Ding, L.; Yang, H.; Gao, H.; Li, N.; Deng, Z.; Guo, J.; Li, N. Terramechanics-based modeling of sinkage and moment for in-situ steering wheels of mobile robots on deformable terrain. Mech. Mach. Theory 2017, 116, 14–33. [Google Scholar] [CrossRef]
- Zhuang, H.; Wang, N.; Gao, H.; Deng, Z. Power Consumption Characteristics Research on Mobile System of Electrically Driven Large-Load-Ratio Six-Legged Robot. Chin. J. Mech. Eng. 2023, 36, 26. [Google Scholar] [CrossRef]
- Liu, Z.; Zhuang, H.-C.; Gao, H.-B.; Deng, Z.-Q.; Ding, L. Static Force Analysis of Foot of Electrically Driven Heavy-Duty Six-Legged Robot under Tripod Gait. Chin. J. Mech. Eng. 2018, 31, 63. [Google Scholar] [CrossRef]
- Bernstein, R. Problems of the experimental mechanics of motor ploughs. Der Motorwagen 1913, 16, 1–10. [Google Scholar]
- Saakyan, S.S. Vzaimodeistrie vedomogo kolesa i pochvi. 1959. [Google Scholar]
- Comin, F.J.; Saaj, C.M. Models for Slip Estimation and Soft Terrain Characterization with Multilegged Wheel–Legs. IEEE Trans. Robot. 2017, 33, 1438–1452. [Google Scholar] [CrossRef]
- Komizunai, S.; Konno, A.; Abiko, S.; Uchiyama, M. Development of a static sinkage model for a biped robot on loose soil. In Proceedings of the 2010 IEEE/SICE International Symposium on System Integration (SII 2010), Sendai, Japan, 21–22 December 2010; pp. 61–66. [Google Scholar] [CrossRef]
- Bekker, M.G. Land Locomotion on the Surface of Planets. ARS J. 1962, 32, 1651–1659. [Google Scholar] [CrossRef]
- Patel, N.; Scott, G.; Ellery, A. Application of Bekker Theory for Planetary Exploration Through Wheeled, Tracked, and Legged Vehicle Locomotion. In Proceedings of the Space 2004 Conference and Exhibit, San Diego, CA, USA, 28–30 September 2004; p. 6091. [Google Scholar] [CrossRef]
- Reece, A.R. Principles of Soil-Vehicle Mechanics. Proc. Inst. Mech. Eng. Automob. Div. 1965, 180, 45–66. [Google Scholar] [CrossRef]
- Gotteland, P.; Benoit, O. Sinkage tests for mobility study, modelling and experimental validation. J. Terramechan. 2006, 43, 451–467. [Google Scholar] [CrossRef]
- Ding, L.; Gao, H.; Deng, Z.; Li, Y.; Liu, G. New perspective on characterizing pressure–sinkage relationship of terrains for estimating interaction mechanics. J. Terramechan. 2014, 52, 57–76. [Google Scholar] [CrossRef]
- Hunt, K.; Crossley, F.R.E. Coefficient of Restitution Interpreted as Damping in Vibroimpact. J. Appl. Mech. 1975, 42, 440–445. [Google Scholar] [CrossRef]
- Wheeler, D.D.; Chavez-Clemente, D.; Sunspiral, V.K. FootSpring: A compliance model for the ATHLETE family of robots. In Proceedings of the 10th International Symposium on Artificial Intelligence, Toronto, ON, Canada, 20–21 June 2010. [Google Scholar]
- Youssef, A.-F.A.; Ali, G.A. Determination of soil parameters using plate test. J. Terramechan. 1982, 19, 129–147. [Google Scholar] [CrossRef]
- Han, D.; Zhang, R.; Zhang, H.; Hu, Z.; Li, J. Mechanical Performances of Typical Robot Feet Intruding into Sands. Energies 2020, 13, 1867. [Google Scholar] [CrossRef]
- Ding, L.; Gao, H.; Deng, Z.; Song, J.; Liu, Y.; Liu, G.; Iagnemma, K. Foot–terrain interaction mechanics for legged robots: Modeling and experimental validation. Int. J. Robot. Res. 2013, 32, 1585–1606. [Google Scholar] [CrossRef]
- Gao, H.; Jin, M.; Ding, L.; Liu, Y.; Li, W.; Yu, X.; Deng, Z.; Liu, Z. A real-time, high fidelity dynamic simulation platform for hexapod robots on soft terrain. Simul. Model. Pract. Theory 2016, 68, 125–145. [Google Scholar] [CrossRef]
- Yang, C.; Ding, L.; Tang, D.; Gao, H.; Deng, Z.; Wang, G. Analysis of the normal bearing capacity of the terrain in case of foot-terrain interaction based on Terzaghi theory. In Proceedings of the 2016 IEEE International Conference on Robotics and Biomimetics (ROBIO), Qingdao, China, 3–7 December 2016; pp. 443–448. [Google Scholar] [CrossRef]
- Vasilev, A.V.; Dokychaeva, E.N.; Utkin-Lubovtsov, O.L. Effect of Tracked Tractor Design Parameters on Tractive Performance; Mashinostroenie: Moscow, Russia, 1969.
- Yeomans, B.; Saaj, C.M. Towards terrain interaction prediction for bioinspired planetary exploration rovers. Bioinspiration Biomim. 2014, 9, 016009. [Google Scholar] [CrossRef] [PubMed]
- Awrejcewicz, J.; Olejnik, P. Analysis of Dynamic Systems with Various Friction Laws. Appl. Mech. Rev. 2005, 58, 389–411. [Google Scholar] [CrossRef]
- Olsson, H.; Åström, K.; de Wit, C.C.; Gäfvert, M.; Lischinsky, P. Friction Models and Friction Compensation. Eur. J. Control 1998, 4, 176–195. [Google Scholar] [CrossRef]
- Haddadi, A.; Hashtrudi-Zaad, K. A New Method for Online Parameter Estimation of Hunt-Crossley Environment Dynamic Models. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 981–986. [Google Scholar] [CrossRef]
- Zapolsky, S.; Drumwright, E. Inverse dynamics with rigid contact and friction. Auton. Robot. 2017, 41, 831–863. [Google Scholar] [CrossRef]
- Senoo, T.; Ishikawa, M. Analysis of sliding behavior of a biped robot in centroid acceleration space. Robotica 2017, 35, 636–653. [Google Scholar] [CrossRef][Green Version]
- Liang, H.; Xie, W.; Zhang, Z.; Wei, P.; Cui, C. A Three-Dimensional Mass-Spring Walking Model Could Describe the Ground Reaction Forces. Math. Probl. Eng. 2021, 2021, 6651715. [Google Scholar] [CrossRef]
- Ding, L.; Xu, P.; Li, Z.; Zhou, R.; Gao, H.; Deng, Z.; Liu, G. Pressing and Rubbing: Physics-Informed Features Facilitate Haptic Terrain Classification for Legged Robots. IEEE Robot. Autom. Lett. 2022, 7, 5990–5997. [Google Scholar] [CrossRef]
- Yang, C.; Ding, L.; Tang, D.; Gao, H.; Niu, L.; Lan, Q.; Li, C.; Deng, Z. Improved Terzaghi-theory-based interaction modeling of rotary robotic locomotors with granular substrates. Mech. Mach. Theory 2020, 152, 103901. [Google Scholar] [CrossRef]
- Iagnemma, K.; Kang, S.; Shibly, H.; Dubowsky, S. Online Terrain Parameter Estimation for Wheeled Mobile Robots with Application to Planetary Rovers. IEEE Trans. Robot. 2004, 20, 921–927. [Google Scholar] [CrossRef]
- Wu, C. Space exploration: Secrets of the martian soil. Nature 2007, 448, 742–744. [Google Scholar] [CrossRef] [PubMed]
- Yen, A.S.; Gellert, R.; Schröder, C.; Morris, R.V.; Bell, J.F.; Knudson, A.T.; Clark, B.C.; Ming, D.W.; Crisp, J.A.; Arvidson, R.E.; et al. An integrated view of the chemistry and mineralogy of martian soils. Nature 2005, 436, 49–54. [Google Scholar] [CrossRef]
- Hecht, M.H.; Kounaves, S.P.; Quinn, R.C.; West, S.J.; Young, S.M.M.; Ming, D.W.; Catling, D.C.; Clark, B.C.; Boynton, W.V.; Hoffman, J.; et al. Detection of Perchlorate and the Soluble Chemistry of Martian Soil at the Phoenix Lander Site. Science 2009, 325, 64–67. [Google Scholar] [CrossRef]
- Shorthill, R.W.; Moore, H.J.; Hutton, R.E.; Scott, R.F.; Spitzer, C.R. The Environs of Viking 2 Lander. Science 1976, 194, 1309–1318. [Google Scholar] [CrossRef]
- Moore, H.J.; Hutton, R.E.; Clow, G.D.; Spitzer, C.R. Physical Properties of the Surface Materials at the Viking Landing Sites on Mars; United States Government Printing Office: Washington, USA, 1987. Available online: https://pubs.usgs.gov/publication/pp1389 (accessed on 1 July 2024).
- Ding, L.; Zhou, R.; Yuan, Y.; Yang, H.; Li, J.; Yu, T.; Liu, C.; Wang, J.; Gao, H.; Deng, Z.; et al. A 2-year locomotive exploration and scientific investigation of the lunar farside by the Yutu-2 rover. Sci. Robot. 2022, 7, eabj6660. [Google Scholar] [CrossRef] [PubMed]
- Heiken, G.H.; Vaniman, D.T.; French, B.M. Lunar Sourcebook: A User’s Guide to the Moon; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Slyuta, E.N. Physical and mechanical properties of the lunar soil (a review). Sol. Syst. Res. 2014, 48, 330–353. [Google Scholar] [CrossRef]





















| Robot | Length × Width × Height (m3) | Legs | Foot Shape | Driving Method | Mass (kg) | Payload (kg) | References |
|---|---|---|---|---|---|---|---|
| TITAN XI | 5.0 × 4.8 × 3.0 | 4 | Cylindrical | Hydraulic | 6800 | 5200 | [16] |
| TITAN IX | 10 × 16 × 5.5 | 4 | Cylindrical | Electric | 170 | - | [17] |
| TITAN III | - | 4 | Cylindrical | - | 80 | - | [18] |
| COMET-IV | 2.8 × 3.3 × 2.5 | 6 | Cylindrical | Hydraulic | 2120 | 424 | [19] |
| Dante II | 3.7 × 2.3 × 3.7 | 8 | Cylindrical | Electric | 770 | 130 | [20] |
| NMIIIA | 1.5 × 0.5 × 1 | 6 | Cylindrical | Electric | 750 | 80 | [1] |
| SILO 4 | 0.31 × 0.31 × 0.3 | 4 | Cylindrical | Electric | 30 | - | [21] |
| ElSpider | 1.9 × 1.9 × 1.0 | 6 | Cylindrical | Electric | 300 | 155 | [22,23] |
| Octopus Robot | 1.5 × 1.5 × 1 | 6 | Cylindrical | Hydraulic | 200 | 200 | [24] |
| Hexapod Robot | - | 6 | Cylindrical | Hydraulic | 3000 | - | [30,31,32] |
| Legged Robot | - | 6 | Cylindrical | Electric | 4200 | - | [33,34] |
| Big Dog | 1.1 × 0.3 × 1 | 4 | Semi-cylindrical | Hydraulic | 109 | 50 | [25,26] |
| MBBOT | 0.85 (Height) | 4 | Semi-cylindrical | Hydraulic | 140 | - | [40,41] |
| HexbotIV | 1.0 × 0.72 ×1 | 4 | Semi-cylindrical | Hydraulic | 268 | 50 | [43,44] |
| LS3 | 1.7 (Height) | 4 | Semi-cylindrical | Hydraulic | 590 | 182 | [45] |
| SCalf-I | 1.0 × 0.4 × 0.68 | 4 | Semi-cylindrical | Hydraulic | 65 | 80 | [46] |
| SCalf-II | 1.1 × 0.45 (Length × Width) | 4 | Semi-cylindrical | Hydraulic | 130 | 140 | [47] |
| SCalf-III | 1.4 × 0.75 (Length × Width) | 4 | Semi-cylindrical | Hydraulic | 200 | 200 | [48] |
| Space Climber1 | 8.2 × 10 × 22 | 6 | Special | Electric | 185 | - | [49] |
| Space Climber2 | 8.5 × 10 × 22 | 6 | Spherical | Electric | 23 | 8 | [50] |
| TITAN XIII | 2.134 × 5.584 × 3.4 | 4 | Spherical | Electric | 5.65 | 5.0 | [51,52] |
| SCOUT II | 0.55 × 0.48 × 0.27 | 4 | Spherical | Electric | 20.86 | - | [53] |
| SILO 6 | 0.88 × 0.45 × 0.26 | 6 | Hemispherical | Electric | 44.34 | - | [54] |
| SDU Hex | 0.98 × 0.4 × 0.1 to 0.6 | 6 | Hemispherical | Electric | 35 | - | [55] |
| Landmaster | 3.6 × 2.3 × 2.6 | 6 | Square | Hydraulic | 3950 | 1000 | [1] |
| Landmaster 3 | 1.4 × 1.3 × 1.0 | 6 | Square | Electric | 82 | 30 | [1] |
| Petman | 1.5 (Height) | 2 | Square | Hydraulic | 80 | - | [56] |
| Altas | 1.8 (Height) | 2 | Square | Electric | 150 | - | [57] |
| Charlie | 8 × 4.4 × 5.4 | 4 | Special | Electric | 21.5 | - | [58,59] |
| Walking Truck | 4 × 3 × 3.3 | 4 | Special | Hydraulic | 1300 | - | [60] |
| TITAN VII | - | 4 | Special | - | - | - | [61] |
| Plate Shape | β |
|---|---|
| Circular | 4 |
| Square | 4 |
| Rectangular | |
| Elliptical |
| Different Feet | Pressure–Sinkage Model |
|---|---|
| Foot with variable cross-sectional area | |
| Foot with constant cross-sectional area |
| Model Name | Model Parameters | Equation Number | References |
|---|---|---|---|
| Bernstein | k, n | (5) | [80,81] |
| Bekker | kc, kΦ, b, n | (6) | [82,83,84] |
| Reece | kc, kΦ, k1, k2, b, n, c, γ | (7), (8) | [86] |
| N2M | Cm, s0, sm | (10) | [87] |
| Ding | kS, λN | (11) | [88] |
| Hunt–Crossley | δ, n1, n2, m, kN, kFN, kTN | (12), (13) | [89] |
| Youssef–Ali | k1, k2, b, n, α, β | (14) | [91] |
| Gao | KN′, CN′, n1, n2, m | (17) | [93] |
| Foot Shape | kTN | nTN | μ | kTT | nTT |
|---|---|---|---|---|---|
| Flat circular | n | 1 | |||
| Flat rectangular | n | 1 | |||
| Cylindrical | 1 | ||||
| Spherical | 1 |
| Model Name | Model Parameters | Equation Number | References |
|---|---|---|---|
| Coulomb | μ | (26) | [99,100] |
| Hunt–Crossley | f, Ct | (27) | [89] |
| Ding | βF | (28) | [93] |
| Ding–Janosi | s, K′, μf, smax, κ | (30), (31) | [94] |
| Feet of Large Legged Animals | Walking Mode | Characteristics | Design Elements |
|---|---|---|---|
| Ostrich feet | Digitigrade | The didactyl foot structure of ostriches comprises only the 3rd and 4th toes. The 3rd toe has a larger contact area with the terrain than the 4th toe. |
|
| Camel feet | Plantigrade | When camel feet walk in the sand, they come into contact with the terrain with a thick finger pillow (subcutaneous layer), which can play an elastic buffering effect and have less impact on the sand. |
|
| Horse feet | Unguligrade | A horse’s hoof usually has a curved shape, similar to an inverted U-shaped shape. The weight of a horse is mainly concentrated on the hoof wall, not the bottom of the hoof. The bottom of a horse’s hoof is usually flat or slightly raised. |
|
| Elephant feet | Semiplantigrade | There is a thick fat foot pad beneath the root bone and metatarsal bone of an elephant’s foot. During the weight-bearing process, the weight is distributed across the entire foot pad, giving the elephant’s feet a stronger load-bearing structure. |
|
| Terrain Mechanical Parameters | Dry Sand | Sandy Loam | Clayey Soil | Snow |
|---|---|---|---|---|
| n | 1.1 | 0.7 | 0.5 | 1.6 |
| c (kPa) | 1.0 | 1.7 | 4.14 | 1.0 |
| φ (°) | 30.0 | 29.0 | 13.0 | 19.7 |
| kc (kPa/mn−1) | 0.9 | 5.3 | 13.2 | 4.4 |
| kΦ (kPa/mn) | 1528.4 | 1515.0 | 692.15 | 196.7 |
| K (m) | 0.025 | 0.025 | 0.01 | 0.04 |
| Property | Viking 1 | Viking 2 | |
|---|---|---|---|
| Sandy Flats | Rocky Flats | Bonneville and Beta | |
| Bulk density (g/cm3) | 1 to 1.6 | 1.8 | 1.5 to 1.8 |
| Particle size (surface and near surface) | |||
| 10 to 100 μm (%) | 60 | 30 | 30 |
| 100 to 2000 μm (%) | 10 | 30 | 30 |
| Angle of internal friction (°) | 20 to 30 | 40 to 45 | 40 to 45 |
| Cohesion (kPa) | - | 0.1 to 1 | 1 |
| Adhesion (kPa) | - | 0.001 to 0.01 | - |
| Symbol | Meaning |
|---|---|
| n | 1 |
| kc (kN/mn+1) | 1.4 |
| kΦ (kN/mn+1) | 820 |
| c (kPa) | 0.17 |
| φ (°) | 35 |
| K (m) | 1.78 |
| Lunar Soil | Lunar Soil Density ρ (g/cm3) |
|---|---|
| Apollo 11 | 1.36 to 1.8 |
| Apollo 12 | 1.15 to 1.93 |
| Apollo 14 | 0.89 to 1.55 |
| Apollo 15 | 0.87 to 1.51 |
| Apollo 16 | 1.1 to 1.89 |
| Luna 16 | 1.115 to 1.793 |
| Luna 20 | 1.040 to 1.798 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, H.; Wang, J.; Wang, N.; Li, W.; Li, N.; Li, B.; Dong, L. A Review of Foot–Terrain Interaction Mechanics for Heavy-Duty Legged Robots. Appl. Sci. 2024, 14, 6541. https://doi.org/10.3390/app14156541
Zhuang H, Wang J, Wang N, Li W, Li N, Li B, Dong L. A Review of Foot–Terrain Interaction Mechanics for Heavy-Duty Legged Robots. Applied Sciences. 2024; 14(15):6541. https://doi.org/10.3390/app14156541
Chicago/Turabian StyleZhuang, Hongchao, Jiaju Wang, Ning Wang, Weihua Li, Nan Li, Bo Li, and Lei Dong. 2024. "A Review of Foot–Terrain Interaction Mechanics for Heavy-Duty Legged Robots" Applied Sciences 14, no. 15: 6541. https://doi.org/10.3390/app14156541
APA StyleZhuang, H., Wang, J., Wang, N., Li, W., Li, N., Li, B., & Dong, L. (2024). A Review of Foot–Terrain Interaction Mechanics for Heavy-Duty Legged Robots. Applied Sciences, 14(15), 6541. https://doi.org/10.3390/app14156541