Multistep Evolution Method to Generate Topological Interlocking Assemblies
Abstract
1. Introduction
2. Related Work
2.1. Block-Shape Analysis
2.2. Concave TI Blocks
2.3. Non-Planar and Curvilinear TI Assemblies
2.4. Free-Form TI Assemblies
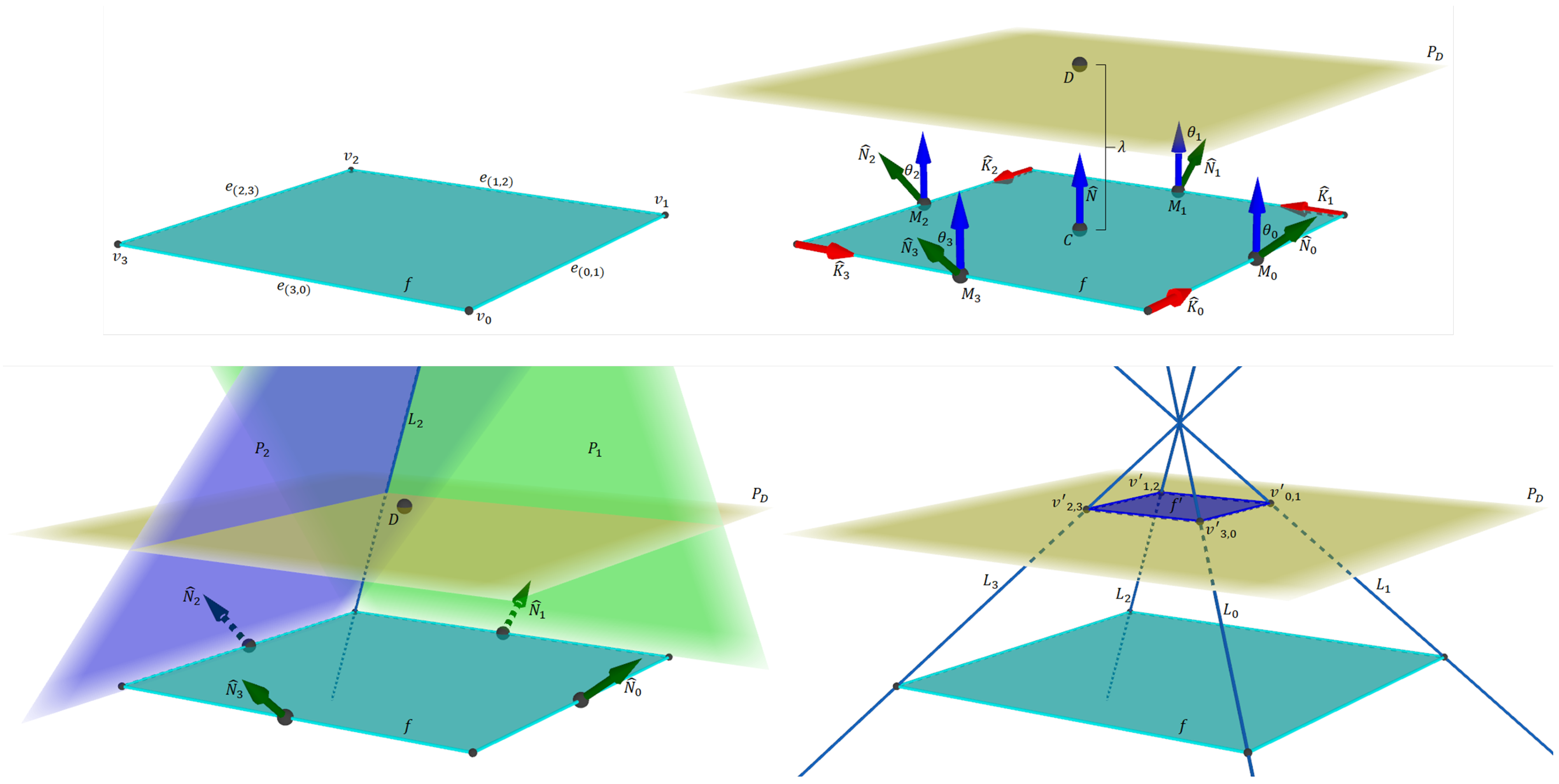
3. Polygon Evolution
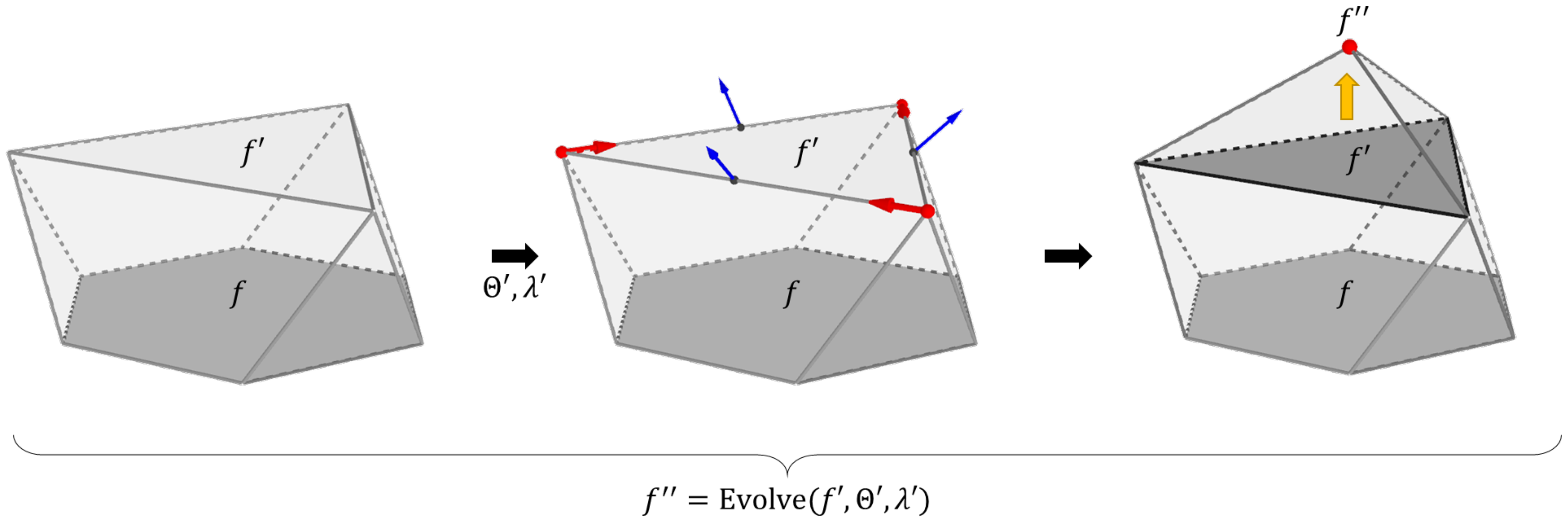
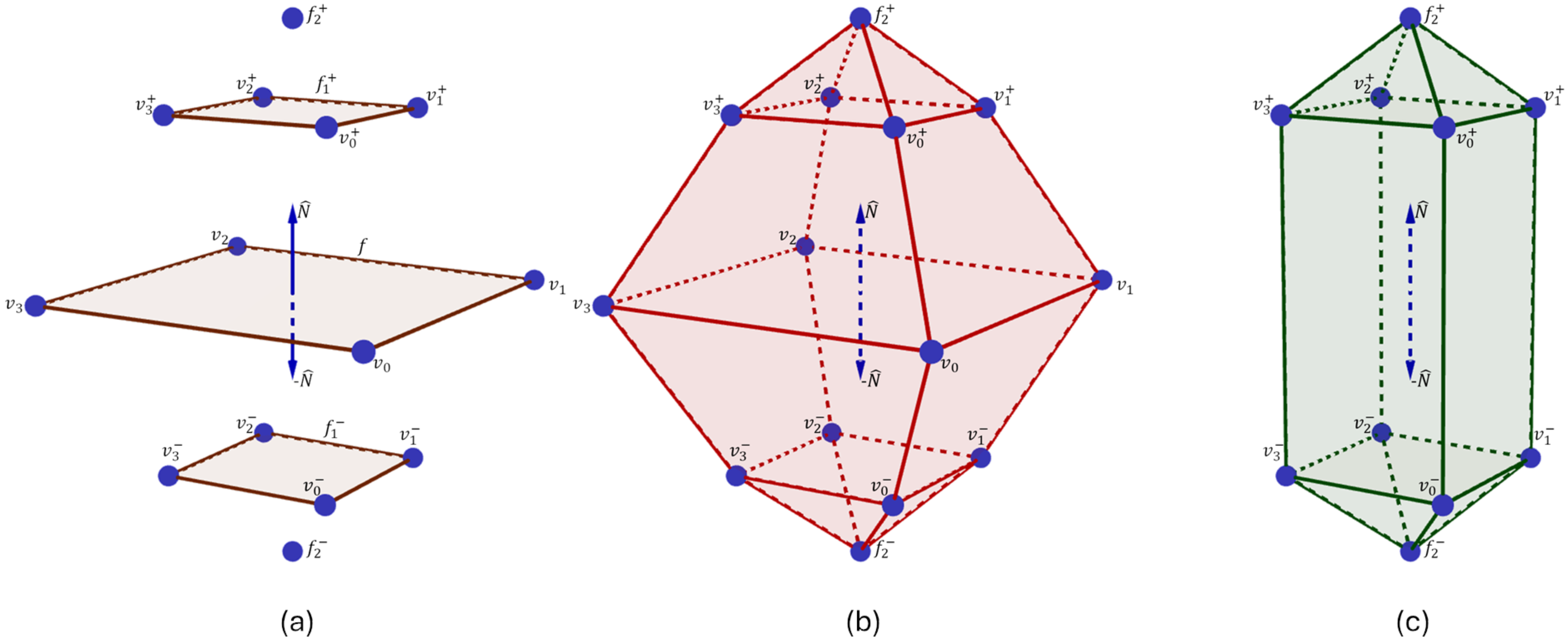
3.1. Evolution Step
| Algorithm 1 Evolve algorithm. |
|
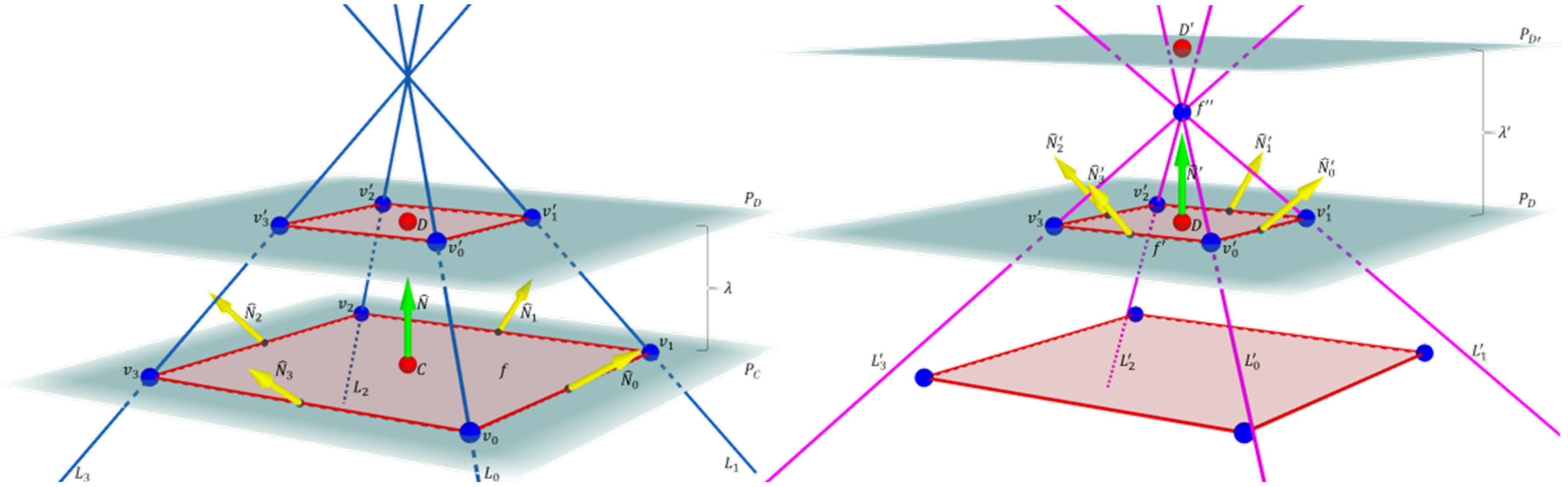
3.2. Single-Direction Polygon–Polyhedron Evolution
3.3. Double-Direction Polygon–Polyhedron Evolution
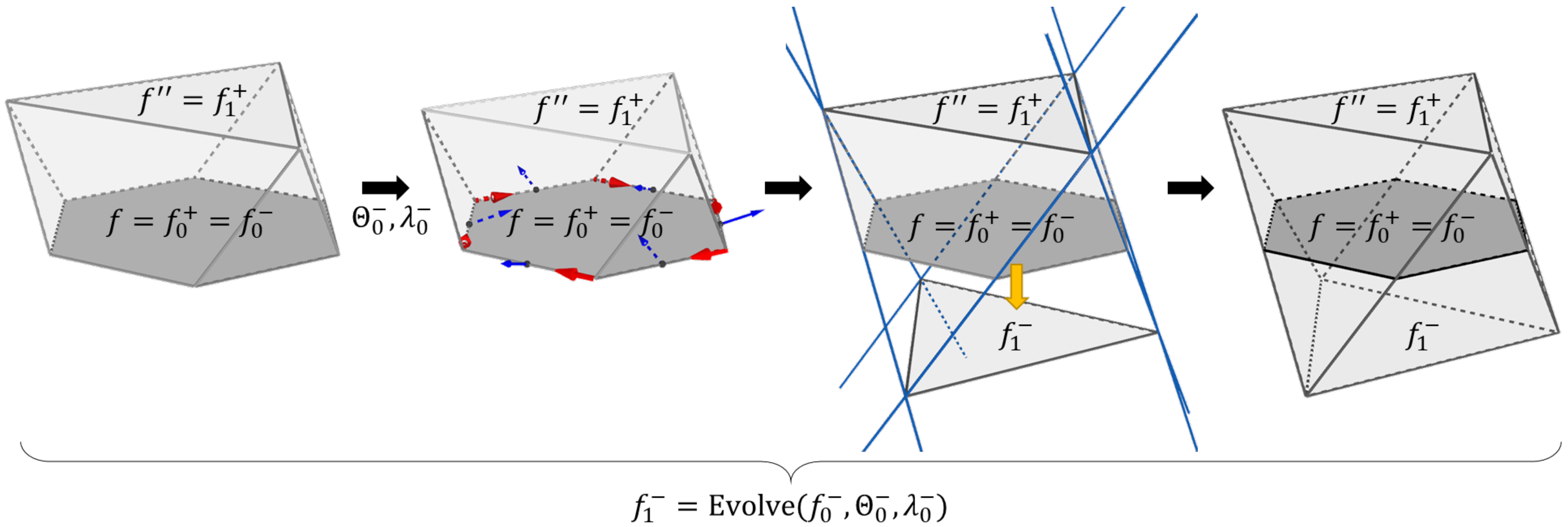
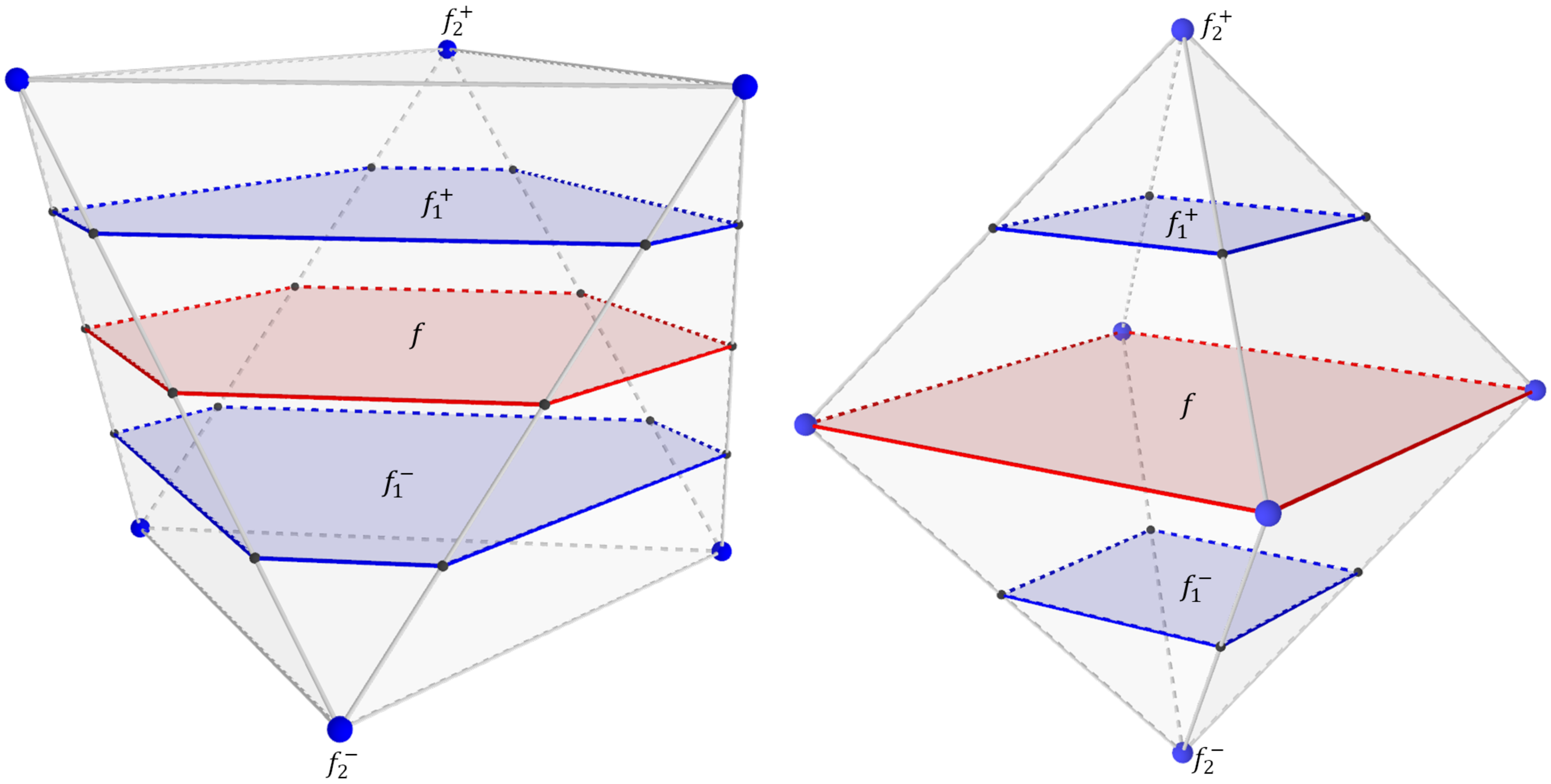
3.4. Reciprocal Evolution Steps
3.5. Uniform Evolution
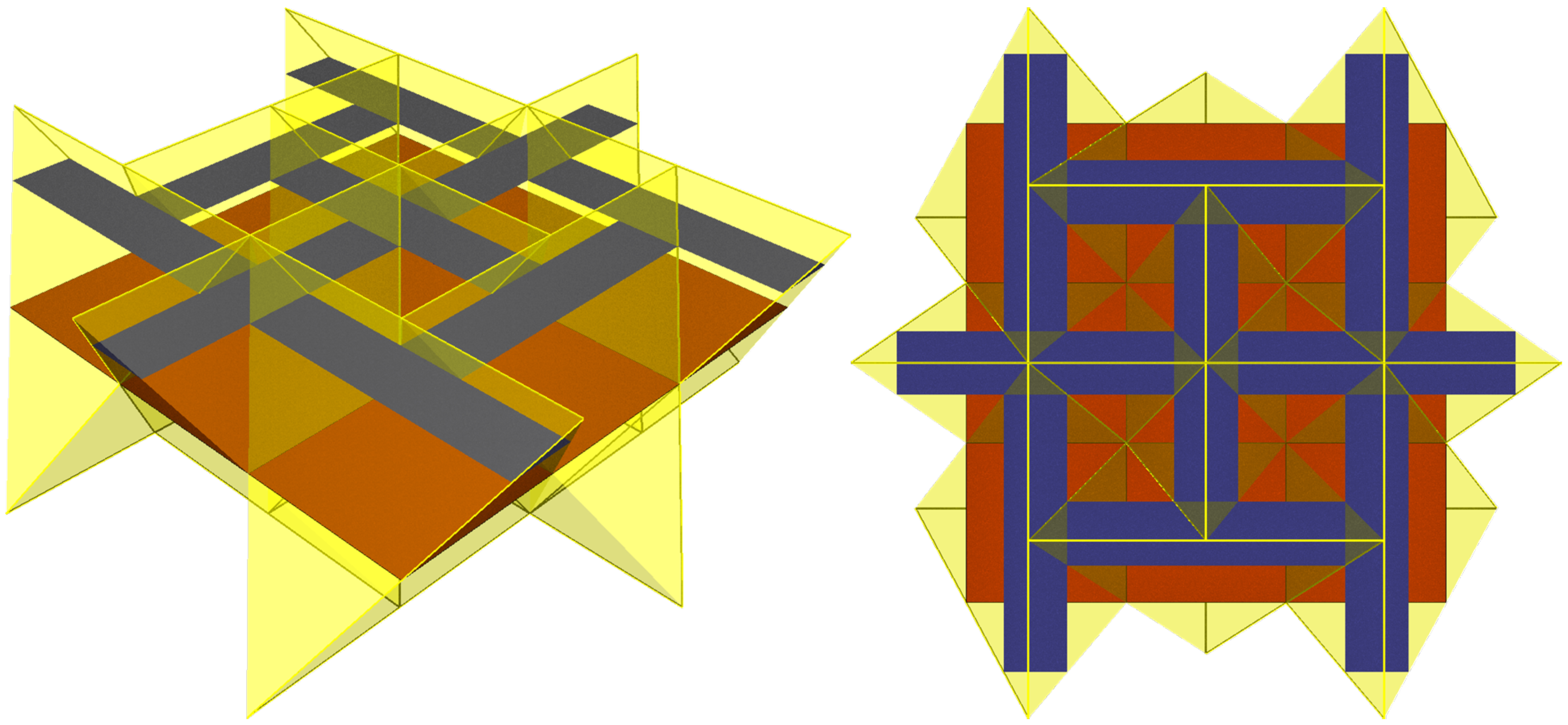
4. General Mid-Section Evolution
4.1. Generation Method
4.2. Fundamental TI Generation Requirement
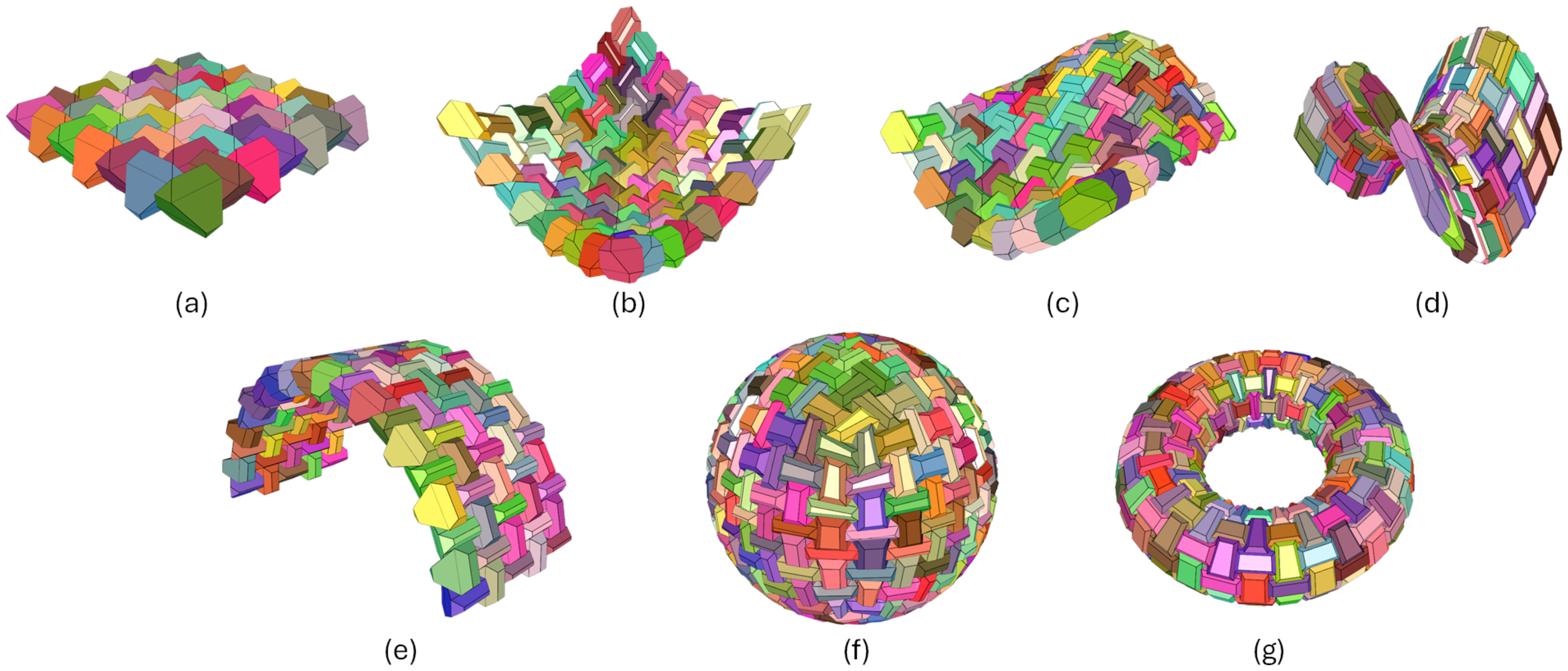
5. Results
5.1. Platonic Solids
5.2. Truncated Platonic Solids and Clipped Solids
5.3. Mixed Solids
5.4. Concave Solids
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dyskin, A.V.; Estrin, Y.; Kanel-Belov, A.J.; Pasternak, E. Toughening by Fragmentation–How Topology Helps. Adv. Eng. Mater. 2001, 3, 885. [Google Scholar] [CrossRef]
- Dyskin, A.V.; Estrin, Y.; Kanel-Belov, A.J.; Pasternak, E. Topological interlocking of platonic solids: A way to new materials and structures. Philos. Mag. Lett. 2003, 83, 197–203. [Google Scholar] [CrossRef]
- Kanel-Belov, A.J.; Dyskin, A.V.; Estrin, Y.; Pasternak, E.; Ivanov-Pogodaev, I.A. Interlocking of convex polyhedra: Towards a geometric theory of fragmented solids. arXiv 2008, arXiv:0812.5089. [Google Scholar] [CrossRef]
- Fallacara, G. Digital Stereotomy and topological transformations: Reasoning about shape building. In Proceedings of the 2nd International Congress on Construction History, Cambridge, UK, 29 March–2 April 2006; Volume 1, pp. 1075–1092. [Google Scholar]
- Fallacara, G. Toward a stereotomic design: Experimental constructions and didactic experiences. In Proceedings of the Third International Congress on Construction History, Cottbus, Germany, 20–24 May 2009; pp. 553–560. [Google Scholar]
- Dyskin, A.V.; Estrin, Y.; Pasternak, E. Topological Interlocking Materials. In Architectured Materials in Nature and Engineering; Estrin, Y., Bréchet, Y., Dunlop, J., Fratzl, P., Eds.; Springer International Publishing: Cham, Switzerland, 2019; Volume 282, pp. 23–49. [Google Scholar] [CrossRef]
- Bejarano, A.; Hoffmann, C. A generalized framework for designing topological interlocking configurations. Int. J. Archit. Comput. 2019, 17, 53–73. [Google Scholar] [CrossRef]
- Mirkhalaf, M.; Zhou, T.; Barthelat, F. Simultaneous improvements of strength and toughness in topologically interlocked ceramics. Proc. Natl. Acad. Sci. USA 2018, 115, 9128–9133. [Google Scholar] [CrossRef] [PubMed]
- Mirkhalaf, M.; Zhou, T.; Hannard, F.; Barthelat, F. Strong and Tough Ceramics Using Architecture and Topological Interlocking. In Proceedings of the IUTAM Symposium Architectured Materials Mechanics, Chicago, IL, USA, 17–19 September 2018; Siegmund, T., Barthelat, F., Eds.; Gleacher Center: Chicago, IL, USA, 2018. [Google Scholar]
- Weizmann, M.; Oded, A.; Grobman, Y.J. Structural Performance of Semi-regular Topological Interlocking Assemblies. In Proceedings of the Symposium on Simulation for Architecture and Urban Design SimAUD 2019, Atlanta, GA, USA, 7–9 April 2019; pp. 217–223. [Google Scholar]
- Williams, A.; Siegmund, T. Mechanics of Topologically Interlocked Material Systems under Point Load: Archimedean and Laves Tiling. arXiv 2020, arXiv:2004.07115. [Google Scholar] [CrossRef]
- Glickman, M. The G-block system of vertically interlocking paving. In Proceedings of the 2nd International Conference on Concrete Block Paving, Delft, The Netherlands, 10–12 April 1984; p. 4. [Google Scholar]
- Dyskin, A.; Estrin, Y.; Kanel-Belov, A.; Pasternak, E. A new concept in design of materials and structures: Assemblies of interlocked tetrahedron-shaped elements. Scr. Mater. 2001, 44, 2689–2694. [Google Scholar] [CrossRef]
- Dyskin, A.; Estrin, Y.; Kanel-Belov, A.; Pasternak, E. Interlocking properties of buckyballs. Phys. Lett. A 2003, 319, 373–378. [Google Scholar] [CrossRef]
- Weizmann, M.; Amir, O.; Grobman, Y.J. Topological Interlocking in Architectural Design. In Emerging Experience in Past, Present and Future of Digital Architecture, Proceedings of the 20th International Conference of the Association for Computer-Aided Architectural Design Research in Asia (CAADRIA 2015), Daegu, Republic of Korea, 20–22 May 2015; The Association for Computer-Aided Architectural Design Research in Asia (CAADRIA): Hong Kong, China, 2015; pp. 107–116. [Google Scholar]
- Weizmann, M.; Amir, O.; Grobman, Y.J. Topological interlocking in buildings: A case for the design and construction of floors. Autom. Constr. 2016, 72, 18–25. [Google Scholar] [CrossRef]
- Weizmann, M.; Amir, O.; Grobman, Y.J. Topological interlocking in architecture: A new design method and computational tool for designing building floors. Int. J. Archit. Comput. 2017, 15, 107–118. [Google Scholar] [CrossRef]
- Weizmann, M.; Amir, O.; Grobman, Y.J. The effect of block geometry on structural behavior of topological interlocking assemblies. Autom. Constr. 2021, 128, 103717. [Google Scholar] [CrossRef]
- Goertzen, T.; Niemeyer, A.; Plesken, W. Topological interlocking via symmetry. In Concrete Innovation for Sustainability, Proceedings of the 6th fib International Congress, Oslo, Norway, 12–16 June 2022; The International Federation for Structural Concrete: Lausanne, Switzerland, 2022; pp. 12–16. [Google Scholar]
- Khor, H.C.; Dyskin, A.; Pasternak, E.; Estrin, Y.; Kanel-Belov, A.J. Integrity and fracture of plate-like assemblies of topologically interlocked elements. In Structural Integrity and Fracture; CRC Press: Leiden, The Netherlands, 2002; pp. 449–456. [Google Scholar]
- Estrin, Y.; Dyskin, A.V.; Kanel-Belov, A.J.; Pasternak, E. Materials with Novel Architectonics: Assemblies of Interlocked Elements. In IUTAM Symposium on Analytical and Computational Fracture Mechanics of Non-Homogeneous Materials, Proceedings of the IUTAM Symposium, Cardiff, UK, 18–22 June 2001; Gladwell, G.M.L., Karihaloo, B.L., Eds.; Springer: Dordrecht, The Netherlands, 2002; Volume 97, pp. 51–55. [Google Scholar] [CrossRef]
- Tessmann, O. Topological Interlocking Assemblies. In Physical Digitality: Proceedings of the 30th eCAADe Conference, Prague, Czech Republic, 12–14 September 2012; eCAADe (Education and research in Computer Aided Architectural Design in Europe): Brussels, Belgium; České Vysoké Učení Technické v Praze: Prague, Czech Republic, 2012; Volume 2, pp. 211–219. [Google Scholar]
- Tessmann, O. Interlocking Manifold Kinematically Constrained Multi-material Systems. In Advances in Architectural Geometry 2012; Hesselgren, L., Sharma, S., Wallner, J., Baldassini, N., Bompas, P., Raynaud, J., Eds.; Springer: Vienna, Austria, 2013; pp. 269–278. [Google Scholar] [CrossRef]
- Tessmann, O.; Becker, M. Extremely heavy and incredibly light: Performative assemblies in dynamic environments. In Proceedings of the 18th International Conference on Computer-Aided Architectural Design Research in Asia: Open Systems, CAADRIA 2013, Singapore, 15–18 May 2013; pp. 469–478. [Google Scholar]
- Akleman, E.; Krishnamurthy, V.R.; Fu, C.A.; Subramanian, S.G.; Ebert, M.; Eng, M.; Starrett, C.; Panchal, H. Generalized abeille tiles: Topologically interlocked space-filling shapes generated based on fabric symmetries. Comput. Graph. 2020, 89, 156–166. [Google Scholar] [CrossRef]
- Ebert, M.; Akleman, E.; Krishnamurthy, V.; Kulagin, R.; Estrin, Y. VoroNoodles: Topological Interlocking with Helical Layered 2-Honeycombs. Adv. Eng. Mater. 2024, 26, 2300831. [Google Scholar] [CrossRef]
- Vella, I.M.; Kotnik, T. Geometric Versatility of Abeille Vault—A Stereotomic Topological Interlocking Assembly. In Complexity & Simplicity, Proceedings of the 34th eCAADe Conference, Oulu, Finland, 22–26 August 2016; Aulikki, H., Österlund, T., Markkanen, P., Eds.; CAADe (Education and Research in Computer Aided Architectural Design in Europe): Brussels, Belgium; Oulu School of Architecture, University of Oulu: Oulu, Finland, 2016; Volume 2, pp. 391–397. [Google Scholar]
- Tessmann, O.; Rossi, A. Parametric and Combinatorial Topological Interlocking Assemblies. In Proceedings of the IUTAM Symposium Architectured Materials Mechanics, Chicago, IL, USA, 17–19 September 2018; Siegmund, T., Barthelat, F., Eds.; Gleacher Center: Chicago, IL, USA, September 2018. [Google Scholar]
- Tessmann, O.; Rossi, A. Geometry as Interface: Parametric and Combinatorial Topological Interlocking Assemblies. J. Appl. Mech. 2019, 86, 111002. [Google Scholar] [CrossRef]
- Xu, W.; Lin, X.; Xie, Y.M. A novel non-planar interlocking element for tubular structures. Tunn. Undergr. Space Technol. 2020, 103, 103503. [Google Scholar] [CrossRef]
- Kurucu, A.T.; İlerisoy, Z.Y. Structural Performance of Topologically Interlocked Flat Vaults According to Joint Details. Period. Polytech. Archit. 2023, 54, 1–11. [Google Scholar] [CrossRef]
- Wang, Z.; Song, P.; Isvoranu, F.; Pauly, M. Design and structural optimization of topological interlocking assemblies. ACM Trans. Graph. 2019, 38, 1–13. [Google Scholar] [CrossRef]
- Loing, V.; Baverel, O.; Caron, J.F.; Mesnil, R. Free-form structures from topologically interlocking masonries. Autom. Constr. 2020, 113, 103117. [Google Scholar] [CrossRef]
- Chen, R.; Qiu, P.; Song, P.; Deng, B.; Wang, Z.; He, Y. Masonry Shell Structures with Discrete Equivalence Classes. ACM Trans. Graph. 2023, 42, 1–12. [Google Scholar] [CrossRef]
- Laccone, F.; Menicagli, S.; Cignoni, P.; Malomo, L. Computational design of segmented concrete shells made of post-tensioned precast flat tiles. Structures 2024, 62, 106156. [Google Scholar] [CrossRef]
- Bejarano, A.; Hoffmann, C. TIGER: Topological Interlocking GEneratoR. In Proceedings of the 2020 IEEE Games, Multimedia, Animation and Multiple Realities Conference (GMAX), Barranquilla, Colombia, 17–18 September 2020; pp. 1–6. [Google Scholar] [CrossRef]






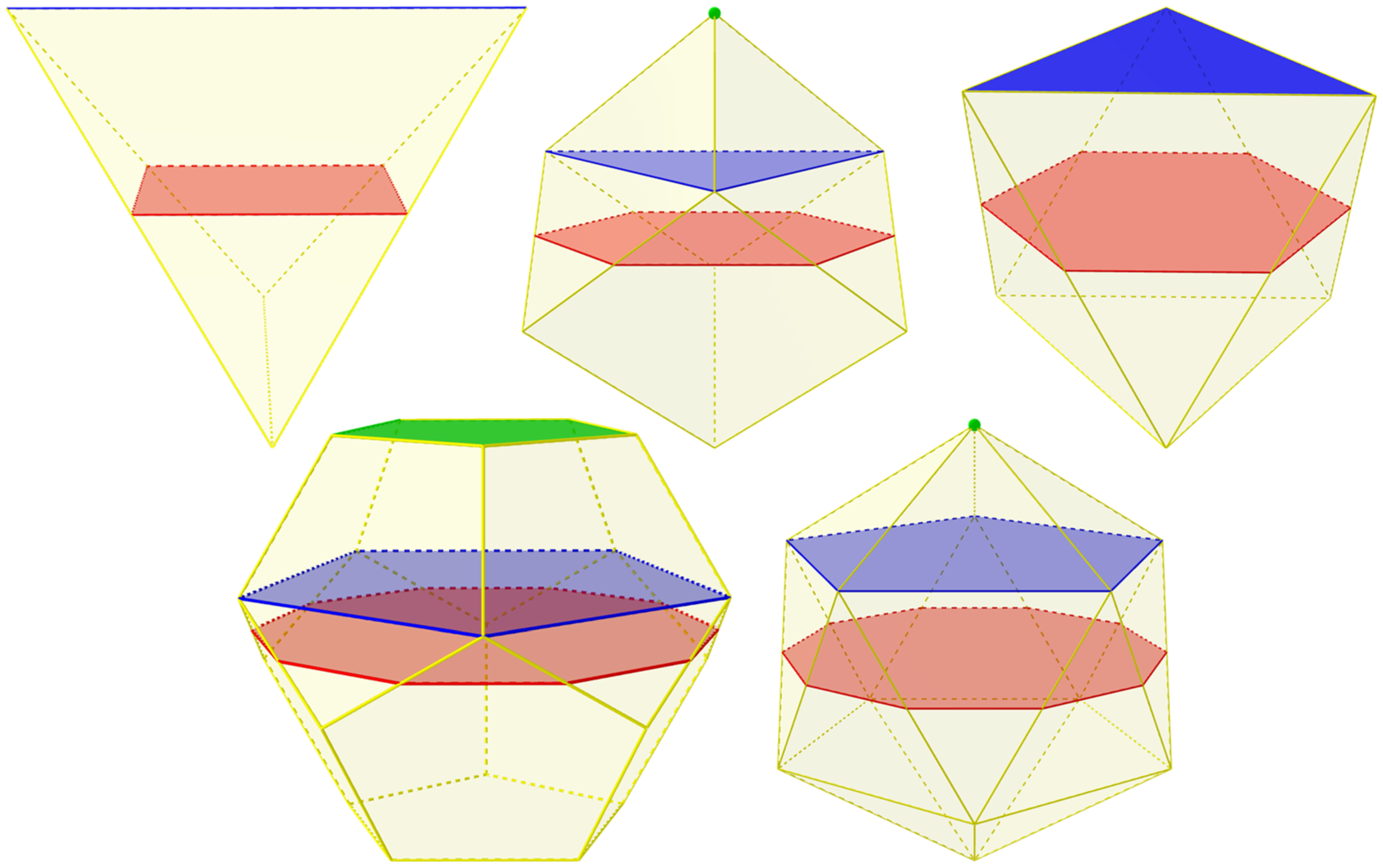

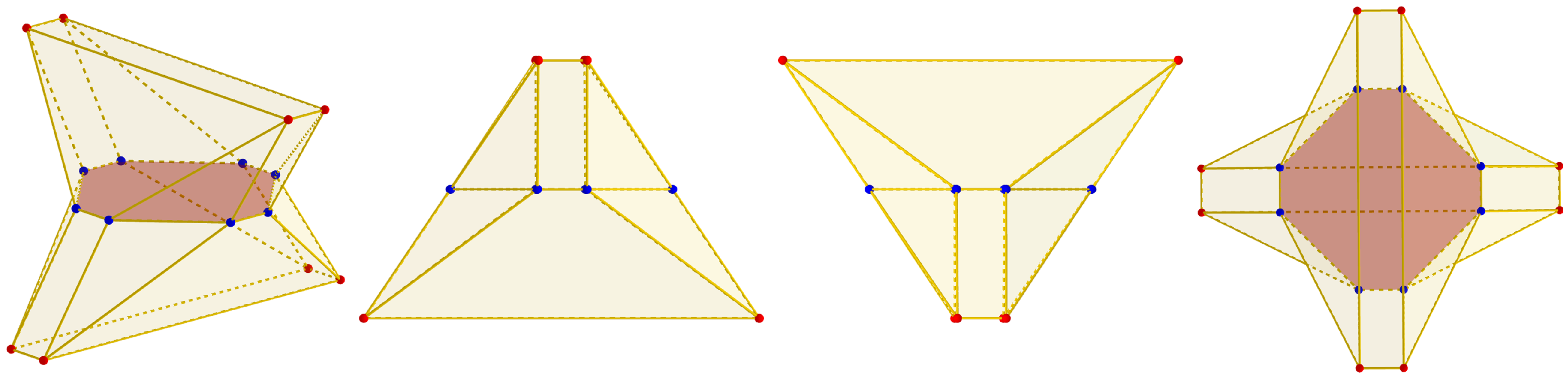

| Family | Vertices | Angles |
|---|---|---|
| Pyramids | ||
| Wedges | ||
| Parallelepipeds | ||
| Prisms | ||
| Cupolae | ||
| Frusta |
| Solid | Seed | Steps | Edge | Radius | ||
|---|---|---|---|---|---|---|
| Tetrahedron | Square | 1 | ||||
| Cube | Hexagon | 2 | ||||
| Octahedron | Hexagon | 1 | ||||
| Dodecahedron | Decagon | 2 | ||||
| Icosahedron | Decagon | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bejarano, A.; Moran, K. Multistep Evolution Method to Generate Topological Interlocking Assemblies. Appl. Sci. 2024, 14, 6542. https://doi.org/10.3390/app14156542
Bejarano A, Moran K. Multistep Evolution Method to Generate Topological Interlocking Assemblies. Applied Sciences. 2024; 14(15):6542. https://doi.org/10.3390/app14156542
Chicago/Turabian StyleBejarano, Andres, and Kathryn Moran. 2024. "Multistep Evolution Method to Generate Topological Interlocking Assemblies" Applied Sciences 14, no. 15: 6542. https://doi.org/10.3390/app14156542
APA StyleBejarano, A., & Moran, K. (2024). Multistep Evolution Method to Generate Topological Interlocking Assemblies. Applied Sciences, 14(15), 6542. https://doi.org/10.3390/app14156542







