Excavation Method Comparison and Optimization for a Super Large Cross-Section Tunnel
Abstract
:1. Introduction
2. Project Overview
2.1. Engineering Background
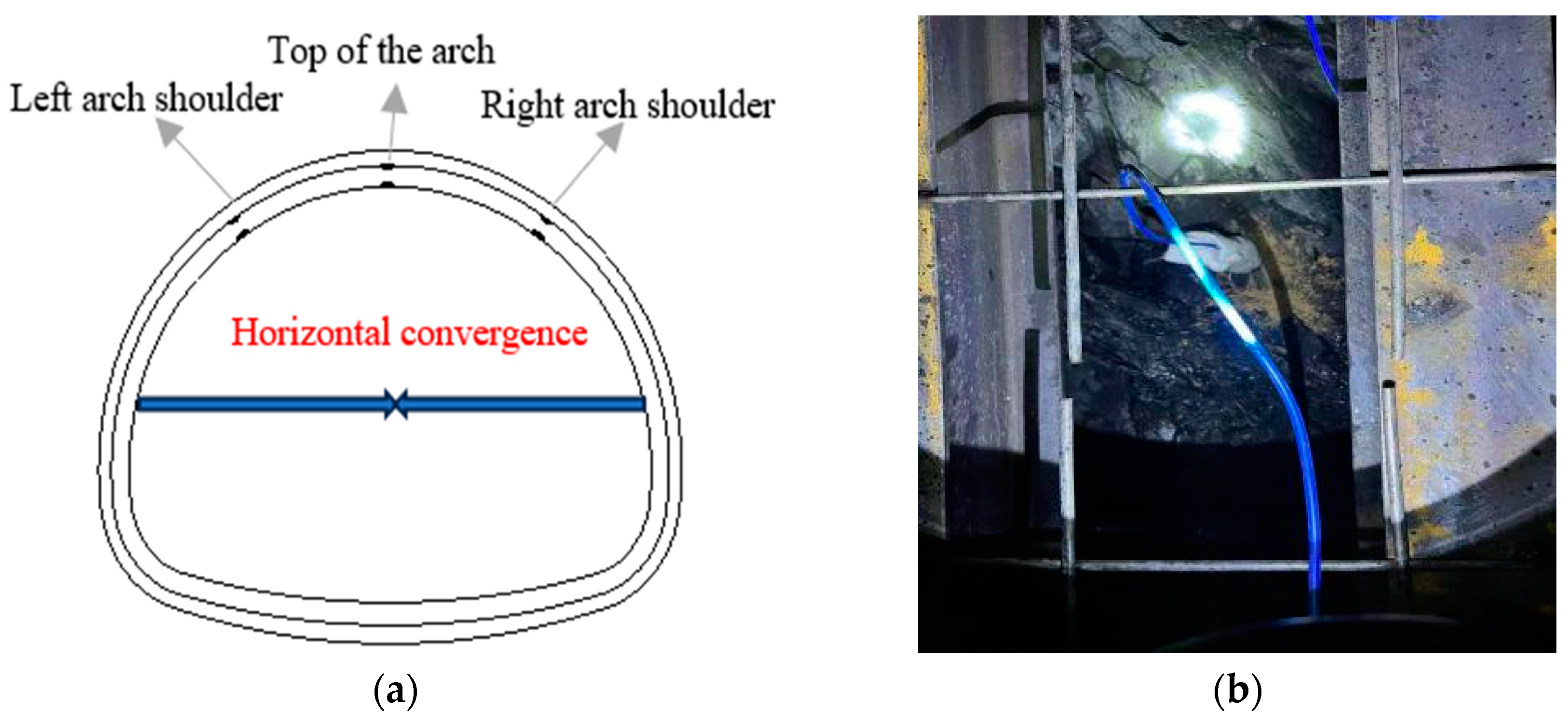
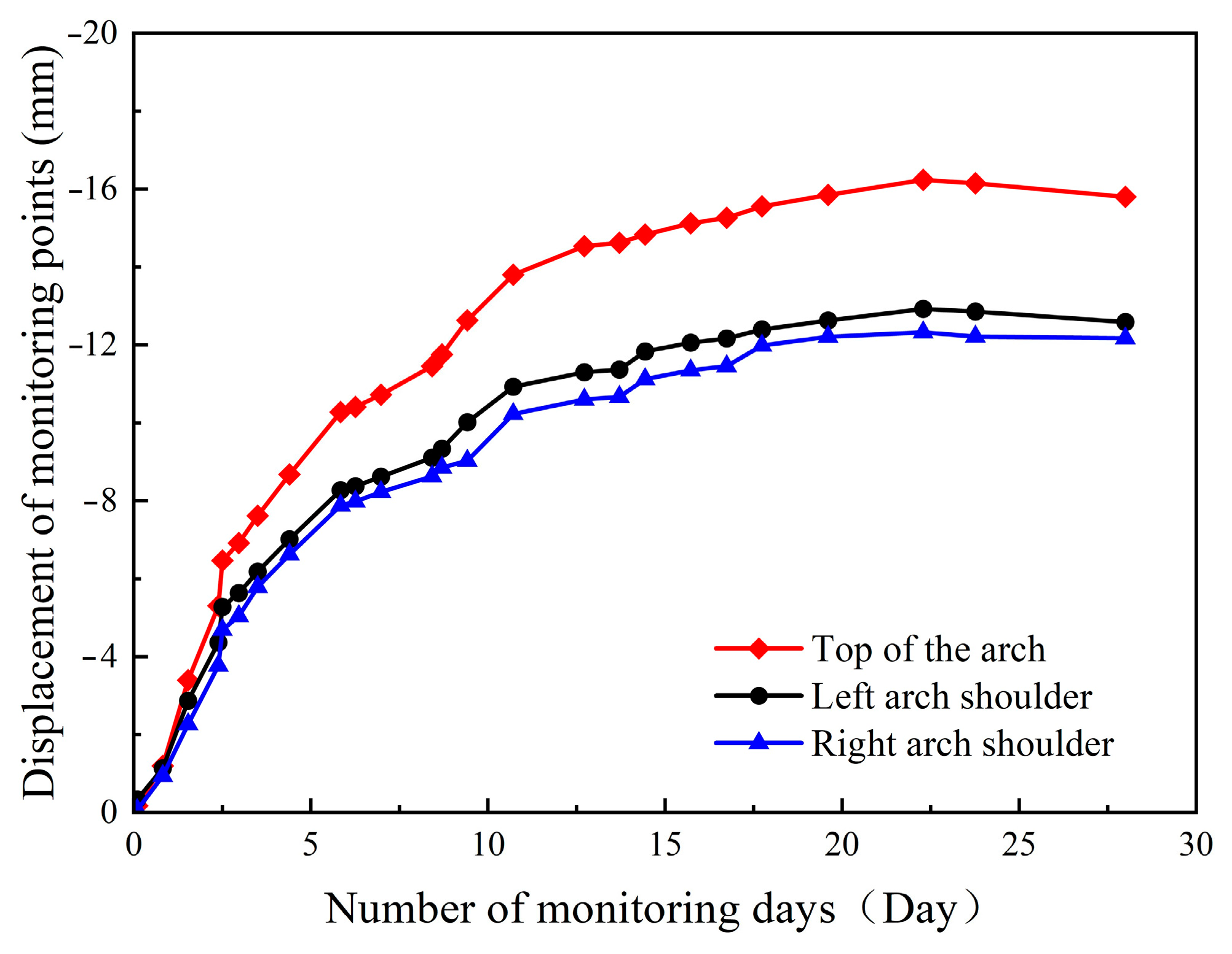
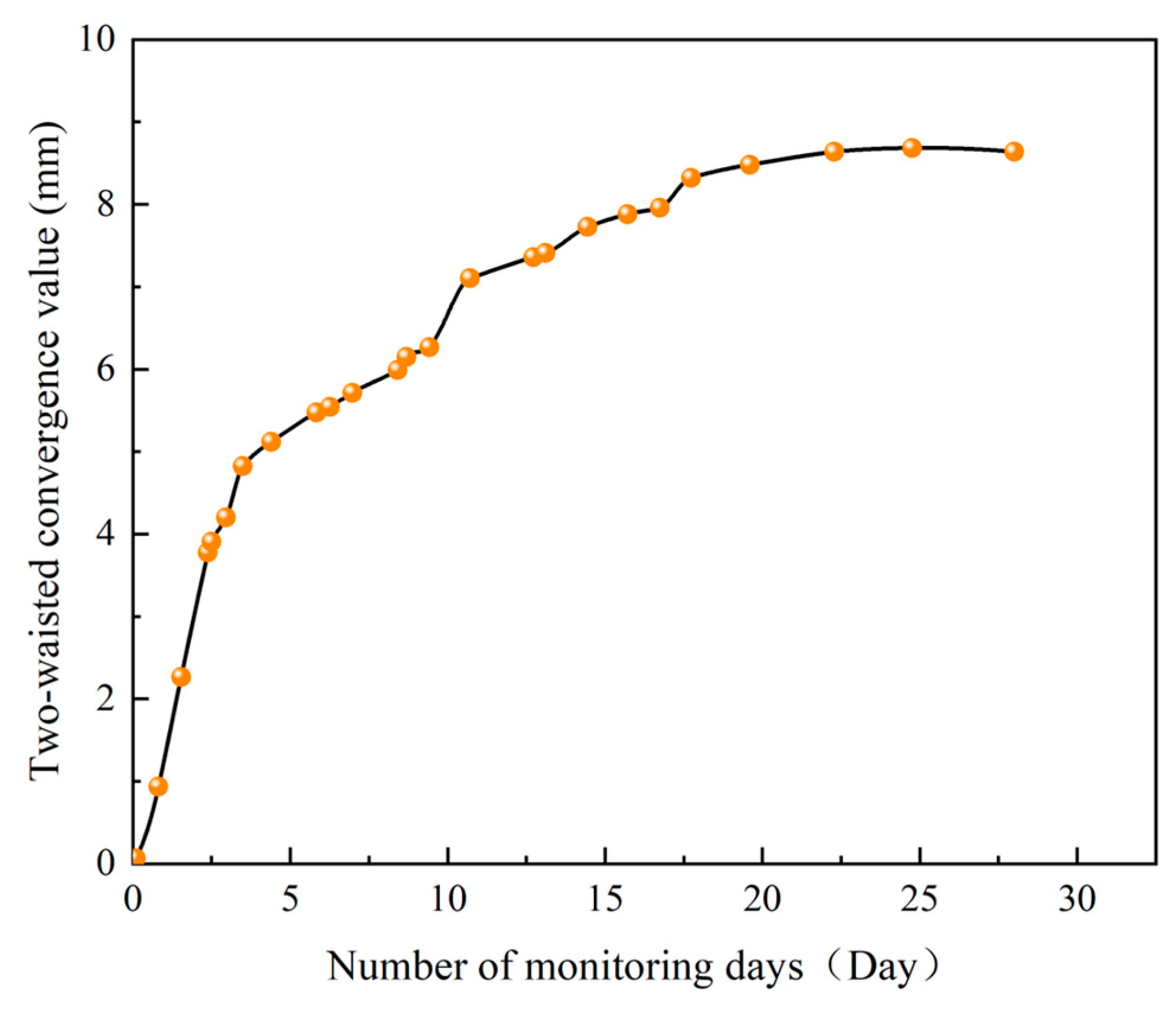
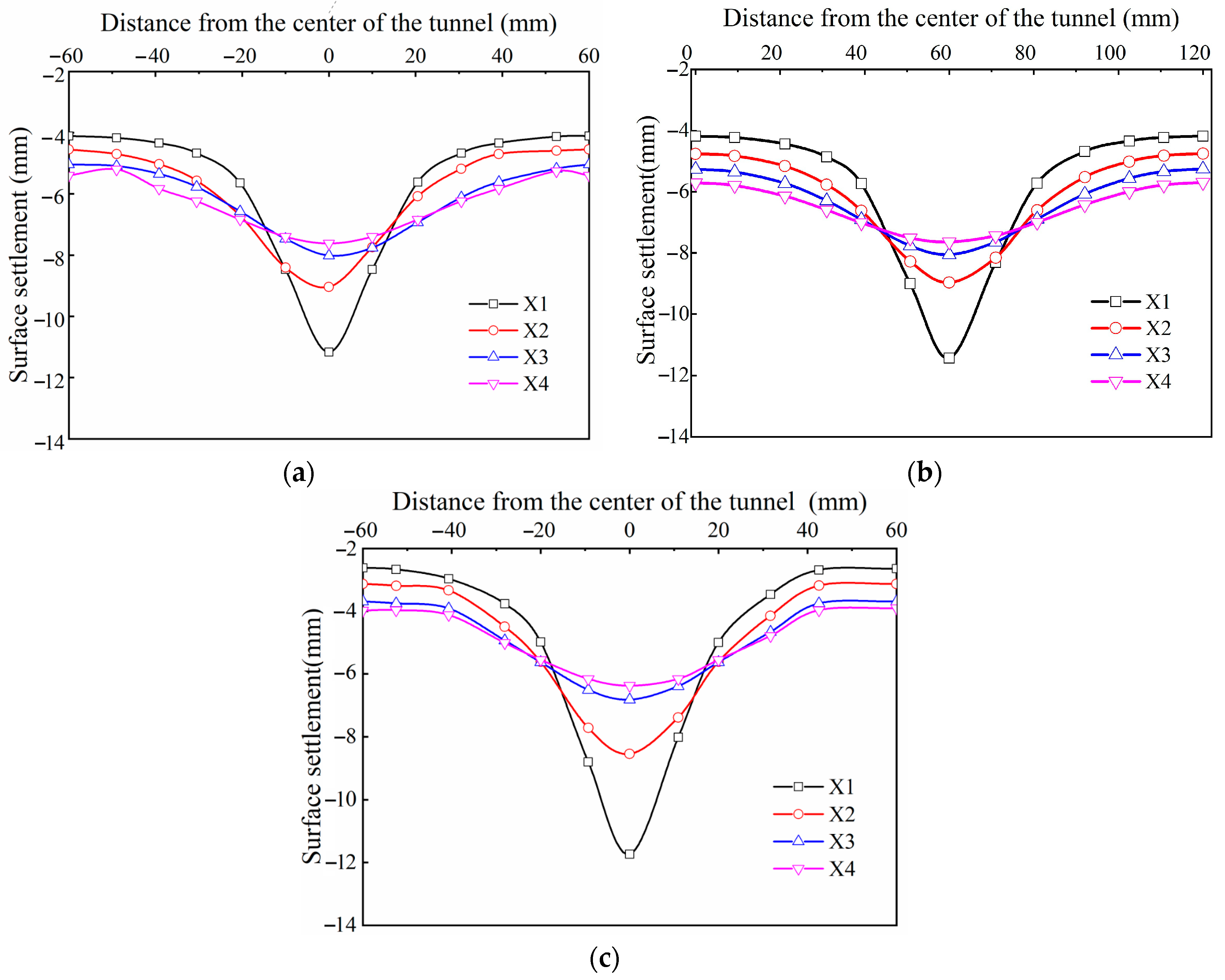
2.2. On-Site Monitoring
3. Comparison of Construction Methods
3.1. Model Building
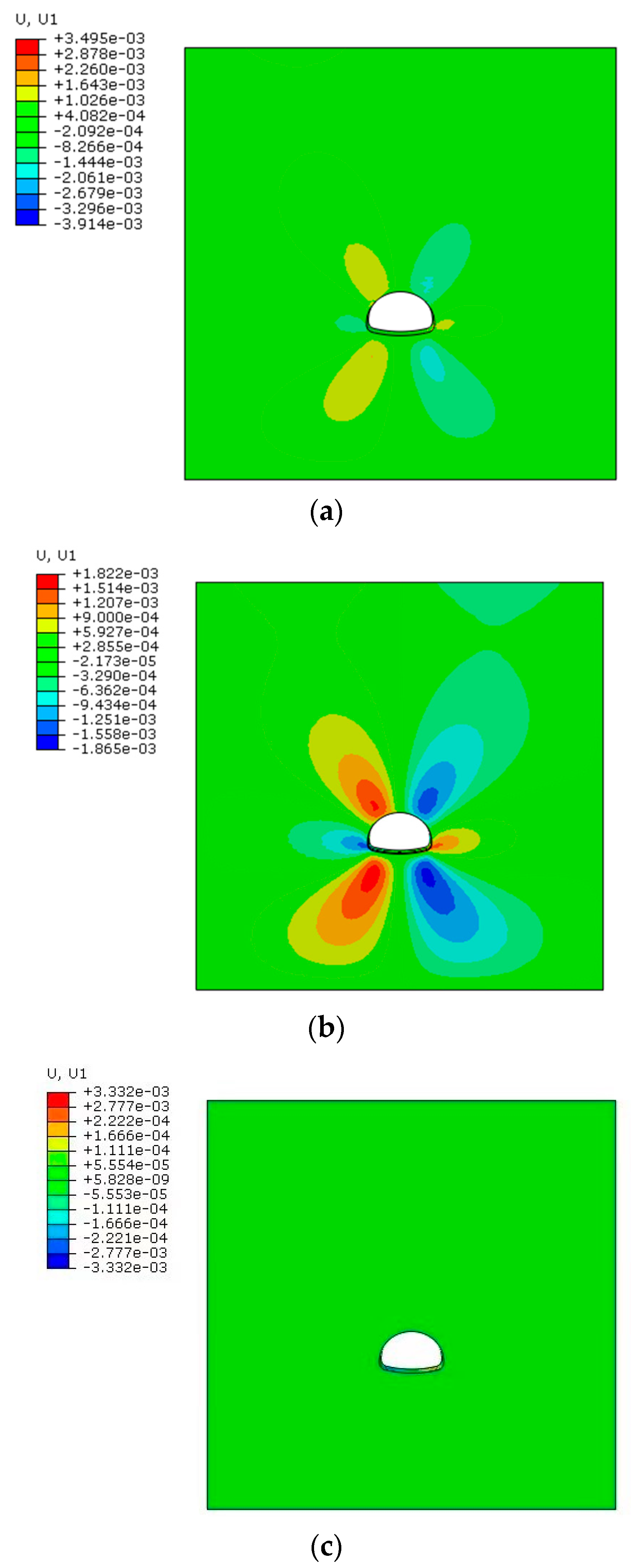
3.2. Model Validation
3.3. Material Properties
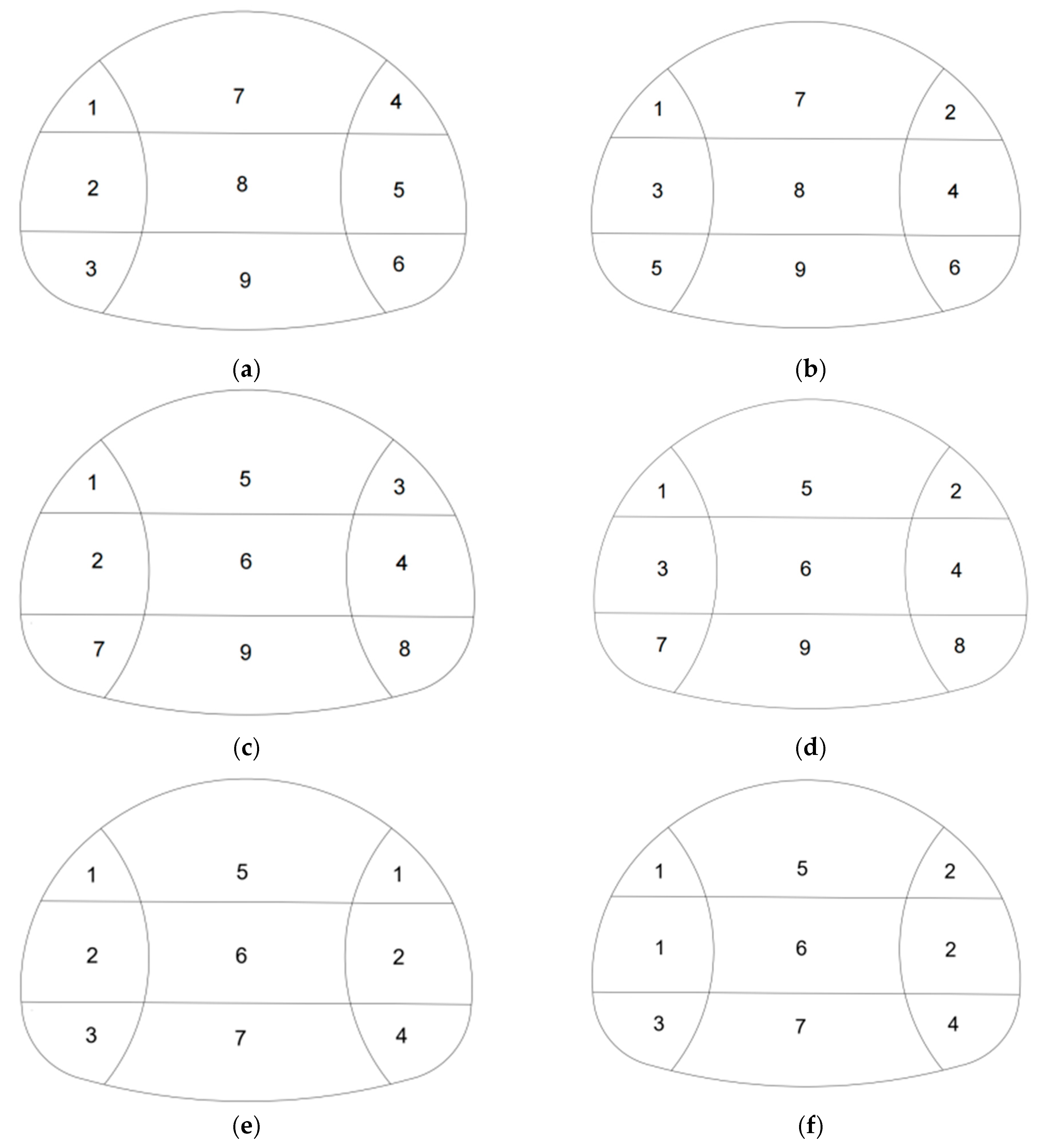
3.4. Different Working Methods to Simulate Working Conditions
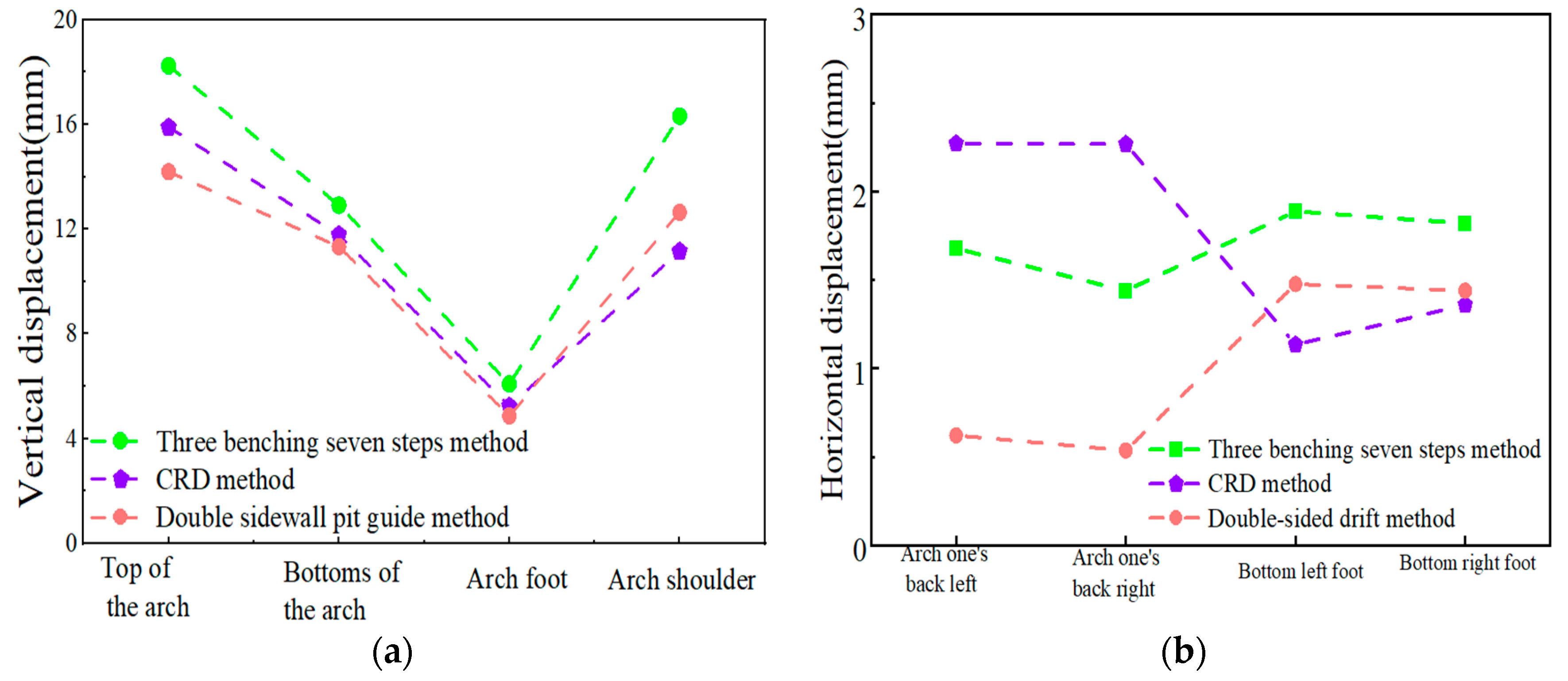
3.5. Surrounding Rock Displacement Analysis
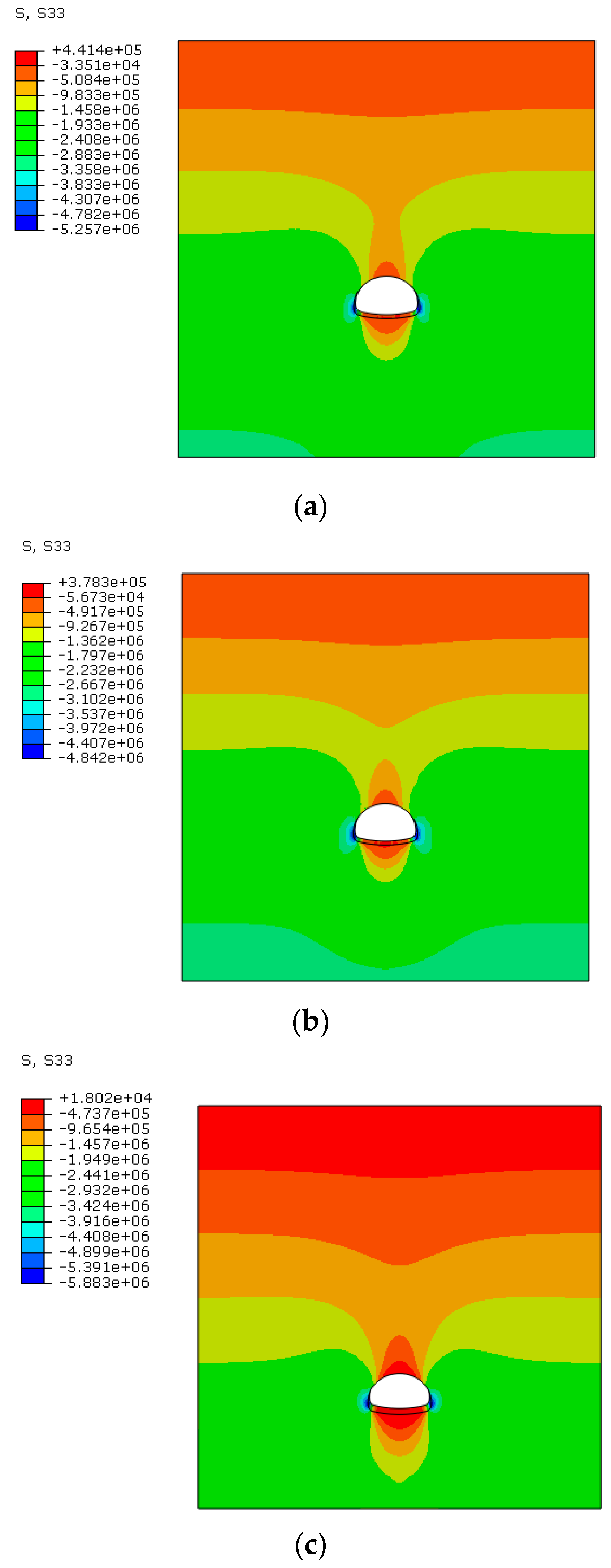
3.6. Surrounding Rock Stress
4. Optimization for the Construction Sequence
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, M.S.; Li, H.; Yu, J.; Zhang, C.R.; Ni, Y.P. On the simplified method for evaluating tunnel response due to overlying foundation pit excavation. Transp. Geotech. 2023, 42, 101048. [Google Scholar] [CrossRef]
- Wei, G.; Feng, F.F.; Cui, Y.L.; Wang, X.Q.; Diao, H.G.; Wu, Y. Research on the influence of foundation pit excavation on the lateral force and deformation of side shield tunnels based on full-scale experiments. Tunn. Undergr. Space Technol. 2023, 140, 105236. [Google Scholar] [CrossRef]
- Zhao, J.P.; Tan, Z.S.; Yu, R.S.; Li, Z.L.; Wang, X.Y. Mechanical responses of a shallow-buried super-large-section tunnel in weak surrounding rock: A case study in Guizhou. Tunn. Undergr. Space Technol. 2023, 131, 104850. [Google Scholar] [CrossRef]
- Zhou, D.H.; Cao, L.Q.; Ma, Y.F.; Shi, Z. Influence analysis of core rock construction in super large section and span tunnel. Model. Comput. Eng. 2010, 1–5. [Google Scholar]
- Tian, Z.X.; Yu, C.; Zhang, B.L.; Zhao, Q.H.; Wang, Z.W. Analysis of Surface and Building Deformation by Shield Tunneling through Geology. Appl. Sci. 2023, 13, 11155. [Google Scholar] [CrossRef]
- Hong, Q.Y.; Lai, H.P.; Liu, Y.Y.; Ma, X.M.; Xie, J.T. Deformation control method of a large cross-section tunnel overlaid by a soft-plastic loess layer: A case study. Bull. Eng. Geol. Environ. 2021, 80, 4717–4730. [Google Scholar] [CrossRef]
- Liu, C.; Li, S.C.; Zhou, Z.Q.; Li, L.P.; Shi, S.S.; Chen, Y.X. Numerical Analysis of Surrounding Rock Stability in Super-Large Section Tunnel Based on Hydro-Mechanical Coupling Model. Geotech. Geol. Eng. 2019, 37, 1297–1310. [Google Scholar] [CrossRef]
- Huang, Y.B.; Zhang, T.T.; Lu, W.; Wei, H.Y.; Liu, Y.; Xiao, Y.C.; Zeng, Z.N. Research on Creep Deformation and Control Mechanism of Weak Surrounding Rock in Super Large Section Tunnel. Geotech. Geol. Eng. 2021, 39, 5213–5227. [Google Scholar] [CrossRef]
- Guo, X.H.; Chen, F.F.; Chu, Y.D.; Qiao, C.J. Research on support technology of highway tunnel in water-rich and weak zone. Geotechnics 2011, 32, 449–454. [Google Scholar]
- Li, L.P.; Li, J.C.; Zhao, Y.; Wang, H.P.; Liu, Q.; Yuan, X.S.; Zhao, Y.; Zhang, Q. Spatial deformation mechanism and load release evolution law of weak and fragmented surrounding rock in mega section tunnel. J. Rock Mech. Eng. 2012, 31, 2109–2118. [Google Scholar]
- Verma, H.K.; Samadhiya, N.K.; Singh, M.; Goel, R.K.; Singh, P.K. Blast induced rock mass damage around tunnels. Tunn. Undergr. Space Technol. 2018, 71, 149–158. [Google Scholar] [CrossRef]
- Li, X.J.; Tang, L.; Ling, J.X.; Chen, C.; Shen, Y.; Zhu, H.H. Digital-twin-enabled JIT design of rock tunnel: Methodology and application. Tunn. Undergr. Space Technol. 2023, 140, 105307. [Google Scholar] [CrossRef]
- Song, S.G.; Li, S.C.; Li, L.P. Model test study on vibration blasting of large cross-section tunnel with small clearance in horizontal stratified surrounding rock. Tunn. Undergr. Space Technol. 2019, 92, 103013. [Google Scholar] [CrossRef]
- Zhang, D.L.; Wang, M.S.; Gao, J.; Liu, Z.W. Research on the construction technology of large-span tunnels under complex surrounding rock conditions. J. Rock Mech. Eng. 2003, 22, 290–296. [Google Scholar]
- Zheng, G.; Wang, R.; Lei, H.; Zhang, T.; Li, H. A novel sequential excavation method for constructing large-cross-section tunnels in soft ground: Practice and theory. Tunn. Undergr. Space Technol. 2022, 128, 104626. [Google Scholar] [CrossRef]
- Wu, B.; Huang, W. Optimization of sequential excavation method for large-section urban subway tunnel: A case study. Adv. Mech. Eng. 2020, 12, 2072264806. [Google Scholar] [CrossRef]
- Gong, J.W. Mechanical Study on the Construction of Highway Tunnels with Flat Large cross Section and Small Clear Distance. Ph.D. Thesis, Tongji University, Shanghai, China, 2008. [Google Scholar]
- Jiang, S.P.; Liu, H.Z.; Xian, X.F. Similar simulation and numerical analysis of dynamic construction of large-span flat tunnels. J. Rock Mech. Eng. 2000, 19, 567–572. [Google Scholar]
- Jiang, S.P.; Li, J.J.; Xie, F. Comparative stability analysis of different excavation methods for tunnel openings. Tunnel Constr. 2007, 16–20. [Google Scholar]
- Jia, X.X. Research on Key Technology of Controlled Blasting for Subway Excavation in Urban Complex Environment. Master’s Thesis, Shijiazhuang Tiedao University, Shijiazhuang, China, 2017. [Google Scholar]
- Liu, C. Study on Mechanical Characteristics of Deeply Buried Large-Section Tunnel Construction. Ph.D. Thesis, Chongqing University, Chongqing, China, 2007. [Google Scholar]
- Yang, H.; Shi, Q.; Xu, X. Intelligent monitoring of tunnel structures based on vision measurement technologies. Mech. Adv. Mater. Struct. 2022, 29, 5906–5910. [Google Scholar] [CrossRef]
- Strauss, A.; Bien, J.; Neuner, H.; Harmening, C.; Seywald, C.; Österreicher, M.; Voit, K.; Pistone, E.; Spyridis, P.; Bergmeister, K. Sensing and monitoring in tunnels testing and monitoring methods for the assessment of tunnels. Struct. Concr. 2020, 21, 1356–1376. [Google Scholar] [CrossRef]
- Tang, Y.; Zheng, Y.; Li, L.; Xian, L.; Guo, D. Experimental Study of Dynamic Responses of Special Tunnel Sections under Near-Fault Ground Motion. Sustainability 2023, 15, 4506. [Google Scholar] [CrossRef]
- Tsinidis, G.; de Silva, F.; Anastasopoulos, I.; Bilotta, E.; Bobet, A.; Hashash, Y.M.A.; He, C.; Kampas, G.; Knappett, J.; Madabhushi, G.; et al. Seismic behaviour of tunnels: From experiments to analysis. Tunn. Undergr. Space Technol. 2020, 99, 103334. [Google Scholar] [CrossRef]
- Chen, J.; Liu, W.; Chen, L.; Luo, Y.; Li, Y.; Gao, H.; Zhong, D. Failure mechanisms and modes of tunnels in monoclinic and soft-hard interbedded rocks: A case study. KSCE J. Civ. Eng. 2020, 24, 1357–1373. [Google Scholar] [CrossRef]
- Galli, G.; Grimaldi, A.; Leonardi, A. Three-dimensional modeling of tunnel excavation and lining. Comput. Geotech. 2004, 31, 171–183. [Google Scholar] [CrossRef]
- Li, P.; Zhao, Y. Performance of a multi-face tunnel excavated in loess ground based on field monitoring and numerical modeling. Arab. J. Geosci. 2016, 9, 1–10. [Google Scholar] [CrossRef]
- Aydin, A.; Ozbek, A.; Cobanoglu, I. Tunnelling in difficult ground: A case study from Dranaz tunnel, Sinop, Turkey. Eng. Geol. 2004, 74, 293–301. [Google Scholar] [CrossRef]








| Name | Grave/KN/m3 | Modulus of Elasticity/GPa | Poisson’s Ratio | Cohesive Force/KPa | Friction Angle/° |
|---|---|---|---|---|---|
| perimeter rock | 24 | 10.7 | 0.26 | 1100 Kpa | 44 |
| primordial branch | 24 | 31.5 | 0.2 | / | / |
| second lining | 25 | 30 | 0.3 | / | / |
| steel arch | 78 | 210 | 0.3 | / | / |
| Working Condition | Sequence I | Sequence II | Sequence III | Sequence IV | Sequence V | Sequence VI |
|---|---|---|---|---|---|---|
| Top of arch settlement (mm) | 14.74 | 14.75 | 14.89 | 14.91 | 14.92 | 14.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Fang, T.; Wang, N. Excavation Method Comparison and Optimization for a Super Large Cross-Section Tunnel. Appl. Sci. 2024, 14, 6544. https://doi.org/10.3390/app14156544
Huang Y, Fang T, Wang N. Excavation Method Comparison and Optimization for a Super Large Cross-Section Tunnel. Applied Sciences. 2024; 14(15):6544. https://doi.org/10.3390/app14156544
Chicago/Turabian StyleHuang, Yingjing, Tao Fang, and Ning Wang. 2024. "Excavation Method Comparison and Optimization for a Super Large Cross-Section Tunnel" Applied Sciences 14, no. 15: 6544. https://doi.org/10.3390/app14156544
APA StyleHuang, Y., Fang, T., & Wang, N. (2024). Excavation Method Comparison and Optimization for a Super Large Cross-Section Tunnel. Applied Sciences, 14(15), 6544. https://doi.org/10.3390/app14156544






