Context-Encoder-Based Image Inpainting for Ancient Chinese Silk
Abstract
1. Introduction
2. Related Work
3. Approach
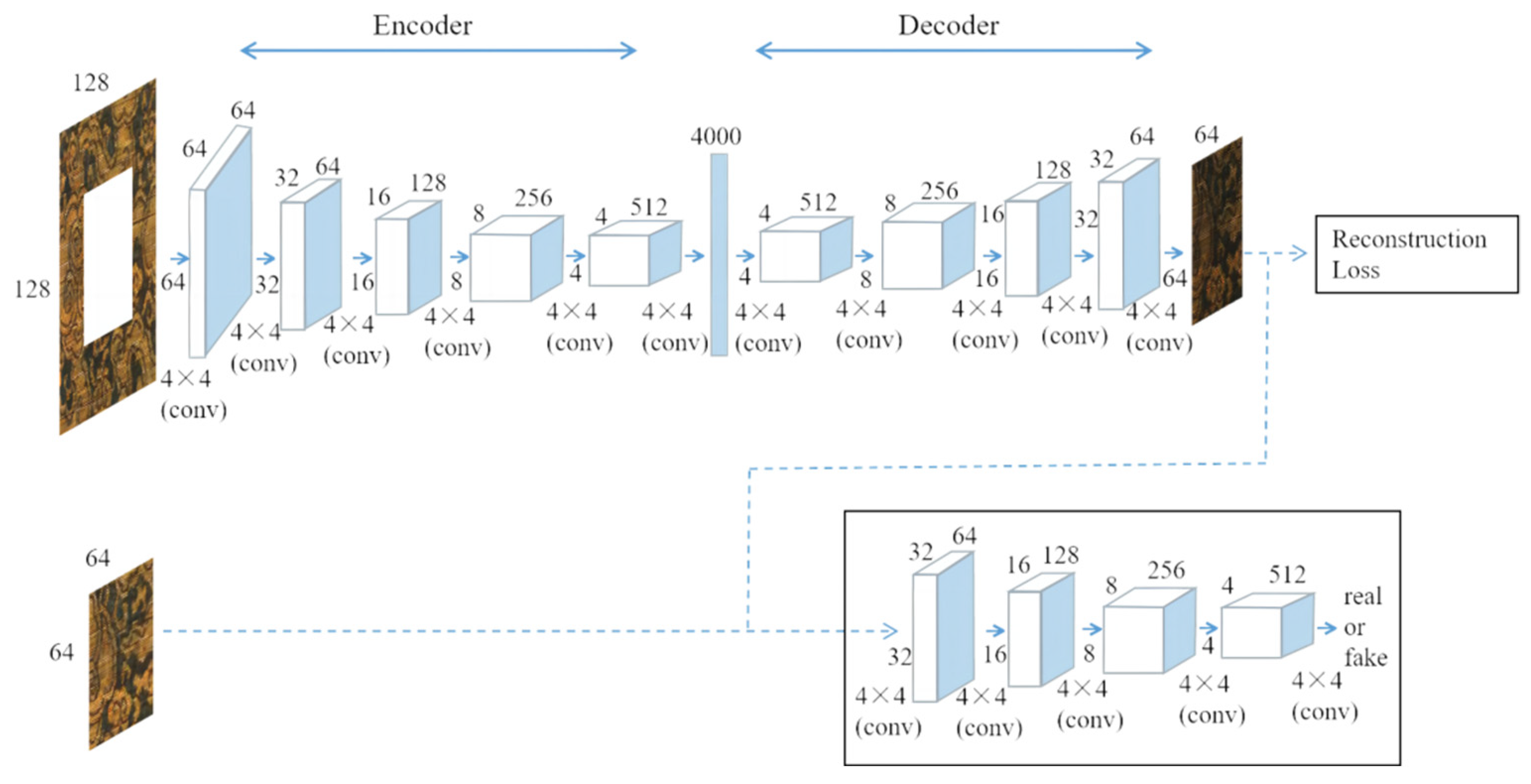
3.1. The Principle of the LISK Model
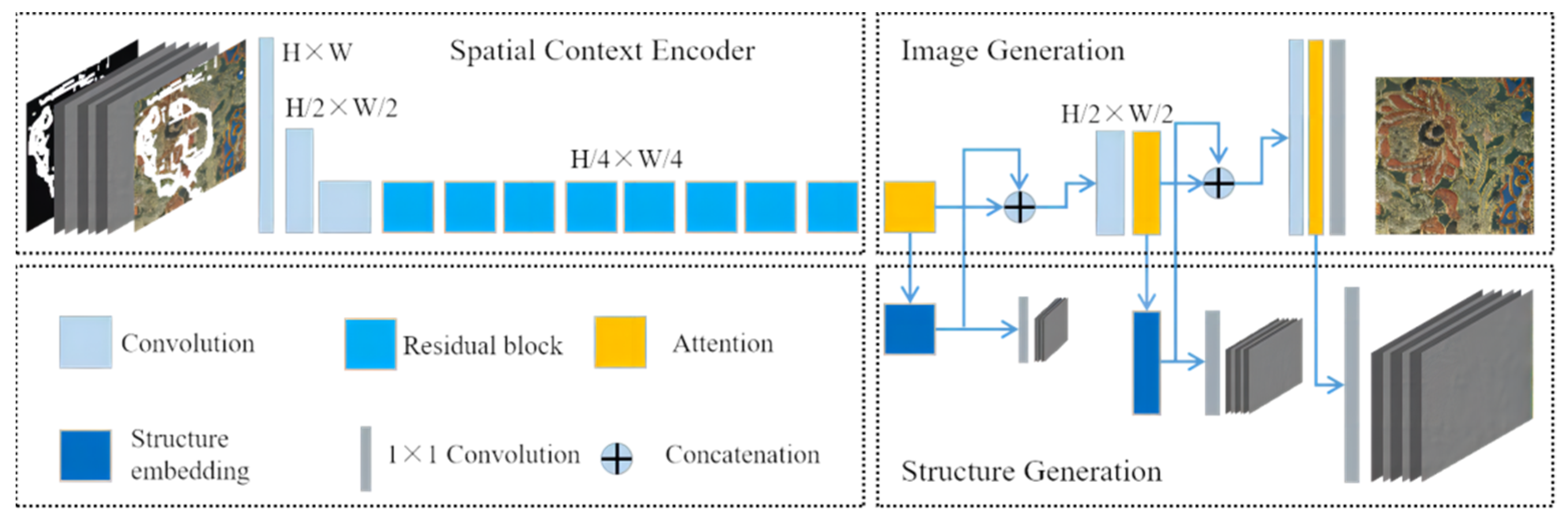
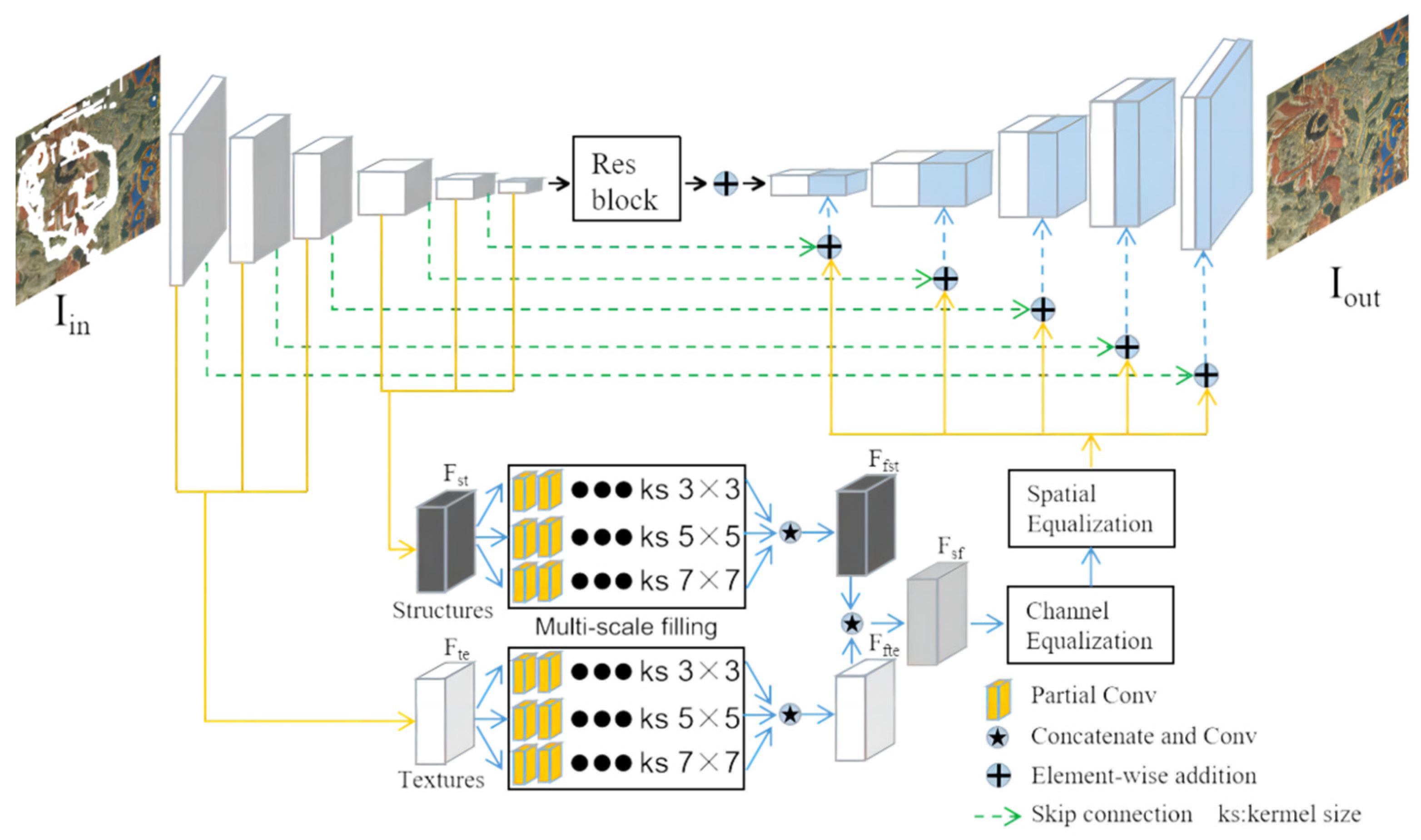
3.2. The Principle of the MEDFE Model
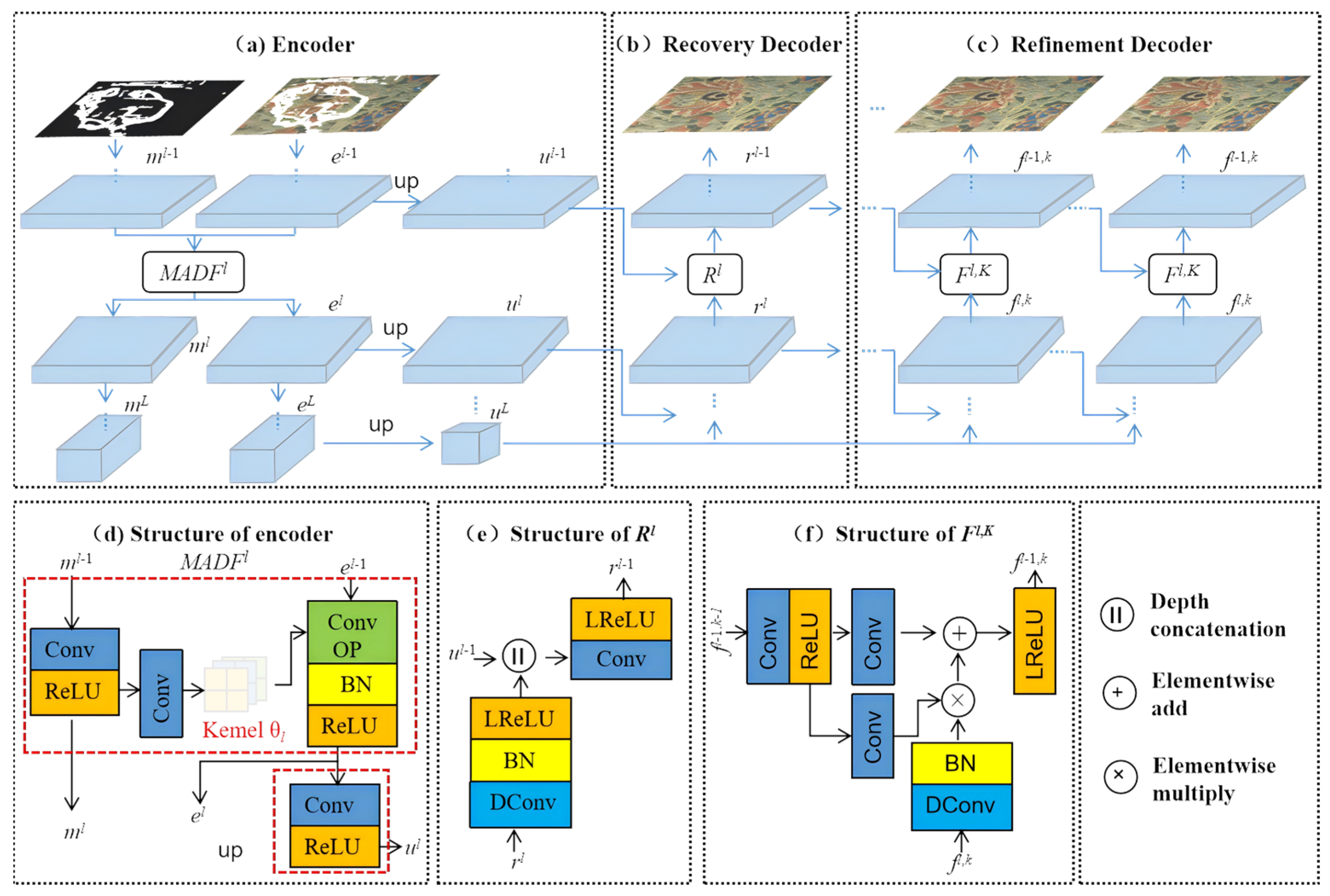
3.3. The Principle of the MADF Model
4. Experiments
4.1. Experimental Settings
4.2. Evaluation Index
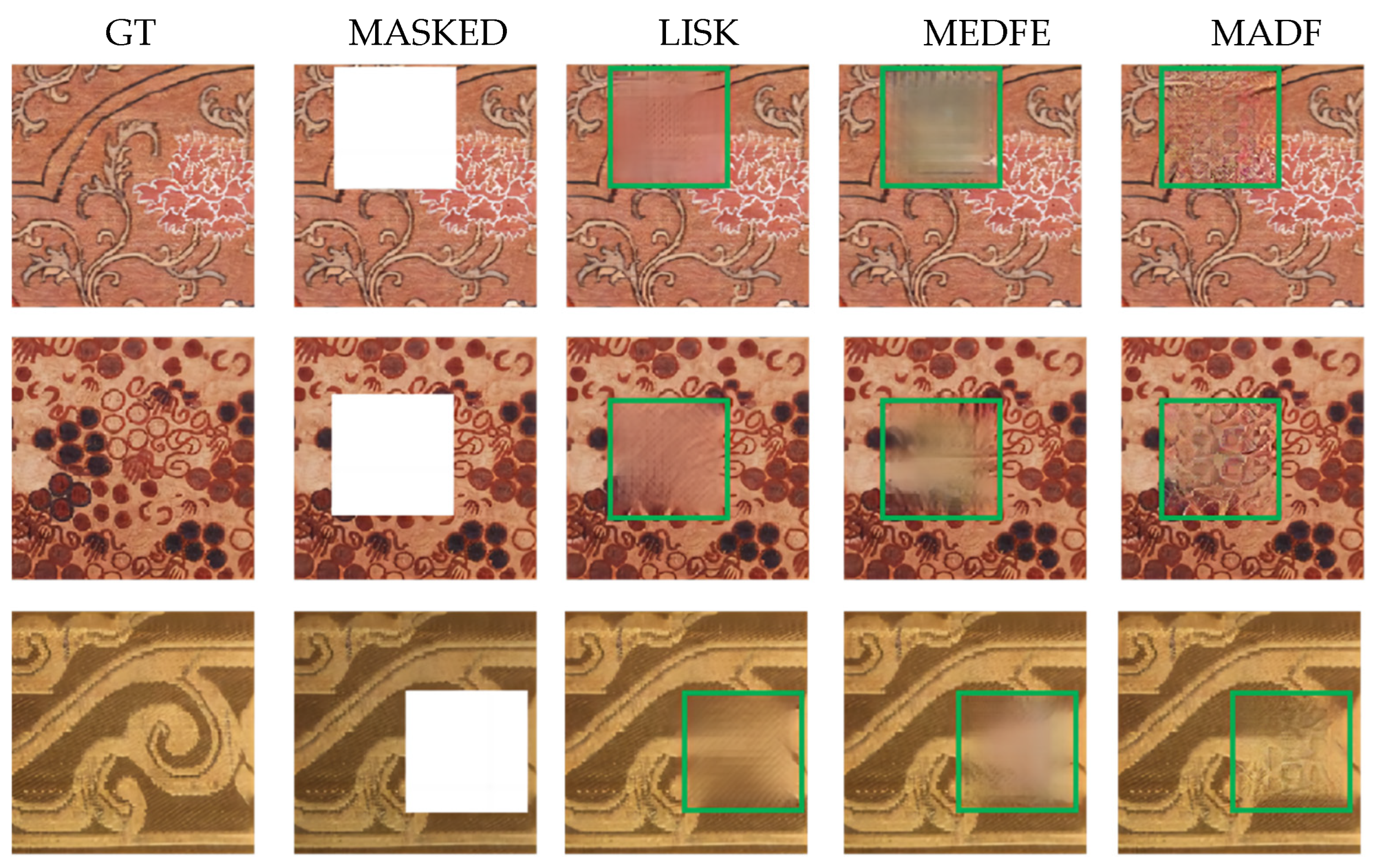
4.3. Qualitative Evaluation
4.4. Quantitative Evaluation
4.5. User Study
4.6. Practice and Challenge
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bertalmio, M.; Sapiro, G.; Caselles, V.; Ballester, C. Image inpainting. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 23–28 July 2000. [Google Scholar]
- Sun, X.; Jia, J.; Xu, P.; Ni, J.; Shi, W.; Li, B. Structure-guided virtual restoration for defective silk cultural relics. J. Cult. Heritage 2023, 62, 78–89. [Google Scholar] [CrossRef]
- Wang, C.; Wu, H.; Jin, Z. Fourllie: Boosting low-light image enhancement by fourier frequency information. In Proceedings of the 31st ACM International Conference on Multimedia, Ottawa, ON, Canada, 29 October–3 November 2023. [Google Scholar]
- Suvorov, R.; Logacheva, E.; Mashikhin, A.; Remizova, A.; Ashukha, A.; Silvestrov, A.; Kong, N.; Goka, H.; Park, K.; Lempitsky, V. Resolution-robust large mask inpainting with fourier convolutions. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Telea, A. An image inpainting technique based on the fast marching method. J. Graph. Tools 2004, 9, 23–34. [Google Scholar] [CrossRef]
- Criminisi, A.; Pérez, P.; Toyama, K. Region filling and object removal by exemplar-based image inpainting. IEEE Trans. Image Process. 2004, 13, 1200–1212. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Gu, T.; Chen, W.; Chen, C. Ootdiffusion: Outfitting fusion based latent diffusion for controllable virtual try-on. arXiv 2024, arXiv:2403.01779. [Google Scholar]
- Gong, L.; Zhu, Y.; Li, W.; Kang, X.; Wang, B.; Ge, T.; Zheng, B. Atomovideo: High fidelity image-to-video generation. arXiv 2024, arXiv:2403.01800. [Google Scholar]
- Huang, W.; Deng, Y.; Hui, S.; Wu, Y.; Zhou, S.; Wang, J. Sparse self-attention transformer for image inpainting. Pattern Recognit. 2024, 145, 109897. [Google Scholar] [CrossRef]
- Yu, Y.; Zhan, F.; Lu, S.; Pan, J.; Ma, F.; Xie, X.; Miao, C. Wavefill: A wavelet-based generation network for image inpainting. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021. [Google Scholar]
- Pathak, D.; Krahenbuhl, P.; Donahue, J.; Darrell, T.; Efros, A.A. Context encoders: Feature learning by inpainting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Rumelhart, D.; Hinton, G.; Williams, R. Learning Internal Representations by Error Propagation; MIT Press: Cambridge, MA, USA, 1985. [Google Scholar]
- Liao, L.; Hu, R.; Xiao, J.; Wang, Z. Edge-aware context encoder for image inpainting. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing, Calgary, AB, Canada, 15–20 April 2018. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Yang, C.; Lu, X.; Lin, Z.; Shechtman, E.; Wang, O.; Li, H. High-resolution image inpainting using multi-scale neural patch synthesis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Vo, H.V.; Duong, N.Q.; Pérez, P. Structural inpainting. In Proceedings of the 26th ACM International Conference on Multimedia, Seoul, Republic of Korea, 22–26 October 2018. [Google Scholar]
- Liu, H.; Jiang, B.; Song, Y.; Huang, W.; Yang, C. Rethinking image inpainting via a mutual encoder-decoder with feature equalizations. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020. [Google Scholar]
- Yang, J.; Qi, Z.; Shi, Y. Learning to incorporate structure knowledge for image inpainting. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020. [Google Scholar]
- Zhu, M.; He, D.; Li, X.; Li, C.; Li, F.; Liu, X.; Ding, E.; Zhang, Z. Image inpainting by end-to-end cascaded refinement with mask awareness. IEEE Trans. Image Process. 2021, 30, 4855–4866. [Google Scholar] [CrossRef] [PubMed]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M. Imagenet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Gatys, L.A.; Ecker, A.S.; Bethge, M. Image style transfer using convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Zhu, J.-Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Xu, L.; Yan, Q.; Xia, Y.; Jia, J. Structure extraction from texture via relative total variation. ACM Trans. Graph. 2012, 31, 1–10. [Google Scholar] [CrossRef]
- Ren, Y.; Yu, X.; Zhang, R.; Li, T.H.; Liu, S.; Li, G. Structureflow: Image inpainting via structure-aware appearance flow. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Jolicoeur-Martineau, A. The relativistic discriminator: A key element missing from standard gan. arXiv 2018, arXiv:1807.00734. [Google Scholar]
- Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual losses for real-time style transfer and super-resolution. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Yu, J.; Lin, Z.; Yang, J.; Shen, X.; Lu, X.; Huang, T.S. Generative image inpainting with contextual attention. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Liu, G.; Reda, F.A.; Shih, K.J.; Wang, T.-C.; Tao, A.; Catanzaro, B. Image inpainting for irregular holes using partial convolutions. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C. A universal image quality index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Sheikh, H.R.; Bovik, A.C. Image information and visual quality. IEEE Trans. Image Process. 2006, 15, 430–444. [Google Scholar] [CrossRef] [PubMed]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. Gans trained by a two time-scale update rule converge to a local nash equilibrium. In Proceedings of the 31st Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]




| Models | (0.01, 0.1] | (0.1, 0.2] | (0.2, 0.3] | (0.3, 0.4] | (0.4, 0.5] | (0.5, 0.6] | ALL | Square | |
|---|---|---|---|---|---|---|---|---|---|
| L1% ¶ | LISK | 0.87 | 2.22 | 4.04 | 6.18 | 8.67 | 12.55 | 5.66 | 5.92 |
| MEDFE | 0.73 | 1.72 | 3.01 | 4.44 | 5.99 | 8.27 | 3.96 | 3.87 | |
| MADF | 0.49 | 1.35 | 2.46 | 3.71 | 5.04 | 7.06 | 3.26 | 3.43 | |
| PSNR † | LISK | 35.19 | 30.49 | 27.56 | 25.31 | 23.55 | 21.48 | 27.40 | 24.91 |
| MEDFE | 32.60 | 27.28 | 24.34 | 22.28 | 20.76 | 18.92 | 24.47 | 22.59 | |
| MADF | 34.24 | 28.57 | 25.46 | 23.32 | 21.80 | 20.01 | 25.73 | 23.11 | |
| SSIM † | LISK | 0.9752 | 0.9344 | 0.8779 | 0.8124 | 0.7402 | 0.6391 | 0.8322 | 0.8263 |
| MEDFE | 0.9703 | 0.9142 | 0.8374 | 0.7485 | 0.6510 | 0.5001 | 0.7718 | 0.7253 | |
| MADF | 0.9775 | 0.9325 | 0.8685 | 0.7919 | 0.7055 | 0.5565 | 0.8082 | 0.7405 | |
| FID ¶ | LISK | 7.77 | 15.51 | 24.26 | 36.19 | 51.32 | 83.80 | 21.26 | 35.54 |
| MEDFE | 6.77 | 18.94 | 37.09 | 61.10 | 87.47 | 126.92 | 36.51 | 45.67 | |
| MADF | 2.06 | 6.12 | 12.35 | 21.34 | 33.41 | 54.72 | 10.43 | 12.22 | |
| UQI † | LISK | 0.9895 | 0.9864 | 0.9824 | 0.9749 | 0.9652 | 0.9472 | 0.9755 | 0.9748 |
| MEDFE | 0.9960 | 0.9888 | 0.9789 | 0.9671 | 0.9542 | 0.9331 | 0.9704 | 0.9701 | |
| MADF | 0.9974 | 0.9922 | 0.9849 | 0.9758 | 0.9658 | 0.9480 | 0.9782 | 0.9737 | |
| VIF † | LISK | 0.9011 | 0.8376 | 0.7666 | 0.6755 | 0.5754 | 0.4487 | 0.7060 | 0.7164 |
| MEDFE | 0.9496 | 0.8545 | 0.7454 | 0.6369 | 0.5367 | 0.4192 | 0.6939 | 0.7150 | |
| MADF | 0.9612 | 0.8912 | 0.8012 | 0.7038 | 0.6085 | 0.4778 | 0.7437 | 0.7326 |
| LISK | MEDFE | MADF | |
|---|---|---|---|
| PRa | 14.00% | 15.20% | 20.40% |
| PRb | 25.00% | 6.00% | 69.00% |
| PRc | 50.40% | 17.40% | 82.20% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; He, S.; Su, M.; Zhao, F. Context-Encoder-Based Image Inpainting for Ancient Chinese Silk. Appl. Sci. 2024, 14, 6607. https://doi.org/10.3390/app14156607
Wang Q, He S, Su M, Zhao F. Context-Encoder-Based Image Inpainting for Ancient Chinese Silk. Applied Sciences. 2024; 14(15):6607. https://doi.org/10.3390/app14156607
Chicago/Turabian StyleWang, Quan, Shanshan He, Miao Su, and Feng Zhao. 2024. "Context-Encoder-Based Image Inpainting for Ancient Chinese Silk" Applied Sciences 14, no. 15: 6607. https://doi.org/10.3390/app14156607
APA StyleWang, Q., He, S., Su, M., & Zhao, F. (2024). Context-Encoder-Based Image Inpainting for Ancient Chinese Silk. Applied Sciences, 14(15), 6607. https://doi.org/10.3390/app14156607






