Structural Design and Analysis of Multi-Directional Foot Mobile Robot
Abstract
1. Introduction
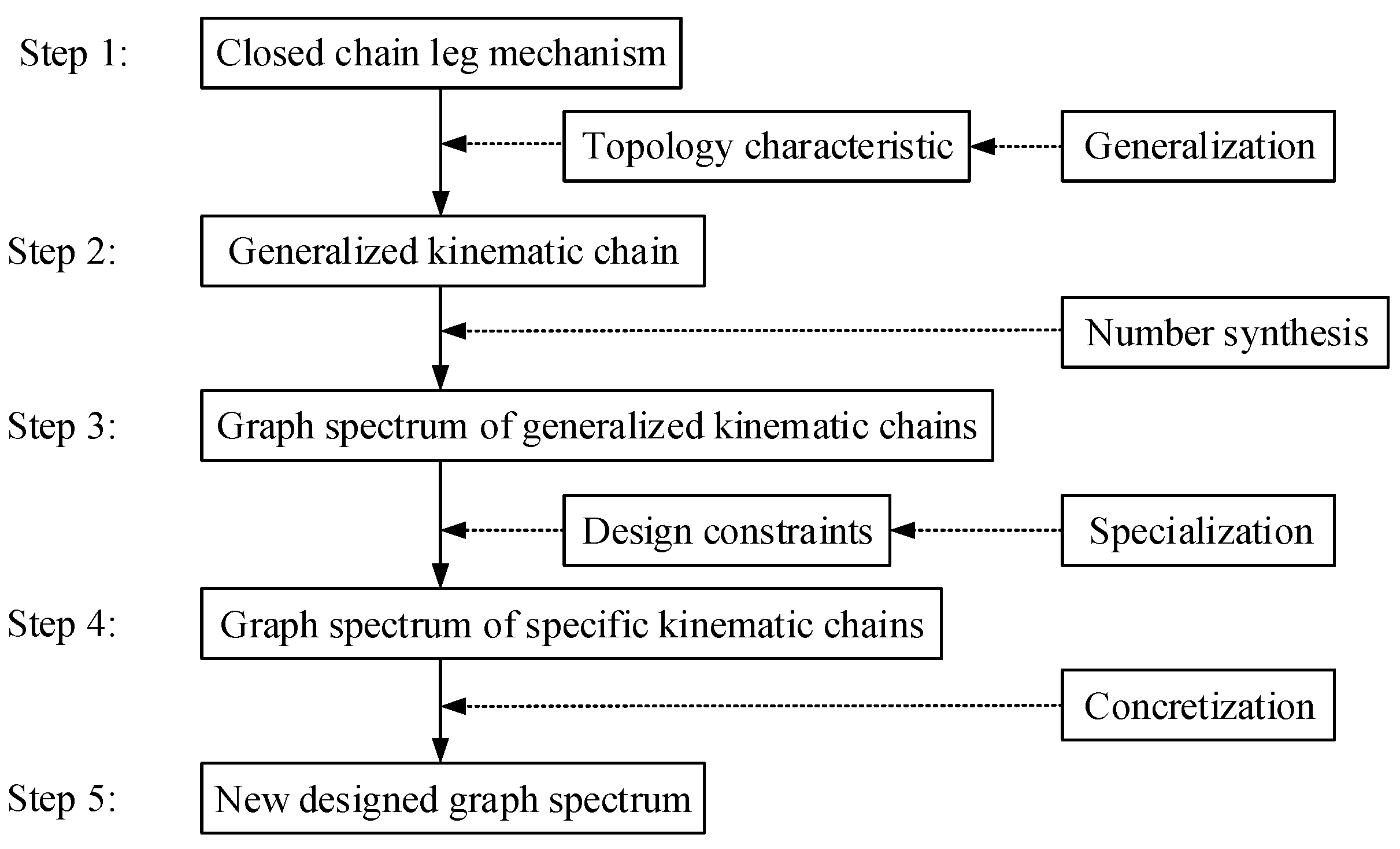
2. Design and Analysis of Closed-Chain Leg Structure
2.1. Selection of Closed-Chain Leg Structure
2.2. Design Evaluation Index
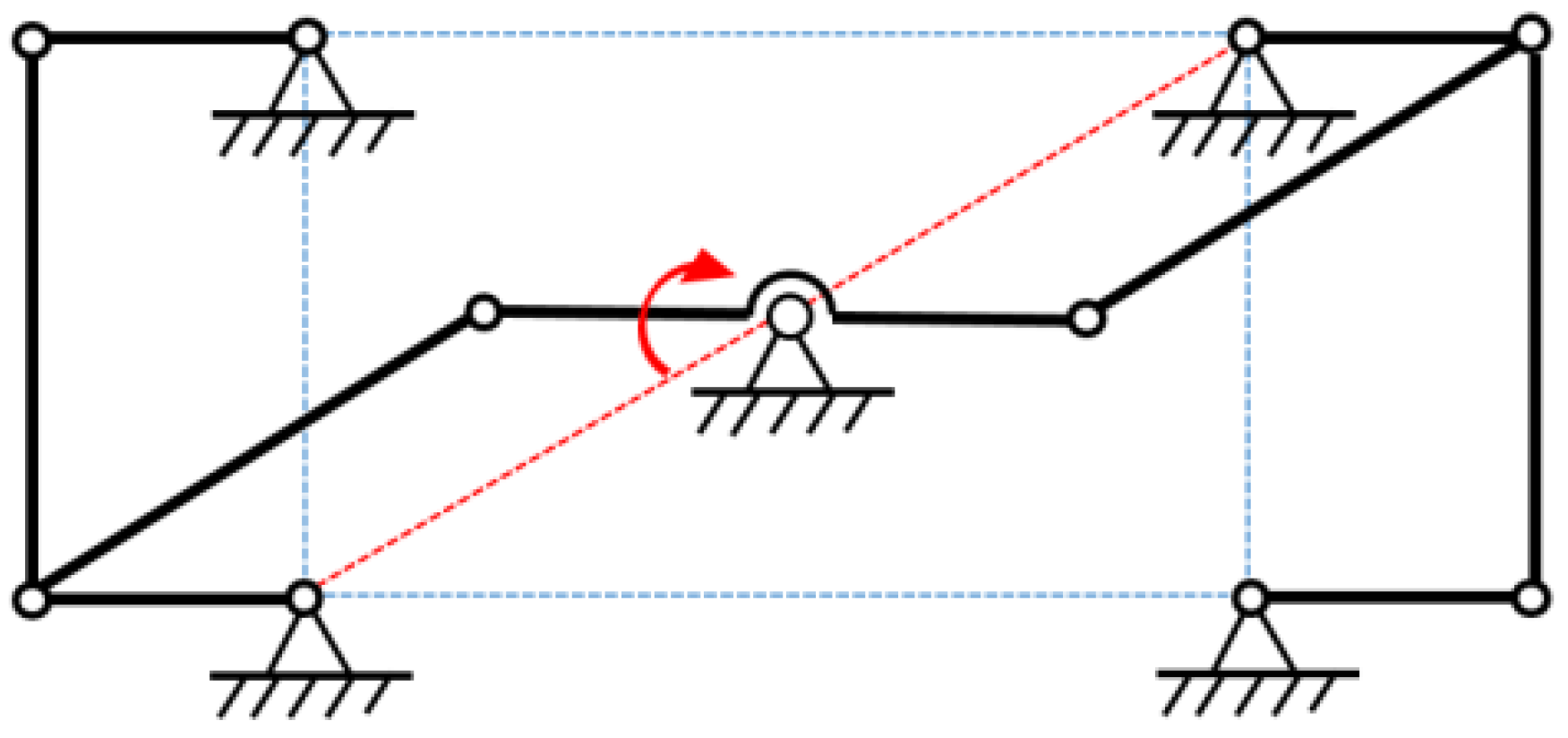
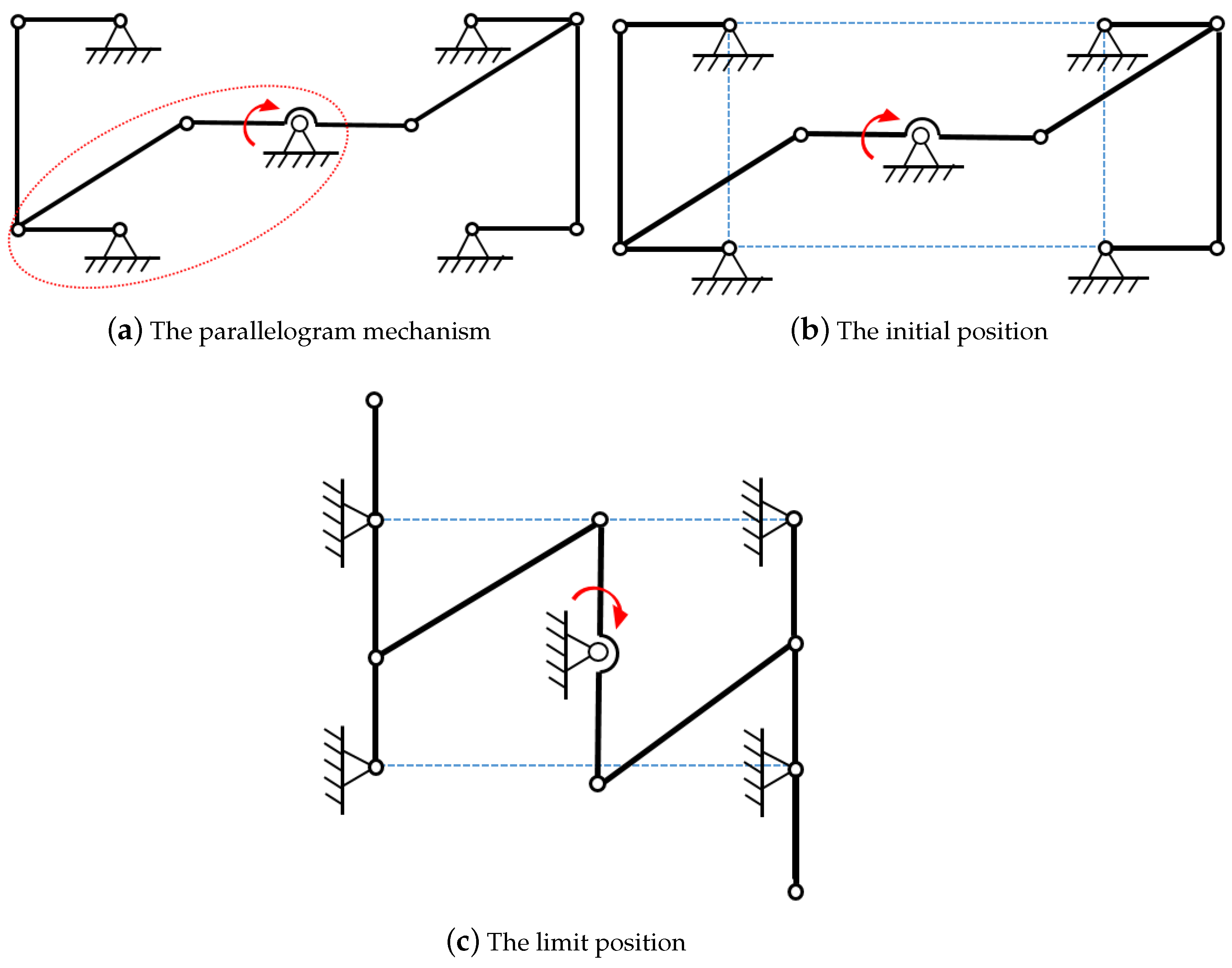
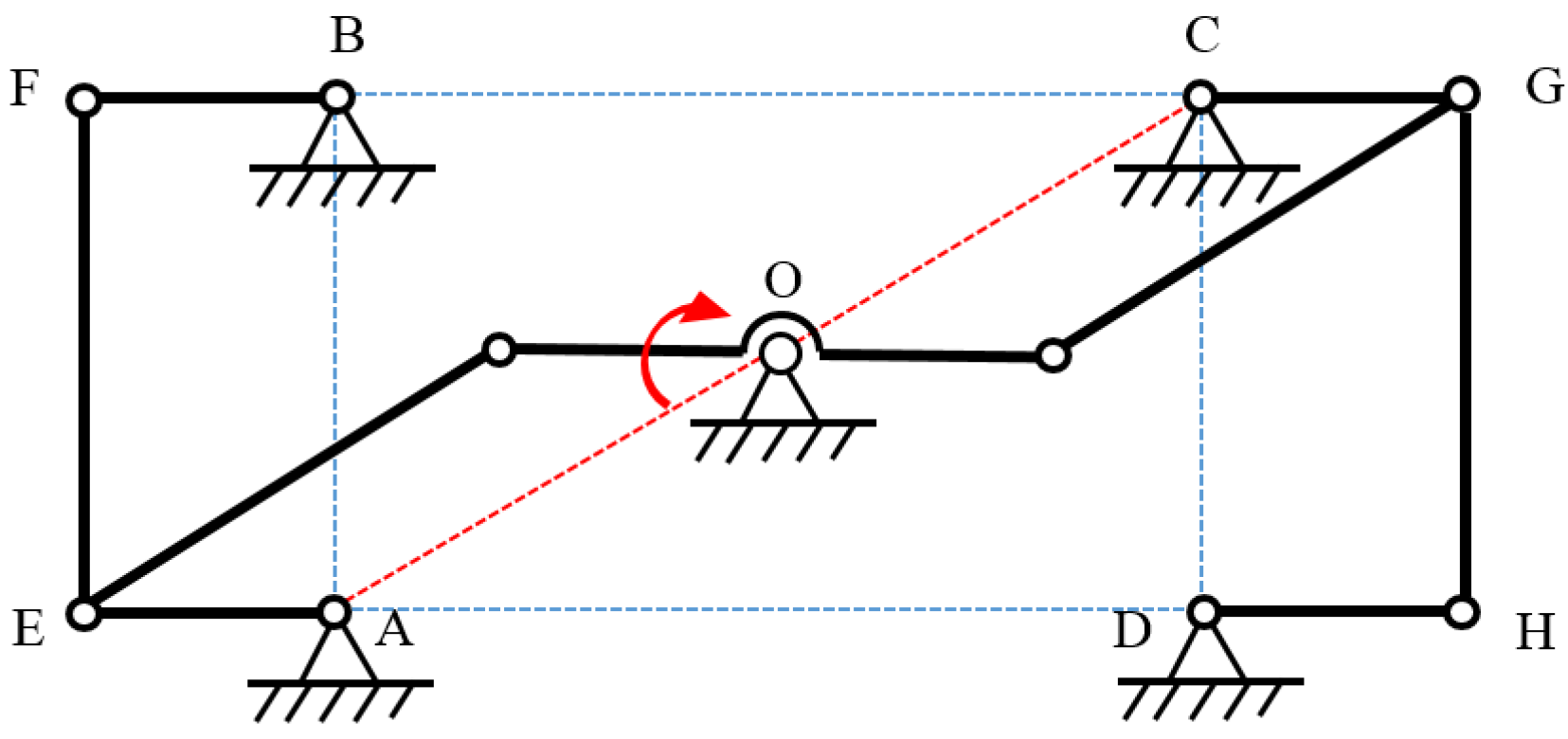
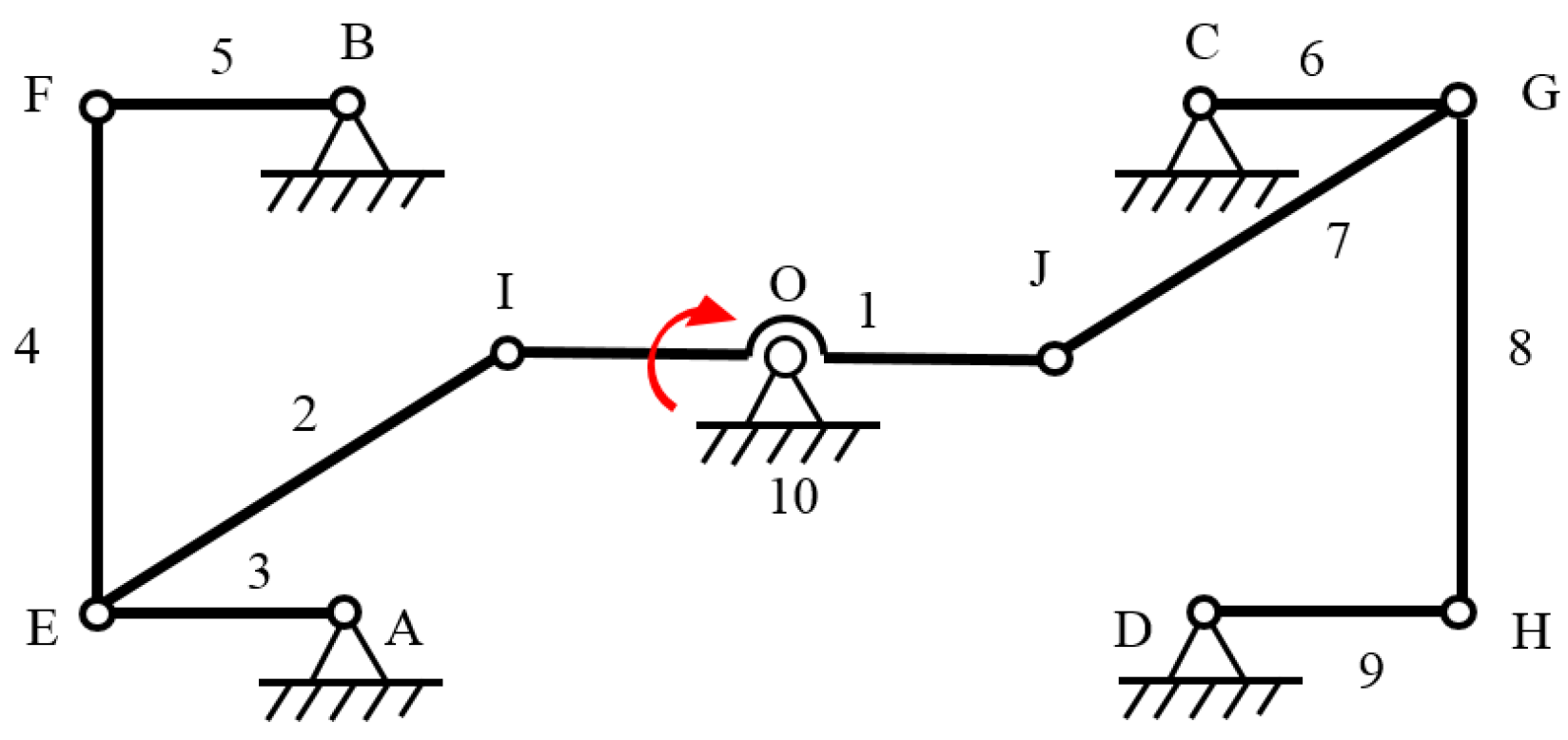
2.3. Degrees of Freedom Analysis of Closed-Chain Single-Leg Mechanism
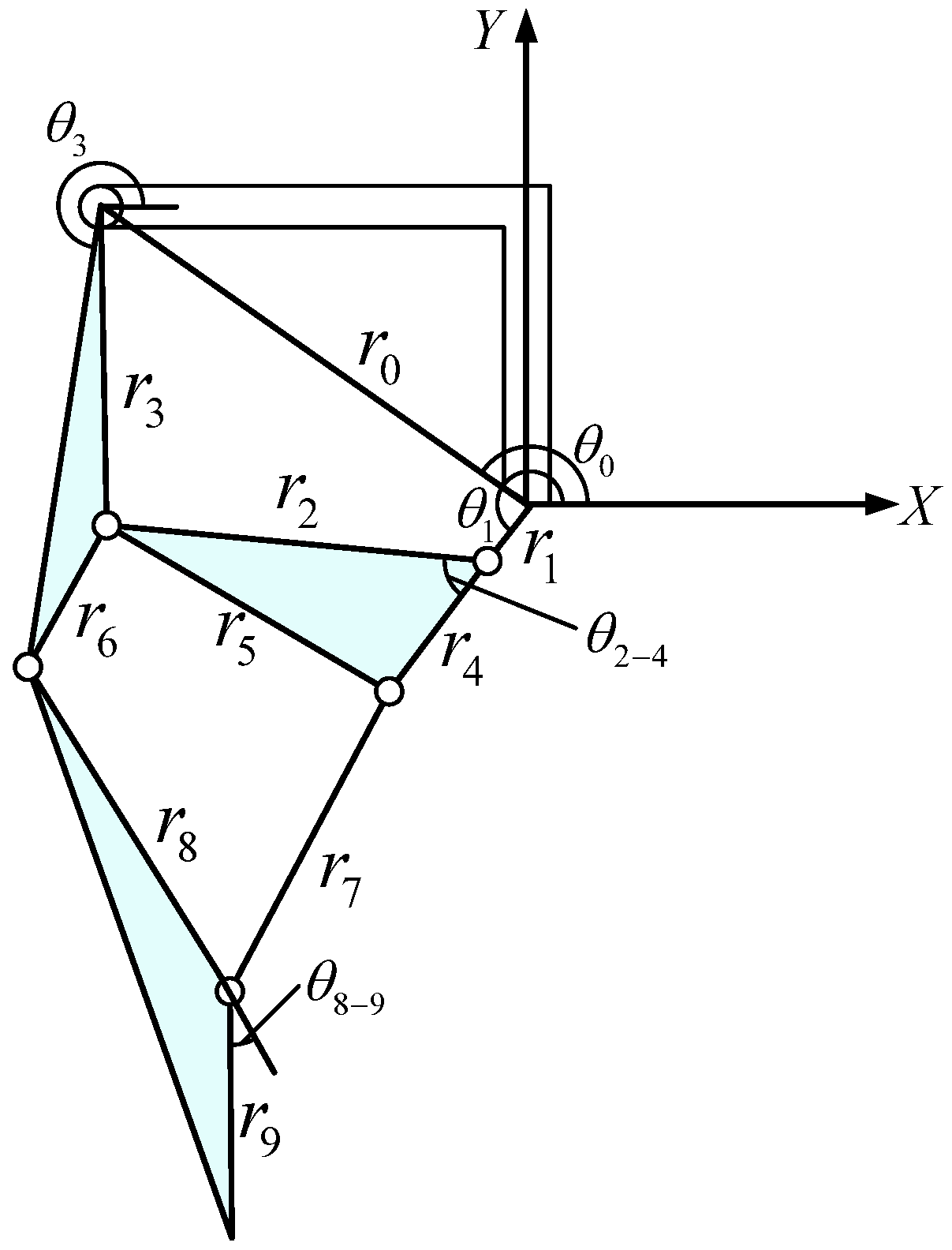
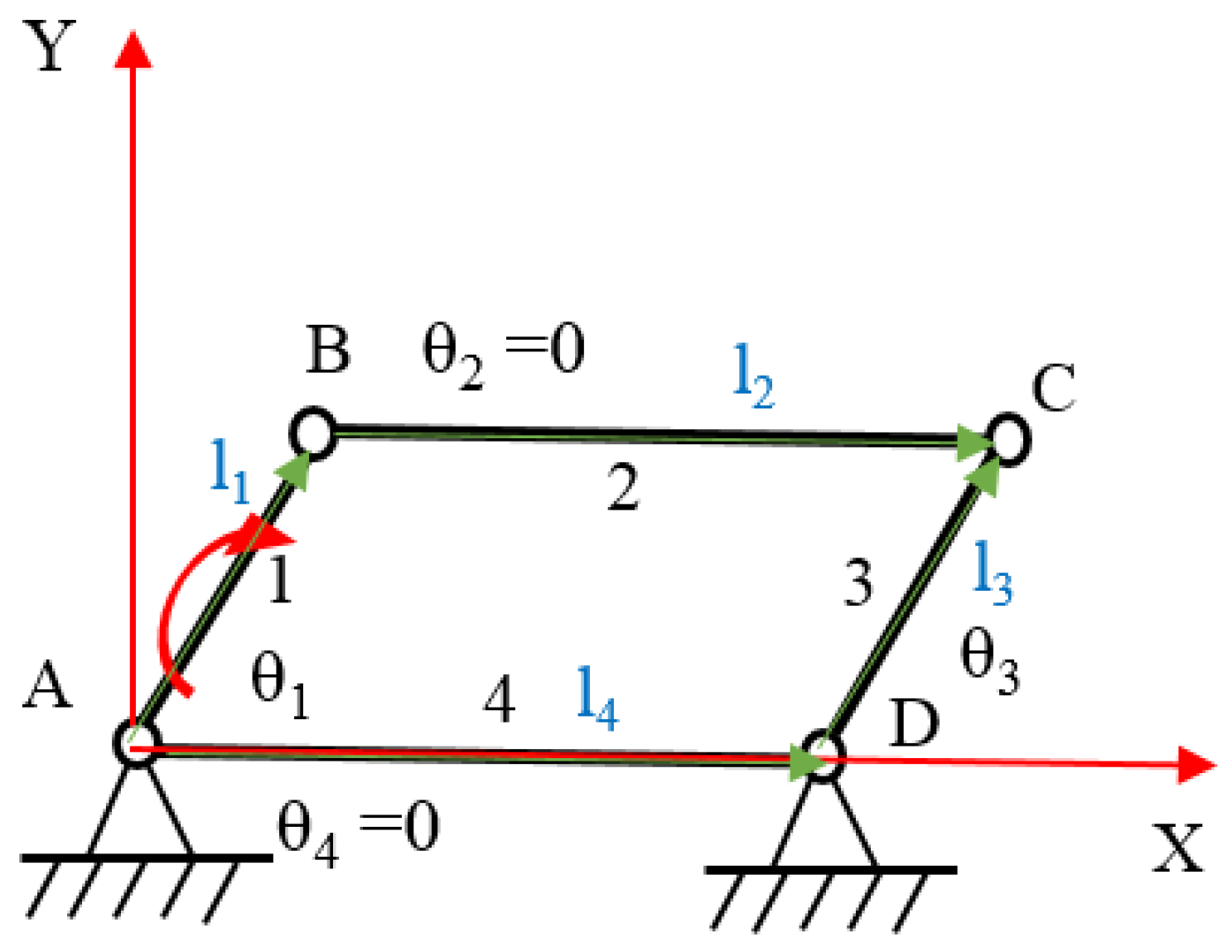
2.4. Kinematics Analysis of Closed-Chain Single-Leg Mechanism
2.5. Singularity Analysis of Closed-Chain Single-Leg Mechanism
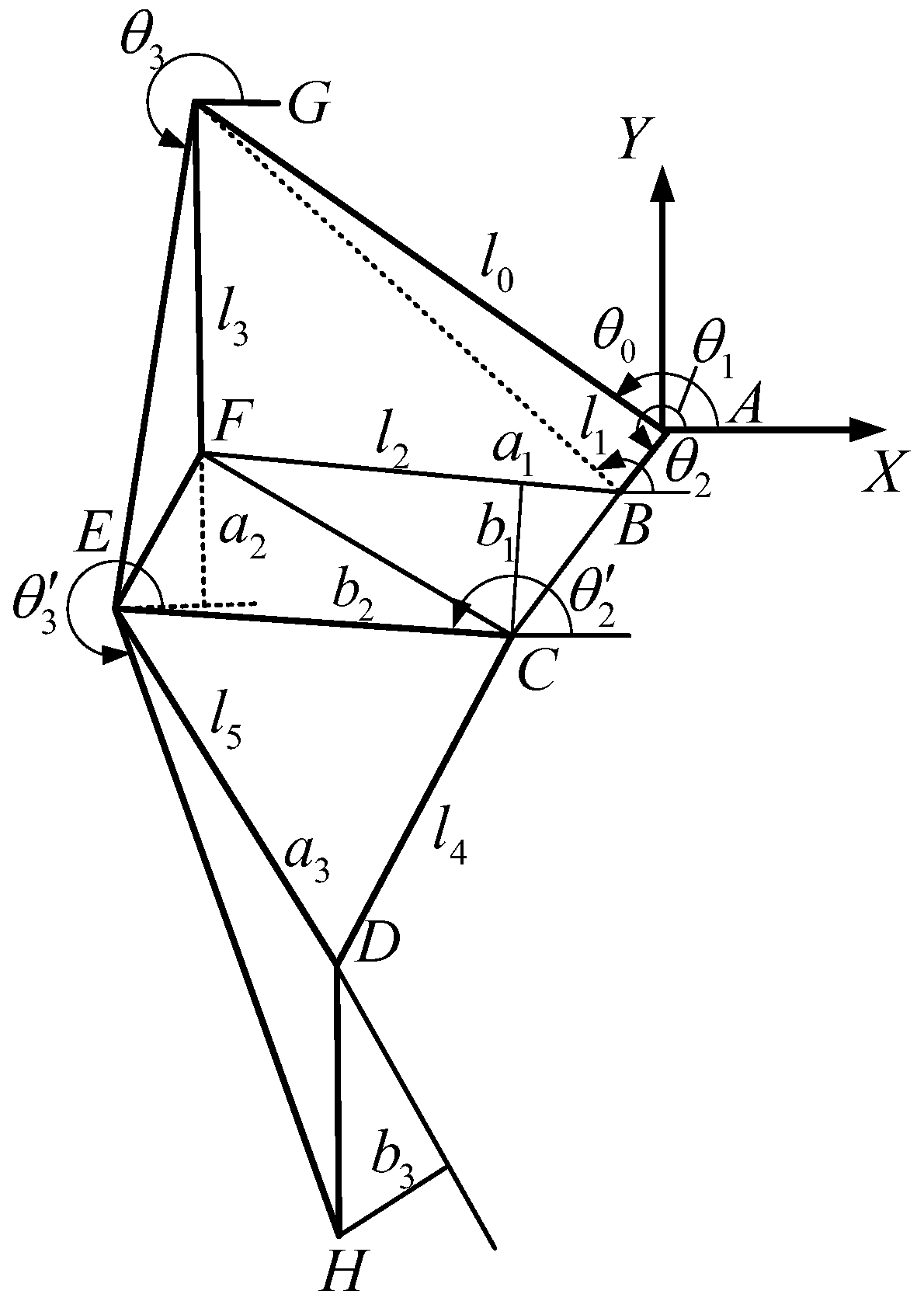
3. Mechanism Size Optimization Based on Trajectory Reproduction
3.1. Basic Research Methods
3.2. Trajectory Reconstruction Based on Traditional Algorithms
3.2.1. Establish an Equivalent Nonlinear Optimization Model with Constraints
3.2.2. Establish Result Evaluation Model
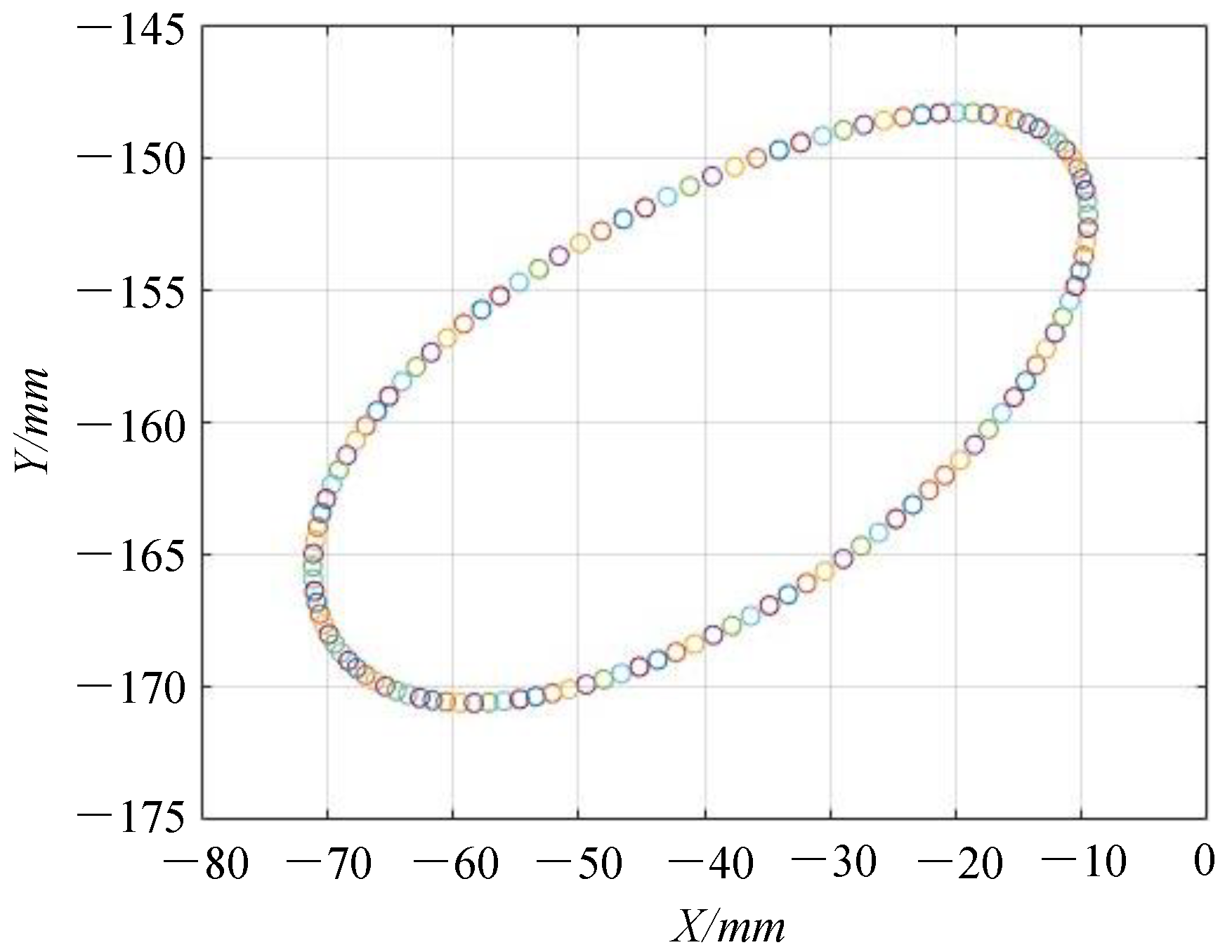
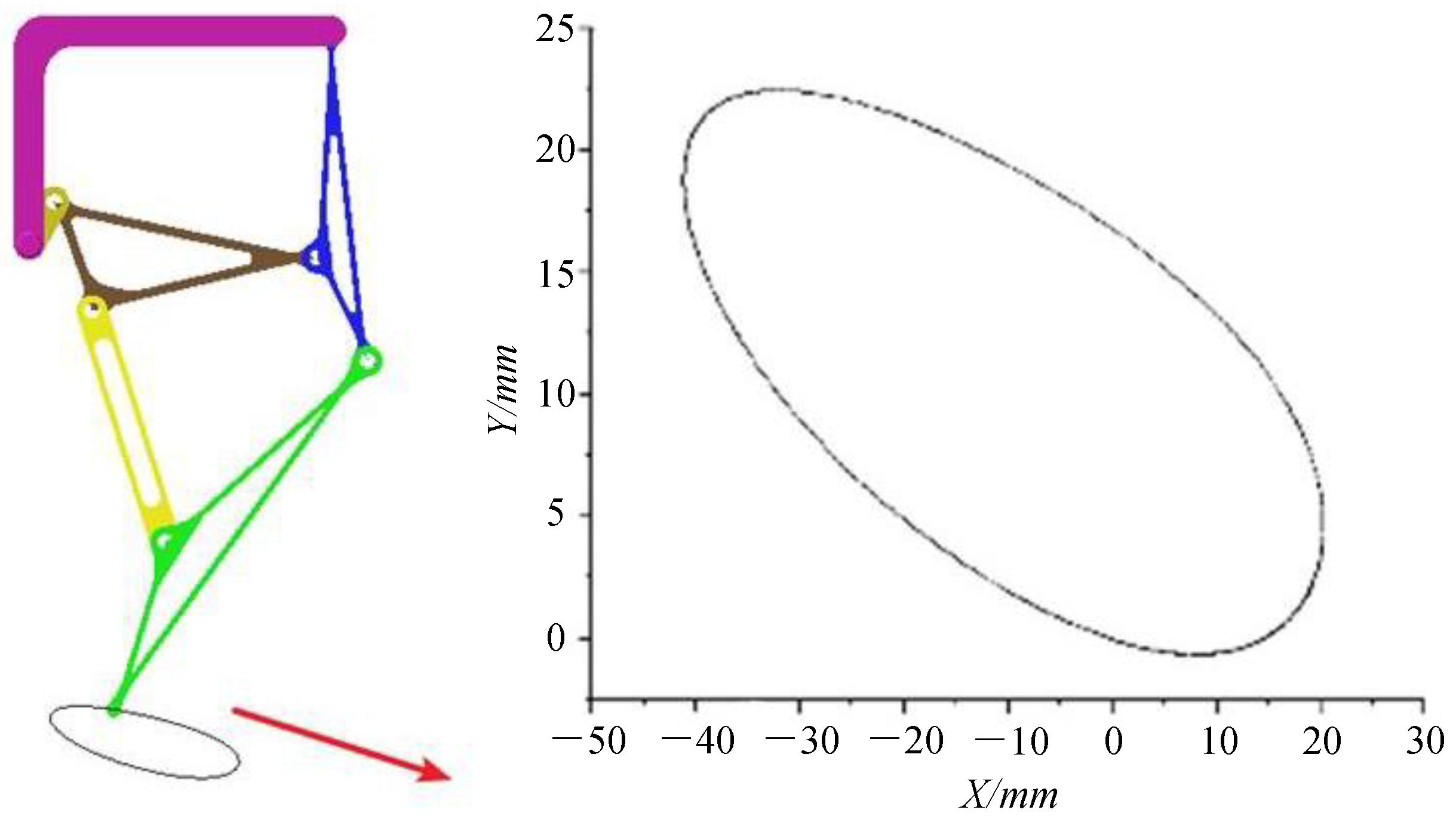
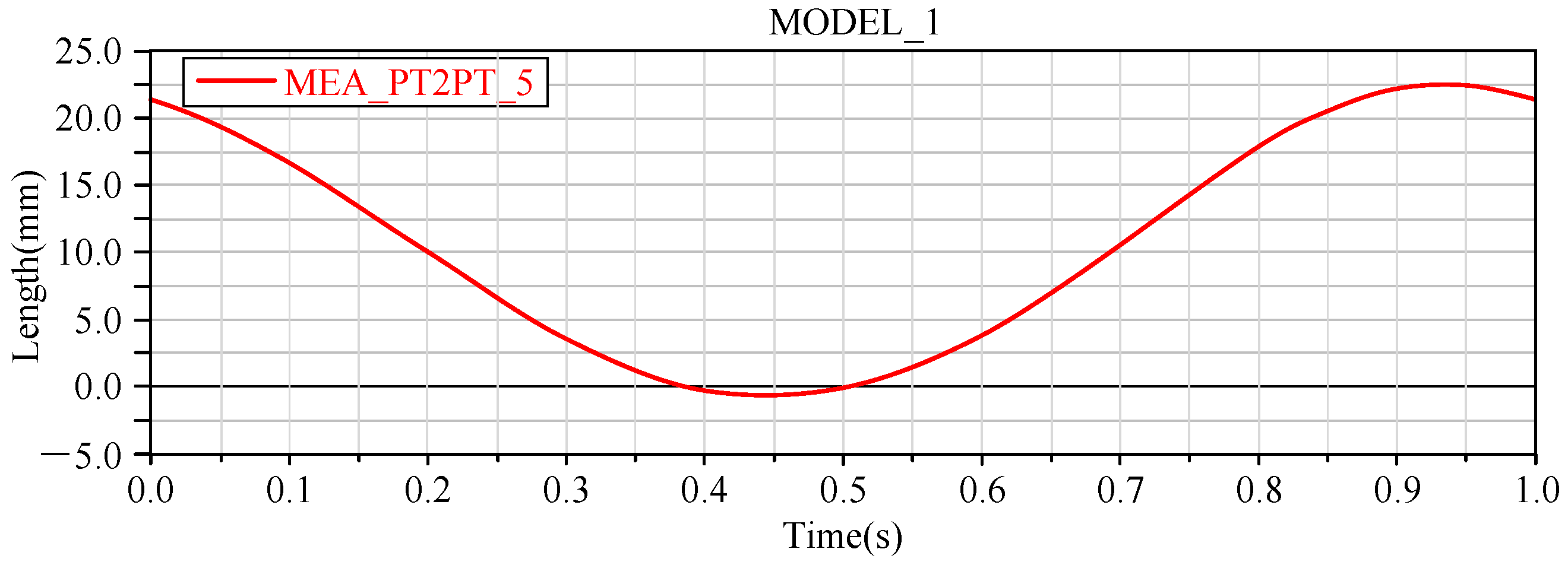
3.2.3. Experimental Verification
3.3. Trajectory Reconstruction Problem Based on Heuristic Algorithm
3.3.1. The Idea of the Particle Swarm Algorithm
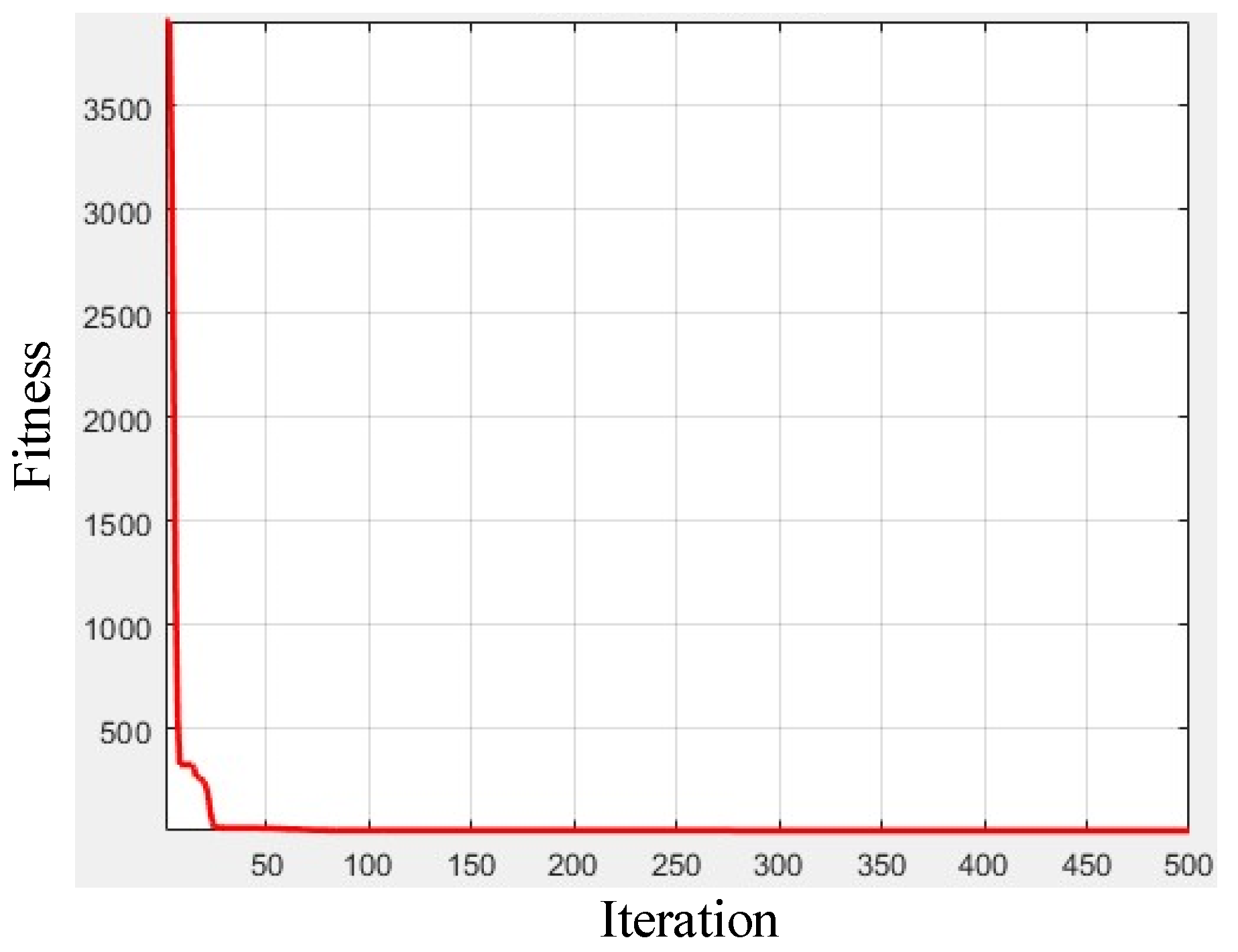
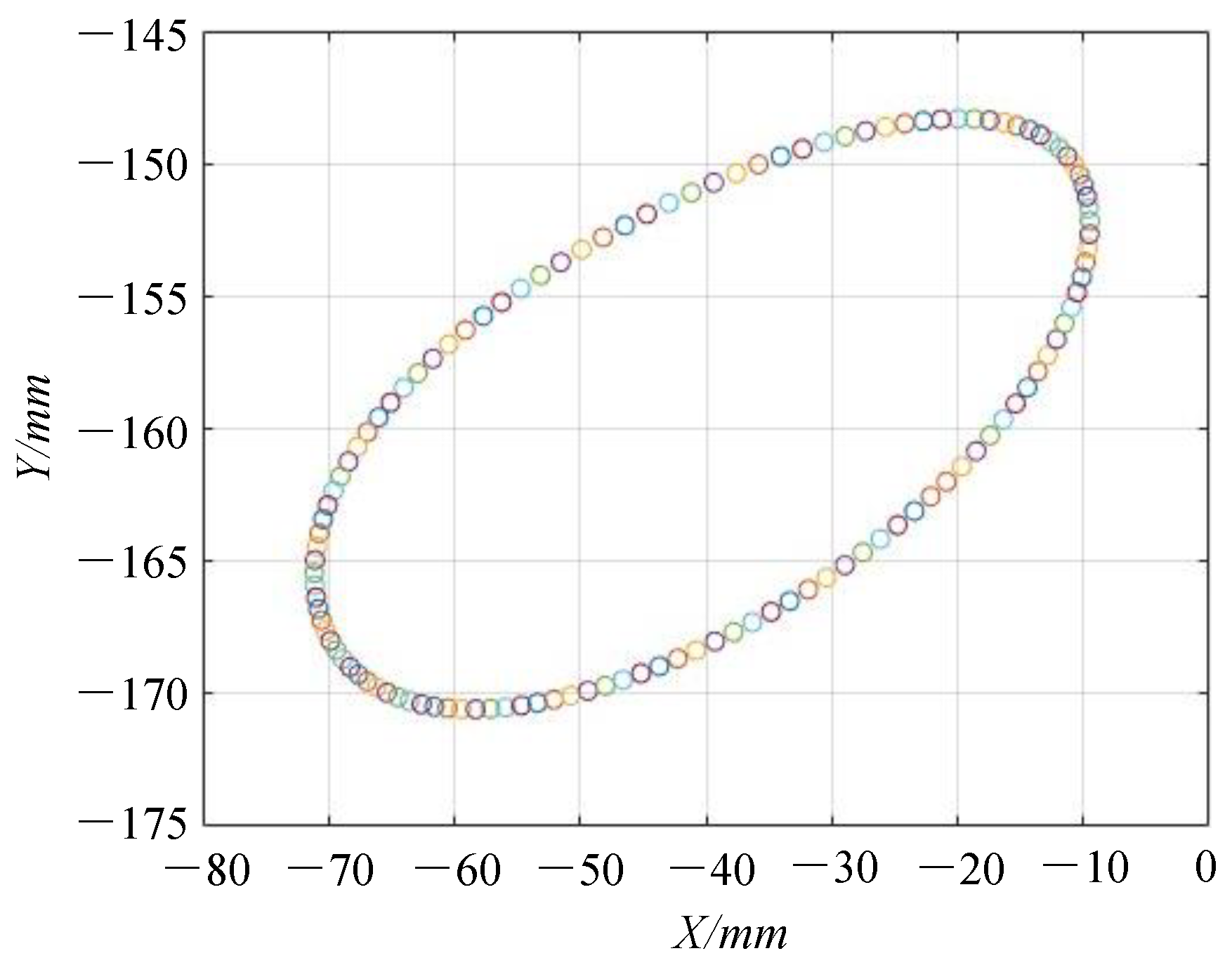
3.3.2. Experimental Verification
4. Design and Analysis of Steering Mechanism
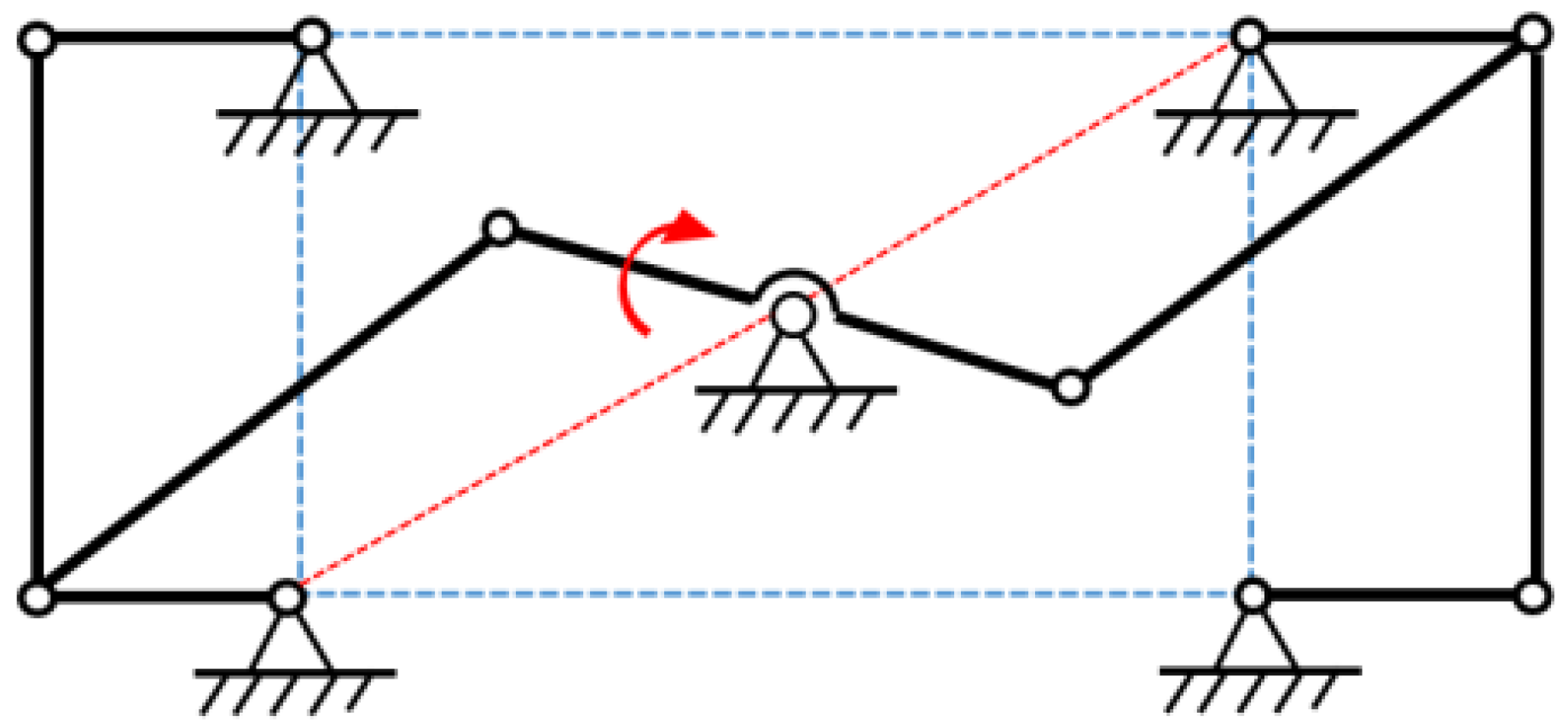
4.1. Design and Selection of Steering Mechanism
4.2. Analysis of Steering Mechanism
4.2.1. Calculation of Degrees of Freedom
4.2.2. Kinematics Analysis
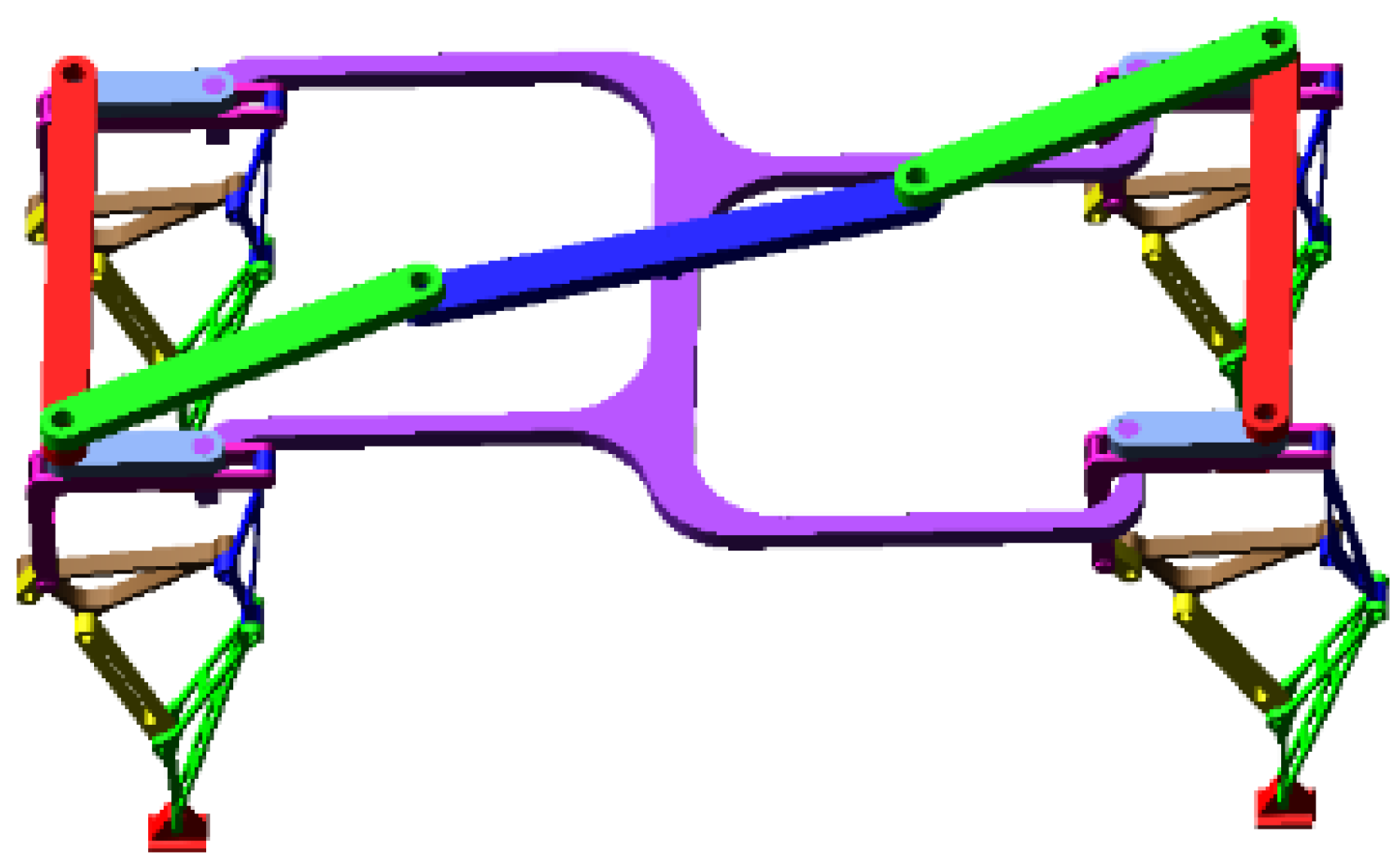
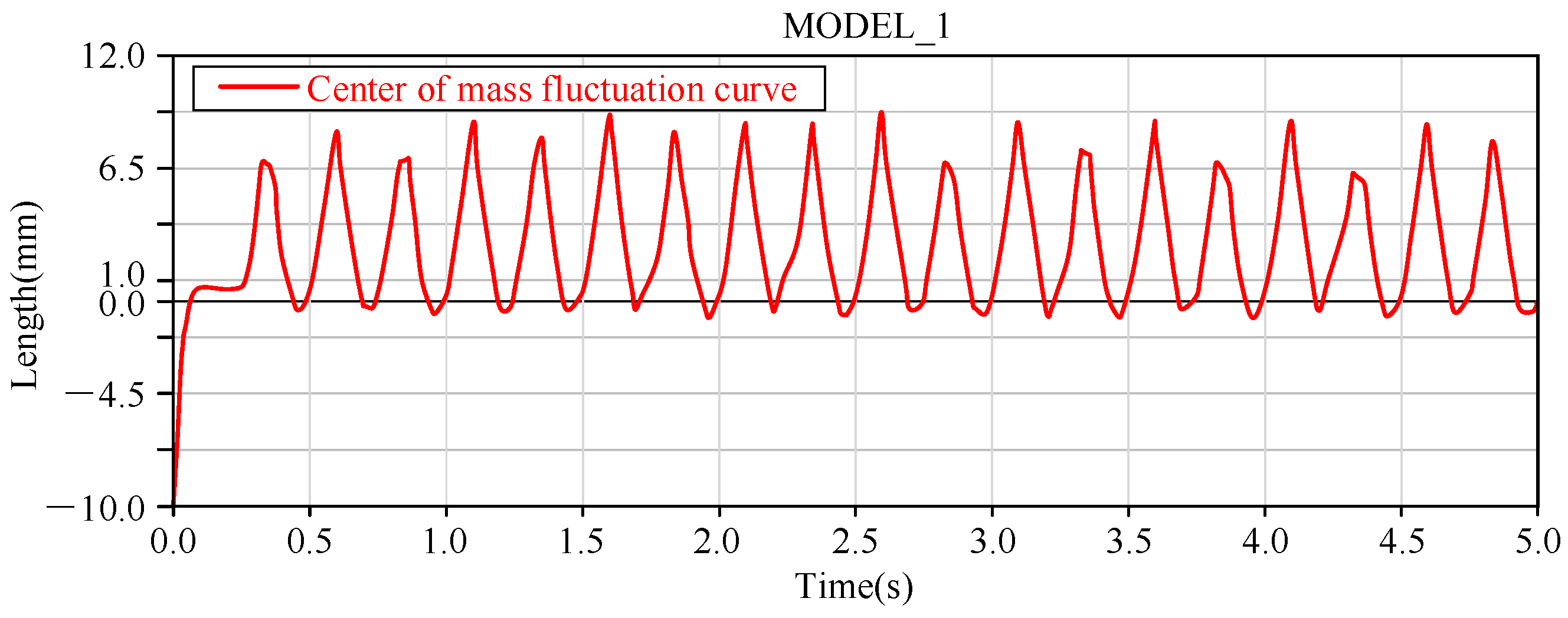
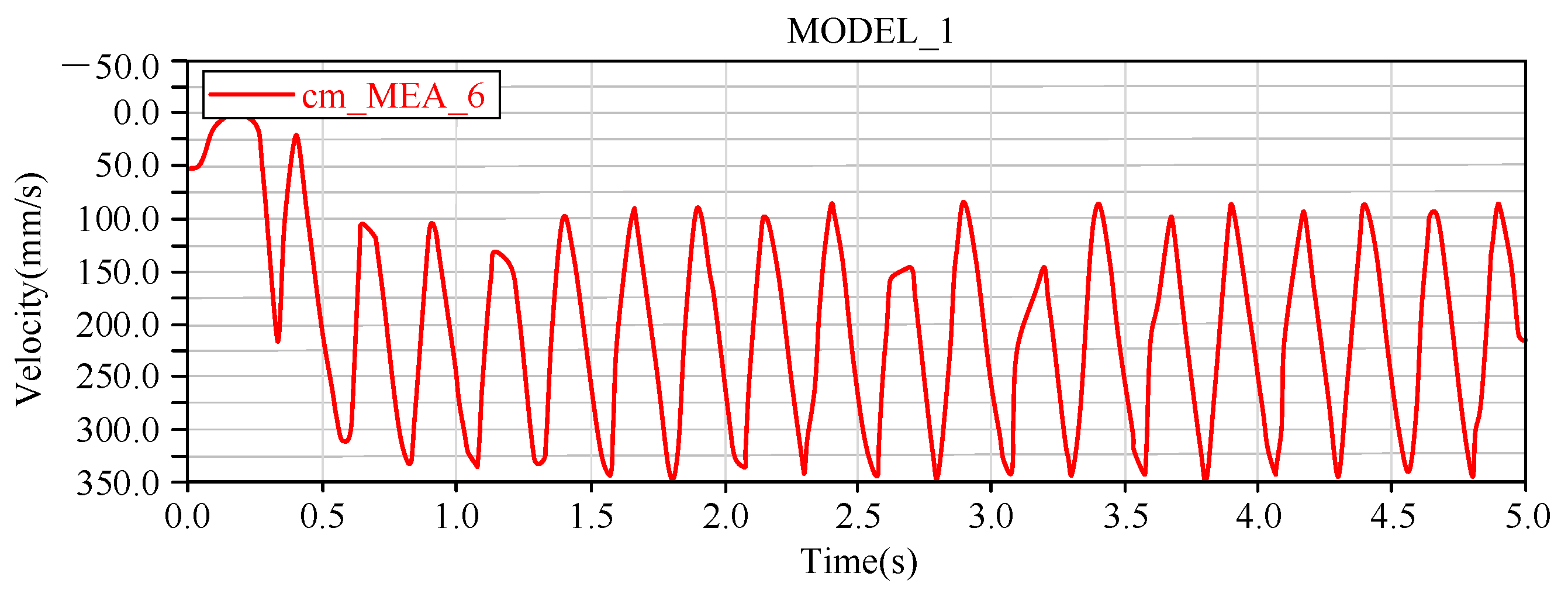
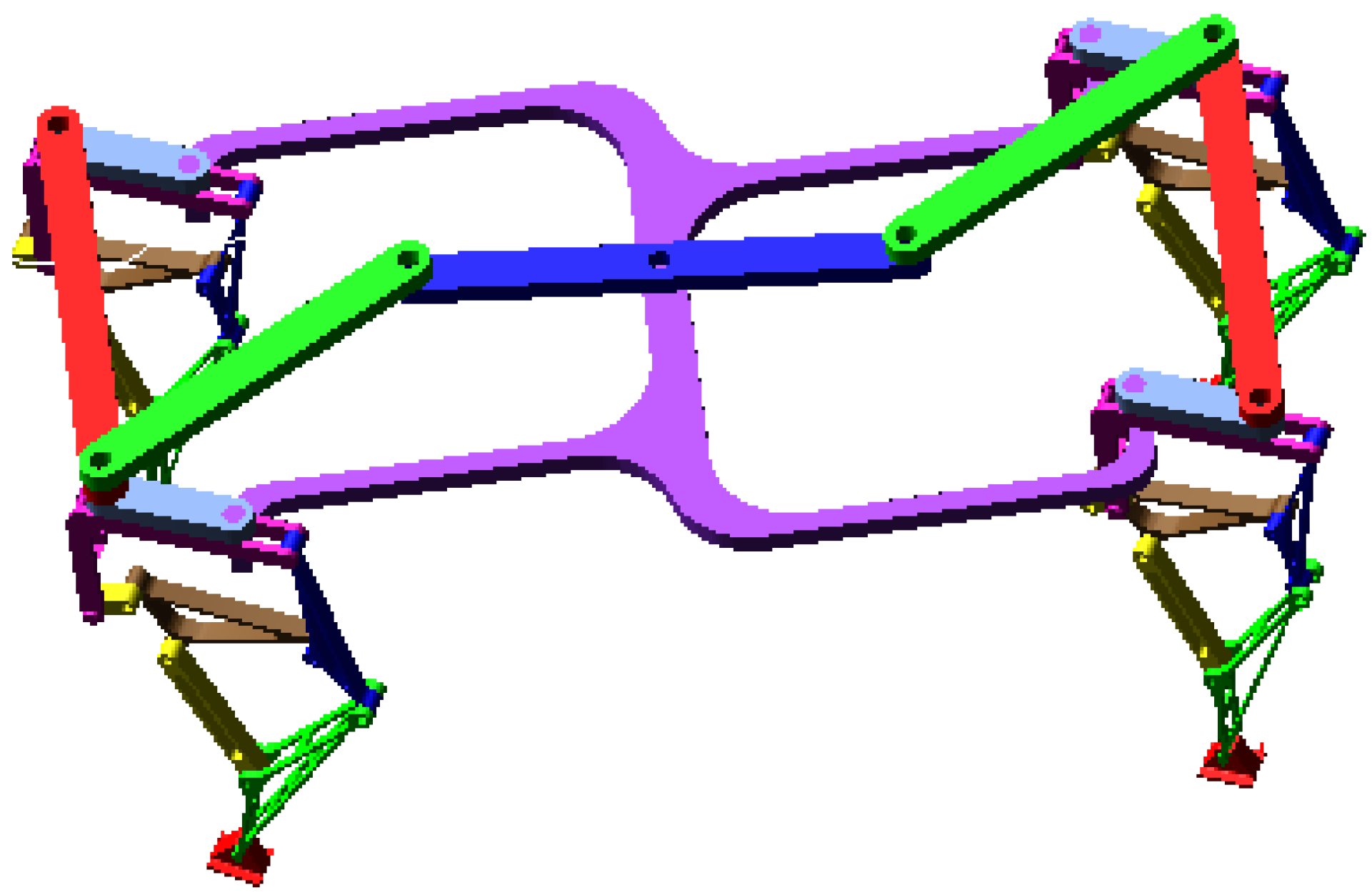
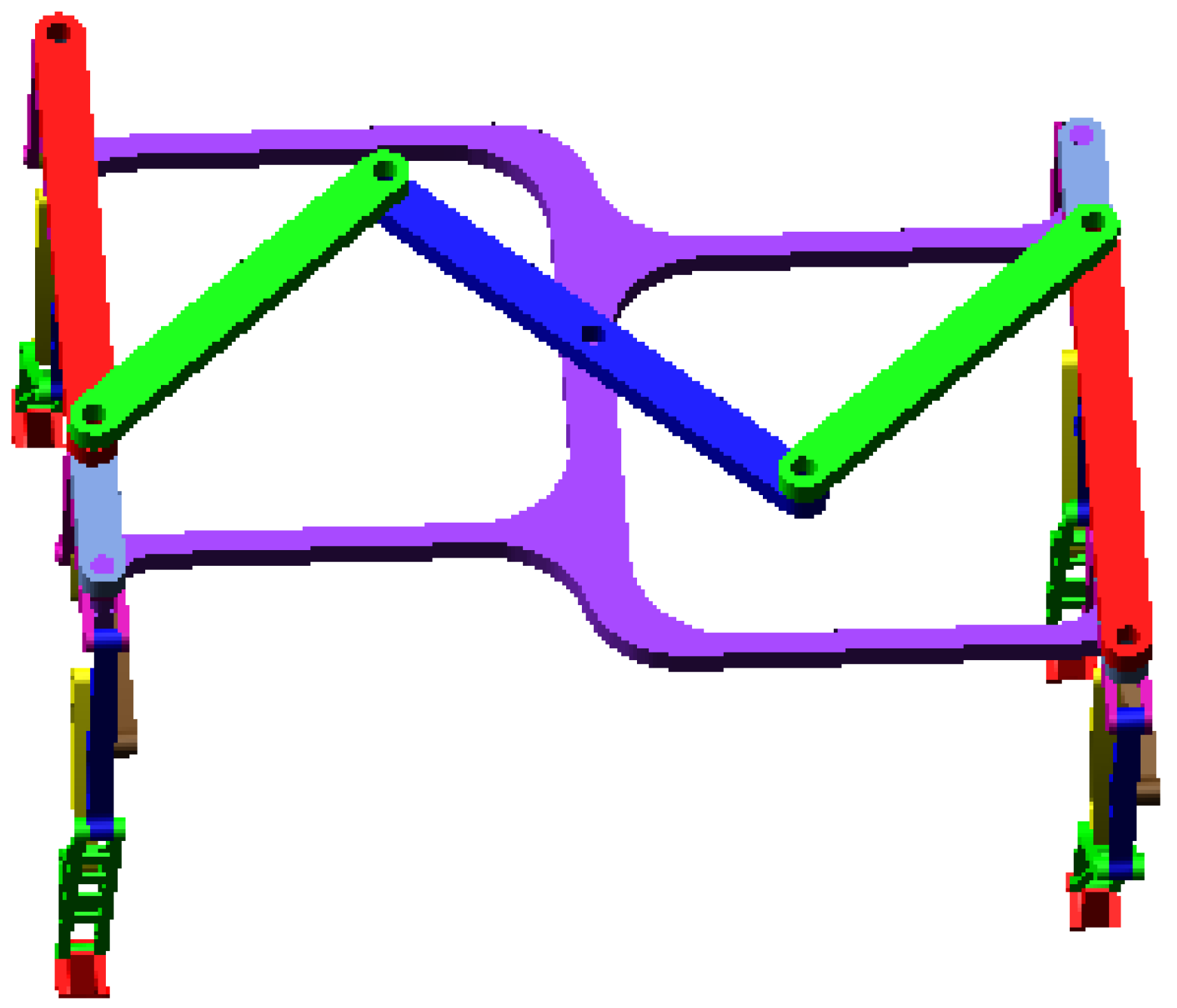
5. Motion Simulation Analysis
5.1. Simulation of Normal Walking Motion
5.2. Steering Motion Simulation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bekker, M.G. Off-the-road locomotion. In Research and Development in Terramechanics; University of Michigan Press: Ann Arbor, MI, USA, 1960. [Google Scholar]
- Patel, N.; Scott, G.; Ellery, A. Application of Bekker theory for planetary exploration through wheeled, tracked, and legged vehicle locomotion. In Proceedings of the Space 2004 Conference and Exhibit, San Diego, CA, USA, 30 September 2004; p. 6091. [Google Scholar]
- Zong, C.; Ji, Z.; Yu, J.; Yu, H. An angle-changeable tracked robot with human–robot interaction in unstructured environments. Assem. Autom. 2020, 40, 565–575. [Google Scholar] [CrossRef]
- Liu, P.; Huang, K.; Chen, C. Design and Motion Simulation of a New Leg-Wheel Robot. In Proceedings of the 2020 Chinese Automation Congress (CAC 2020), Shanghai, China, 6–8 November 2020. [Google Scholar] [CrossRef]
- Chu, H.; Qi, B.; Qiu, X.; Zhou, Y. 6-DOF wheeled parallel robot and its automatic type synthesis method. Mech. Mach. Theory 2022, 169, 104646. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, X.; Tan, M. Legged robots: A review. Robot 2006, 28, 81–88. [Google Scholar]
- Tan, M.; Wang, S. Research progress on robotics. Acta Autom. Sin. 2013, 39, 963–972. [Google Scholar] [CrossRef]
- García Armada, E.; Jiménez Ruiz, M.A.; González de Santos, P.; Armada, M. The Evolution of Robotics Research: From Industrial Robotics to Field and Service Robotics; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2007; Number 1; pp. 90–103. [Google Scholar]
- Catalano, M.G.; Pollayil, M.J.; Grioli, G.; Valsecchi, G.; Kolvenbach, H.; Hutter, M.; Bicchi, A.; Garabini, M. Adaptive Feet for Quadrupedal Walkers. IEEE Trans. Robot. 2022, 38, 302–316. [Google Scholar] [CrossRef]
- Fu, Q.; Guan, Y.; Liu, S.; Zhu, H. A Novel Modular Wheel-legged Mobile Robot with High Mobility. In Proceedings of the 2021 IEEE International Conference on Robotics and Biomimetics (IEEE-ROBIO 2021), Sanya, China, 27–31 December 2021; pp. 577–582. [Google Scholar] [CrossRef]
- Li, L.; Fang, Y.; Yao, J.; Wang, L. Type synthesis of a family of novel parallel leg mechanisms driven by a 3-DOF drive system. Mech. Mach. Theory 2022, 167, 104572. [Google Scholar] [CrossRef]
- Zang, L.; Yang, S.; Wu, C.; Wang, X.; Teng, F. Design and kinematics analysis of coordinated variable wheel-track walking mechanism. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420930577. [Google Scholar] [CrossRef]
- Desai, S.G.; Annigeri, A.R.; TimmanaGouda, A. Analysis of a new single degree-of-freedom eight link leg mechanism for walking machine. Mech. Mach. Theory 2019, 140, 747–764. [Google Scholar] [CrossRef]
- Miler, D.; Birt, D.; Hoic, M. Multi-Objective Optimization of the Chebyshev Lambda Mechanism. Stroj.-Vestn.-J. Mech. Eng. 2022, 68, 725–734. [Google Scholar] [CrossRef]
- Alizade, R.I.; Kiper, G.; Bagdadioglu, B.; Dede, M.I.C. Function synthesis of Bennett 6R mechanisms using Chebyshev approximation. Mech. Mach. Theory 2014, 81, 62–78. [Google Scholar] [CrossRef]
- Nansai, S.; Elara, M.R.; Iwase, M. Dynamic Analysis and Modeling of Jansen Mechanism. In Proceedings of the International Conference on Design and Manufacturing (ICONDM2013), Chennai, India, 18–20 July 2013; Volume 64, pp. 1562–1571. [Google Scholar] [CrossRef]
- Patnaik, L.; Umanand, L. Kinematics and dynamics of Jansen leg mechanism: A bond graph approach. Simul. Model. Pract. Theory 2016, 60, 160–169. [Google Scholar] [CrossRef]
- Singh, R.; Bera, T.K. Walking Model of Jansen Mechanism-Based Quadruped Robot and Application to Obstacle Avoidance. Arab. J. Sci. Eng. 2020, 45, 653–664. [Google Scholar] [CrossRef]
- Sheba, J.K.; Elara, M.R.; Martinez-Garcia, E.; Tan-Phuc, L. Design and Evaluation of Reconfigurable Klann Mechanism based Four Legged Walking Robot. In Proceedings of the 2015 10th International Conference on Information, Communications and Signal Processing (ICICS), Singapore, 2–4 December 2015. [Google Scholar]
- Komoda, K.; Wagatsuma, H. Energy-efficacy comparisons and multibody dynamics analyses of legged robots with different closed-loop mechanisms. Multibody Syst. Dyn. 2017, 40, 123–153. [Google Scholar] [CrossRef]
- Rafeeq, M.; Toha, S.F.; Ahmad, S.; Yusof, M.S.M.; Razib, M.A.M.; Bahrin, M.I.H.S. Design and Modeling of Klann Mechanism-Based Paired Four Legged Amphibious Robot. IEEE Access 2021, 9, 166436–166445. [Google Scholar] [CrossRef]
- Li, T.; Ceccarelli, M. Design and simulated characteristics of a new biped mechanism. Robotica 2015, 33, 1568–1588. [Google Scholar] [CrossRef]
- Baskar, A.; Plecnik, M.; Hauenstein, J.D. Finding straight line generators through the approximate synthesis of symmetric four-bar coupler curves. Mech. Mach. Theory 2023, 188, 105310. [Google Scholar] [CrossRef]
- Yin, L.; Huang, L.; Huang, J.; Xu, P.; Peng, X.; Zhang, P. Synthesis Theory and Optimum Design of Four-bar Linkage with Given Angle Parameters. Mech. Sci. 2019, 10, 545–552. [Google Scholar] [CrossRef]
- Jaiswal, A.; Jawale, H.P. Comparative study of four-bar hyperbolic function generation mechanism with four and five accuracy points. Arch. Appl. Mech. 2017, 87, 2037–2054. [Google Scholar] [CrossRef]
- Bai, S.; Angeles, J. Coupler-curve synthesis of four-bar linkages via a novel formulation. Mech. Mach. Theory 2015, 94, 177–187. [Google Scholar] [CrossRef]
- Ivolga, D.V.; Borisov, I.I.; Nasonov, K.V.; Kolyubin, S.A. Computational Design of Closed-Chain Linkages: Respawn Algorithm for Generative Design. In Proceedings of the 2023 IEEE/RSJ International Conference on Intelligent Robots Furthermore, Systems, (IROS), Detroit, MI, USA, 1–5 October 2023; pp. 481–486. [Google Scholar] [CrossRef]
- Tole, G.; Williams, G.; Holland, A.E.; Clark, R.A. Lower limb muscle performance during a closed chain single leg squat and a squat jump in people with leg weakness after stroke: A comparative study. Brain Impair. 2022, 25, IB22031. [Google Scholar] [CrossRef]
- Liu, G.; Trinkle, J.; Yang, Y.; Luo, S. Motion Planning of Planar Closed Chains Based on Structural Sets. IEEE Access 2020, 8, 117203–117217. [Google Scholar] [CrossRef]
- Shafei, A.M.; Shafei, H.R. Dynamic modeling of planar closed-chain robotic manipulators in flight and impact phases. Mech. Mach. Theory 2018, 126, 141–154. [Google Scholar] [CrossRef]
- Wu, J.; Yao, Y.A. Design and analysis of a novel walking vehicle based on leg mechanism with variable topologies. Mech. Mach. Theory 2018, 128, 663–681. [Google Scholar] [CrossRef]
- Wu, J.; Yao, Y.; Ruan, Q.; Liu, X. Design and optimization of a dual quadruped vehicle based on whole close-chain mechanism. Proc. Inst. Mech. Eng. Part-J. Mech. Eng. Sci. 2017, 231, 3601–3613. [Google Scholar] [CrossRef]
- Yan, H.; Yao, Y. Creative Design of Mechanical Devices; China Machine Press: Beijing, China, 2002. [Google Scholar]
- Huang, Z.; Zhao, Y.S.; Zhao, T.S. Advanced Spatial Mechanism; China Higher Education Press: Beijing, China, 2006; pp. 89–201. [Google Scholar]
- Gu, R. Optimal design of planar four-bar mechanism with trajectory representation. J. Nantong Vocat. Univ. 2011, 25, 97–100. [Google Scholar]
- Wu, J. The Design and Application of the Link Type Integral Closed Chain Multi Sufficient Transportation Platform; Beijing Jiaotong University: Beijing, China, 2019. [Google Scholar]
- Li, P.; Peng, S.; Che, L.; Du, L.; Wu, Z. Application of hybrid artificial bee colony algorithm in scale optimization of parallel mechanism. Mech. Des. 2019, 36, 90–96. [Google Scholar]

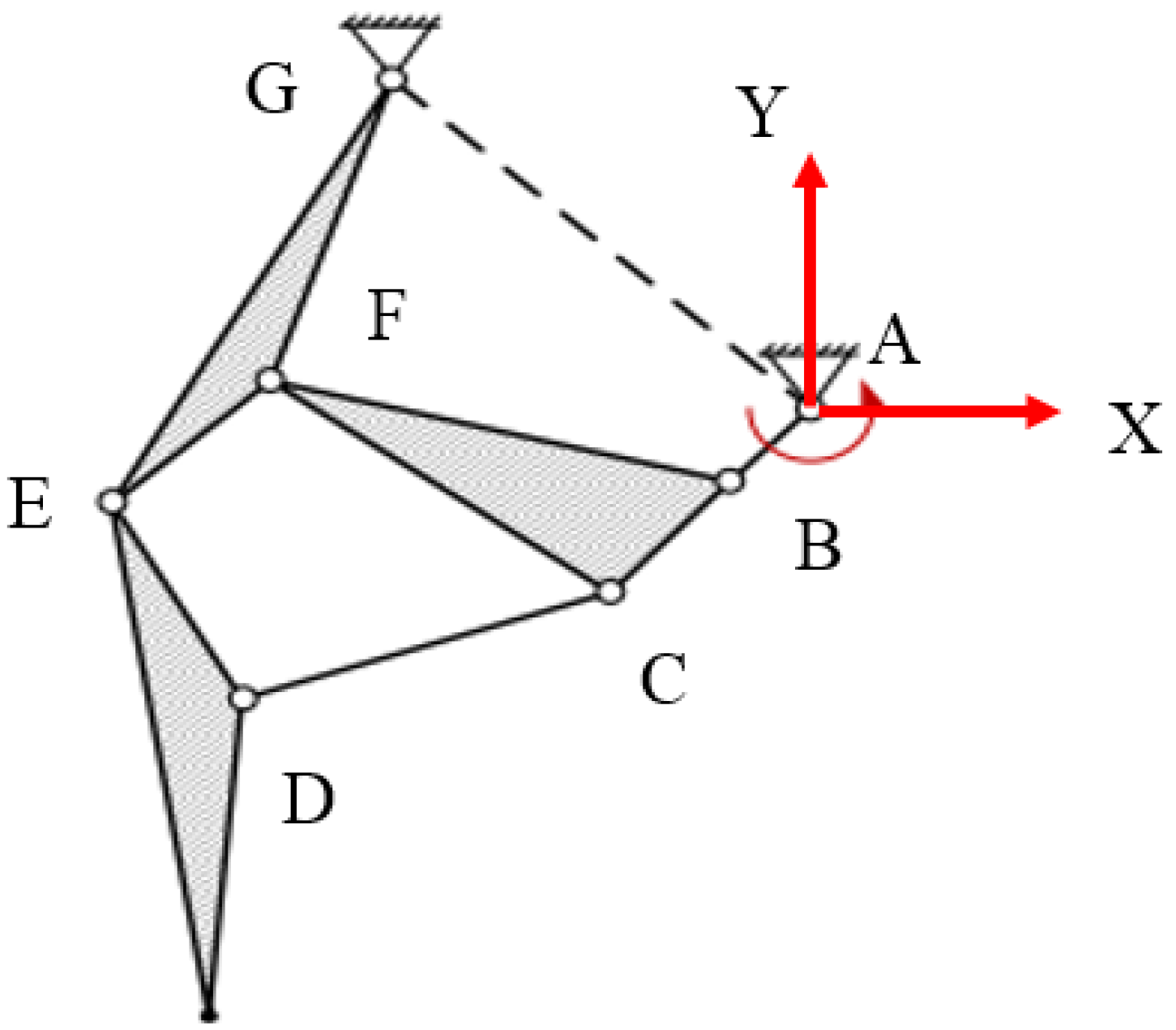



| (n,f) | (6,7) | (8,10) | (10,13) |
|---|---|---|---|
| Generalized kinematic chain | 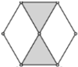 | 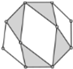 | 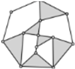 |
| Specific kinematic chain | 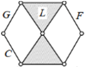 | 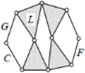 | 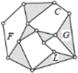 |
| Schematic diagram of the new closed -chain leg mechanism | 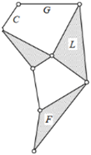 | 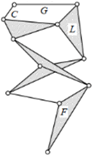 |  |
| Serial Number | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Mechanism type | WATT-I | WATT-II | Stephenson-II | Stephenson-III | Stephenson-III |
| Specific kinematic chain | 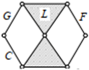 |  | 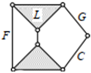 | 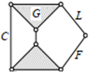 | 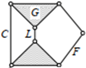 |
| Schematic diagram of the new closed -chain leg mechanism | 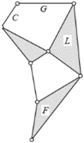 |  | 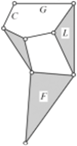 | 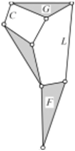 |  |
| Parameters | Numerical Value (mm) | Parameters | Numerical Value (mm) |
|---|---|---|---|
| 15.9 | 105 | ||
| −96.9 | 18.5 | ||
| 70.4 | 78.2 | ||
| 87.4 | 87.9 | ||
| 73.1 | 126.2 | ||
| 19.3 | 29.2 | ||
| 31.8 |
| (deg) | 0 | 60 | 120 | 180 | 240 | 300 |
|---|---|---|---|---|---|---|
| (mm) | −22.368 | −9.6286 | −30.5297 | −63.0965 | −69.6808 | −50.6535 |
| (mm) | −162.530 | −151.182 | −149.276 | −157.858 | −168.004 | −170.216 |
| Method/Initial Error | 1 mm | 3 mm | 5 mm | 7 mm | 9 mm | 11 mm |
|---|---|---|---|---|---|---|
| SQP | 4 | 402 | 1502 | 8206 | 17,483 | 28,606 |
| Interior point | 1 | 1 | 33 | 9791 | 10,810 | 9868 |
| Active set | 1 | 18 | 87 | 13,634 | 32,300 | 27,356 |
| Particle Swarm Scale | The Maximum Number of Iterations | Inertia Weight | Learning Factor | Learning Factor | Particle Velocity |
|---|---|---|---|---|---|
| 500 | 500 | 0.7298 | 1.4961 | 1.4961 | [−1, 1] |
| Theoretical Value (mm) | Calculated Value (mm) | |
|---|---|---|
| 15.9 | 15.9 | |
| −96.9 | −93.9 | |
| 70.4 | 79.0 | |
| 87.4 | 85.2 | |
| 73.1 | 78.1 | |
| 19.3 | 7.43 | |
| 31.8 | 42.3 | |
| 105 | 111 | |
| 18.5 | 18.8 | |
| 78.2 | 75.8 | |
| 87.9 | 102 | |
| 126.2 | 137 | |
| 29.2 | 33.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Shi, W.; Long, Z.; Jiang, Z. Structural Design and Analysis of Multi-Directional Foot Mobile Robot. Appl. Sci. 2024, 14, 6805. https://doi.org/10.3390/app14156805
Yang H, Shi W, Long Z, Jiang Z. Structural Design and Analysis of Multi-Directional Foot Mobile Robot. Applied Sciences. 2024; 14(15):6805. https://doi.org/10.3390/app14156805
Chicago/Turabian StyleYang, Hui, Wen Shi, Zhongjie Long, and Zhouxiang Jiang. 2024. "Structural Design and Analysis of Multi-Directional Foot Mobile Robot" Applied Sciences 14, no. 15: 6805. https://doi.org/10.3390/app14156805
APA StyleYang, H., Shi, W., Long, Z., & Jiang, Z. (2024). Structural Design and Analysis of Multi-Directional Foot Mobile Robot. Applied Sciences, 14(15), 6805. https://doi.org/10.3390/app14156805






