Coupled Non-Ordinary State-Based Peridynamics Model for Ductile and Brittle Solids Subjected to Thermal Shocks
Abstract
:1. Introduction
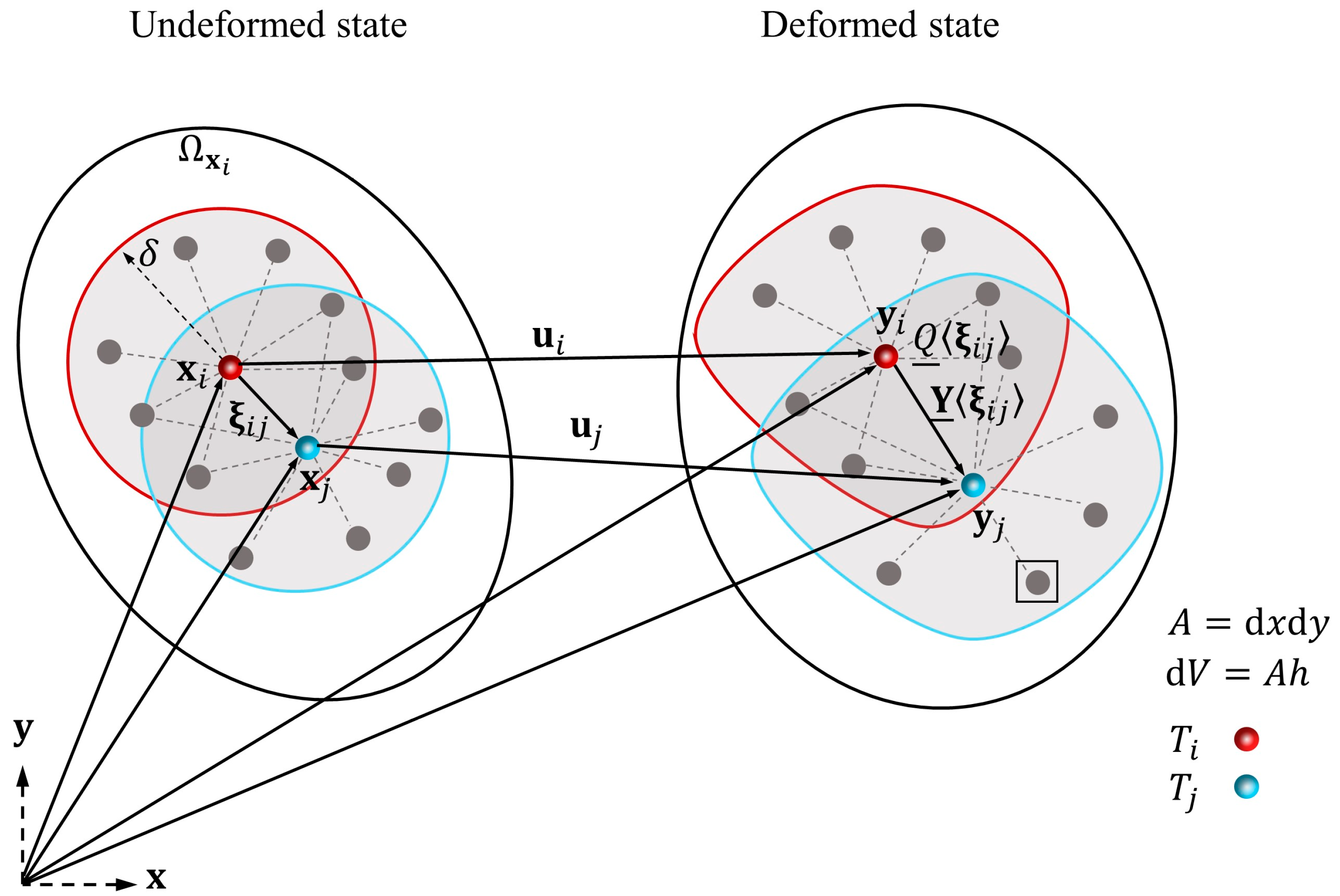
2. Basic Theory of the Non-Ordinary State-Based Peridynamics Model
2.1. Thermomechanical PD Equations
2.2. Correspondence Material Model for Thermomechanical Problems
2.3. Stabilization Method
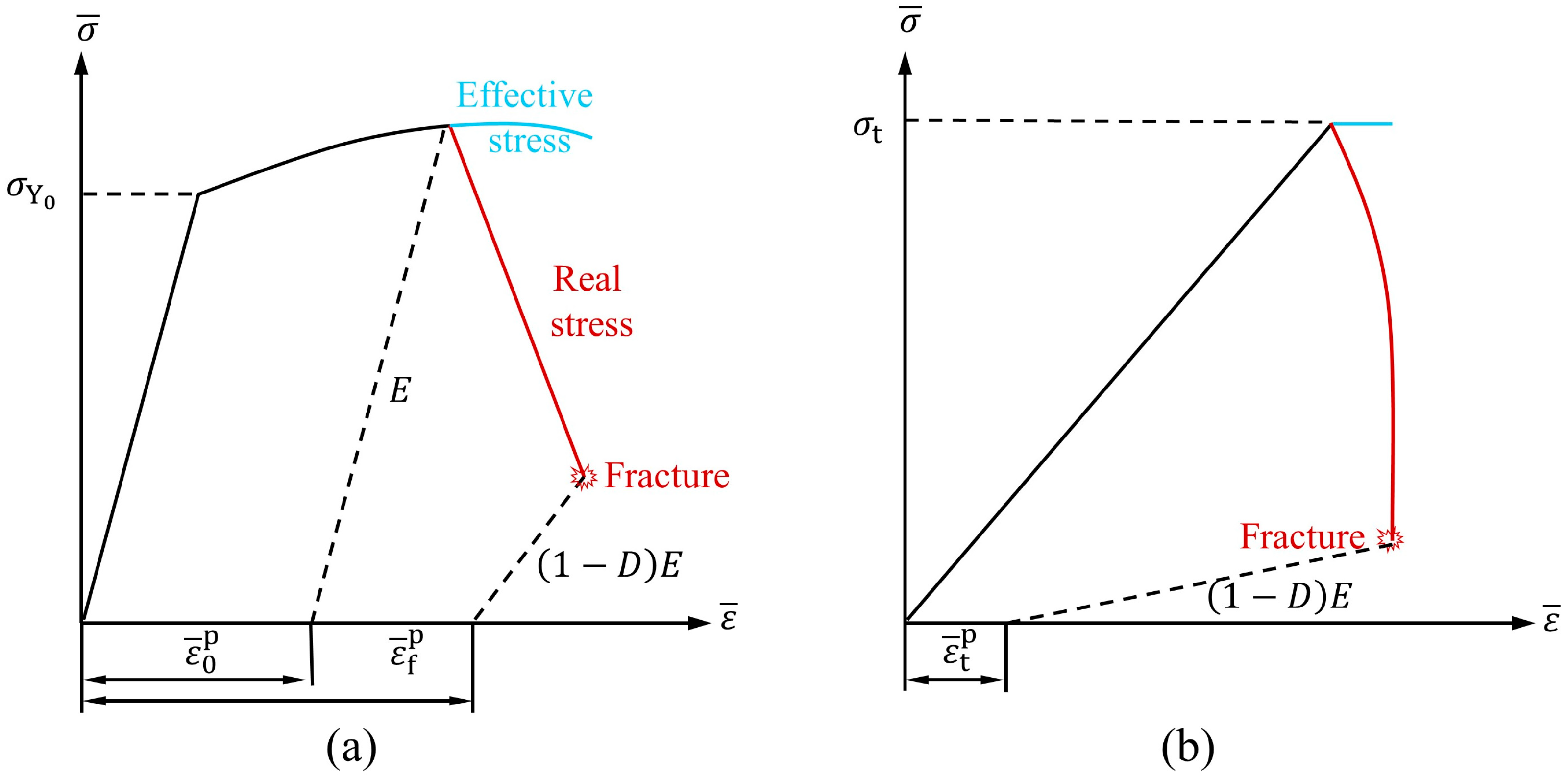
3. Constitutive Model
3.1. Multiaxial Constitutive Model with Damage
3.2. Failure Criterion
4. Numerical Implementation
4.1. Time Integration
4.2. Stress Integration
5. Numerical Examples
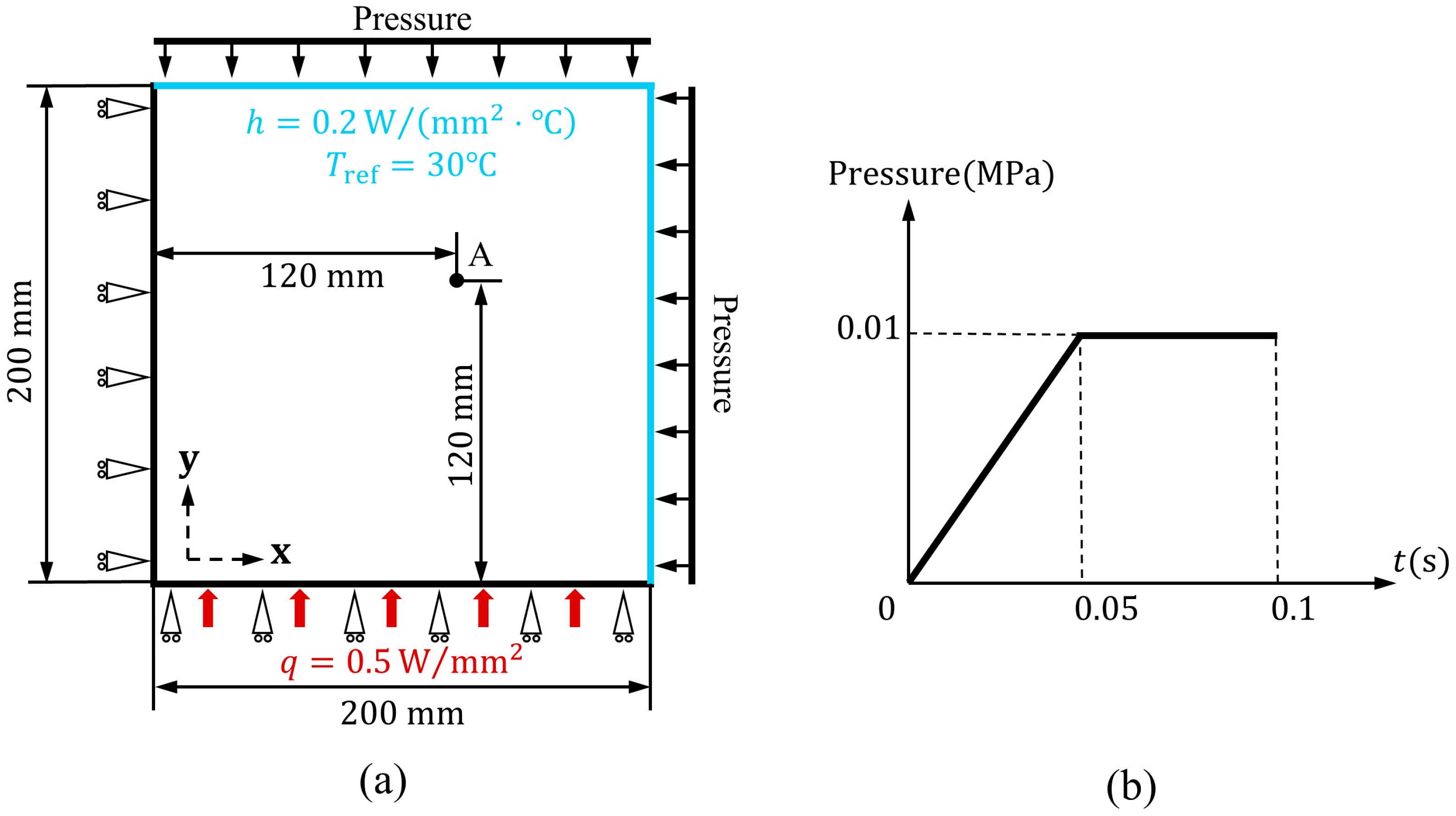
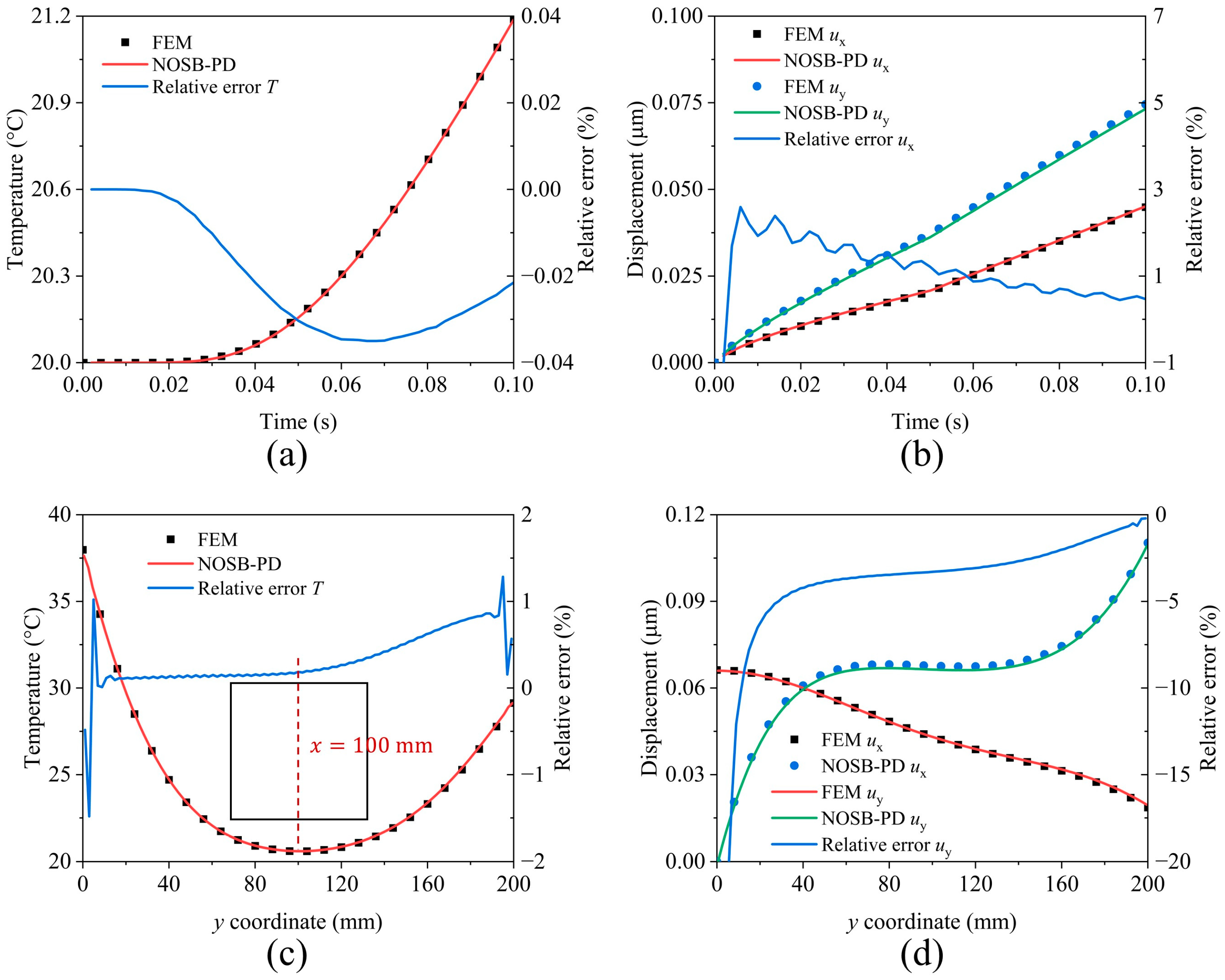
5.1. Thermodynamic Analysis of Plate
5.2. Kalthoff–Winkler Impact Test
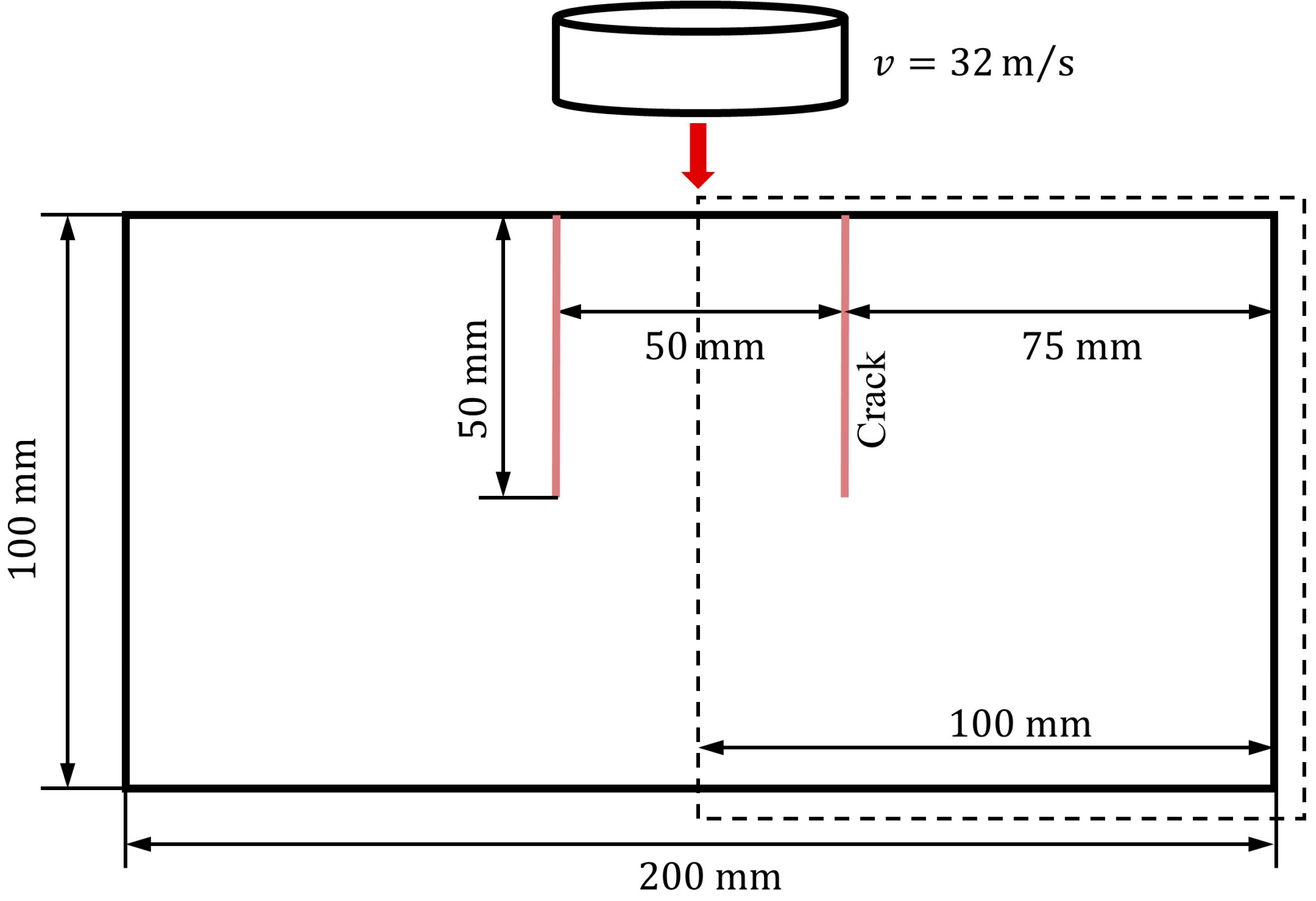
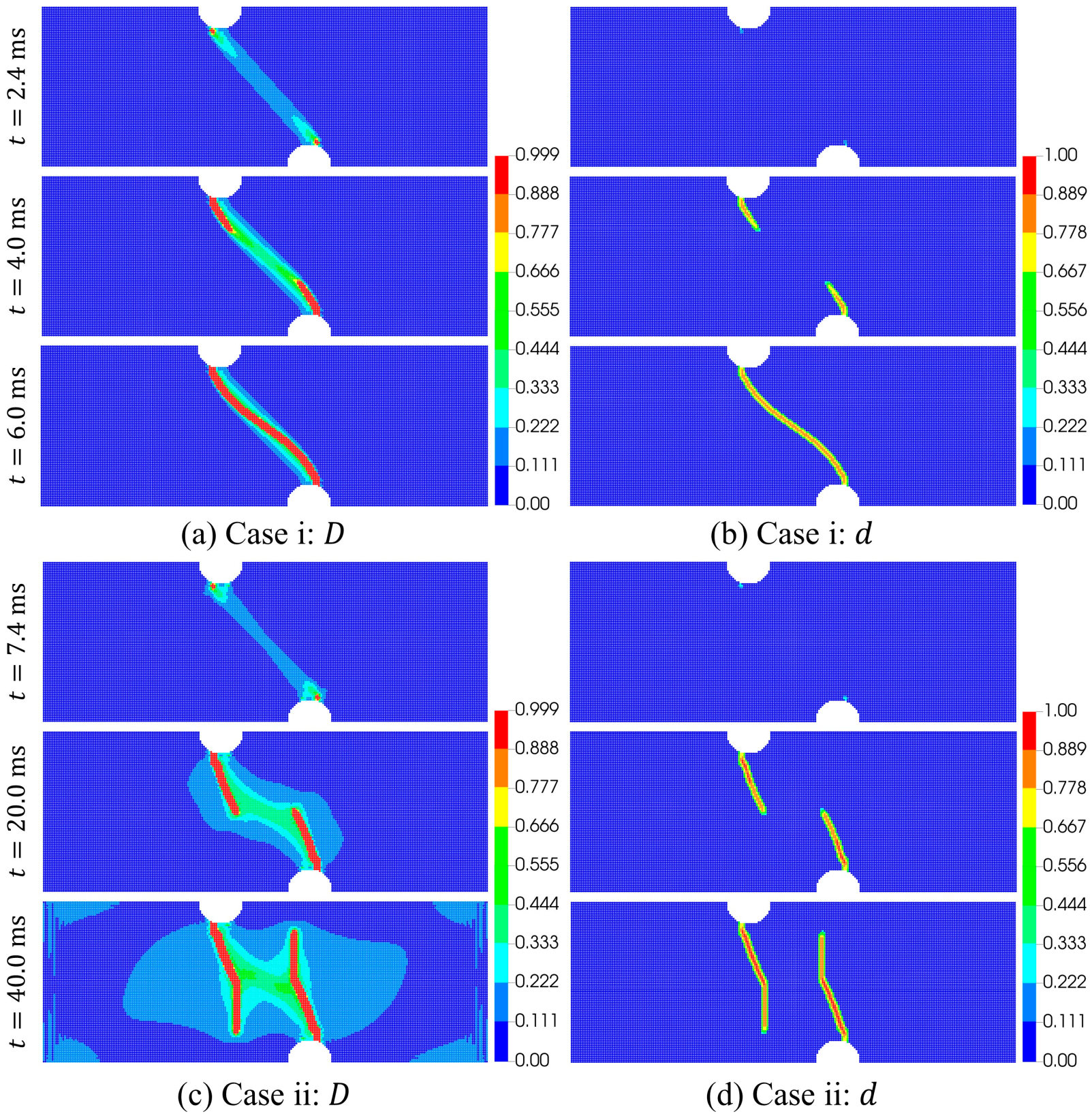
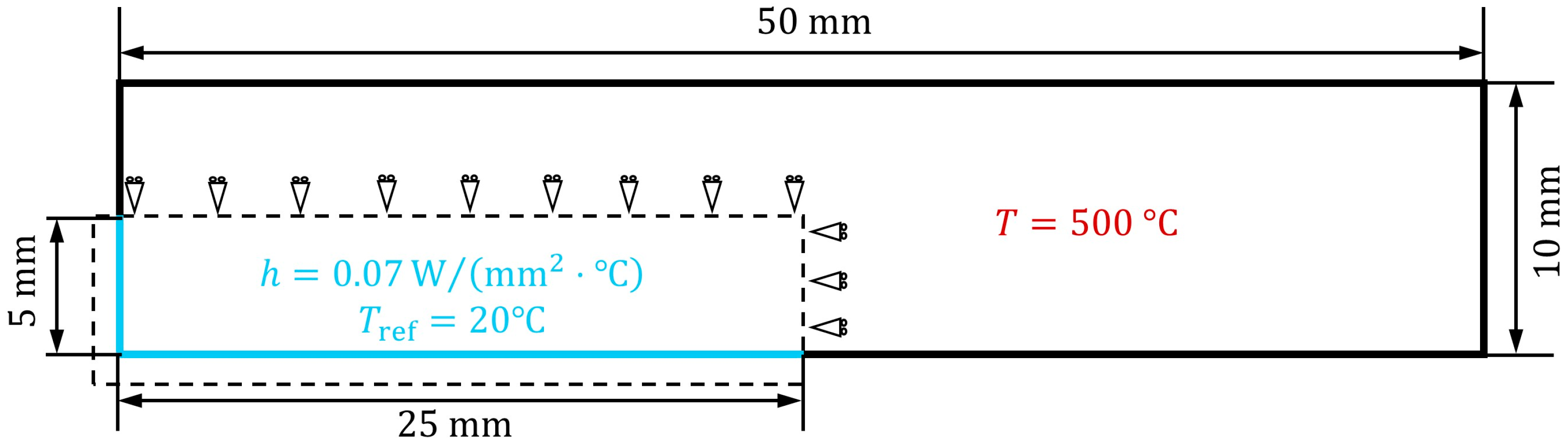
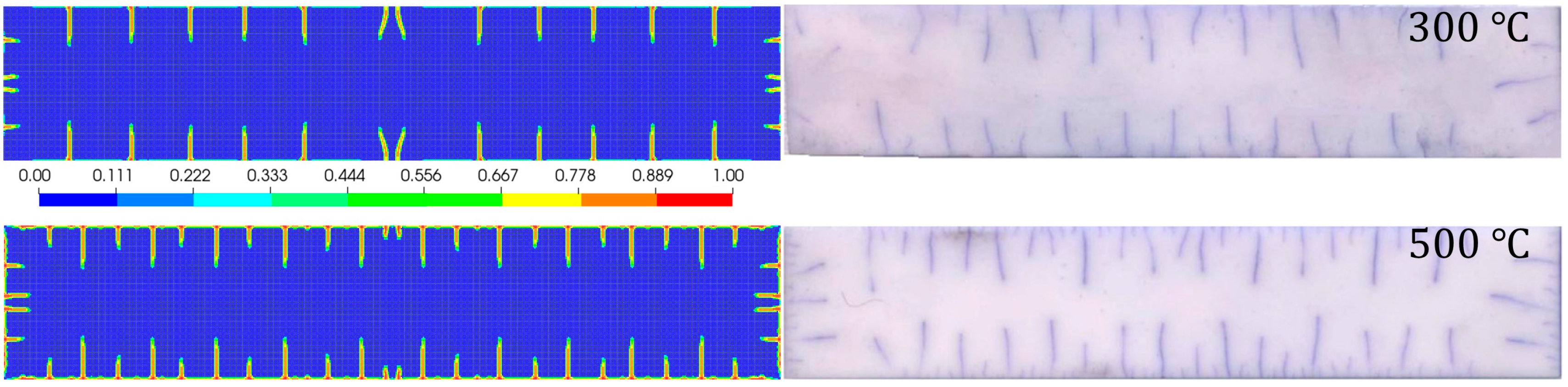
5.3. Thermal Effect in the Fracture
- The velocity of is applied to both ends of the specimen while the temperature is set to be constant.
- The specimen is fixed at both ends while a temperature change is applied.
5.4. The 2D Quenching Test
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Material points | |
| The number of material points | |
| The position in the deformed configuration | |
| The displacement vector | |
| The neighborhood horizon of | |
| The radius of the neighborhood horizon | |
| The bond between two interacting points | |
| The corresponding deformation vector state | |
| The temperature | |
| The heat temperature scalar state | |
| The density | |
| The acceleration vector | |
| The derivative of the temperature | |
| The volume associated with point | |
| The external body force | |
| The specific heat capacity | |
| The volumetric heat generation per unit mass | |
| The force vector state | |
| The heat flow scalar state | |
| The non-local deformation gradient | |
| The non-local temperature gradient | |
| The influence function | |
| The shape tensor | |
| The Cauchy stress tensor | |
| The heat flux density vector | |
| The elastic tensor | |
| The total strain tensor | |
| The plastic strain tensor | |
| The thermal strain tensor | |
| The coefficient of thermal expansion | |
| The thermal conductivity tensor | |
| The stabilized force vector state | |
| A positive constant on the order of 1 | |
| The nonuniform deformation state | |
| The stabilized heat flow scalar state | |
| The nonuniform temperature state | |
| The damage variable | |
| The yield function | |
| The von Mises equivalent stress | |
| The yield stress | |
| The accumulated plastic strain | |
| The initial yield stress | |
| The hardening parameter | |
| The incremental plastic strain | |
| The plastic multiplier | |
| The incremental damage | |
| The triaxiality function | |
| The hydrostatic pressure | |
| The critical damage value | |
| The fracture strain | |
| The corresponding strain at the beginning of damage | |
| The tensile strength | |
| Young’s modulus | |
| The scalar reflecting fracture state | |
| The bond stretch | |
| The critical value of bond stretch | |
| The fracture level | |
| The time increment | |
| The size of material points | |
| The speed of the stress wave in materials | |
| The material integrity | |
| The effective elastic trial von Mises equivalent stress | |
| he deviatoric trial stress tensor | |
| The elastic trial stress tensor | |
| The heat flux | |
| The reference temperature | |
| Poisson’s ratio | |
| The time | |
| The velocity |
References
- Bahr, H.A.; Weiss, H.J.; Maschke, H.G.; Meissner, F. Multiple crack propagation in a strip caused by thermal shock. Theor. Appl. Fract. Mech. 1988, 10, 219–226. [Google Scholar] [CrossRef]
- Tarasovs, S.; Ghassemi, A. Self-similarity and scaling of thermal shock fractures. Phys. Rev. E 2014, 90, 012403. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Song, F.; Jiang, C.P. Direct numerical simulations on crack formation in ceramic materials under thermal shock by using a non-local fracture model. J. Eur. Ceram. Soc. 2013, 33, 2677–2687. [Google Scholar] [CrossRef]
- Menouillard, T.; Belytschko, T. Analysis and computations of oscillating crack propagation in a heated strip. Int. J. Fract. 2011, 167, 57–70. [Google Scholar] [CrossRef]
- Wang, H.S. An extended element-free Galerkin method for thermo-mechanical dynamic fracture in linear and nonlinear materials. Comput. Mater. Sci. 2015, 98, 366–371. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Bui, T.Q.; Nguyen, M.N.; Truong, T.T. Meshfree thermomechanical crack growth simulations with new numerical integration scheme. Eng. Fract. Mech. 2020, 235, 107121. [Google Scholar] [CrossRef]
- Ba, K.; Gakwaya, A. Thermomechanical total Lagrangian SPH formulation for solid mechanics in large deformation problems. Comput. Methods Appl. Mech. Eng. 2018, 342, 458–473. [Google Scholar] [CrossRef]
- Chen, J.Y.; Feng, D.L.; Liu, J.H.; Yu, S.Y.; Lu, Y. Numerical modeling of the damage mechanism of concrete-soil multilayered medium subjected to underground explosion using the GPU-accelerated SPH. Eng. Anal. Boundary Elem. 2023, 151, 265–274. [Google Scholar] [CrossRef]
- Zhuo, X.R.; Ma, A.B. Molecular dynamics-based cohesive zone model for Mg/Mg17Al12 interface. Metals 2020, 10, 836. [Google Scholar] [CrossRef]
- Miehe, C.; Welschinger, F.; Hofacker, M. Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations. Int. J. Numer. Methods Eng. 2010, 83, 1273–1311. [Google Scholar] [CrossRef]
- Zhou, Q.Q.; Yang, L.; Luo, C.; Chen, F.W.; Zhou, Y.C.; Wei, Y.G. Thermal barrier coatings failure mechanism during the interfacial oxidation process under the interaction between interface by cohesive zone model and brittle fracture by phase-field. Int. J. Solids Struct. 2021, 214–215, 18–34. [Google Scholar] [CrossRef]
- Piska, R.; El-Borgi, S.; Nafees, M.; Rajagopal, A.; Reddy, J.N. A thermodynamically consistent phase field model for brittle fracture in graded coatings under thermo-mechanical loading. Theor. Appl. Fract. Mech. 2024, 131, 104414. [Google Scholar] [CrossRef]
- Song, J.H.; Wang, H.W.; Belytschko, Y. A comparative study on finite element methods for dynamic fracture. Comput. Mech. 2008, 42, 239–250. [Google Scholar] [CrossRef]
- Li, M.; Wang, B.; Hu, J.; Wang, B.; Fang, G. A non-local damage model-based FFT framework for elastic-plastic failure analysis of UD fiber-reinforced polymer composites. Compos. Commun. 2023, 43, 101730. [Google Scholar] [CrossRef]
- Silling, S.A. Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids 2000, 48, 175–209. [Google Scholar] [CrossRef]
- Silling, S.A.; Askari, E. A meshfree method based on the peridynamic model of solid mechanics. Comput. Struct. 2005, 83, 1526–1535. [Google Scholar] [CrossRef]
- Demmie, P.N.; Silling, S.A. An approach to modeling extreme loading of structures using peridynamics. J. Mech. Mater. Struct. 2007, 2, 1921–1945. [Google Scholar] [CrossRef]
- Silling, S.A.; Epton, M.; Weckner, O.; Xu, J.; Askari, E. Peridynamic states and constitutive modeling. J. Elast. 2007, 88, 151–184. [Google Scholar] [CrossRef]
- Madenci, E.; Oterkus, S. Ordinary state-based peridynamics for plastic deformation according to von Mises yield criteria with isotropic hardening. J. Mech. Phys. Solids 2016, 86, 192–219. [Google Scholar] [CrossRef]
- Madenci, E.; Oterkus, S. Ordinary state-based peridynamics for thermoviscoelastic deformation. Eng. Fract. Mech. 2017, 175, 31–45. [Google Scholar] [CrossRef]
- Wu, L.W.; Wang, L.; Huang, D.; Xu, Y.P. An ordinary state-based peridynamic modeling for dynamic fracture of laminated glass under low-velocity impact. Compos. Struct. 2020, 234, 111722. [Google Scholar] [CrossRef]
- Wu, C.T.; Ren, B. A stabilized non-ordinary state-based peridynamics for the nonlocal ductile material failure analysis in metal machining process. Comput. Methods Appl. Mech. Eng. 2015, 291, 197–215. [Google Scholar] [CrossRef]
- Hu, Y.M.; Feng, G.Q.; Li, S.F.; Sheng, W.J.; Zhang, C.Y. Numerical modelling of ductile fracture in steel plates with non-ordinary state-based peridynamics. Eng. Fract. Mech. 2019, 225, 106446. [Google Scholar] [CrossRef]
- Wu, L.W.; Wang, H.; Huang, D.; Cai, X.; Guo, J.B. A reformulated non-ordinary state-based peridynamic method for dynamic failure of ductile materials. Eng. Fract. Mech. 2023, 283, 109196. [Google Scholar] [CrossRef]
- Gu, X.; Zhang, Q.; Madenci, E. Non-ordinary state-based peridynamic simulation of elastoplastic deformation and dynamic cracking of polycrystal. Eng. Fract. Mech. 2019, 218, 106568. [Google Scholar] [CrossRef]
- Liu, Z.H.; Zhang, J.Y.; Zhang, H.B.; Ye, H.F.; Zhang, H.W.; Zheng, Y.G. Time-discontinuous state-based peridynamics for elasto-plastic dynamic fracture problems. Eng. Fract. Mech. 2022, 266, 108392. [Google Scholar] [CrossRef]
- Wang, H.; Xu, Y.P.; Huang, D. A non-ordinary state-based peridynamic formulation for thermo-visco-plastic deformation and impact fracture. Int. J. Mech. Sci. 2019, 159, 336–344. [Google Scholar] [CrossRef]
- Li, C.X.; Zhang, H.B.; Ye, H.F.; Zhang, H.W.; Zheng, Y.G. An improved stabilized peridynamic correspondence material model for the crack propagation of nearly incompressible hyperelastic materials. Comput. Methods Appl. Mech. Eng. 2023, 404, 115840. [Google Scholar] [CrossRef]
- Bobaru, F.; Duangpanya, M. The peridynamic formulation for transient heat conduction. Int. J. Heat Mass Transfer 2010, 53, 4047–4059. [Google Scholar] [CrossRef]
- Bobaru, F.; Duangpanya, M. A peridynamic formulation for transient heat conduction in bodies with evolving discontinuities. J. Comput. Phys. 2012, 231, 2764–2785. [Google Scholar] [CrossRef]
- Gao, Y.; Oterkus, S. Non-local modeling for fluid flow coupled with heat transfer by using peridynamic differential operator. Eng. Anal. Boundary Elem. 2019, 105, 104–121. [Google Scholar] [CrossRef]
- Gao, Y.; Oterkus, S. Ordinary state-based peridynamic modelling for fully coupled thermoelastic problems. Continuum Mech. Thermodyn. 2018, 31, 907–937. [Google Scholar] [CrossRef]
- Amani, J.; Oterkus, E.; Areias, P.; Zi, G.; Nguyen-Thoi, T.; Rabczuk, T. A non-ordinary state-based peridynamics formulation for thermoplastic fracture. Int. J. Impact Eng. 2016, 87, 83–94. [Google Scholar] [CrossRef]
- Li, M.Y.; Lu, W.; Oterkus, E.; Oterkus, S. Thermally-induced fracture analysis of polycrystalline materials by using peridynamics. Eng. Anal. Boundary Elem. 2020, 117, 167–187. [Google Scholar] [CrossRef]
- Madenci, E.; Barut, A.; Phan, N. Peridynamic unit cell homogenization for thermoelastic properties of heterogenous microstructures with defects. Compos. Struct. 2018, 188, 104–115. [Google Scholar] [CrossRef]
- Xue, T.; Zhang, X.B.; Tamma, K.K. A non-local dissipative Lagrangian modelling for generalized thermoelasticity in solids. Appl. Math. Modell. 2019, 73, 247–265. [Google Scholar] [CrossRef]
- Wang, Y.T.; Zhou, X.P.; Kou, M.M. An improved coupled thermo-mechanic bond-based peridynamic model for cracking behaviors in brittle solids subjected to thermal shocks. Eur. J. Mech. A-Solid 2019, 73, 282–305. [Google Scholar] [CrossRef]
- Sun, W.K.; Yin, B.B.; Akbar, A.; Kodur, V.K.R.; Liew, K.M. A coupled 3D thermo-mechanical peridynamic model for cracking analysis of homogeneous and heterogeneous materials. Comput. Methods Appl. Mech. Eng. 2024, 418, 116577. [Google Scholar] [CrossRef]
- Bazazzadeh, S.; Mossaiby, F.; Shojaei, A. An adaptive thermo-mechanical peridynamic model for fracture analysis in ceramics. Eng. Fract. Mech. 2020, 223, 106708. [Google Scholar] [CrossRef]
- Gao, Y.; Oterkus, S. Fully coupled thermomechanical analysis of laminated composites by using ordinary state based peridynamic theory. Compos. Struct. 2019, 207, 397–424. [Google Scholar] [CrossRef]
- Griffith, A.A. The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. A 1921, 221, 163–198. [Google Scholar]
- Yu, H.C.; Li, S.F. On energy release rates in peridynamics. J. Mech. Phys. Solids 2020, 142, 104024. [Google Scholar] [CrossRef]
- Madenci, E.; Oterkus, E. Peridynamic Theory and Its Applications; Springer: New York, NY, USA, 2014. [Google Scholar]
- Chen, Z.; Wan, J.; Xiu, C.X.; Chu, X.H.; Guo, X.Y. A bond-based correspondence model and its application in dynamic plastic fracture analysis for quasi-brittle materials. Theor. Appl. Fract. Mech. 2021, 113, 102941. [Google Scholar] [CrossRef]
- Warren, T.L.; Silling, S.A.; Askari, A.; Weckner, O.; Epton, M.A.; Xu, J. A non-ordinary state-based peridynamic method to model solid material deformation and fracture. Int. J. Solids Struct. 2009, 46, 1186–1195. [Google Scholar] [CrossRef]
- Yu, H.T.; Sun, Y.Q. Bridging the gap between local and nonlocal numerical methods—A unified variational framework for non-ordinary state-based peridynamics. Comput. Methods Appl. Mech. Eng. 2021, 384, 113962. [Google Scholar] [CrossRef]
- Tupek, M.R.; Rimoli, J.J.; Radovitzky, R. An approach for incorporating classical continuum damage models in state-based peridynamics. Comput. Methods Appl. Mech. Eng. 2013, 263, 20–26. [Google Scholar] [CrossRef]
- Zhang, H.B.; Li, J.Y.; Li, H.; Ye, H.F.; Zhang, H.W.; Zheng, Y.G. A coupled axisymmetric peridynamics with correspondence material model for thermoplastic and ductile fracture problems. Int. J. Fract. 2023, 244, 85–111. [Google Scholar] [CrossRef]
- Silling, S.A. Stability of peridynamic correspondence material models and their particle discretizations. Comput. Methods Appl. Mech. Eng. 2017, 322, 42–57. [Google Scholar] [CrossRef]
- Wan, J.; Chen, Z.G.; Chu, X.H.; Liu, H. Improved method for zero-energy mode suppression in peridynamic correspondence model. Acta Mech. Sin. 2019, 35, 1021–1032. [Google Scholar] [CrossRef]
- Tavoosi, M.; Sharifian, M.; Sharifian, M. A hybrid method to update stress for perfect von-Mises plasticity coupled with Lemaitre damage mechanics. Eng. Comput. 2019, 37, 705–729. [Google Scholar] [CrossRef]
- Lubliner, J. A maximum-dissipation principle in generalized plasticity. Acta Mech. 1984, 52, 225–237. [Google Scholar] [CrossRef]
- Lemaitre, J. Coupled elasto-plasticity and damage constitutive equations. Comput. Methods Appl. Mech. Eng. 1985, 51, 31–49. [Google Scholar] [CrossRef]
- Casolo, S.; Diana, V. Modelling laminated glass beam failure via stochastic rigid body-spring model and bond-based peridynamics. Eng. Fract. Mech. 2018, 190, 331–346. [Google Scholar] [CrossRef]
- Dong, Y.J.; Su, C.; Qiao, P.Z. A stability-enhanced peridynamic element to couple non-ordinary state-based peridynamics with finite element method for fracture analysis. Finite Elem. Anal. Des. 2020, 181, 103480. [Google Scholar] [CrossRef]
- de Souza Neto, E.A. A fast, one-equation integration algorithm for the Lemaitre ductile damage model. Commun. Numer. Methods Eng. 2002, 18, 541–554. [Google Scholar] [CrossRef]
- Bobaru, F.; Yang, M.J.; Alves, L.F.; Silling, S.A.; Askari, E.; Xu, J.F. Convergence, adaptive refinement, and scaling in 1D peridynamics. Int. J. Numer. Methods Eng. 2010, 77, 852–877. [Google Scholar] [CrossRef]
- Silling, S.A. Dynamic fracture modeling with a meshfree peridynamic code. In Computational Fluid and Solid Mechanics; Elsevier: Amsterdam, The Netherlands, 2003; pp. 641–644. [Google Scholar]
- Kalthoff, J.F. Modes of dynamic shear failure in solids. Int. J. Fract. 2000, 101, 1–31. [Google Scholar] [CrossRef]
- Ren, H.L.; Zhuang, X.Y.; Anitescu, C.; Rabczuk, T. An explicit phase field method for brittle dynamic fracture. Comput. Struct. 2019, 217, 45–56. [Google Scholar] [CrossRef]
- Trask, N.; You, H.Q.; Yu, Y.; Parks, M.L. An asymptotically compatible meshfree quadrature rule for nonlocal problems with applications to peridynamics. Comput. Methods Appl. Mech. Eng. 2019, 343, 151–165. [Google Scholar] [CrossRef]
- Kramer, S.L.B.; Jones, A.; Mostafa, A.; Ravaji, B.; Tancogne-Dejean, T.; Roth, C.C.; Bandpay, M.G.; Pack, K.; Foster, J.T.; Behzadinasab, M.; et al. The third Sandia fracture challenge: Predictions of ductile fracture in additively manufactured metal. Int. J. Fract. 2019, 218, 5–61. [Google Scholar] [CrossRef]
- Bogaard, R.H.; Desai, P.D.; Li, H.H.; Ho, C.Y. Thermophysical properties of stainless steels. Thermochim. Acta 1993, 218, 373–393. [Google Scholar] [CrossRef]
- Ruan, H.; Rezaei, S.; Yang, Y.; Gross, D.; Xu, B.X. A thermo-mechanical phase-field fracture model: Application to hot cracking simulations in additive manufacturing. J. Mech. Phys. Solids 2023, 172, 105169. [Google Scholar] [CrossRef]




| c | k | ||||
| c | k | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Zhang, H.; Zhang, Y.; Bai, X.; Shao, X.; Wu, B. Coupled Non-Ordinary State-Based Peridynamics Model for Ductile and Brittle Solids Subjected to Thermal Shocks. Appl. Sci. 2024, 14, 6927. https://doi.org/10.3390/app14166927
Li H, Zhang H, Zhang Y, Bai X, Shao X, Wu B. Coupled Non-Ordinary State-Based Peridynamics Model for Ductile and Brittle Solids Subjected to Thermal Shocks. Applied Sciences. 2024; 14(16):6927. https://doi.org/10.3390/app14166927
Chicago/Turabian StyleLi, Hui, Hanbo Zhang, Yixiong Zhang, Xiaoming Bai, Xuejiao Shao, and Bingyang Wu. 2024. "Coupled Non-Ordinary State-Based Peridynamics Model for Ductile and Brittle Solids Subjected to Thermal Shocks" Applied Sciences 14, no. 16: 6927. https://doi.org/10.3390/app14166927





