Proposal of a Design Procedure for Steel Frames with Viscoelastic Dampers
Abstract
:Featured Application
Abstract
1. Introduction
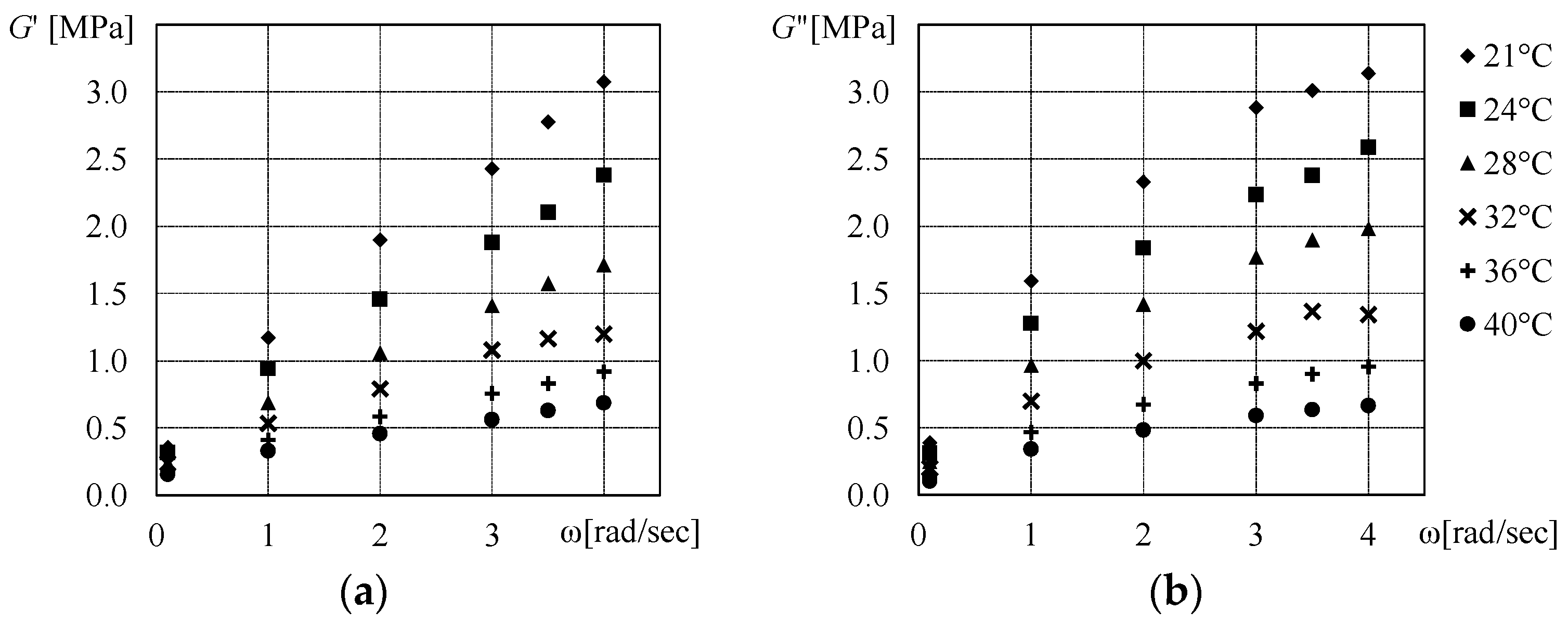
2. Dynamic Characteristics of Viscoelastic Materials
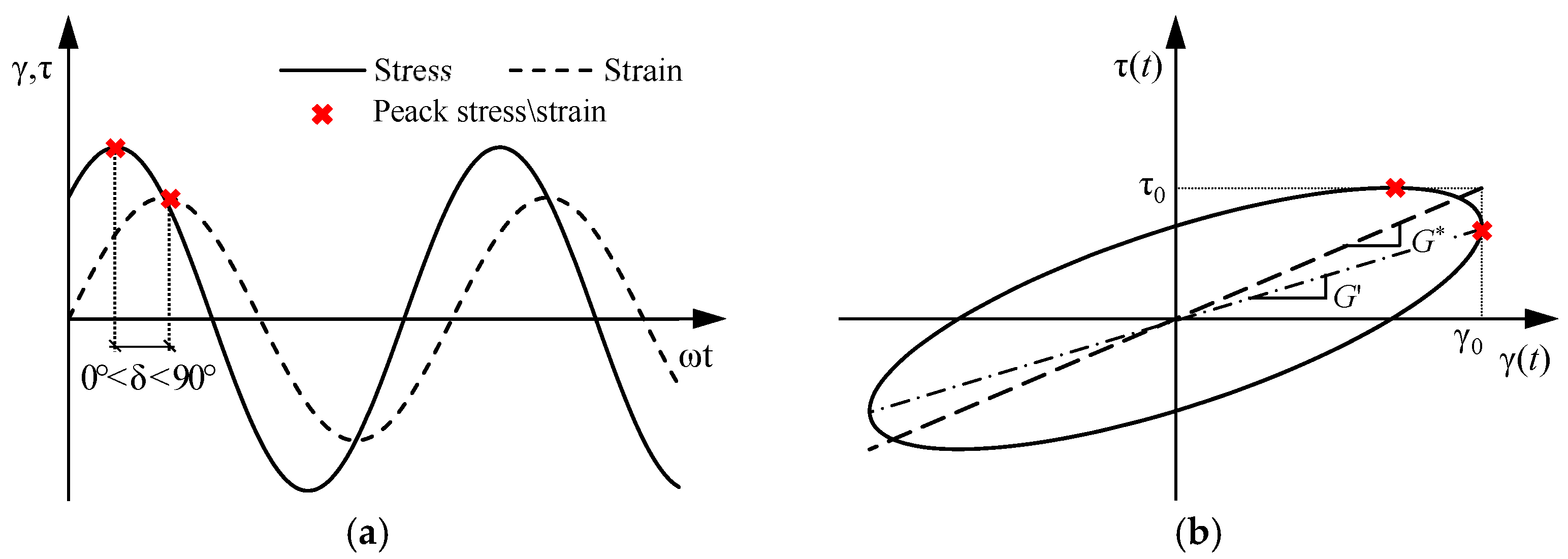
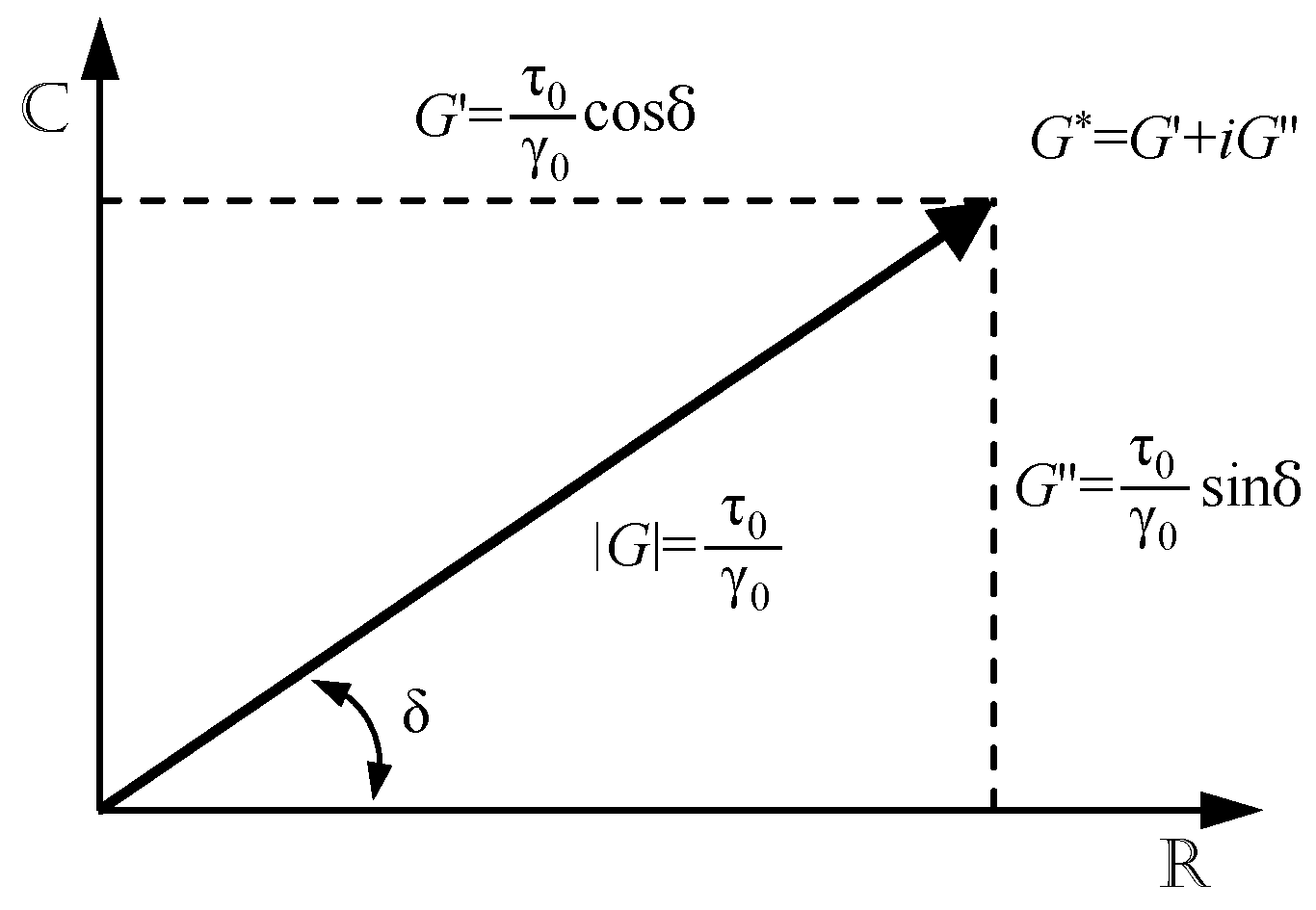
3. Numerical Model of Viscoelastic Dampers
3.1. Generalized Maxwell Model

| γ0 = 100% | f [Hz] | |||
|---|---|---|---|---|
| 0.1 | 0.3 | 1.0 | 2.0 | |
| G’ [MPa] | 0.123 | 0.191 | 0.327 | 0.446 |
| G” [MPa] | 0.101 | 0.183 | 0.366 | 0.517 |
| η [-] | 0.82 | 0.96 | 1.12 | 1.16 |
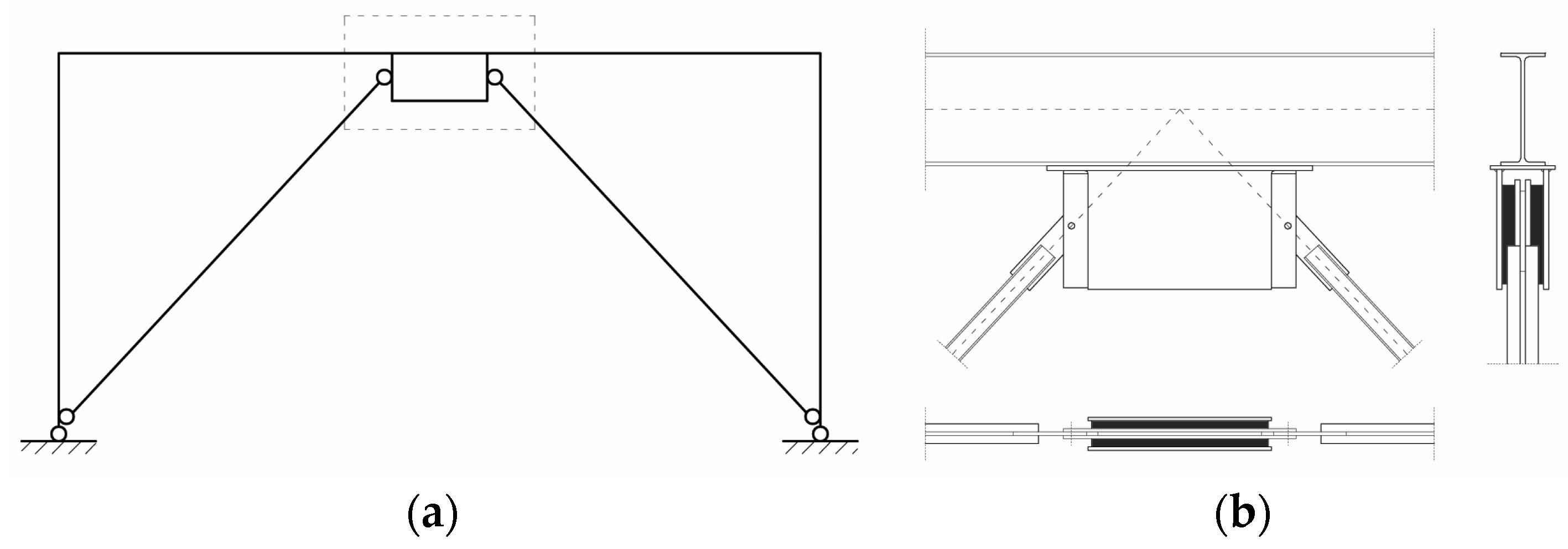
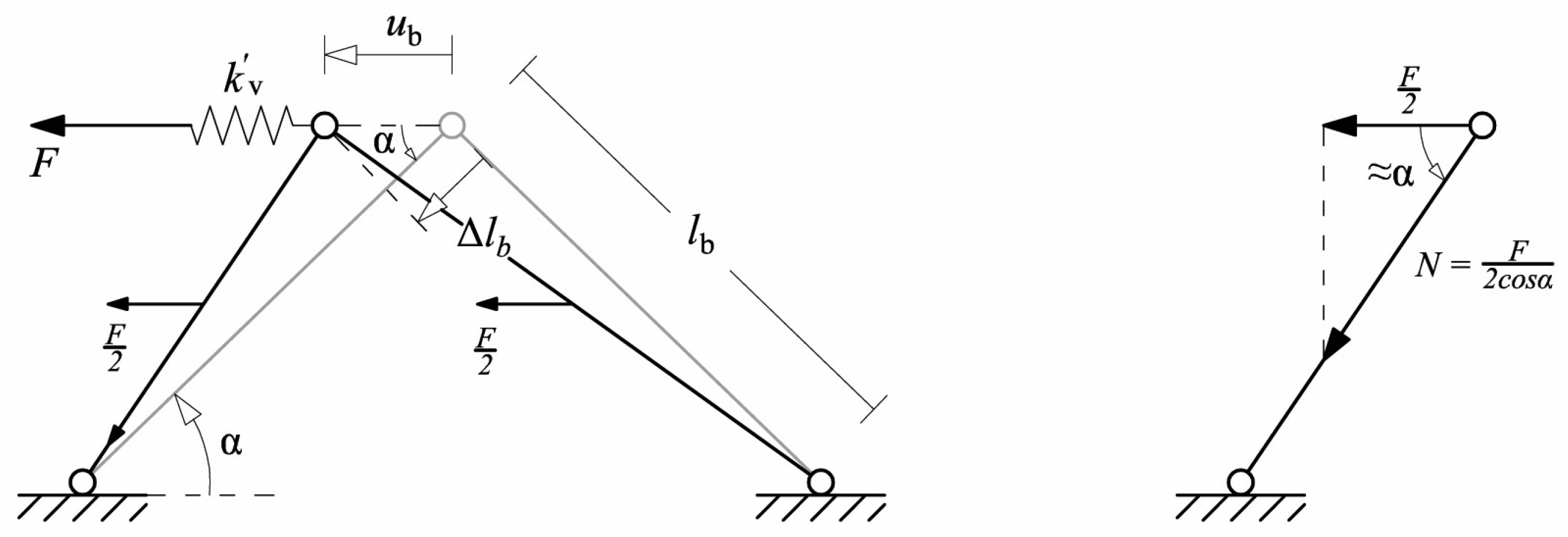
3.2. Equivalent Brace Model
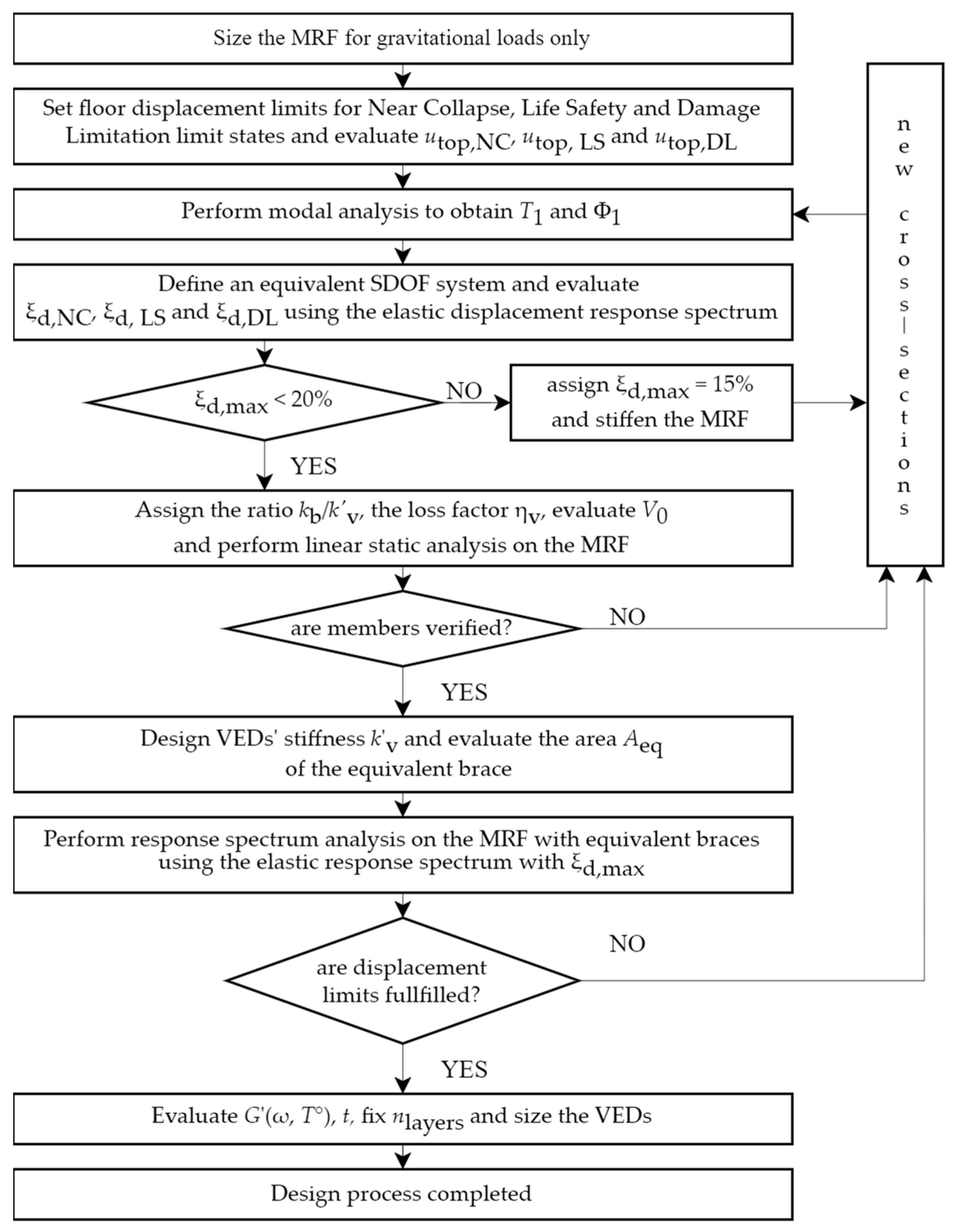
4. Proposed Design Procedure
4.1. Design of the MRF
4.2. Design of the Braces
4.3. Check on Drift Limits
4.4. Design of the VEDs
5. Application to a Case Study
5.1. Numerical Model for Design Analyses

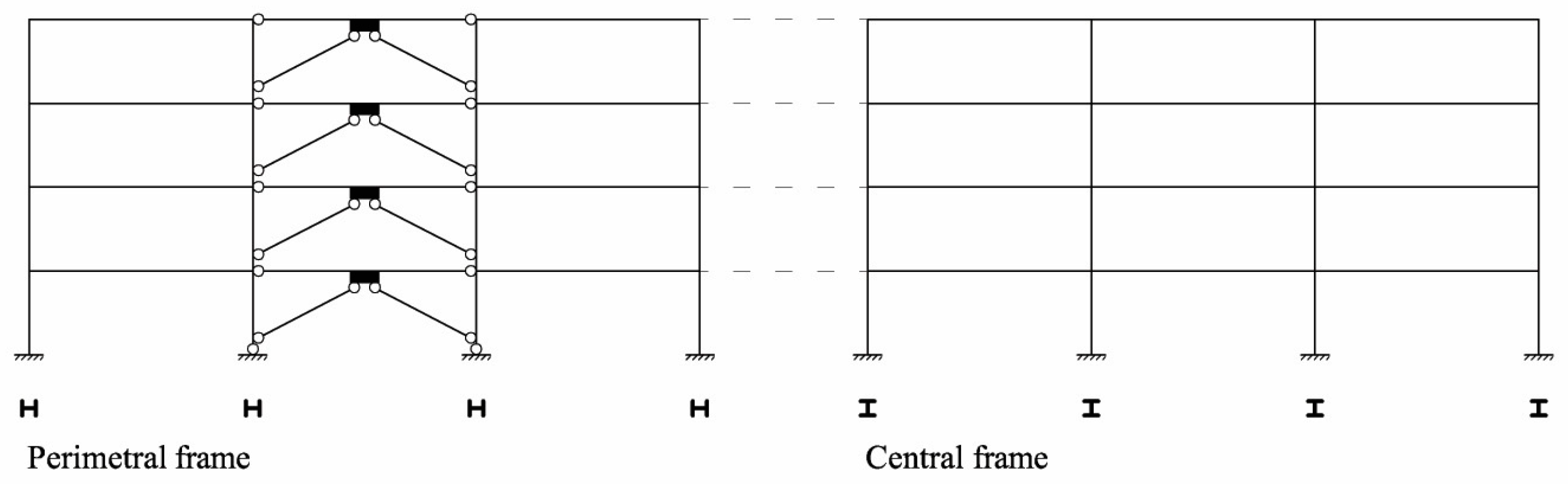
5.2. Design of the MRF
5.3. Design of the Braces
| Piano | αMSE [-] | k0,I [kN/mm] | kv-b,I [kN/mm] | k’v,I [kN/mm] |
|---|---|---|---|---|
| 1 | 0.162 | 21.599 | 3.490 | 3.494 |
| 2 | 17.824 | 2.880 | 2.883 | |
| 3 | 12.767 | 2.063 | 2.065 | |
| 4 | 11.777 | 1.903 | 1.905 |
5.4. Check on Drift Limits
5.5. Design of the VEDs
| Floor | T1 [s] | G’ [N/mm2] | t [mm] | nl | Al,i [cm2] | bl × hl [cm] |
|---|---|---|---|---|---|---|
| 1 | 1.548 | 0.268 | 25.7 | 4 | 838.80 | 42 × 20 |
| 2 | 692.19 | 35 × 20 | ||||
| 3 | 495.79 | 25 × 20 | ||||
| 4 | 457.38 | 23 × 20 |
6. Nonlinear Dynamic Analyses
- The values of the PGA corresponding to the achievement of yielding, or buckling of the members of the MRF and to the limit displacement established for the VEDs;
- The lateral story displacements;
- The internal forces in the dampers, braces, and C0-columns.
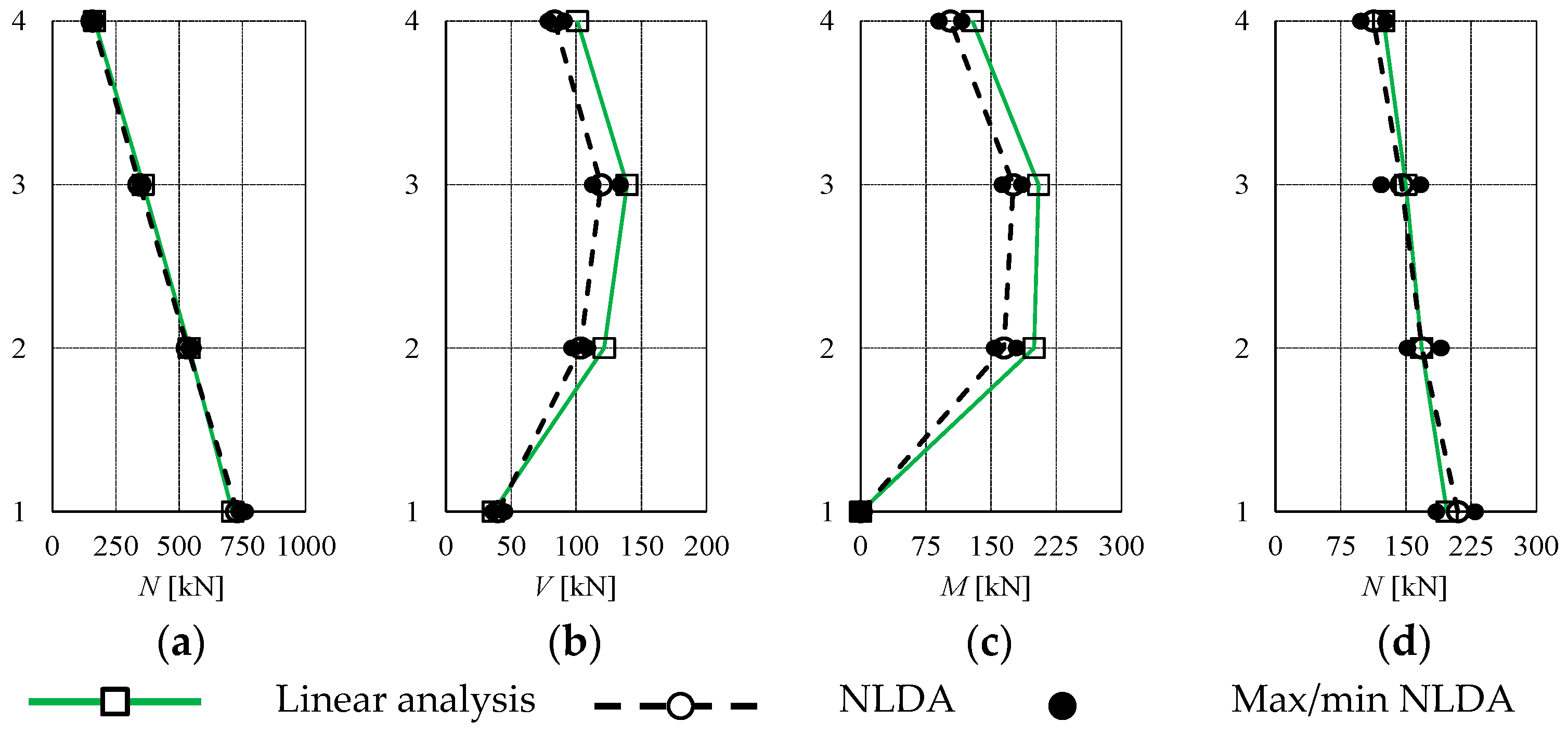
6.1. Seismic Response of the Case Study
6.2. Seismic Response of the Other Buildings
| Case | PGASD | PGANC | PGAbeams | PGAcolMRF | PGAVED | |
|---|---|---|---|---|---|---|
| 4-story | Soil A | 0.250 | 0.429 | 0.241 | - | 0.443 |
| 0.350 | 0.600 | 0.309 | - | 0.603 | ||
| Soil C | 0.250 | 0.429 | 0.273 | - | 0.437 | |
| 0.350 | 0.600 | 0.340 | - | 0.541 | ||
| 6-story | Soil A | 0.250 | 0.429 | 0.330 | 0.312 | 0.544 |
| 0.350 | 0.600 | 0.341 | 0.386 | 0.572 | ||
| Soil C | 0.250 | 0.429 | 0.222 | 0.273 | 0.376 | |
| 0.350 | 0.600 | 0.292 | - | 0.513 | ||
| 8-story | Soil A | 0.250 | 0.429 | 0.304 | 0.361 | 0.505 |
| 0.350 | 0.600 | 0.353 | 0.432 | 0.560 | ||
| Soil C | 0.250 | 0.429 | 0.223 | 0.291 | 0.357 | |
| 0.350 | 0.600 | 0.281 | 0.372 | 0.489 | ||
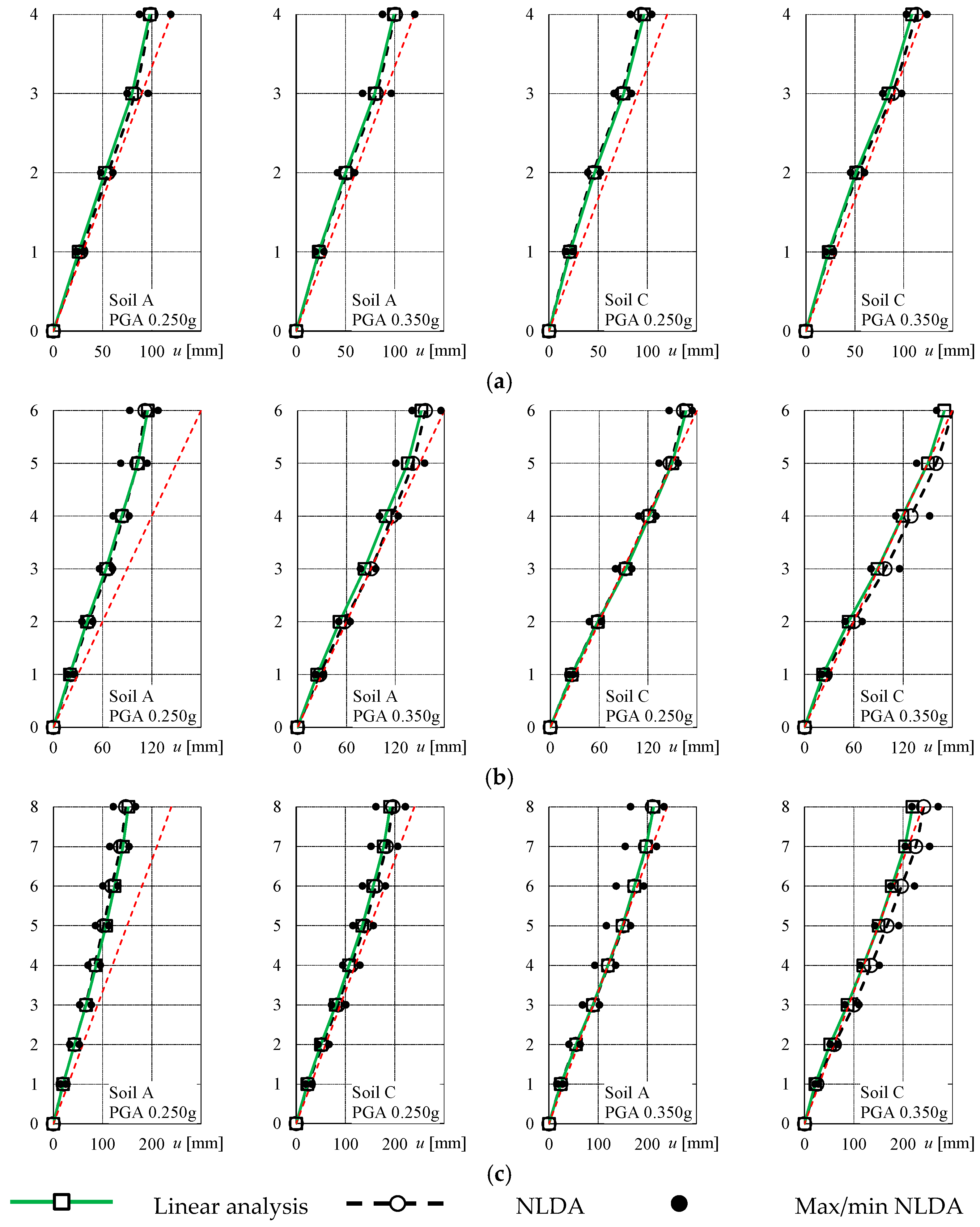
7. Conclusions
- The fulfillment of the main design objective, i.e., the control of the story drifts below prefixed limits, is achieved for all cases. At the same time, the internal forces of the braces and of the other members of the MRF are well predicted. This proves the effectiveness of the procedure based on the MSE method.
- The GMM4 model is effective in reproducing the hysteretic behavior of the VEDs as a function of frequency and for a given ambient temperature.
- VEDs are effective in conferring the demanded damping to the structure, although in the cases in which high damping is demanded, at least one of the dampers of the dissipative system exceeds the maximum allowed displacement for a value of the PGA that is lower than the expected value.
- Optimal arrangement of the dampers in the structure;
- Comparison of the seismic performance and construction costs of the frames designed by means of the proposed procedure with those of the frames designed by means of other procedures available in the literature;
- Study of the response of viscoelastically damped structures in the case of near-fault design scenarios.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
| Floor | Columns | Beams | Braces | |||
|---|---|---|---|---|---|---|
| C0 | C1 | C2 | Braced bay | MRF | ||
| 4 Stories, Soil A, PGA 0.25 g | ||||||
| 4 | HEB 220 | HEB 160 | HEB 200 | IPE 300 * | IPE 360 * | HEB 120 ** |
| 3 | HEB 220 | HEB 160 | HEB 200 | IPE 300 * | IPE 360 * | HEB 120 ** |
| 2 | HEB 220 | HEB 180 | HEB 360 | IPE 300 * | IPE 360 * | HEB 120 ** |
| 1 | HEB 220 | HEB 180 | HEB 360 | IPE 300 * | IPE 360 * | HEB 140 ** |
| 4 Stories, Soil A, PGA 0.35 g | ||||||
| 4 | HEB 240 | HEB 180 | HEB 240 | IPE 300 * | IPE 360 * | HEB 140 ** |
| 3 | HEB 240 | HEB 180 | HEB 240 | IPE 300 * | IPE 360 * | HEB 140 ** |
| 2 | HEB 260 | HEB 220 | HEM 300 | IPE 300 * | IPE 360 * | HEB 160 ** |
| 1 | HEB 260 | HEB 220 | HEM 300 | IPE 300 * | IPE 360 * | HEB 200 ** |
| 4 Stories, Soil C, PGA 0.25 g | ||||||
| 4 | HEB 260 | HEB 180 | HEB 260 | IPE 300 * | IPE 360 * | HEB 140 ** |
| 3 | HEB 260 | HEB 180 | HEB 260 | IPE 300 * | IPE 360 * | HEB 160 ** |
| 2 | HEB 280 | HEB 240 | HEM 300 | IPE 300 * | IPE 400 * | HEB 200 ** |
| 1 | HEB 280 | HEB 240 | HEM 300 | IPE 300 * | IPE 400 * | HEB 240 ** |
| 4 Stories, Soil C, PGA 0.35 g | ||||||
| 4 | HEB 280 | HEB 180 | HEB 260 | IPE 300 * | IPE 360 * | HEB 180 ** |
| 3 | HEB 280 | HEB 180 | HEB 260 | IPE 300 * | IPE 360 * | HEB 200 ** |
| 2 | HEB 300 | HEB 260 | HEM 300 | IPE 300 * | IPE 400 * | HEB 260 ** |
| 1 | HEB 300 | HEB 260 | HEM 300 | IPE 300 * | IPE 400 * | HEB 300 ** |
| Floor | γ [%] | tl [mm] | nl [-] | k’v [kN/mm] | T1 [s] | G’ [N/mm2] | Ai [cm2] | ξadd [%] |
|---|---|---|---|---|---|---|---|---|
| 4 Stories, Soil A, PGA 0.25 g | ||||||||
| 4 | 200 | 25.7 | 4 | 2.0321 | 1.541 | 0.268 | 486.74 | 7 |
| 3 | 4 | 2.2027 | 527.61 | |||||
| 2 | 4 | 3.0753 | 736.63 | |||||
| 1 | 4 | 3.7266 | 892.64 | |||||
| 4 Stories, Soil A, PGA 0.35 g | ||||||||
| 4 | 200 | 25.7 | 4 | 3.5618 | 1.273 | 0.293 | 781.48 | 9.5 |
| 3 | 4 | 4.2573 | 934.09 | |||||
| 2 | 4 | 7.1050 | 1558.90 | |||||
| 1 | 4 | 9.2980 | 2040.05 | |||||
| 4 Stories, Soil C, PGA 0.25 g | ||||||||
| 4 | 200 | 25.7 | 4 | 5.2586 | 1.124 | 0.311 | 1087.76 | 11.5 |
| 3 | 4 | 6.3045 | 1304.12 | |||||
| 2 | 4 | 9.6773 | 2001.81 | |||||
| 1 | 4 | 12.9529 | 2679.38 | |||||
| 4 Stories, Soil C, PGA 0.35 g | ||||||||
| 4 | 200 | 25.7 | 4 | 7.7447 | 1.039 | 0.323 | 1543.77 | 15 |
| 3 | 4 | 9.5688 | 1907.35 | |||||
| 2 | 4 | 14.7518 | 2940.50 | |||||
| 1 | 4 | 20.2874 | 4043.90 | |||||
| Floor | Columns | Beams | Braces | |||
|---|---|---|---|---|---|---|
| C0 | C1 | C2 | Braced bay | MRF | ||
| 6 Stories, Soil A, PGA 0.25 g | ||||||
| 6 | HEB 180 | HEB 140 | HEB 200 | IPE 300 * | IPE 360 * | HEB 120 ** |
| 5 | HEB 180 | HEB 140 | HEB 200 | IPE 300 * | IPE 360 * | HEB 120 ** |
| 4 | HEB 200 | HEB 160 | HEB 240 | IPE 300 * | IPE 360 * | HEB 120 ** |
| 3 | HEB 200 | HEB 160 | HEB 240 | IPE 300 * | IPE 360 * | HEB 120 ** |
| 2 | HEB 220 | HEB 180 | HEB 300 | IPE 300 * | IPE 360 * | HEB 120 ** |
| 1 | HEB 220 | HEB 180 | HEB 300 | IPE 300 * | IPE 360 * | HEB 140 ** |
| 6 Stories, Soil A, PGA 0.35 g | ||||||
| 6 | HEB 200 | HEB 140 | HEB 200 | IPE 300 * | IPE 360 * | HEB 120 ** |
| 5 | HEB 200 | HEB 140 | HEB 200 | IPE 300 * | IPE 360 * | HEB 140 ** |
| 4 | HEB 240 | HEB 180 | HEB 240 | IPE 300 * | IPE 360 * | HEB 140 ** |
| 3 | HEB 240 | HEB 180 | HEB 240 | IPE 300 * | IPE 360 * | HEB 140 ** |
| 2 | HEB 260 | HEB 220 | HEB 320 | IPE 300 * | IPE 360 * | HEB 140 ** |
| 1 | HEB 260 | HEB 220 | HEB 320 | IPE 300 * | IPE 360 * | HEB 160 ** |
| 6 Stories, Soil C, PGA 0.25 g | ||||||
| 6 | HEB 220 | HEB 160 | HEB 220 | IPE 300 * | IPE 360 * | HEB 140 ** |
| 5 | HEB 220 | HEB 160 | HEB 220 | IPE 300 * | IPE 360 * | HEB 140 ** |
| 4 | HEB 260 | HEB 200 | HEB 260 | IPE 300 * | IPE 360 * | HEB 140 ** |
| 3 | HEB 260 | HEB 200 | HEB 260 | IPE 300 * | IPE 360 * | HEB 160 ** |
| 2 | HEB 280 | HEB 240 | HEB 320 | IPE 300 * | IPE 360 * | HEB 160 ** |
| 1 | HEB 280 | HEB 240 | HEB 320 | IPE 300 * | IPE 360 * | HEB 200 ** |
| 6 Stories, Soil C, PGA 0.35 g | ||||||
| 6 | HEB 240 | HEB 200 | HEB 220 | IPE 300 * | IPE 360 * | HEB 160 ** |
| 5 | HEB 240 | HEB 200 | HEB 220 | IPE 300 * | IPE 360 * | HEB 180 ** |
| 4 | HEB 280 | HEB 240 | HEB 280 | IPE 300 * | IPE 400 * | HEB 200 ** |
| 3 | HEB 280 | HEB 240 | HEB 280 | IPE 300 * | IPE 400 * | HEB 200 ** |
| 2 | HEB 300 | HEB 340 | HEB 340 | IPE 300 * | IPE 400 * | HEB 240 ** |
| 1 | HEB 300 | HEB 340 | HEB 340 | IPE 300 * | IPE 400 * | HEB 280 ** |
| Floor | γ [%] | tl [mm] | nl [-] | k’v [kN/mm] | T1 [s] | G’ [N/mm2] | Ai [cm2] | ξadd [%] | |
|---|---|---|---|---|---|---|---|---|---|
| 4 Stories, Soil A, PGA 0.25 g | |||||||||
| 6 | 200 | 25.7 | 4 | 1.8232 | 2.326 | 0.225 | 520.11 | 10 | |
| 5 | 4 | 1.8755 | 535.06 | ||||||
| 4 | 4 | 3.1539 | 899.77 | ||||||
| 3 | 4 | 3.2270 | 920.62 | ||||||
| 2 | 4 | 4.1055 | 1171.23 | ||||||
| 1 | 4 | 4.5794 | 1306.43 | ||||||
| 4 Stories, Soil A, PGA 0.35 g | |||||||||
| 6 | 200 | 25.7 | 4 | 2.6487 | 2.108 | 0.235 | 725.87 | 10 | |
| 5 | 4 | 2.7978 | 766.72 | ||||||
| 4 | 4 | 3.9674 | 1087.25 | ||||||
| 3 | 4 | 4.1353 | 1133.26 | ||||||
| 2 | 4 | 5.3604 | 1468.99 | ||||||
| 1 | 4 | 6.8299 | 1871.70 | ||||||
| 4 Stories, Soil C, PGA 0.25 g | |||||||||
| 6 | 200 | 25.7 | 4 | 3.5385 | 1.948 | 0.242 | 938.38 | 12 | |
| 5 | 4 | 3.8398 | 1018.29 | ||||||
| 4 | 4 | 5.1871 | 1375.56 | ||||||
| 3 | 4 | 5.4881 | 1455.38 | ||||||
| 2 | 4 | 7.1881 | 1906.21 | ||||||
| 1 | 4 | 9.5327 | 2527.98 | ||||||
| 4 Stories, Soil C, PGA 0.35 g | |||||||||
| 6 | 200 | 25.7 | 4 | 6.1181 | 1.496 | 0.272 | 1446.15 | 15 | |
| 5 | 4 | 7.6185 | 1800.80 | ||||||
| 4 | 4 | 11.3658 | 2686.56 | ||||||
| 3 | 4 | 12.1210 | 2865.07 | ||||||
| 2 | 4 | 15.6574 | 3700.98 | ||||||
| 1 | 4 | 22.9575 | 5426.54 | ||||||
| Floor | Columns | Beams | Braces | |||
|---|---|---|---|---|---|---|
| C0 | C1 | C2 | Braced bay | MRF | ||
| 8 Stories, Soil A, PGA 0.25 g | ||||||
| 8 | HEB 200 | HEB 140 | HEB 220 | IPE 300 * | IPE 360 * | HEB 120 ** |
| 7 | HEB 200 | HEB 140 | HEB 220 | IPE 300 * | IPE 360 * | HEB 120 ** |
| 6 | HEB 220 | HEB 160 | HEB 260 | IPE 300 * | IPE 360 * | HEB 120 ** |
| 5 | HEB 220 | HEB 160 | HEB 260 | IPE 300 * | IPE 360 * | HEB 120 ** |
| 4 | HEB 240 | HEB 180 | HEB 300 | IPE 300 * | IPE 360 * | HEB 120 ** |
| 3 | HEB 240 | HEB 180 | HEB 300 | IPE 300 * | IPE 360 * | HEB 120 ** |
| 2 | HEB 260 | HEB 220 | HEB 360 | IPE 300 * | IPE 360 * | HEB 120 ** |
| 1 | HEB 260 | HEB 220 | HEB 360 | IPE 300 * | IPE 360 * | HEB 140 ** |
| 8 Stories, Soil A, PGA 0.35 g | ||||||
| 8 | HEB 200 | HEB 140 | HEB 220 | IPE 300 * | IPE 360 * | HEB 120 ** |
| 7 | HEB 200 | HEB 140 | HEB 220 | IPE 300 * | IPE 360 * | HEB 120 ** |
| 6 | HEB 220 | HEB 160 | HEB 260 | IPE 300 * | IPE 360 * | HEB 140 ** |
| 5 | HEB 220 | HEB 160 | HEB 260 | IPE 300 * | IPE 360 * | HEB 140 ** |
| 4 | HEB 240 | HEB 180 | HEB 300 | IPE 300 * | IPE 360 * | HEB 160 ** |
| 3 | HEB 240 | HEB 180 | HEB 300 | IPE 300 * | IPE 360 * | HEB 160 ** |
| 2 | HEB 280 | HEB 240 | HEB 360 | IPE 300 * | IPE 360 * | HEB 180 ** |
| 1 | HEB 280 | HEB 240 | HEB 360 | IPE 300 * | IPE 360 * | HEB 220 ** |
| 8 Stories, Soil C, PGA 0.25 g | ||||||
| 8 | HEB 200 | HEB 140 | HEB 220 | IPE 300 * | IPE 360 * | HEB 140 ** |
| 7 | HEB 200 | HEB 140 | HEB 220 | IPE 300 * | IPE 360 * | HEB 140 ** |
| 6 | HEB 220 | HEB 180 | HEB 260 | IPE 300 * | IPE 360 * | HEB 160 ** |
| 5 | HEB 220 | HEB 180 | HEB 260 | IPE 300 * | IPE 360 * | HEB 160 ** |
| 4 | HEB 240 | HEB 180 | HEB 300 | IPE 300 * | IPE 360 * | HEB 180 ** |
| 3 | HEB 240 | HEB 180 | HEB 300 | IPE 300 * | IPE 360 * | HEB 200 ** |
| 2 | HEB 280 | HEB 260 | HEB 360 | IPE 300 * | IPE 360 * | HEB 220 ** |
| 1 | HEB 280 | HEB 260 | HEB 360 | IPE 300 * | IPE 360 * | HEB 260 ** |
| 8 Stories, Soil C, PGA 0.35 g | ||||||
| 8 | HEB 220 | HEB 180 | HEB 220 | IPE 300 * | IPE 400 * | HEB 160 ** |
| 7 | HEB 220 | HEB 180 | HEB 220 | IPE 300 * | IPE 400 * | HEB 160 ** |
| 6 | HEB 260 | HEB 200 | HEB 280 | IPE 300 * | IPE 400 * | HEB 180 ** |
| 5 | HEB 260 | HEB 200 | HEB 280 | IPE 300 * | IPE 400 * | HEB 180 ** |
| 4 | HEB 280 | HEB 220 | HEB 320 | IPE 300 * | IPE 400 * | HEB 220 ** |
| 3 | HEB 280 | HEB 220 | HEB 320 | IPE 300 * | IPE 400 * | HEB 220 ** |
| 2 | HEB 320 | HEB 360 | HEB 400 | IPE 300 * | IPE 400 * | HEB 260 ** |
| 1 | HEB 320 | HEB 360 | HEB 400 | IPE 300 * | IPE 400 * | HEB 320 ** |
| Floor | γ [%] | tl [mm] | nl [-] | k’v [kN/mm] | T1 [s] | G’ [N/mm2] | Ai [cm2] | ξadd [%] |
|---|---|---|---|---|---|---|---|---|
| 8 Stories, Soil A, PGA 0.25 g | ||||||||
| 8 | 200 | 25.7 | 4 | 0.9364 | 2.898 | 0.206 | 291.72 | 5 |
| 7 | 4 | 0.9945 | 309.83 | |||||
| 6 | 4 | 1.5977 | 497.74 | |||||
| 5 | 4 | 1.6458 | 512.73 | |||||
| 4 | 4 | 1.9597 | 610.52 | |||||
| 3 | 4 | 1.9979 | 622.41 | |||||
| 2 | 4 | 2.3373 | 728.16 | |||||
| 1 | 4 | 2.9864 | 930.36 | |||||
| 8 Stories, Soil A, PGA 0.35 g | ||||||||
| 8 | 200 | 25.7 | 4 | 2.0529 | 2.759 | 0.21 | 627.14 | 8 |
| 7 | 4 | 2.1806 | 666.15 | |||||
| 6 | 4 | 2.7679 | 845.56 | |||||
| 5 | 4 | 2.8301 | 864.56 | |||||
| 4 | 4 | 3.3709 | 1029.76 | |||||
| 3 | 4 | 3.4469 | 1052.96 | |||||
| 2 | 4 | 4.2593 | 1301.14 | |||||
| 1 | 4 | 5.6326 | 1720.68 | |||||
| 8 Stories, Soil C, PGA 0.25 g | ||||||||
| 8 | 200 | 25.7 | 4 | 2.6984 | 2.665 | 0.213 | 812.98 | 10 |
| 7 | 4 | 2.8663 | 863.55 | |||||
| 6 | 4 | 3.6385 | 1096.19 | |||||
| 5 | 4 | 3.7200 | 1120.76 | |||||
| 4 | 4 | 4.4310 | 1334.97 | |||||
| 3 | 4 | 4.5306 | 1364.98 | |||||
| 2 | 4 | 5.5989 | 1686.81 | |||||
| 1 | 4 | 7.4037 | 2230.57 | |||||
| 8 Stories, Soil C, PGA 0.25 g | ||||||||
| 8 | 200 | 25.7 | 4 | 5.4841 | 2.069 | 0.236 | 1491.25 | 15 |
| 7 | 4 | 5.8908 | 1601.83 | |||||
| 6 | 4 | 7.8005 | 2121.13 | |||||
| 5 | 4 | 8.8216 | 2398.78 | |||||
| 4 | 4 | 11.0738 | 3011.18 | |||||
| 3 | 4 | 11.5056 | 3128.60 | |||||
| 2 | 4 | 14.6208 | 3975.70 | |||||
| 1 | 4 | 21.2937 | 5790.19 | |||||
References
- EN 1998-1-1; Eurocode 8—Design of Structures for Earthquake Resistance—Part 1-1: General Rules, Seismic Action and Rules for Buildings. European Committee for Standardization: Bruxelles, Belgium, 2005.
- Christopoulos, C.; Filiatrault, A. Principles of Passive Supplemental Damping and Seismic Isolation; IUSS Press: Pavia, Italy, 2006; Volume 133, p. 1192. [Google Scholar]
- Sadek, F.; Mohraz, B.; Taylor, A.W.; Chung, R.M. Passive Energy Dissipation Devices for Seismic Applications; US Department of Commerce, National Institute of Standards and Technology: Gaithersburg, MD, USA, 1996. [Google Scholar]
- Symans, M.D.; Charney, F.A.; Whittaker, A.S.; Constantinou, M.C.; Kircher, C.A.; Johnson, M.W.; McNamara, R.J. Energy Dissipation Systems for Seismic Applications: Current Practice and Recent Developments. J. Struct. Eng. 2008, 134, 3–21. [Google Scholar] [CrossRef]
- Titirla, M.D. A State-of-the-Art Review of Passive Energy Dissipation Systems in Steel Braces. Buildings 2023, 13, 851. [Google Scholar] [CrossRef]
- Kasai, K.; Fu, Y.; Watanabe, A. Passive Control Systems for Seismic Damage Mitigation. J. Struct. Eng. 1998, 124, 501–512. [Google Scholar] [CrossRef]
- Mazza, F.; Vulcano, A. Control of the earthquake and wind dynamic response of steel-framed buildings by using additional braces and/or viscoelastic dampers. Earthq. Eng. Struct. Dyn. 2011, 40, 155–174. [Google Scholar] [CrossRef]
- Chang, K.; Soong, T.T.; Oh, S.-T.; Lai, M.L. Seismic Response of a 2/5 Scale Steel Structure with Added Viscoelastic Dampers; Technical Report NCEER 91-0012; State University of New York: Buffalo, NY, USA, 1991. [Google Scholar]
- Kulak, R.F.; Hughes, T.H. Frequency and Temperature Dependence of High Damping Elastomers. Report No. ANL/RE/CP-78944; CONF-930803-22; CONF-930803-22; Argonne National Lab.: Lemont, IL, USA, 1993. [Google Scholar]
- Shen, K.L.; Soong, T.T. Modeling of Viscoelastic Dampers for Structural Applications. J. Eng. Mech. 1995, 121, 694–701. [Google Scholar] [CrossRef]
- Inaudi, J.A.; Blondet, M.; Kelly, J.M. Heat Generation Effects on Viscoelastic Dampers in Structures. In Proceedings of the 11th World Conference on Earthquake Engineering, Acapulco, Mexico, 23–28 June 1996. [Google Scholar]
- Dall’Asta, A.; Ragni, L. Experimental tests and analytical model of high damping rubber dissipating devices. Eng. Struct. 2006, 28, 1874–1884. [Google Scholar] [CrossRef]
- Lai, M.L.; Lu, P.; Lunsford, D.A.; Kasai, K.; Chang, K.C. Viscoelastic damper: A damper with linear or nonlinear material? In Proceedings of the 11th World Conference on Earthquake Engineering, Acapulco, Mexico, 23–28 June 1996.
- Lai, M.L.; Kasai, K.; Chang, K. Relationship between temperature rise and nonlinearity of a viscoelastic damper. ISET J. Earthq. Technol. 1999, 36, 61–71. [Google Scholar]
- Blondet, M. Dynamic Response of Two Viscoelastic Dampers; Report to County of Santa Clara Construction Services Division; Service to Industry, Project No. ES-2046; Department of Civil Engineering, University of California at Berkeley: Berkeley, CA, USA, 1993. [Google Scholar]
- Crosby, P.; Kelly, J.M.; Singh, J.P. Utilizing viscoelastic dampers in the seismic retrofit of a thirteen-story steel framed building. In Proceedings of the ASCE Structures Congress XII, Atlanta, GA, USA, 24–28 April 1994; pp. 1286–1291. [Google Scholar]
- Kanitkar, R.; Harms, M.; Patrick, C.; Lai Lai, M. Seismic Retrofit of A Steel Moment Frame Structure Using Viscoelastic Dampers. ISET J. Earthq. Tecnol. 1998, 35, 207–219. [Google Scholar]
- Antonucci, R.; Balducci, F.; Castellano, M.G.; Ahmadi, H.; Goodchild, I.; Fuller, K. Viscoelastic dampers for seismic protection of buildings: An application to an existing building. In Proceedings of the 5th World Congress on Joints, Bearings and Seismic System for Concrete Structures, Rome, Italy, 7–11 October 2001. [Google Scholar]
- Christopoulos, C.; Montgomery, M. Viscoelastic coupling dampers (VCDs) for enhanced wind and seismic performance of high-rise buildings. Earthq. Eng. Struct. Dyn. 2013, 42, 2217–2233. [Google Scholar] [CrossRef]
- Zhou, Y.; Aguaguiña, M.; Beskos, D.E.; Gong, S. A displacement-based seismic design method for building structures with nonlinear viscoelastic dampers. Bull. Earthq. Eng. 2021, 19, 4535–4585. [Google Scholar] [CrossRef]
- Mahmoodi, P.; Robertson, L.E.; Yontar, M.; Moy, C.; Feld, I. Performances of Viscoelastic Dampers in World Trade Centre Towers. In Proceedings of the Session at Structures Congress ’87, Orlando, FL, USA, 17–20 August 1987. [Google Scholar]
- Mehrabi, M.H.; Suhatril, M.; Ibrahim, Z.; Ghodsi, S.S.; Khatibi, H. Modeling of a viscoelastic damper and its application in structural control. PLoS ONE 2017, 12, e0176480. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.; Zhou, Y.; Huang, Z. Efficient direct displacement-based seismic design approach for structures with viscoelastic dampers. Structures 2021, 29, 1699–1708. [Google Scholar] [CrossRef]
- Dall’Asta, A.; Ragni, L.; Tubaldi, E. Dissipative Braces Based On High Damping Rubber: Analysis and Design. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Zhang, R.; Soong, T.T. Seismic Design of Viscoelastic Dampers for Structural Applications. J. Struct. Eng. 1992, 118, 1375–1392. [Google Scholar] [CrossRef]
- Chang, K.C.; Lai, M.L.; Soong, T.T.; Hao, D.S.; Yeh, Y.C. Seismic Behavior and Design Guidelines for Steel Frame Structures with Added Viscoelastic Dampers; Technical Report NCEER 91-0009; National Center for Earthquake Engineering Research (NCEER): Buffalo, NY, USA, 1993. [Google Scholar]
- Kasai, K.; Munshi, J.A.; Lai, M.L.; Maison, B.F. Viscoelastic damper hysteretic model: Theory, experiment and application. In Proceedings of the ATC17-1 Seminar, San Francisco, CA, USA, 11–12 March 1993; Applied Technology Council: Redwood City, CA, USA, 1993; Volume 12, pp. 521–532. [Google Scholar]
- Higgins, C.; Chen, S.-J.; Chou, F. Testing and Analysis of Steel Frames with viscoelastic dampers. In Proceedings of the 11th World Conference on Earthquake Engineering, Acapulco, Mexico, 23–28 June 1996. [Google Scholar]
- prEN 1998-1-2:2022; Eurocode 8—Design of Structures for Earthquake Resistance—Part 1-1: General Rules and Seismic Action. CEN (Comité européen de normalisation): Brussels, Belgium, 2022.
- Fu, Y.; Kasai, K. Comparative Study of Frames Using Viscoelastic and Viscous Dampers. J. Struct. Eng. 1998, 124, 513–522. [Google Scholar] [CrossRef]
- Zhang, L.; Su, M.; Zhang, C.; Shen, H.; Islam, M.M.; Zhang, R. A design method of viscoelastic damper parameters based on the elastic-plastic response reduction curve. Soil Dyn. Earthq. Eng. 2019, 117, 149–163. [Google Scholar] [CrossRef]
- Hareen, C.B.V.; Mohan, S.C. Energy-based seismic retrofit and design of building frames with passive dampers. Eng. Struct. 2022, 250, 113412. [Google Scholar] [CrossRef]
- Lin, Y.Y.; Tsai, M.H.; Hwang, J.S.; Chang, K.C. Direct displacement-based design for building with passive energy dissipation systems. Eng. Struct. 2003, 25, 25–37. [Google Scholar] [CrossRef]
- Mazza, F.; Vulcano, A. Displacement-based design procedure of damped braces for the seismic retrofitting of R.C. framed buildings. Bull. Earthq. Eng. 2015, 13, 2121–2143. [Google Scholar] [CrossRef]
- Chang, K.C.; Soong, T.T.; Lai, M.L.; Nielsen, E.J. Development of a design procedure for structures with added viscoelastic dampers. In Proceedings of the ATC17-1 Seminar, San Francisco, CA, USA, 11–12 March 1993; Applied Technology Council: Redwood City, CA, USA, 1993; Volume 12, pp. 473–484. [Google Scholar]
- Chang, K.C.; Lin, Y.Y.; Lai, M.L. Seismic Analysis and Design of Structures with Added Viscoelastic Dampers. ISET J. Earthq. Technol. 1998, 4, 143–166. [Google Scholar]
- Tsai, M.; Chang, K. A study of the modal strain energy method for viscoelastically damped structures. J. Chin. Inst. Eng. 2001, 24, 311–320. [Google Scholar] [CrossRef]
- Tchamo, J.M.; Zhou, Y. An alternative practical design method for structures with viscoelastic dampers. Earthq. Eng. Eng. Vib. 2018, 17, 459–473. [Google Scholar] [CrossRef]
- Ungar, E.E.; Kerwin, E.M. Loss Factors of Viscoelastic Systems in Terms of Energy Concepts. J. Acoust. Soc. Am. 1962, 34, 954–957. [Google Scholar] [CrossRef]
- Johnson, C.D.; Kienholz, D.A. Finite element prediction of damping in structures with constrained viscoelastic layers. Am. Inst. Aeronaut. Astronaut. 1982, 20, 1284–1290. [Google Scholar] [CrossRef]
- Naqi, A.; Saito, T. Seismic performance evaluation of steel buildings with oil dampers using capacity spectrum method. Appl. Sci. 2021, 11, 2687. [Google Scholar] [CrossRef]
- Bantilasa, K.E.; Kavvadias, I.E.; Vasiliadisb, L.K. Capacity spectrum method based on inelastic spectra for high viscous damped buildings. Earthq. Struct. 2017, 13, 337–351. [Google Scholar] [CrossRef]
- Diotallevi, P.P.; Landi, L.; Dellavalle, A. A methodology for the direct assessment of the damping ratio of structures equipped with nonlinear viscous dampers. J. Earthq. Eng. 2012, 16, 350–373. [Google Scholar] [CrossRef]
- Wang, S.; Yuan, Y.; Tan, P.; Li, Y.; Zheng, W.; Zhang, D. Experimental study and numerical model of a new passive adaptive isolation bearing. Eng. Struct. 2024, 308, 118044. [Google Scholar] [CrossRef]
- Zheng, W.; Tan, P.; Li, J.; Wang, H.; Liu, Y.; Xian, Z. Superelastic pendulum isolator with multi-stage variable curvature for seismic resilience enhancement of cold-regional bridges. Eng. Struct. 2023, 284, 115960. [Google Scholar] [CrossRef]
- Zheng, W.; Wang, H.; Tan, P.; Li, J.; Liu, Y. Numerical modeling and experimental validation of Sliding-LRBs considering hysteretic strength degradation. Eng. Struct. 2022, 262, 114374. [Google Scholar] [CrossRef]
- Carfagni, M.; Lenzi, E.; Pierini, M. Loss factor as a measure of mechanical damping. In Proceedings of the International Modal Analysis Conference-IMAC, Santa Barabara, CA, USA, 2–5 February 1998; Volume 1, pp. 580–584. [Google Scholar]
- Hanson, R.D.; Aiken, I.D.; Nims, D.K.; Richter, P.J.; Bachman, R.E. State-of-the-art and state-of -the-practice in seismic energy dissipation. In Proceedings of the ATC17-1 Seminar, San Francisco, CA, USA, 11–12 March 1993; Applied Technology Council: Redwood City, CA, USA, 1993; Volume 12, pp. 449–471. [Google Scholar]
- Daniel, Y.; Montgomery, M.; Christopoulos, C. Testing and modeling of ISD-111H viscoelastic dampers under wind and earthquake loading. In Proceedings of the NCEE 2014—10th U.S. National Conference on Earthquake Engineering: Frontiers of Earthquake Engineering, Anchorage, AK, USA, 21–25 July 2014. [Google Scholar]
- Aprile, A.; Inaudi, J.A.; Kelly, J.M. Evolutionary Model of Viscoelastic Dampers for Structural Applications. J. Eng. Mech. 1997, 123, 551–560. [Google Scholar] [CrossRef]
- Di Paola, M.; Pinnola, F.P. Calcolo Frazionario & Viscoelasticità; Dipartimento di Ingegneria Civile Ambientale e Aerospaziale, Università degli Studi di Palermo: Palermo, Italy, 2011. [Google Scholar]
- Montgomery, M.S. Fork Configuration Dampers (FCDs) for Enhanced Dynamic Performance of High-Rise Buildings. Ph.D. Thesis, Department of Civil Engineering, University of Toronto, Toronto, ON, Canada, 2011. [Google Scholar]
- Fan, C.-P. Seismic Analysis, Behavior, and Retrofit of Non-Ductile Reinforced Concrete Frame Buildings with Viscoelastic Dampers. Ph.D. Thesis, Lehigh University, Bethlehem, PA, USA, 1998. [Google Scholar]
- Biggerstaff, J.M. Vibrational Damping of Composite Materials. Master’s Thesis, University of California, San Diego, CA, USA, 2006. [Google Scholar]
- EN 1993-1-3; Eurocode 3—Design of Steel Structures Part 1-3: General Rules—Supplementary Rules for Cold-Formed Members and Sheeting. European Committee for Standardization: Bruxelles, Belgium, 2007.
- Montgomery, M.; Christopoulos, C. Experimental Validation of Viscoelastic Coupling Dampers for Enhanced Dynamic Performance of High-Rise Buildings. J. Struct. Eng. 2015, 141, 04014145. [Google Scholar] [CrossRef]
- FEMA 356; Pre-Standard and Commentary for the Seismic Rehabilitation of Building. Fed Emerg Manag Agency: Washington, DC, USA, 2000.
- Mazzoni, S.; McKenna, F.; Scott, H.M.; Fenves, L.G. OpenSees Command Language Manual. Pac. Earthq. Eng. Res. Cent. 2006, 246, 137–158. [Google Scholar]
- Gasparini, D.A.; Vanmarcke, E.H. SIMQKE—A Program for Artificial Motion Generation (User’s Manual and Documentation); Grant ATA 74-06935; MIT—Department of Civil Engineering: Cambridge, MA, USA, 1976. [Google Scholar]

| T = 20 °C | Spring 0 | Spring 1 | Spring 2 | Spring 3 | Spring 4 |
|---|---|---|---|---|---|
| GE [MPa] | 0.033337 | 0.311289 | 0.099964 | 0.003002 | 0.080206 |
| Dashpot 0 | Dashpot 1 | Dashpot 2 | Dashpot 3 | Dashpot 4 | |
| GC [MPa/ω] | 0.029715 | 0.038467 | 0.069748 | 0.065506 | 0.439183 |
| δmax,NC | δmax,LS | δmax,DL | |
|---|---|---|---|
| FEMA 365 (Table C1-3) | 5% | 2.5% | 0.7% |
| Adopted limits | 2.5% | 1% | 0.5% |
| Columns | Beams | ||||
|---|---|---|---|---|---|
| Floor | C0 | C1 | C2 | Braced Bay | MRF |
| 1 | HEB200 | HEB140 | HEB260 | IPE 300 * | IPE 360 * |
| 2 | HEB200 | HEB140 | HEB260 | IPE 300 * | IPE 360 * |
| 3 | HEB160 | HEB120 | HEB180 | IPE 300 * | IPE 360 * |
| 4 | HEB160 | HEB120 | HEB180 | IPE 300 * | IPE 360 * |
| Limit State | Φ(1)4 [-] | Γ(1) [-] | T1 [s] | umaxMDOF [m] | uSDOF [mm] | ξd [%] |
|---|---|---|---|---|---|---|
| DL | 0.0592 | 22.004 | 2.096 | 0.06 | 46.271 | 8.77 |
| LS | 0.12 | 92.542 | 9.62 | |||
| NC | 0.30 | 231.355 | 3.48 |
| T1 [s] | ξadd [%] | kb/kv [-] | ηv [-] | ηv-b [-] | βMSE | Vbase [kN] | V0 [kN] |
|---|---|---|---|---|---|---|---|
| 2.096 | 6.62 | 40 | 1.00 | 0.952 | 0.799 | 733.14 | 585.42 |
| 1.668 | 0.928 | 965.5 | 770.9 |
| Columns | Beams | ||||
|---|---|---|---|---|---|
| Floor | C0 | C1 | C2 | Braced Bay | MRF |
| 1 | HEB 220 | HEB 180 | HEB 360 | IPE 360 * | IPE 300 * |
| 2 | HEB 220 | HEB 180 | HEB 360 | IPE 360 * | IPE 300 * |
| 3 | HEB 220 | HEB 160 | HEB 200 | IPE 360 * | IPE 300 * |
| 4 | HEB 220 | HEB 160 | HEB 200 | IPE 360 * | IPE 300 * |
| Floor | Initial Values | Final Values | ||
|---|---|---|---|---|
| kb/k’v | Profile | kb/k’v | kb/k’v | |
| 1 | 40.07 | HEB 100 | 66.10 | HEB 140 |
| 2 | 48.55 | HEB 100 | 63.41 | HEB 120 |
| 3 | 67.78 | HEB 100 | 88.53 | HEB 120 |
| 4 | 73.48 | HEB 100 | 95.97 | HEB 120 |
| Floor | Spring Stiffness [kN/mm] | Damper Viscous Factors [kN/mm] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| kE,0 | kE,1 | kE,2 | kE,3 | kE,4 | cC,0 | cC,1 | cC,2 | cC,3 | cC,4 | |
| 1 | 0.376 | 3.512 | 1.128 | 0.034 | 0.905 | 0.335 | 0.434 | 0.787 | 0.739 | 4.954 |
| 2 | 0.310 | 2.898 | 0.931 | 0.028 | 0.747 | 0.277 | 0.358 | 0.649 | 0.610 | 4.088 |
| 3 | 0.222 | 2.076 | 0.667 | 0.020 | 0.535 | 0.198 | 0.256 | 0.465 | 0.437 | 2.928 |
| 4 | 0.205 | 1.915 | 0.615 | 0.018 | 0.493 | 0.183 | 0.237 | 0.429 | 0.403 | 2.702 |
| Floor | PGA [g] | Fmax [kN] | umax [mm] | F(umax) [kN] | u(Fmax) [mm] | ulim/umax |
|---|---|---|---|---|---|---|
| 1 | 0.443 | 277.28 | 49.75 | 186.86 | 34.91 | 96.7% |
| 2 | 210.09 | 44.00 | 136.86 | 29.38 | 85.6% | |
| 3 | 172.38 | 46.70 | 111.26 | 31.95 | 90.8% | |
| 4 | 119.99 | 31.51 | 75.75 | 19.68 | 61.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bosco, M.; Floridia, A.; Rossi, P.P. Proposal of a Design Procedure for Steel Frames with Viscoelastic Dampers. Appl. Sci. 2024, 14, 6937. https://doi.org/10.3390/app14166937
Bosco M, Floridia A, Rossi PP. Proposal of a Design Procedure for Steel Frames with Viscoelastic Dampers. Applied Sciences. 2024; 14(16):6937. https://doi.org/10.3390/app14166937
Chicago/Turabian StyleBosco, Melina, Andrea Floridia, and Pier Paolo Rossi. 2024. "Proposal of a Design Procedure for Steel Frames with Viscoelastic Dampers" Applied Sciences 14, no. 16: 6937. https://doi.org/10.3390/app14166937






