Back to the Metrics: Exploration of Distance Metrics in Anomaly Detection
Abstract
1. Introduction
1.1. Two-Dimensional Industrial Anomaly Detection
- Supervised Learning: These algorithms treat anomaly detection as an imbalanced binary classification problem. This approach suffers from the scarcity of abnormal samples and the high cost of labeling. To deal with these problems, various methods have been proposed to generate anomalous samples so as to alleviate the labeling cost. For example, CutPaste [10] and DRAEM [11] manually construct anomalous samples; SimpleNet [12] samples anomalous features near positive sample features; NSA [13] and GRAD [14] synthesize anomalous samples based on normal samples. Despite the diversity of anomaly generation methods, they consistently fail to address the underlying issue of discrepancies between the distributions of generated and real data [15,16,17].
- Unsupervised Learning: These algorithms operate under the assumption that data follow a normal distribution. For example, SROC [18] and SRR [19] rely on this assumption to identify and remove minor anomalies from normal data. When combined with semi-supervised learning techniques, these algorithms achieve enhanced performance.
- Semi-supervised Learning: The concentration assumption, which supposes the normal data are usually bound if the features extracted are good enough, is commonly used when designing semi-supervised learning AD&S methods. These algorithms require only labels for normal data and assume boundaries in the normal data distribution for anomaly detection. Examples include the following: autoencoder-based [20,21,22], GAN-based [20,23,24,25], flow-based [26,27,28,29,30], and SVDD-based methods [31,32,33]. Some memory bank-based methods (MBBM) [16,17,34,35,36,37] that combine pre-trained features from deep neural networks with traditional semi-supervised algorithms have achieved particularly outstanding results and also possess strong interpretability. In rough chronological order, we summarize the main related algorithms as follows:
- (a)
- (b)
- SPADE, building on DN2, [35] employs feature pyramid matching to achieve image AD&S.
- (c)
- PaDiM [36] models pre-train feature patches with Gaussian distributions for better AD&S performance.
- (d)
- Panda [33] sets subtasks based on pre-trained features for model tuning to achieve better feature extraction and improve model performance.
- (e)
1.2. Three-Dimensional Industrial Anomaly Detection
1.3. Evaluation Metrics
- I-AUROC (instance-based AUROC): This metric measures the AUROC at the instance level, which is crucial for image anomaly detection. It calculates the AUROC value for each image or object, providing an evaluation of the model’s performance on individual instances (detection performance). The formula is as follows:where is the true label of instance i, and is the predicted probability for instance i. This metric ranges from 0 to 1. A value closer to 1 indicates better detection performance by the model. A value close to 0.5 suggests that the model is ineffective, and its predictive performance can be considered equivalent to that of a random prediction model.
- P-AUROC (pixel-based AUROC): This metric calculates the AUROC at the pixel level, which is essential for evaluating the performance of anomaly segmentation tasks. It considers the predictions and true labels of each pixel within the images. The formula is as follows:where is the true label of pixel j, and is the predicted probability for pixel j. This metric ranges from 0 to 1. A value closer to 1 indicates better segmentation performance by the model. A value close to 0.5 suggests that the model is ineffective, and its predictive performance can be considered equivalent to that of a random prediction model. Due to the special nature of anomaly detection tasks, where normal pixels vastly outnumber abnormal ones, the reference value of this metric for segmentation performance is relatively low.
- PRO (per-region overlap): This metric evaluates the overlap between predicted anomaly regions and ground truth regions, specifically for anomaly segmentation. The formula is as follows:where K is the number of ground truth anomaly regions, P is the set of predicted anomaly regions (multiple connected components), and is the k-th ground truth anomaly region (a single connected component). denotes the number of pixels in a connected component. PRO considers the size and location of anomaly regions, making it useful for evaluating segmentation performance.
- AUPRO (area under the PRO curve): This metric evaluates the performance of anomaly segmentation by calculating the area under the PRO curve. PRO measures the overlap between predicted and ground truth anomaly regions. The formula is as follows:where T is the true segmentation label (pixel-level) of a image (a binary matrix, the set of connected pixels with a value of 1 represents a connected component), is the set of predicted anomaly scores for each pixel in the image, FPR represents the false positive rate at different thresholds , and is the PRO score at the corresponding threshold . is initialized to the minimum prediction score that makes FPR 0, and as decreases, FPR exhibits a discrete upward trend, with the actual integral computed through numerical integration methods. This metric ranges from 0 to 1. A value closer to 1 indicates better segmentation performance by the model. A value close to 0.5 suggests that the model is ineffective, and its predictive performance can be considered equivalent to that of a random prediction model. AUPRO is similar to AUROC but is specifically designed for anomaly segmentation tasks, summarizing the model’s performance across different thresholds.
1.4. Contributions and Paper Organization
- Methodological clarification (PatchCore and BTF): We compare and analyze the theoretical framework and official implementation of PatchCore and BTF. Then, we make improvements to some details found in the paper or code while clarifying the framework of BTM.
- Distance metric analysis: We visualize and analyze the distance measure in the anomaly scoring algorithm, providing initial insights into its strengths and weaknesses. Based on these analyses, we also propose some assumptions.
- Method proposed: On the basis of BTF, a method named back to the metrics (BTM) is proposed in Section 2.1, which achieves the performance improvement of (I-AUROC 5.7% ↑, AURPO 0.5% ↑, and P-AUROC 0.2% ↑). It is also competitive against other leading methods.
- Section 2 optimizes k-nearest neighbor feature fusion, feature alignment, and distance metrics based on BTF and proposes the BTM method. Then, the basis of modification is introduced, including a summary of the framework of MBBM method and an analysis of the implementation details of MBBM (anomaly score calculation, feature fusion, and the downsampling method).
- Section 4 summarizes the conclusions drawn in this work and explores future research directions.
2. Methodology
2.1. Back to the Metric
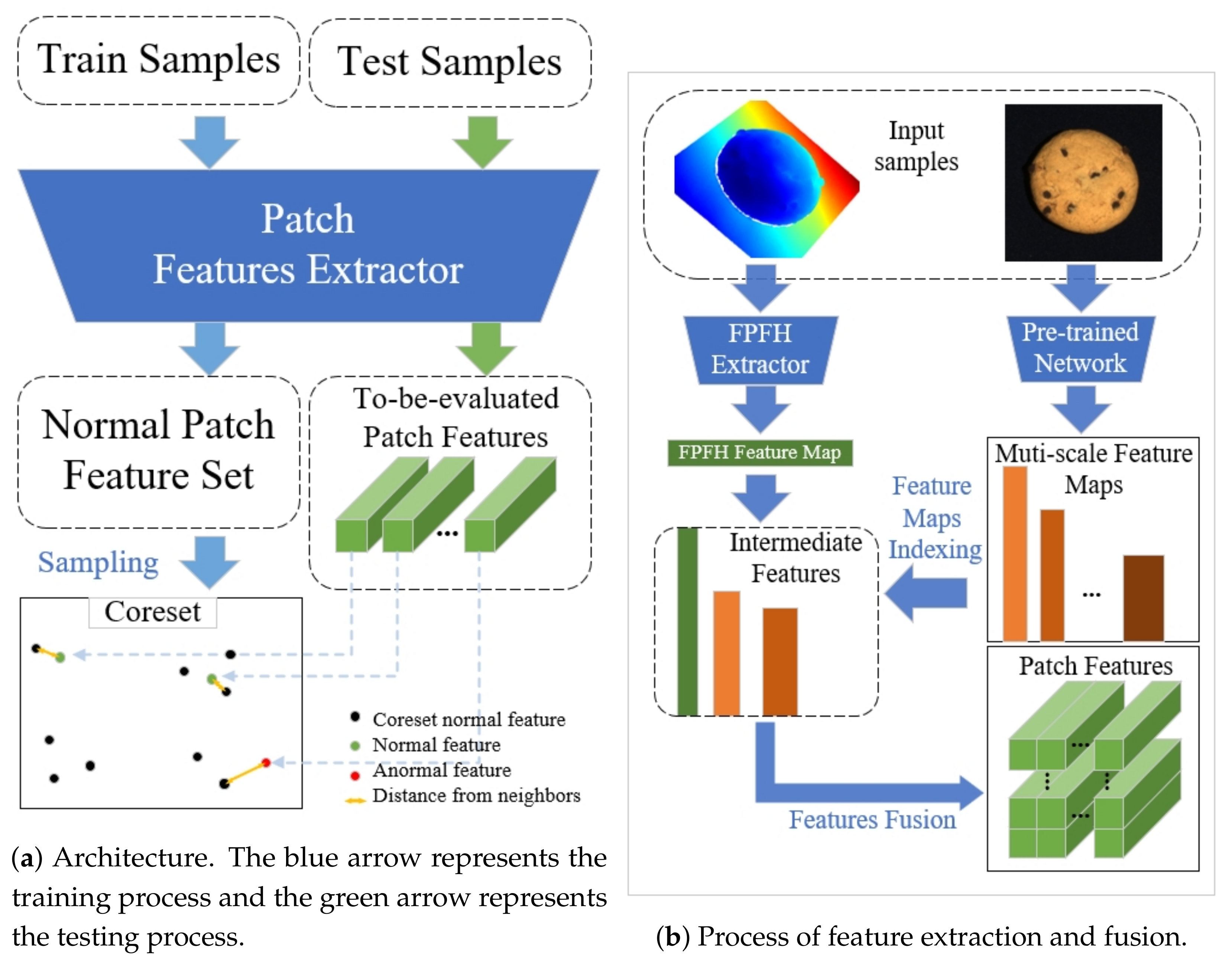
2.1.1. Framework
2.1.2. Optimization
2.2. The Structure of Memory Bank-Based Methods (MBBM)
2.2.1. Anomaly Score Metrics
2.2.2. Feature Fusion
2.2.3. The Iterative Greedy Approximation Algorithm
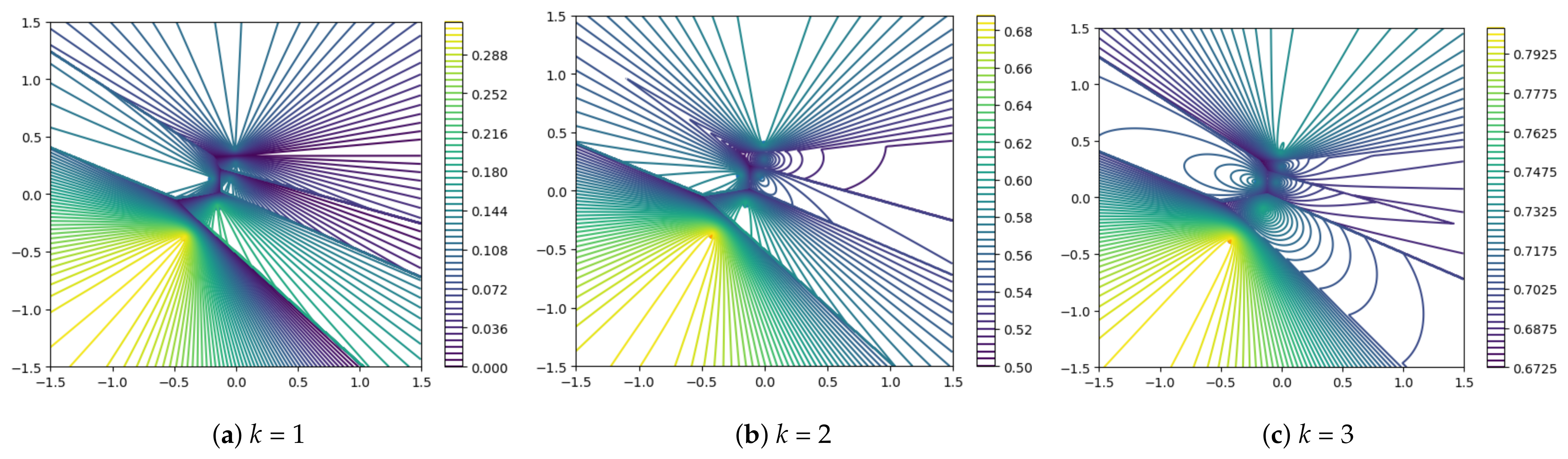
2.3. Visualization Analysis of Different Metrics
2.3.1. k-Nearest Neighbor Squared Distance Mean
2.3.2. PatchCore Anomaly Score Calculation Function
2.3.3. Summary
3. Experiments
3.1. Datasets
3.2. Evaluation Metrics
3.3. Implementation Details
3.4. Performance Comparison
3.4.1. Anomaly Detection on MVTec-3D AD
3.4.2. Anomaly Segmentation on MVTec-3D AD
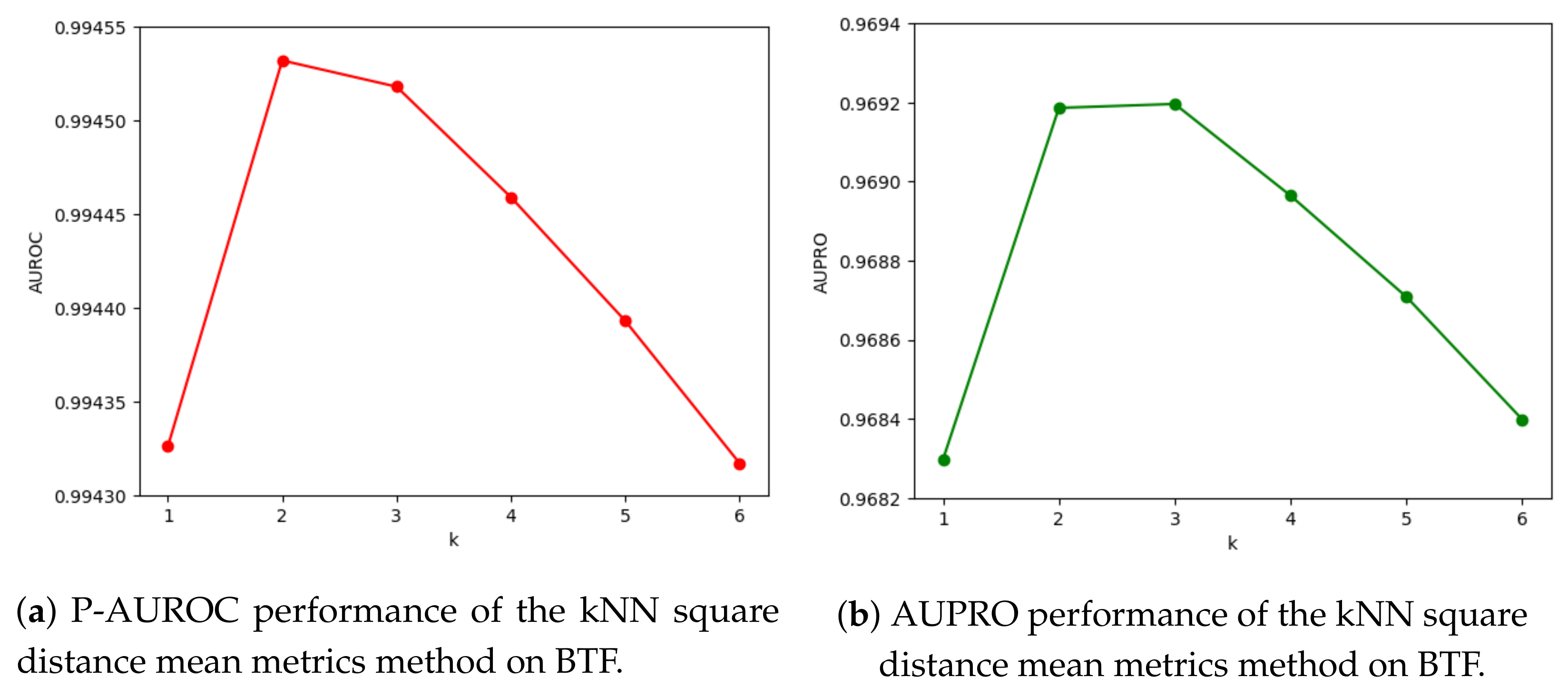
3.5. Performance of kNN Reweight Metrics on BTF
| Method | Bagel | Cable Gland | Carrot | Cookie | Dowel | Foam | Peach | Potato | Rope | Tire | Mean | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3D | Depth GAN [40] | 0.111 | 0.072 | 0.212 | 0.174 | 0.160 | 0.128 | 0.003 | 0.042 | 0.446 | 0.075 | 0.143 |
| Depth AE [40] | 0.147 | 0.069 | 0.293 | 0.217 | 0.207 | 0.181 | 0.164 | 0.066 | 0.545 | 0.142 | 0.203 | |
| Depth VM [40] | 0.280 | 0.374 | 0.243 | 0.526 | 0.485 | 0.314 | 0.199 | 0.388 | 0.543 | 0.385 | 0.374 | |
| Voxel GAN [40] | 0.440 | 0.453 | 0.875 | 0.755 | 0.782 | 0.378 | 0.392 | 0.639 | 0.775 | 0.389 | 0.583 | |
| Voxel AE [40] | 0.260 | 0.341 | 0.581 | 0.351 | 0.502 | 0.234 | 0.351 | 0.658 | 0.015 | 0.185 | 0.348 | |
| Voxel VM [40] | 0.453 | 0.343 | 0.521 | 0.697 | 0.680 | 0.284 | 0.349 | 0.634 | 0.616 | 0.346 | 0.492 | |
| 3D-ST [41] | 0.950 | 0.483 | 0.986 | 0.921 | 0.905 | 0.632 | 0.945 | 0.988 | 0.976 | 0.542 | 0.833 | |
| M3DM [44] | 0.943 | 0.818 | 0.977 | 0.882 | 0.881 | 0.743 | 0.958 | 0.974 | 0.95 | 0.929 | 0.906 | |
| FPFH (BTF) [43] | 0.972 | 0.849 | 0.981 | 0.939 | 0.963 | 0.693 | 0.975 | 0.981 | 0.980 | 0.949 | 0.928 | |
| FPFH (BTM) | 0.974 | 0.861 | 0.981 | 0.937 | 0.959 | 0.661 | 0.978 | 0.983 | 0.98 | 0.947 | 0.926 | |
| RGB | PatchCore [44] | 0.901 | 0.949 | 0.928 | 0.877 | 0.892 | 0.563 | 0.904 | 0.932 | 0.908 | 0.906 | 0.876 |
| M3DM [44] | 0.952 | 0.972 | 0.973 | 0.891 | 0.932 | 0.843 | 0.97 | 0.956 | 0.968 | 0.966 | 0.942 | |
| RGB iNet (BTF) [43] | 0.898 | 0.948 | 0.927 | 0.872 | 0.927 | 0.555 | 0.902 | 0.931 | 0.903 | 0.899 | 0.876 | |
| RGB iNet (BTM) | 0.901 | 0.958 | 0.942 | 0.905 | 0.951 | 0.615 | 0.906 | 0.938 | 0.927 | 0.916 | 0.896 | |
| RGB+3D | Depth GAN [40] | 0.421 | 0.422 | 0.778 | 0.696 | 0.494 | 0.252 | 0.285 | 0.362 | 0.402 | 0.631 | 0.474 |
| Depth AE [40] | 0.432 | 0.158 | 0.808 | 0.491 | 0.841 | 0.406 | 0.262 | 0.216 | 0.716 | 0.478 | 0.481 | |
| Depth VM [40] | 0.388 | 0.321 | 0.194 | 0.570 | 0.408 | 0.282 | 0.244 | 0.349 | 0.268 | 0.331 | 0.335 | |
| Voxel GAN [40] | 0.664 | 0.620 | 0.766 | 0.740 | 0.783 | 0.332 | 0.582 | 0.790 | 0.633 | 0.483 | 0.639 | |
| Voxel AE [40] | 0.467 | 0.750 | 0.808 | 0.550 | 0.765 | 0.473 | 0.721 | 0.918 | 0.019 | 0.170 | 0.564 | |
| Voxel VM [40] | 0.510 | 0.331 | 0.413 | 0.715 | 0.680 | 0.279 | 0.300 | 0.507 | 0.611 | 0.366 | 0.471 | |
| M3DM * | 0.966 | 0.971 | 0.978 | 0.949 | 0.941 | 0.92 | 0.977 | 0.967 | 0.971 | 0.973 | 0.961 | |
| BTF [43] | 0.976 | 0.967 | 0.979 | 0.974 | 0.971 | 0.884 | 0.976 | 0.981 | 0.959 | 0.971 | 0.964 | |
| BTM | 0.979 | 0.972 | 0.980 | 0.976 | 0.977 | 0.905 | 0.978 | 0.982 | 0.968 | 0.975 | 0.969 |
| Method | Bagel | Cable Gland | Carrot | Cookie | Dowel | Foam | Peach | Potato | Rope | Tire | Mean | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3D | M3DM [44] | 0.981 | 0.949 | 0.997 | 0.932 | 0.959 | 0.925 | 0.989 | 0.995 | 0.994 | 0.981 | 0.970 |
| FPFH (BTF) [43] | 0.995 | 0.955 | 0.998 | 0.971 | 0.993 | 0.911 | 0.995 | 0.999 | 0.998 | 0.988 | 0.980 | |
| FPFH (BTM) | 0.995 | 0.96 | 0.998 | 0.97 | 0.991 | 0.894 | 0.996 | 0.999 | 0.998 | 0.987 | 0.979 | |
| RGB | PatchCore [44] | 0.983 | 0.984 | 0.980 | 0.974 | 0.972 | 0.849 | 0.976 | 0.983 | 0.987 | 0.977 | 0.967 |
| M3DM [44] | 0.992 | 0.990 | 0.994 | 0.977 | 0.983 | 0.955 | 0.994 | 0.990 | 0.995 | 0.994 | 0.987 | |
| RGB iNet (BTF) [43] | 0.983 | 0.984 | 0.980 | 0.974 | 0.985 | 0.836 | 0.976 | 0.982 | 0.989 | 0.975 | 0.966 | |
| RGB iNet (BTM) | 0.984 | 0.987 | 0.984 | 0.979 | 0.991 | 0.872 | 0.976 | 0.983 | 0.992 | 0.979 | 0.973 | |
| RGB+3D | M3DM * | 0.994 | 0.994 | 0.997 | 0.985 | 0.985 | 0.98 | 0.996 | 0.994 | 0.997 | 0.995 | 0.992 |
| BTF [43] | 0.996 | 0.991 | 0.997 | 0.995 | 0.995 | 0.972 | 0.996 | 0.998 | 0.995 | 0.994 | 0.993 | |
| BTM | 0.997 | 0.993 | 0.998 | 0.995 | 0.996 | 0.979 | 0.997 | 0.999 | 0.996 | 0.995 | 0.995 |
3.6. Performance of k Squared Distance Mean Metrics on BTF
3.7. Performance of kNN Squared Distance Mean Metrics on 2D Datasets with the PatchCore Method
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Formula Mentioned in the Original Article of PatchCore
Appendix A.1. Expressed in the Original Article
Appendix A.2. Expressed in Our Context
References
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. (CSUR) 2009, 41, 1–58. [Google Scholar] [CrossRef]
- Ruff, L.; Kauffmann, J.R.; Vandermeulen, R.A.; Montavon, G.; Samek, W.; Kloft, M.; Dietterich, T.G.; Müller, K.R. A unifying review of deep and shallow anomaly detection. Proc. IEEE 2021, 109, 756–795. [Google Scholar] [CrossRef]
- Rippel, O.; Merhof, D. Anomaly Detection for Automated Visual Inspection: A Review. In Bildverarbeitung in der Automation: Ausgewählte Beiträge des Jahreskolloquiums BVAu 2022; Springer: Berlin/Heidelberg, Germany, 2023; pp. 1–13. [Google Scholar]
- Liu, J.; Xie, G.; Wang, J.; Li, S.; Wang, C.; Zheng, F.; Jin, Y. Deep industrial image anomaly detection: A survey. Mach. Intell. Res. 2024, 21, 104–135. [Google Scholar] [CrossRef]
- Bergmann, P.; Fauser, M.; Sattlegger, D.; Steger, C. MVTec AD—A comprehensive real-world dataset for unsupervised anomaly detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9592–9600. [Google Scholar] [CrossRef]
- Bergmann, P.; Batzner, K.; Fauser, M.; Sattlegger, D.; Steger, C. The MVTec anomaly detection dataset: A comprehensive real-world dataset for unsupervised anomaly detection. Int. J. Comput. Vis. 2021, 129, 1038–1059. [Google Scholar] [CrossRef]
- Mishra, P.; Verk, R.; Fornasier, D.; Piciarelli, C.; Foresti, G.L. VT-ADL: A vision transformer network for image anomaly detection and localization. In Proceedings of the 2021 IEEE 30th International Symposium on Industrial Electronics (ISIE), Kyoto, Japan, 20–23 June 2021; pp. 1–6. [Google Scholar]
- Huang, Y.; Qiu, C.; Yuan, K. Surface defect saliency of magnetic tile. Vis. Comput. 2020, 36, 85–96. [Google Scholar] [CrossRef]
- Bergmann, P.; Batzner, K.; Fauser, M.; Sattlegger, D.; Steger, C. Beyond dents and scratches: Logical constraints in unsupervised anomaly detection and localization. Int. J. Comput. Vis. 2022, 130, 947–969. [Google Scholar] [CrossRef]
- Li, C.L.; Sohn, K.; Yoon, J.; Pfister, T. Cutpaste: Self-supervised learning for anomaly detection and localization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 9664–9674. [Google Scholar]
- Zavrtanik, V.; Kristan, M.; Skočaj, D. Draem—A discriminatively trained reconstruction embedding for surface anomaly detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 8330–8339. [Google Scholar]
- Liu, Z.; Zhou, Y.; Xu, Y.; Wang, Z. Simplenet: A simple network for image anomaly detection and localization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 20402–20411. [Google Scholar]
- Schlüter, H.M.; Tan, J.; Hou, B.; Kainz, B. Natural synthetic anomalies for self-supervised anomaly detection and localization. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 474–489. [Google Scholar]
- Dai, S.; Wu, Y.; Li, X.; Xue, X. Generating and reweighting dense contrastive patterns for unsupervised anomaly detection. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–28 February 2024; Volume 38, pp. 1454–1462. [Google Scholar]
- Ye, Z.; Chen, Y.; Zheng, H. Understanding the effect of bias in deep anomaly detection. arXiv 2021, arXiv:2105.07346. [Google Scholar]
- Rippel, O.; Mertens, P.; König, E.; Merhof, D. Gaussian anomaly detection by modeling the distribution of normal data in pretrained deep features. IEEE Trans. Instrum. Meas. 2021, 70, 1–13. [Google Scholar] [CrossRef]
- Rippel, O.; Mertens, P.; Merhof, D. Modeling the distribution of normal data in pre-trained deep features for anomaly detection. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 6726–6733. [Google Scholar]
- Cordier, A.; Missaoui, B.; Gutierrez, P. Data refinement for fully unsupervised visual inspection using pre-trained networks. arXiv 2022, arXiv:2202.12759. [Google Scholar]
- Yoon, J.; Sohn, K.; Li, C.L.; Arik, S.O.; Lee, C.Y.; Pfister, T. Self-supervise, refine, repeat: Improving unsupervised anomaly detection. arXiv 2021, arXiv:2106.06115. [Google Scholar]
- Davletshina, D.; Melnychuk, V.; Tran, V.; Singla, H.; Berrendorf, M.; Faerman, E.; Fromm, M.; Schubert, M. Unsupervised anomaly detection for X-ray images. arXiv 2020, arXiv:2001.10883. [Google Scholar]
- Nguyen, D.T.; Lou, Z.; Klar, M.; Brox, T. Anomaly detection with multiple-hypotheses predictions. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 4800–4809. [Google Scholar]
- Sakurada, M.; Yairi, T. Anomaly detection using autoencoders with nonlinear dimensionality reduction. In Proceedings of the MLSDA 2014 2nd Workshop on Machine Learning for Sensory Data Analysis, Gold Coast, QLD, Australia, 2 December 2014; pp. 4–11. [Google Scholar]
- Pidhorskyi, S.; Almohsen, R.; Doretto, G. Generative probabilistic novelty detection with adversarial autoencoders. Adv. Neural Inf. Process. Syst. 2018, 31, 6823–6834. [Google Scholar]
- Sabokrou, M.; Khalooei, M.; Fathy, M.; Adeli, E. Adversarially learned one-class classifier for novelty detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3379–3388. [Google Scholar]
- Akcay, S.; Atapour-Abarghouei, A.; Breckon, T.P. Ganomaly: Semi-supervised anomaly detection via adversarial training. In Proceedings of the Computer Vision—ACCV 2018: 14th Asian Conference on Computer Vision, Perth, Australia, 2–6 December 2018; Revised Selected Papers, Part III 14. Springer: Berlin/Heidelberg, Germany, 2019; pp. 622–637. [Google Scholar]
- Rudolph, M.; Wandt, B.; Rosenhahn, B. Same same but differnet: Semi-supervised defect detection with normalizing flows. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Virtual, 5–9 January 2021; pp. 1907–1916. [Google Scholar]
- Gudovskiy, D.; Ishizaka, S.; Kozuka, K. Cflow-ad: Real-time unsupervised anomaly detection with localization via conditional normalizing flows. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2022; pp. 98–107. [Google Scholar]
- Rudolph, M.; Wehrbein, T.; Rosenhahn, B.; Wandt, B. Fully convolutional cross-scale-flows for image-based defect detection. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2022; pp. 1088–1097. [Google Scholar]
- Zhou, Y.; Xu, X.; Song, J.; Shen, F.; Shen, H.T. MSFlow: Multiscale Flow-Based Framework for Unsupervised Anomaly Detection. IEEE Trans. Neural Netw. Learn. Syst. 2024, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Zheng, Y.; Wang, X.; Li, W.; Wu, Y.; Zhao, R.; Wu, L. Fastflow: Unsupervised anomaly detection and localization via 2d normalizing flows. arXiv 2021, arXiv:2111.07677. [Google Scholar]
- Ruff, L.; Vandermeulen, R.A.; Görnitz, N.; Binder, A.; Müller, E.; Müller, K.R.; Kloft, M. Deep semi-supervised anomaly detection. arXiv 2019, arXiv:1906.02694. [Google Scholar]
- Yi, J.; Yoon, S. Patch svdd: Patch-level svdd for anomaly detection and segmentation. In Proceedings of the Asian Conference on Computer Vision, Kyoto, Japan, 30 November–4 December 2020. [Google Scholar]
- Reiss, T.; Cohen, N.; Bergman, L.; Hoshen, Y. Panda: Adapting pretrained features for anomaly detection and segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 2806–2814. [Google Scholar]
- Bergman, L.; Cohen, N.; Hoshen, Y. Deep nearest neighbor anomaly detection. arXiv 2020, arXiv:2002.10445. [Google Scholar]
- Cohen, N.; Hoshen, Y. Sub-image anomaly detection with deep pyramid correspondences. arXiv 2020, arXiv:2005.02357. [Google Scholar]
- Defard, T.; Setkov, A.; Loesch, A.; Audigier, R. Padim: A patch distribution modeling framework for anomaly detection and localization. In Proceedings of the International Conference on Pattern Recognition, Virtual Event, 10–15 January 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 475–489. [Google Scholar]
- Roth, K.; Pemula, L.; Zepeda, J.; Schölkopf, B.; Brox, T.; Gehler, P. Towards total recall in industrial anomaly detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 14318–14328. [Google Scholar]
- D’oro, P.; Nasca, E.; Masci, J.; Matteucci, M. Group Anomaly Detection via Graph Autoencoders. Proceedings of the NIPS Workshop. 2019, Volume 2. Available online: https://api.semanticscholar.org/CorpusID:247021966 (accessed on 2 May 2024).
- Hyun, J.; Kim, S.; Jeon, G.; Kim, S.H.; Bae, K.; Kang, B.J. ReConPatch: Contrastive patch representation learning for industrial anomaly detection. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2024; pp. 2052–2061. [Google Scholar]
- Bergmann, P.; Jin, X.; Sattlegger, D.; Steger, C. The MVTec 3D-AD Dataset for Unsupervised 3D Anomaly Detection and Localization. In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications, Virtual Event, 6–8 February 2022; SCITEPRESS—Science and Technology Publications: Setubal, Portugal, 2022; pp. 202–213. [Google Scholar] [CrossRef]
- Bergmann, P.; Sattlegger, D. Anomaly detection in 3d point clouds using deep geometric descriptors. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 2–7 January 2023; pp. 2613–2623. [Google Scholar]
- Rudolph, M.; Wehrbein, T.; Rosenhahn, B.; Wandt, B. Asymmetric student-teacher networks for industrial anomaly detection. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 2–7 January 2023; pp. 2592–2602. [Google Scholar]
- Horwitz, E.; Hoshen, Y. Back to the feature: Classical 3d features are (almost) all you need for 3d anomaly detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 2967–2976. [Google Scholar]
- Wang, Y.; Peng, J.; Zhang, J.; Yi, R.; Wang, Y.; Wang, C. Multimodal industrial anomaly detection via hybrid fusion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 8032–8041. [Google Scholar]
- Zavrtanik, V.; Kristan, M.; Skočaj, D. Cheating Depth: Enhancing 3D Surface Anomaly Detection via Depth Simulation. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2024; pp. 2164–2172. [Google Scholar]
- Chu, Y.M.; Liu, C.; Hsieh, T.I.; Chen, H.T.; Liu, T.L. Shape-guided dual-memory learning for 3D anomaly detection. In Proceedings of the 40th International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023; pp. 6185–6194. [Google Scholar]
- Peterson, L.E. K-nearest neighbor. Scholarpedia 2009, 4, 1883. [Google Scholar] [CrossRef]
- Sener, O.; Savarese, S. Active Learning for Convolutional Neural Networks: A Core-Set Approach. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Muhr, D.; Affenzeller, M.; Küng, J. A Probabilistic Transformation of Distance-Based Outliers. Mach. Learn. Knowl. Extr. 2023, 5, 782–802. [Google Scholar] [CrossRef]
- Rousseeuw, P.J.; Hubert, M. Anomaly detection by robust statistics. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1236. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J.; Wang, C. Systematic testing of the data-poisoning robustness of KNN. In Proceedings of the 32nd ACM SIGSOFT International Symposium on Software Testing and Analysis, Seattle, WA, USA, 17–21 July 2023; pp. 1207–1218. [Google Scholar]
- Classmate-Huang. The Anomaly Detection Process [GitHub Issue]. 2022. Available online: https://github.com/amazon-science/patchcore-inspection/issues/27 (accessed on 2 May 2024).
- nuclearboy95. Anomaly Score Calculation is Different from the Paper [GitHub Issue]. 2022. Available online: https://github.com/amazon-science/patchcore-inspection/issues/54 (accessed on 2 May 2024).




| Method | Bagel | Cable Gland | Carrot | Cookie | Dowel | Foam | Peach | Potato | Rope | Tire | Mean | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3D | Depth GAN [40] | 0.538 | 0.372 | 0.580 | 0.603 | 0.430 | 0.534 | 0.642 | 0.601 | 0.443 | 0.577 | 0.532 |
| Depth AE [40] | 0.648 | 0.502 | 0.650 | 0.488 | 0.805 | 0.522 | 0.712 | 0.529 | 0.540 | 0.552 | 0.595 | |
| Depth VM [40] | 0.513 | 0.551 | 0.477 | 0.581 | 0.617 | 0.716 | 0.450 | 0.421 | 0.598 | 0.623 | 0.555 | |
| Voxel GAN [40] | 0.680 | 0.324 | 0.565 | 0.399 | 0.497 | 0.482 | 0.566 | 0.579 | 0.601 | 0.482 | 0.517 | |
| Voxel AE [40] | 0.510 | 0.540 | 0.384 | 0.693 | 0.446 | 0.632 | 0.550 | 0.494 | 0.721 | 0.413 | 0.538 | |
| Voxel VM [40] | 0.553 | 0.772 | 0.484 | 0.701 | 0.751 | 0.578 | 0.480 | 0.466 | 0.689 | 0.611 | 0.609 | |
| 3D-ST | 0.862 | 0.484 | 0.832 | 0.894 | 0.848 | 0.663 | 0.763 | 0.687 | 0.958 | 0.486 | 0.748 | |
| M3DM [44] | 0.941 | 0.651 | 0.965 | 0.969 | 0.905 | 0.760 | 0.880 | 0.974 | 0.926 | 0.765 | 0.874 | |
| FPFH (BTF) [43] | 0.820 | 0.533 | 0.877 | 0.769 | 0.718 | 0.574 | 0.774 | 0.895 | 0.990 | 0.582 | 0.753 | |
| FPFH (BTM) | 0.939 | 0.553 | 0.916 | 0.844 | 0.823 | 0.588 | 0.718 | 0.928 | 0.976 | 0.633 | 0.792 | |
| RGB | PatchCore [44] | 0.876 | 0.880 | 0.791 | 0.682 | 0.912 | 0.701 | 0.695 | 0.618 | 0.841 | 0.702 | 0.770 |
| M3DM [44] | 0.944 | 0.918 | 0.896 | 0.749 | 0.959 | 0.767 | 0.919 | 0.648 | 0.938 | 0.767 | 0.850 | |
| RGB iNet (BTF) [43] | 0.854 | 0.840 | 0.824 | 0.687 | 0.974 | 0.716 | 0.713 | 0.593 | 0.920 | 0.724 | 0.785 | |
| RGB iNet (BTM) | 0.909 | 0.895 | 0.838 | 0.745 | 0.975 | 0.714 | 0.79 | 0.605 | 0.93 | 0.759 | 0.816 | |
| RGB+3D | Depth GAN [40] | 0.530 | 0.376 | 0.607 | 0.603 | 0.497 | 0.484 | 0.595 | 0.489 | 0.536 | 0.521 | 0.523 |
| Depth AE [40] | 0.468 | 0.731 | 0.497 | 0.673 | 0.534 | 0.417 | 0.485 | 0.549 | 0.564 | 0.546 | 0.546 | |
| Depth VM [40] | 0.510 | 0.542 | 0.469 | 0.576 | 0.609 | 0.699 | 0.450 | 0.419 | 0.668 | 0.520 | 0.546 | |
| Voxel GAN [40] | 0.383 | 0.623 | 0.474 | 0.639 | 0.564 | 0.409 | 0.617 | 0.427 | 0.663 | 0.577 | 0.537 | |
| Voxel AE [40] | 0.693 | 0.425 | 0.515 | 0.790 | 0.494 | 0.558 | 0.537 | 0.484 | 0.639 | 0.583 | 0.571 | |
| Voxel VM [40] | 0.750 | 0.747 | 0.613 | 0.738 | 0.823 | 0.693 | 0.679 | 0.652 | 0.609 | 0.690 | 0.699 | |
| M3DM * | 0.998 | 0.894 | 0.96 | 0.963 | 0.954 | 0.901 | 0.958 | 0.868 | 0.962 | 0.797 | 0.926 | |
| BTF [43] | 0.938 | 0.765 | 0.972 | 0.888 | 0.960 | 0.664 | 0.904 | 0.929 | 0.982 | 0.726 | 0.873 | |
| BTM | 0.980 | 0.860 | 0.980 | 0.963 | 0.978 | 0.726 | 0.958 | 0.953 | 0.980 | 0.926 | 0.930 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.; Li, X. Back to the Metrics: Exploration of Distance Metrics in Anomaly Detection. Appl. Sci. 2024, 14, 7016. https://doi.org/10.3390/app14167016
Lin Y, Li X. Back to the Metrics: Exploration of Distance Metrics in Anomaly Detection. Applied Sciences. 2024; 14(16):7016. https://doi.org/10.3390/app14167016
Chicago/Turabian StyleLin, Yujing, and Xiaoqiang Li. 2024. "Back to the Metrics: Exploration of Distance Metrics in Anomaly Detection" Applied Sciences 14, no. 16: 7016. https://doi.org/10.3390/app14167016
APA StyleLin, Y., & Li, X. (2024). Back to the Metrics: Exploration of Distance Metrics in Anomaly Detection. Applied Sciences, 14(16), 7016. https://doi.org/10.3390/app14167016







