Numerical Simulation and Flow Field Analysis of Porous Water Jet Nozzle Based on Fluent
Abstract
:1. Introduction
2. Physical Model and Control Equation
2.1. Physical Model and Simulation Scheme
2.2. Governing Equation
- (1)
- Continuity equation:
- (2)
- Navier–Stokes equations:
- (3)
- The momentum equation:
- (4)
- Turbulent kinetic energy equation:
2.3. Turbulent Eddy Viscosity Model
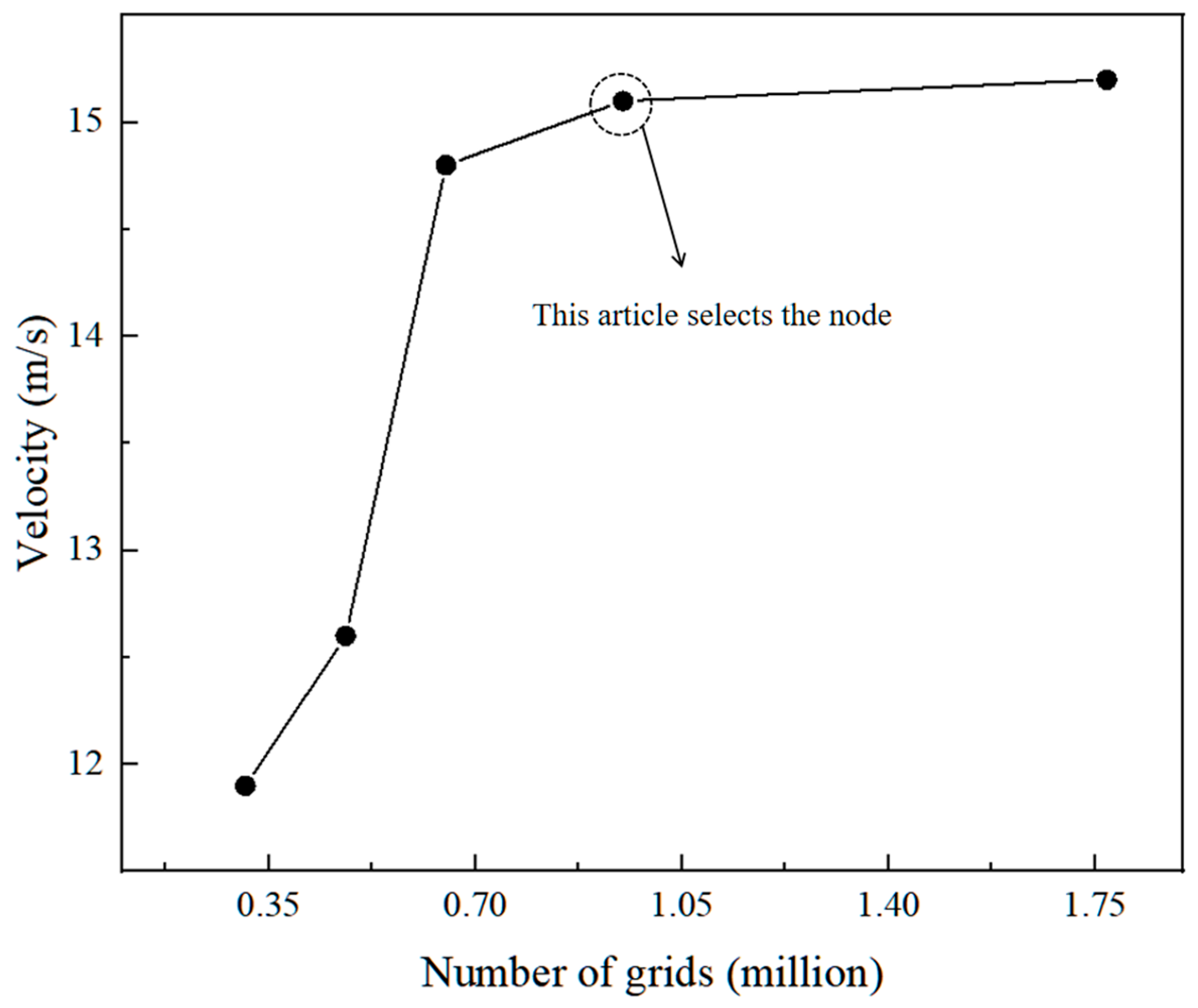
2.4. Mesh Setting and Mesh Independence Verification
2.5. Solution Method and Boundary Condition Setting
- (1)
- The RNG model in the k-ε (2 eqn) model was selected. The wall function selects the standard wall function.
- (2)
- The model constants were Cmu = 0.0845, C1-Epsilon = 1.42, C2-Epsilon = 1.68.
- (3)
- The material is liquid water, the nozzle outlet is the inlet of the fluid domain, the inlet is the velocity inlet, the velocity is 25 m/s, and the turbulence intensity is 5%. Considering the influence of gravity, the initial velocity of the y-axis is set to −9.81 m/s.
- (4)
- The outlet condition is the pressure outlet, the initial gauge pressure is 0, the reflux turbulence intensity is 5%, and the reflux turbulence viscosity ratio is 10.
- (5)
- Set the wall as a non-slip solid wall.
- (6)
- The time step method is set to “Automatic”. The length scale method is set to “Conservative”. The time scale factor is set to 1. The number of iterations is set to five hundred. The report interval is set to 0.5. The data update interval is set to 1.
3. Analysis of Jet Flow Field in Pipe
3.1. Flow Field Analysis of 25° Tilt Angle Rear Nozzle
3.2. Flow Field Analysis of 30° Tilt Angle Rear Nozzle
3.3. Flow Field Analysis of 35° Tilt Angle Rear Nozzle
3.4. Flow Field Analysis of 40° Tilt Angle Rear Nozzle
4. Flow Velocity Analysis
4.1. Velocity Analysis of Front Nozzle
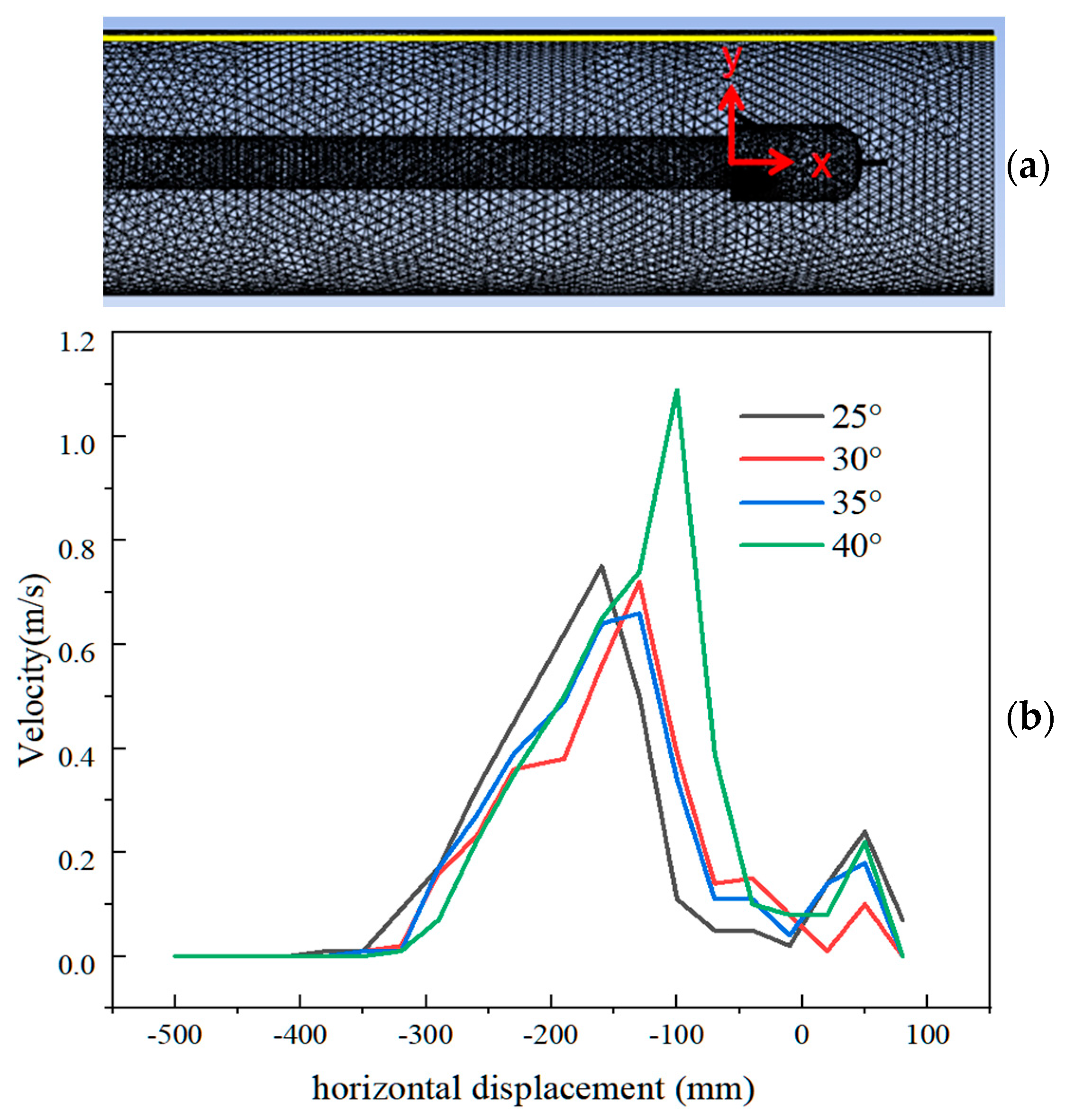
4.2. Velocity Analysis of Pipe Wall Flow Field
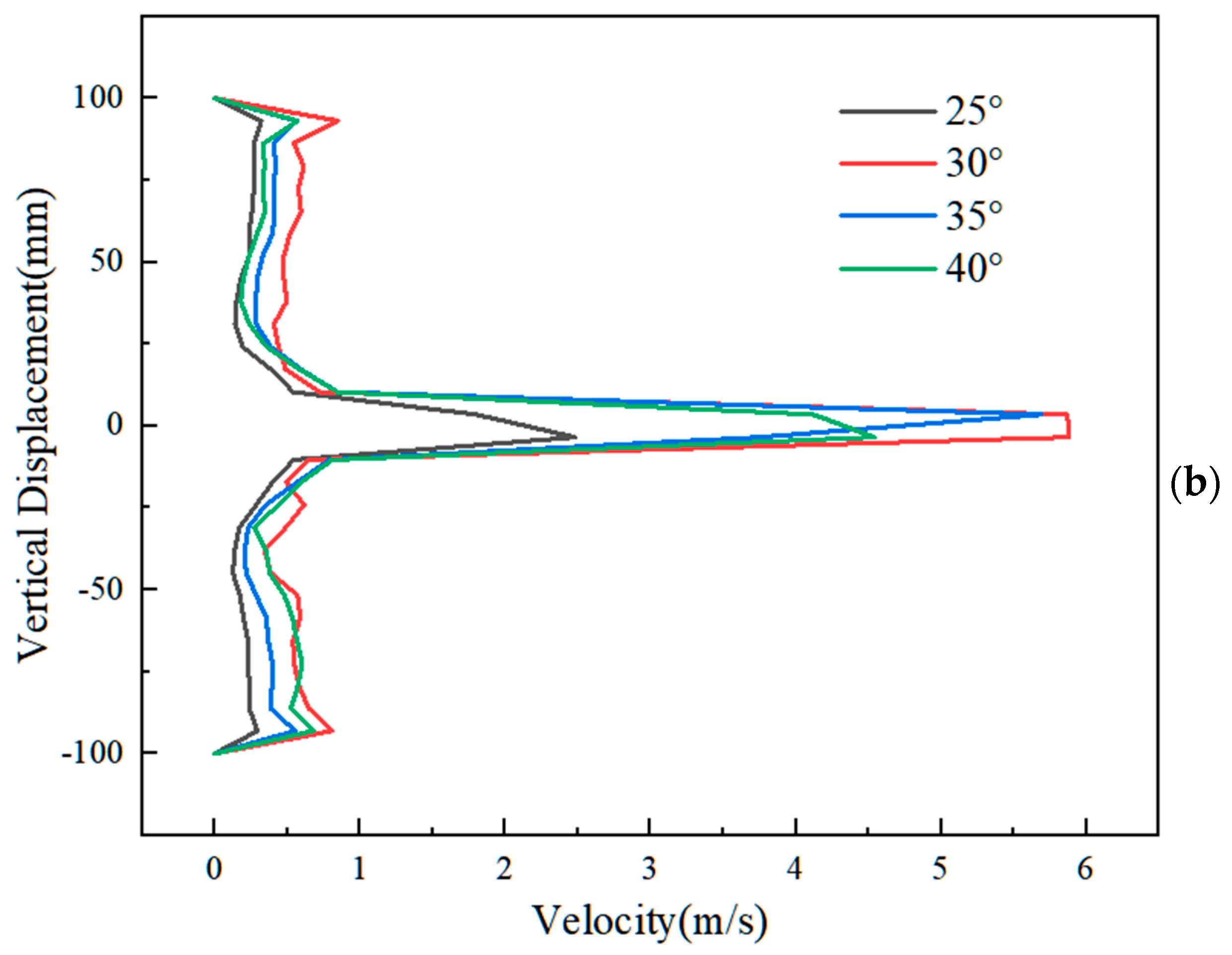
4.3. Analysis of Velocity Displacement Relationship in y Direction
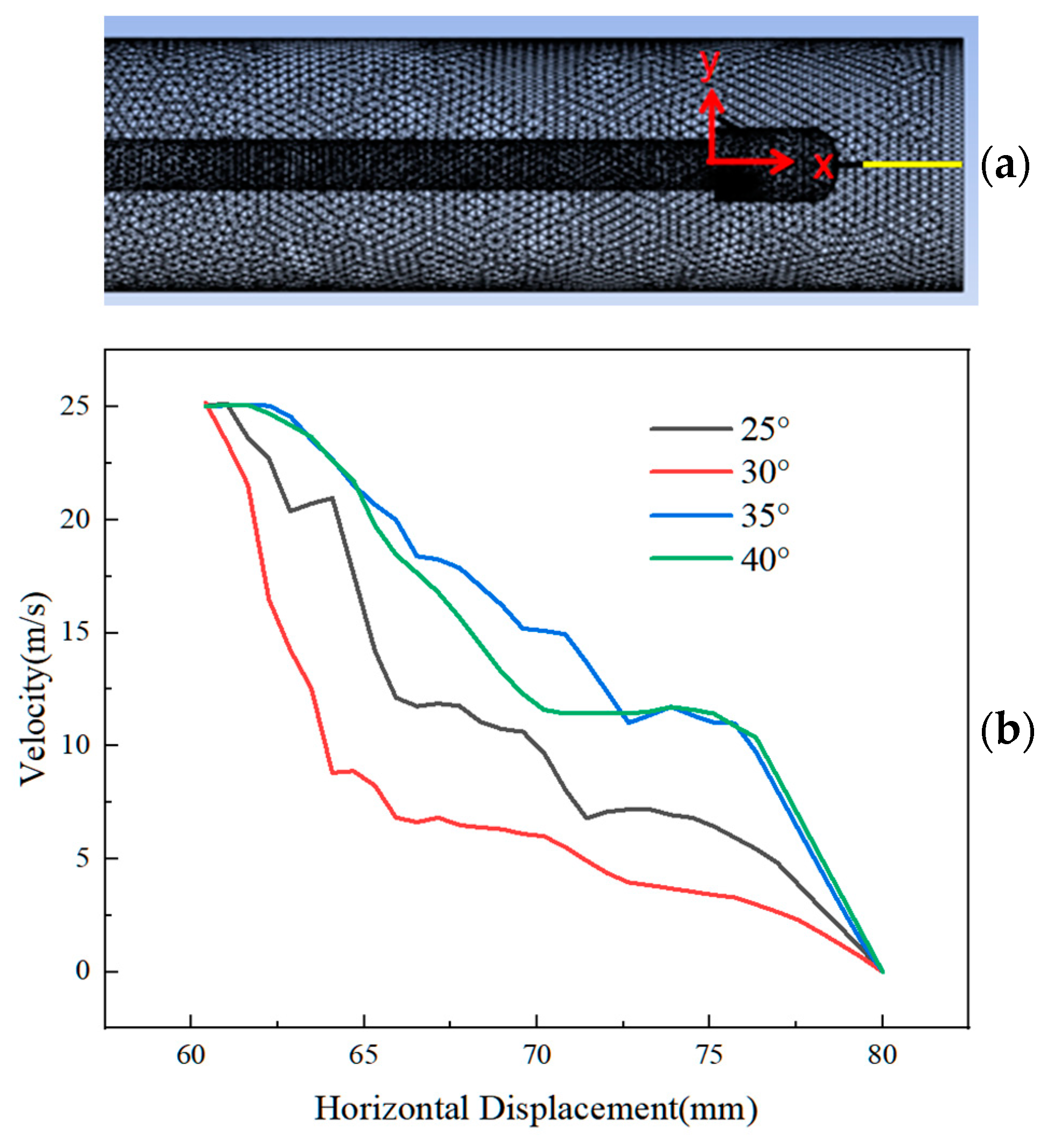
4.4. Comparison of Velocity Displacement of Different Aperture Jets
5. Conclusions
- (1)
- The rear nozzle’s varying inclination angles significantly influence the internal flow field of the pipeline. Specifically, when the inclination angle is set at 35°, further increasing the angle leads to a shortened stroke from the outlet to the wall surface, resulting in an elevated instantaneous velocity of the rear jet upon contact with the wall. However, this does not translate to a continual increase in the overall wall velocity.
- (2)
- The interplay between the rear and front jets creates vortex zones and wall backflow within the pipeline, subsequently affecting the jet velocity of the front nozzle. Notably, at an inclination angle of 35° for the rear nozzle, the impact on the flow velocity within the front jet pipe is minimized. Taking the 35° inclined rear nozzle scheme as an example, the jet velocity of the 2 mm aperture front nozzle experiences an attenuation of 77.2%, while the jet velocity of the 3.5 mm aperture front nozzle undergoes an attenuation of 67.7%.
- (3)
- When the inclination angle of the rear nozzle remains constant, augmenting the nozzle aperture from 2 mm to 3.5 mm effectively decreases the size of the vortex area. The vortex area of the 3.5 mm aperture nozzle comprises 63% of that of the 2 mm aperture nozzle. The reduction in this vortex can improve the dredging efficiency and reduce the damage to the workpiece.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Y.Q.; Ren, Q.L.; Xue, S.X.; Chen, Z.W.; Zhu, H.Q.; Pang, L. Research on new application technology and equipment of water jet. Fluid Mach. 2018, 46, 36–40. [Google Scholar]
- Peng, H.; Zhang, P. Numerical Simulation of High Speed Rotating Waterjet Flow Field in a Semi Enclosed Vacuum Chamber. CMES Comput. Model. Eng. Sci. 2018, 114, 59–73. [Google Scholar]
- Chen, J.; Yang, R.; Huang, Z.; Li, G.; Qin, X.; Li, J.; Wu, X. Detached eddy simulation on the structure of swirling jet flow field. Pet. Explor. Dev. Online 2022, 49, 929–941. [Google Scholar] [CrossRef]
- Qin, C.; Loth, E. Numerical description of a pressure-swirl nozzle spray. Chem. Eng. Process. Process Intensif. 2016, 107, 68–79. [Google Scholar] [CrossRef]
- Zhao, L.; Li, Y.Q.; Zhang, D.; Shen, S.Q. Experimental study on the characteristics of internal and external flow field of spiral nozzle. J. Chem. Ind. 2024, 8, 1–16. Available online: http://kns.cnki.net/kcms/detail/11.1946.TQ.20240618.1113.004.html (accessed on 1 January 2024).
- Shaji, K.; Lee, K.-K.; Salmani, F.; Kim, H.D. Numerical analysis and an approach for optimization of the Ranque–Hilsch vortex tube for a compressible flow. Appl. Therm. Eng. 2024, 243, 122590. [Google Scholar] [CrossRef]
- Liu, Y.; Dai, S.; Wei, J.P.; Guo, X.H.; Yuan, Y.W. Study on the motion equation and key parameters of self-propelled rotary drill hole repair. J. Henan Polytech. Univ. 2023, 9, 2021110075. [Google Scholar]
- Liu, Y.; Liang, B.C.; He, A.; Wei, J.P. Research on Drilling REPAIR theory and Key Parameters of Self-Propelled Rotary Drill Bit; China Safety Production Science and Technology: Beijing, China, 2016; Volume 12, pp. 39–44. [Google Scholar]
- Xiao, S. Study on the Flow Field Characteristics of Self-Rotating Jet and the Mechanism of Coal and Rock Breaking. Ph.D. Dissertation, Chongqing University, Chongqing, China, 2019. [Google Scholar] [CrossRef]
- Mitra, A.; Murugan, S.; van Hout, R.; Kleiman, A.; Raizner, M.; Cukurel, B. Near-field flow characteristics of a free coaxial jet. Int. J. Heat Fluid Flow 2023, 103, 109186. [Google Scholar] [CrossRef]
- Li, M.; Wang, J. Numerical simulation of flow field in self-propelled nozzle wellbore. J. Cent. South Univ. 2015, 46, 3656–3662. [Google Scholar]
- Du, P.; Peng, X.; Wei, Z.; Xu, B. Flow field investigation of a straight–swirling integrated jet for radial jet drilling. Energy Rep. 2022, 8, 7434–7443. [Google Scholar] [CrossRef]
- Wen, J.; Chen, C. Optimizing the Structure of the Straight Cone Nozzle and the Parameters of Borehole Hydraulic Mining for Huadian Oil Shale Based on Experimental Research. Energies 2017, 10, 2021. [Google Scholar] [CrossRef]
- Li, J.C.; Li, H.Y.; Chen, J.; Yang, Y.M. Study on the effect of nozzle structure on the performance of vacuum jet atomization. J. Vac. Sci. Technol. 2014, 34, 101–105. [Google Scholar]
- Yang, G.L.; Zhou, W.H.; Liu, F. Flow field simulation of high pressure water jet nozzle based on fluent. J. Lanzhou Univ. Technol. 2008, 2, 49–52. [Google Scholar]
- Tang, M.Z.; Cai, Y.; Chen, L.Y.; Li, Y.F. Design of high pressure water jet nozzle structure and flow field simulation based on CFD. Mech. Des. 2023, 12, 25. [Google Scholar] [CrossRef]
- Chen, Z.S.; Huang, L.Y.; Du, B.X.; Chen, Y.J.; Ni, L.X.; Jiang, H. Study on hydrodynamic characteristics of ultra-high pressure water jet nozzle. Explos. Shock. 2022, 42, 158–171. [Google Scholar]
- Wang, Y.X.; Wang, Z.W.; Zhang, M.J.; Meng, F.G.; Song, Y.X.; Zhang, L.H. Research on flow mechanism and structural optimization design of high pressure nozzle. J. Vac. Sci. Technol. 2024, 08, 1–8. [Google Scholar] [CrossRef]
- Niazi, M.; Ashrafizadeh, S.N.; Hashemabadi, S.H.; Karami, H. CFD simulation of drag-reducing fluids in a non-Newtonian turbulent pipe flow. Chem. Eng. Sci. 2024, 285, 119612. [Google Scholar] [CrossRef]
- Wang, G.; Yang, F.; Wu, K.; Ma, Y.; Peng, C.; Liu, T.; Wang, L. Estimation of the dissipation rate of turbulent kinetic energy: A review. Chem. Eng. Sci. 2020, 229, 116133. [Google Scholar] [CrossRef]
- Yang, Y.; Li, W.; Shi, W.; Zhang, W.; El-Emam, M.A. Numerical Investigation of a High-Pressure Submerged Jet Using a Cavitation Model Considering Effects of Shear Stress. Processes 2019, 7, 541. [Google Scholar] [CrossRef]
- Moghadam, M.M.; Islami, H.R.; Ezam, M.; Mousavi, S.A. Optimizing flow uniformity and velocity fields in aquaculture tanks by modifying water inlets and nozzles arrangement: A computational fluid dynamics study. Aquac. Eng. 2024, 106, 102431. [Google Scholar] [CrossRef]
- Adarsh, V.; Kaustav, C. The vortex structures of the mean turbulent flow field in a 90-degree bend pipe. Eur. J. Mech.-B/Fluids 2023, 98, 21–31. [Google Scholar]
- Wei, Y.; Zhang, D.; Wang, L. Calculation of self-propelled rotating water jet self-propelled force. Coal Mine Mach. 2007, 8, 14–15. [Google Scholar] [CrossRef]
- Feng, Q.; Bu, Q.; Liu, S. Similarity analysis and numerical simulation of flow field in rotating disk cavity with pre-swirl nozzle. J. Northw. Polytech. Univ. 2003, 2, 239–243. [Google Scholar]
- Dong, Z.Z.; Fu, B.W.; Guo, C.; Xi, Y.Q. Flow field simulation analysis of high pressure water jet nozzle based on CFD. Pet. Petro Chem. Equip. 2016, 19, 20–23. [Google Scholar]
- Zhang, S.; Tao, X.; Lu, J.; Wang, X.; Zeng, Z. Structure Optimization and Numerical Simulation of High Pressure Water Jet Nozzle. Mater. Sci. Eng. Prog. 2015, 2015, 732054. [Google Scholar]
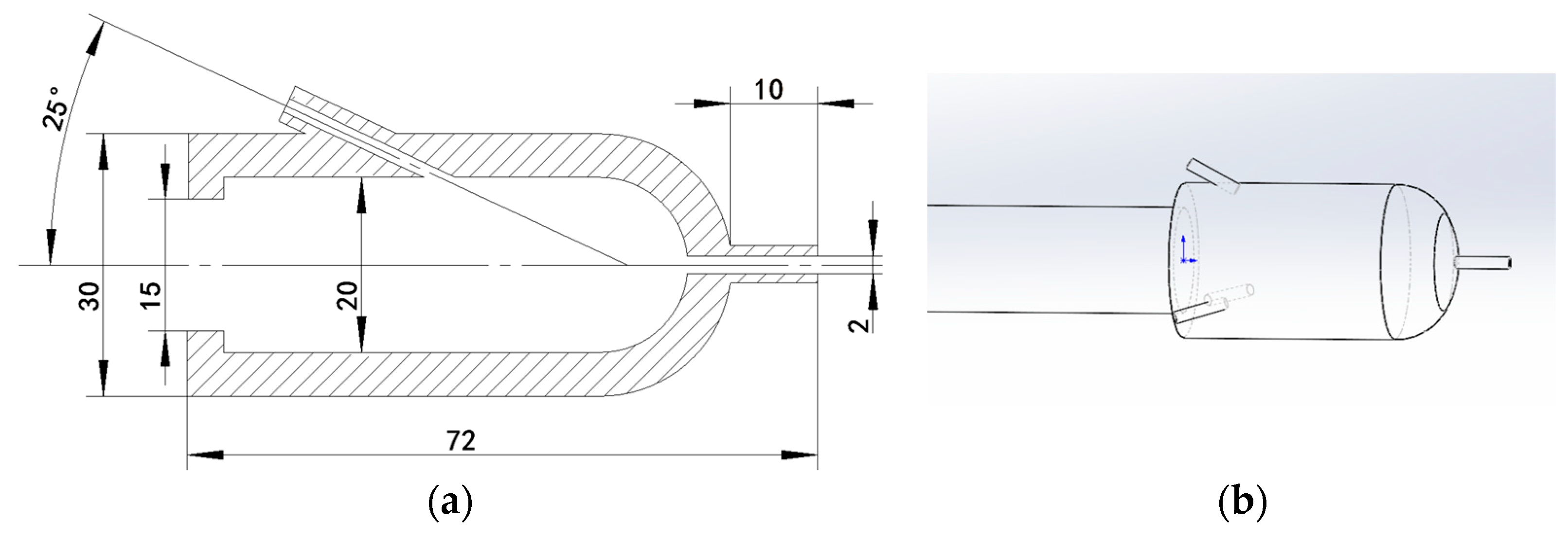







| Scheme | Nozzle Diameters (mm) | Rear Nozzle Inclination | Initial Velocity (m/s) |
|---|---|---|---|
| 1 | 2 | 25° | 25 |
| 2 | 2 | 30° | 25 |
| 3 | 2 | 35° | 25 |
| 4 | 2 | 40° | 25 |
| 5 | 3.5 | 30° | 25 |
| 6 | 3.5 | 35° | 25 |
| 7 | 3.5 | 40° | 25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, Y.; Geng, Z.; Yuan, H.; Zhai, S.; Huo, F. Numerical Simulation and Flow Field Analysis of Porous Water Jet Nozzle Based on Fluent. Appl. Sci. 2024, 14, 7075. https://doi.org/10.3390/app14167075
Pan Y, Geng Z, Yuan H, Zhai S, Huo F. Numerical Simulation and Flow Field Analysis of Porous Water Jet Nozzle Based on Fluent. Applied Sciences. 2024; 14(16):7075. https://doi.org/10.3390/app14167075
Chicago/Turabian StylePan, Yue, Zhongcheng Geng, Hao Yuan, Shengyu Zhai, and Fulin Huo. 2024. "Numerical Simulation and Flow Field Analysis of Porous Water Jet Nozzle Based on Fluent" Applied Sciences 14, no. 16: 7075. https://doi.org/10.3390/app14167075
APA StylePan, Y., Geng, Z., Yuan, H., Zhai, S., & Huo, F. (2024). Numerical Simulation and Flow Field Analysis of Porous Water Jet Nozzle Based on Fluent. Applied Sciences, 14(16), 7075. https://doi.org/10.3390/app14167075







