An Assessment Method for the Step-Down Stress Accelerated Degradation Test Considering Random Effects and Detection Errors
Abstract
:1. Introduction
- (1)
- This article proposes a new method for assessing storage life under the SDSADT to solve the problem of slow product performance degradation at the beginning of the step-stress ADT. This article mainly focuses on the assessment method for the storage life of high-reliability and long-life products under the SDSADT.
- (2)
- A new IG performance degradation model is proposed. This model introduces the Gamma distribution to characterize the randomness of and difference in the degradation paths of different products and uses the normal distribution to describe the detection errors of performance parameters. This model can solve the problem of the product storage life assessment caused by random effects and detection errors.
- (3)
- The Monte Carlo (MC) technique is employed to estimate the unknown parameters in the IG model to solve the problem that the calculation of the likelihood function is complicated and there is no explicit expression. This method can improve the calculation accuracy and efficiency.
- (4)
- Parameter estimation and storage life assessment are carried out on the SDSADT data from a specific missile tank to verify the effectiveness and feasibility of the proposed method.
2. Theoretical Background
2.1. Step-Down Stress Accelerated Degradation Test
2.2. Life Assessment Method Based on IG Process for Accelerated Degradation Test
- (1)
- The value of is always 0.
- (2)
- For any , and are independent degradation increments.
- (3)
- For any , follows the IG process with mean and variance , which is denoted as . Here, and are constants. , , and is the monotone increasing function of time .
3. Proposed Method
3.1. Model Assumption
- (1)
- In the SDSADT, the degradation path of the product follows the IG process. Without loss of generality, it is assumed that the performance degradation increases monotonically with time.
- (2)
- The failure mechanism of the product under accelerated stress levels is unchanged and the same as under normal stress levels.
- (3)
- The remaining life of the product depends only on the current stress level and the parts that have accumulated degradation. It has nothing to do with the accumulation method [25].
3.2. IG Model Considering Random Effects and Detection Errors
3.3. Parameter Estimation and Storage Life Assessment
4. Case Study
4.1. Data Description
4.2. Comparison Method
- (1)
- SNADM: This method is based on an equivalent approach of the cumulative damage theory to derive the piecewise expression for the overall cumulative degradation function. It then combines the nonlinear function to obtain a Segmented Nonlinear Accelerated Degradation Model (SNADM). Subsequently, numerical iterative methods are used to estimate the model parameters [22].
- (2)
- Simple IG process: This method uses an IG process-based approach described in Section 2.2 of this article, which ignores the randomness of the degradation paths among different samples. It assumes that all samples share the same performance degradation process and uses the MLE method to estimate the model parameters.
- (3)
- IG model considering random effects (IG-RE): This method only considers the randomness of the product degradation paths and uses the Markov Chain Monte Carlo (MCMC) method to estimate the unknown parameters in the degradation model [21].
4.3. Parameter Estimation and Result Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, Y.; Zhang, Q.; Cai, Z.; Wang, L. Storage Reliability Assessment Model Based on Competition Failure of Multi-Components in Missile. J. Syst. Eng. Electron. 2017, 28, 606–616. [Google Scholar]
- Wang, X.; Wang, B.; Wu, W.; Hong, Y. Reliability Analysis for Accelerated Degradation Data Based on the Wiener Process with Random Effects. Qual. Reliab. Eng. 2020, 36, 1969–1981. [Google Scholar] [CrossRef]
- Jiang, P.; Wang, B.; Wang, X.; Zhou, Z. Inverse Gaussian Process Based Reliability Analysis for Constant-Stress Accelerated Degradation Data. Appl. Math. Model. 2022, 105, 137–148. [Google Scholar] [CrossRef]
- Feng, X.; Tang, J.; Tan, Q.; Yin, Z. Reliability Model for Dual Constant-Stress Accelerated Life Test with Weibull Distribution under Type-I Censoring Scheme. Commun. Stat. Theory Methods 2022, 51, 8579–8597. [Google Scholar] [CrossRef]
- Lim, H.; Yum, B. Optimal Design of Accelerated Degradation Tests Based on Wiener Process Models. J. Appl. Stat. 2011, 38, 309–325. [Google Scholar] [CrossRef]
- Wang, L.; Pan, R.; Li, X.; Jiang, T.A. Bayesian Reliability Evaluation Method with Integrated Accelerated Degradation Testing and Field Information. Reliab. Eng. Syst. Saf. 2013, 112, 38–47. [Google Scholar] [CrossRef]
- Méndez-González, L.; Rodríguez-Picón, L.; Pérez Olguin, I.; Garcia, V.; Quezada-Carreón, A. Reliability Analysis for DC Motors under Voltage Step-Stress Scenario. Electr. Eng. 2020, 102, 1433–1440. [Google Scholar] [CrossRef]
- Tang, S.; Guo, X.; Yu, C.; Xue, H.; Zhou, Z. Accelerated Degradation Tests Modeling Based on the Nonlinear Wiener Process with Random Effects. Math. Probl. Eng. 2014, 2014, 1–11. [Google Scholar] [CrossRef]
- Sun, L.; Gu, X.; Song, P. Accelerated Degradation Process Analysis Based on the Nonlinear Wiener Process with Covariates and Random Effects. Math. Probl. Eng. 2016, 2016, 1–13. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, Y.; Ma, X. Mechanism Equivalence in Designing Optimum Step-Stress Accelerated Degradation Test Plan under Wiener Process. IEEE Access 2018, 6, 4440–4451. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, X.; Wen, X. Step-Down-Stress Accelerated Life Test-Methodology. Acta Armamentarii 2005, 26, 661–665. [Google Scholar]
- Cai, M.; Yang, D.; Zheng, J.; Mo, Y.; Huang, J.; Xu, J.; Chen, W.; Zhang, G.; Chen, X. Thermal Degradation Kinetics of LED Lamps in Step-Up-Stress and Step-Down-Stress Accelerated Degradation Testing. Appl. Therm. Eng. Des. Process. Equip. Econ. 2016, 107, 918–926. [Google Scholar] [CrossRef]
- Qi, H.; Zhang, X.; Xie, X.; Lv, C.; Chen, C.; Zhao, L. Storage Life of Power Switching Transistors Based on Performance Degradation Data. J. Semicond. 2014, 35, 044006. [Google Scholar] [CrossRef]
- Hong, Y.; Duan, Y.; Meeker, W.; Stanley, D.; Gu, X. Statistical Methods for Degradation Data with Dynamic Covariates Information and an Application to Outdoor Weathering Data. Technometrics 2015, 57, 180–193. [Google Scholar] [CrossRef]
- Liu, T.; Sun, Q.; Pan, Z.; Feng, J.; Tang, Y. Irregular Time-Varying Stress Degradation Path Modeling: A Case Study on Lithium-ion Cell Degradation. Qual. Reliab. Eng. Int. 2016, 32, 1889–1902. [Google Scholar] [CrossRef]
- Tang, J.; Su, T.S. Estimating Failure Time Distribution and Its Parameters Based on Intermediate Data from a Wiener Degradation Model. Nav. Res. Logist. 2008, 55, 265–276. [Google Scholar] [CrossRef]
- Wang, X.; Xu, W. An Inverse Gaussian Process Model for Degradation Data. Technometrics 2010, 52, 188–197. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, W.; Qin, H. Inverse Gaussian Process-Based Corrosion Growth Model for Energy Pipelines Considering the Sizing Error in Inspection Data. Corros. Sci. 2013, 73, 309–320. [Google Scholar] [CrossRef]
- Peng, W.; Li, Y.; Yang, Y.; Huang, H.; Zuo, M. Inverse Gaussian Process Models for Degradation Analysis: A Bayesian Perspective. Reliab. Eng. Syst. Saf. 2014, 130, 175–189. [Google Scholar] [CrossRef]
- Tsai, T.; Sung, W.; Lio, Y.; Chang, S.; Lu, J. Optimal Two-Variable Accelerated Degradation Test Plan for Gamma Degradation Processes. IEEE Trans. Reliab. 2016, 65, 459–468. [Google Scholar] [CrossRef]
- Kou, H.; Wei, K. The Evaluation Method for Step-Down-Stress Accelerated Degradation Testing Based on Inverse Gaussian Process. IEEE Access 2021, 9, 73194–73200. [Google Scholar]
- Yao, J.; Xu, M.; Zhong, W. Research of Step-Down Stress Accelerated Degradation Data Assessment Method of a Certain Type of Missile Tank. Chin. J. Aeronaut. 2012, 25, 917–924. [Google Scholar] [CrossRef]
- Gao, L.; Chen, W.; Qian, P.; Pan, J.; He, Q. Optimal Design of Multiple Stresses Accelerated Life Test Plan Based on Transforming the Multiple Stresses to Single Stress. Chin. J. Mech. Eng. 2014, 27, 309–325. [Google Scholar] [CrossRef]
- Smith, A.; Roberts, G. Bayesian Computation via the Gibbs Sampler and Related Markov Chain Monte Carlo Methods. J. R. Stat. Soc. Ser. B (Methodol.) 1993, 55, 3–23. [Google Scholar] [CrossRef]
- Lee, Y.; Lu, M. Damage-Based Models for Step-Stress Accelerated Life Testing. J. Test. Eval. 2012, 34, 1–10. [Google Scholar] [CrossRef]
- Peng, C.Y. Inverse Gaussian Processes with Random Effects and Explanatory Variables for Degradation Data. Technometrics 2015, 57, 100–111. [Google Scholar] [CrossRef]
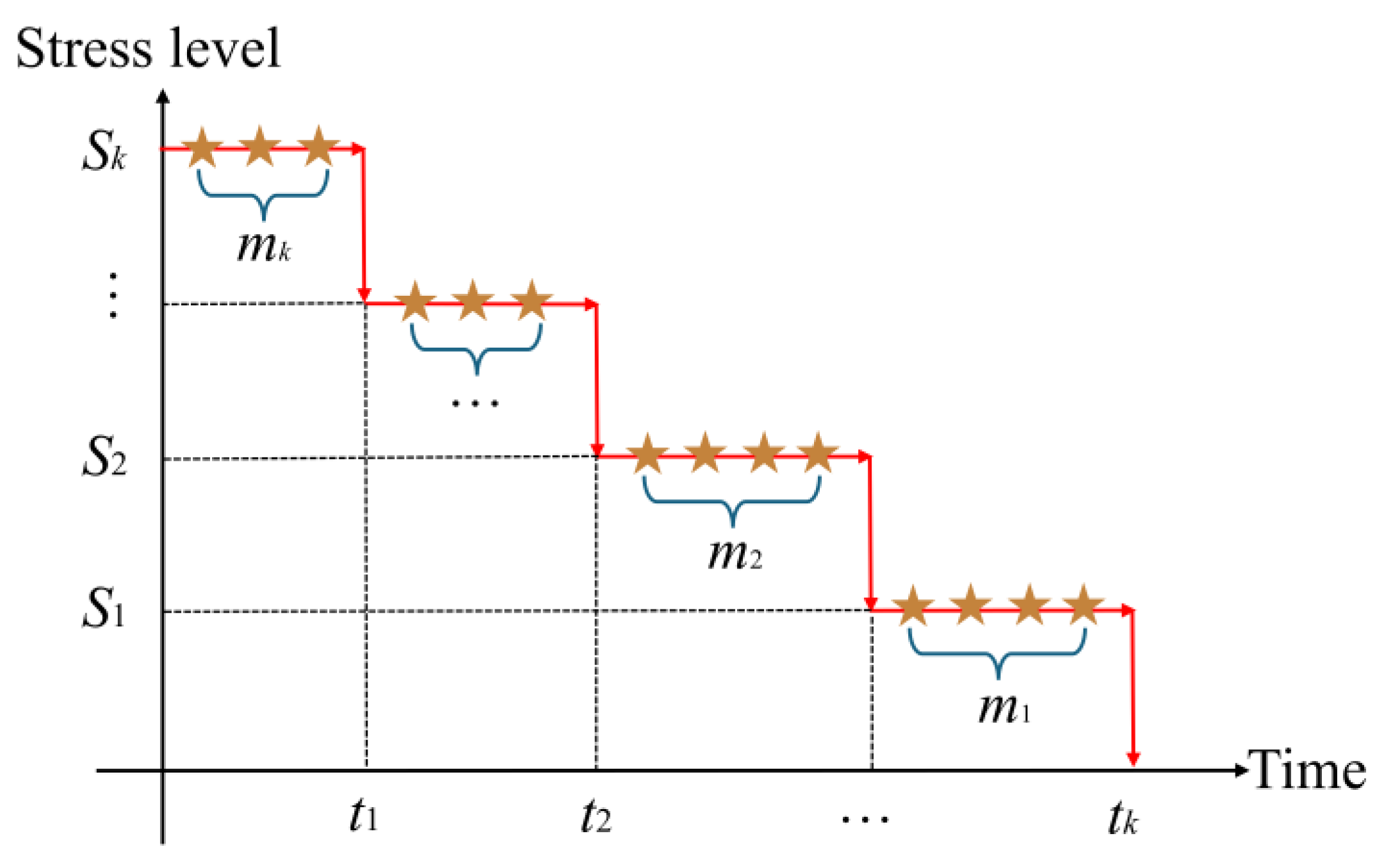
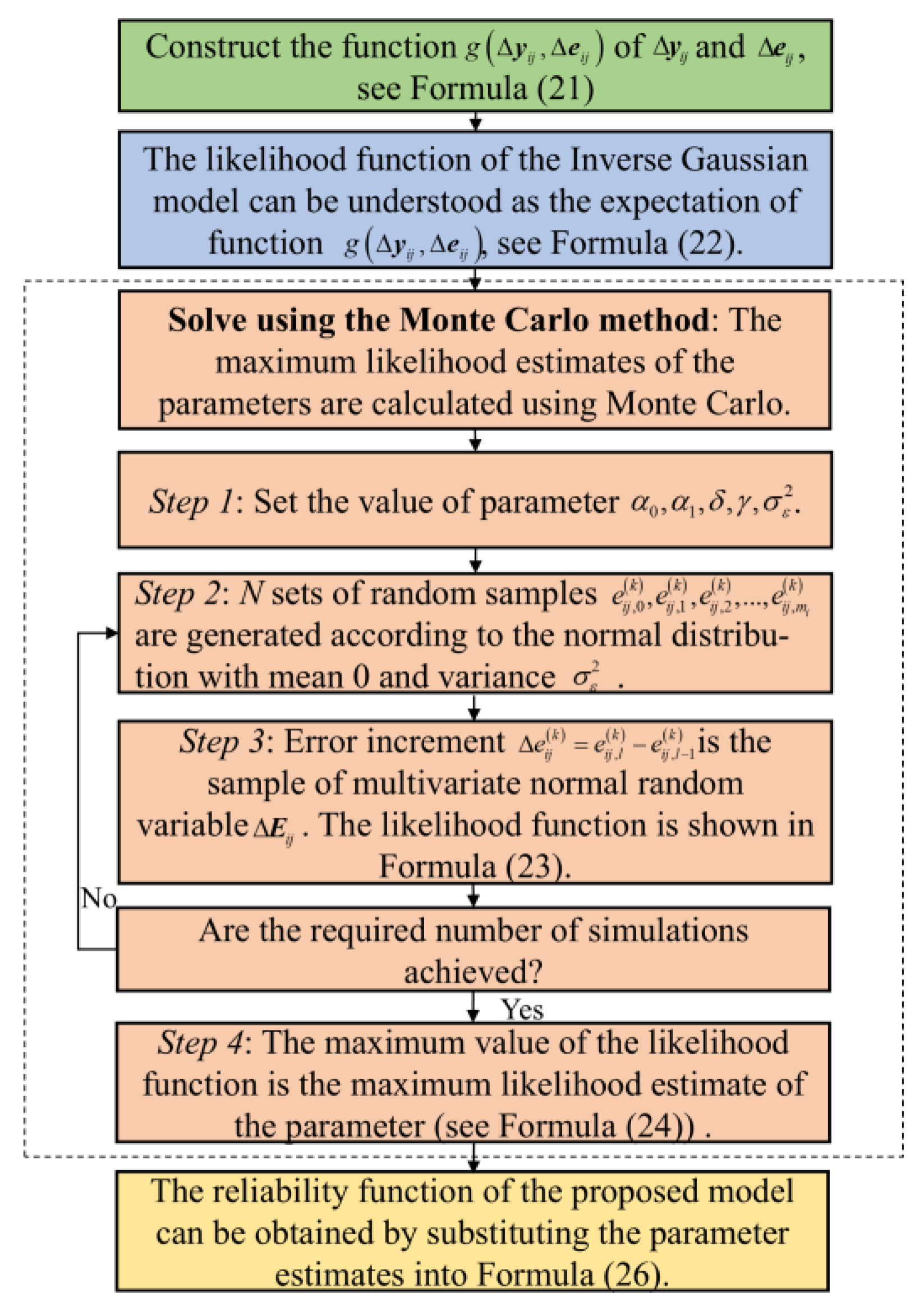
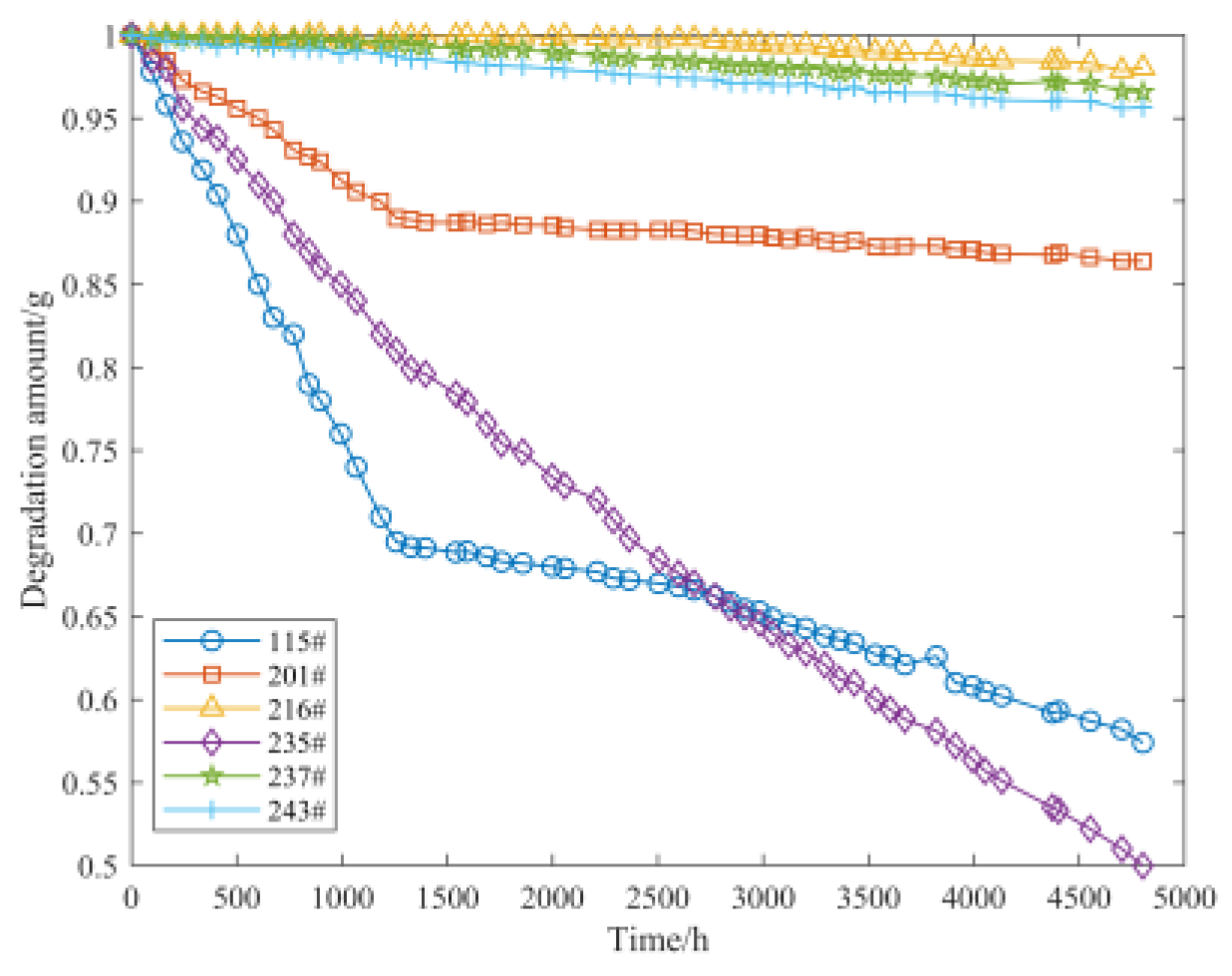
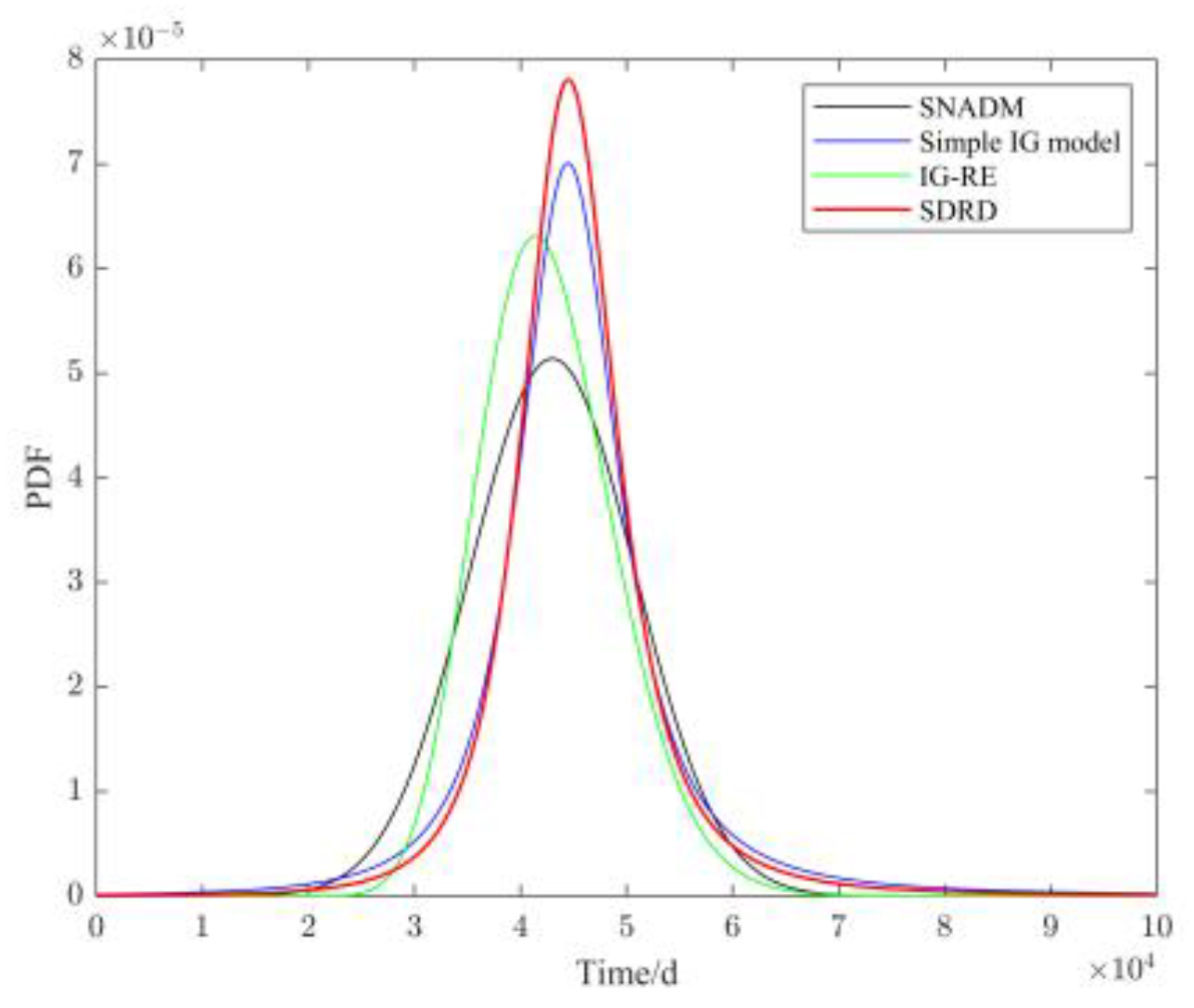
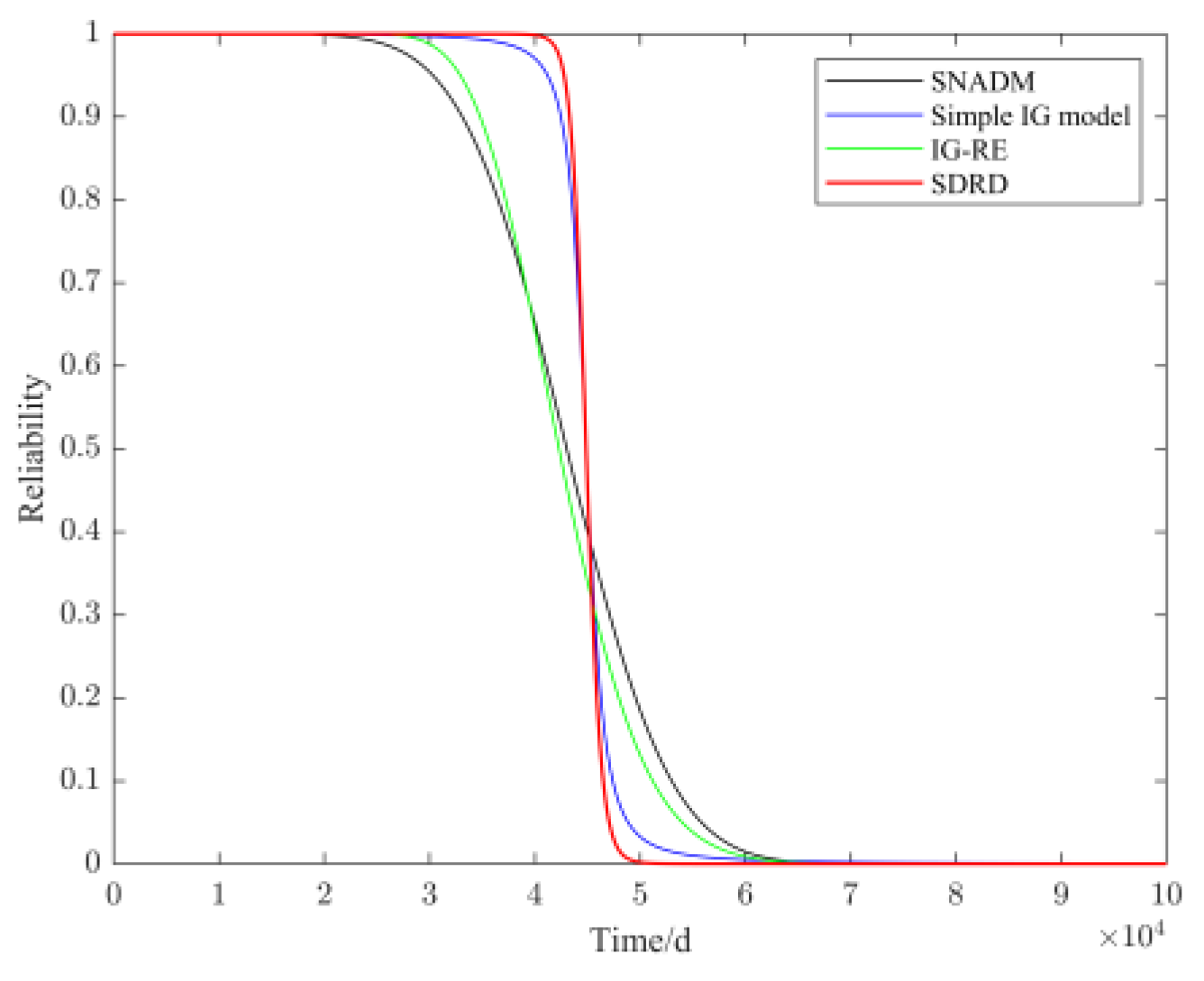
| No. | Test Parameter | Specific Details |
|---|---|---|
| 1 | Sample size | |
| 2 | The number of stress levels | |
| 3 | Stress levels/K 1 | |
| 4 | Normal stress level/K 1 | |
| 5 | Detection number | |
| 6 | Stress transition moment/h | |
| 7 | Failure threshold/g 2 | |
| 8 | Test period/h | About 72 |
| 9 | Index storage life/h 3 | 43,800 |
| Models | Index Storage Life/h | Storage Life Assessment Value/h |
|---|---|---|
| SNADM 1 | 43,800 | 42,291 |
| Simple IG model 2 | 43,028 | |
| IG-RE 3 | 43,359 | |
| SDRD 4 | 43,401 |
| Models | SNADM | Simple IG Model | IG-RE | SDRD |
|---|---|---|---|---|
| AIC | −10.15 | −32.23 | −60.89 | −72.28 |
| BIC | −10.77 | −32.85 | −61.72 | −73.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, J.; Zhao, H.; Peng, Z. An Assessment Method for the Step-Down Stress Accelerated Degradation Test Considering Random Effects and Detection Errors. Appl. Sci. 2024, 14, 7209. https://doi.org/10.3390/app14167209
Cui J, Zhao H, Peng Z. An Assessment Method for the Step-Down Stress Accelerated Degradation Test Considering Random Effects and Detection Errors. Applied Sciences. 2024; 14(16):7209. https://doi.org/10.3390/app14167209
Chicago/Turabian StyleCui, Jie, Heming Zhao, and Zhiling Peng. 2024. "An Assessment Method for the Step-Down Stress Accelerated Degradation Test Considering Random Effects and Detection Errors" Applied Sciences 14, no. 16: 7209. https://doi.org/10.3390/app14167209





