An Extensive Parametric Analysis and Optimization to Design Unidimensional Periodic Acoustic Metamaterials for Noise Attenuation
Abstract
:1. Introduction
2. Materials and Methods
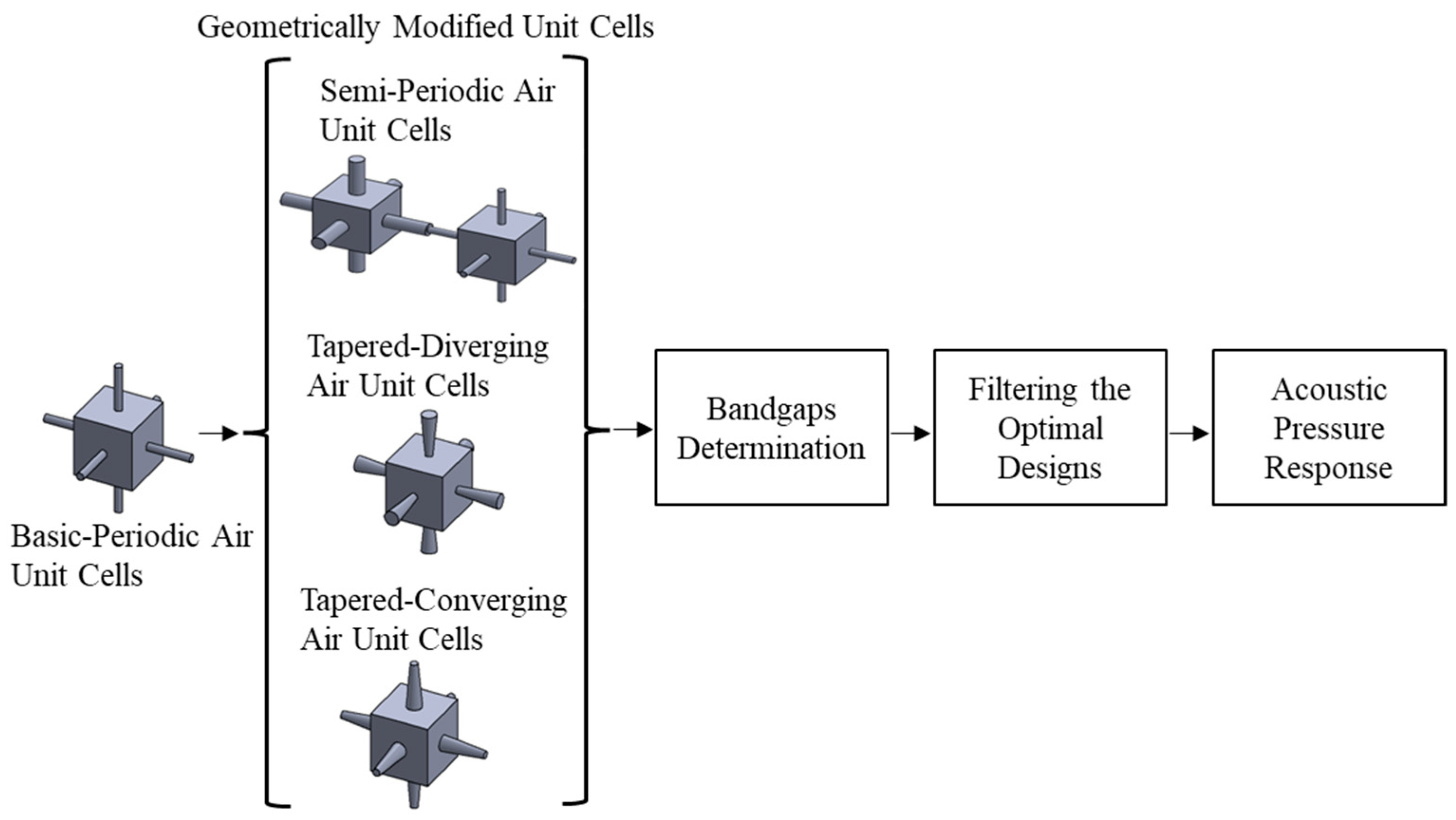
2.1. Design Framework
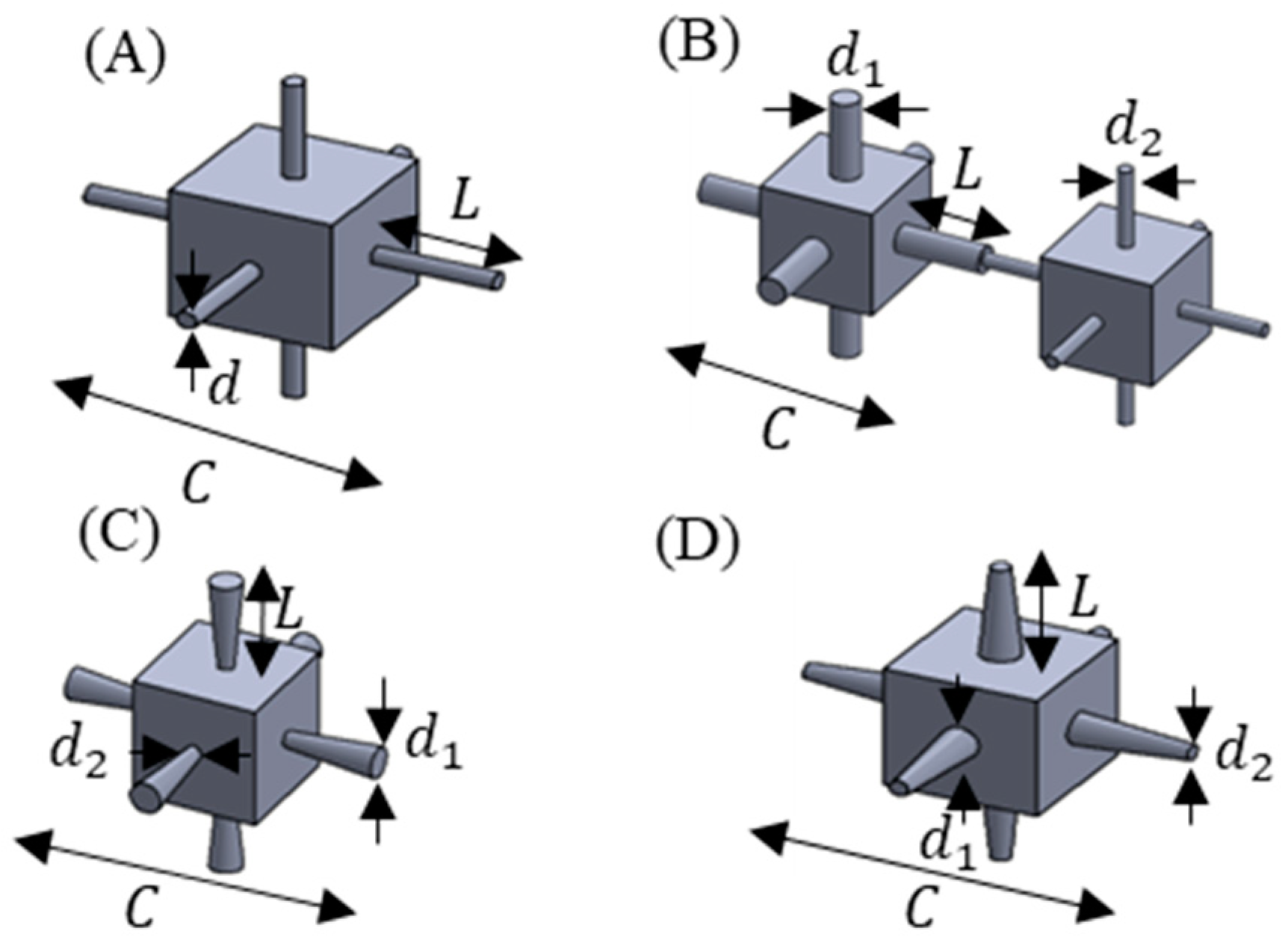
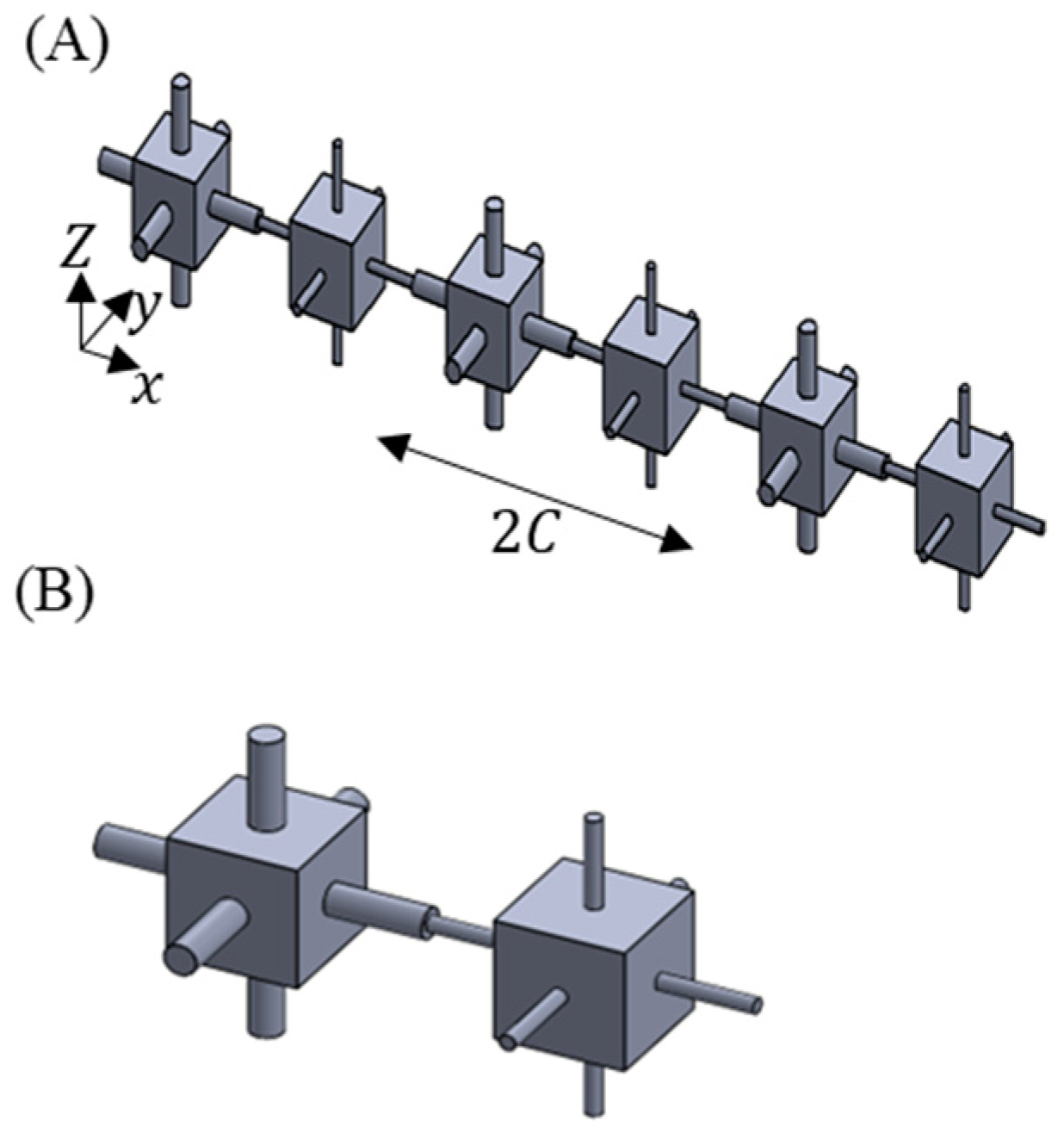
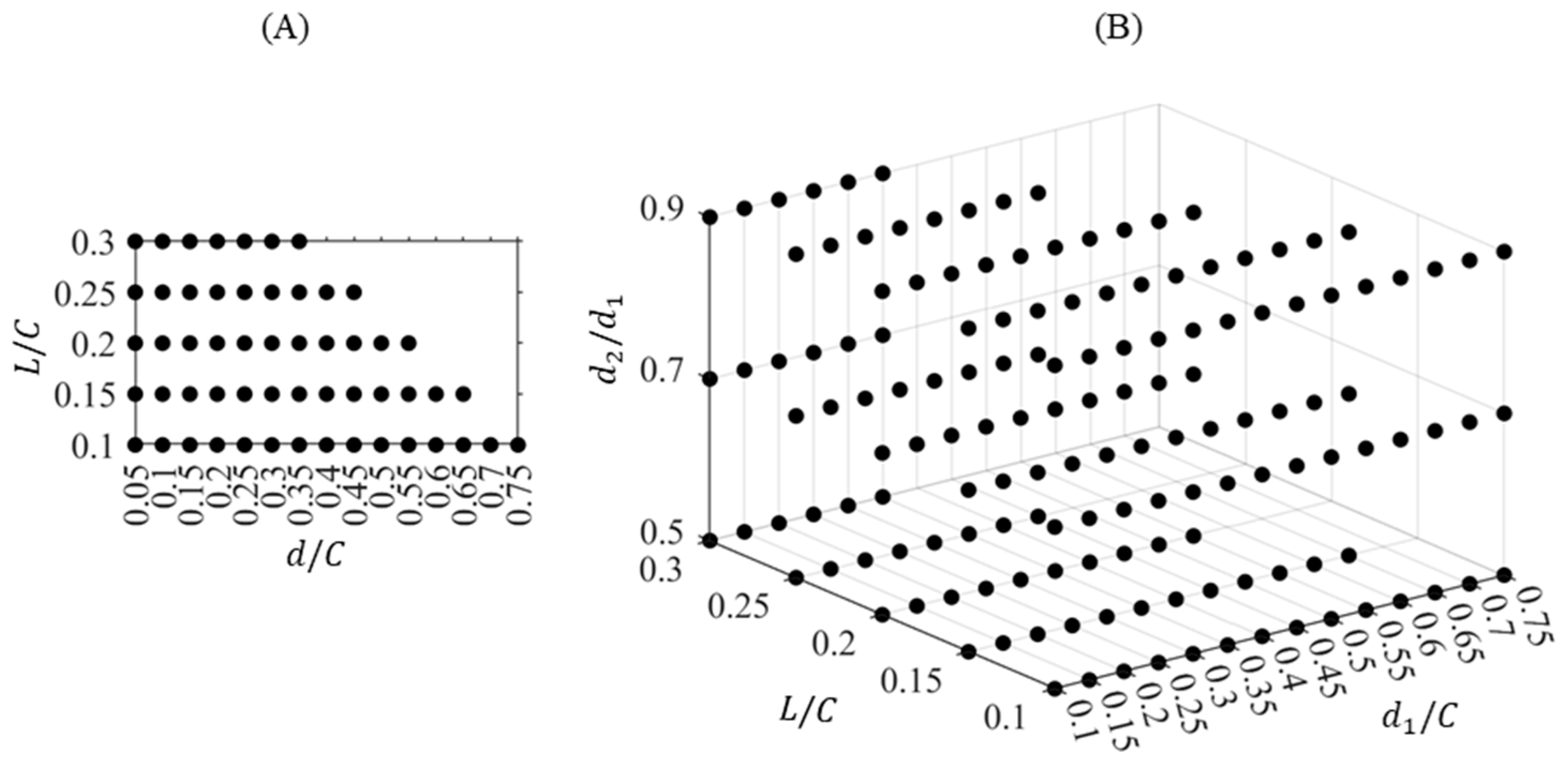
2.2. Unit Cell Designs and Geometrical Parameters
2.3. Bandgaps Determination through Utilization of FE—Bloch’s Theorem Method
3. Results
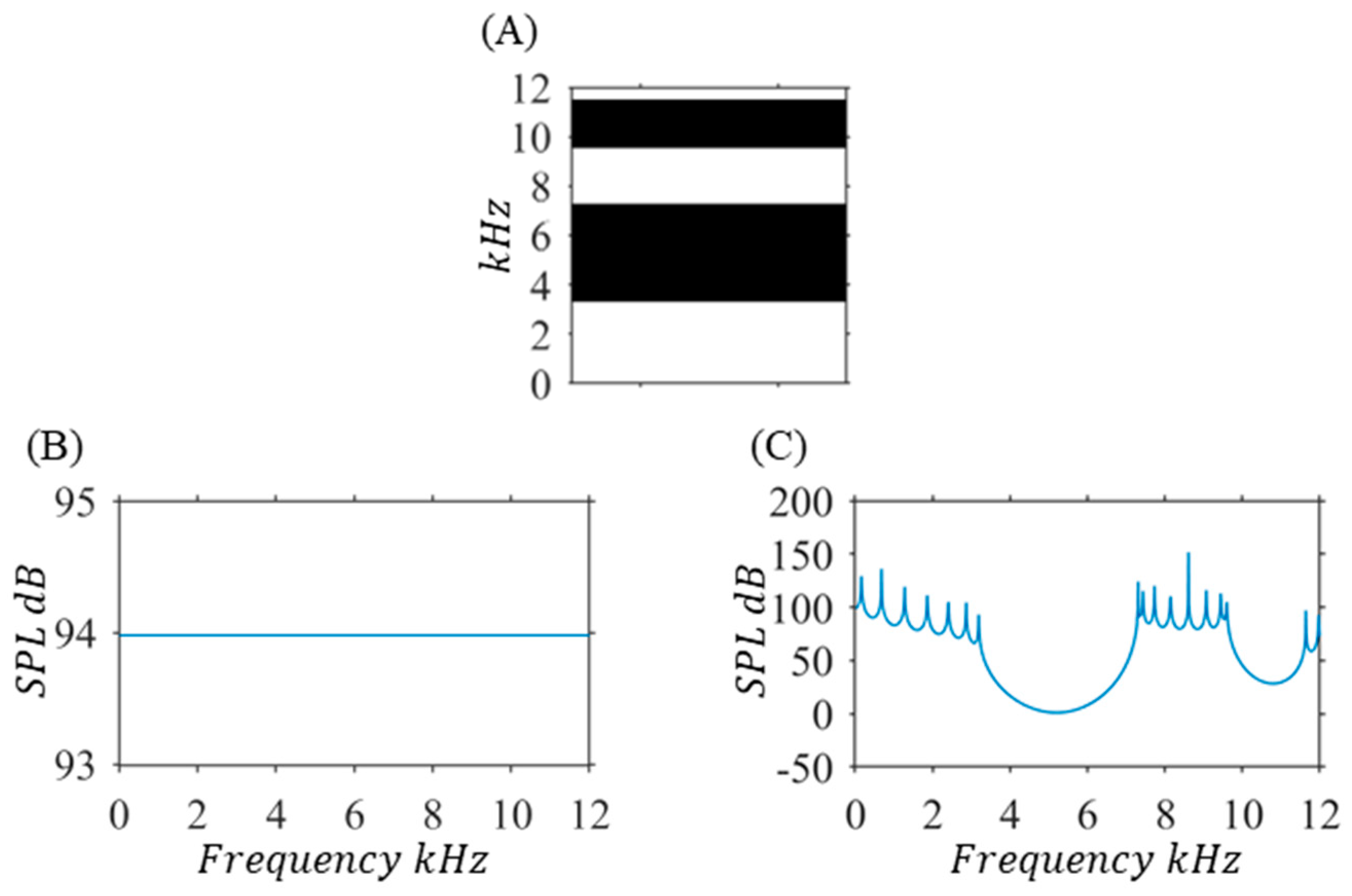
3.1. Benchmarking the Bandgaps through Using FE—Bloch’s Theorem Single Unit Cell—Dependent Methodology
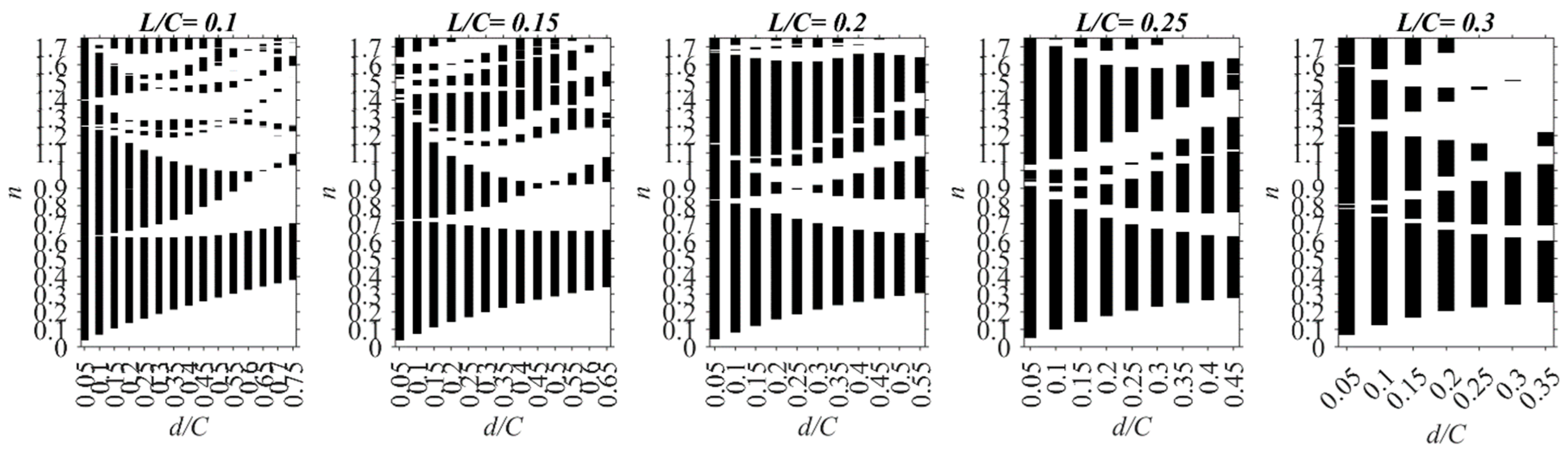
3.2. Bandgaps for All Considered Unit Cells
4. Discussion
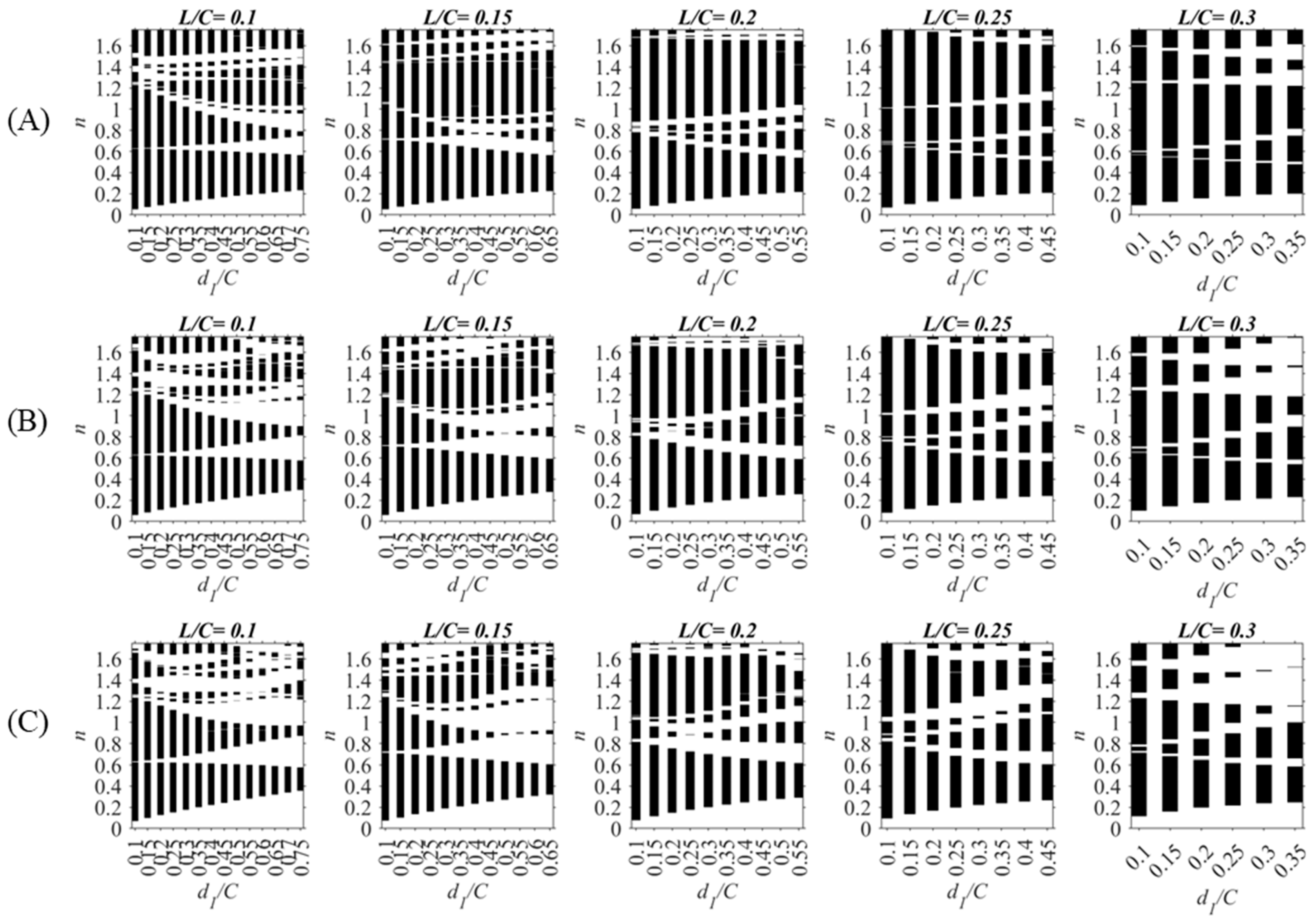
4.1. Filtering Function of the Optimal Unit Cell Design Combinations in Each Considered Unit Cell Configuration
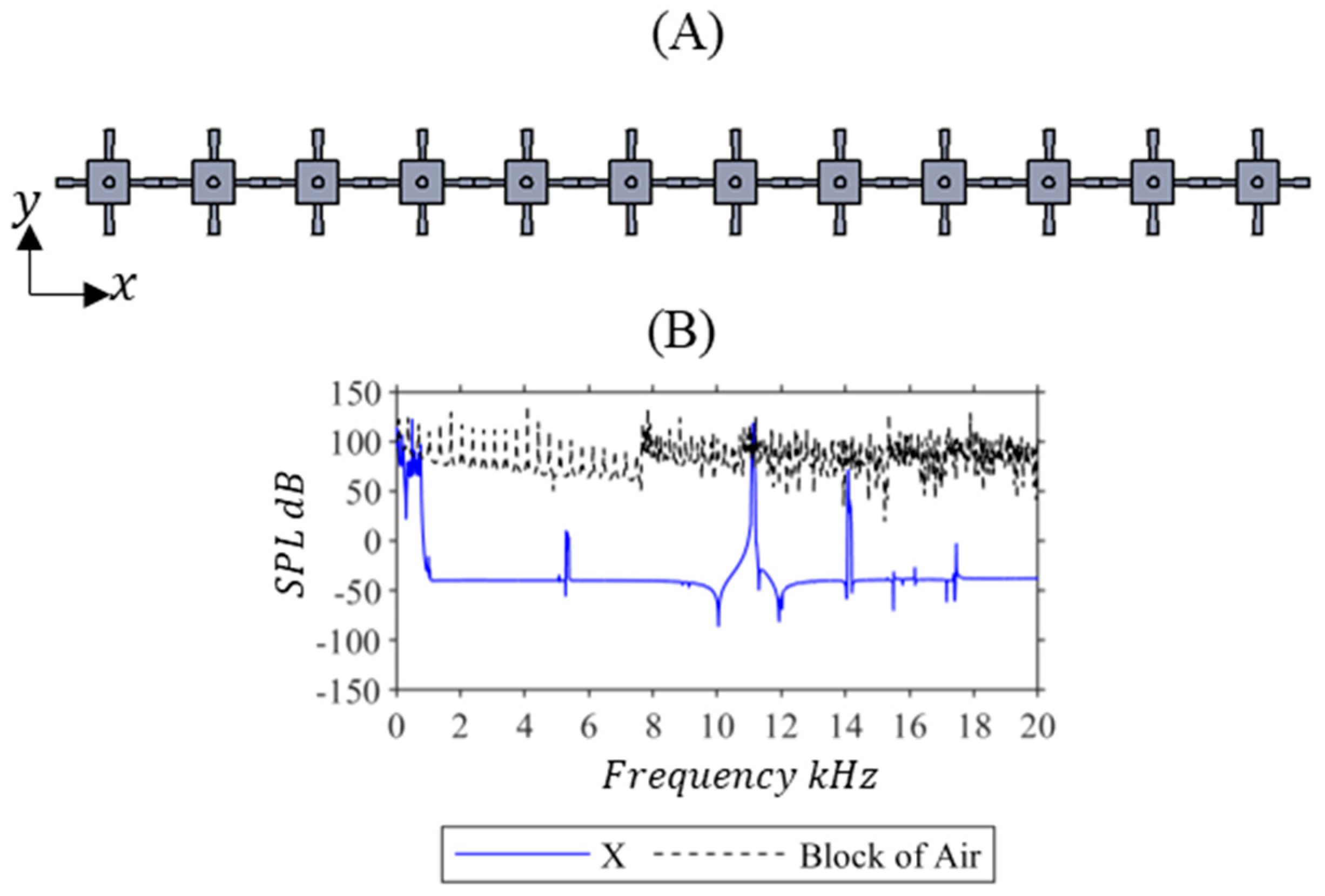
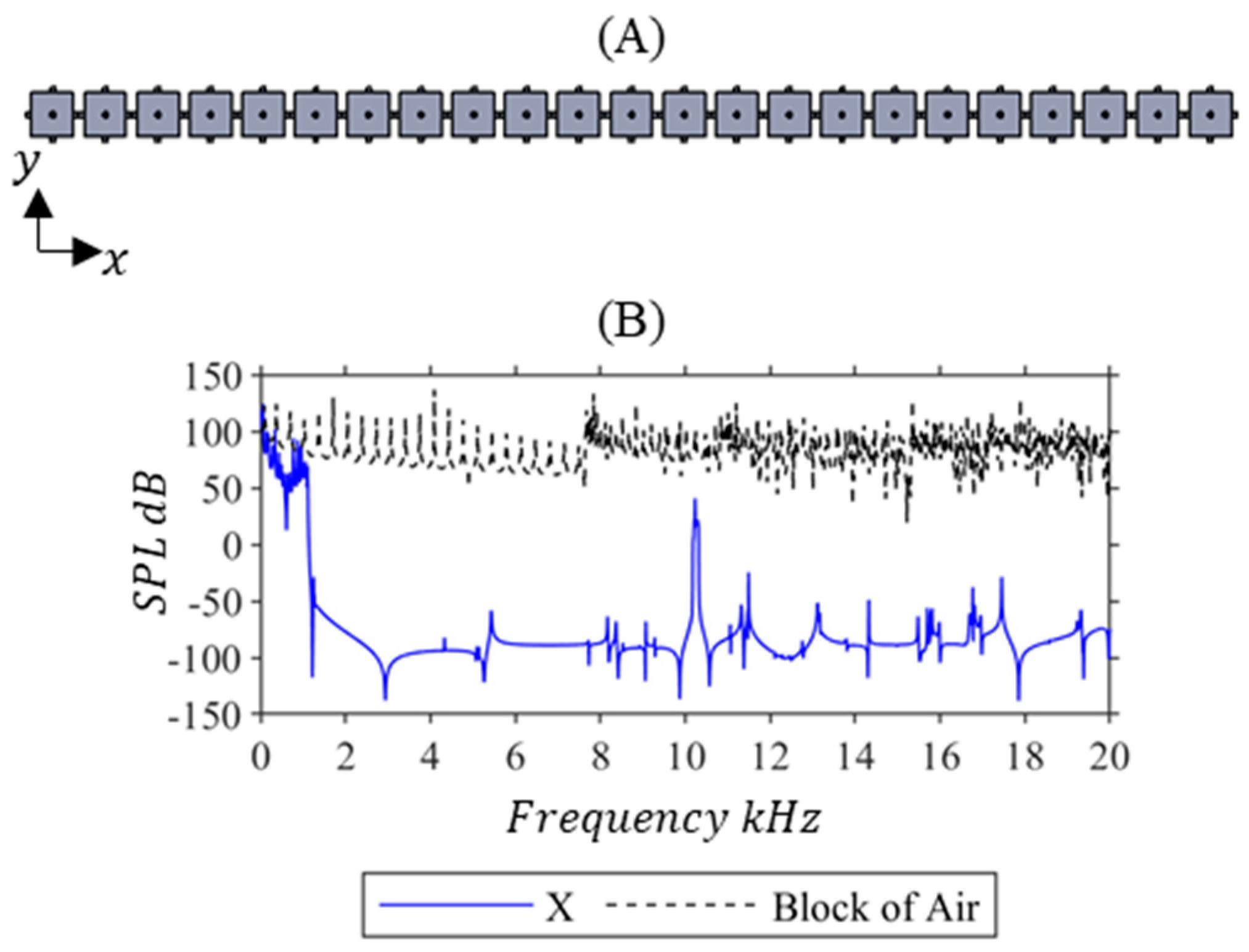
4.2. Acoustic Pressure Response of 1D Acoustic Metamaterials Made from Repeated Optimal Unit Cell
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Charakida, M.; Deanfield, J.E. Nighttime Aircraft Noise Exposure: Flying towards Arterial Disease. Eur. Heart J. 2013, 34, 3472–3474. [Google Scholar] [CrossRef] [PubMed]
- Stansfeld, S.A.; Berglund, B.; Clark, C.; Lopez-Barrio, I.; Fischer, P.; Öhrström, E.; Haines, M.M.; Head, J.; Hygge, S.; van Kamp, I.; et al. Aircraft and Road Traffic Noise and Children’s Cognition and Health: A Cross-National Study. Lancet 2005, 365, 1942–1949. [Google Scholar] [CrossRef] [PubMed]
- Dalton, B.H.; Behm, D.G. Effects of Noise and Music on Human and Task Performance: A Systematic Review. Occup. Ergon. 2007, 7, 143–152. [Google Scholar] [CrossRef]
- Padhye, R.; Nayak, R. Textile Science and Clothing Technology Acoustic Textiles; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Rao, M.D. Recent Applications of Viscoelastic Damping for Noise Control in Automobiles and Commercial Airplanes. J. Sound Vib. 2003, 262, 457–474. [Google Scholar] [CrossRef]
- Asdrubali, F.; Schiavoni, S.; Horoshenkov, K.V. A Review of Sustainable Materials for Acoustic Applications. Build. Acoust. 2012, 19, 283–312. [Google Scholar] [CrossRef]
- Yilmaz, N.D. Acoustic Properties of Biodegradable Nonwovens. Ph.D Thesis, North Carolina State University, Raleigh, NC, USA, 2009. [Google Scholar]
- Eco-Indicator 99 Manual for Designers; Ministry of Housing, Spatial Planning and the Environment: Dutch, The Netherlands, 2000.
- Yilmaz, N. Agro-Residual Fibers as Potential Reinforcement Elements for Biocomposites. In Lignocellulosic Polymer Composites: Processing, Characterization, and Properties; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014; pp. 231–270. ISBN 9781118773574. [Google Scholar]
- Phani, A.S.; Woodhouse, J.; Fleck, N.A. Wave Propagation in Two-Dimensional Periodic Lattices. J. Acoust. Soc. Am. 2006, 119, 1995–2005. [Google Scholar] [CrossRef] [PubMed]
- Alkhader, M.; Iyer, S.; Shi, W.; Venkatesh, T.A. Low Frequency Acoustic Characteristics of Periodic Honeycomb Cellular Cores: The Effect of Relative Density and Strain Fields. Compos. Struct. 2015, 133, 77–84. [Google Scholar] [CrossRef]
- Spadoni, A.; Ruzzene, M.; Gonella, S.; Scarpa, F. Phononic Properties of Hexagonal Chiral Lattices. Wave Motion 2009, 46, 435–450. [Google Scholar] [CrossRef]
- Nimmagadda, C.; Matlack, K.H. Thermally Tunable Band Gaps in Architected Metamaterial Structures. J. Sound Vib. 2019, 439, 29–42. [Google Scholar] [CrossRef]
- Pajunen, K.; Celli, P.; Daraio, C. Prestrain-Induced Bandgap Tuning in 3D-Printed Tensegrity-Inspired Lattice Structures. Extrem. Mech. Lett. 2021, 44, 101236. [Google Scholar] [CrossRef]
- Matlack, K.H.; Bauhofer, A.; Krödel, S.; Palermo, A.; Daraio, C. Composite 3D-Printed Metastructures for Lowfrequency and Broadband Vibration Absorption. Proc. Natl. Acad. Sci. USA 2016, 113, 8386–8390. [Google Scholar] [CrossRef]
- Scarpa, F.; Ouisse, M.; Collet, M.; Saito, K. Kirigami Auxetic Pyramidal Core: Mechanical Properties and Wave Propagation Analysis in Damped Lattice. J. Vib. Acoust. 2013, 135, 041001. [Google Scholar] [CrossRef]
- Shendy, M.; Alkhader, M.; Abu-Nabah, B.A.; Jaradat, M.A.; Venkatesh, T.A. Machine Learning Assisted Approach to Design Lattice Materials with Prescribed Band Gap Characteristics. Eur. J. Mech. A/Solids 2023, 102, 105125. [Google Scholar] [CrossRef]
- Zhao, P.; Zhang, K.; Deng, Z. Elastic Wave Propagation in Lattice Metamaterials with Koch Fractal. Acta Mech. Solida Sin. 2020, 33, 600–611. [Google Scholar] [CrossRef]
- Chen, Y.; Zuo, L.; Scarpa, F.; Wang, L. Broadband and Multiband Vibration Mitigation in Lattice Metamaterials with Sinusoidally-Shaped Ligaments. Extrem. Mech. Lett. 2017, 17, 24–32. [Google Scholar] [CrossRef]
- Zhao, P.; Zhang, K.; Zhao, C.; Deng, Z. Mechanism of Band Gaps in Self-Similar Triangular Lattice with Koch Fractal. J. Vib. Acoust. 2022, 144, 031009. [Google Scholar] [CrossRef]
- Zhao, P.; Zhang, K.; Zhao, C.; Qi, L.; Deng, Z. In-Plane Wave Propagation Analysis for Waveguide Design of Hexagonal Lattice with Koch Snowflake. Int. J. Mech. Sci. 2021, 209, 106724. [Google Scholar] [CrossRef]
- Zhu, Z.; Deng, Z.; Du, J. Elastic Wave Propagation in Hierarchical Honeycombs with Woodpile-like Vertexes. J. Vib. Acoust. 2019, 141, 041020. [Google Scholar] [CrossRef]
- Bilal, O.R.; Hussein, M.I. Ultrawide Phononic Band Gap for Combined In-Plane and out-of-Plane Waves. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2011, 84, 065701. [Google Scholar] [CrossRef]
- Elmadih, W.; Chronopoulos, D.; Syam, W.P.; Maskery, I.; Meng, H.; Leach, R.K. Three-Dimensional Resonating Metamaterials for Low-Frequency Vibration Attenuation. Sci. Rep. 2019, 9, 11503. [Google Scholar] [CrossRef]
- Wang, P.; Casadei, F.; Kang, S.H.; Bertoldi, K. Locally Resonant Band Gaps in Periodic Beam Lattices by Tuning Connectivity. Phys. Rev. B Condens. Matter Mater. Phys. 2015, 91, 020103. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, X.Z.; Jiang, W.Z.; Gu, Y. Tuning of Bandgap Structures in Three-Dimensional Kagome-Sphere Lattice. J. Vib. Acoust. 2014, 136, 021016. [Google Scholar] [CrossRef]
- Bilal, O.R.; Ballagi, D.; Daraio, C. Architected Lattices for Simultaneous Broadband Attenuation of Airborne Sound and Mechanical Vibrations in All Directions. Phys. Rev. Appl. 2018, 10, 054060. [Google Scholar] [CrossRef]
- Elmadih, W.; Chronopoulos, D.; Zhu, J. Metamaterials for Simultaneous Acoustic and Elastic Bandgaps. Sci. Rep. 2021, 11, 14635. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Chen, Y. Lightweight Architected Hollow Sphere Foams for Simultaneous Noise and Vibration Control. J. Phys. D Appl. Phys. 2019, 52, 325303. [Google Scholar] [CrossRef]
- Aravantinos-Zafiris, N.; Kanistras, N.; Sigalas, M.M. Acoustoelastic Phononic Metamaterial for Isolation of Sound and Vibrations. J. Appl. Phys. 2021, 129, 105108. [Google Scholar] [CrossRef]
- Li, G.; Chen, Y.; Chen, W.; Liu, J.; He, H. Local Resonance—Helmholtz Lattices with Simultaneous Solid-Borne Elastic Waves and Air-Borne Sound Waves Attenuation Performance. Appl. Acoust. 2022, 186, 108450. [Google Scholar] [CrossRef]
- Xia, B.; Li, L.; Liu, J.; Yu, D. Acoustic Metamaterial with Fractal Coiling Up Space for Sound Blocking in a Deep Subwavelength Scale. J. Vib. Acoust. 2018, 140, 011011. [Google Scholar] [CrossRef]
- Li, J.B.; Wang, Y.S.; Zhang, C. Tuning of Acoustic Bandgaps in Phononic Crystals with Helmholtz Resonators. J. Vib. Acoust. 2013, 135, 031015. [Google Scholar] [CrossRef]
- Chen, Y.; Yao, H.; Wang, L. Acoustic Band Gaps of Three-Dimensional Periodic Polymer Cellular Solids with Cubic Symmetry. J. Appl. Phys. 2013, 114, 043521. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Jasiuk, I.; Sobh, N.A. Acoustic Band Gaps and Elastic Stiffness of PMMA Cellular Solids Based on Triply Periodic Minimal Surfaces. Mater. Des. 2018, 145, 20–27. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, X.; Lu, G. Tunable Bandgaps and Acoustic Characteristics of Perforated Miura-Ori Phononic Structures. Int. J. Mech. Sci. 2023, 253, 108389. [Google Scholar] [CrossRef]
- Kheybari, M.; Daraio, C.; Bilal, O.R. Tunable Auxetic Metamaterials for Simultaneous Attenuation of Airborne Sound and Elastic Vibrations in All Directions. Appl. Phys. Lett. 2022, 121, 081702. [Google Scholar] [CrossRef]
- Chen, J.S.; Chang, I.L.; Huang, W.T.; Chen, L.W.; Huang, G.H. Asymmetric Transmission of Acoustic Waves in a Layer Thickness Distribution Gradient Structure Using Metamaterials. AIP Adv. 2016, 6, 095020. [Google Scholar] [CrossRef]
- Shuaib, M.; Haleem, A.; Kumar, S.; Javaid, M. Impact of 3D Printing on the Environment: A Literature-Based Study. Sustain. Oper. Comput. 2021, 2, 57–63. [Google Scholar] [CrossRef]
- Mousanezhad, D.; Babaee, S.; Ghosh, R.; Mahdi, E.; Bertoldi, K.; Vaziri, A. Honeycomb Phononic Crystals with Self-Similar Hierarchy. Phys. Rev. B Condens. Matter Mater. Phys. 2015, 92, 104304. [Google Scholar] [CrossRef]
- Brillouin, L. Wave Propagation in Periodic Structures: Electric Filters and Crystal Lattices; Dover Publications: Mineola, NY, USA, 1953. [Google Scholar]
- Pierce, A.D. Acoustics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Wang, Z.; Xian, W.; Baccouche, M.R.; Lanzerath, H.; Li, Y.; Xu, H. Design of Phononic Bandgap Metamaterials Based on Gaussian Mixture Beta Variational Autoencoder and Iterative Model Updating. J. Mech. Des. 2022, 144, 041705. [Google Scholar] [CrossRef]
- Wang, W.; Cheney, W.; Amirkhizi, A.V. Generative Design of Graded Metamaterial Arrays for Dynamic Response Modulation. Mater. Des. 2024, 237, 112550. [Google Scholar] [CrossRef]
- Ha, C.S.; Yao, D.; Xu, Z.; Liu, C.; Liu, H.; Elkins, D.; Kile, M.; Deshpande, V.; Kong, Z.; Bauchy, M.; et al. Rapid Inverse Design of Metamaterials Based on Prescribed Mechanical Behavior through Machine Learning. Nat. Commun. 2023, 14, 5765. [Google Scholar] [CrossRef]




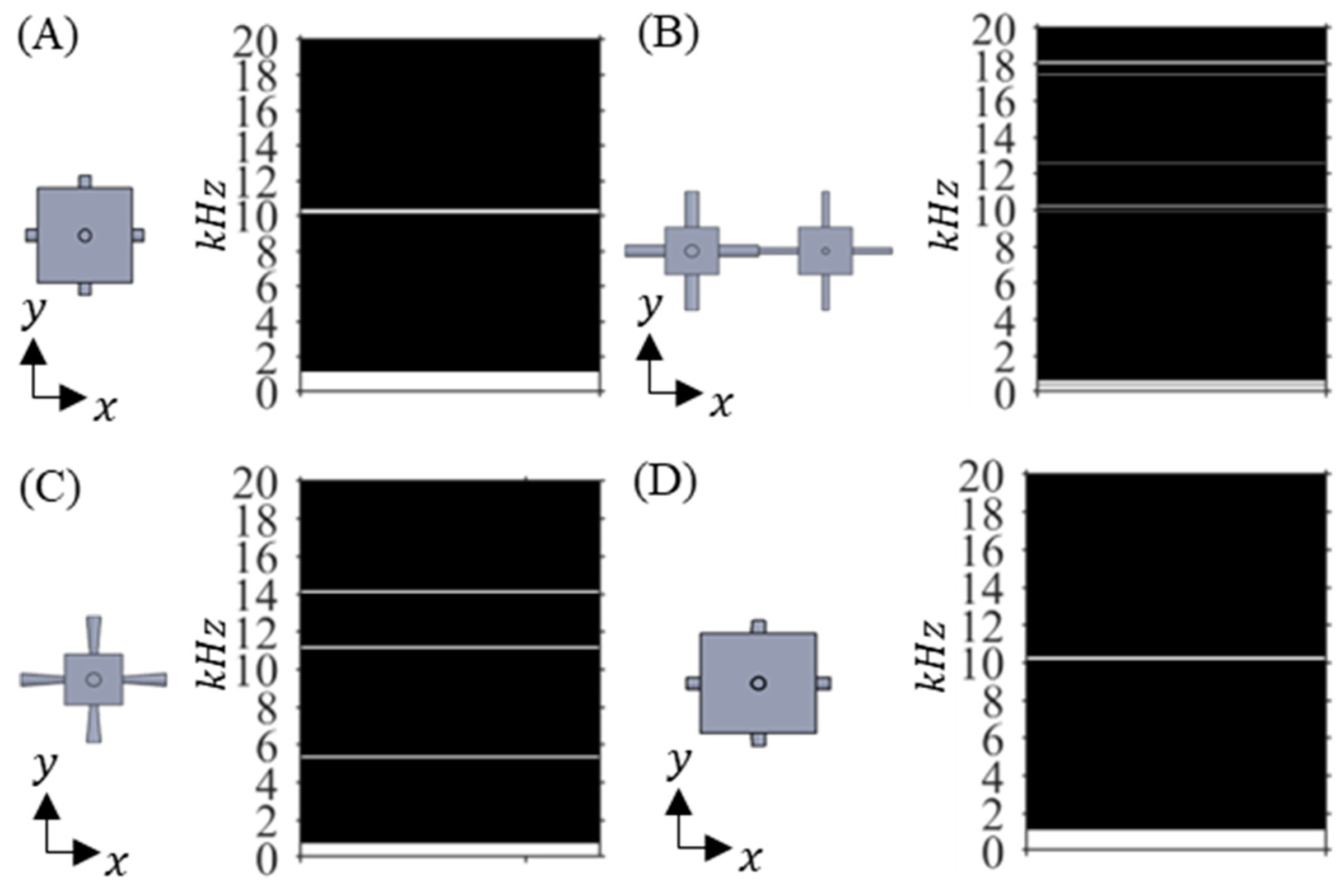
| Metamaterial | Design Combination | Bandgaps Coverage | |||||
| Semi—Periodic | 42.9 | 0.3 | 0.1 | 0.5 | 0.955 | ||
| Tapered—Diverging | 38.7 | 0.3 | 0.1 | 0.5 | 0.944 | ||
| Tapered—Converging | 21.1 | 0.1 | 0.1 | 0.9 | 0.936 | ||
| Metamaterial | Design Combination | Bandgaps Coverage | |||||
| Basic—Periodic | 21.1 | 0.1 | 0.1 | 0.935 | |||
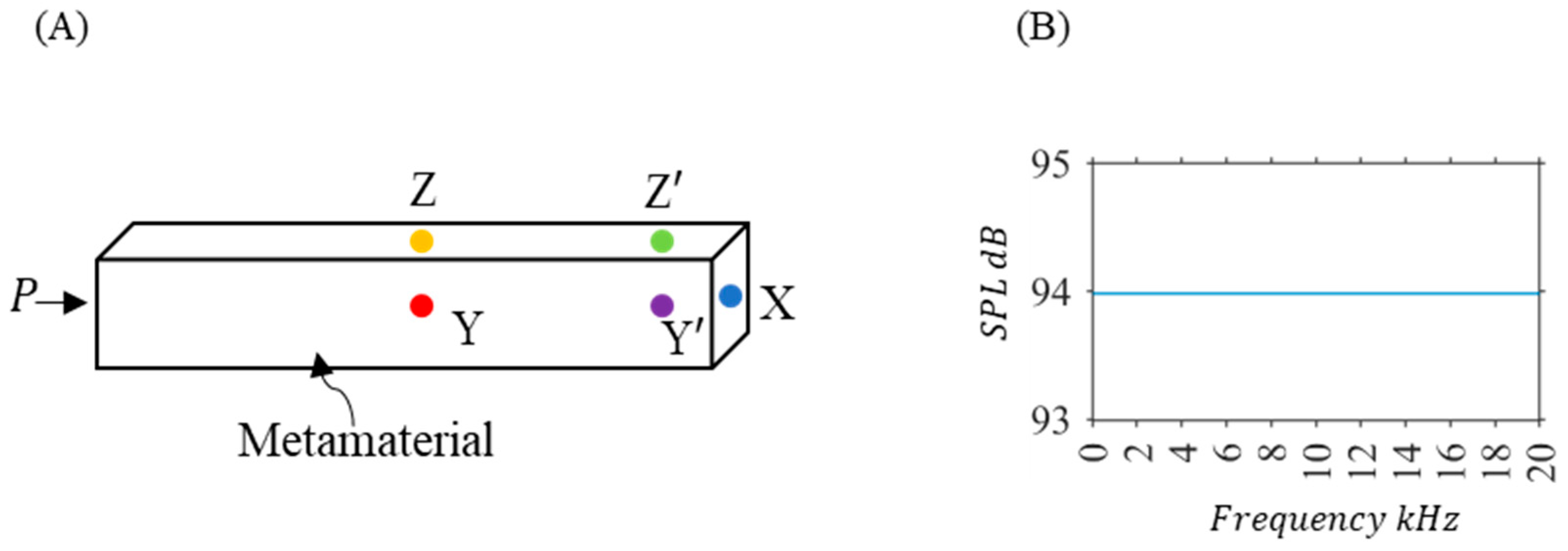
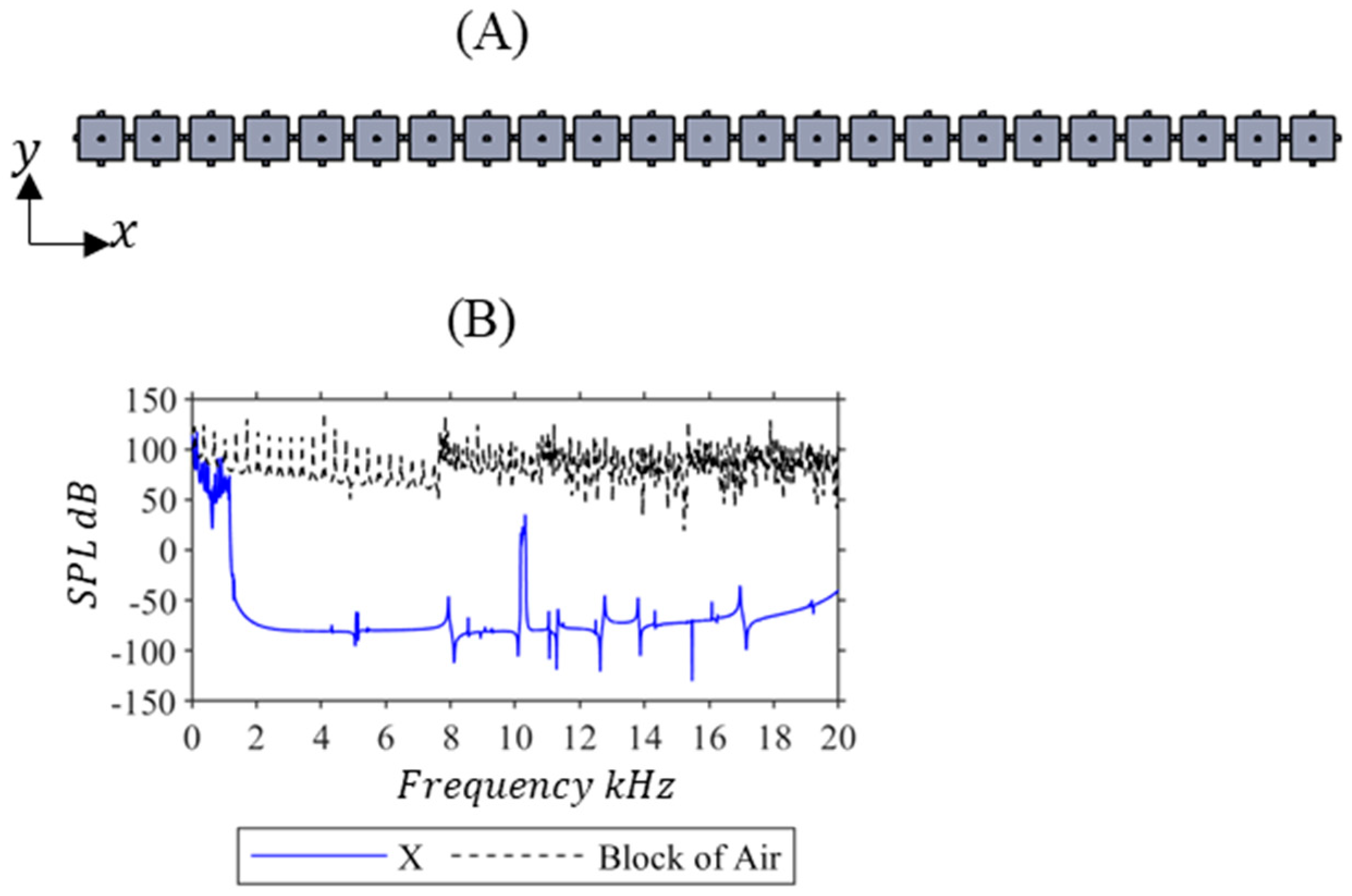
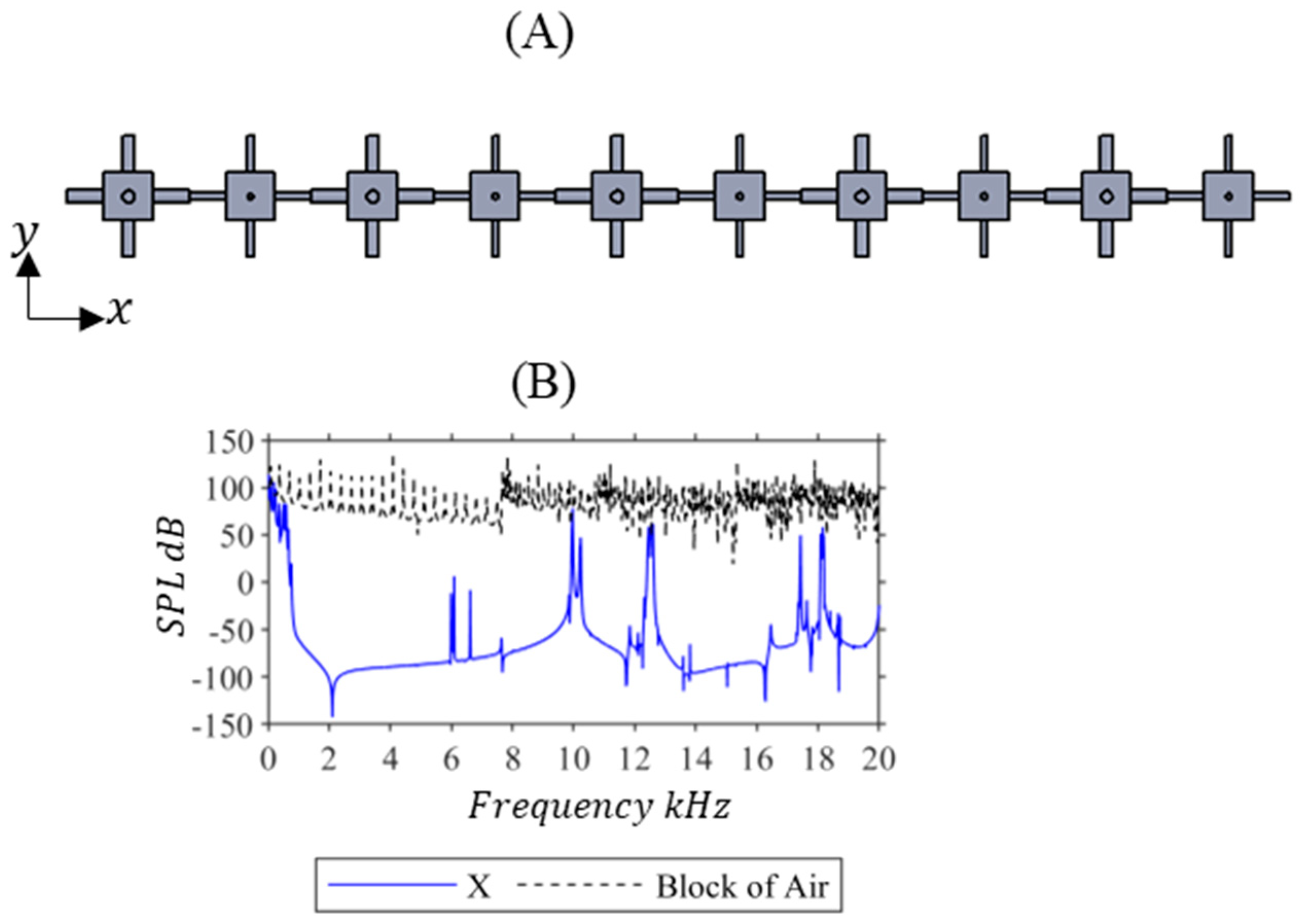
| Metamaterial | X ) | Y ) | Z ) | ) | ) | ) | Reduction to Basic—Periodic (%) |
|---|---|---|---|---|---|---|---|
| Semi—Periodic | 3.46 | 5.23 | 5.16 | 3.04 | 3.05 | 3.99 | 11.33 |
| Tapered— Diverging | 3.84 | 5.07 | 5.07 | 3.65 | 3.69 | 4.26 | 5.33 |
| Tapered— Converging | 3.77 | 5.14 | 5.13 | 3.68 | 3.68 | 4.28 | 4.89 |
| Basic—Periodic | 3.98 | 5.39 | 5.40 | 3.88 | 3.88 | 4.50 | |
| Block of Air | 80.45 | 70.62 | 71.45 | 70.01 | 70.57 | 72.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shendy, M.; Oluyemi, M.; Maftoon, N.; Salehian, A. An Extensive Parametric Analysis and Optimization to Design Unidimensional Periodic Acoustic Metamaterials for Noise Attenuation. Appl. Sci. 2024, 14, 7272. https://doi.org/10.3390/app14167272
Shendy M, Oluyemi M, Maftoon N, Salehian A. An Extensive Parametric Analysis and Optimization to Design Unidimensional Periodic Acoustic Metamaterials for Noise Attenuation. Applied Sciences. 2024; 14(16):7272. https://doi.org/10.3390/app14167272
Chicago/Turabian StyleShendy, Mohamed, Momoiyioluwa Oluyemi, Nima Maftoon, and Armaghan Salehian. 2024. "An Extensive Parametric Analysis and Optimization to Design Unidimensional Periodic Acoustic Metamaterials for Noise Attenuation" Applied Sciences 14, no. 16: 7272. https://doi.org/10.3390/app14167272





