Visual Odometry in GPS-Denied Zones for Fixed-Wing Unmanned Aerial Vehicle with Reduced Accumulative Error Based on Satellite Imagery
Abstract
1. Introduction
- Multirotor drones: These UAVs are characterized by their design, which has multiple rotor blades. These drones are similar in concept to traditional helicopters but are typically smaller. The main distinguishing ability of rotary-wing drones is their ability to hover, take off, and land vertically (VTOL).
- Fixed-wing: These are similar to traditional airplanes. Unlike rotary-wing drones, they achieve lift through the aerodynamic forces generated by their wings as they move through the air.
- Altitude, speed, and heading information.
- Battery status and remaining flight time.
- Sensor data such as temperature, humidity, or camera feed.
- GPS coordinates for position tracking.
- Manual.
- Altitude hold.
- Loiter mode.
- Autonomous (pre-programmed missions).
Problem Statement
2. Related Work
3. Methodology
- Visual Odometry: At the moment of GPS loss, the algorithm estimates a latitude and longitude coordinate based only on monocular vision. The accumulated error in this phase will depend on the precision with which the scale is calculated. This phase is explained in detail in Section 3.1.
- Satellite image preprocessing: This stage is carried out offline before the flight and is described in detail in Section 3.2. This phase is composed of the following subprocesses: We start with a flight plan, which can either be provided by the user or calculated using an exploration algorithm, in this case, Rapidly-exploring Random Trees (Section 3.2.1). From the flight plan, the keypoints of the satellite image are filtered to reduce their cardinality (Section 3.2.2). Finally, the problem of spatial indexing is solved using a Quad-tree to efficiently find the 2D points closest to the path (Section 3.2.3).
- Reduction in accumulated error: We search for correspondences between the UAV image and the geo-referenced map to correct the estimation errors from the previous phase. The reduction error phase is explained in Section 3.3. This process is performed online and onboard the UAV.
3.1. Visual Odometry
3.2. Satellite Image Preprocessing
- Onboard processing: In areas without GPS coverage, communication can be unreliable or nonexistent. As a result, the UAV must be capable of performing GPS estimation on board.
- Altitude estimation: While low-altitude multirotors can achieve high precision with laser or ultrasonic sensors, in our case, we would require expensive LiDAR equipment that exceeds the payload capacity of the vehicle. In our situation, we estimate the altitude using a barometer, which can introduce errors of up to several hundred meters.
- High-range missions: Tactical UAVs can operate over distances of up to 200 km. Therefore, the algorithms used must be able to handle long-duration flights.
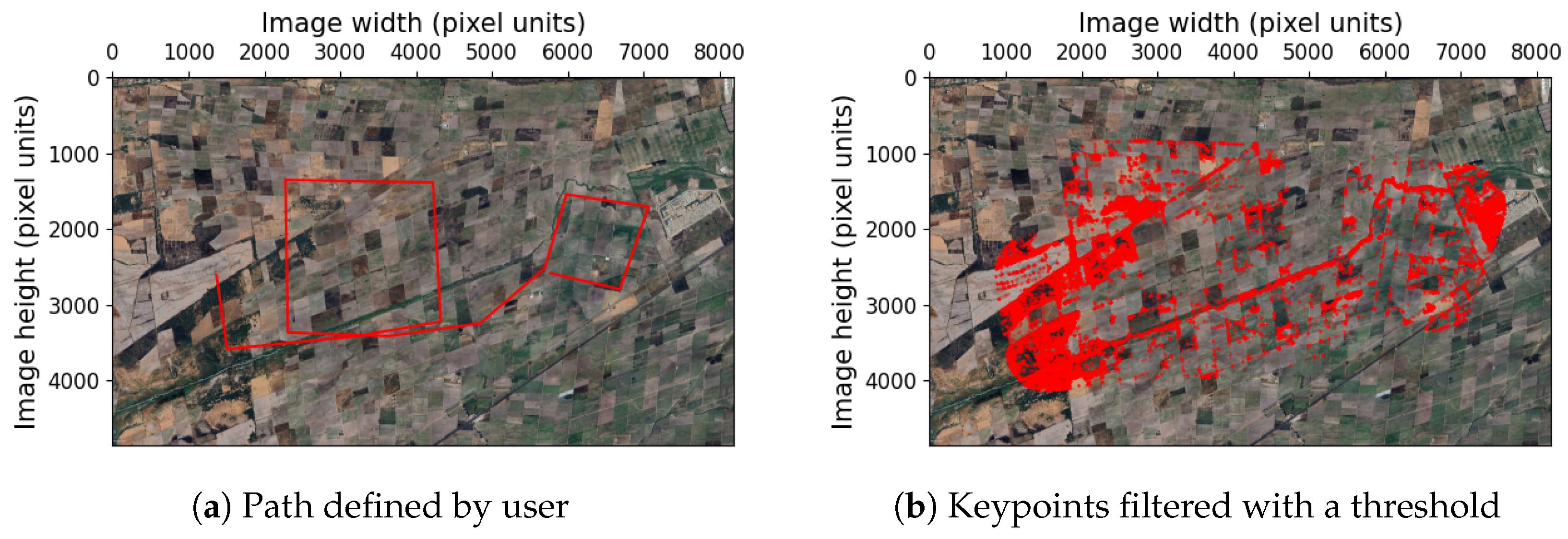
3.2.1. Calculate Flight Plan
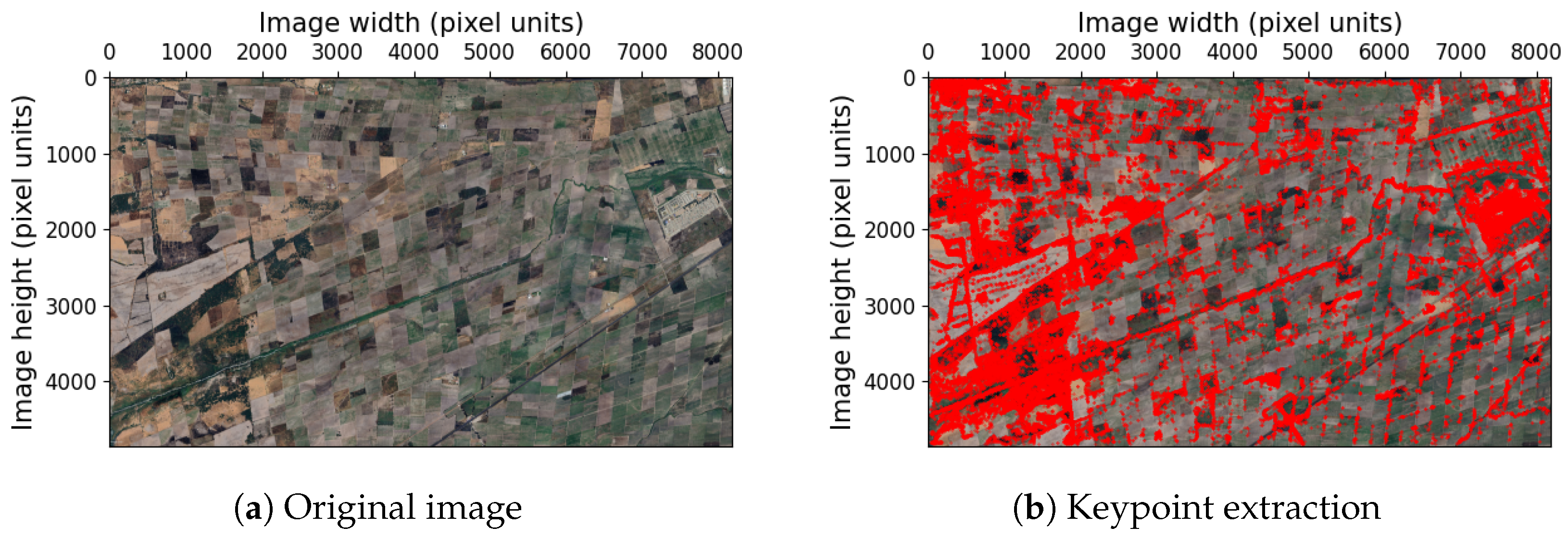
3.2.2. Filter Keypoints with the Flight Plan
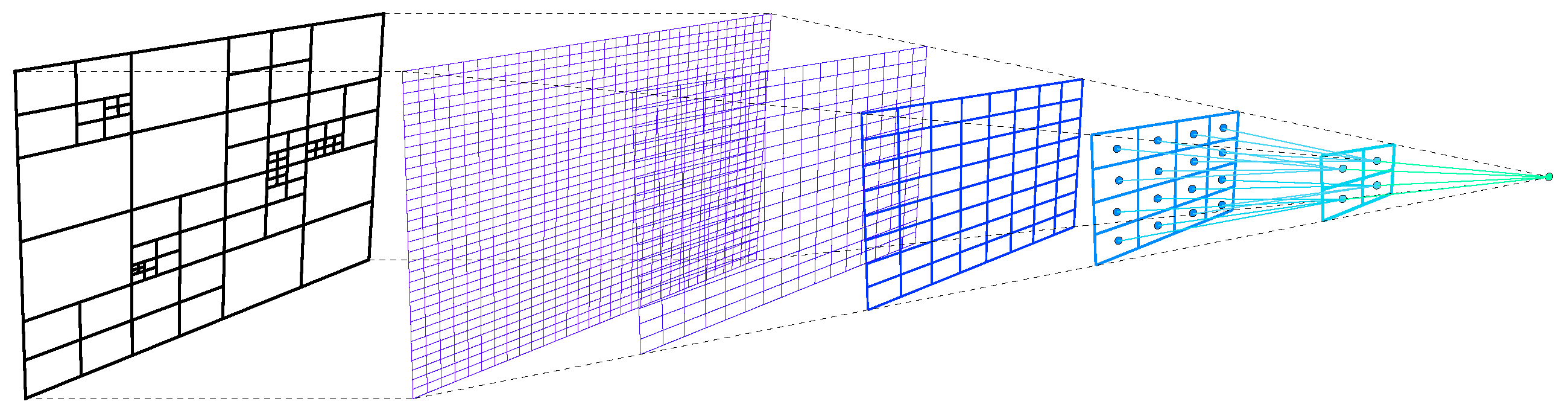
3.2.3. Spatial Indexing
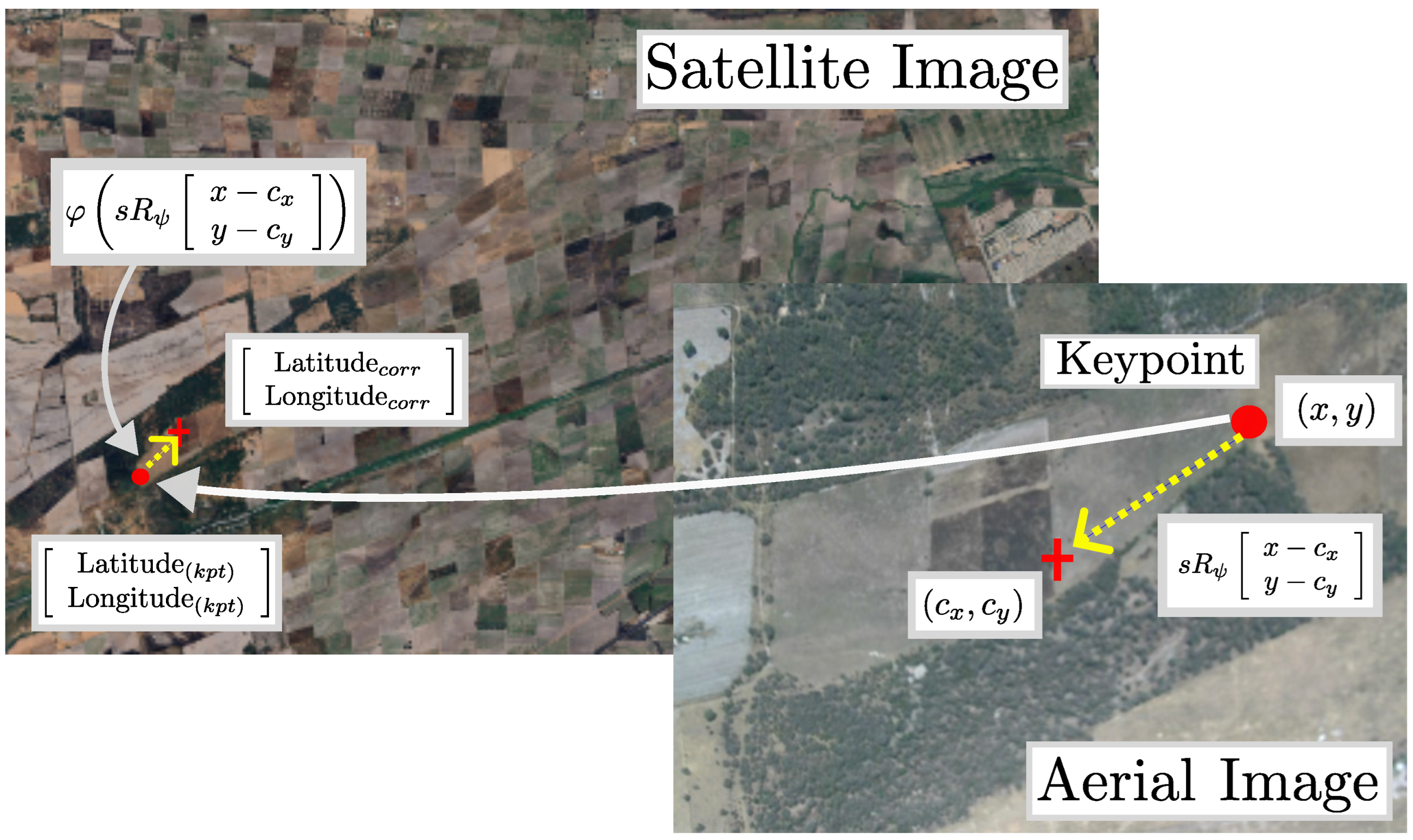
3.3. Reduction in Accumulated Error
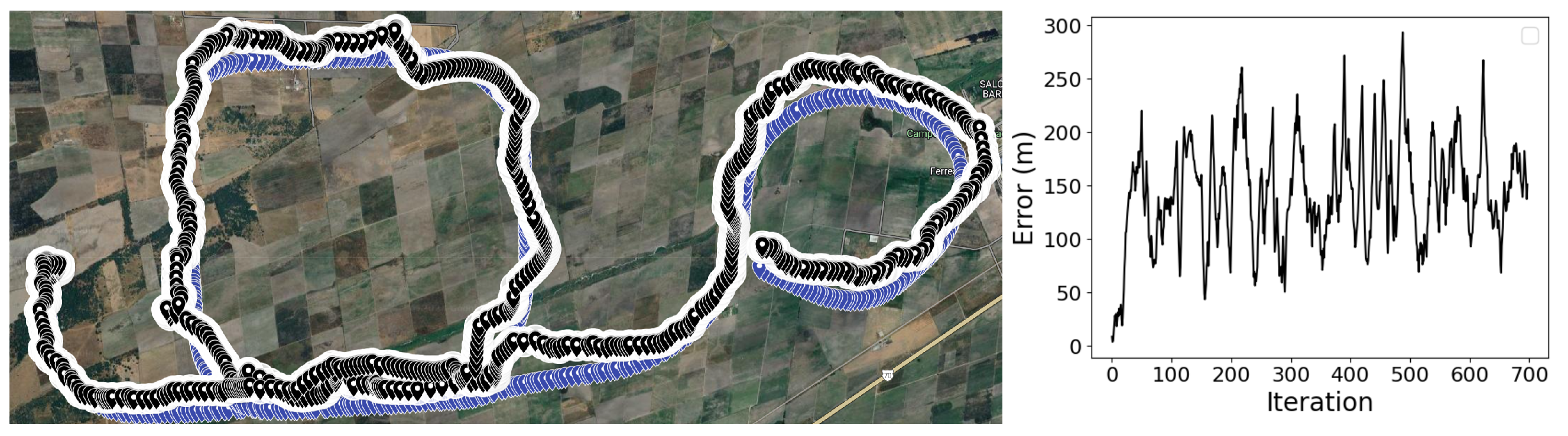
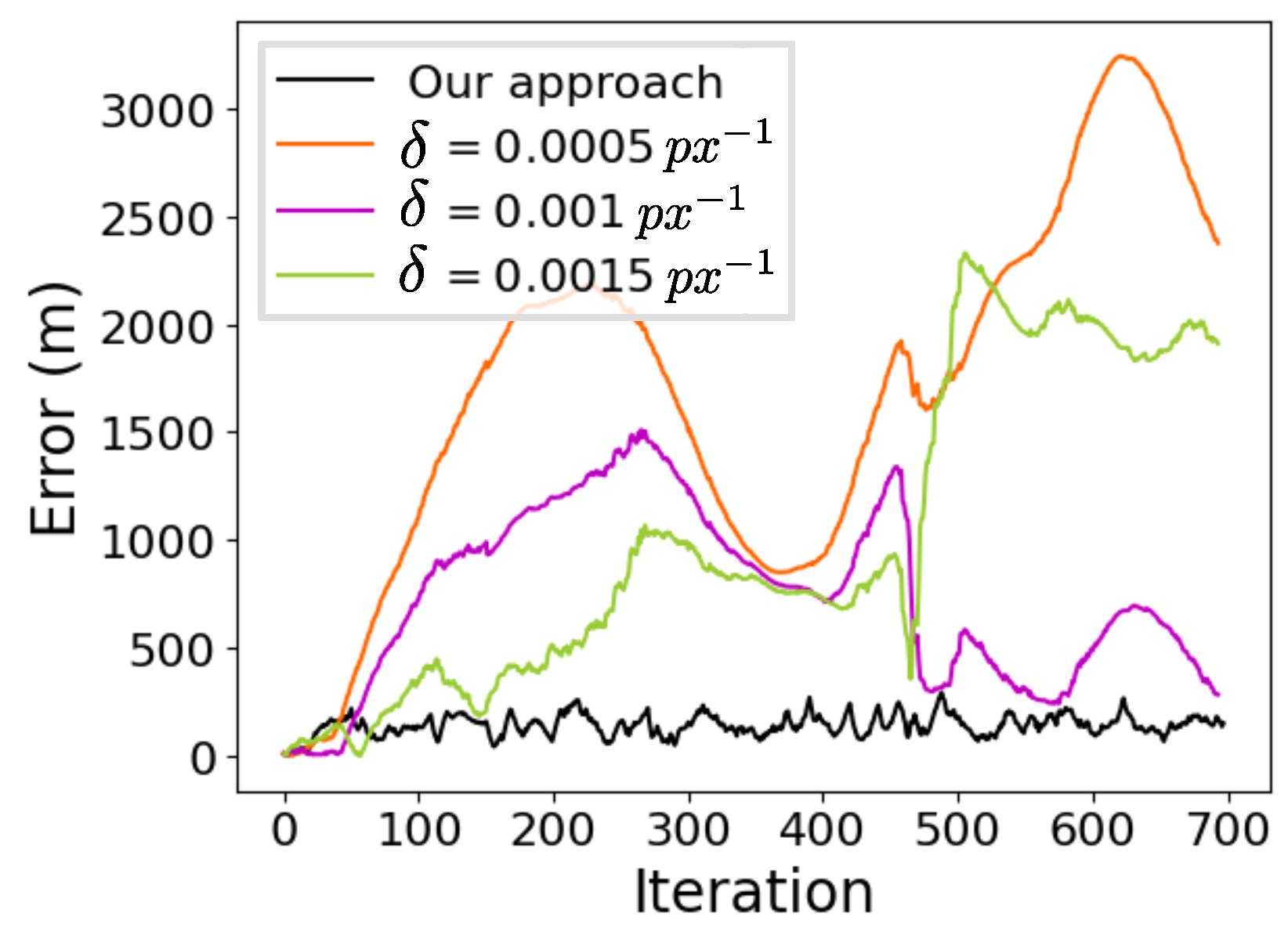
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BVLOS | Beyond Visual Line of Sight |
| DEM | Digital Elevation Model |
| GCS | Ground Control Station |
| GDAL | Geospatial Data Abstraction Library |
| GPS | Global Positioning System |
| HALE | High-Altitude Long-Endurance |
| IMU | Inertial Measurement Unit |
| INS | Inertial Navigation System |
| LIDAR | Light Detection And Ranging |
| LSTM | Long Short-Term Memory |
| MALE | Medium-Altitude Long-Endurance |
| ORB | Oriented Fast and Rotated Brief |
| RNN | Recurrent Neural Network |
| SVD | Singular Value Decomposition |
| UAV | Unmanned Aerial Vehicle |
| UGS | Unattended Ground Sensor |
| UTM | Universal Transverse Mercator |
| SLAM | Simultaneous Localization And Mapping |
| VLOS | Visual Line Of Sight |
| VTOL | Vertical Take Off and Landing |
References
- Radoglou-Grammatikis, P.; Sarigiannidis, P.; Lagkas, T.; Moscholios, I. A compilation of UAV applications for precision agriculture. Comput. Netw. 2020, 172, 107148. [Google Scholar] [CrossRef]
- Van den Bergh, B.; Pollin, S. Keeping UAVs under control during GPS jamming. IEEE Syst. J. 2018, 13, 2010–2021. [Google Scholar] [CrossRef]
- Grayson, B.; Penna, N.T.; Mills, J.P.; Grant, D.S. GPS precise point positioning for UAV photogrammetry. Photogramm. Rec. 2018, 33, 427–447. [Google Scholar] [CrossRef]
- Gutiérrez, G.; Searcy, M.T. Introduction to the UAV special edition. SAA Archaeol. Rec. Spec. Issue Drones Archaeol. 2016, 16, 6–9. [Google Scholar]
- Muchiri, G.; Kimathi, S. A review of applications and potential applications of UAV. In Proceedings of the Sustainable Research and Innovation Conference, Pretoria, South Africa, 20–24 June 2022; pp. 280–283. [Google Scholar]
- Ozdemir, U.; Aktas, Y.O.; Vuruskan, A.; Dereli, Y.; Tarhan, A.F.; Demirbag, K.; Erdem, A.; Kalaycioglu, G.D.; Ozkol, I.; Inalhan, G. Design of a commercial hybrid VTOL UAV system. J. Intell. Robot. Syst. 2014, 74, 371–393. [Google Scholar] [CrossRef]
- U.S. Army Unmanned Aircraft Systems Center of Excellence. U.S. Army Unmanned Aircraft Systems Roadmap 2010–2035: Eyes of the Army; U.S. Army Unmanned Aircraft Systems Center of Excellence: Fort Rucker, AL, USA, 2010. [Google Scholar]
- Davies, L.; Bolam, R.C.; Vagapov, Y.; Anuchin, A. Review of unmanned aircraft system technologies to enable beyond visual line of sight (BVLOS) operations. In Proceedings of the 2018 X International conference on electrical power drive systems (ICEPDS), Novocherkassk, Russia, 3–6 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Roos, J.C.J.C. Autonomous Take-Off and Landing of a Fixed Wing Unmanned Aerial Vehicle. Ph.D. Thesis, Stellenbosch University, Stellenbosch, South Africa, 2007. [Google Scholar]
- Qu, Y.; Zhang, Y. Cooperative localization of low-cost UAV using relative range measurements in multi-UAV flight. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Toronto, ON, Canada, 2–5 August 2010; p. 8187. [Google Scholar]
- Chakraborty, A.; Taylor, C.N.; Sharma, R.; Brink, K.M. Cooperative localization for fixed wing unmanned aerial vehicles. In Proceedings of the 2016 IEEE/ION Position, Location and Navigation Symposium (PLANS), Savannah, GA, USA, 11–14 April 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 106–117. [Google Scholar]
- Iyidir, B.; Ozkazanc, Y. Jamming of GPS receivers. In Proceedings of the IEEE 12th Signal Processing and Communications Applications Conference, Kusadasi, Turkey, 30 April 2004; IEEE: Piscataway, NJ, USA, 2004; pp. 747–750. [Google Scholar]
- Navigation, T.R.; Foundation, T. Prioritizing Dangers to the United States from Threats to GPS: Ranking Risks and Proposed Mitigations. Available online: https://rntfnd.org/wp-content/uploads/12-7-Prioritizing-Dangers-to-US-fm-Threats-to-GPS-RNTFoundation.pdf (accessed on 13 August 2024).
- Borio, D.; O’driscoll, C.; Fortuny, J. GNSS jammers: Effects and countermeasures. In Proceedings of the 2012 6th ESA Workshop on Satellite Navigation Technologies (Navitec 2012) & European Workshop on GNSS Signals and Signal Processing, Noordwijk, The Netherlands, 5–7 December 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–7. [Google Scholar]
- Westbrook, T. Will GPS Jammers Proliferate in the smart city? Salus J. 2019, 7, 45–67. [Google Scholar]
- Psiaki, M.L.; O’Hanlon, B.W.; Bhatti, J.A.; Shepard, D.P.; Humphreys, T.E. GPS spoofing detection via dual-receiver correlation of military signals. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 2250–2267. [Google Scholar] [CrossRef]
- Manfredini, E.G.; Akos, D.M.; Chen, Y.H.; Lo, S.; Walter, T.; Enge, P. Effective GPS spoofing detection utilizing metrics from commercial receivers. In Proceedings of the 2018 International Technical Meeting of The Institute of Navigation, Reston, VA, USA, 29 January–1 February 2018; pp. 672–689. [Google Scholar]
- O’Hanlon, B.W.; Psiaki, M.L.; Bhatti, J.A.; Shepard, D.P.; Humphreys, T.E. Real-time GPS spoofing detection via correlation of encrypted signals. Navigation 2013, 60, 267–278. [Google Scholar] [CrossRef]
- Khanafseh, S.; Roshan, N.; Langel, S.; Chan, F.C.; Joerger, M.; Pervan, B. GPS spoofing detection using RAIM with INS coupling. In Proceedings of the 2014 IEEE/ION Position, Location and Navigation Symposium-PLANS 2014, Monterey, CA, USA, 5–8 May 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1232–1239. [Google Scholar]
- Jung, J.H.; Hong, M.Y.; Choi, H.; Yoon, J.W. An analysis of GPS spoofing attack and efficient approach to spoofing detection in PX4. IEEE Access 2024, 12, 46668–46677. [Google Scholar] [CrossRef]
- Chen, J.; Wang, X.; Fang, Z.; Jiang, C.; Gao, M.; Xu, Y. A Real-Time Spoofing Detection Method Using Three Low-Cost Antennas in Satellite Navigation. Electronics 2024, 13, 1134. [Google Scholar] [CrossRef]
- Fan, Z.; Tian, X.; Wei, S.; Shen, D.; Chen, G.; Pham, K.; Blasch, E. GASx: Explainable Artificial Intelligence For Detecting GPS Spoofing Attacks. In Proceedings of the 2024 International Technical Meeting of The Institute of Navigation, Long Beach, CA, USA, 23–25 January 2024; pp. 441–453. [Google Scholar]
- Rady, S.; Kandil, A.; Badreddin, E. A hybrid localization approach for UAV in GPS denied areas. In Proceedings of the 2011 IEEE/SICE International Symposium on System Integration (SII), Kyoto, Japan, 20–22 December 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1269–1274. [Google Scholar]
- Conte, G.; Doherty, P. An integrated UAV navigation system based on aerial image matching. In Proceedings of the 2008 IEEE Aerospace Conference, Big Sky, MT, USA, 1–8 March 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1–10. [Google Scholar]
- Quist, E. UAV Navigation and Radar Odometry. Ph.D. Thesis, Bringham Young University, Provo, UT, USA, 2015. [Google Scholar]
- Sharma, R.; Taylor, C. Cooperative navigation of MAVs in GPS denied areas. In Proceedings of the 2008 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems, Seoul, Republic of Korea, 20–22 August 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 481–486. [Google Scholar]
- Russell, J.S.; Ye, M.; Anderson, B.D.; Hmam, H.; Sarunic, P. Cooperative localization of a GPS-denied UAV using direction-of-arrival measurements. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 1966–1978. [Google Scholar] [CrossRef]
- Misra, S.; Chakraborty, A.; Sharma, R.; Brink, K. Cooperative simultaneous arrival of unmanned vehicles onto a moving target in gps-denied environment. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami Beach, FL, USA, 17–19 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 5409–5414. [Google Scholar]
- Manyam, S.G.; Rathinam, S.; Darbha, S.; Casbeer, D.; Cao, Y.; Chandler, P. Gps denied uav routing with communication constraints. J. Intell. Robot. Syst. 2016, 84, 691–703. [Google Scholar] [CrossRef]
- Srisomboon, I.; Lee, S. Positioning and Navigation Approaches using Packet Loss-based Multilateration for UAVs in GPS-Denied Environments. IEEE Access 2024, 12, 13355–13369. [Google Scholar] [CrossRef]
- Griffin, B.; Fierro, R.; Palunko, I. An autonomous communications relay in GPS-denied environments via antenna diversity. J. Def. Model. Simul. 2012, 9, 33–44. [Google Scholar] [CrossRef]
- Zahran, S.; Mostafa, M.; Masiero, A.; Moussa, A.; Vettore, A.; El-Sheimy, N. Micro-radar and UWB aided UAV navigation in GNSS denied environment. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 469–476. [Google Scholar] [CrossRef]
- Asher, M.S.; Stafford, S.J.; Bamberger, R.J.; Rogers, A.Q.; Scheidt, D.; Chalmers, R. Radionavigation alternatives for US Army Ground Forces in GPS denied environments. In Proceedings of the 2011 International Technical Meeting of the Institute of Navigation, San Diego, CA, USA, 24–26 January 2011; Citeseer: Princeton, NJ, USA, 2011; Volume 508, p. 532. [Google Scholar]
- Trujillo, J.C.; Munguia, R.; Guerra, E.; Grau, A. Cooperative monocular-based SLAM for multi-UAV systems in GPS-denied environments. Sensors 2018, 18, 1351. [Google Scholar] [CrossRef] [PubMed]
- Radwan, A.; Tourani, A.; Bavle, H.; Voos, H.; Sanchez-Lopez, J.L. UAV-assisted Visual SLAM Generating Reconstructed 3D Scene Graphs in GPS-denied Environments. arXiv 2024, arXiv:2402.07537. [Google Scholar]
- Kim, J.; Sukkarieh, S. 6DoF SLAM aided GNSS/INS navigation in GNSS denied and unknown environments. Positioning 2005, 1, 120–128. [Google Scholar] [CrossRef]
- Kayi, A.; Erdoğan, M.; Eker, O. OPTECH HA-500 ve RIEGL LMS-Q1560 ile gerçekleştirilen LİDAR test sonuçları. Harit. Derg. 2015, 153, 42–46. [Google Scholar]
- Matyja, T.; Stanik, Z.; Kubik, A. Automatic correction of barometric altimeters using additional air temperature and humidity measurements. GPS Solut. 2024, 28, 40. [Google Scholar] [CrossRef]
- Simonetti, M.; Crespillo, O.G. Geodetic Altitude from Barometer and Weather Data for GNSS Integrity Monitoring in Aviation. Navig. J. Inst. Navig. 2024, 71, navi.637. [Google Scholar] [CrossRef]
- Guang, X.; Gao, Y.; Liu, P.; Li, G. IMU data and GPS position information direct fusion based on LSTM. Sensors 2021, 21, 2500. [Google Scholar] [CrossRef] [PubMed]
- Yol, A.; Delabarre, B.; Dame, A.; Dartois, J.E.; Marchand, E. Vision-based absolute localization for unmanned aerial vehicles. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 3429–3434. [Google Scholar]
- Gurgu, M.M.; Queralta, J.P.; Westerlund, T. Vision-based gnss-free localization for uavs in the wild. In Proceedings of the 2022 7th International Conference on Mechanical Engineering and Robotics Research (ICMERR), Krakow, Poland, 9–11 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 7–12. [Google Scholar]
- Jurevičius, R.; Marcinkevičius, V.; Šeibokas, J. Robust GNSS-denied localization for UAV using particle filter and visual odometry. Mach. Vis. Appl. 2019, 30, 1181–1190. [Google Scholar] [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 2564–2571. [Google Scholar]
- Tareen, S.A.K.; Saleem, Z. A comparative analysis of sift, surf, kaze, akaze, orb, and brisk. In Proceedings of the 2018 International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 3–4 March 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–10. [Google Scholar]
- Leutenegger, S.; Chli, M.; Siegwart, R.Y. BRISK: Binary robust invariant scalable keypoints. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 2548–2555. [Google Scholar]
- Alcantarilla, P.F.; Bartoli, A.; Davison, A.J. KAZE features. In Proceedings of the Computer Vision–ECCV 2012: 12th European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; Proceedings, Part VI 12. Springer: Berlin/Heidelberg, Germany, 2012; pp. 214–227. [Google Scholar]
- Alcantarilla, P.F.; Solutions, T. Fast explicit diffusion for accelerated features in nonlinear scale spaces. IEEE Trans. Patt. Anal. Mach. Intell. 2011, 34, 1281–1298. [Google Scholar]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-up robust features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Weberruss, J.; Kleeman, L.; Drummond, T. ORB feature extraction and matching in hardware. In Proceedings of the Australasian Conference on Robotics and Automation, Canberra, Australia, 2–4 December 2015; pp. 2–4. [Google Scholar]
- Arun, K.S.; Huang, T.S.; Blostein, S.D. Least-squares fitting of two 3-D point sets. IEEE Trans. Pattern Anal. Mach. Intell. 1987, PAMI-9, 698–700. [Google Scholar] [CrossRef]
- Sorkine-Hornung, O.; Rabinovich, M. Least-squares rigid motion using svd. Computing 2017, 1, 1–5. [Google Scholar]
- Fernández-Coppel, I.A. La Proyección UTM. In Área de Ingeniería Cartográfica, Geodesia y Fotogrametría, Departamento de Ingeniería Agrícola y Forestal, Escuela Técnica Superior de Ingenierías Agrarias, Palencia; Universidad de Valladolid: Valladolid, Spain, 2001. [Google Scholar]
- Franco, A.R. Características de las Coordenadas UTM y Descripción de Este Tipo de Coordenadas. 1999. Available online: http://www.elgps.com/documentos/utm/coordenadas_utm.html (accessed on 12 August 2024).
- Langley, R.B. The UTM grid system. GPS World 1998, 9, 46–50. [Google Scholar]
- Dana, P.H. Coordinate systems overview. In The Geographer’s Craft Project, Department of Geography, The University of Colorado at Boulder; Available online: https://foote.geography.uconn.edu/gcraft/notes/coordsys/coordsys_f.html (accessed on 13 August 2024).
- Wu, C.; Fraundorfer, F.; Frahm, J.M.; Snoeyink, J.; Pollefeys, M. Image localization in satellite imagery with feature-based indexing. In Proceedings of the XXIst ISPRS Congress: Technical Commission III. ISPRS, Beijing, China, 3–11 July 2008; Volume 37, pp. 197–202. [Google Scholar]
- Hu, S.; Lee, G.H. Image-based geo-localization using satellite imagery. Int. J. Comput. Vis. 2020, 128, 1205–1219. [Google Scholar] [CrossRef]
- Bianchi, M.; Barfoot, T.D. UAV localization using autoencoded satellite images. IEEE Robot. Autom. Lett. 2021, 6, 1761–1768. [Google Scholar] [CrossRef]
- Gay, W. Raspberry Pi Hardware Reference; Apress: New York, NY, USA, 2014. [Google Scholar]
- Orange Pi 5 plus User Manual. Available online: https://agelectronica.lat/pdfs/textos/O/ORANGEPLUS5GB.PDF (accessed on 13 August 2024).
- Noreen, I.; Khan, A.; Habib, Z. A comparison of RRT, RRT* and RRT*-smart path planning algorithms. Int. J. Comput. Sci. Netw. Secur. (IJCSNS) 2016, 16, 20. [Google Scholar]
- Begum, S.A.N.; Supreethi, K. A survey on spatial indexing. J. Web Dev. Web Des. 2018, 3, 1–25. [Google Scholar]
- Ram, P.; Sinha, K. Revisiting kd-tree for nearest neighbor search. In Proceedings of the 25th ACM Sigkdd International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 1378–1388. [Google Scholar]
- Huang, K.; Li, G.; Wang, J. Rapid retrieval strategy for massive remote sensing metadata based on GeoHash coding. Remote Sens. Lett. 2018, 9, 1070–1078. [Google Scholar] [CrossRef]
- Tobler, W.; Chen, Z.t. A quadtree for global information storage. Geogr. Anal. 1986, 18, 360–371. [Google Scholar] [CrossRef]
- Ready, B.B.; Taylor, C.N. Inertially aided visual odometry for miniature air vehicles in gps-denied environments. J. Intell. Robot. Syst. 2009, 55, 203–221. [Google Scholar] [CrossRef]
- Ellingson, G.; Brink, K.; McLain, T. Relative visual-inertial odometry for fixed-wing aircraft in GPS-denied environments. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 786–792. [Google Scholar]
- McConville, A.; Bose, L.; Clarke, R.; Mayol-Cuevas, W.; Chen, J.; Greatwood, C.; Carey, S.; Dudek, P.; Richardson, T. Visual odometry using pixel processor arrays for unmanned aerial systems in gps denied environments. Front. Robot. AI 2020, 7, 126. [Google Scholar] [CrossRef]
- Sharifi, M.; Chen, X.; Pretty, C.G. Experimental study on using visual odometry for navigation in outdoor GPS-denied environments. In Proceedings of the 2016 12th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA), Auckland, New Zealand, 29–31 August 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–5. [Google Scholar]
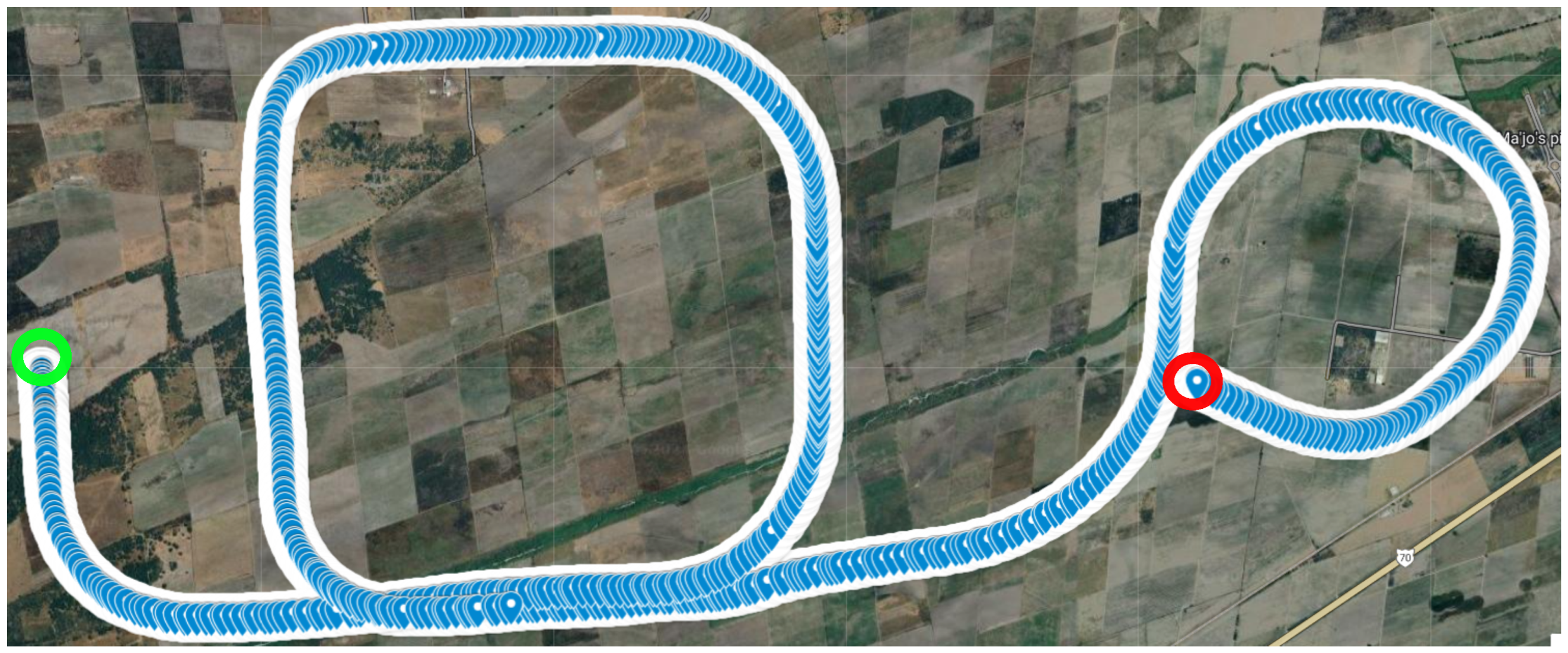



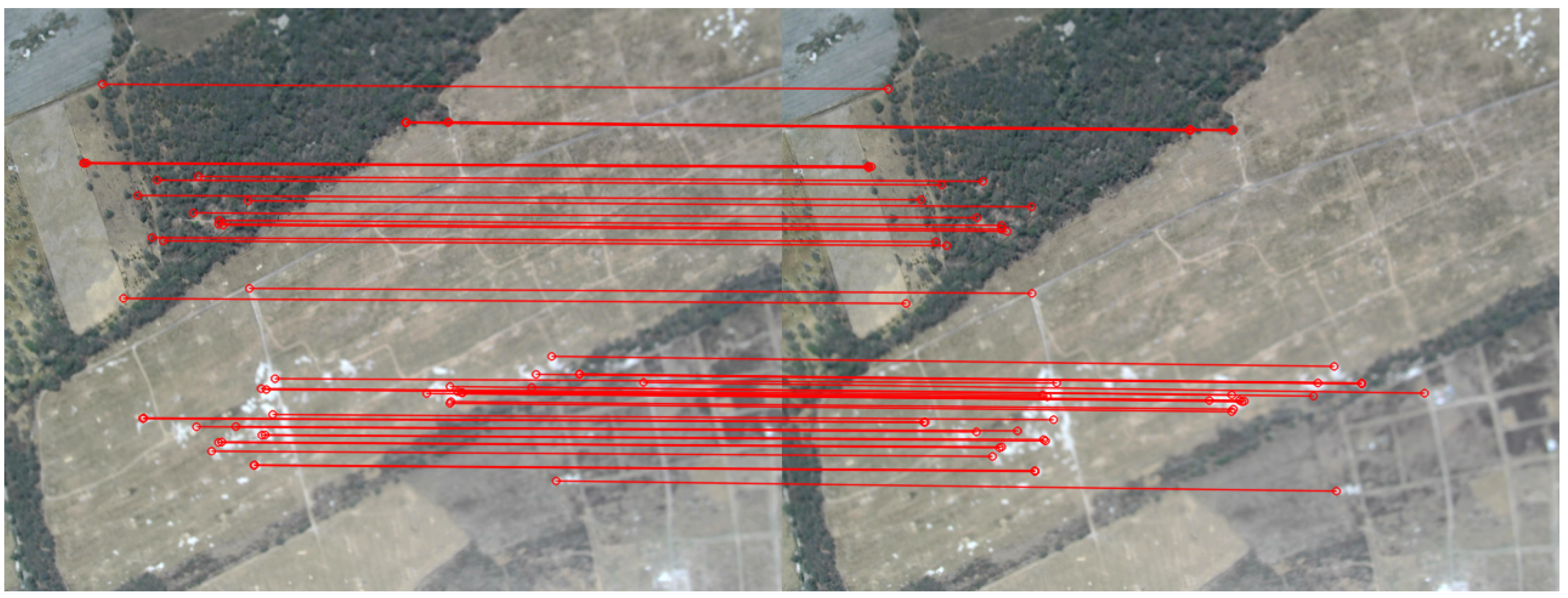


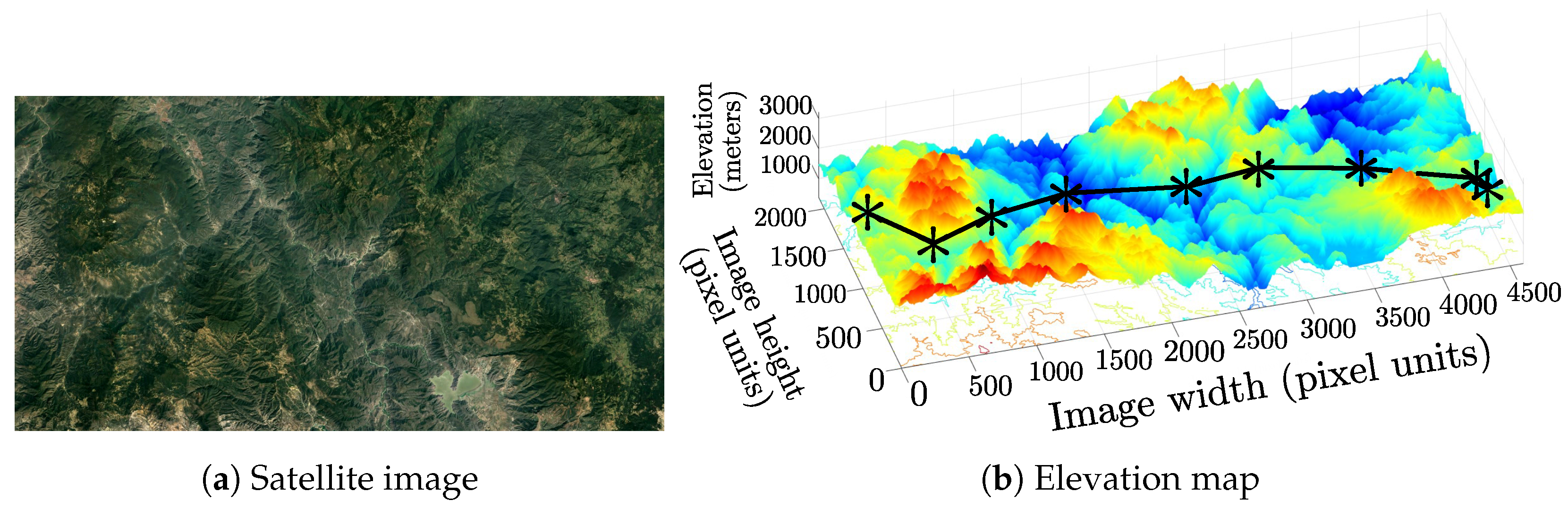




| Class | Category | Operating Altitude (ft) | Range (km) | Payload (kg) |
|---|---|---|---|---|
| I | Micro (<2 kg) | <3000 | 5 | 0.2–0.5 |
| I | Mini (2–20 kg) | <3000 | 25 | 0.5–10 |
| II | Small (<150 kg) | <5000 | 50–150 | 5–50 |
| III | Tactical | <10,000 | <200 | 25–200 |
| IV | Medium-Altitude Long-Endurance (MALE) | <18,000 | >1000 | >200 |
| V | High-Altitude Long-Endurance (HALE) | >18,000 | >1000 | >200 |
| Class | Accumulated Error | Root Mean Square Error (RMSE) | Mean Error | Std | Mean Error (%) |
|---|---|---|---|---|---|
| 0.0005 | 1,184,118.53 | 1893.99 | 1706.22 | 822.20 | 9.86 |
| 0.001 | 516,631.52 | 845.68 | 744.42 | 401.27 | 4.30 |
| 0.0015 | 696,712.03 | 1230.59 | 1003.90 | 711.71 | 5.80 |
| Our Approach | 99,732.63 | 150.79 | 142.88 | 48.19 | 0.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mateos-Ramirez, P.; Gomez-Avila, J.; Villaseñor, C.; Arana-Daniel, N. Visual Odometry in GPS-Denied Zones for Fixed-Wing Unmanned Aerial Vehicle with Reduced Accumulative Error Based on Satellite Imagery. Appl. Sci. 2024, 14, 7420. https://doi.org/10.3390/app14167420
Mateos-Ramirez P, Gomez-Avila J, Villaseñor C, Arana-Daniel N. Visual Odometry in GPS-Denied Zones for Fixed-Wing Unmanned Aerial Vehicle with Reduced Accumulative Error Based on Satellite Imagery. Applied Sciences. 2024; 14(16):7420. https://doi.org/10.3390/app14167420
Chicago/Turabian StyleMateos-Ramirez, Pablo, Javier Gomez-Avila, Carlos Villaseñor, and Nancy Arana-Daniel. 2024. "Visual Odometry in GPS-Denied Zones for Fixed-Wing Unmanned Aerial Vehicle with Reduced Accumulative Error Based on Satellite Imagery" Applied Sciences 14, no. 16: 7420. https://doi.org/10.3390/app14167420
APA StyleMateos-Ramirez, P., Gomez-Avila, J., Villaseñor, C., & Arana-Daniel, N. (2024). Visual Odometry in GPS-Denied Zones for Fixed-Wing Unmanned Aerial Vehicle with Reduced Accumulative Error Based on Satellite Imagery. Applied Sciences, 14(16), 7420. https://doi.org/10.3390/app14167420






