Large-Area Coverage Path Planning Method Based on Vehicle–UAV Collaboration
Abstract
1. Introduction
- A vehicle–UAV collaboration methodology is proposed for the large-area efficient coverage path planning problem.
- A dynamically adjusted region segmentation algorithm is proposed based on the construction of regular hexagons and a Voronoi diagram.
- An ant colony optimization algorithm is adopted to generate the vehicle paths from the supply points for connecting each sub-area, and a zigzag coverage path method is utilized to ensure the UAV paths to fill the contours of each sub-area.
- Simulation experiments are provided to verify the effectiveness and feasibility of the proposed vehicle–UAV collaboration method, and two comparative experiments are constructed to demonstrate that the proposed method excels at large-scale coverage path planning scenarios, and achieves a significant improvement in coverage efficiency.
2. Related Works
- Vehicle–UAV independent mode: Drones and vehicles perform their tasks independently without affecting each other. Fikar et al. [18] proposed a simulation and optimization based decision-support system to facilitate disaster relief coordination between private and relief organizations, in which the trucks and UAVs are adopted to transport the relief goods from transfer points to demand points, but more attention is paid to the coordination between the private and relief organizations. Marlin et al. [19] presented a dynamic vehicle routine problem with heterogeneous fleets to improve same-day delivery performance and proposed a policy function approximation based on geographical districting to decide whether an order is delivered by a drone or by a vehicle in the same-day context.
- UAV-first mode: UAVs take the primary role in the mission, with vehicles acting as support vehicles. Tokekar et al. [20] studied an approximation algorithm for the traveling salesperson problem with neighborhoods to choose sampling locations from disks and generate a route to visit these locations while minimizing the sum of the travel and measurement times. Garone et al. [21] introduced cooperative mission planning for a class of carrier-vehicle system and presented a heuristic solution for cooperation between a ship and a helicopter to solve two mission planning problems: one involving visiting a list of points sequentially under the hypothesis that the takeoff/landing sequence is not determined a priori, and a second in which the visiting sequence of points is optimized. Mathew et al. [22] addressed the task scheduling and path planning problem for a team of cooperating vehicles performing autonomous deliveries while ensuring the quadrotor delivered items at all requested locations along the shortest cooperative route.
- Vehicle-first model: The vehicle has a higher priority in the task, and the cooperative optimization problem mainly describes the objective function of the vehicle, with the UAV acting as an auxiliary tool. Savuran et al. [23] designed a solution based on the genetic algorithm and the nearest-neighbor heuristic to generate a route with minimization of total route length while ensuring take-off and land-on locations. Fawaz et al. [24] explored a UAV-based method to minimize the path availability’s dependence on vehicular density and cooperation while enhancing the availability of a connectivity path, as well as reducing the end-to-end package delivery delay.
- Vehicle–UAV Collaboration Model: In this model, the vehicle and the UAV must work together, and one may need to wait for the other. Despite the high cost of collaboration, Poikonen et al. [25] and Wang et al. [26] demonstrated that the delivery time in the vehicle–UAV collaboration mode is usually less than that of using the vehicle alone. Campbell et al. [27] showed that using UAV-equipped trucks for cargo delivery saves about 10% to 40% of the transportation cost. Grocholsky et al. [28] constructed a model and algorithmic framework for vehicle and UAV collaboration for aerial and ground surveillance. DeFreitas et al. [29] optimized the initial solution using a stochastic variable domain heuristic and verified that the method works better in solving large-scale cases. Liu Yao et al. [30] modeled the effect of UAV load on its energy consumption and used a simulated annealing algorithm to solve a two-tier path planning problem for vehicle-mounted UAVs for collaborative distribution. Ropero et al. [31] proposed a method for exploring planetary surfaces based on a hybrid UGV–UAV system. Phan et al. [32] proposed a hierarchical UAV/ UGV platform.
3. Coverage Path Planning Method Based on Vehicle–UAV Collaboration
3.1. Overview of the Methodologies
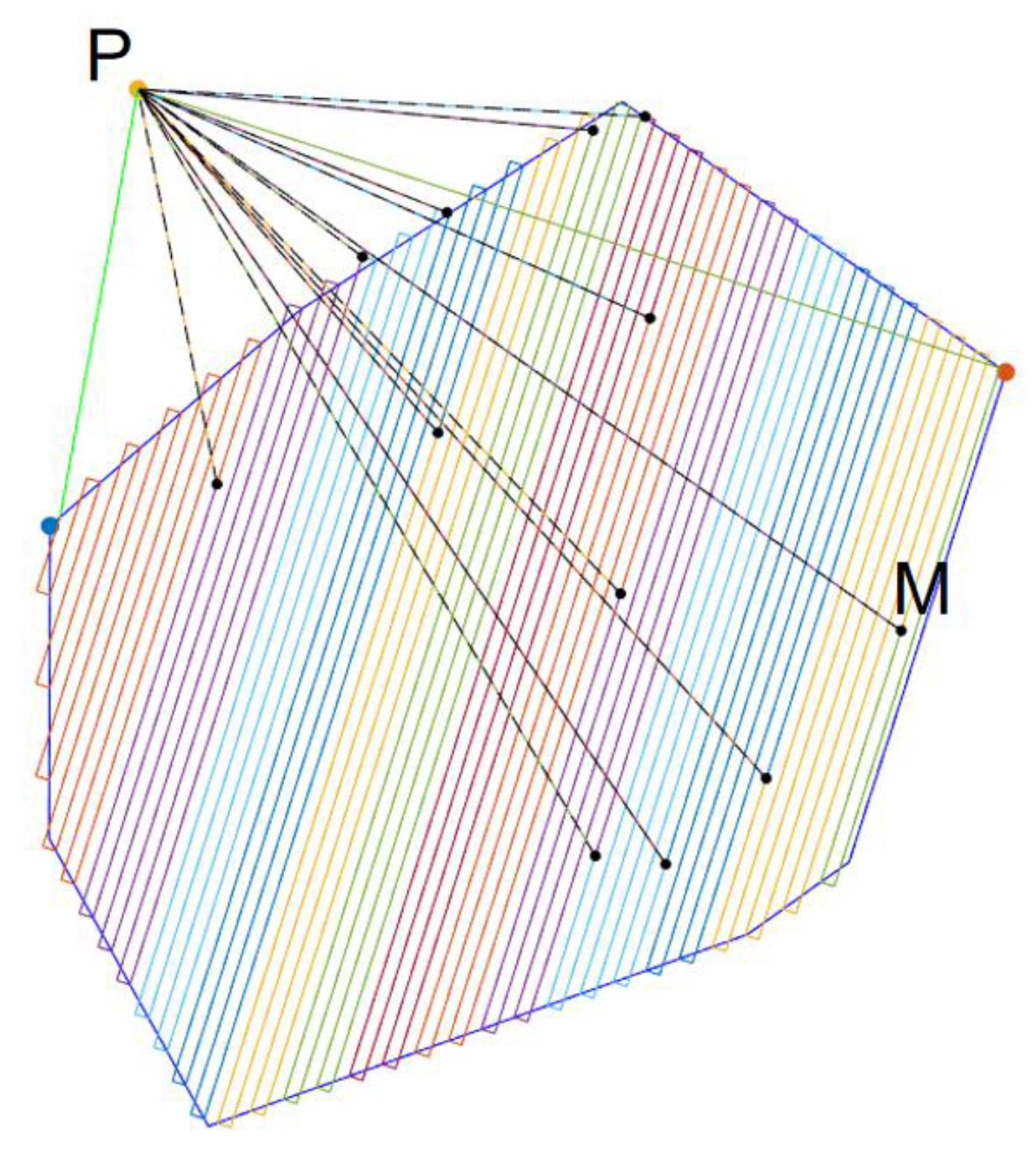
3.2. Modeling of Coverage Path Planning Problem
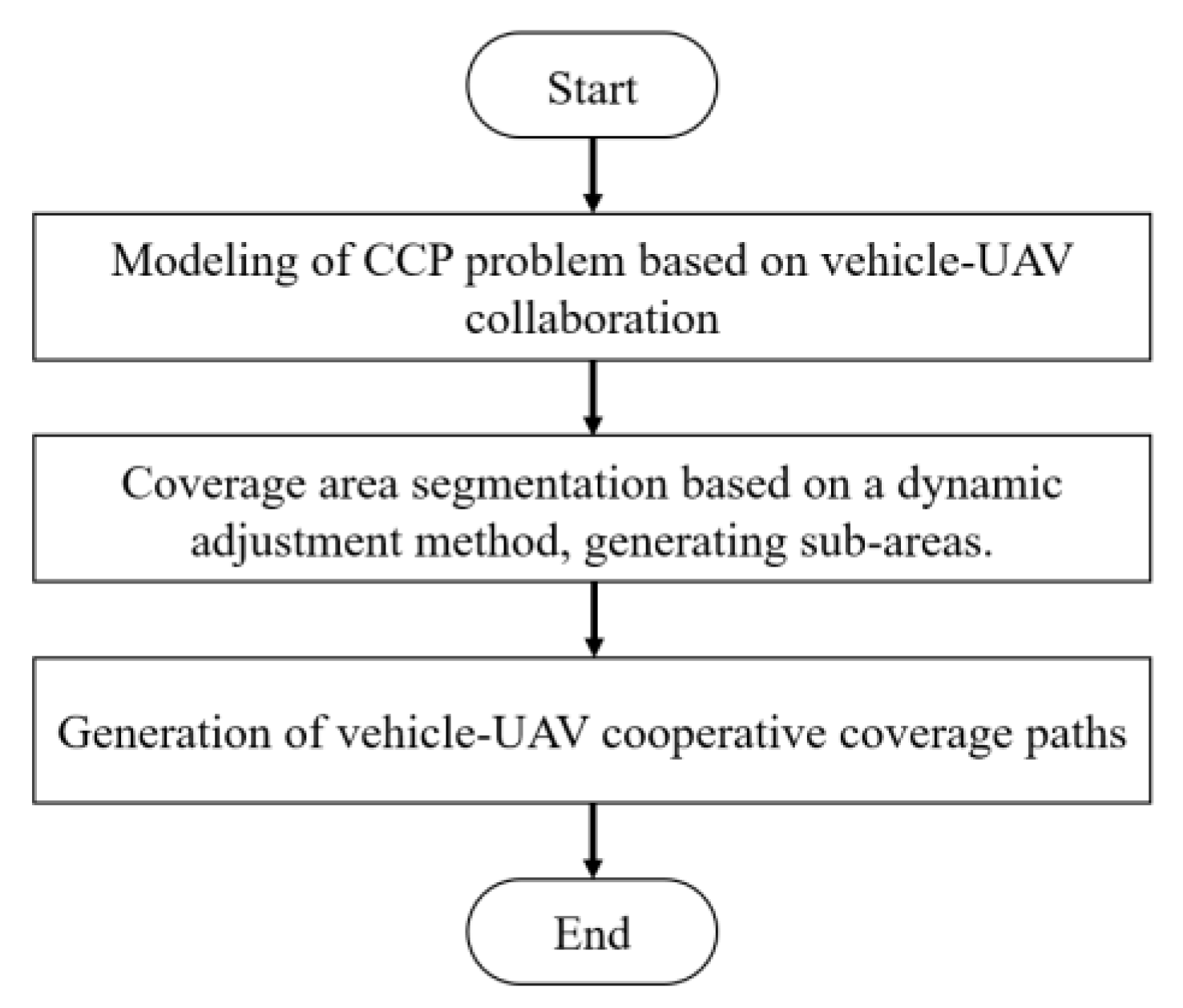
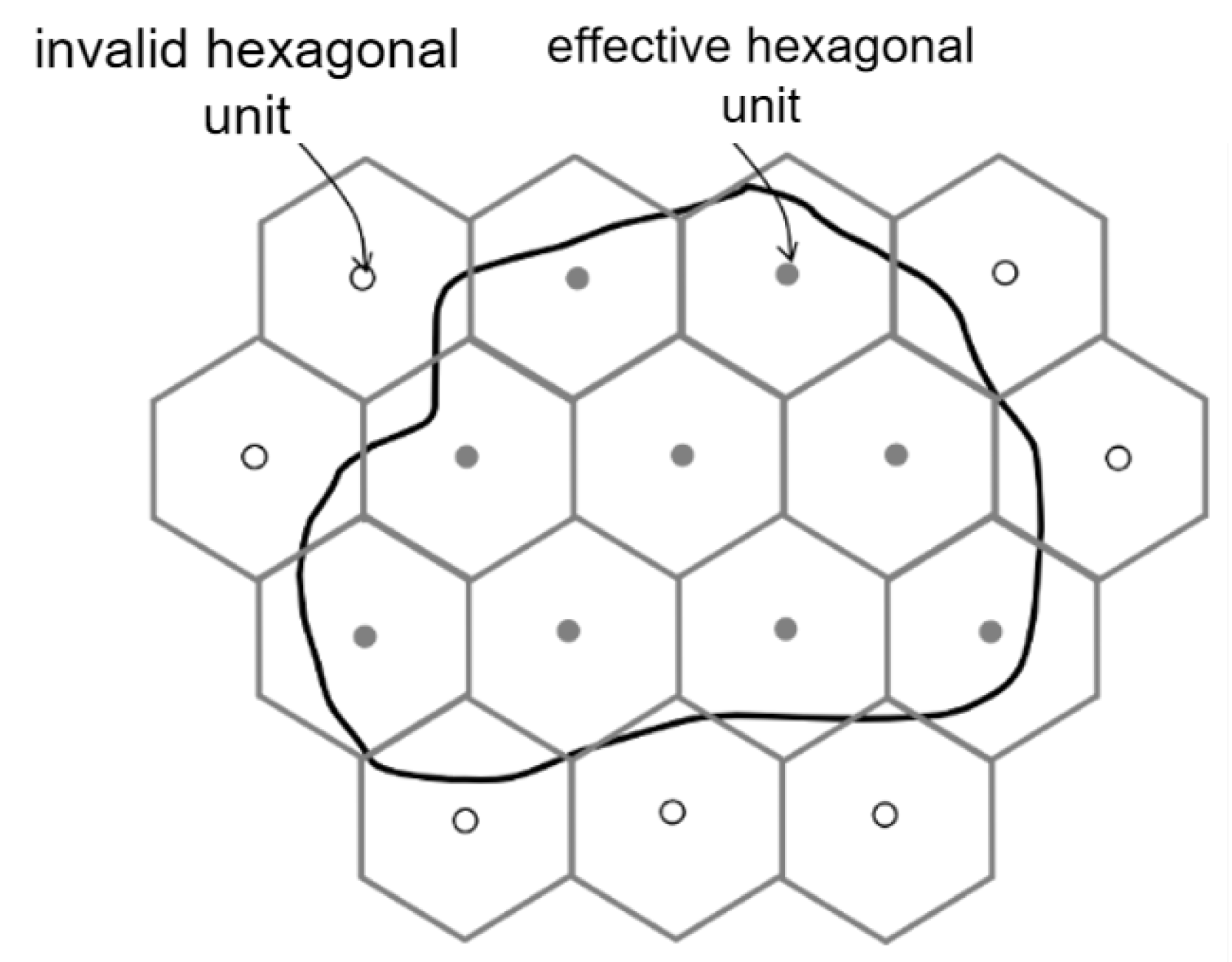
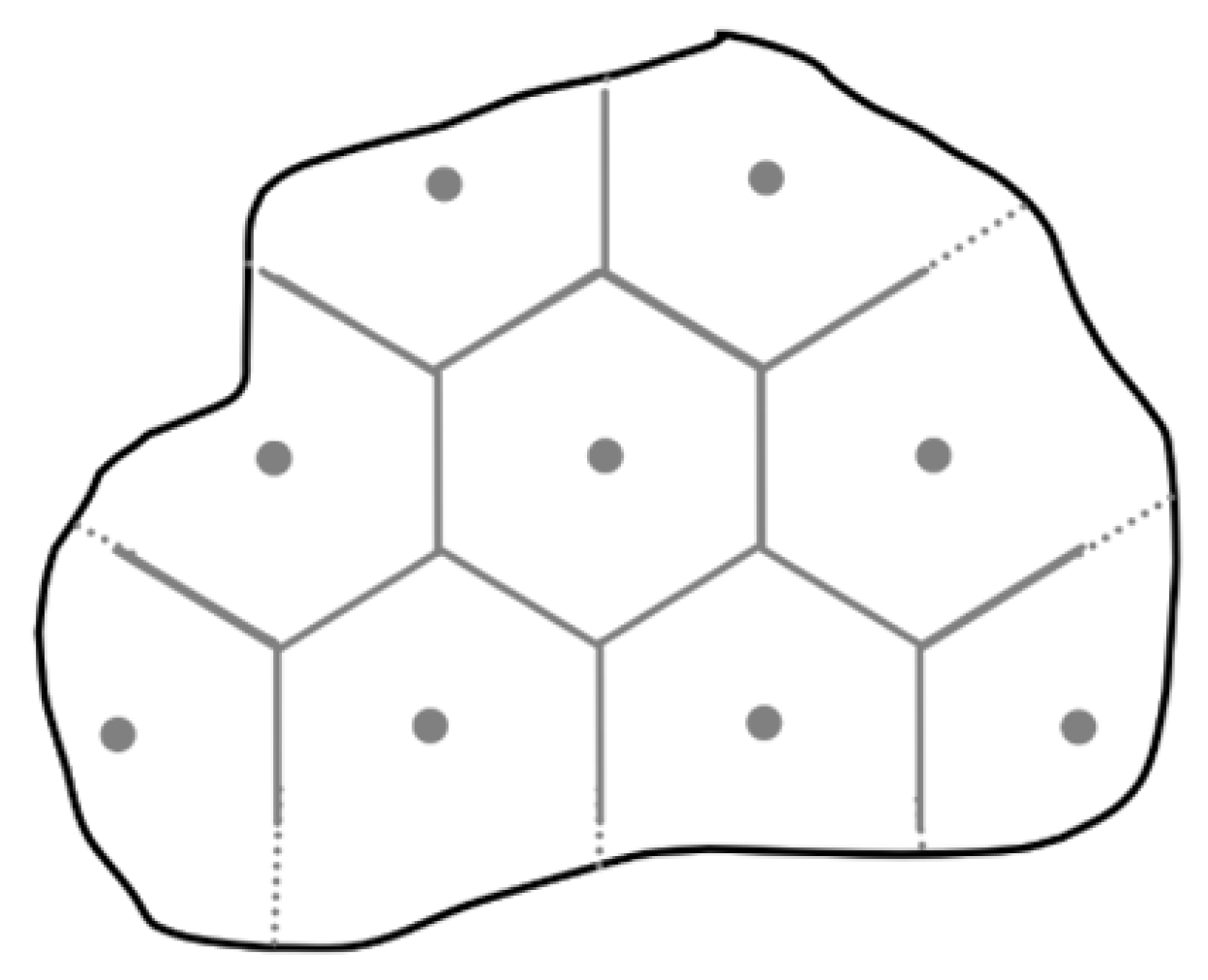
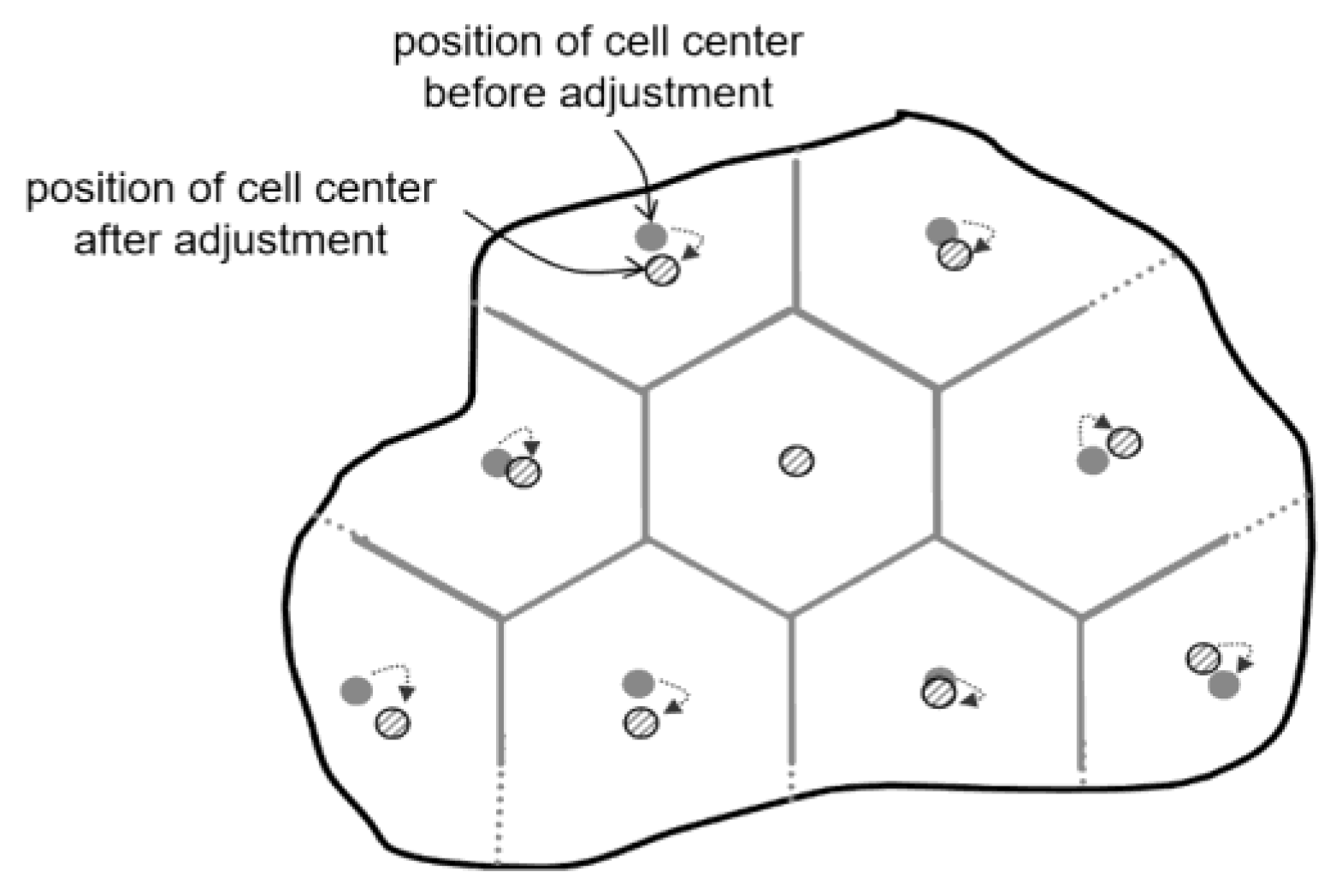
3.3. Coverage Area Segmentation Method Based on Dynamic Adjustment
3.4. Generation of Vehicle–UAV Cooperative Coverage Paths
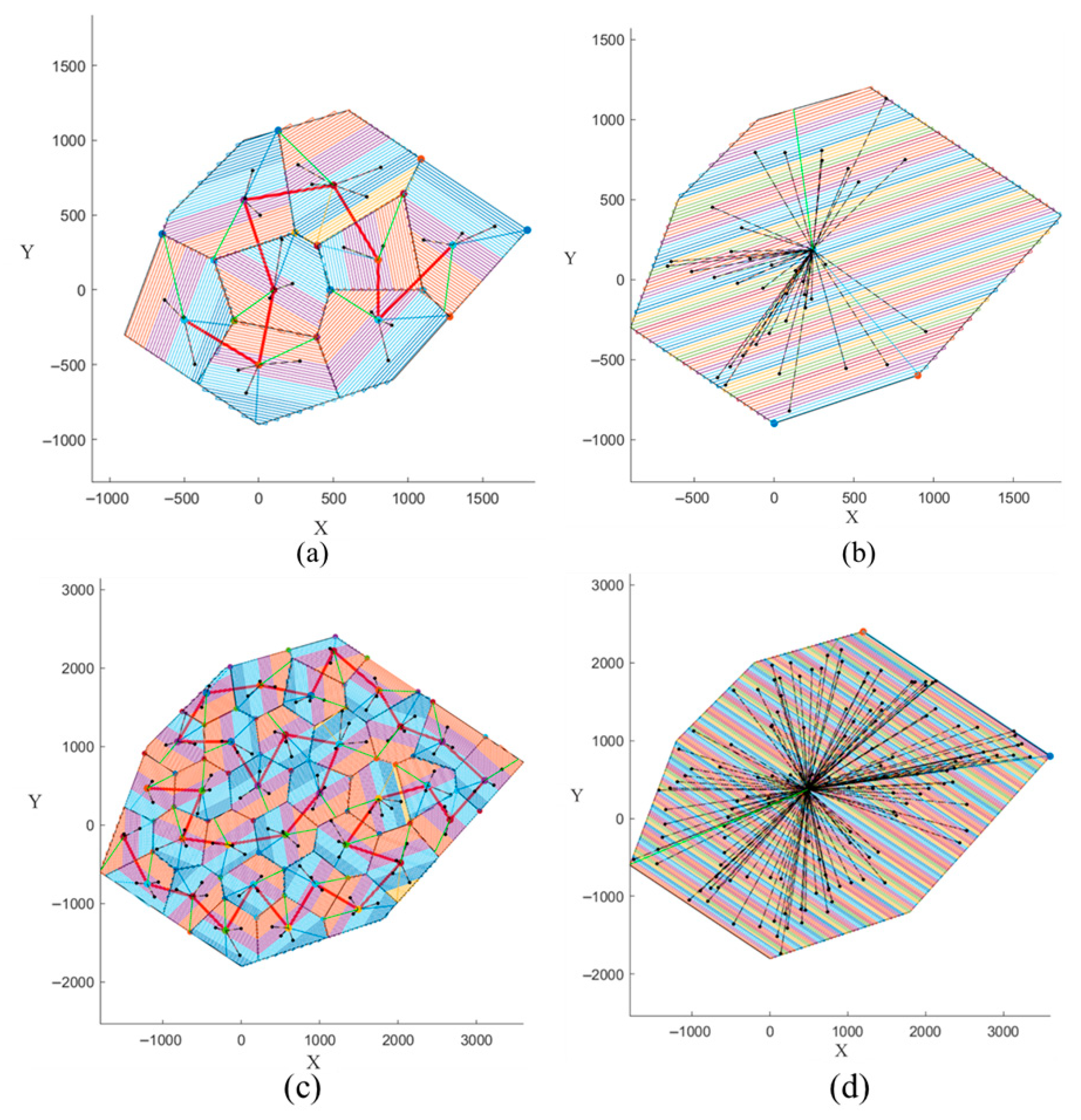
4. Simulation and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| UAV | Unmanned Aerial Vehicle |
| CCP | Coverage Path Planning |
| VG | Voronoi Diagram |
| TSP | Traveling Salesman Problem |
| ACO | Ant Colony Optimization |
| KML | Keynote markup language |
| 3D | Three Dimensional |
| 2D | Two Dimensional |
References
- Hashim, H.A. Advances in UAV avionics systems architecture, classification and integration: A comprehensive review and future perspectives. Results Eng. 2024, 25, 103786. [Google Scholar] [CrossRef]
- Barazzetti, L.; Remondino, F.; Scaioni, M. Extraction of accurate tie points for automated pose estimation of close-range blocks. In International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences; ISPRS Archives: Saint-Mandé, France, 2010; Volume 38. [Google Scholar]
- Gao, H.; Yu, Y.; Huang, X.; Song, L.; Li, L.; Li, L.; Zhang, L. Enhancing the localization accuracy of UAV images under GNSS denial conditions. Sensors 2023, 23, 9751. [Google Scholar] [CrossRef] [PubMed]
- Lucieer, A.; Turner, D.; King, D.H.; Robinson, S.A. Using an unmanned aerial vehicle (UAV) to capture micro-topography of antarctic moss beds. Int. J. Appl. Earth Obs. Geoinf. 2014, 27, 53–62. [Google Scholar] [CrossRef]
- Ahmed, N.; Pawase, C.J.; Chang, K. Distributed 3-d path planning for multi-UAVs with full area surveillance based on particle swarm optimization. Appl. Sci. 2021, 11, 3417. [Google Scholar] [CrossRef]
- Pérez-González, A.; Benítez-Montoya, N.; Jaramillo-Duque, Á.; Cano-Quintero, J.B. Coverage path planning with semantic segmentation for UAV in PV plants. Appl. Sci. 2021, 11, 12093. [Google Scholar] [CrossRef]
- Valente, J.; Sanz, D.; Del Cerro, J.; Barrientos, A.; de Frutos, M.Á. Near-optimal coverage trajectories for image mosaicing using a mini quad-rotor over irregular-shaped fields. Precis. Agric. 2013, 14, 115–132. [Google Scholar] [CrossRef]
- Guo, F.; Gao, W. Batch reconstruction from UAV images with prior information. Acta Autom. Sin. 2013, 39, 834–845. [Google Scholar] [CrossRef]
- Casbeer, D.W.; Kingston, D.B.; Beard, R.W.; McLain, T.W. Cooperative forest fire surveillance using a team of small unmanned air vehicles. Int. J. Syst. Sci. 2006, 37, 351–360. [Google Scholar] [CrossRef]
- Delmerico, J.; Mintchev, S.; Giusti, A.; Gromov, B.; Melo, K.; Horvat, T.; Cadena, C.; Hutter, M.; Ijspeert, A.; Floreano, D.; et al. The current state and future outlook of rescue robotics. J. Field Robot. 2019, 36, 1171–1191. [Google Scholar] [CrossRef]
- Cong, W.; Yi, H.; Yu, F.; Chen, J.; Chen, X.; Xu, F. An improved pied kingfisher optimizer for maritime UAV path planning. Appl. Sci. 2024, 14, 11816. [Google Scholar] [CrossRef]
- Han, D.; Yu, Q.; Jiang, H.; Chen, Y.; Zhu, X.; Wang, L. Three-dimensional path planning for post-disaster rescue UAV by integrating improved grey wolf optimizer and artificial potential field method. Appl. Sci. 2024, 14, 4461. [Google Scholar] [CrossRef]
- Ahmed, G.; Sheltami, T.; Ghaleb, M.; Hamdan, M.; Mahmoud, A.; Yasar, A. Energy-efficient internet of drones path-planning study using meta-heuristic algorithms. Appl. Sci. 2024, 14, 2418. [Google Scholar] [CrossRef]
- Murray, C.C.; Chu, A.G. The flying sidekick traveling salesman problem: Optimization of drone-assisted parcel delivery. Transp. Res. Part C Emerg. Technol. 2015, 54, 86–109. [Google Scholar] [CrossRef]
- Manyam, S.; Casbeer, D.; Sundar, K. Path planning for cooperative routing of air-ground vehicles. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016. [Google Scholar]
- Agatz, N.; Bouman, P.; Schmidt, M. Optimization approaches for the traveling salesman problem with drone. Transp. Sci. 2018, 52, 965–981. [Google Scholar] [CrossRef]
- Deng, C.; Wang, S.; Huang, Z.; Tan, Z.; Liu, J. Unmanned aerial vehicles for power line inspection: A cooperative way in platforms and communications. J. Commun. 2014, 9, 687–692. [Google Scholar] [CrossRef]
- Fikar, C.; Gronalt, M.; Hirsch, P. A decision support system for coordinated disaster relief distribution. Expert Syst. Appl. 2016, 57, 104–116. [Google Scholar] [CrossRef]
- Ulmer, M.W.; Thomas, B.W. Same-day delivery with heterogeneous fleets of drones and vehicles. Networks 2018, 72, 475–505. [Google Scholar] [CrossRef]
- Tokekar, P.; Vander Hook, J.; Mulla, D.; Isler, V. Sensor planning for a symbiotic UAV and UGV system for precision agriculture. IEEE Trans. Robot. 2016, 32, 1498–1511. [Google Scholar] [CrossRef]
- Garone, E.; Naldi, R.; Casavola, A.; Frazzoli, E. Cooperative mission planning for a class of carrier-vehicle systems. In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010. [Google Scholar]
- Mathew, N.; Smith, S.; Waslander, S. Planning paths for package delivery in heterogeneous multirobot teams. IEEE Trans. Autom. Sci. Eng. 2015, 12, 1298–1308. [Google Scholar] [CrossRef]
- Savuran, H.; Karakaya, M. Route optimization method for unmanned air vehicle launched from a carrier. Lect. Notes Softw. Eng. 2015, 3, 279. [Google Scholar] [CrossRef]
- Fawaz, W.; Atallah, R.; Assi, C.; Khabbaz, M. Unmanned aerial vehicles as store-carry-forward nodes for vehicular networks. IEEE Access 2017, 5, 23710–23718. [Google Scholar] [CrossRef]
- Poikonen, S.; Wang, X.; Golden, B. The vehicle routing problem with drones: Extended models and connections. Networks 2017, 70, 34–43. [Google Scholar] [CrossRef]
- Wang, X.; Poikonen, S.; Golden, B. The vehicle routing problem with drones: Several worst-case results. Optim. Lett. 2017, 11, 679–697. [Google Scholar] [CrossRef]
- Sweeney, D.C.; Campbell, J.F.; Zhang, J. Strategic design for delivery with trucks and drones. Supply Chain Anal. Rep. SCMA 2017, 47–55. Available online: https://www.updwg.org/wp-content/uploads/2019/05/StrategicDesignforDeliverywithDronesandTrucks_4-17-17_SCMA-2017-0201.pdf (accessed on 10 December 2024).
- Grocholsky, B.; Keller, J.; Kumar, V.; Pappas, G. Cooperative air and ground surveillance. IEEE Robot. Autom. Mag. 2006, 13, 16–25. [Google Scholar] [CrossRef]
- de Freitas, J.C.; Penna, P.H.V. A randomized variable neighborhood descent heuristic to solve the flying sidekick traveling salesman problem. Electron. Notes Discret. Math. 2018, 66, 95–102. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Z.; Shi, J.; Wu, G.; Pedrycz, W. Two-echelon routing problem for parcel delivery by cooperated truck and drone. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 7450–7465. [Google Scholar] [CrossRef]
- Ropero, F.; Muñoz, P.; R-Moreno, M.D. TERRA: A path planning algorithm for cooperative UGV–UAV exploration. Eng. Appl. Artif. Intell. 2019, 78, 260–272. [Google Scholar] [CrossRef]
- Phan, C.; Liu, H. A cooperative UAV/UGV platform for wildfire detection and fighting. In Proceedings of the 2008 Asia Simulation Conference—7th International Conference on System Simulation and Scientific Computing, Beijing, China, 10–12 October 2008. [Google Scholar]
- Cabreira, T.; Franco, C.; Ferreira, P.; Buttazzo, G. Energy-aware spiral coverage path planning for UAV photogrammetric applications. IEEE Robot. Autom. Lett. 2018, 3, 3662–3668. [Google Scholar] [CrossRef]
- Nagy, I.; Laufer, E. Energy-optimized 3d path planning for unmanned aerial vehicles. Appl. Sci. 2024, 14, 6988. [Google Scholar] [CrossRef]
- Jung, S. Development of path planning tool for unmanned system considering energy consumption. Appl. Sci. 2019, 9, 3341. [Google Scholar] [CrossRef]
- Aurenhammer, F. Voronoi diagrams—A survey of a fundamental geometric data structure. ACM Comput. Surv. 1991, 23, 345–405. [Google Scholar] [CrossRef]
- Song, Q.; Zhao, Q.; Wang, S.; Liu, Q.; Chen, X. Dynamic path planning for unmanned vehicles based on fuzzy logic and improved ant colony optimization. IEEE Access 2020, 8, 62107–62115. [Google Scholar] [CrossRef]
- Ajaj, R.M.; Saavedra Flores, E.I.; Friswell, M.I.; Allegri, G.; Woods, B.K.S.; Isikveren, A.T.; Dettmer, W.G. The zigzag wingbox for a span morphing wing. Aerosp. Sci. Technol. 2013, 28, 364–375. [Google Scholar] [CrossRef]


| Coverage Path Planning Methods | Total Path Length (m) | |
|---|---|---|
| Small Area Case | Large Area Case | |
| The Proposed Coverage Path Planning Method Based on Vehicle–UAV Collaboration | 202,626 | 820,678 |
| The Classic Zigzag Coverage Path Planning Method Based Entirely on UAV | 224,943 | 1,127,467 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, N.; Zhang, B.; Zhang, Q.; Gao, C.; Feng, J.; Yue, L. Large-Area Coverage Path Planning Method Based on Vehicle–UAV Collaboration. Appl. Sci. 2025, 15, 1247. https://doi.org/10.3390/app15031247
Zhang N, Zhang B, Zhang Q, Gao C, Feng J, Yue L. Large-Area Coverage Path Planning Method Based on Vehicle–UAV Collaboration. Applied Sciences. 2025; 15(3):1247. https://doi.org/10.3390/app15031247
Chicago/Turabian StyleZhang, Nan, Bingbing Zhang, Qiang Zhang, Chaojun Gao, Jiahao Feng, and Linkai Yue. 2025. "Large-Area Coverage Path Planning Method Based on Vehicle–UAV Collaboration" Applied Sciences 15, no. 3: 1247. https://doi.org/10.3390/app15031247
APA StyleZhang, N., Zhang, B., Zhang, Q., Gao, C., Feng, J., & Yue, L. (2025). Large-Area Coverage Path Planning Method Based on Vehicle–UAV Collaboration. Applied Sciences, 15(3), 1247. https://doi.org/10.3390/app15031247






