Advances in the Neural Network Quantization: A Comprehensive Review
Abstract
:1. Introduction
2. Quantization Fundamentals
3. Quantization Techniques
3.1. PTQ
3.2. QAT
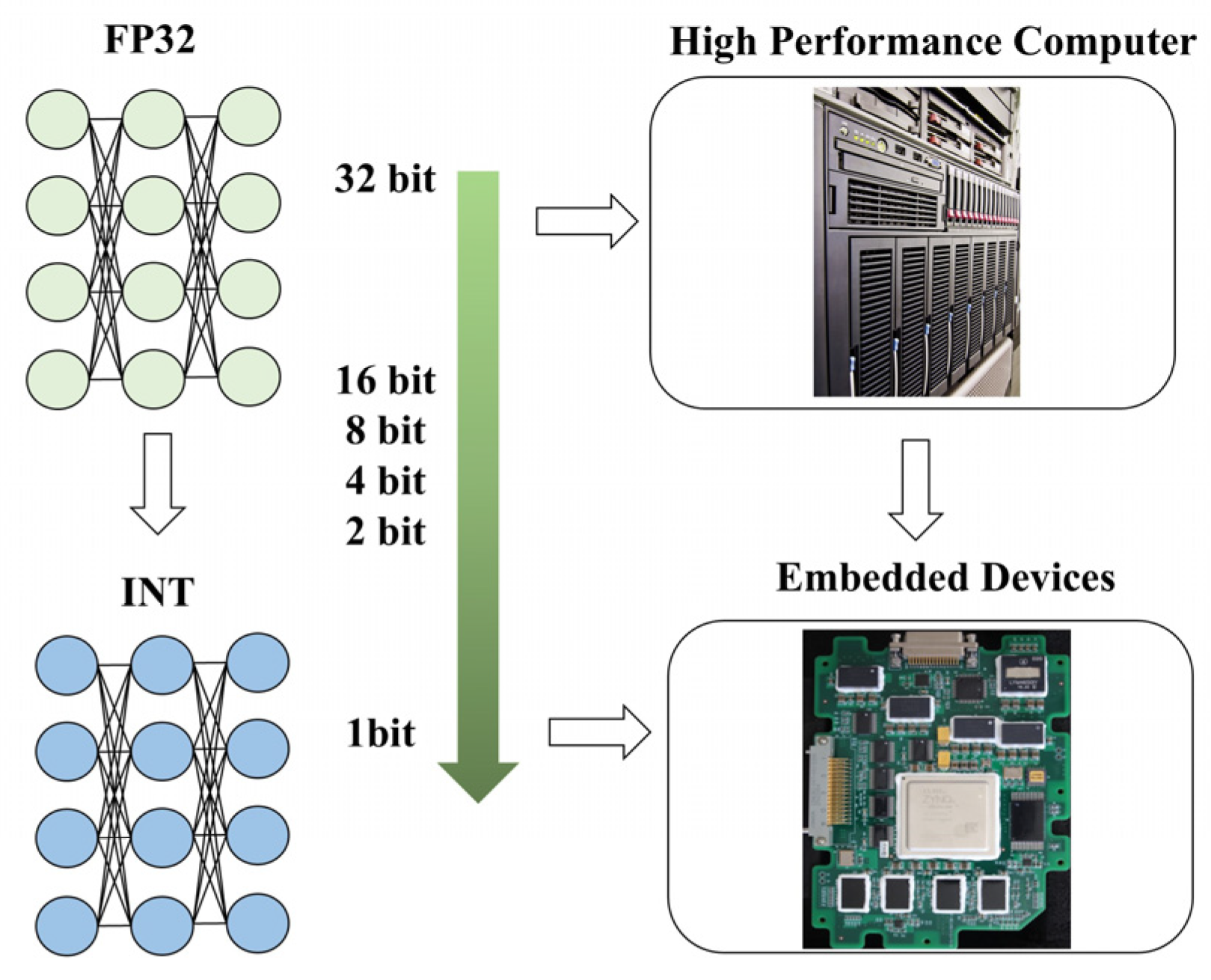
3.3. The Selection of Quantization Bitwidth
3.4. The Accuracy Loss Evaluation of the Quantized Models
3.5. Quantization of LLMs
4. Experimental Results
4.1. Experimental Setting
4.2. Results
5. Future Challenges and Trends
Author Contributions
Funding
Conflicts of Interest
References
- Liu, Z.; Hu, H.; Lin, Y.; Yao, Z.; Xie, Z.; Wei, Y.; Ning, J.; Cao, Y.; Zhang, Z.; Dong, L.; et al. Swin transformer v2: Scaling up capacity and resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021. [Google Scholar]
- Zhang, H.; Li, F.; Liu, S.; Zhang, L.; Su, H.; Zhu, J.; Ni, L.M.; Shum, H.-Y. DINO: DETR with improved denoising anchor boxes for end-to-end object detection. In International Conference on Learning Representations. arXiv 2023, arXiv:2203.03605. [Google Scholar]
- Zong, Z.; Song, G.; Liu, Y. Detrs with collaborative hybrid assignments training. In Proceedings of the International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 6725–6735. [Google Scholar]
- Zhou, X.S.; Wu, W.L. Unmanned system swarm intelligence and its research progresses. Microelectron. Comput. 2021, 38, 1–7. [Google Scholar] [CrossRef]
- Chen, Z.; Duan, Y.; Wang, W.; He, J.; Lu, T.; Dai, J.; Qiao, Y. Vision transformer adapter for dense predictions. In International Conference on Learning Representations. arXiv 2023, arXiv:2205.08534. [Google Scholar]
- Fang, Y.; Wang, W.; Xie, B.; Sun, Q.; Wu, L.; Wang, X.; Huang, T.; Wang, X.; Cao, Y. EVA: Exploring the limits of masked visual representation learning at scale. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 19358–19369. [Google Scholar]
- Su, W.; Zhu, X.; Tao, C.; Lu, L.; Li, B.; Huang, G.; Qiao, Y.; Wang, X.; Zhou, J.; Dai, J. Towards all-in-one pre-training via maximizing multi-modal mutual information. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 15888–15899. [Google Scholar]
- Wang, W.; Dai, J.; Chen, Z.; Huang, Z.; Li, Z.; Zhu, X.; Hu, X.; Lu, T.; Lu, L.; Li, H.; et al. Internimage: Exploring large-scale vision foundation models with deformable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 14408–14419. [Google Scholar]
- Tang, L.; Ma, Z.; Li, S.; Wang, Z.X. The present situation and developing trends of space-based intelligent computing technology. Microelectron. Comput. 2022, 39, 1–8. [Google Scholar] [CrossRef]
- Bianco, S.; Cadene, R.; Celona, L.; Napoletano, P. Benchmark analysis of representative deep neural network architectures. IEEE Access 2018, 6, 64270–64277. [Google Scholar] [CrossRef]
- Hong, J.; Duan, J.; Zhang, C.; Li, Z.; Xie, C.; Lieberman, K.; Diffenderfer, J.; Bartoldson, B.; Jaiswal, A.; Xu, K.; et al. Decoding Compressed Trust: Scrutinizing the Trustworthiness of Efficient LLMs under Compression. Computing Research Repository. arXiv 2024, arXiv:2403.15447. [Google Scholar]
- Agustsson, E.; Theis, L. Universally quantized neural compression. Adv. Neural Inf. Process. Syst. 2020, 33, 12367–12376. [Google Scholar]
- Banner, R.; Nahshan, Y.; Soudry, D. Post-training 4-bit quantization of convolution networks for rapid-deployment. arXiv 2018, arXiv:1810.05723. [Google Scholar]
- Bulat, A.; Martinez, B.; Tzimiropoulos, G. High-capacity expert binary networks. International Conference on Learning Representations. arXiv 2021, arXiv:2010.03558. [Google Scholar]
- Liang, T.; Glossner, J.; Wang, L.; Shi, S.; Zhang, X. Pruning and quantization for deep neural network acceleration: A survey. arXiv 2021, arXiv:2101.09671. [Google Scholar] [CrossRef]
- Garg, S.; Jain, A.; Lou, J.; Nahmias, M. Confounding tradeoffs for neural network quantization. arXiv 2021, arXiv:2102.06366. [Google Scholar]
- Garg, S.; Lou, J.; Jain, A.; Guo, Z.; Shastri, B.J.; Nahmias, M. Dynamic precision analog computing for neural networks. arXiv 2021, arXiv:2102.06365. [Google Scholar] [CrossRef]
- Devlin, J.; Chang, M.-W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. North American Chapter of the Association for Computational Linguistics. arXiv 2018, arXiv:1810.04805, 4171–4186. [Google Scholar]
- Tom, B.B.; Benjamin, M.; Nick, R.; Melanie, S.; Jared, K. Language Models are Few-Shot Learners. Conf. Neural Inf. Process. Syst. 2020, 33, 1877–1901. [Google Scholar]
- Zhu, X.; Li, J.; Liu, Y.; Ma, C.; Wang, W. A Survey on Model Compression for Large Language Models. CoRR arXiv 2023, arXiv:2308.07633. [Google Scholar]
- Zhang, Y.; Huang, D.; Liu, B.; Tang, S.; Lu, Y.; Chen, L.; Bai, L.; Chu, Q.; Yu, N.; Ouyang, W. MotionGPT: Finetuned LLMs Are General-Purpose Motion Generators. Proc. AAAI Conf. Artif. Intell. 2024, 38, 7368–7376. [Google Scholar] [CrossRef]
- Xu, Z.; Cristianini, N. QBERT: Generalist Model for Processing Questions. In Advances in Intelligent Data Analysis XXI; Springer: Berlin/Heidelberg, Germany, 2022; pp. 472–483. [Google Scholar]
- Frantar, E.; Ashkboos, S.; Hoefler, T.; Alistarh, D. GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers. arXiv 2023, arXiv:2210.17323. [Google Scholar]
- Zhou, S.; Wu, Y.; Ni, Z.; Zhou, X.; Wen, H.; Zou, Y. Dorefa-net: Training low bitwidth convolutional neural networks with low bitwidth gradients. arXiv 2016, arXiv:1606.06160. [Google Scholar]
- Gholami, A.; Kim, S.; Dong, Z.; Yao, Z.; Mahoney, M.W.; Keutzer, K. A Survey of Quantization Methods for Efficient Neural Network Inference. arXiv 2021, arXiv:2103.13630. [Google Scholar]
- Nagel, M.; Fournarakis, M.; Amjad, R.A.; Bondarenko, Y.; Van Baalen, M.; Blankevoort, T. A White Paper on Neural Network Quantization. arXiv 2021, arXiv:2106.08295. [Google Scholar]
- Li, Y.; Dong, X.; Wang, W. Additive Powers-of-Two Quantization: An Efficient Non-uniform Discretization for Neural Networks. arXiv 2020, arXiv:1909.13144. [Google Scholar]
- Liu, Z.; Wang, Y.; Han, K.; Zhang, W.; Ma, S.; Gao, W. Post-training quantization for vision transformer. Adv. Neural Inf. Process. Syst. 2021, 34, 28092–28103. [Google Scholar]
- Jacob, B.; Kligys, S.; Chen, B.; Zhu, M.; Tang, M.; Howard, A.; Adam, H.; Kalenichenko, D. Quantization and training of neural networks for efficient integerarithmetic-only inference. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2704–2713. [Google Scholar]
- Li, Y.; Xu, S.; Zhang, B.; Cao, X.; Gao, P.; Guo, G. Q-vit: Accurate and fully quantized low-bit vision transformer. Adv. Neural Inf. Process. Syst. 2022, 35, 34451–34463. [Google Scholar]
- Yao, Z.; Dong, Z.; Zheng, Z.; Gholami, A.; Yu, J.; Tan, E.; Wang, L.; Huang, Q.; Wang, Y.; Mahoney, M. Hawqv3: Dyadic neural network quantization. arXiv 2020, arXiv:2011.10680. [Google Scholar]
- McKinstry, J.L.; Esser, S.K.; Appuswamy, R.; Bablani, D.; Arthur, J.V.; Yildiz, I.B.; Modha, D.S. Discovering low-precision networks close to full-precision networks for efficient embedded inference. arXiv 2018, arXiv:1809.04191. [Google Scholar]
- Krishnamoorthi, R. Quantizing deep convolutional net-works for efficient inference: A whitepaper. arXiv 2018, 8, 667–668. [Google Scholar]
- Wu, H.; Judd, P.; Zhang, X.; Isaev, M.; Micikevicius, P. Integer quantization for deep learning inference: Principles and empirical evaluation. arXiv 2020, arXiv:2004.09602. [Google Scholar]
- Migacz, S. 8-Bit Inference with TensorRT. GPU Technology Conference 2, 7. 2017. Available online: https://on-demand.gputechconf.com/gtc/2017/presentation/s7310-8-bit-inference-with-tensorrt.pdf (accessed on 8 May 2017).
- Chen, T.; Moreau, T.; Jiang, Z.; Zheng, L.; Yan, E. TVM: An automated end-to-end optimizing compiler for deep learning. In Proceedings of the 13th fUSENIXg Symposium on Operating Systems Design and Implementation (fOSDIg 18), Carlsbad, CA, USA, 8–10 October 2018; pp. 578–594. [Google Scholar]
- Choukroun, Y.; Kravchik, E.; Yang, F.; Kisilev, P. Low-bit quantization of neural networks for efficient inference. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Republic of Korea, 27–28 October 2019; pp. 3009–3018. [Google Scholar]
- Shin, S.; Hwang, K.; Sung, W. Fixed-point performance analysis of recurrent neural networks. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 976–980. [Google Scholar]
- Sung, W.; Shin, S.; Hwang, K. Resiliency of deep neural networks under quantization. arXiv 2015, arXiv:1511.06488. [Google Scholar]
- Zhao, R.; Hu, Y.W.; Dotzel, J. Improving neural network quantization without retraining using outlier channel splitting. arXiv 2019, arXiv:1901.09504. [Google Scholar]
- Park, E.; Ahn, J.; Yoo, S. Weighted-entropy-based quantization for deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 26 July 2017; pp. 5456–5464. [Google Scholar]
- Wei, L.; Ma, Z.; Yang, C. Activation Redistribution Based Hybrid Asymmetric Quantization Method of Neural Networks. CMES 2024, 138, 981–1000. [Google Scholar] [CrossRef]
- Choi, J.; Wang, Z.; Venkataramani, S.; Chuang, P.I.-J.; Srinivasan, V.; Gopalakrishnan, K. Pact: Parameterized clipping activation for quantized neural networks. arXiv 2018, arXiv:1805.06085. [Google Scholar]
- Gong, R.; Liu, X.; Jiang, S.; Li, T.; Hu, P.; Lin, J.; Yu, F.; Yan, J. Differentiable soft quantization: Bridging full-precision and low-bit neural networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 4852–4861. [Google Scholar]
- Jin, Q.; Yang, L.; Liao, Z. Towards efficient training for neural network quantization. arXiv 2019, arXiv:1912.10207. [Google Scholar]
- Liu, J.; Cai, J.; Zhuang, B. Sharpness-aware Quantization for Deep Neural Networks. arXiv 2021, arXiv:2111.12273. [Google Scholar] [CrossRef]
- Zhuang, B.; Liu, L.; Tan, M.; Shen, C.; Reid, I. Training Quantized Neural Networks With a Full-Precision Auxiliary Module. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 1488–1497. [Google Scholar] [CrossRef]
- Diao, H.; Li, G.; Xu, S.; Kong, C.; Wang, W. Attention Round for post-training quantization. Neurocomputing 2024, 565, 127012. [Google Scholar] [CrossRef]
- Wu, B.; Wang, Y.; Zhang, P.; Tian, Y.; Vajda, P.; Keutzer, K. Mixed precision quantization of convnets via differentiable neural architecture search. arXiv 2018, arXiv:1812.00090. [Google Scholar]
- Wang, K.; Liu, Z.; Lin, Y.; Lin, J.; Han, S. Haq: Hardware-aware automated quantization with mixed precision. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 8612–8620. [Google Scholar]
- Dong, Z.; Yao, Z.; Gholami, A.; Mahoney, M.; Keutzer, K. Hawq: Hessian aware quantization of neural networks with mixed-precision. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 293–302. [Google Scholar]
- Dong, P.; Li, L.; Wei, Z.; Niu, X.; Tian, Z.; Pan, H. Emq: Evolving training-free proxies for automated mixed precision quantization. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 17076–17086. [Google Scholar]
- Tang, C.; Ouyang, K.; Chai, Z.; Bai, Y.; Meng, Y.; Wang, Z.; Zhu, W. SEAM: Searching Transferable Mixed-Precision Quantization Policy through Large Margin Regularization. In Proceedings of the 31st ACM International Conference on Multimedia, Ottawa, ON, Canada, 29 October–3 November 2023; pp. 7971–7980. [Google Scholar]
- Dong, Z.; Yao, Z.; Cai, Y.; Arfeen, D.; Gholami, A.; Mahoney, M.W.; Keutzer, K. Hawq-v2: Hessian aware trace-weighted quantization of neural networks. In Advances in Neural Information Processing Systems; JMLR: New York, NY, USA, 2020; pp. 18518–18529. [Google Scholar]
- Tang, C.; Ouyang, K.; Wang, Z.; Zhu, Y.; Ji, W.; Wang, Y.; Zhu, W. Mixed-Precision Neural Network Quantization via Learned Layer-wise Importance. In Proceedings of the Computer Vision—ECCV 2022, Tel Aviv, Israel, 23–27 October 2022. [Google Scholar] [CrossRef]
- Sheng, T.; Feng, C.; Zhuo, S.; Zhang, X.; Shen, L.; Aleksic, M. A quantization-friendly separable convolution for mobilenets. In Proceedings of the 2018 1st Workshop on Energy Efficient Machine Learning and Cognitive Computing for Embedded Applications (EMC2), Williamsburg, VA, USA, 25 March 2018. [Google Scholar]
- Feng, P.; Yu, L.; Tian, S.W.; Geng, J.; Gong, G.L. Quantization of 8-bit deep neural networks based on mean square error. Comput. Eng. Des. 2022, 43, 1258–1264. [Google Scholar]
- Wang, T.; Wang, K.; Cai, H.; Lin, J.; Liu, Z.; Wang, H.; Lin, Y.; Han, S. APQ: Joint Search for Network Architecture, Pruning and Quantization Policy. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; Volume 2006.08509, pp. 2075–2084. [Google Scholar]
- Wang, P.; Yang, A.; Men, R.; Lin, J.; Bai, S.; Li, Z. Unifying Architectures, Tasks, and Modalities Through a Simple Sequence-to-Sequence Learning Framework. In Proceedings of the International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022; pp. 23318–23340. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Advances in Neural Information Processing Systems 30; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S.V.N., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2017; pp. 5998–6008. [Google Scholar]
- Dettmers, T.; Pagnoni, A.; Holtzman, A.; Zettlemoyer, L. Qlora: Efficient finetuning of quantized llms. arXiv 2023, arXiv:2305.14314. [Google Scholar]
- Wei, X.; Zhang, Y.; Zhang, X.; Gong, R.; Zhang, S.; Zhang, Q.; Yu, F.; Liu, X. Outlier suppression: Pushing the limit of low-bit transformer language models. NeurIPS 2022, 35, 17402–17414. [Google Scholar]




| Task | Model | PC Accuracy (FP32) | Method [42] | Method [41] | Method [43] |
|---|---|---|---|---|---|
| Image Classification | GoogleNet | 67.04 | 65.22 | 65.91 | 66.65 |
| Image Classification | VGG16 | 66.13 | 64.72 | 62.53 | 65.61 |
| Object Detection | YOLOv1 | 61.99 | 59.41 | 60.94 | 61.27 |
| Image Segmentation | U-net | 82.78 | 82.13 | 81.71 | 82.14 |
| Method | W-Bits | B-Bits | Top-1 | W-C |
|---|---|---|---|---|
| PACT [44] | 3 | 3 | 67.57 | 10.67x |
| HAWQv2 [55] | 3-Mixed-Precision | 3-Mixed-Precision | 68.62 | 12.2x |
| LIMPQ [56] | 3-Mixed-Precision | 4-Mixed-Precision | 70.15 | 12.3x |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, L.; Ma, Z.; Yang, C.; Yao, Q. Advances in the Neural Network Quantization: A Comprehensive Review. Appl. Sci. 2024, 14, 7445. https://doi.org/10.3390/app14177445
Wei L, Ma Z, Yang C, Yao Q. Advances in the Neural Network Quantization: A Comprehensive Review. Applied Sciences. 2024; 14(17):7445. https://doi.org/10.3390/app14177445
Chicago/Turabian StyleWei, Lu, Zhong Ma, Chaojie Yang, and Qin Yao. 2024. "Advances in the Neural Network Quantization: A Comprehensive Review" Applied Sciences 14, no. 17: 7445. https://doi.org/10.3390/app14177445
APA StyleWei, L., Ma, Z., Yang, C., & Yao, Q. (2024). Advances in the Neural Network Quantization: A Comprehensive Review. Applied Sciences, 14(17), 7445. https://doi.org/10.3390/app14177445






