Techno-Economic Assessment of Coaxial HTS HVAC Transmission Cables with Critical Current Grading between Phases Using the OSCaR Tool
Abstract
1. Introduction
2. Methodology Overview
2.1. Cable System Structure Represented in the Tool
2.2. System Variables Selected for the Optimization and Grading Approach
3. Main Simplifying Hypotheses Assumed in the Optimization Tool
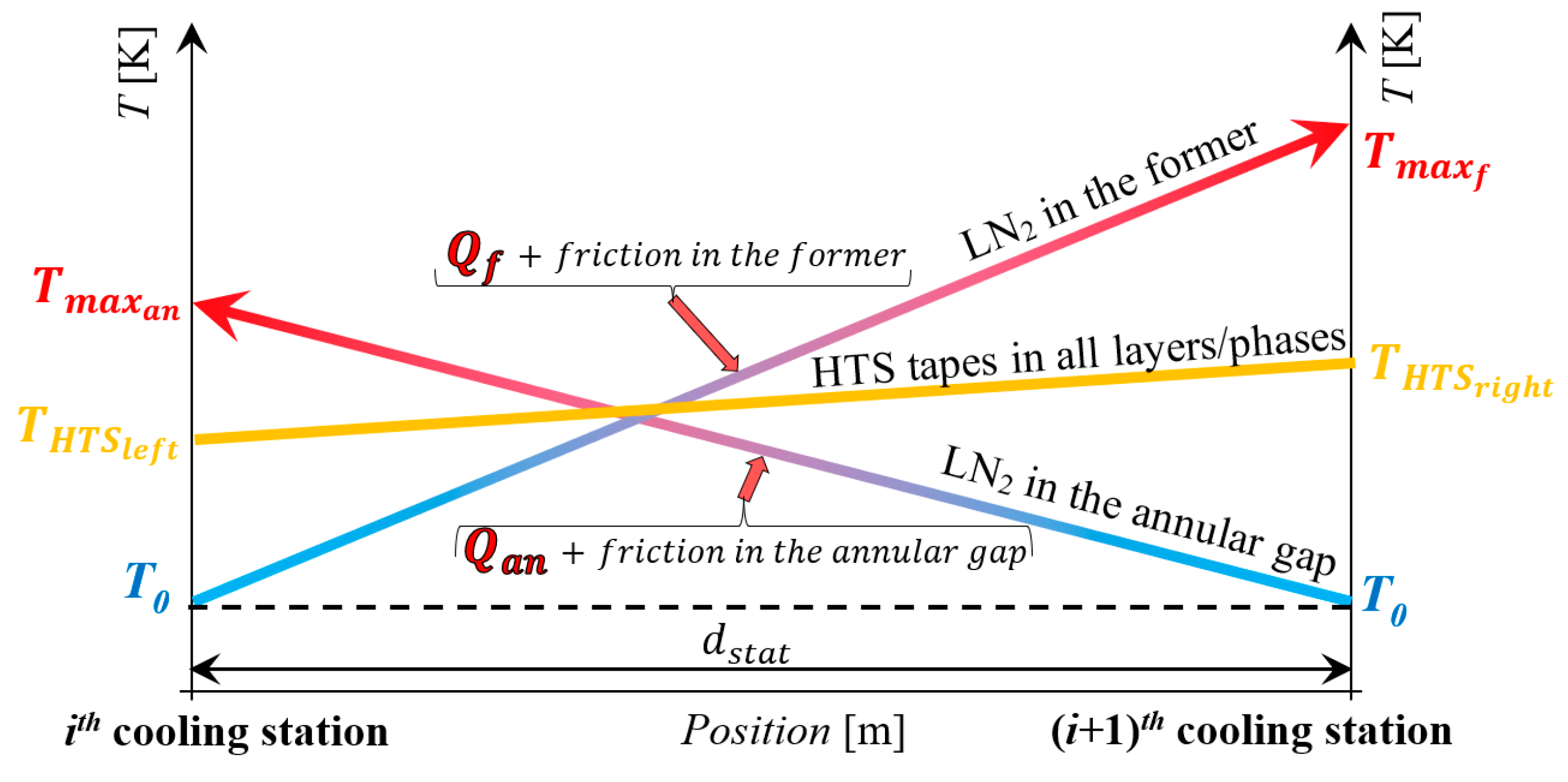
3.1. Thermo-Hydraulic Model
3.2. Electrical Model
3.3. Magnetic Model
3.4. Time-Varying Power Transferred by the Line
3.5. Calculation of the Thicknesses of the Dielectric Layers
4. Cost Function to Be Minimized
4.1. Approach for the Quantitative Discounting of Selected Cost Indexes
- (1)
- A reference quantity (called , where the subscript x can be replaced with the corresponding cost term) is set for each discounted index, whether it be a length, a weight, a volume, or the number of components. These quantities correspond to the reference case for which the authors have assumed fixed unit costs (), such as the materials required for a 50 km HTS cable. By carrying out parametric analyses with the proposed tool, different case studies from the reference one can be investigated, resulting in different optimized designs and material or component quantities.If these quantities are greater than their reference values, then a reduction in the unit cost is expected. Conversely, if the optimized quantities fall below their reference values, then it is reasonable that the buyer will have to pay a higher unit price.
- (2)
- A multiplicative coefficient relative to the reference quantity is set (referred to as ), corresponding to a discount of the unit cost, called . To give a quantitative example, supposing is equal to 100 km, is equal to 5, and is equal to 20%, if the optimized cable design requires purchasing a quantity of the material or component x equal to = 500 km, then the corresponding unit cost of that material or component will be lowered by 20% compared with the one set for the reference quantity. The parameter is also used as a divisor of the reference quantity, resulting in an increase in the unit cost when the optimized quantity is lower than the reference one, corresponding again to .
- (3)
- It is assumed that the discount of the unit cost is linearly proportional to the optimized quantity. This discounting process is applied within maximum and minimum discounting rates compared with the reference unit cost. This corresponds to assuming that the buyer’s or manufacturer’s leverage on the unit price is limited to a certain range. For simplicity, both thresholds are set equal to , which might then be positive or negative.
4.2. Cost of the Superconducting Material
- (1)
- At each algorithm step, a specific set of system variables is examined, including the ratios.
- (2)
- Based on each ratio and the calculation of for the innermost layer of each phase (as detailed in Section 3.2), the values of are derived. These correspond to the lowest critical current values for the tapes belonging to the innermost layer of each phase occurring in a cable segment.
- (3)
- From the results of the thermal model (Section 3.1) and the magnetic model (Section 3.3), the higher temperature and magnetic field values within a cable segment are determined for the innermost layer of each phase. These represent the most stressful scenarios for the coated conductor in each phase, where the upper limit of the ratios between the transport currents and the critical currents are conservatively determined.
- (4)
- Then, the characteristic curves of the chosen coated conductor are considered. These curves are generally provided by the manufacturer for a reference tape and are not always reported in dimensionless terms. These curves enable calculation of the critical current values of the reference tape under the same temperature and magnetic field conditions identified in the previous step, with one for each phase, called .
- (5)
- Similarly, using the manufacturer’s characteristic curves, the critical current value of the reference tape at 77 K and self-field is known, called .
- (6)
- It is assumed that the same characteristic curves valid to the reference tape can be scaled for the actual tape adopted in each phase of the optimized structure. By solving a simple proportion for each phase, the corresponding values of can be obtained:
- (7)
- Then, the values (before quantitative discounting) are computed by multiplying the values for the cost per unit length and per kiloampere of current carried by the tape at 77 K and the self-field tape (), for which statistical data can be gathered from the literature:
- (8)
- Finally, the values are calculated by applying the quantitative discounting approach described in Section 4.1 to .
4.3. Cost of the Insulating Material
4.4. Cost of the Cryogenic Fluid
4.5. Cost of the Copper for the Neutral Conductor
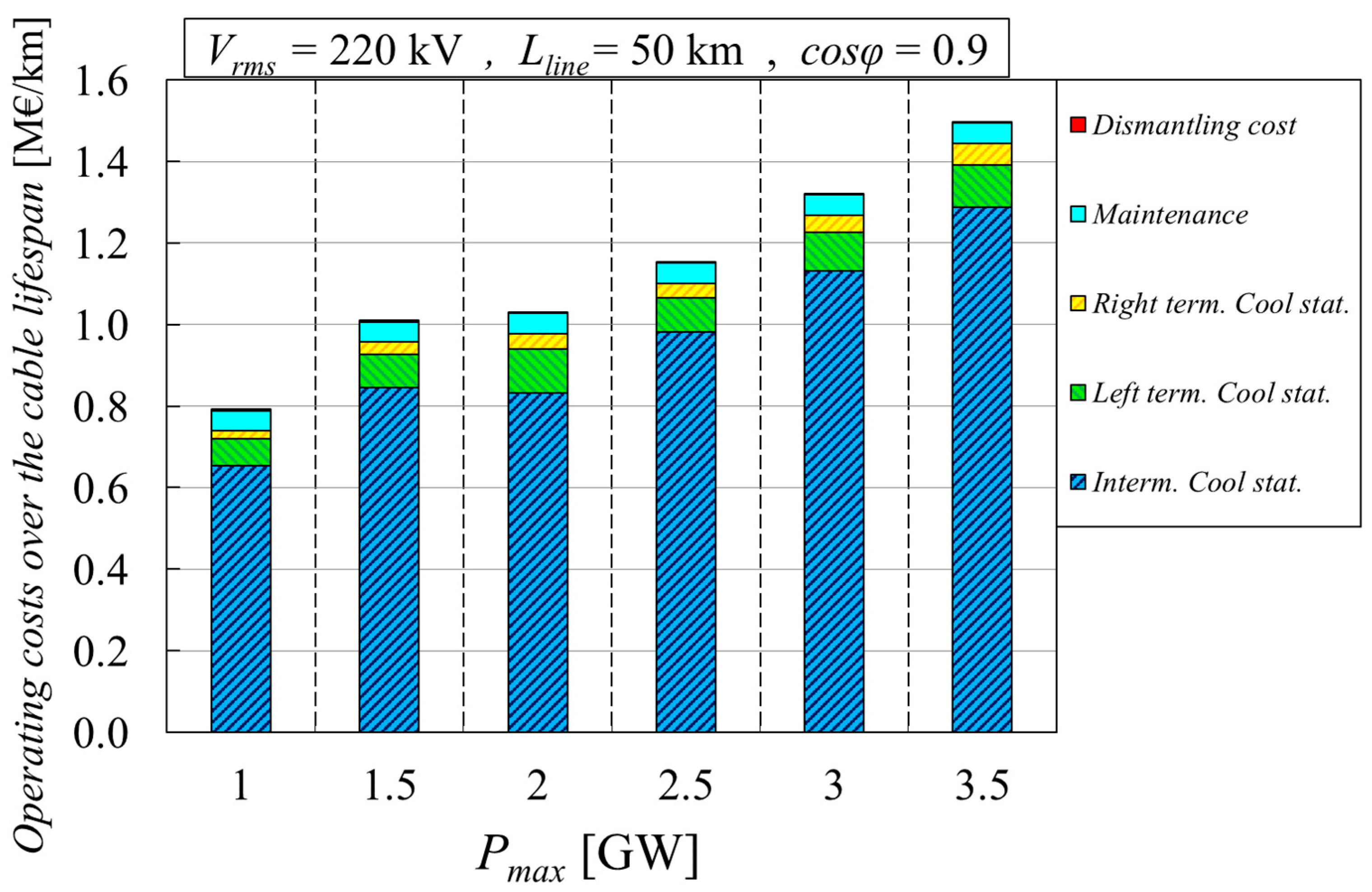
4.6. Capital and Operating Costs for the Cooling Stations
4.7. Cost for the Land to Be Purchased to Install the Cable
4.8. Other Cost Indexes
5. Calculation of the Loss Contributions
5.1. AC Losses Generated in the HTS Tapes
5.2. Losses Generated in the Insulating Layers
5.3. Losses Due to Eddy Currents
5.4. Heat Entering the Cable Cryostat from the Outside
6. Constraints Applied to the Optimization Algorithm
6.1. Constraints on the Correlations among Phase Currents and among Layer Currents
6.2. Constraints on the Maximum LN2 Temperature Rise and Pressure Drop
6.3. Constraints on the Values of
7. References Values Adopted for the Parametric Analyses
7.1. References Values for the Economic Parameters
7.2. References Values for the Geometrical Parameters of the Cable
7.3. References Values for the Dielectric Parameters
7.4. References Values for the Constraint Parameters
7.5. Values of the Other User-Defined Parameters
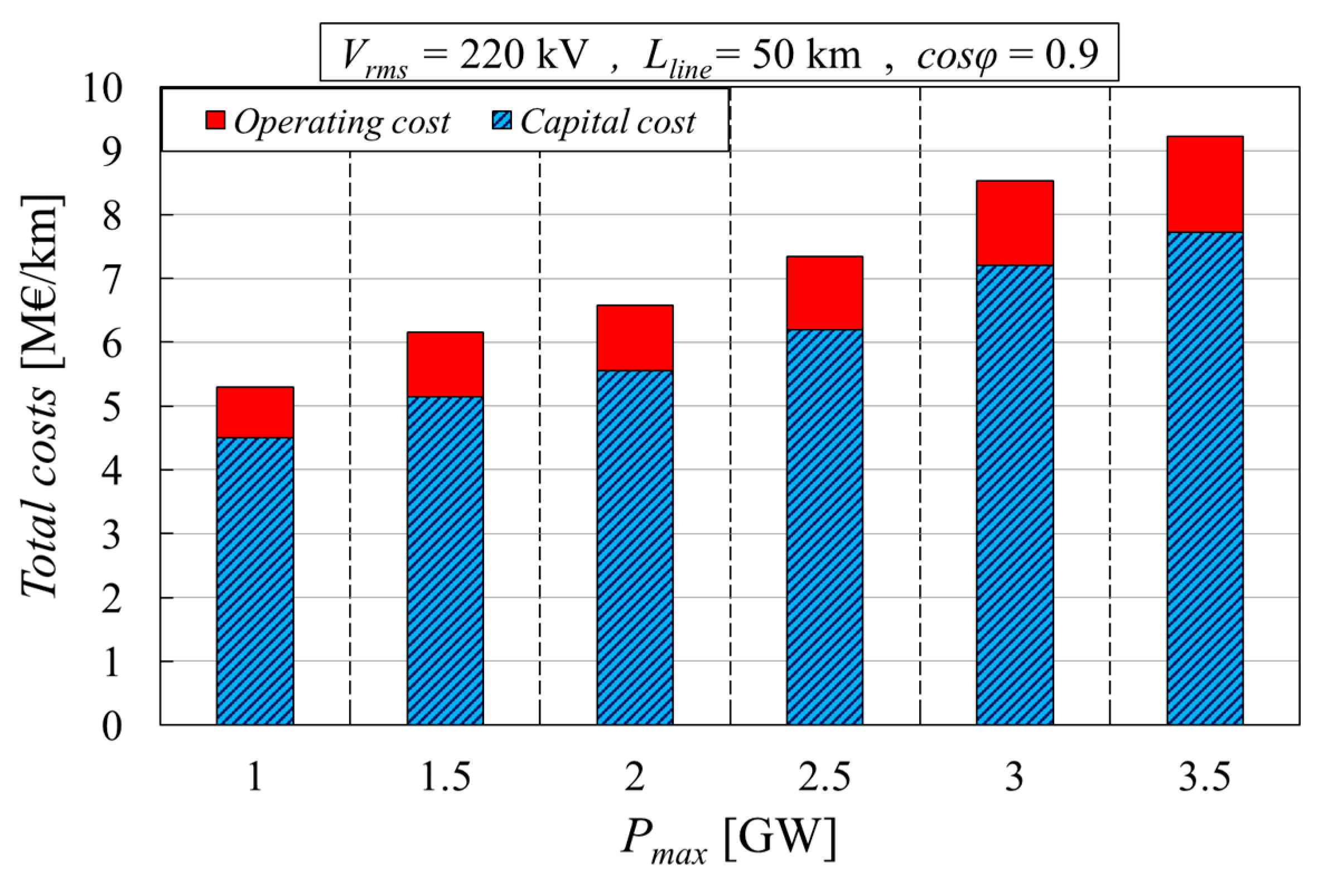
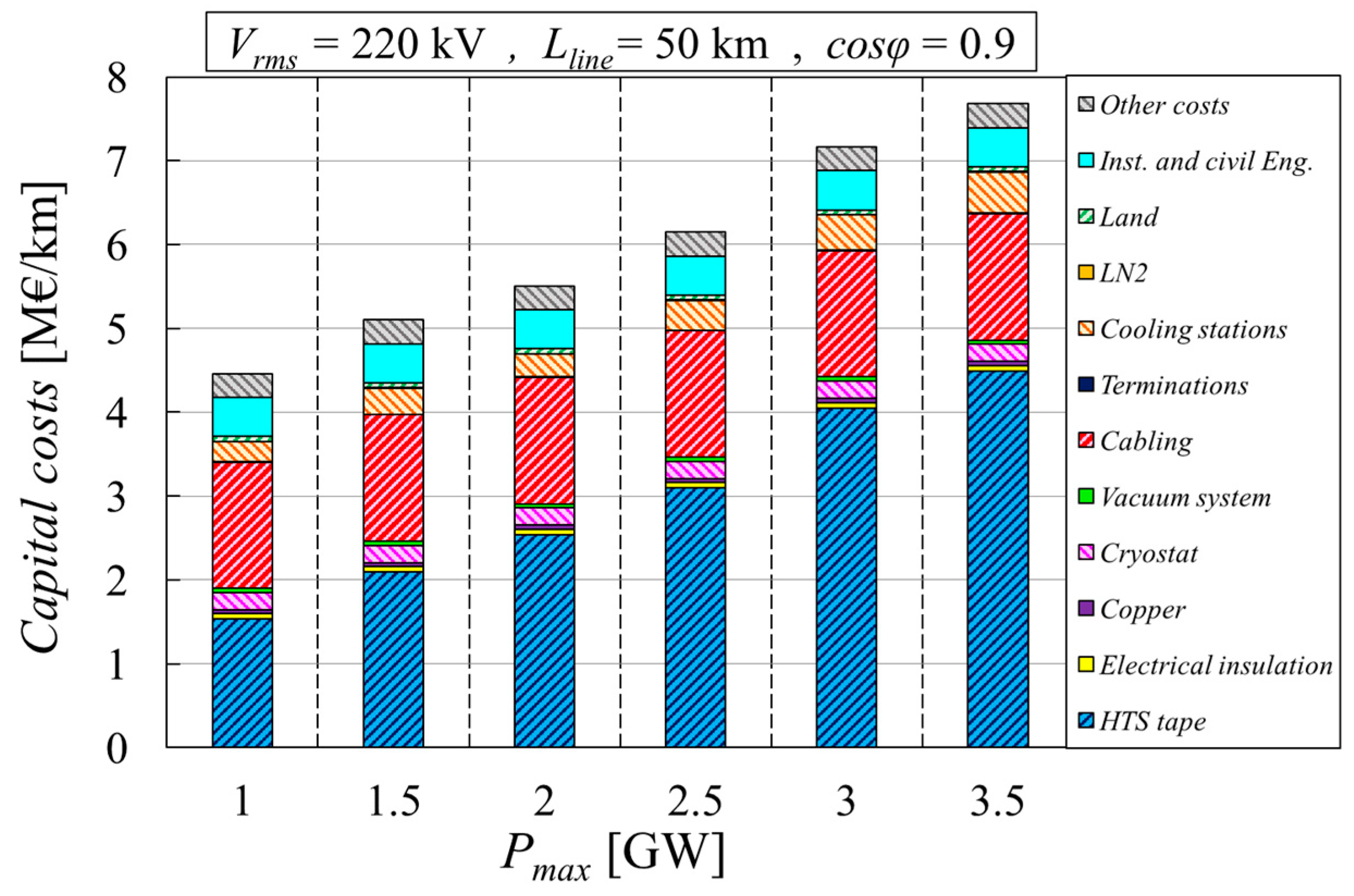
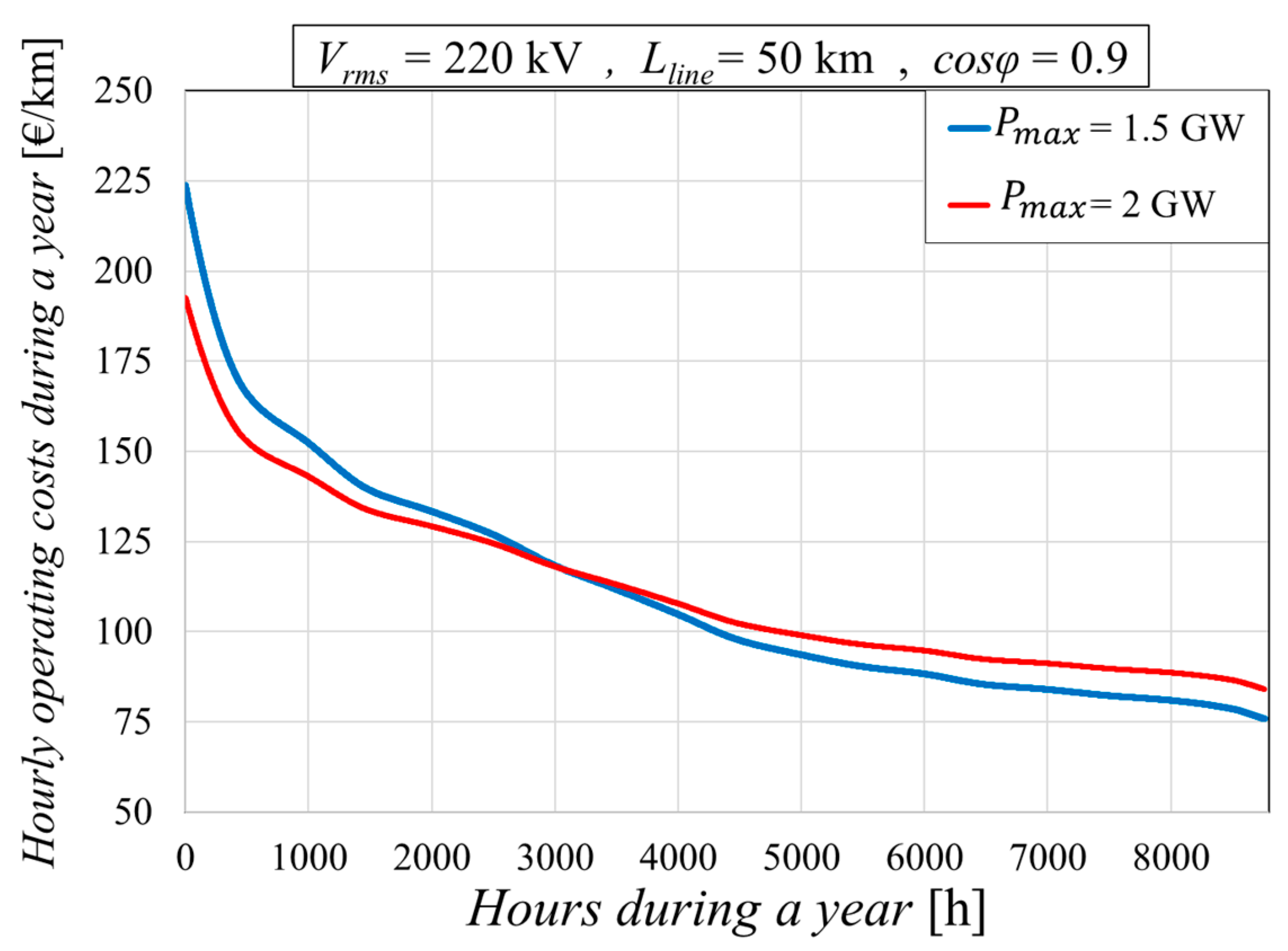
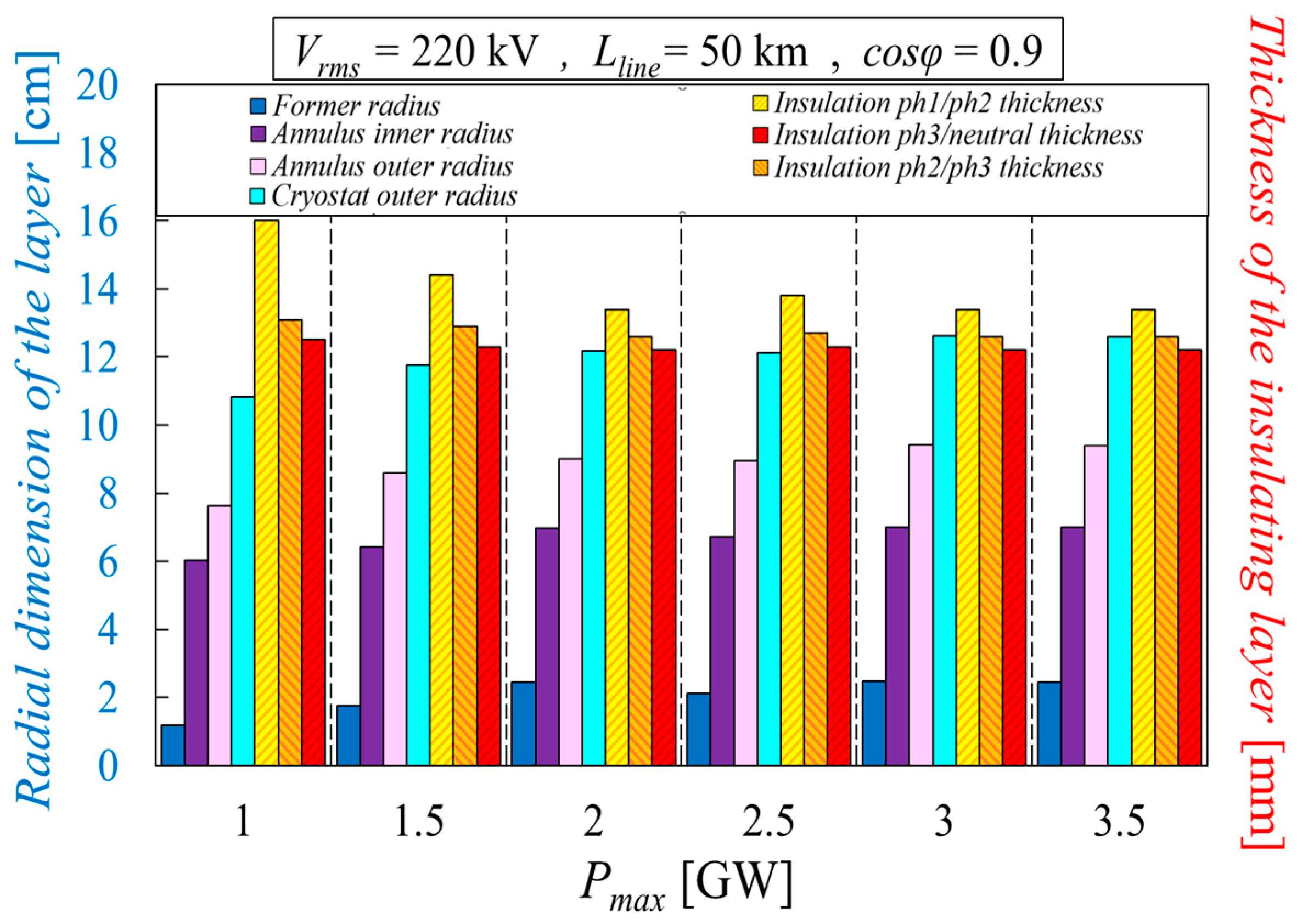
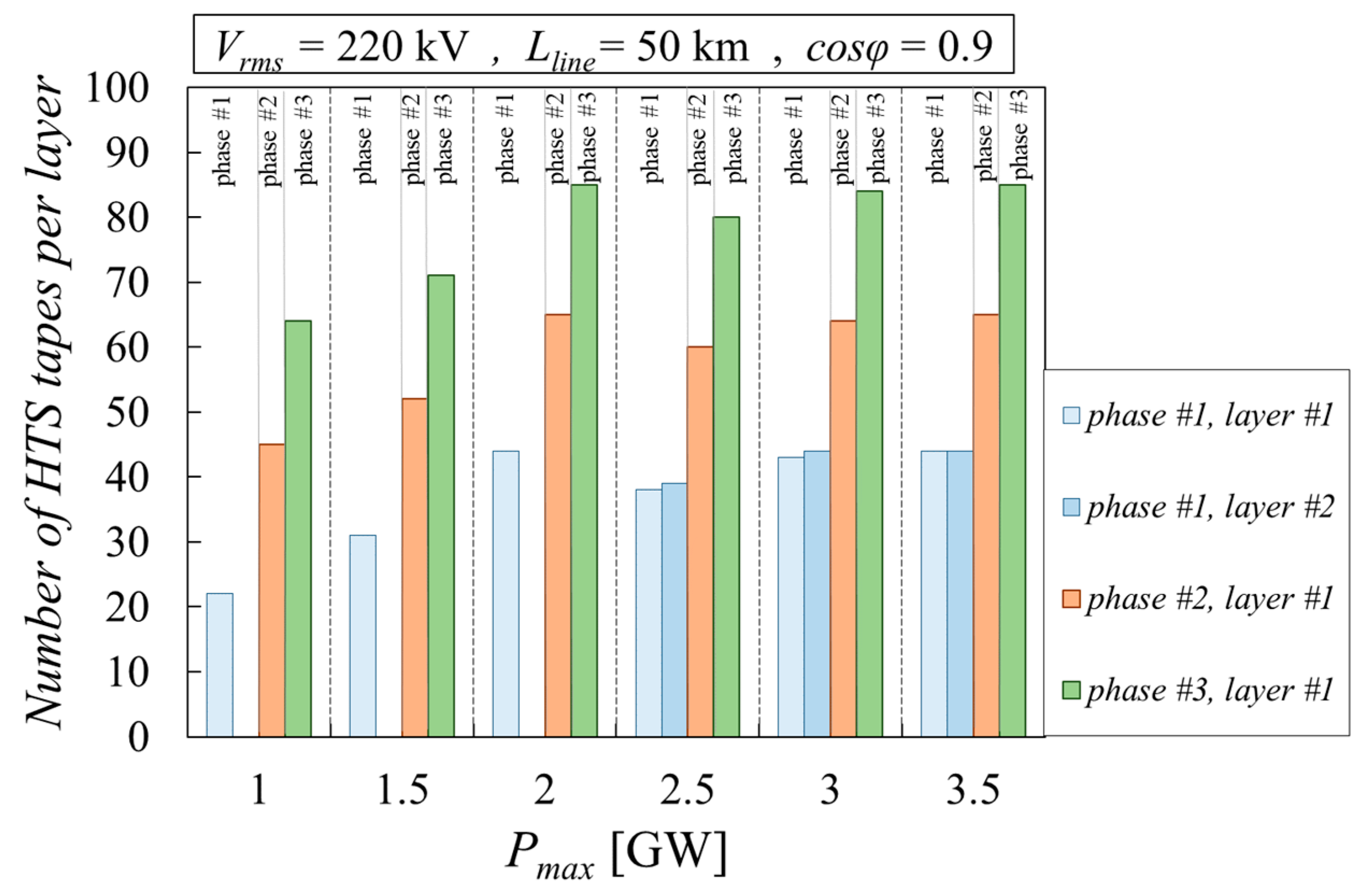
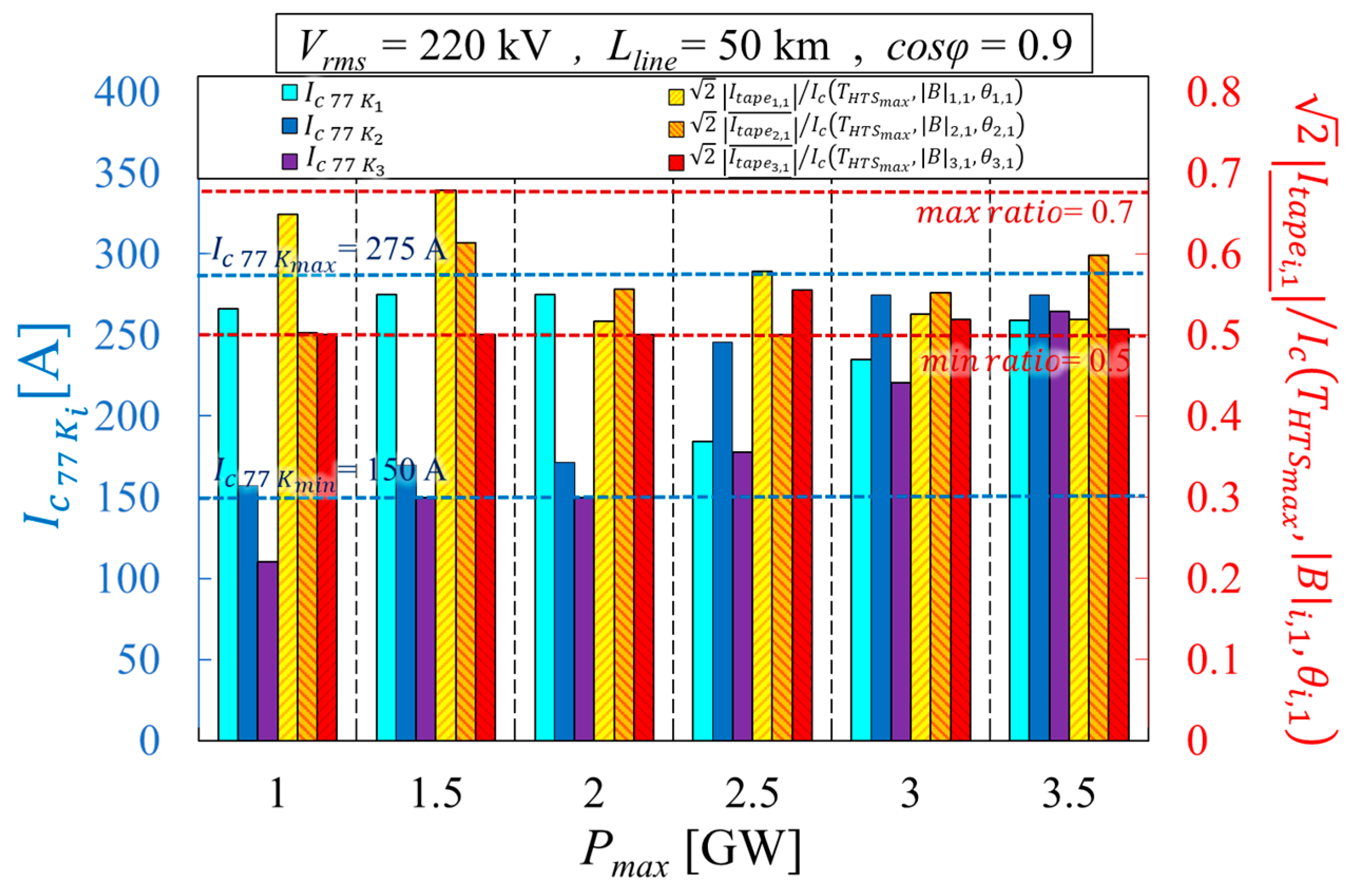
8. Results of the Parametric Analyses Carried Out with the Proposed Tool
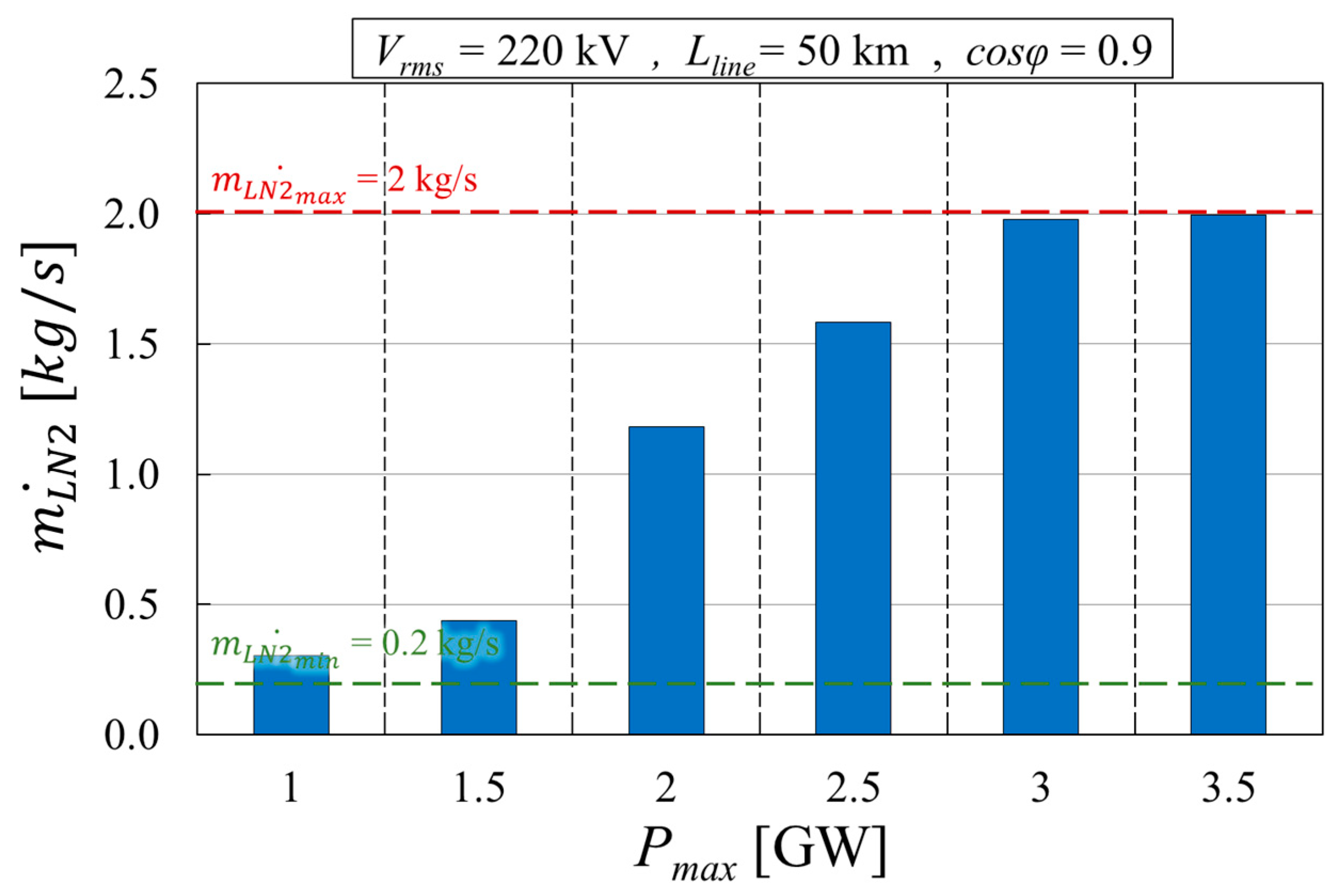
8.1. Impact of the Cable’s Active Power
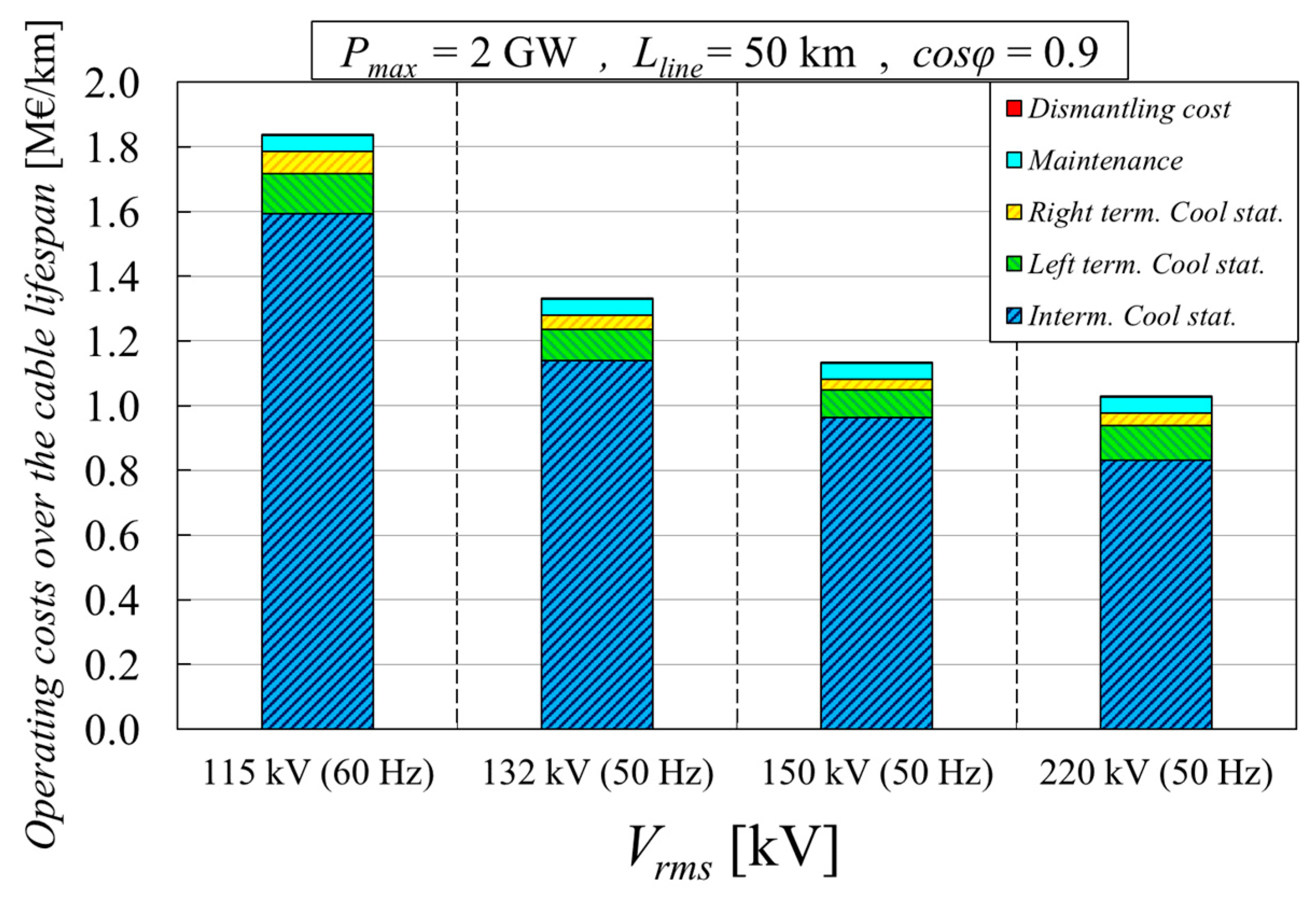
8.2. Impact of the Cable’s Voltage Level
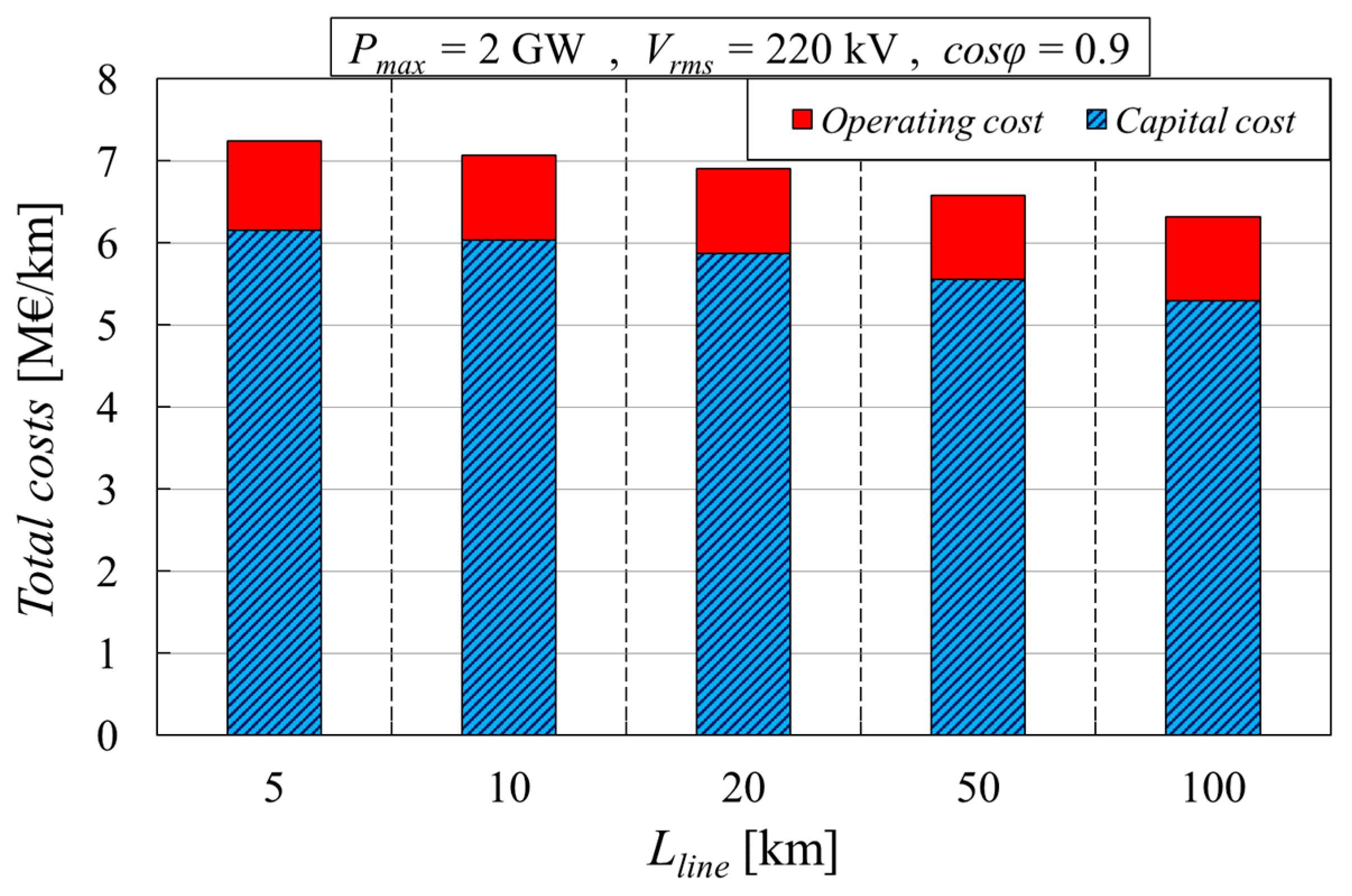
8.3. Impact of the Line Length
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Garwin, R.L.; Matisoo, J. Superconducting lines for the transmission of large amounts of electric power over great distances. Proc. IEEE 1967, 55, 538–548. [Google Scholar] [CrossRef]
- Forsyth, E.B.; Thomas, R.A. Performance summary of the Brookhaven superconducting power transmission system. Cryogenics 1986, 26, 599–614. [Google Scholar] [CrossRef]
- Kim, D.W.; Jang, H.-M.; Lee, C.-H.; Kim, J.-H.; Ha, C.-W.; Kwon, Y.-H.; Kim, D.-W.; Cho, J.-W. Development of the 22.9-kV class HTS power cable in LG cable. IEEE Trans. Appl. Supercond. 2005, 15, 1723–1726. [Google Scholar] [CrossRef]
- Sim, K.; Kim, S.; Cho, J.; Kim, D.; Kim, C.; Jang, H.; Sohn, S.; Hwang, S. DC critical current and AC loss measurement of the 100 m 22.9 kV/50 MVA HTS cable. Physica C 2008, 468, 2018–2022. [Google Scholar] [CrossRef]
- Lee, S.; Yoon, J.; Lee, B.; Yang, B. Modeling of a 22.9 kV 50 MVA superconducting power cable based on PSCAD/EMTDC for application to the Icheon substation in Korea. Phys. C Supercond. Its Appl. 2011, 471, 1283–1289. [Google Scholar] [CrossRef]
- Lee, C.; Hyukchan, S.; Youngjin, W.; Youngwoong, K.; Cheolhwi, R.; Minwon, P.; Masataka, I. Progress of the first commercial project of high-temperature superconducting cables by KEPCO in Korea. Supercond. Sci. Technol. 2020, 33, 044006. [Google Scholar] [CrossRef]
- Takahashi, T.; Suzuki, H.; Ichikawa, M.; Okamoto, T.; Akita, S.; Mukoyama, S.; Ishii, N.; Kimura, A.; Yasuda, K. Demonstration and verification tests of 500 m long HTS power cable. IEEE Trans. Appl. Supercond. 2005, 15, 1823–1826. [Google Scholar] [CrossRef]
- Maruyama, O.; Ohkuma, T.; Masuda, T.; Ashibe, Y.; Mukoyama, S.; Yagi, M.; Saitoh, T.; Hasegawa, T.; Amemiya, N.; Ishiyama, A.; et al. Development of 66 kV and 275 kV class REBCO HTS power cables. IEEE Trans. Appl. Supercond. 2013, 23, 5401405. [Google Scholar] [CrossRef]
- Masuda, T.; Watanabe, M.; Mimura, T.; Tanazawa, M.; Yamaguchi, H. The 2nd in-grid operation of superconducting cable in Yokohama project. J. Phys. Conf. Ser. 2020, 1559, 012083. [Google Scholar] [CrossRef]
- Li, J.; Zhang, L.; Ye, X.; Xia, F.; Cao, Y. Demonstration Project of 35 kV/1 kA Cold Dielectric High Temperature Superconducting Cable System in Tianjin. IEEE Trans. Appl. Supercond. 2020, 30, 5400205. [Google Scholar] [CrossRef]
- Zong, X.H.; Han, Y.W.; Huang, C.Q. Introduction of 35-kV kilometer-scale high-temperature superconducting cable demonstration project in Shanghai. Superconductivity 2022, 22, 100008. [Google Scholar] [CrossRef]
- Stemmle, M.; Merschel, F.; Noe, M.; Hobl, A. AmpaCity—Installation of advanced superconducting 10 kV system in city center replaces conventional 110 kV cables. In Proceedings of the IEEE International Conference on Applied Superconductivity and Electromagnetic Devices, Beijing, China, 25–27 October 2013; pp. 323–326. [Google Scholar]
- Soika, R.; Granados Garcia, X.; Cascante Nogales, S. ENDESA supercable, a 3.2 kA, 138 MVA, medium voltage superconducting power cable. IEEE Trans. Appl. Supercond. 2011, 21, 972–975. [Google Scholar] [CrossRef]
- Volkov, E.P.; Vysotsky, V.S.; Firsov, V.P. First Russian long length HTS power cable. Physica C 2012, 482, 87–91. [Google Scholar] [CrossRef]
- Allais, A.; Saugrain, J.-M.; West, B.; Lallouet, N.; Caron, H.; Ferandelle, D.; Terrien, L.; Bouvier, G.; Hajiri, G.; Berger, K.; et al. SuperRail–World-First HTS Cable to be Installed on a Railway Network in France. IEEE Trans. Appl. Supercond. 2024, 34, 4802207. [Google Scholar] [CrossRef]
- Magnusson, N.; Allais, A.; Angeli, G.; Bouvier, G.; Bruzek, C.E.; Candido, J.; Creusot, C.; Gammelsæter, M.; Garofalo, E.; Gömöry, F.; et al. SCARLET—A European Effort to Develop HTS and MgB2 Based MVDC Cables. IEEE Trans. Appl. Supercond. 2024, 34, 5400205. [Google Scholar] [CrossRef]
- Maguire, J.F.; Folts, D.; Yuan, J.; Henderson, N.; Lindsay, D.; Knoll, D.; Rey, C.; Duckworth, R.; Gouge, M.; Wolff, Z.; et al. Status and progress of a fault current limiting HTS cable to be installed in the Con Edison grid. Adv. Cryog. Eng. 2009, 55A, 445–452. [Google Scholar]
- Maguire, J.F.; Yuan, J.; Romanosky, W.; Schmidt, F.; Soika, R.; Bratt, S.; Durand, F.; King, C.; McNamara, J.; Welsh, T.E. Progress and status of a 2G HTS power cable to be installed in the Long Island Power Authority (LIPA) grid. IEEE Trans. Appl. Supercond. 2011, 21, 961–966. [Google Scholar] [CrossRef]
- Schmidt, F.; Allais, A. Superconducting cables for power transmission applications—A review. In Proceedings of the Workshop on Accelerator Magnet Super-Conductors (WAMS) Proceedings, Archamps, France, 22–24 March 2004; p. 352. [Google Scholar]
- Malozemoff, A.P.; Yuan, J.; Rey, C.M. High-temperature superconducting (HTS) AC cables for power grid applications. In Superconductors in the Power Grid Materials and Applications; Woodhead Publishing Series in Energy; Woodhead Publishing: Cambridge, UK, 2015; pp. 133–188. [Google Scholar]
- Ren, L.; Tang, Y.; Shi, J.; Li, L.; Li, J.; Cheng, S.C. Techno-Economic Feasibility Study on HTS Power Cables. IEEE Trans. Appl. Supercond. 2009, 19, 1774–1777. [Google Scholar] [CrossRef]
- Venuturumilli, S.H.; Zhang, Z.; Zhang, M.; Yuan, W. Superconducting Cables-Network Feasibility Study Work Package 3. 2017. Available online: https://www.westernpower.co.uk/downloads-view-reciteme/2152 (accessed on 1 February 2024).
- Yuan, W.; Venuturumilli, S.; Zhang, Z.; Mavrocostanti, Y.; Zhang, M. Economic Feasibility Study of using High Temperature Superconducting cables in UK’s Electrical Distribution Networks. IEEE Trans. Appl. Supercond. 2018, 28, 5401505. [Google Scholar] [CrossRef]
- Yu, Z.; Ren, Y.; Cao, B.; Liu, J.; Zhou, Z. Feasibility and Economical Analysis of the Superconducting Cable and Hydrogen Hybrid Transmission Gallery. In Proceedings of the 2020 IEEE International Conference on Applied Superconductivity and Electromagnetic Devices, Tianjin, China, 16–18 October 2020. [Google Scholar]
- Guarino, R.; Wesche, R.; Sedlak, K. Technical and economic feasibility study of high-current HTS bus bars for fusion reactors. Phys. C Supercond. Its Appl. 2022, 592, 1353996. [Google Scholar] [CrossRef]
- Ferran, P.C. Economical Study of Electric Power Transmission with Superconducting Lines for HVDC Systems. Ph.D. Thesis, Escola Tècnica Superior d’Enginyeria Industrial de Barcelona, Barcelona, Spain, 2021. [Google Scholar]
- Long, J.; Ren, L.; Li, J.; Xu, Y.; Shi, J.; Tang, Y. High-Temperature Superconducting Cable Optimization Design Software Based on 2-D Finite Element Model. IEEE Trans. Appl. Supercond. 2022, 32, 4801405. [Google Scholar] [CrossRef]
- Peng, S.; Cai, C.; Cai, J.; Zheng, J.; Zhou, D. Optimum Design and Performance Analysis of Superconducting Cable with Different Conductor Layout. Energies 2022, 15, 8893. [Google Scholar] [CrossRef]
- Politano, D.; Sjostrom, M.; Schnyder, G.; Rhyner, J. Technical and Economical Assessment of HTS Cables. IEEE Trans. Appl. Supercond. 2001, 11, 2477–2480. [Google Scholar] [CrossRef]
- Elsherif, M.; Taylor, P.; Blake, S. Investigating the potential impact of superconducting distribution networks. In Proceedings of the 22nd International Conference on Electricity Distribution, Stockholm, Sweden, 10–13 June 2013; p. 0816. [Google Scholar]
- Buchholz, A.; Noe, M.; Kottonau, D.; Shabagin, E.; Weil, M. Environmental Life-Cycle Assessment of a 10 kV High-Temperature Superconducting Cable System for Energy Distribution. IEEE Trans. Appl. Supercond. 2021, 31, 4802405. [Google Scholar] [CrossRef]
- Sadeghi, A.; Seyyedbarzegar, S. An accurate model of the high-temperature superconducting cable by using stochastic methods. Transform. Mag. 2021, 8 (Suppl. 5), 70–76. [Google Scholar]
- Kloppel, S.; Marian, A.; Haberstroh, C.; Bruzek, C.-E. Thermo-hydraulic and economic aspects of long-length high-power MgB2 superconducting cables. Cryogenics 2020, 113, 103211. [Google Scholar] [CrossRef]
- Altov, V.A.; Balashov, N.N.; Degtyarenko, P.N.; Ivanov, S.S.; Kopylov, S.I.; Sytnikov, V.E.; Zheltov, V.V. Optimization of Three- and Single-Phase AC HTS Cables Design by Numerical Simulation. IEEE Trans. Appl. Supercond. 2017, 27, 4801606. [Google Scholar] [CrossRef]
- Musso, A.; Angeli, G.; Bocchi, M.; Ribani, P.L.; Breschi, M. OSCaR: A Cost Analysis of HTS Coaxial Cables With a Novel Optimization Method. IEEE Trans. Appl. Supercond. 2023, 33, 4803516. [Google Scholar] [CrossRef]
- Musso, A.; Angeli, G.; Bocchi, M.; Ribani, P.L.; Breschi, M. A method to quantify technical-economic aspects of HTS electric power cables. IEEE Trans. Appl. Supercond. 2022, 32, 4803516. [Google Scholar] [CrossRef]
- Musso, A.; Cavallucci, L.; Angeli, G.; Bocchi, M.; Breschi, M. A conceptual design optimization for a MgB2 DC transmission line. IEEE Trans. Appl. Supercond. 2024, 34, 6200607. [Google Scholar] [CrossRef]
- de Sousa, W.T.B.; Shabagin, E.; Kottonau, D.; Noe, M. An open-source 2D finite difference based transient electro-thermal simulation model for three-phase concentric superconducting power cables. Supercond. Sci. Technol. 2021, 34, 015014. [Google Scholar] [CrossRef]
- Kottonau, D.; de Sousa, W.T.B.; Bock, J.; Noe, M. Design Comparisons of Concentric Three-Phase HTS Cables. IEEE Trans. Appl. Supercond. 2019, 29, 5401508. [Google Scholar] [CrossRef]
- Morandi, A. HTS dc transmission and distribution: Concepts, applications and benefits. Supercond. Sci. Technol. 2015, 28, 123001. [Google Scholar] [CrossRef]
- Kottonau, D.; Shabagin, E.; de Sousa, W.T.B.; Geisbüsch, J.; Noe, M.; Stagge, H.; Fechner, S.; Woiton, H.; Küsters, T. Evaluation of the Use of Superconducting 380 kV Cable; KIT Scientific Publishing: Karlsruhe, Germany, 2020. [Google Scholar]
- Colebrook, C. Turbulent Flow in Pipes with Particular Reference to the Transition Region between the Smooth and Rough Pipe Laws. J. Inst. Civ. Eng. 1939, 11, 133–156. [Google Scholar] [CrossRef]
- Haaland, S.E. Simple and Explicit formulas for friction factor in turbulent pipe flow. J. Fluid. Eng. 1983, 105, 89–90. [Google Scholar] [CrossRef]
- Nguyen, T.; Lee, W.-G.; Lee, S.-J.; Park, M.; Kim, H.-M.; Won, D.; Yoo, J.; Yang, H.S. A Simplified Model of Coaxial, Multilayer High-Temperature Superconducting Power Cables with Cu Formers for Transient Studies. Energies 2019, 12, 1514. [Google Scholar] [CrossRef]
- Seog Whan, K.; Jinho, J.; Jeonwook, C.; Joonhan, B.; Hae-jong, K.; Kichul, S. Effect of winding direction on four-layer HTS power transmission cable. Cryogenics 2003, 43, 629–635. [Google Scholar]
- Jiahui, Z.; Zhenyu, Z.; Huiming, Z.; Min, Z.; Ming, Q.; Weijia, Y. Inductance and Current Distribution Analysis of a Prototype HTS Cable. J. Phys. Conf. Ser. 2014, 507, 022047. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics; John Wiley & Sons: Hoboken, NJ, USA, 1975. [Google Scholar]
- Thomas, H.; Marian, A.; Chervyakov, A.; Stückrad, S.; Rubbia, C. Efficiency of superconducting transmission lines: An analysis with respect to the load factor and capacity rating. Renew. Sustain. Energy Rev. 2016, 141, 381–391. [Google Scholar] [CrossRef]
- Jovcic, D.; Li, P.; Hodge, E.; Fitzgerald, J. Assessment of interconnection options for 1GW remote offshore wind farm utilizing superconducting HVDC cable without offshore platform. In Proceedings of the 41st CIGRE Symposium, Ljubljana, Slovenia, 21–24 November 2021. [Google Scholar]
- Cullinane, M.; Judge, F.; O’Shea, M.; Thandayutham, K.; Murphy, J. Subsea superconductors: The future of offshore renewable energy transmission? Renew. Sustain. Energy Rev. 2022, 156, 111943. [Google Scholar] [CrossRef]
- Choi, J.; Cheon, H.-G.; Choi, J.-H.; Kim, H.-J.; Cho, J.-W.; Kim, S.-H. A Study on Insulation Characteristics of Laminated Polypropylene Paper for an HTS Cable. IEEE Trans. Appl. Supercond. 2010, 20, 1280–1283. [Google Scholar] [CrossRef]
- Kwag, D.S.; Nguyen, V.D.; Baek, S.M.; Kim, H.J.; Cho, J.W.; Kim, S.H. A Study on the Composite Dielectric Properties for an HTS Cable. IEEE Trans. Appl. Supercond. 2005, 15, 1731–1734. [Google Scholar] [CrossRef]
- Pi, W.; Yang, Q.; Wang, T.; Peng, C.; Wang, Y.; Shi, Q.; Dong, J. Insulation Design and Simulation for Three-Phase Concentric High-Temperature Superconducting Cable under 10-kV Power System. IEEE Trans. Appl. Supercond. 2019, 29, 7700104. [Google Scholar] [CrossRef]
- Hayakawa, N. Insulation Technologies for HTS Apparatus; ESAS Summer School on HTS Technology for Sustainable Energy and Transport Systems: Bologna, Italy, 2016. [Google Scholar]
- Norris, W.T. Calculation of hysteresis losses in hard superconductors carrying AC isolated conductors and edges of thin sheets. J. Phys. Appl. Phys. 1970, 3, 489–507. [Google Scholar] [CrossRef]
- Amemiya, N.; Jiang, Z.; Nakahata, M.; Yagi, M.; Mukoyama, S.; Kashima, N.; Nagaya, S.; Shiohara, Y. AC Loss Reduction of Superconducting Power Transmission Cables Composed of Coated Conductors. IEEE Trans. Appl. Supercond. 2017, 17, 1712–1717. [Google Scholar] [CrossRef]
- Musso, A.; Breschi, M.; Ribani, P.L.; Grilli, F. Analysis of AC loss contributions from different layers of HTS tapes using the A−V. formulation model. IEEE Trans. Appl. Supercond. 2021, 31, 5900411. [Google Scholar] [CrossRef]
- Kottonau, D.; Shabagin, E.; Noe, M.; Grohmann, S. Opportunities for High-Voltage AC Superconducting Cables as Part of New Long-Distance Transmission Lines. IEEE Trans. Appl. Supercond. 2017, 27, 5400405. [Google Scholar] [CrossRef]
- Trevisani, L. Design and Simulation of a Large Scale Energy Storage and Power Transmission System for Remote Renewable Energy Sources Exploitation. Ph.D. Dissertation, University of Bologna, Bologna, Italy, 2006. [Google Scholar]
- Gouge, M.J.; Lindsay, D.T.; Demko, J.A.; Duckworth, R.C.; Ellis, A.R.; Fisher, P.W.; James, D.R.; Lue, J.W.; Roden, M.L.; Sauers, I.; et al. Tests of tri-axial HTS cables. IEEE Trans. Appl. Supercond. 2005, 15, 1827–1830. [Google Scholar] [CrossRef]
- Masuda, T.; Ashibe, Y.; Watanabe, M.; Suzawa, C.; Ohkura, K.; Hirose, M.; Isojima, S.; Honjo, S.; Matsuo, K.; Mimura, T. Development of a 100 m, 3-core 114MVA HTSC cable system. Physica C 2002, 372–376, 1580–1584. [Google Scholar] [CrossRef]
- Mukoyama, S.; Yagi, M.; Ishii, N.; Kimura, H.; Suzuki, H.; Ichikawa, M.; Takahashi, T.; Okamoto, T.; Kimura, A.; Yasuda, K. Demonstration and verification tests of a 500 m HTS cable in the super-ACE project. Physica C 2005, 426–431, 1365–1373. [Google Scholar]
- Demko, J.A.; Lue, J.W.; Gouge, M.J.; Lindsay, D.; Roden, M.; Willen, D.; Daumling, M.; Fesmire, J.E.; Augustynowicz, S.D. Cryostat vacuum thermal considerations for HTS power transmission cable systems. IEEE Trans. Appl. Supercond. 2003, 13, 1930–1933. [Google Scholar] [CrossRef]
- Zuijderduin, R. Integration of High-Tc Superconducting Cables in the Dutch Power Grid of the Future. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2016. [Google Scholar]
- Herzog, F. Cooling unit for the AmpaCity project—One year successful operation. Cryogenics 2016, 80, 204–209. [Google Scholar] [CrossRef]
- Preuß, A. Development of High-Temperature Superconductor Cables for High Direct Current Applications. Ph.D. Dissertation, KIT Scientific Publishing, Institut für Technische Physik (ITEP), Karlsruhe, Germany, 2022. [Google Scholar]
- Hayakawa, N.; Nishimachi, S.; Maruyama, O.; Ohkuma, T.; Liu, J.; Yagi, M. A Novel Electrical Insulating Material for 275 kV High-Voltage HTS Cable with Low Dielectric Loss. J. Phys. Conf. Ser. 2024, 507, 032021. [Google Scholar] [CrossRef]
- Allen, N.C.; Chiesa, L.; Takayasu, M. Numerical and experimental investigation of the electromechanical behaviour of REBCO tapes. IOP Conf. Ser. Mater. Sci. Eng. 2015, 102, 012025. [Google Scholar] [CrossRef]
- Weedy, B.M.; Cory, B.I. Electric Power Systems; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- International Energy Agency. Electricity Grids and Secure Energy Transitions—Enhancing the Foundations of Resilient, Sustainable and Affordable Power Systems. November 2023. Available online: https://www.iea.org/reports/electricity-grids-and-secure-energy-transitions/executive-summary (accessed on 1 February 2024).
- ANSI C84.1-2011; American National Standard for Electric Power Systems and Equipment—Voltage Ratings (60 Hertz). American National Standards Institute: Washington, DC, USA, 2011.







| Parameter | Unit | Value | Reference |
|---|---|---|---|
| EUR/kA∙m | 100.0 | ||
| EUR M/ton | 0.02 | [41] | |
| EUR/liter | 0.16 | [26] | |
| EUR/kg | 7.0 | ||
| EUR M/km | 0.22 | [64] | |
| EUR/m | 52.0 | [65] | |
| EUR M/km | 2.0 | ||
| EUR M/km | 0.11 | [41] | |
| EUR M/km | 0.02 | [41] | |
| EUR/m2 | 60 | ||
| EUR M/km | 0.04 | ||
| EUR M/km | 0.46 | ||
| EUR M/km | 0.28 | ||
| EUR M | 0.4 | [66] | |
| EUR M | 0.5 | ||
| EUR/W | 25.0 | ||
| 1.1 | |||
| 1.1 | |||
| EUR/kWh | 0.053 | ||
| % | 5.0 |
| Parameter | Unit | Value |
|---|---|---|
| km | 100 | |
| 5 | ||
| tons | 20 | |
| 10 | ||
| liters | 104 | |
| 10 | ||
| km | 20 | |
| 5 | ||
| n° cool. stat. | 8 | |
| 3 | ||
| km | 5 | |
| 10 | ||
| 20% | ||
| 30% | ||
| 50% |
| Parameter | Unit | Value | Reference |
|---|---|---|---|
| mm | 2.0 | [41] | |
| mm | 1.7 | [39] | |
| mm | 0.15 | ||
| mm | 0.05 | ||
| mm | 2.0 | [38] | |
| mm | 0.8 | [39] | |
| mm | 31.8 | [41] | |
| mm | 4.0 | ||
| mm | 1.4 | [41] | |
| m | 1.0 |
| Parameter | Unit | Value | Reference |
|---|---|---|---|
| 1.3 ×10−4 | [67] | ||
| 1.73 | [67] | ||
| ton/m3 | 0.34 | [41] | |
| kV | 750 | ||
| MV/m | 75 | ||
| MV/m | 52 | ||
| 1.2 | |||
| 1.0 | |||
| 1.0 | |||
| 1.1 | |||
| 1.1 |
| Parameter | Unit | Lower Boundary | Upper Boundary |
|---|---|---|---|
| cm | 0.5 | 2.5 | |
| cm | 1.5 | 5.0 | |
| 1 | 4 | ||
| ° | |||
| Kg/s | 0.2 | 2.0 | |
| 0 | |||
| 0.5 | 0.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Musso, A.; Cavallucci, L.; Angeli, G.; Bocchi, M.; L’Abbate, A.; Vitulano, L.C.; Dambone Sessa, S.; Sanniti, F.; Breschi, M. Techno-Economic Assessment of Coaxial HTS HVAC Transmission Cables with Critical Current Grading between Phases Using the OSCaR Tool. Appl. Sci. 2024, 14, 7488. https://doi.org/10.3390/app14177488
Musso A, Cavallucci L, Angeli G, Bocchi M, L’Abbate A, Vitulano LC, Dambone Sessa S, Sanniti F, Breschi M. Techno-Economic Assessment of Coaxial HTS HVAC Transmission Cables with Critical Current Grading between Phases Using the OSCaR Tool. Applied Sciences. 2024; 14(17):7488. https://doi.org/10.3390/app14177488
Chicago/Turabian StyleMusso, Andrea, Lorenzo Cavallucci, Giuliano Angeli, Marco Bocchi, Angelo L’Abbate, Lorenzo Carmine Vitulano, Sebastian Dambone Sessa, Francesco Sanniti, and Marco Breschi. 2024. "Techno-Economic Assessment of Coaxial HTS HVAC Transmission Cables with Critical Current Grading between Phases Using the OSCaR Tool" Applied Sciences 14, no. 17: 7488. https://doi.org/10.3390/app14177488
APA StyleMusso, A., Cavallucci, L., Angeli, G., Bocchi, M., L’Abbate, A., Vitulano, L. C., Dambone Sessa, S., Sanniti, F., & Breschi, M. (2024). Techno-Economic Assessment of Coaxial HTS HVAC Transmission Cables with Critical Current Grading between Phases Using the OSCaR Tool. Applied Sciences, 14(17), 7488. https://doi.org/10.3390/app14177488








