Analysis and Optimization of the Stray Capacitance of Rogowski Coils
Abstract
:1. Introduction
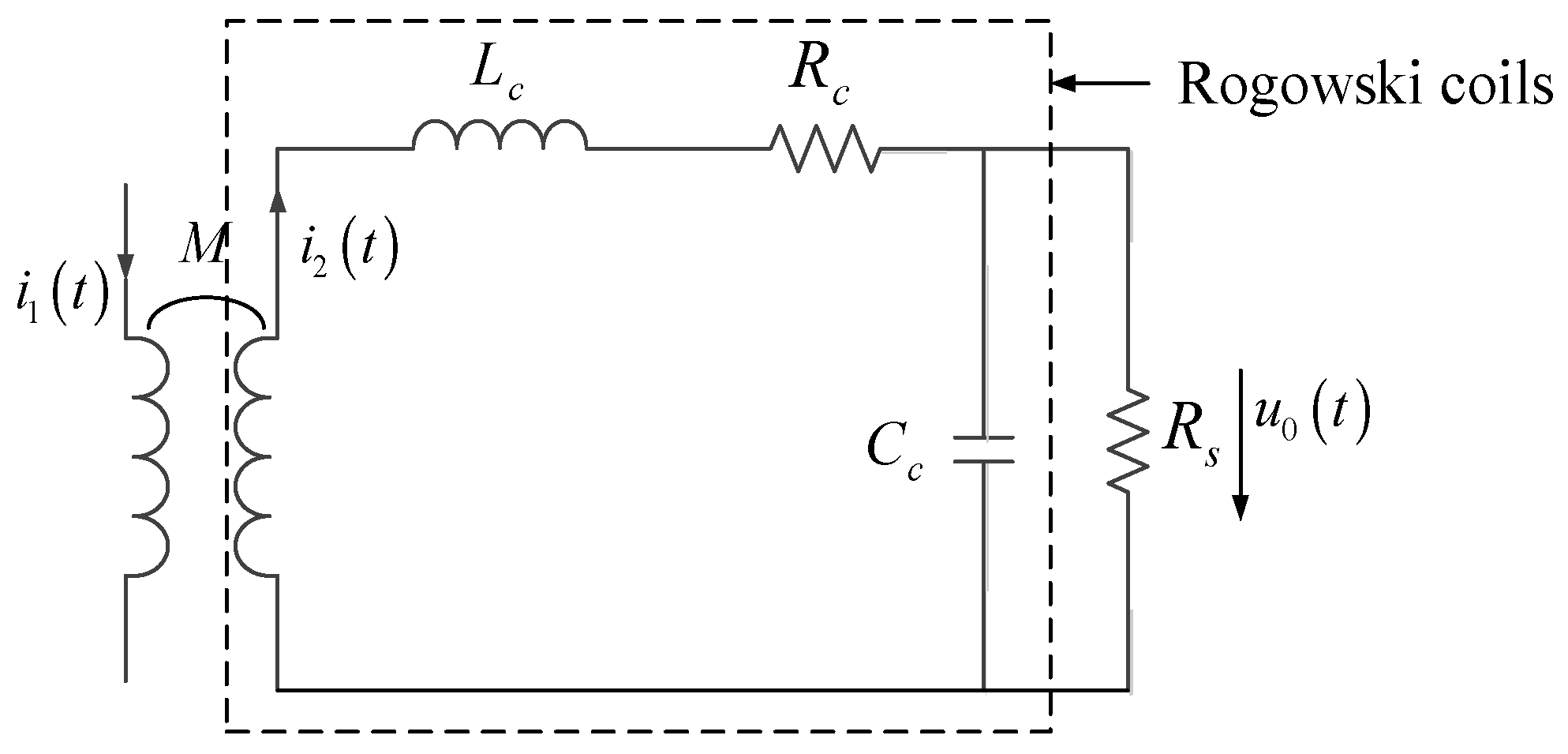
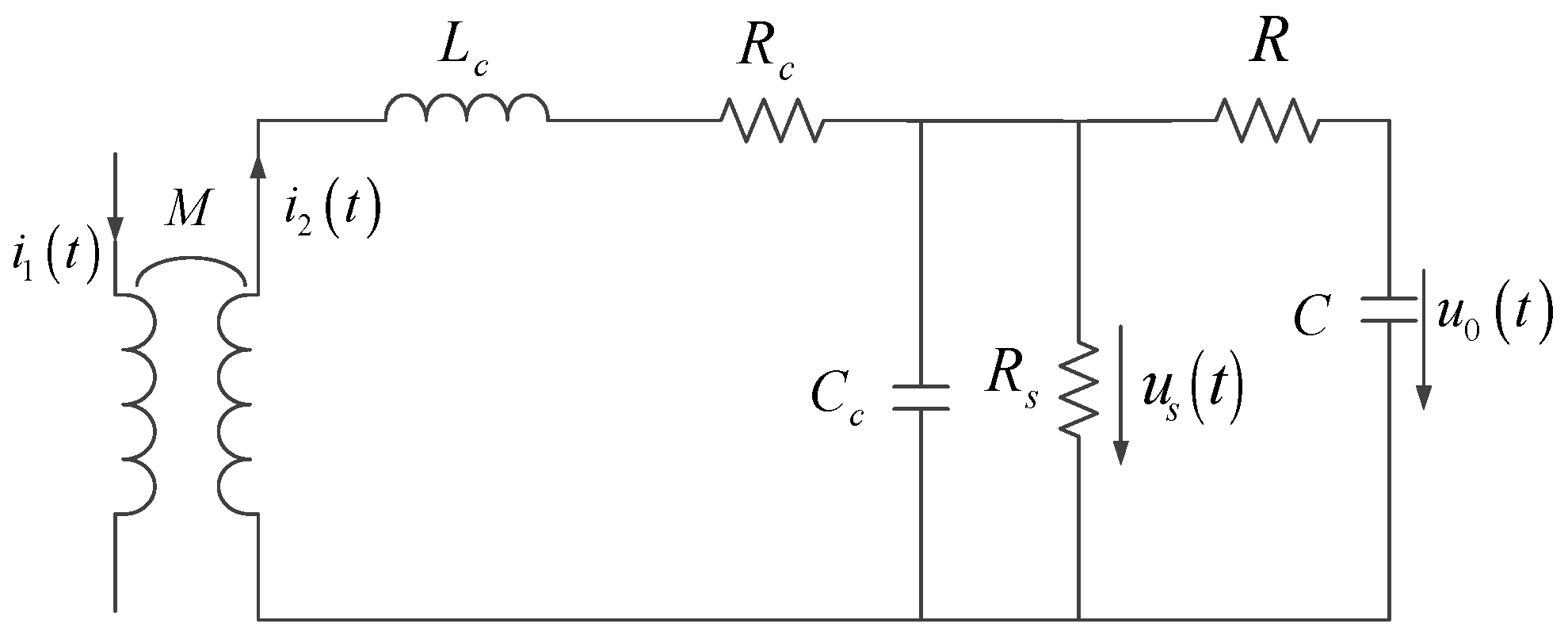
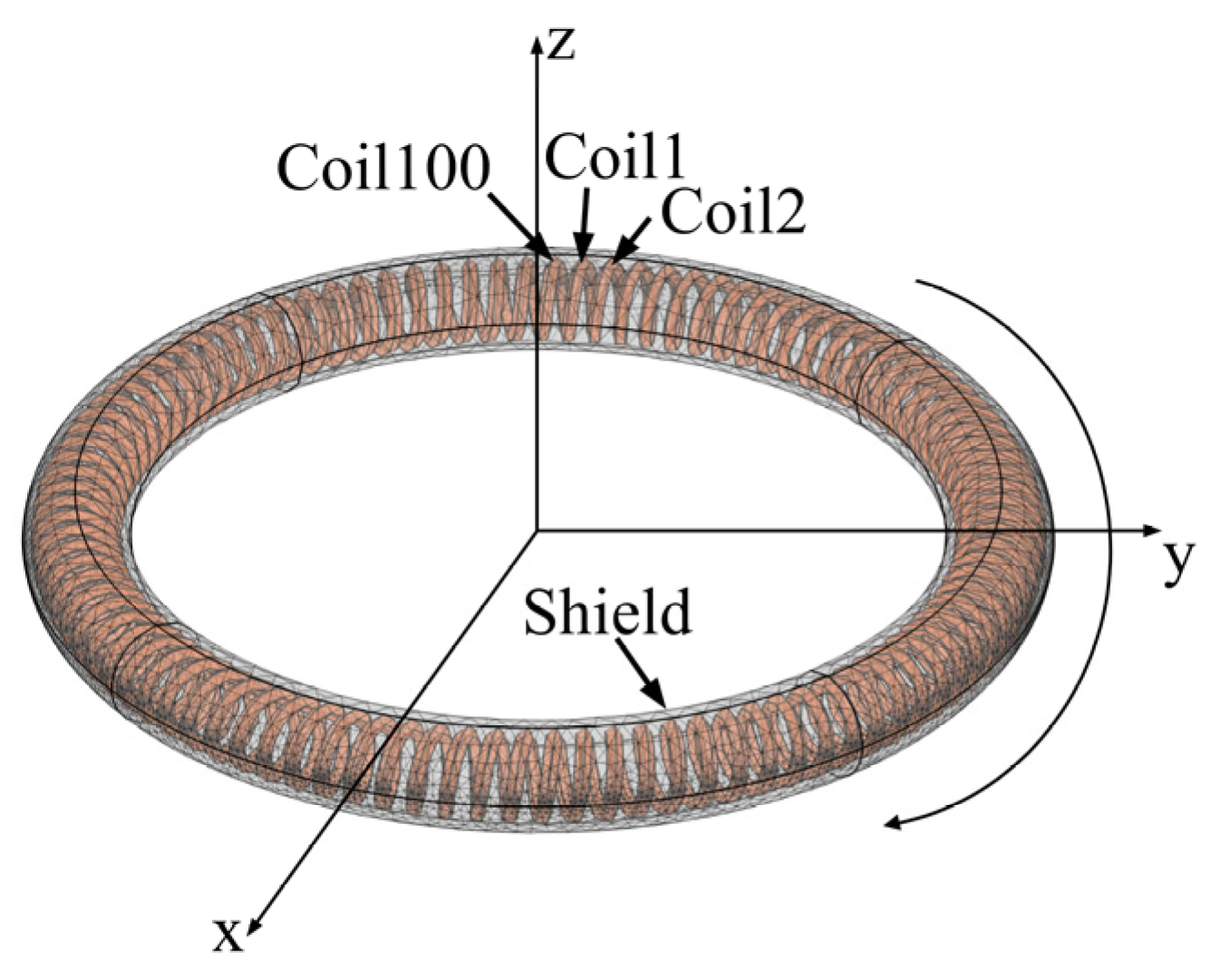
2. Analysis of Dynamic Characteristics of Rogowski Coils
3. Stray Capacitance of Rogowski Coils
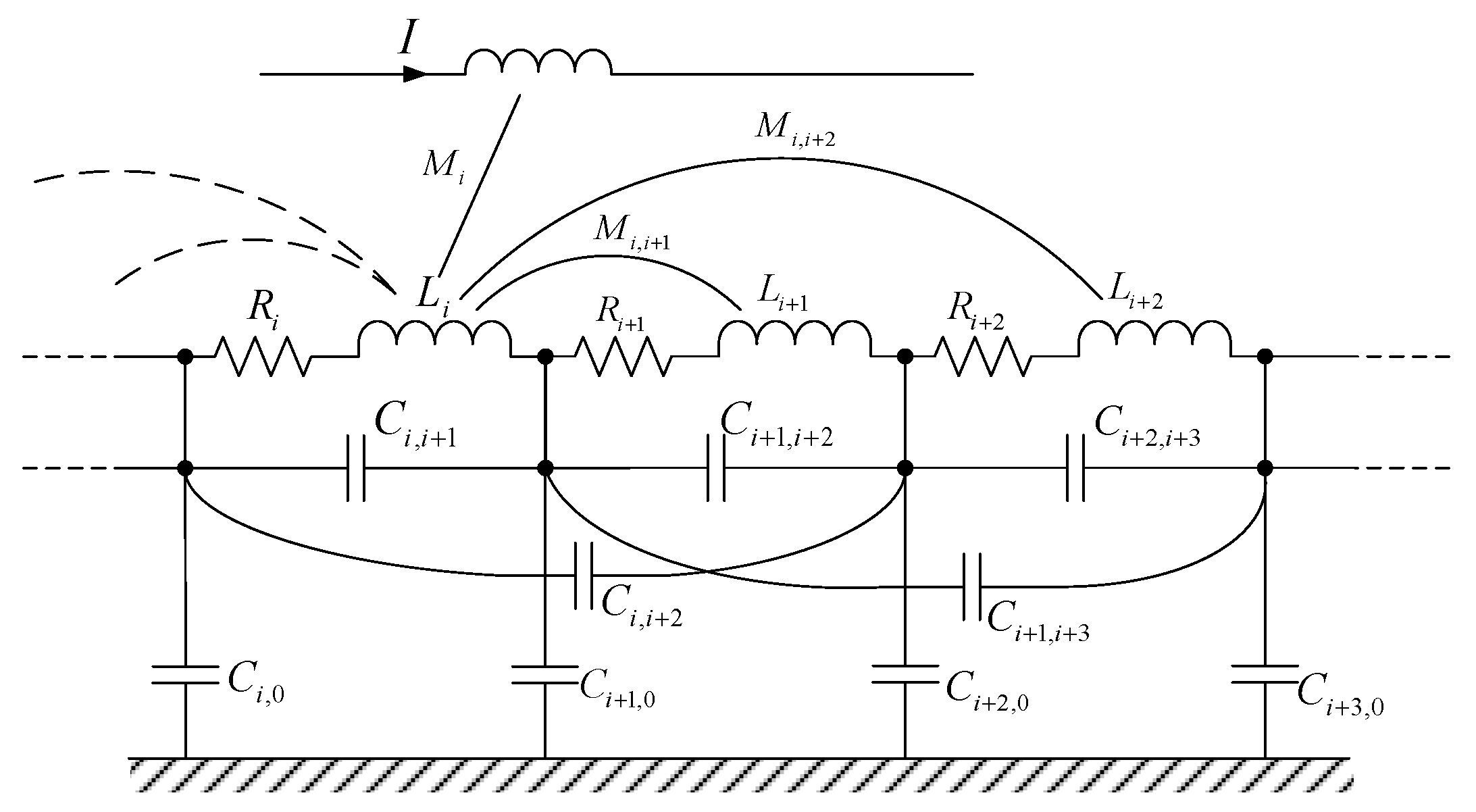
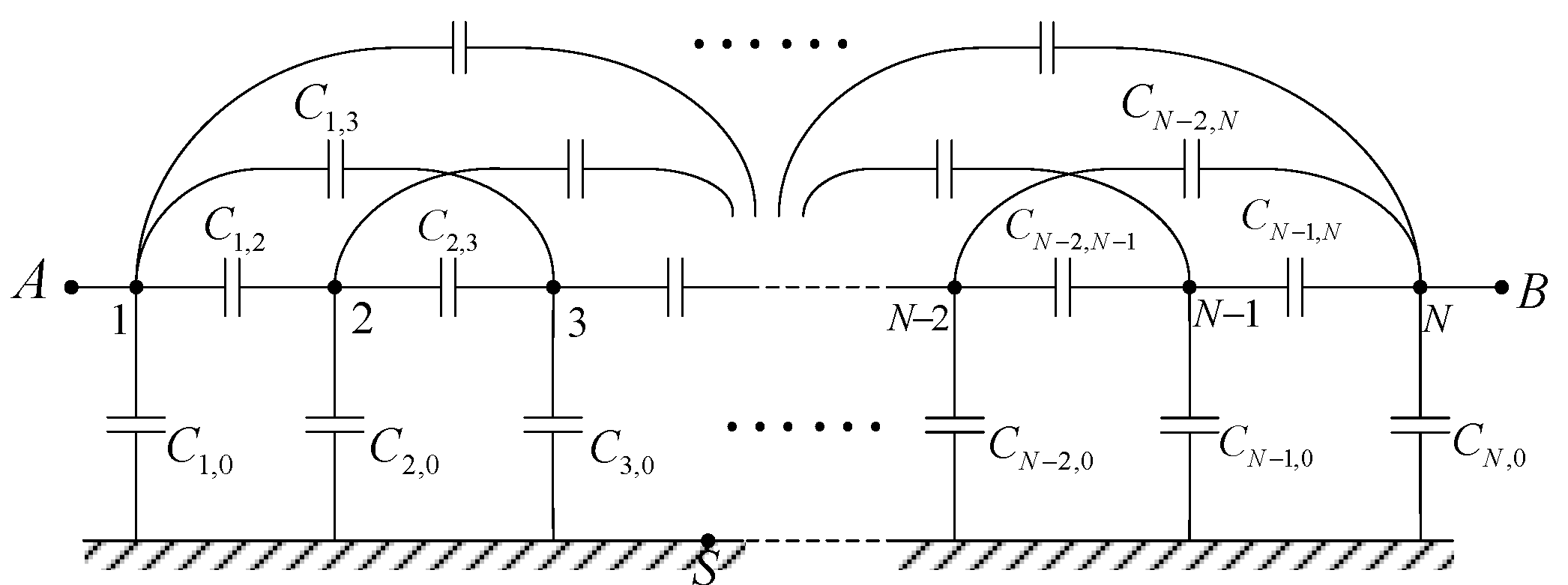
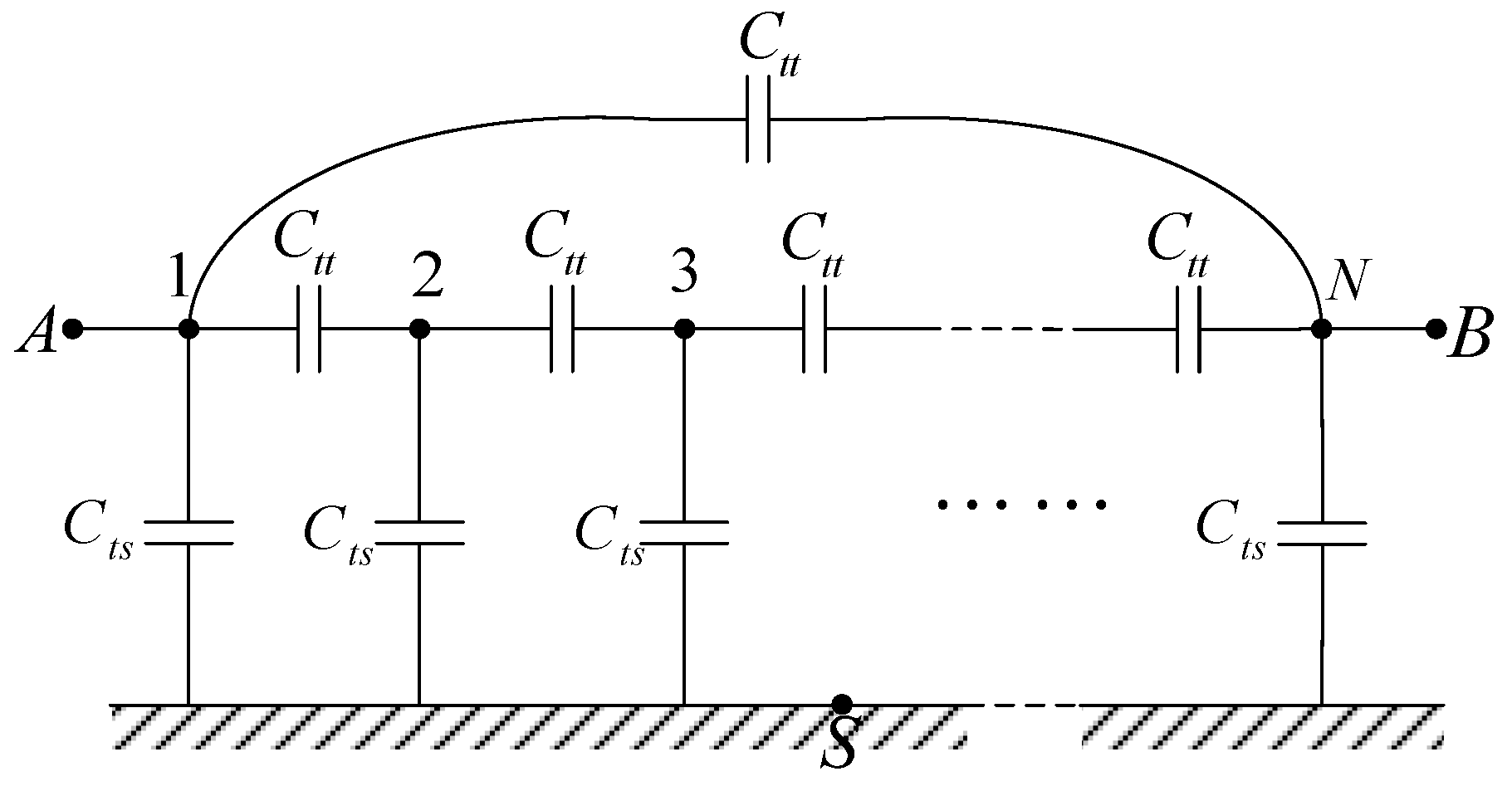
3.1. A Network Model of the Stray Capacitance of Rogowski Coils
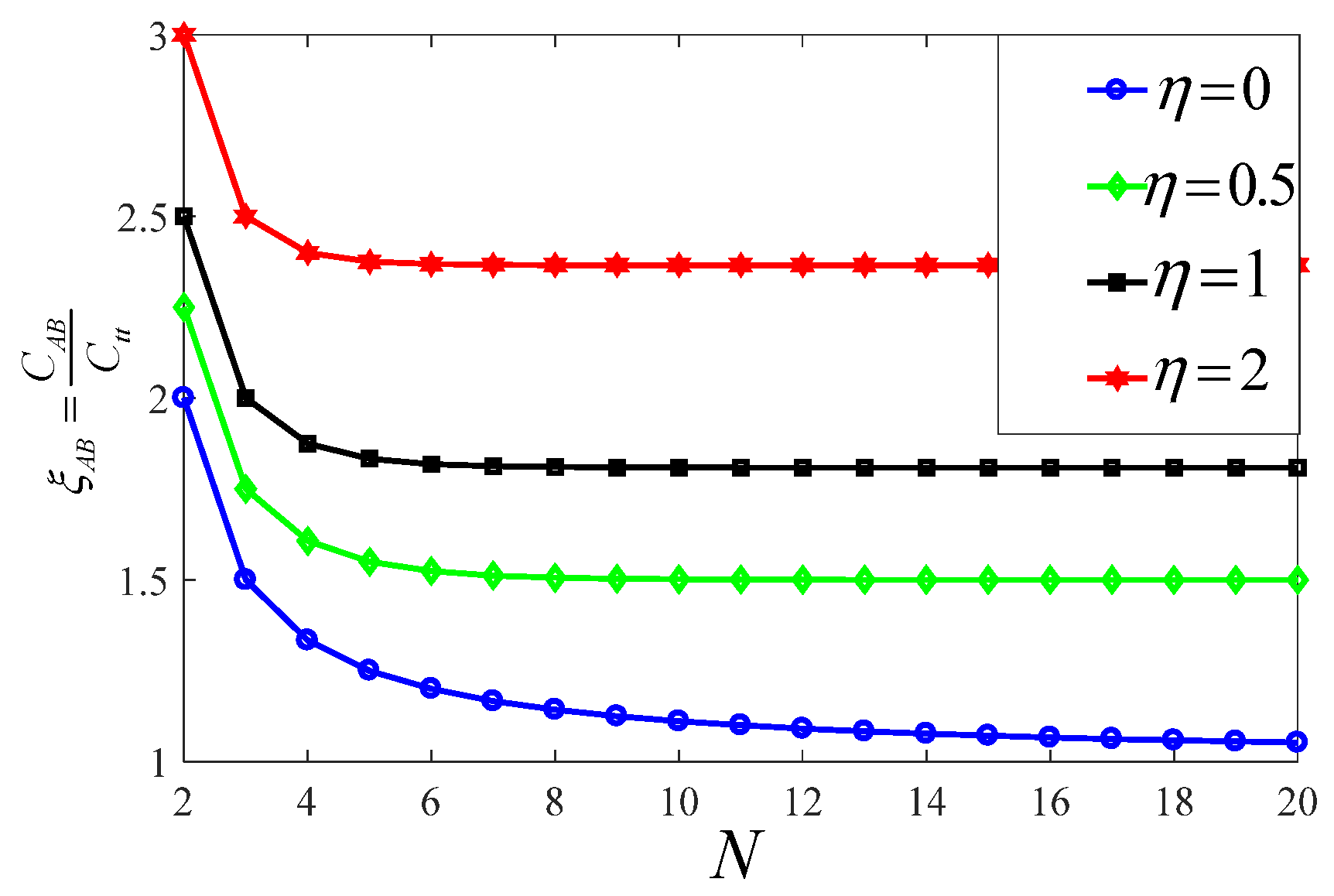
3.2. Simplified Model of the Stray Capacitance Network
3.3. Discussions of the Factors Affecting Stray Capacitance
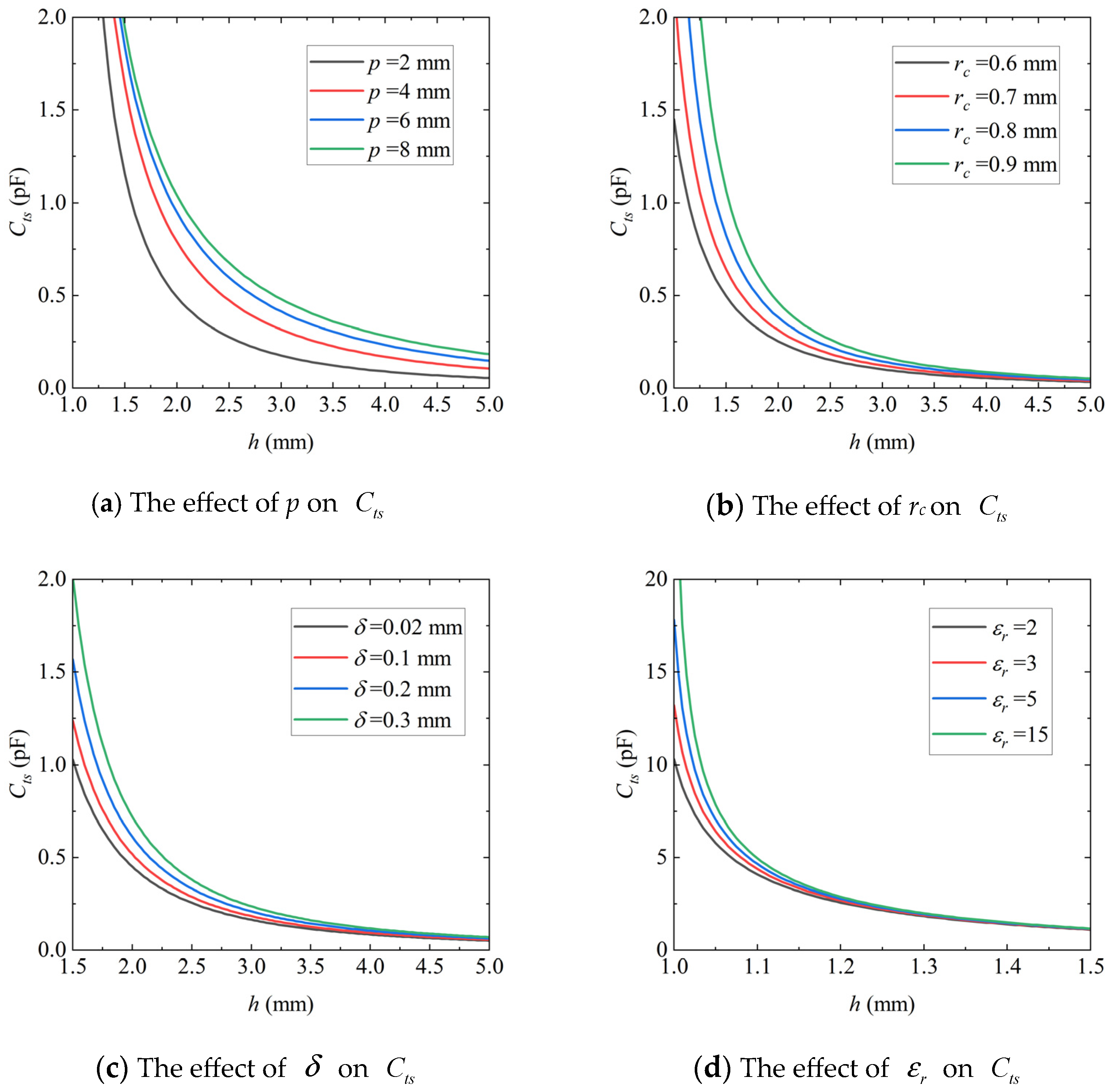
3.3.1. Investigations of Factors Affecting
3.3.2. Investigations of Factors Affecting
3.3.3. Measures to Reduce Stray Capacitance
4. Optimization of the Skeleton Cross-Section
4.1. Optimization of Skeletons of Three Common Shapes
4.1.1. Rectangular Cross-Section
4.1.2. Circular Cross-Section
4.1.3. Oval Cross-Section
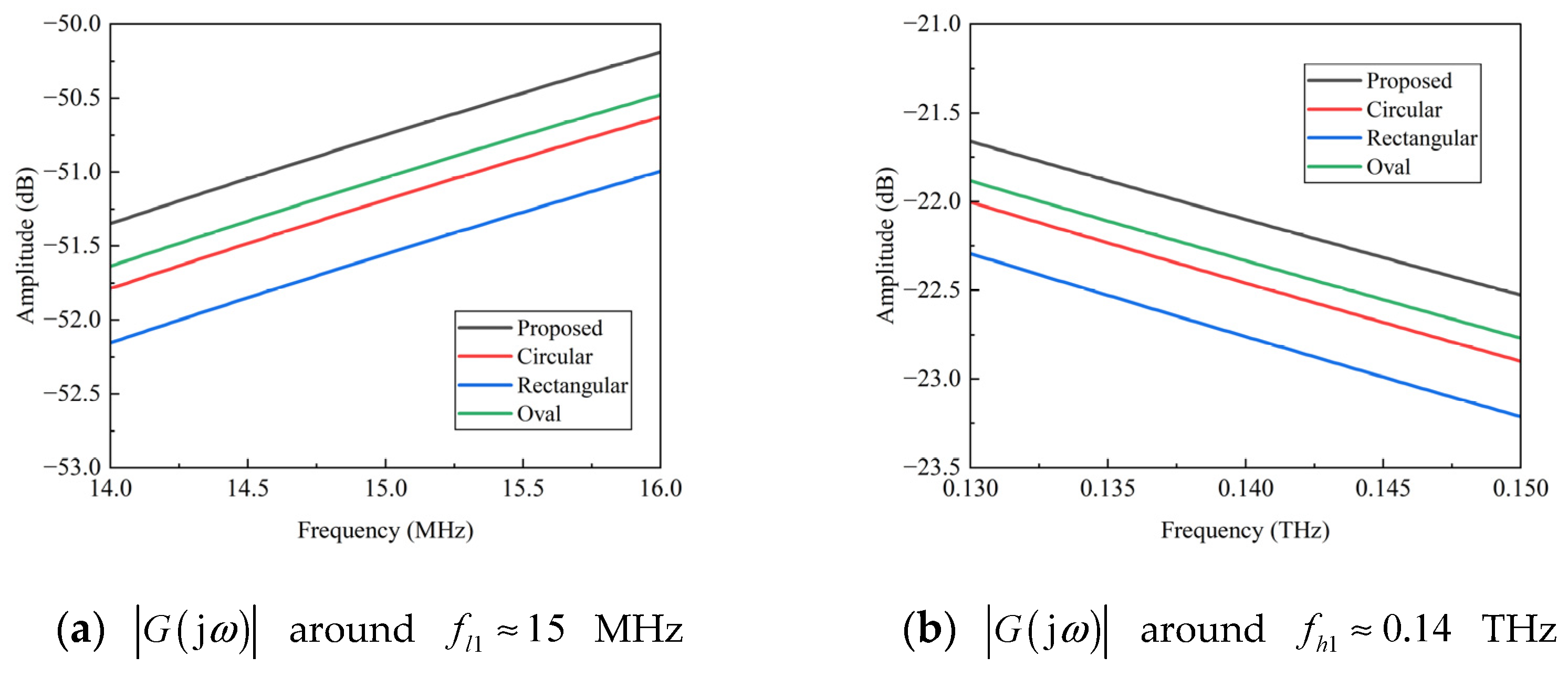
4.2. Optimal Design of the Skelenton Cross-Section
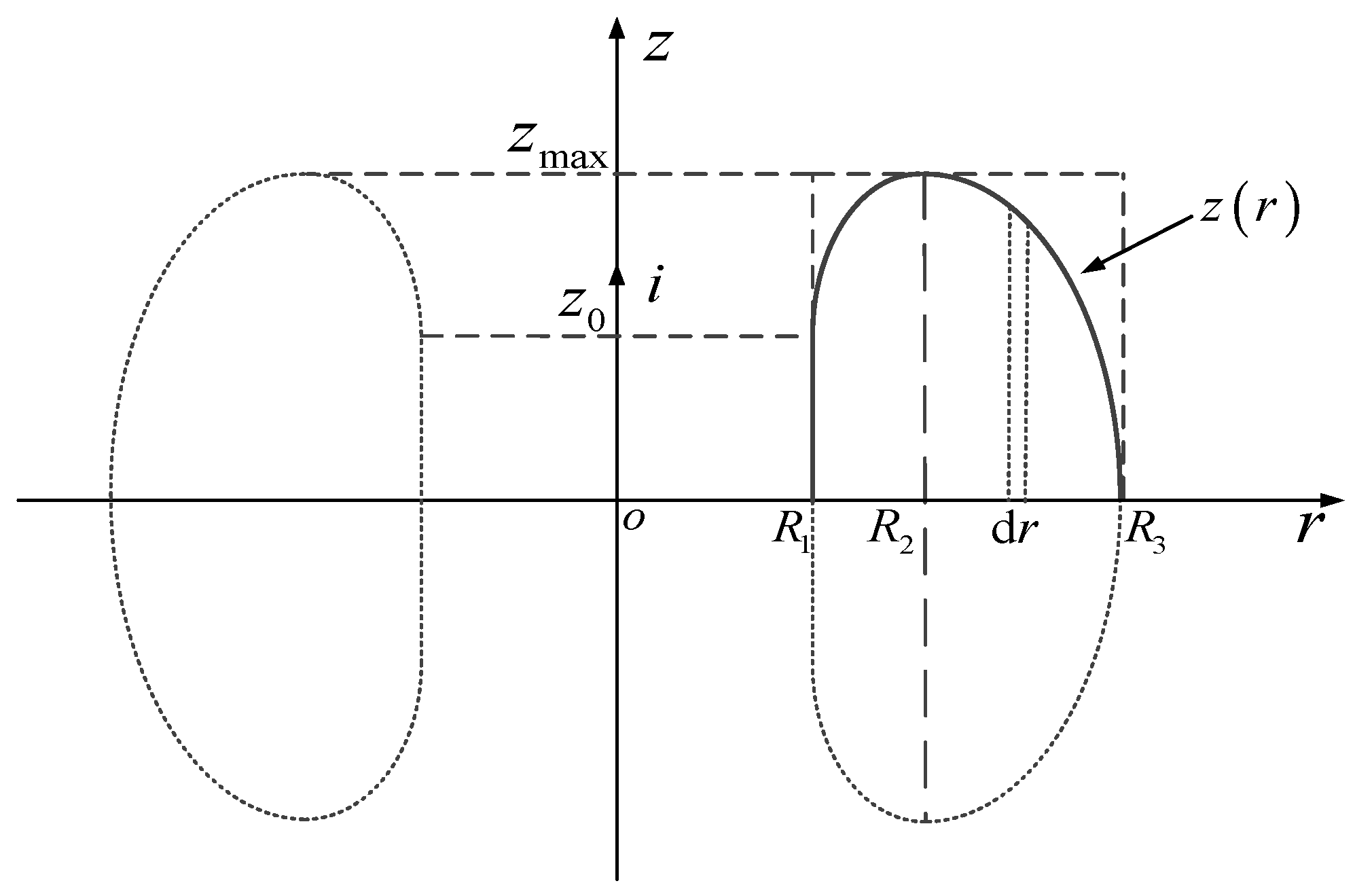
4.2.1. The Constrained Variational Problem
4.2.2. Solution to the Constrained Variational Problem via Euler’s Method
4.3. Numerical Example
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Abdi-Jalebi, E.; McMahon, R. High-Performance Low-Cost Rogowski Transducers and Accompanying Circuitry. IEEE Trans. Instrum. Meas. 2007, 56, 753–759. [Google Scholar] [CrossRef]
- Samimi, M.H.; Mahari, A.; Farahnakian, M.A.; Mohseni, H. The Rogowski Coil Principles and Applications: A Review. IEEE Sens. J. 2015, 15, 651–658. [Google Scholar] [CrossRef]
- Ramboz, J.D. Machinable Rogowski Coil, Design, and Calibration. Trans. Instrum. Meas. 1996, 45, 511–515. [Google Scholar] [CrossRef]
- Chen, Q.; Li, H.-b.; Huang, B.-x.; Dou, Q.-q. Rogowski Sensor for Plasma Current Measurement in J-TEXT. IEEE Sens. J. 2009, 9, 293–296. [Google Scholar]
- Liu, X.; Huang, H.; Jiao, C. Modeling and Analyzing the Mutual Inductance of Rogowski Coils of Arbitrary Skeleton. Sensors 2019, 19, 3397. [Google Scholar] [CrossRef] [PubMed]
- Ferkovic, L.; Ilic, D.; Lenicek, I. Influence of Axial Inclination of the Primary Conductor on Mutual Inductance of a Precise Rogowski Coil. IEEE Trans. Instrum. Meas. 2015, 64, 3045–3054. [Google Scholar] [CrossRef]
- Tao, T.; Zhao, Z.; Ma, W.; Pan, Q.; Hu, A. Design of PCB Rogowski Coil and Analysis of Anti-interference Property. IEEE Trans. Electromagn. Compat. 2016, 58, 344–355. [Google Scholar] [CrossRef]
- Jie, B. High Current Measurement; China Machine Press: Beijing, China, 1987; pp. 181–198. (In Chinese) [Google Scholar]
- Chiampi, M.; Crotti, G.; Morando, A. Evaluation of Flexible Rogowski Coil Performances in Power Frequency Applications. IEEE Trans. Instrum. Meas. 2011, 60, 854–862. [Google Scholar] [CrossRef]
- Li, W. Theoretical Research and Practice of Large Current Measurement Sensing Based on Rogowski Coil. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2005. (In Chinese). [Google Scholar]
- Mingotti, A.; Costa, F.; Peretto, L.; Tinarelli, R.; Mazza, P. Modeling Stray Capacitances of High-Voltage Capacitive Dividers for Conventional Measurement Setups. Energies 2021, 14, 1262. [Google Scholar] [CrossRef]
- Yue, X.; Zhu, G.; Wang, J.V.; Deng, X.; Wang, Q. PCB Rogowski Coils for Capacitors Current Measurement in System Stability Enhancement. Electronics 2023, 12, 1099. [Google Scholar] [CrossRef]
- Robles, G.; Shafiq, M.; Martínez-Tarifa, J.M. Designing a Rogowski Coil with Particle Swarm Optimization. Proceedings 2019, 4, 10. [Google Scholar]
- Zhao, T. Optimized Design of Rogowski Coil for Pulse Current Measurement. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2005. (In Chinese). [Google Scholar]
- Metwally, I.A. Self-Integrating Rogowski Coil for High-Impulse Current Measurement. IEEE Trans. Instrum. Meas. 2010, 59, 353–360. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, C.; Wang, C. High Voltage Test Technology; Tsinghua University Press: Beijing, China, 2009. (In Chinese) [Google Scholar]
- Jiao, C.; Zhang, J.; Zhao, Z.; Zhang, Z.; Fan, Y. Research on Small Square PCB Rogowski Coil Measuring Transient Current in the Power Electronics Devices. Sensors 2019, 19, 4176. [Google Scholar] [CrossRef]
- Dalessandro, L.; Cavalcante, F.S.; Kolar, J.W. Self-Capacitance of High-Voltage Transformers. IEEE Trans. Power Electron. 2007, 22, 2081–2092. [Google Scholar] [CrossRef]
- Qin, Y.; Holmes, T.W. A Study on Stray Capacitance Modeling of Inductors by Using the Finite Element Method. IEEE Trans. Electromagn. Compat. 2001, 43, 88–93. [Google Scholar] [CrossRef]
- Atabekov, G.I. Several Problems of Theoretical Electro-Engineering; National Defence Industry Press: Beijing, China, 1958. (In Chinese) [Google Scholar]
- Liang, L. Variational Principles and Their Applications in Mechanics and Electromagnetism; Harbin Engineering University Press: Harbin, China, 2011; ISBN 978-7-5661-0044-3. (In Chinese) [Google Scholar]
- Reddy, J.N. Energy Principles and Variational Methods in Applied Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]




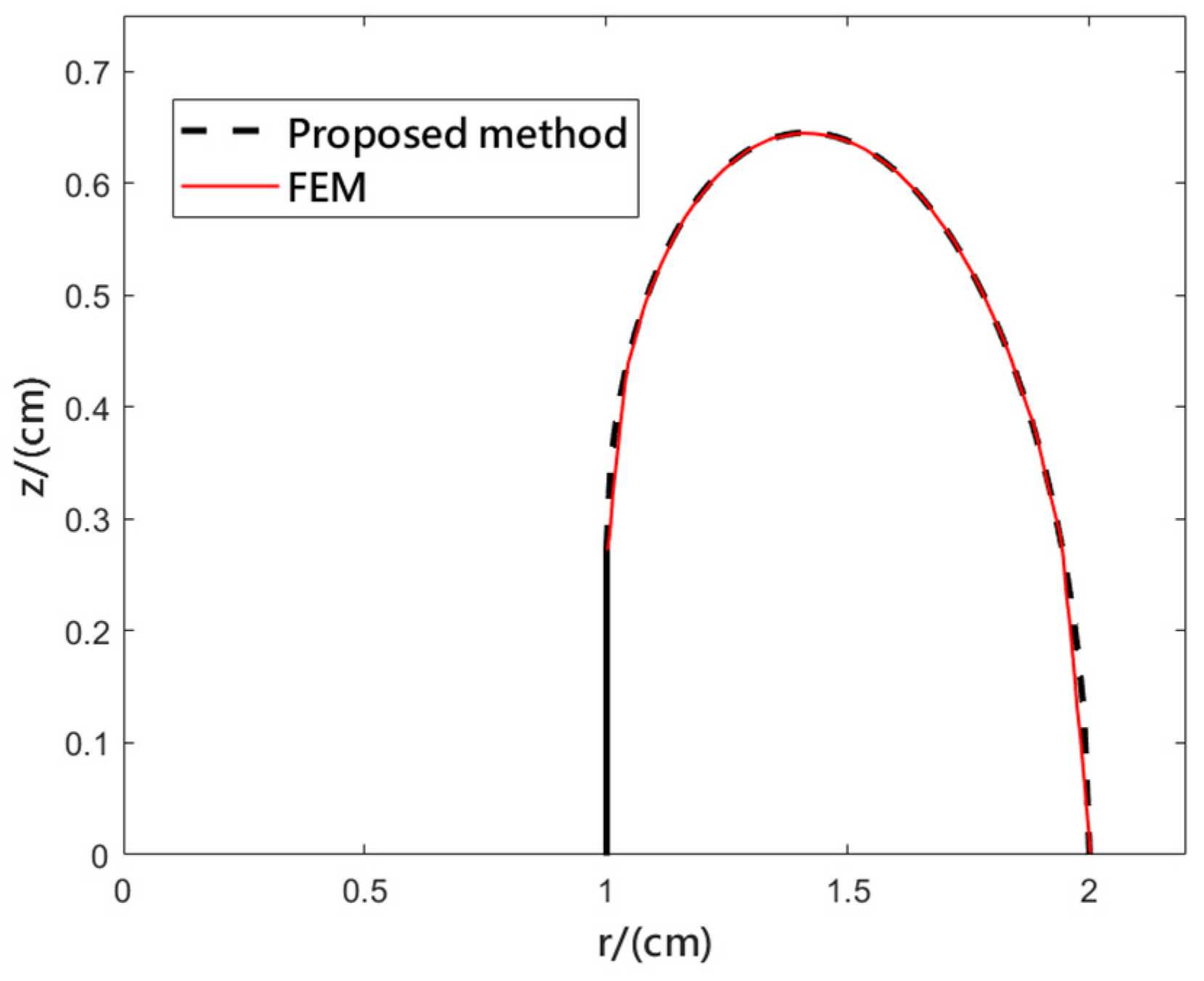

| Stray Capacitance | FEM | Proposed Method | Relative Error |
|---|---|---|---|
| Cts | 7.74 pF | 8.05 pF | 4.0% |
| Ctt | 2.66 pF | 2.81 pF | 5.9% |
| CAB | 7.52 pF | 7.94 pF | 5.6% |
| Shape of the Cross-Section | Perimeter (cm) | Rc () | Lc () | Cc (pF) | ||
|---|---|---|---|---|---|---|
| Rectangular | 4.22 | 0.0760 | 0.1044 | 1.230 | 1 | 1 |
| Circular | 3.93 | 0.0711 | 0.1044 | 1.151 | 1.069 | 1.034 |
| Oval | 3.85 | 0.0697 | 0.1044 | 1.128 | 1.090 | 1.044 |
| Proposed | 3.71 | 0.0671 | 0.1044 | 1.086 | 1.133 | 1.064 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Wang, H.; Mao, M.; Ma, X. Analysis and Optimization of the Stray Capacitance of Rogowski Coils. Appl. Sci. 2024, 14, 7748. https://doi.org/10.3390/app14177748
Wang J, Wang H, Mao M, Ma X. Analysis and Optimization of the Stray Capacitance of Rogowski Coils. Applied Sciences. 2024; 14(17):7748. https://doi.org/10.3390/app14177748
Chicago/Turabian StyleWang, Jiawei, Huifu Wang, Minyu Mao, and Xikui Ma. 2024. "Analysis and Optimization of the Stray Capacitance of Rogowski Coils" Applied Sciences 14, no. 17: 7748. https://doi.org/10.3390/app14177748





